Stretching and Bending Fluctuations of Short DNA Molecules

Abstract

Recent measurements of the distribution of end-to-end distance in short DNA molecules infer cooperative stretching fluctuations. The assumptions underlying the analysis can be questioned if transient, thermally induced defects producing a localized decrease in bending stiffness are present in thermal equilibrium, such as regions in which DNA melts locally (bubbles), sustains large-angle bends (kinks), or can locally transform into an alternative (S-DNA) state. We study a generalized discrete worm-like chain model for DNA, capable of describing these experiments, showing that the model yields accurate fits to available experimental data. Our results indicate that DNA bending arising from such localized defects, rather than solely stretching, can be an equal contributor to end-to-end distance fluctuations for 35-bp DNA and contributes nontrivially to such fluctuations at all scales below the persistence length. The analysis suggests that such fluctuations should exhibit a scale-dependent cooperativity, specifically relevant in determining the behavior of short chains, but which saturates rapidly to a length-independent value for longer DNA, to ensure a consistent physical description of DNA across multiple scales. Our approach provides a minimal, yet accurate, coarse-grained description of DNA at the subpersistence length scales of current experimental interest.

Introduction

Understanding several recent biophysical experiments on short DNA molecules requires bridging the gap between coarse-grained polymeric descriptions of DNA at length scales of microns and atomistic representations appropriate at the basepair level. DNA molecules at length scales several orders of magnitude larger than the size of a single basepair are accurately modeled as semiflexible polymers or worm-like chains (WLC), with conformational properties deriving from a single parameter, the persistence length ${\ell }_p$ (47–50 nm or ∼150 bp of B-DNA) (1,2). With the persistence length as a fitting parameter, an interpolation formula proposed by Marko and Siggia and its subsequent generalizations provides an accurate description of measured force-extension relations of DNA for forces below ∼40 pN (3). Increasing the force still further, to around 65 pN, leads to an abrupt increase in length of around $70\%$ over the B-form value. This overstretching transition is manifest as a plateau in the force at varying extensions (4–9). The physical state of DNA in such force regimes is only gradually being elucidated, but may reflect competing pathways involving separate transitions, including the possibility of strand separation or a transition into a novel S-DNA state, sensitively tuned by factors such as temperature and salt concentration (10–12).

It is conventionally assumed that the WLC description should remain valid over length scales ranging from the micron scale at which single molecule experiments measure canonical DNA force extension curves, down to microscopic scales of a few tens of basepairs (13). However, a number of experiments, which probe short DNA molecules with length between 10 and 100 bp challenge this view (14–16). The cyclization assays of Cloutier and Widom (CW) measure the propensity of DNA to form loops, finding an anomalous enhancement, by up to four orders of magnitude, of the cyclization J-factor for DNA of size 100 bp or less. This indicates that DNA at these length scales is far more bendable than would be suggested by persistence length estimates. It has been argued that this discrepancy might arise as a consequence of transient bubbles or kinks in the DNA molecule, which could act as localized regions where the cost of making a large-angle bend is substantially reduced (17–19). Consistent with this, fluorescence resonance energy transfer and small-angle x-ray scattering-based measurements of the end-to-end distance and radius of gyration of short (∼15–90 bp) DNA molecules in solution infer considerably reduced persistence lengths, around 20 nm for the 20 bp case (20). A recent experiment of Vafabakhsh and Ha uses single-molecule fluorescence resonance energy transfer experiments, thus avoiding potential problems of the ligation-based cyclization assays of CW, to monitor the looping of single short DNA molecules between 67 and 106 bp in length. These experiments also find that short DNA strands are far more flexible than simple WLC models would predict.

The molecular-ruler experiments of Matthew-Fenn, Das and Harbury (MDH) suggest one more way in which the WLC picture of DNA may need to be revised (16). MDH obtain the probability distribution $P\left(\left|\mathbf{R}\right|\right)$, and the related quantity $S\left(R\right)=4\pi R^{2}P\left(\left|\mathbf{R}\right|\right)$, as a function of end-to-end distance R in short (10–35 bp) DNA molecules. If bending is neglected, the width of these distributions can be interpreted as arising from stretching fluctuations alone (16,21,22). The data indicate an anomalous enhancement of this width relative to WLC predictions, also yielding a quadratic variation of the variance of $S\left(R\right)$ with N, the number of basepairs, suggestive of strong cooperativity. These experiments would seem to suggest that simple WLC-based approaches, which assume that DNA is inextensible, cannot describe DNA at these scales.

The analysis of the experimental data of MDH assumes that there is no significant bending of the DNA molecule if it is short enough, an assumption questioned by the prior experiments. It is reasonable to require that any model description of this problem should be capable of describing both short-scale bending fluctuations whose energy cost is reduced below WLC predictions based on assuming a uniform bending rigidity (we will refer to this as rigidity softening), as well as local stretching. Furthermore, importantly, predictions from such a model should remain consistent with the force-extension relation measurements documented extensively for DNA at larger scales, including the overstretching behavior. Although models containing the requisite ingredients have been proposed, calculations of $P\left(\mathbf{R}\right)$ and its moments, which incorporate the physics of inhomogeneous local bending costs and stretching have, hitherto, been unavailable, making the direct comparison of experiment with theory difficult.

This work derives and studies such end-to-end distribution functions in a model, first proposed by Storm and Nelson (23), which incorporates those aspects of DNA mechanics required for the interpretation of the CW and MDH experiments. These include inhomogeneities in bending rigidity arising from the spontaneous formation of local defects in thermal equilibrium (24,29), the possibility of local stretching, and cooperative effects affecting both rigidity softening and stretching fluctuations. Such defects can arise as a consequence of the local melting of DNA (bubbles), from nonlinear elastic effects leading to a reduced cost for large-angle bends (kinks), or the local transformation into a structure preferred at large forces, which recent work assigns to S-DNA provided the strands are not locally separated (10–12); an alternative structure, likely dictated by GC content, is a force-induced melted state resembling single-stranded DNA. The model, despite its relatively simple structure, has previously been shown to yield accurate and unified results for different regimes of the force-extension behavior of long chains (23). Unlike the long-chain limit exclusively studied earlier in the continuum limit, our study uses the discrete model and concentrates on short chains, as appropriate to the cyclization and molecular ruler experiments, calculating distribution functions and related quantities accessed in experiments on such chains. These quantities have not been studied in detail previously, but assume importance in light of recent advances that make them accessible to experiments.

Our results are summarized as follows: First, we show how $P\left(\mathbf{R}\right)$ and its moments can be calculated within a coarse-grained model for DNA structure, which accounts for contributions from rigidity softening, as well as from length fluctuations originating in local stretching. Such distribution functions, optimized using parameter values in an experimentally reasonable range, fit the experimental data of (16) to high accuracy, providing a way of parametrizing data from molecular ruler-based experiments. Second, we demonstrate that bending as a consequence of localized rigidity softening contributes substantially to the width of the distribution function. This rules out interpretations of the experimental results of MDH, which assume that the DNA molecule is relatively rigid with highly suppressed bending fluctuations, at these scales. We illustrate calculations of the moments of the full probability distribution of end-to-end distances for DNA molecules over a wide range of lengths. These can be probed by experiments similar to those of MDH, because molecular-ruler experiments yield data of sufficient accuracy for the computation of higher order moments to yield meaningful results. Such higher order moments can be used to illuminate the relative importance of bending and stretching in the short-chain case. Third, we calculate effective persistence lengths in our model across a range of model parameters, thus providing estimates for the Kuhn length appropriate to our coarse-grained polymer representation of DNA. Finally, we illustrate the importance of imposing a lowered cooperativity of rigidity softening at short scales for obtaining good fits to data, presumably a consequence of the increased importance of end effects for short polymers with the complex internal structure of the DNA molecule.

The parameter values we use are inferred largely from experiments, are physically reasonable, and yield results that match experiment closely. Our model of DNA interpolates to the conventional WLC model appropriate at large length scales while describing short-range fluctuations quantitatively. Our parameter values are chosen to be consistent with a persistence length of 150 bp (50 nm) at these large scales; the costs for defect formation range from $1-3k_{B}T$ per basepair in our calculation, consistent with several current estimates that stress the importance of entropic effects in determining bubble free energy costs (25,26). The analytic tools we use here provide essentially numerically exact results for quantities such as $P\left(\mathbf{R}\right),S\left(R\right)$, and their moments. These quantities are experimentally accessible and their measurement should yield stringent tests of models of DNA structure and mechanics at length scales comparable to ${\ell }_p$.

Model and Methodology

Conventional approaches to WLC models of DNA begin with continuum energy of the form

$$\mathcal{H}=\frac{1}{2}\underset{0}{\overset{L}{\int }}ds\kappa \left(s\right){\left|\frac{d\hat{t}\left(s\right)}{ds}\right|}^2,$$ (1)

supplemented by the inextensibility constraint ${\left|\hat{t}\left(s\right)\right|}^2=1$, for a chain parametrized by a unit tangent vector $\hat{t}\left(s\right)$ at every point along its contour, indexed by the one-dimensional coordinate s. The constraint must be relaxed, at least at a phenomenological level, to accurately describe DNA force-extension curves above applied forces of ∼10 pN. The previous expression accounts for a varying bending stiffness $\kappa \left(s\right)$ along the chain and can strictly only be justified for fluctuations at scales considerably exceeding a molecular scale cutoff, given the approximations inherent in a continuum approach. For the chain lengths appropriate to the CW and MDH experiments, one must specifically account for fluctuations at short (the scale of the rigidity softening, typically 1–2 basepairs) length scales. We thus work with the standard discretization of the WLC model in which the polymer is discretized into N units, with each unit, a unit tangent vector ${\hat{t}}_i$ labeled by the index i, provides a coarse-grained representation of DNA at the length scale of 1–2 basepairs. Semiflexibility is incorporated through an interaction coupling neighboring ${\hat{t}}_i$ -values, which takes the general form ${\sum }_i{A}_{i,i+1}\left(1-{\hat{t}}_i·{\hat{t}}_{i+1}\right)$, with $A_{i,i+1}>0$. This interaction yields a minimum energy when the vectors ${\hat{t}}_i$ are all parallel to each other, representing a straight polymer filament. The local curvature cost $A_{i,i+1}$ can be inhomogeneous, reflecting microscopic variation of this quantity arising both from basepair sequence variation as well as from softening attributable to local defects and is equivalent to the physicists model of an inhomogeneous Heisenberg spin model in an external field, a connection exploited in our numerical work (27,28).

We represent the conformation of the DNA molecule through its backbone, thus ignoring, as is customary for WLC models for DNA, its double-helical character. We also ignore twist couplings, although the physics of the defect-induced chain-length relaxation we model could potentially arise as an indirect consequence of twist-stretch coupling (8). Accounting for these effects, in particular for DNA helicity, would be expected to superimpose an overall oscillatory component to the results we obtain. We expect that they should not qualitatively alter the broader structure of our results.

This model is extended to include stretching fluctuations following the discrete persistent chain model of Storm and Nelson (23), originally proposed as a model for the DNA overstretching transition. Each subunit of the polymer can be either in a high-energy stretched state or in a low-energy unstretched state. The length of the subunit in the stretched state is $\zeta b$, where b is the subunit length in the unstretched state and $\zeta >1$. A two-state Ising variable ${\sigma }_i$ at every site denotes whether the subunit there is stretched $\left({\sigma }_i=-1\right)$ or unstretched $\left({\sigma }_i=1\right)$. A lower bending stiffness is assigned to the junction of two stretched subunits or the junction between a stretched and an unstretched subunit vis-á-vis the junction of two unstretched subunits. A chemical potential term as well as a cooperativity term controls the relative proportion of stretched and unstretched units.

Thus, the energy of a particular configuration of tangent vectors and the Ising variable, the Hamiltonian of the system, is then

$$\begin{array}{c}\beta H=\sum _{i=1}^{N-1}\left[\frac{J_{dd}}{2}\frac{\left(1+{\sigma }_i\right)\left(1+{\sigma }_{i+1}\right)}{4}+\frac{J_{ss}}{2}\frac{\left(1-{\sigma }_i\right)\left(1-{\sigma }_{i+1}\right)}{4}+\frac{J_{ds}}{2}\left|{\sigma }_i-{\sigma }_{i+1}\right|\right]\left(1-{\hat{\text{t}}}_i·{\hat{\text{t}}}_{i+1}\right)\\ -\sum _{i=1}^{N-1}\left[\frac{\alpha }{2}\left({\sigma }_i+{\sigma }_{i+1}\right)+\gamma \left({\sigma }_i{\sigma }_{i+1}-1\right)\right].\end{array}$$ (2)

The first three terms, all multiplying $\left(1-{\hat{\text{t}}}_i·{\hat{\text{t}}}_{i+1}\right)$, represent the bending cost in different configurations of stretched and unstretched units. The first term gives the bending energy of two neighboring unstretched subunits $\left({\sigma }_i=+1,{\sigma }_{i+1}=+1\right)$ where J_dd is the dimensionless bending stiffness, scaled with $k_{\text{B}}Tb$ to render it dimensionless. The second term represents the bending of two neighboring stretched subunits i.e., $\left({\sigma }_i=-1,{\sigma }_{i+1}=-1\right)$, with a bending modulus J_ss. When a stretched subunit appears near an unstretched one, i.e., $\left({\sigma }_i=+1,{\sigma }_{i+1}=-1\right)$ or $\left({\sigma }_i=-1,{\sigma }_{i+1}=+1\right)$, the third term yields a bending modulus $J_{ds}=J_{sd}$.

The last two terms control the stretching of subunits and their cooperativity: $\alpha k_{B}T$ is the free energy cost for generating a stretched subunit, whereas $2\gamma k_{B}T$ is the cost of creating an interface between stretched and unstretched subunits. The continuum limit for the bending energy terms follows from taking $b\to 0$, $N\to \infty$ with $Nb=L$ constant. The model describes the overstretching transition of DNA accurately, fitting force-extension relations over a regime of forces extending from the $F=0$ case to values of ∼100 pN (23). Although Storm and Nelson use a variational approach, valid only in the large N limit, to solve for the force-extension relation in their model, the methodology described here can obtain such relations for arbitrary N, as well as $P\left(\mathbf{R}\right)$ and a host of similar quantities of direct relevance to experiments.

The relation of this model to previous models in the literature is the following: If we fix all ${\sigma }_i=1$, the model reduces to the discrete WLC, with fixed subunit length. We have earlier reported a comprehensive comparison of results for this model to the numerical calculations, showing that the loop formation probabilities we calculate precisely reproduce the results of analytic calculations for the WLC (29). In the absence of cooperativity $\left(\gamma =0\right)$ and stretching fluctuations $\left(\zeta =1\right)$, but allowing inhomogeneous curvature costs, so the ${\sigma }_i$ -values fluctuate, the bending rigidity $J_s$ of an inhomogeneous region is reduced from the bending rigidity in homogeneous regions, because this locally replaces $J_d$ with $J_s$, with $J_s<J_d$. This model is then that of several independent groups for the CW cyclization results (17,18,29). The full model, including subunit size fluctuations, cooperativity, and inhomogeneous curvature costs, is the Storm-Nelson model for DNA overstretching, which has been shown to yield accurate fits for the overstretching transition. Thus, our model reduces to various models studied earlier in appropriate limits, providing accurate benchmarks for validation.

The distribution of the end-to-end vector R is obtained using a methodology proposed in (29). for DNA with bubbles and further generalized here to deal with stretching. The end-to-end distance is obtained from

$$\mathbf{R}=\sum _i\left(\frac{1+{\sigma }_i}{2}+\frac{1-{\sigma }_i}{2}\zeta \right){\hat{\text{t}}}_i,$$ (3)

where R is measured in units of subunit length b. In thermal equilibrium, $P\left(\mathbf{R}\right)$ is thus defined through the path integral

$$P\left(\mathbf{R}\right)=\mathcal{N}\int d{\text{t}}_1\dots \int d{\text{t}}_N\sum _{{\sigma }_i=\pm 1}\text{exp}\left(-\beta H\right)\delta \left(\sum _i\left(\frac{1+{\sigma }_i}{2}+\frac{1-{\sigma }_i}{2}\zeta \right){\hat{\text{t}}}_i-\mathbf{R}\right),$$ (4)

where N is a normalization constant and the delta function enforces the constraint that the end-to-end distance is R.

A numerically exact approach to this problem is enabled through the following: We exploit the equivalence of the discretized polymer chain to a model of interacting Heisenberg and Ising spins. We use a generalized transfer matrix method to solve for the equilibrium behavior of this system, using a mapping between associated quantities in the spin model and the polymer model. We calculate the partition function corresponding to the Hamiltonian in the fixed force ensemble, $Z\left(f\right)$, where the force enters as a magnetic field in the spin analogy. The transfer matrix method is generalized from that used in (29) to accommodate the local stretching variable ${\sigma }_i$, resulting in a block structure of the transfer matrix (23). Once $Z\left(f\right)$ is obtained, a Laplace transformation in the field variable f yields the partition function computed at fixed magnetization, equivalently at fixed end-to-end separation in the associated polymer model. This partition function is then related, exploiting symmetries and tomographic reconstructions, to the normalized probability distribution of the end-to-end distance (see the Supporting Material). From this distribution, a variety of quantities can be calculated, including force-extension relations, moments measuring the statistics of fluctuations, and loop formation probabilities from the limiting value $P\left(0\right)$. In addition, matrix computations based on the generalized transfer matrix can be used to calculate correlation functions, yielding estimates for the persistence length for tangent vector fluctuations.

Results and Discussion

We summarize results for our model across a broad variety of regimes, based on the methodology described in the previous section. Unless specified otherwise, we assume the following. We take 1 bp per Heisenberg spin, implying $L=N$, and measure energies in units of $k_{B}T$. We assume the parameters listed in Table 1, based on the fits of Storm and Nelson, but choose to vary the other model parameters, specifically the chemical potential for defects α, and the cooperativity energy γ. The quantities we vary to obtain our best fits, α and γ, are taken to have values close to those used in (23). Physically, the free energy cost for defects is expected to be sequence dependent, whereas the cooperativity γ might be expected to be both force and sequence-dependent, potentially differing at zero force from the value assumed by Storm and Nelson to fit the high-force limit of the force-extension relation (23). However, although (23) uses fits to the force-extension relation at large N to determine these, our numbers are optimized with respect to the full probability distribution for end-to-end distances for short chains. All these values are as specified in the appropriate subsections below and in the figure captions.

Table 1.

Summary of parameter values

Parameter	Value
$J_{dd}$	150 (1)
$J_{ds}$	50 (23)
$J_{ss}$	40 (23)
ζ	1.76 (4,7,23)
α	$1.0\le \alpha \le 3.0$ (17,37)
γ	$0.0\le \gamma \le 3.0$

Parameter ζ is quoted in units of subunit length b. All other parameter values are quoted in units of the thermal energy $k_{B}T$. We optimize this parameter for the 35 bp DNA strands through comparison with the experimental $P\left(R\right)$.

Role of Cooperativity

Because the anomalous scaling of the width of $P\left(\mathbf{R}\right)$ in the MDH experiments is attributed to cooperative interactions governed by γ between DNA subunits, we first examine how $\gamma$ influences the end-to-end distance distribution. These results are presented in Fig. 1, where we plot $S\left(R\right)=4\pi R^{2}P\left(R\right)$ for several values of γ with $N=35$ (the units are basepairs, here and below). Other parameter values are as listed in Table 1. For small cooperativity γ, we note that the distribution is broad and skewed toward larger lengths. As γ is increased, the distribution becomes narrower and more symmetric for intermediate values of γ, with its peak moving toward shorter lengths. For large γ, we obtain a sharp peak, together with a tail toward shorter lengths. The inset compares these numerical results with the experimental data of MDH (16). Our best fits to the distribution function are obtained for $\gamma =0.5$. We fix that value as an optimal choice in the calculations we describe below.

Figure 1.

The end-to-end distribution function $S\left(R\right)$, calculated for finite chains of size $N=35$, with parameter values $\zeta =1.76,\alpha =2.77$, for a range of γ values (from right to left): $\gamma =0$ (rightmost), 0.5, 1, and 3 (leftmost). Other parameter values are as in Table 1. In the inset we compare our results for $\gamma =0.5$ (continuous curve) with experimental data (points) from (16).

Importance of stretching fluctuations and curvature energy inhomogeneities

To isolate the relative contributions of stretching and bending fluctuations to enhanced DNA flexibility, we present, in Fig. 2, results for $S\left(R\right)$ in some special limiting cases, for $N=35$. These special cases include: i), the pure WLC model, obtained by setting $J_{dd}=J_{ss}=J_{ds}$, and $\zeta =1$, thereby eliminating stretching fluctuations as well as rigidity softening, as shown in Fig. 2 a; ii), the WLC model with stretching alone, in the absence of defects, as shown in Fig. 2 b; iii), the WLC model with contributions from rigidity softening, in the absence of stretching, as in Fig. 2 c; and, finally iv), the general case, with contributions from both stretching and rigidity softening, Fig. 2 d. For each case, we also present results for two different values of the cooperativity parameter, $\gamma =0$ and $\gamma =0.5$, to illustrate the shifts in these distributions with cooperativity.

Figure 2.

The end-to-end distribution function $S\left(R\right)$, calculated for finite chains of size $N=35$, with parameter values (a) $\zeta =1,\alpha =\infty$ (the worm-like chain model); (b) $\zeta =1.76,\alpha =2.77$, (the pure stretching model) with $\gamma =0$ (marked as g0) and $\gamma =0.5$; (c) $\zeta =1.0,\alpha =2.77$, (the model for DNA with bending energy inhomogeneities and no stretching) with $\gamma =0$ (marked as g0) and $\gamma =0.5$; (d) $\zeta =1.76,\alpha =2.77$, with $\gamma =0$ (marked as g0) and $\gamma =0.5$, (the full model with bending energy inhomogeneities and stretching). Other parameters are as in Table 1.

These probability distributions can be used to compute the variance in $P\left(\mathbf{R}\right)$ within these different scenarios. The end-to-end distance in the pure WLC, Fig. 2 a, has a very small variance of $7.7{\AA }^2$, consistent with the expectation that bending fluctuations, and the consequent broadening of $P\left(R\right)$ are greatly suppressed for $L\ll {\ell }_p$. The intermediate case shown in Fig. 2 b, with stretching alone and no rigidity softening, yields a variance of $23.6{\AA }^2$. The introduction of stretching fluctuations in the absence of a reduced bending rigidity thus contributes to broadening the end-to-end distribution function, leading to a threefold increase above the pure WLC value of the variance. Note that the mode of the distribution has shifted perceptibly to larger lengths, especially with the addition of cooperativity, reflecting the importance of the role of stretching. Allowing inhomogeneous bending energy fluctuations and the consequent softening of bending energy cost as in Fig. 2 c, but eliminating stretching fluctuations, yields a variance of $34.04{\AA }^2$. Note that this result is comparable, with this choice of parameters, to the result for the pure stretching case, indicating that a roughly equal contribution to the total width of the distribution can be assigned to both stretching and bending. Thus, including defect energetics increases the variance, above the WLC value, by a factor of ∼5. Finally, our case (d) (Fig. 2 d), modeling the full combination of stretching fluctuations and defects leading to rigidity softening, together with cooperativity, yields a variance of $58.7{\AA }^2$. This is comfortingly close to the value of $58.4{\AA }^2$ obtained in the experiments.

Note that the peak value of the distribution shifts to larger values as contributions from stretching and the softening of the rigidity are accounted for. In the case where stretching fluctuations are disallowed but we allow for bending energy inhomogeneities, the average length is seen to decrease slightly. This is because allowing for such inhomogeneities effectively reduces the persistence length, leading to a shift toward a more Gaussian distribution, centered closer to zero, with a $P\left(R\right)$ peaking at $R=0$ in the extreme Gaussian limit. With cooperative stretching fluctuations but no rigidity softening, we see the average length increasing substantially for this choice of parameter values. Thus, the incorporation of stretching fluctuations is essential for the shift in most probable length to values above the naive contour length estimate.

Comparison with experiments

With our parameter values now optimized, we compare our results for end-to-end distance distribution with the experimental data of Mathew-Fenn et al (16) for different values of L, in Fig. 3. We find that a single value of α, the parameter representing the energy cost for defect formation, does not suffice to accurately fit the data for different lengths, but that α must be varied between 1 and 3. Because α is expected to be strongly DNA sequence-dependent, it is reasonable to expect that some variation of α should be imposed for an optimal fit. The numerics provide an accurate fit to the data, as can be seen.

Figure 3.

Comparing our prediction (curve) with MDH data from (16). (points) for N = 25, 30, and 35 (left to right). The parameter values that fit are $\gamma =0.5$, $\zeta =1.76$, $\alpha =1$ (for N = 25 and N = 30) and $\alpha =2.77$ (for N = 35). Other parameters are as in Table 1. The additional small-scale oscillations in the experimental data are artefacts, arising from ringing in the Fourier transforms used in analysis.

Length dependence of variance

Next, we examine how the variance $\left(\langle R^2\rangle -{\langle R\rangle }^2\right)$ of the end-to-end distance varies with length (L) of the DNA filament. These results are shown in Fig. 4. In Fig. 4 a, we show the calculated trends for the variance across several decades in length, ranging from ∼35 to 5000 bp. The variance for short chains $\left(L<150\text{bp}\right)$ fits to a power of 3.4, as indicated by the line. For longer chains $\left(L>300\text{bp}\right)$, the variance grows linearly with the size of the chain, as is expected because once chain lengths exceed correlation lengths of Ising and Heisenberg spin degrees of freedom, the central limit theorem should accurately predict the statistics of the variance. Pure bending fluctuations in an intermediate length-scale regime for semiflexible polymers have been proposed to scale as $L^4$, although the data of Fig. 1 of (22) appears to be more consistent with our numerically computed exponent value of 3.4, which includes all fluctuation contributions. In Fig. 4 b, we compare our results with those of MDH. The experimental data (asterisks) agree reasonably well with our calculations, given that the amount of energy per basepair to form a localized defect can be expected to be strongly sequence dependent, an effect not directly accounted for in this calculation.

Figure 4.

Variance versus L plot for a fixed gamma value. Both plots use $\gamma =0.5$. The subfigure (a) has $\alpha =2.77$, whereas (b) has 3 different α values (2.77 (bottom), 2 (middle), and 1 (top)). The asterisks are data points from the experiments of MHD. In Fig 4(a) the line for large L has a slope of 1, whereas the line for small L has a slope around 3.5. Parameter values are as in Table 1.

Loop formation probability

We now discuss results for loop formation in our model, obtained via computations of the quantity $P\left(R=0\right)$, which is proportional to the loop formation probability. Fig. 5 presents this loop formation probability for the different cases described below. First, we vary the cooperativity parameter γ, finding that the loop formation probability increases as we decrease cooperativity. From bottom to top are $\gamma =1,\zeta =1.76$; $\gamma =1,\zeta =1$ (no stretching); $\gamma =0.5,\zeta =1.76$; $\gamma =0,\zeta =1.76$. All data are for $\alpha =2.77$ with other parameters as in Table 1. To examine the effects of stretching, we calculate the loop formation probability with $\zeta =1$ and $\gamma =1$ (red squares), finding that the effect of stretching is small. We also varied the defect cost α across the three values 2.77, 2 and 1 (solid circles from bottom to top). These results are compared with the experimental results of CW for cyclization of short DNA (open circles, black), and are broadly consistent with the experiments for an appropriate choice of parameters. Note that the loop formation probability should generically be larger than the experimental cyclization J-factor, as DNA cyclization probed by ligation imposes special constraints on the end tangent vectors.

Figure 5.

The calculation of the loop formation probability density $P\left(R=0\right)$, as a function of the size of the DNA molecule L, for a range of lengths. The curves from bottom to top are $\gamma =1,\zeta =1.76$ (bottommost squares); $\gamma =1,\zeta =1$; $\gamma =0.5,\zeta =1.76$; $\gamma =0,\zeta =1.76$ (topmost squares). All data are for $\alpha =2.77$. Other parameters are as in Table 1. The open circles are CW data from (14,15). The solid circles are for different α values (bottom to top: α = 2.77, α = 2, and α = 1).

Effective persistence length and length dependence of assumed parameter values

We have also calculated the force-extension relation in the chain length $L\to \infty$ limit. This is shown in the Supporting Material (Fig. S2) for a range of values of the cooperativity parameter γ. Note that for the values of γ used to fit the data of Fig. 3 and Fig. 4, the force-extension curve exhibits a relatively gentle variation. In contrast, for larger values of γ $\left(>2.2\right)$, the curve exhibits a sharp rise at the experimentally measured threshold of 65 pN (11). Also plotted in the same figure is experimental data, digitized from Fig. 8 of (23). Our calculations thus provide a very accurate representation of the experimental data for the overstretching transition at these values of γ.

We have also calculated the effective persistence length for a range of parameters α and γ as shown in Fig. 6. For small values of γ and defect energy α, ${\ell }_p\approx 40$ bp. As γ and α increase, ${\ell }_p$ approaches 150 bp—the value corresponding to the persistence length of B-DNA. Thus, to fit the data on both short and long chains requires that one must take the effective Kuhn length to be length-dependent through its implicit dependence on the (length-dependent) parameters α and γ for short chains. This Kuhn length is length-independent for somewhat longer chains, consistent with the discussion previously.

Figure 6.

Effective persistence length calculated from tangent-tangent correlation for different values of α and γ. From bottom to top $\gamma =0,0.5,1,1.5,2,2.5$.

Moments of the distribution function

To further analyze end-to-end distance distribution functions we compute the skewness and kurtosis of the numerically obtained distribution functions. Using central moments defined via $\int dRRS\left(R\right)={\mu }_1$ and for $\mu >1,\int dR{\left(R-{\mu }_1\right)}^{m}S\left(R\right)={\mu }_m$, we obtain the skewness via $Sk={\mu }_3/{\mu }_2^{3/2}$ and the kurtosis through $Ku={\mu }_4/{\left({\mu }_2\right)}^2$. These are computed directly from the distribution functions. The skewness measures the degree of asymmetry of a probability distribution about its mean, whereas the kurtosis measures how peaked it is. These quantities are good indicators of deviations from Gaussian behavior and we expect that the contrast between the highly asymmetric distributions originating in the WLC at small persistence length and similar distributions including the effects of bending energy inhomogeneities and stretching should be most clearly seen with these.

Our results for skewness and kurtosis are shown in Fig. 7. We compare results from our model (skewness: solid squares below; kurtosis: solid squares above) with results from the standard WLC (skewness: solid circles below; kurtosis: solid circles above). The continuous curves represent skewness and kurtosis and are calculated from a highly accurate analytical formula for the WLC distribution function (30). In the $N\to \infty$ limit both the WLC and our model yield the same answer, as expected. In this long-chain limit, where $P\left(R\right)$ is Gaussian, $Sk\to 0$ and $Ku\to 3$. However, in the small length regime below ∼70 basepairs the two models yield qualitative different answers for these moments. As the filament length decreases, the WLC distribution function becomes highly peaked and asymmetric. This is reflected in high kurtosis and negative skewness, consistent with a distribution function with a long tail below the mean value. For our model we find that, for very short chains, the kurtosis becomes less negative, returning to a valuer close to zero, whereas the skewness decreases to a smaller value. These results indicate that the combined effect of rigidity softening and stretching is to make the distribution function more symmetric and less peaked, in the manner qualitatively described previously. In the Supporting Material, we show Sk and Ku in two additional limits: i), the WLC with stretching alone in the absence of rigidity softening and ii), the WLC with contributions from softening, in the absence of stretching (Fig. S1). These results show that, for short chains, stretching is the dominant factor contributing to a more symmetric and less peaked distribution function. Compared to the WLC, for a given length, rigidity softening decreases the amount of asymmetry and peakedness; however, both increase as the length decreases, as expected, because the softening chiefly acts to reduce the persistence length of the DNA. Comparing these model results to those from experiments should clarify the relative contributions of rigidity softening and stretching in modifying the distribution functions for end-to-end separations in DNA molecules at such subpersistence length scales. It is worth noting that substantial qualitative deviations from the WLC predictions, as seen in these higher order moments, appear to set in only below ∼60–70 basepairs.

Figure 7.

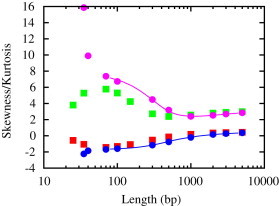
Skewness and kurtosis of the distribution function $S\left(R\right)$. We compare results from our model (skewness: solid squares below; kurtosis: solid squares above) with that of the standard WLC (skewness: solid circles below; kurtosis: solid circles above). The continuous curves represent skewness and kurtosis calculated from an analytical formula for the WLC distribution function, from (30).

The physics of these results is the following. For DNA lengths far exceeding persistence lengths, localized rigidity softening only serves to mildly renormalize persistence lengths, while leaving distribution functions largely unaltered. This is because chain tangent vectors are already decorrelated at scales of order the Kuhn length $\left(2l_p\right)$, therefore an additional softening arising from fluctuations at scales much larger than these is practically irrelevant. For short chains however, although such localized rigidity softening is vastly suppressed by thermal factors, its influence on the distribution functions is nevertheless anomalously large. For example, for short chains, as outlined in (29), accounting for a single defect near the center of the chain leads to a $P\left(\left|\mathbf{R}\right|\right)$, which diverges at the origin, from a mapping to a two-step random walk, in sharp contrast to the case for chains with no such defects. Such anomalously large contributions from anomalously rare events lie at the root of the enhancement of the cyclization probabilities in the CW experiments as well as the behavior of the skewness and kurtosis for short chains.

Conclusion

We have presented a detailed study of end-to-end distance distribution functions $P\left(R\right)$ in a model for short double-stranded DNA, aimed at understanding the implications of bending and stretching fluctuations for the interpretation of results from molecular ruler and similar experiments. We show that obtaining accurate fits to the experimental data requires that we account for local fluctuations in bending rigidity, although stretching is, however, indeed necessary to shift the mode of the distribution to larger values than contour length estimates would suggest. Our results allow us to quantify, within reasonable estimates for parameter values, the interplay of the relative contributions of bending and stretching for DNA strands across multiple scales. We can thus rule out interpretations of the experimental results of MDH, which assume that the DNA molecule is relatively rigid, with highly suppressed bending fluctuations, at these scales. We report a detailed study of the moments of the distribution function in the presence of both bending and stretching fluctuations, showing how characteristic features in these may be used to discriminate between different proposals for the configurations of short double-stranded DNA.

The experiments of both CW and of MDH have been critically assessed (22,31,32). Although (31) sees no anomalous enhancement in cyclization in experiments on chains of similar length, attributing the CW results to a lack of equilibration between circularization and dimerization in the ligation experiments, their specific experimental conditions do not appear to fully replicate those of CW. In particular, the large enthalpic factors crucial to the cost of defect formation are much enhanced at the closer-to-physiological temperatures at which the CW experiments were performed (33,34). The Vafabakhsh-Ha experiments see the same anomalous increase in flexibility as CW, as inferred via an approximately length-independent behavior of the cyclization probability for short chains (see (17,18,29) for predictions of this behavior). Overall, the broad experimental situation appears to be consistent with the view that fairly short DNA strands have larger angle bending fluctuations than a naive WLC-based theory would predict.

The axial displacement of the nanocrystal centers used to tag DNA molecule ends in the molecular ruler experiments from the ends of the DNA duplex has been proposed to act like a lever arm to amplify bending fluctuations (22); alternatively, enhanced linker flexibility could yield to large variances (32). In (21), in connection with the possibility of kinking raised in (22), it is suggested that the dominant Gaussian feature in end-to-end distributions might correspond to an exclusively unbent DNA population, with fits to the Gaussian feature unaffected by bending phenomena. Kinked DNA molecules could then contribute a separate broad probability feature, possibly hidden in the baseline of the distribution. Our results clarify that if increased local flexibility arising from defects are accounted for, the dominant feature in the $P\left(R\right)$ is composed of contributions both from stretching and from bending fluctuations that cannot be decomposed separately. A numerical simulation suggests that accounting for the exclusion volume of the attached nanoparticles in the MDH experiments as well as electrostatic repulsions between them might account for the inferred stretching fluctuations (35). Our own estimates of the contribution of stretching in the MDH experiments suggest that it was overestimated by more than a factor of two in the earlier analysis, rendering such a comparison somewhat moot. Furthermore, note that the potentials used in the related all-atom simulations do not, to the best of our knowledge, reproduce any of the experimentally seen short-scale rigidity softening in DNA.

Although this work refers to defects responsible both for rigidity softening and localized stretching, preferring this usage to the more specific bubbles and kinks, we speculate that these defects might actually correspond to localized regions of one (possibly both) of the two types of DNA structures stabilized in the large force $\left(>65\text{pN}\right)$ limit. One of these states is reached through a hysteretic transition, likely involving force-induced melting and strand separation. The other is obtained through a smooth transition, putatively to the novel strand-joined S-DNA state. The hysteretic transition appears to be favored by increased AT content, whereas the reversible transition is favored by increased GC content (36). The extension parameter in our model is $\zeta =1.76$, which corresponds to an extension of $\approx 0.58$ nm/bp, a number comparable to the known extension of S-DNA. Furthermore, the measured bending stiffness of the S-DNA state is comparable to the J_ss values we use (10,11); see also (23). These observations lend some credence to our proposal that the defects discussed here might represent fluctuations of S-DNA in a background of B-DNA.

Overall, we may conclude the following: Our choice of J_ss and J_dd provides accurate fits to the overstretching data on long chains, consistent with earlier work in the continuum limit. However, for short chains we must use smaller values both for the cooperativity (γ) as well as the defect energy cost (α), than those that provide the best fits for long chains. Taken together, our results imply that reducing the cooperativity of bending fluctuations produces distribution functions as well as moments which fit the experimental data on short chains, whereas such cooperativity should saturate to a somewhat larger, L-independent value for long chains. Such a short-scale length dependence of parameters such as cooperativity might have been physically expected, because the presence of open ends should, in general, be expected to reduce cooperativity for short chains in comparison to longer chains for which such end effects should be negligible.

In mesoscale regimes, of a few tens of basepairs, the obvious convenience and simplicity of a coarse-grained polymer description must be balanced by the requirement that short-scale fluctuations, such as the rigidity softening and the subunit length fluctuations suggested in earlier work, must be accounted for. Our approach here extends the successful WLC paradigm to such scales through calculations on a relatively simple discrete model that reduces to the WLC for large L. The incorporation of twist effects and the sequence dependence of bending rigidities and basepair length fluctuations into our model would be a logical next step, albeit at the expense of several additional layers of complexity.