Free Energy Cost of Stretching mRNA Hairpin Loops Inhibits Small RNA Binding

Abstract

Small RNA-mRNA binding is an essential step in RNA interference, an important cellular regulatory process. Calculations of binding free energy have been used in binding site prediction, but the cost of stretching the mRNA loop when the small RNA-mRNA duplex forms requires further exploration. Here, using both polymer physics theory and simulations, we estimate the free energy of a stretched mRNA loop. We find loop stretching significantly increases the free energy of 3′ supplementary/compensatory miRNA binding and siRNA binding to mRNA hairpin loops. We also make the observation that sites where 3′ supplementary binding is available may bind at the seed only, and that loop stretching often favors seed-only binding over seed plus 3′ supplementary binding in mRNA hairpins.

Introduction

RNA interference functions both as an important cellular regulatory mechanism and an experimental and therapeutic tool in posttranscriptional gene repression. Two types of small RNAs bind to mRNA to effect RNA interference: small interfering RNAs (siRNAs) and microRNAs (miRNAs).

The siRNAs bind with nearly full complementarity along their length of ∼21 nucleotides (nts) (1). The miRNAs bind to mRNA in two ways: seed-only binding and 3′ supplementary/compensatory (3′ supp/comp) binding. The seed-only binding occurs at miRNA nts ∼1–8. The 3′ supp binding supplements seed-binding with at least three basepairs centered around miRNA nts 13–16. The 3′ comp binding compensates for a seed mismatch or bulge with at least four basepairs centered around miRNA nts 13–16 (2).

Binding-site prediction initially relied on primary sequence complementarity or free energy of duplex formation and evolutionary conservation (3–7), but other factors, such as AU content near the site, proximity to sites for coexpressed miRNAs, and positioning of site within 3′ UTR, have been considered (8). The role of mRNA secondary structure has also been explored in recent years. The accessibility of the mRNA target site and the free energy cost of disrupting local mRNA secondary structure have been factored into the analysis (9–13).

As we see in Fig. 1, when a small RNA binds to an mRNA loop, the resulting helical structure stretches the rest of the loop, posing an entropic cost to the free energy of binding (14). To quantify this cost, we first use polymer theory to estimate the free energy of a stretched mRNA chain and use random-walk simulations to confirm our formula. We then apply our theory to calculate the free energy of small RNA binding to mRNA loops and show that chain stretching inhibits 3′ supp/comp miRNA binding and siRNA binding to mRNA hairpins. We also find that when 3′ supp miRNA binding is available in mRNA hairpin loops, the miRNA often prefers to bind only to the seed.

Figure 1.

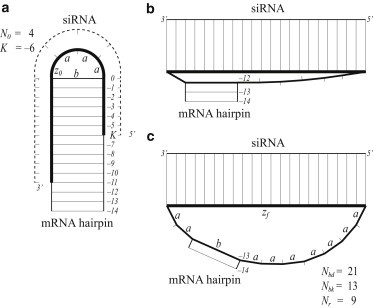
An example of siRNA binding. (a) Before binding, there are N₀ = 4 a-segments in the mRNA hairpin loop. K = −6 marks the binding position of the first nucleotide of the siRNA. To calculate loop free energy, the loop is modeled as a chain of three a-segments and one b-segment held at end-to-end separation z₀ = a. (b) After breaking 12 stem basepairs, the loop has just enough contour length to accommodate the binding helix, but is still highly stretched. (c) The minimum free energy is reached after another stem basepair is broken. There are N_bd = 21 a-segments involved in binding. N_bk = 13 basepairs (labeled 0 to $-12$) were broken in the mRNA hairpin stem. N_r = 9 a-segments remain in the hairpin loop, which is modeled as a chain of nine a-segments and one b-segment held at separation z_f = z(21) = 57.5 Å.

Theory

Formula for the free energy of a stretched mRNA loop

If the small RNA binds to s + 1 nucleotides in the loop, those nucleotides become part of a helix and are removed from the flexible portion of the loop. The helix stretches the remainder of the loop to an end-to-end separation of

$$\begin{array}{c}z\left(s\right)={\left\{{\left(hs\right)}^2+r^2{\left[1-\text{cos}\left(\frac{2\pi s}{11}\right)\right]}^2+r^2{\text{sin}}^2\left(\frac{2\pi s}{11}\right)\right\}}^{1/2},\\ ={\left[{\left(hs\right)}^2+4r^2{\text{sin}}^2\left(\frac{\pi s}{11}\right)\right]}^{1/2},\end{array}$$ (1)

where h = 2.7 Å and r = 9.9 Å describe A-form RNA (15).

Let the remainder of the loop be made of N single-stranded backbone segments (of length a = 6.2 Å) and M helix-crossing segments (of length b = 15 Å) in a two-length-scale freely jointed chain model (16). The contour length S = Na + Mb is the upper limit of z(s) in stretching. The Flory radius

$$R_F={\left(\langle R^2\rangle \right)}^{1/2}={\left(N^{6/5}{a}^2+M^{6/5}{b}^2\right)}^{1/2},$$ (2)

represents the characteristic end-to-end separation of a self-avoiding chain (16).

We will now derive the free energy G(N,M,z) of an mRNA loop with N a-segments, M b-segments, and a helix of length z, which arises from binding a small RNA. We will find the leading behavior in three regimes: z ≪ R_F, z ≳ R_F, and z ≈ S, and develop an interpolation formula.

According to scaling theory, if we place one end of a self-avoiding chain at the origin, the probability density per unit volume of the other end of the chain depends on dimensionless separation variable x = z/R_F and takes the form

$$p\left(z\right)=\frac{1}{R_F^3}\varphi \left(x\right),$$ (3)

where ϕ(x) is a universal function (17). For z ≳ R_F, the universal function scales like

$$\varphi \left(x\right)=\text{exp}\left\{-x^{5/2}\right\}.$$

The probability that the other end of the chain is within a small volume ΔV around z = R_F (i.e., the probability that a loop with a helical segment of length z = R_F is made) is

$$p_{\text{loop}}=p\left(z\right)\Delta V=\left(\Delta V/R_F^3\right)\text{exp}\left\{-x^{5/2}\right\}.$$ (4)

Using the Boltzmann relation p_loop ∝ e^−βG, where β = 1/RT, we have

$$\begin{array}{c}\beta G\left(N,M,z\right)=3/2\text{ln}\left(N^{6/5}{a}^2+M^{6/5}{b}^2\right)+{\left(z/R_F\right)}^{5/2}+\beta C_0-1,\\ =3/2\text{ln}\left(N^{6/5}{a}^2+M^{6/5}{b}^2\right)+5/2\left(z-R_F\right)+\beta C_0.\end{array}$$ (5)

The second line is obtained by Taylor-expanding to first-order around z = R_F. In our final free energy formula, we will require that (∂/∂z)βG(N,M,z) be consistent with Eq. 5 at z = R_F. The constant C₀ depends on ΔV and could be set on the basis of an experiment.

Compression or extension causes an entropic force; we calculate the free energy in both regimes. When the scaled separation x = z/R_F ≪ 1, the universal function in Eq. 3 scales like ϕ(x) = x^v, with $\nu =5/18$ (18), so the leading behavior is

$$\beta G_{\text{short}}\sim -\nu \text{ln}z+\beta C_1,$$ (6)

for z ≪ R_F, where C₁ is a constant with respect to z.

Next, we derive the free energy for a freely jointed chain stretched so z approaches the contour length S = Na + Mb. Each segment points in a random direction, and the probability density function of the displacement along the z axis is p = 1/(2a) for an a-segment and p = 1/(2b) for a b-segment. Thus the total probability of being within a short distance D = S − z from full extension is

$$\begin{array}{c}P(0\le \xi \le D)=\underset{0}{\overset{D}{\int }}d{\xi }_1\cdots \underset{0}{\overset{D-{\xi }_1-\dots -{\xi }_{N+M-1}}{\int }}d{\xi }_{N+M}{p}_1\cdots p_{N+M},\\ =\frac{1}{{\left(2a\right)}^N{\left(2b\right)}^M}\frac{D^{N+M}}{\left(N+M\right)!},\end{array}$$ (7)

where the net deviation from maximum extension

$$\xi =\sum _{i=1}^{N+M}{\xi }_i,$$

is the sum of the deviations of individual segments. Taking the derivative of Eq. 7, we have the linear probability density function in the z direction of

$$p\left(D\right)=\frac{dP(0\le \xi \le D)}{dD}=\frac{1}{{\left(2a\right)}^N{\left(2b\right)}^M}\frac{D^{N+M-1}}{\left(N+M-1\right)!}.$$ (8)

We then consider fluctuations in the xy plane. For an a-segment, we have x_i² + y_i² + z_i² = a² and z_i = a − ξ_i. Thus x_i² + y_i² + z_i² = a² – (a − ξ_i)² ≈ 2aξ_i. Similarly, for a b-segment, x_i² + y_i² ≈ 2bξ_i. Summing the xy fluctuations for all segments gives

$$\langle R_{\perp }^2\rangle \approx \frac{2\left(Na+Mb\right)D}{N+M},$$

which is similar to a result derived for the wormlike chain (19). The probability that the end of the chain is within a small volume $\Delta V=\Delta x\Delta y\Delta z$ of position (0,0,z) is

$$p\left(z\right)\Delta V\propto \left(\frac{\Delta x\Delta y}{\langle R_{\perp }^2\rangle }\right)\left(\frac{\Delta z}{{\left(2a\right)}^N{\left(2b\right)}^M}\frac{D^{N+M-1}}{\left(N+M-1\right)!}\right)\propto D^{N+M-2},$$ (9)

where D = S − z. Thus, the free energy of making a highly stretched loop goes like

$$\beta G_{\text{long}}\sim -\left(N+M-2\right)\text{ln}\left(S-z\right)+\beta C_2,$$ (10)

for z ≈ S.

Equations 5, 6, and 10 describe the leading behavior for z ≈ R_F, z ≪ R_F, and z ≈ S. Our formula for the free energy G(N, M, z) of a loop with N a-segments and M b-segments held at end-to-end separation z incorporates all of those contributions:

$$\beta G\left(N,M,z\right)=3/2\text{ln}\left(N^{6/5}{a}^2+M^{6/5}{b}^2\right)+\beta C_0-\nu \text{ln}\left(\frac{z-r}{R_F-r}\right)-\left(N+M-2\right)\text{ln}\left(\frac{S-z}{S-R_F}\right)+\left(\frac{5}{2R_F}+\frac{\nu }{R_F-r}-\frac{N+M-2}{S-R_F}\right)\left(z-R_F\right).$$ (11)

Note that at z = R_F, Eq. 11 is consistent with both the value and the derivative with respect to z of Eq. 5. We have introduced the radius r = 2.4 Å of beads used in the self-avoiding simulations described in the next section.

Simulated free energy of a stretched mRNA chain

We test the validity of Eq. 11 with self-avoiding random-walk computer simulations, conducted as previously (16) with 10⁹ walkers. Let Ω_total (N,M) be the total number of chains with a particular specification (N,M). We examine the number Ω_z (N,M) of chains with end-to-end separation belonging to a spherical shell (z, z + 0.1Å), going from 4.8 to 64 Å.

The probability of forming a loop with a helical segment of length z is

$$p_{\text{loop}}\left(N,M,z\right)=\frac{{\Omega }_z\left(N,M\right)}{4\pi z^2\Delta z{\Omega }_{\text{total}}\left(N,M\right)}\Delta V\propto e^{-\beta G_{\text{sim}}\left(N,M,z\right)},$$ (12)

so

$$\beta G_{\text{sim}}\left(N,M,z\right)=-\text{ln}\frac{{\Omega }_z\left(N,M\right)}{4\pi z^2\Delta z{\Omega }_{\text{total}}\left(N,M\right)}$$ (13)

for discrete z from 4.8 Å to 64 Å in steps of Δz = 0.1 Å.

In Fig. 2, with r = 2.4 Å, ν = 1.4, and C₀ = 2.8 kcal/mol, we show that theory (Eq. 11) and simulations (Eq. 13) are in excellent agreement when plotted as a function of z. Fig. S2 in the Supporting Material shows that there is good agreement at z = R_F for different values of N and M. Though scaling theory describes the properties of long chains, even short loops are well represented.

Figure 2.

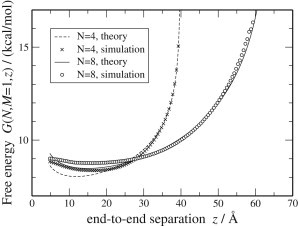
The theoretical and simulated free energies of a stretched mRNA chain with N = 4 or 8 and M = 1.

Other authors recently have enumerated configurations with a discrete number of possibilities at each step (14,20–25), many based on a virtual bond representation (26,27).

Application to small RNA binding to mRNA hairpin loops

Hairpins are the smallest mRNA loops and thus the most susceptible to the effects of chain stretching. The net free energy of binding is derived from the cost of initiating binding, the making and breaking of basepairs, and the change in loop free energy, as

$$\Delta G_{\text{binding}}=\Delta G_{\text{init}}+\Delta G_{\text{bp}}\left(N_{bk}-N_{bd}\right)+G\left(N_r,1,z_f\right)-G\left(N_0-1,1,z_0=a\right),$$ (14)

where N_bd is the number a-segments involved in basepairing between the small RNA and the mRNA; N_bk is the number of mRNA stem basepairs broken; N_r is the number of remaining a-segments in the hairpin after binding; N₀ is the initial number of a-segments in the loop; and z₀ and z_f are the end-to-end distances at which the mRNA chain is held before and after binding, respectively. In addition, we define a parameter K to indicate the position of the binding site within the loop. These variables are also described in Fig. 1.

The initiation cost of forming a small RNA-mRNA helix (28) is ΔG_init = 4.1 kcal/mol. For binding free energy, we use the average value per basepair (15) of ΔG_bp = 2.14 kcal/mol to highlight the effects of the length of the binding region within the loop independent of sequence. To estimate the free energy of the mRNA loop before binding, we think of it as a chain with one fewer a-segment than the loop, held at an end-to-end distance of z₀ = a.

A previous model (13) takes into account the free energy cost of breaking mRNA stem basepairs overlapping with the small RNA binding site, but not the cost of stretching the mRNA loop. Instead, it simply calculates the change in Turner loop free energy, treating the bound mRNA nucleotides as if part of a single-stranded loop. Our model, on the other hand, accounts for loop stretching and breaks additional stem basepairs one by one as long as the resulting benefit in loop free energy is greater than the cost of breaking the basepair. In the interest of developing a general theory, we assume that the stem is never completely broken.

Results

The free energy of small RNA binding to mRNA hairpins

Hairpins, with only one helix-crossing b-segment, are the smallest mRNA loops and thus the most susceptible to the effects of chain stretching. We consider three types of small RNA-mRNA binding: siRNA; seed-only miRNA; and 3′ supplementary/compensatory miRNA. In each case, we compare the binding energies predicted by our theory, our simulations, and a previous model (13) that uses Turner hairpin energies.

For siRNA binding, we choose N_bd = 21 (with 22 contiguous basepairs between the siRNA and the mRNA) as a representative case. The end-to-end separation of the mRNA chain after binding is z_f = z(21) = 57.5 Å. In Fig. 3 (a), we compare our model with a previous model (13) that did not account for the free energy of stretching a loop. When the binding site is at the center of the hairpin loop, the previous model would allow the loop after binding to be composed of the 22-bp binding helix, one b-segment, and only two a-segments. This configuration, however, is not possible: to geometrically bridge a helix of length 57.5 Å requires a b = 15 Å segment and at least seven a = 6.2 Å segments (Fig. 1 b). In fact, even then the loop is so highly stretched that the minimum free energy is reached when another basepair in the stem is broken, increasing the contour length by 2a (Fig. 1 c). This relaxation process stops when the benefit of relieving chain stretching no longer outweighs the cost of breaking an extra stem basepair. In the end, the chain is still partially stretched beyond R_F. Thus, the offset in binding free energy between our model and the previous model consists of the costs of partial chain stretching and of breaking stem basepairs.

Figure 3.

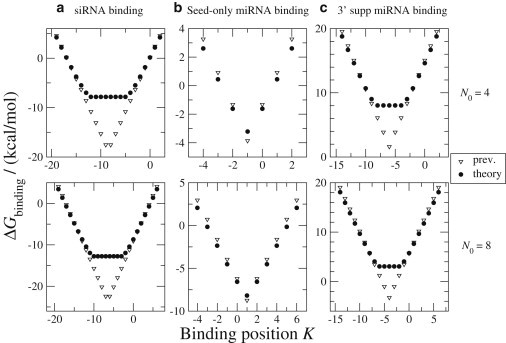
The free energy of small RNA binding in mRNA hairpin loops with initial hairpin sizes N₀ = 4 or 8. In (a) siRNA binding and (c) 3′ supplementary/compensatory miRNA binding, our theory offers an improvement over those of the previous model (13). (b) In seed-only miRNA binding, our theory and the previous model largely agree.

Because siRNA binding to the center requires several stem basepairs to be broken, the binding site is free to shift a few nucleotides in either direction without further invading the stem, which would increase binding free energy. Thus, our binding free energy gives equal values for binding sites within a few nucleotides of the center of the loop (Fig. 3, a). Similarly, asymmetry in internal loops has little effect on free energy (25).

For seed-only miRNA binding, we choose a 7-nt seed as a representative case. Then, N_bd = 6 and z_f = z(6) = 25.5 Å. Our predicted energies differ little from results of the previous model (Fig. 3, b). Introducing a miRNA-mRNA helix of seven basepairs with length 25.5 Å is not much of a constraint because the helix can be easily bridged by the b-segment (b = 15 Å) plus two a-segments (a = 6.2 Å).

For 3′ supp/comp miRNA binding, the miRNA and mRNA form two helical segments, connected by an internal loop. As a representative case, we choose to bind at miRNA nts 1–7 and 13–17. Thus, N_bd = 10. The binding initiation energy of 4.1 kcal/mol is applied only once for the two helices, because once one helix forms, the formation of the other is an intramolecular reaction. We also add the free energy cost of forming the symmetric internal loop between the two binding regions, which is G_internal = 2.34 kcal/mol according to the Turner rules (28). The conformational freedom of the two binding helices relative to each other is limited by the protein complex RISC. Using a ternary crystal structure of Ago (a part of RISC), a 12-nt target RNA (a surrogate for mRNA), and a 21-nt guide DNA (a surrogate for siRNA) (29), we estimate that the length of this rigid segment is roughly z_f = 44 Å, which is sufficiently long to stretch the hairpin loop. Thus, when the binding site is located near the center of the loop, our predictions of binding free energies are higher than those of the previous model (Fig. 3, c). Notably, most of the binding free energies are positive, indicating that 3′ supp/comp miRNA binding is usually unfavorable in small mRNA hairpin loops, though binding of GC-rich sequences may still be possible.

Two binding motifs of 3′ supplementary miRNA: comparing seed-only and 3′ supp binding

Given the high free energy cost of 3′ supp/comp miRNA binding in small mRNA hairpins, we explore alternative binding possibilities in these interactions. In 3′ comp miRNA binding, extensive 3′ pairing is required to compensate seed mismatches. In 3′ supplementary miRNA binding, however, 3′ pairing is nonessential (2). While providing extra basepairing free energy, 3′ pairing also involves the costs of forming an internal loop between the two binding regions and of stretching the mRNA loop with a longer binding segment [z_f = 44 Å vs. z_f = z(6) = 25.5 Å]. Our free energy predictions show that in mRNA hairpin loops, due to loop constraints, seed-only binding is usually preferred (Fig. 4). The exception is that when the seed binds in the stem of the mRNA hairpin with negative K, adding a-segments to the loop, the 3′ region of the miRNA may bind with a benefit in free energy (Fig. 4), but then the binding free energy is often positive so binding is unfavorable. Thus, many putative 3′ supp binding interactions in hairpins may effectively be seed-only interactions. The net binding free energy derives from the partition function of the binding energies of the two modes,

$$\beta \Delta G_{\text{net}}=-\text{ln}\left(e^{-\beta \Delta G_{\text{seed}-\text{only}}}+e^{-\beta \Delta G_{3^{\prime }\text{supp}}}\right),$$ (15)

plotted in Fig. 4.

Figure 4.

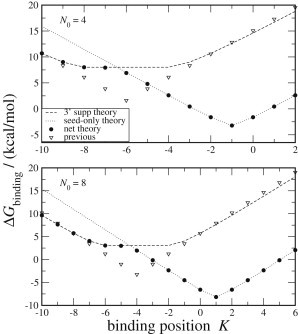
Binding free energies at 3′ supplementary sites in mRNA hairpins with initial hairpin sizes N₀ = 4 and 8. Our model (solid circles) takes the net free energy of seed-only and 3′ supplementary binding modalities, while the previous model (triangles) considers only 3′ supp binding. (Dotted line) Seed-only binding component of our theory. (Dashed line) 3′ supplementary binding.

Extending the hairpin binding model: mRNA loop constraints are insignificant in bulges, internal loops, and multibranch loops

In addition to hairpins (M = 1), there are also bulges and internal loops (M = 2) and multibranch loops (M > 2). Because the other types have additional b-segments, these loops tend to be too large to be significantly stretched by even siRNAs, which create the longest binding helix.

Conclusion

We have derived a theoretical formula for the free energy of a stretched mRNA chain that agrees beautifully with self-avoiding random-walk simulations; we have shown, using the formula, that mRNA loop stretching inhibits siRNA and 3′ supp/comp miRNA binding to mRNA hairpins; and we have shown that sites in mRNA hairpins where 3′ supplementary binding is available often prefers to bind only to the seed. We encourage target site prediction models to use Eqs. 11 and 14 to take into account the thermodynamic effect of mRNA loop stretching.