Abstract
The superior colliculus (SC) integrates relevant sensory information (visual, auditory, somatosensory) from several cortical and subcortical structures, to program orientation responses to external events. However, this capacity is not present at birth, and it is acquired only through interactions with cross-modal events during maturation. Mathematical models provide a quantitative framework, valuable in helping to clarify the specific neural mechanisms underlying the maturation of the multisensory integration in the SC. We extended a neural network model of the adult SC (Cuppini et al. 2010) to describe the development of this phenomenon starting from an immature state, based on known or suspected anatomy and physiology, in which: 1) AES afferents are present but weak, 2) Responses are driven from non-AES afferents, and 3) The visual inputs have a marginal spatial tuning. Sensory experience was modelled by repeatedly presenting modality-specific and cross-modal stimuli. Synapses in the network were modified by simple Hebbian learning rules. As a consequence of this exposure, 1) Receptive fields shrink and come into spatial register, and 2) SC neurons gained the adult characteristic integrative properties: enhancement, depression, and inverse effectiveness. Importantly, the unique architecture of the model guided the development so that integration became dependent on the relationship between the cortical input and the SC. Manipulations of the statistics of the experience during the development changed the integrative profiles of the neurons, and results matched well with the results of physiological studies.
Keywords: Visual-acoustic neurons, Anterior ectosylvian sulcus, Enhancement, Hebb rule Learning mechanisms, Inverse effectiveness principle, Neural network modeling
1. INTRODUCTION
Neurons in the cat superior colliculus (SC) are unisensory at birth and continue to be so until roughly four weeks of age. These neonatal neurons have large receptive fields (RFs) and weak sensory responses with long latencies that fatigue readily (Stein et al. 1973a; Stein et al. 1973b). As they mature, the neurons become responsive to multiple sensory modalities, their responses become more robust, their modality-specific RFs shrink into spatial register with one another, and they eventually gain the ability to integrate signals across the senses to boost sensory responsiveness (Wallace et al. 2004; Wallace and Stein 1997). This process requires months of cross-modal experience before achieving adult-like status. If that experience is prohibited by disallowing the animal access to the requisite experience, multisensory neurons develop, but do not have the capacity to integrate inputs across sensory modalities for signal enhancement.
The mechanisms underlying adaptation of the underlying neural circuitry to cross-modal experience are not well understood. It is believed to involve areas of association cortex which project to the SC, because they must be intact in order for SC neurons (and behaving animals) to acquire and maintain the ability to integrate cross-modal cues (Alvarado et al. 2008; Fuentes-Santamaria et al. 2009; Jiang et al. 2002; Jiang et al. 2001; Jiang et al. 2007). If these afferents are removed early in development or are functionally compromised in the adult, SC neurons and behaving animals will still respond to multiple sensory modalities but not be capable of integrating signals across them (i.e., the response to two concurrent cross-modal stimuli is not grater than the stronger of the two modality-specific responses acting separately).
Previously developed neural network models are able to account for many aspects of SC responsiveness (Cuppini et al. 2010; Magosso et al. 2008; Ursino et al. 2009), but are limited by having parameters “hard-wired” a priori and do not describe maturation or adaptation. Here, we present a model that describes how internal circuitry can develop and change as a consequence of simulated multisensory and unisensory experience. It thereby provides viable hypotheses for how the underlying biological circuit is altered and comes to instantiate multisensory integration.
A preliminary version of this study analyzed the maturation of the RFs and the appearance of cross-modal enhancement in a single SC neuron (Cuppini et al. 2011); that work showed that Hebbian learning in a cross-modal environment can explain the development of neurons with adult-like behavior. The present study extends the previous by considering not a single neuron, but a network of neurons coding for different spatial positions. This allows investigation of several aspects not considered before: i) how, as a consequence of the random nature of cross-modal and within-modal inputs, neurons can exhibit different characteristics after maturation, i.e. there exists a mixture of neurons with various multisensory integrative products; ii) how the different characteristics in the SC population depend on the exposure to cross-modal experience and on some crucial parameters of the network; iii) how lateral synapses among SC neurons in the network, refined by experience, can explain cross-modal depression of misaligned stimuli, a property not present in the immature stage.
2. METHODS
2.1 General model structure
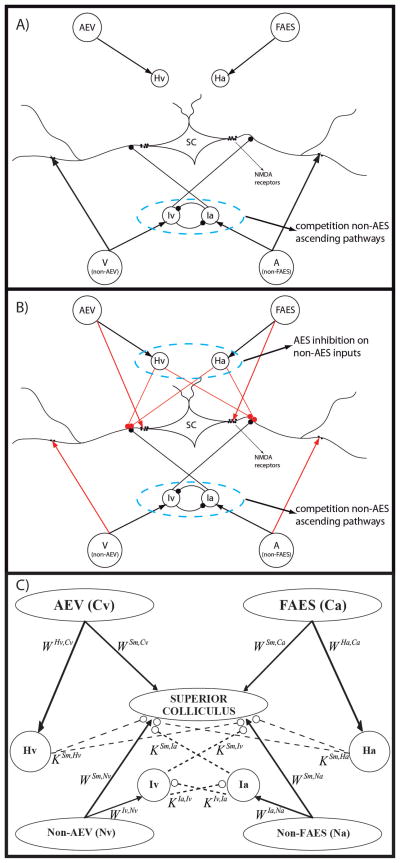
The model was designed to simulate the development of circuits involved in the maturation of multisensory integration in the cat SC, starting with a configuration corresponding to approximately 4 weeks postnatal (Fig. 1A), when the SC neurons can respond to multiple sensory modalities but not integrate signals across them, and ending with an adult-like configuration (Fig. 1B), when the majority of multisensory SC neurons show multisensory integration capabilities. Two fundamental aspects of the model are: i) the use of simple Hebbian rules for long term potentiation and depression; ii) the close dependence of SC maturation on exposure to correlated cross-modal signals. For simplicity only two senses are modeled, based on vision (V) and audition (A), but the model can be generalized to other sensory combinations as well.
Fig. 1. The general structure of the network in neonatal (fig. 1A) and in mature (fig. 1B – 1C) phase.
The four projection areas make excitatory synapses with their target interneurons (arrows). In the neonatal configuration (fig. 1A) only non-AEV and non-FAES input regions are connected with their target SC neurons and their correlated interneurons are effective; on the contrary, projections from AES subregions are not mature and their interneurons haven’t influence on the SC activity. In the adult configuration (fig. 1B) all the four unisensory input areas send excitatory synapses to the SC and the four interneuron populations are effective. These interneurons provide two competitive mechanisms: 1) Ha and Hv provide the bases through which the inhibitory effect of AES is imposed on non-AES inputs; 2) Ia and Iv provide the substrate for a competition between two non-AES inputs in which the stronger one overwhelms the weaker. In panel C, a schematic picture of the network is reported to highlight the more important parameters of the model.
Three different regions are modeled: i) sensory inputs derived from unisensory cortical areas of the anterior ectosylvian sulcus (AES) referred to as “descending inputs”, ii) sensory inputs derived from other cortical and subcortical regions (non-AES) referred to as “ascending inputs”, and iii) the SC itself. AES inputs are divided into those derived from a visual subregion (AEV) and unisensory auditory subregion (FAES). A similar subdivision is made for the unisensory non-AES regions (visual=non-AEV, auditory=non-FAES).
The SC itself contains populations of output neurons (“units”) and four populations of inhibitory interneurons that receive input from the sensory sources and from one another, and inhibit SC. The interneurons are divided into four groups depending on their excitatory input source: Iv receives input from the ascending visual source, Ia from the ascending auditory source, Hv from the descending visual source, and Ha from the descending auditory source. The inhibitory interneuron populations receiving ascending inputs (Iv, Ia) also exchange lateral connections and mutually inhibit one another.
Modeling the individual units
According to the previous description, the model contains four unisensory input arrays, four arrays of SC inhibitory units, and a single array of SC output units. Each of these nine different arrays contains 100 units and is referenced as follows:
Ca (cortical auditory): auditory AES (FAES) units:
Cv (cortical visual): visual AES (AEV) units;
Na: non-FAES auditory units;
Nv: non-AEV visual units;
Hv: SC inhibitory units which receive input from AEV;
Ha: SC inhibitory units which receive input from FAES;
Ia: SC inhibitory units which receive input from the non-FAES (auditory) region;
Iv: SC inhibitory units which receive input from the non-AEV (visual) region;
Sm: SC output neurons
Each unit in the model is taken to represent the aggregate activity of an ensemble of real neurons on a given experimental trial, and the response of a single unit can be compared to the magnitude of a real neuron’s output (i.e., # impulses) averaged over multiple trials.
Individual units are referenced with superscripts indicating their array assignment and subscripts that indicate their position within that array (i.e., indicating their spatial position/sensitivity). u(t) and z(t) are used to represent the net input and output of a given unit at time t, respectively. Thus, represents the output of a unit receiving net input at location i within array h at time t.
The strength (i.e., “weight”) of an excitatory projection to a unit at position i in array h from a unit at position j in array k is denoted . Inhibitory connection strengths use the same convention but are denoted by a capital K instead of W. The weight of the lateral connection from a projecting unit at position i to a receiving unit j within an array h is denoted , and may be positive or negative.
The output of each unit in the network at each simulated moment is a continuous variable and is computed from its input, which is passed through a static sigmoidal relationship, and a first-order dynamic. Specifically, for a unit i in region s with time constant τ s receiving net input at a moment in time t, its output is determined by the following differential equation (Eq. (1)):
| (1) |
where ϕ(us(t)) is a sigmoidal function with parameters ϑs (the central point) and ps, which sets the slope at the central point (Eq. 2):
| (2) |
Thus, in this model, unit activity is limited to the range (0, 1) as a convention (i.e., all neuronal activities are normalized to a maximum of 1). Units are initialized at zero.
The input regions
Units within each input area (AEV, FAES, non-AEV non-FAES) are modeled as having topographically organized and overlapping receptive fields (RFs). To represent the higher spatial resolution of the visual system, auditory RFs are assumed to be larger than visual RFs. Units within each input area are reciprocally connected via lateral synapses that are excitatory among nearby units and inhibitory among distant units, according to a classical “Mexican Hat” pattern. Consequently, although a single stimulus is modeled as existing only at a single point in space, it produces a shaped population of activity in the corresponding sensory input regions.
External stimuli are described through inputs Is(x,t) that are functions of time (t) and space (x) to a particular input area s. The receptive field of a generic unit i of an input area s is defined by a Gaussian function of space having a default maximum amplitude , center xi, and standard deviation :
| (3) |
As a consequence of Eq. (3), a stimulus simulated as present at a particular position xi maximally excites unit i but can also excite adjacent units. The external input, to a generic unit i in an input area s, is determined as the inner product of the receptive field and the external stimulus:
| (4) |
where the integral has been approximated with a sum, and Δx is the integration step.
Unisensory input units within an area s also receive input through intrinsic lateral connections. The net lateral input, , is defined by the sum of products of the weights of lateral connections and the output of projecting units for each location:
| (5) |
Lateral connections are symmetric and their weights ( ) are defined by a “Mexican hat” function constructed by subtracting an inhibitory Gaussian function (max amplitude = Lins, std = σins) from an excitatory one (max amplitude = Lexs, std = σexs):
| (6) |
In this equation, dx represents the distance between the projecting and target units. Elements at the extreme ends of a linear array potentially might not receive the same number of connections as other units (e.g., there are no units to the “left” of i=1), which can produce undesired border effects. To avoid this complication, the array is imagined as having a circular structure so that each unit within an area receives the same number of lateral connections:
| (7) |
The net input received by a unit at position i in a unisensory input area s, , is the sum of the inputs from the external stimulus (Eq. 4) and the intrinsic connections (Eq. 5):
| (8) |
The output of each of these units in the unisensory input areas is determined by Eq. 1, 2, and 8 where s is either Ca, Cv, Na, or Nv (i.e., the previous equations separately hold for both AES and non-AES areas, and for both auditory and visual modalities).
The SC inhibitory populations
The four arrays of 100 topographically-organized SC inhibitory units receive input from specific sensory input sources and send projections to a paired SC output unit and (in some cases) to each other. SC inhibitory units Ha and Hv, that receive input from AES subregions, have net inputs defined as the product of the activity of the topographically-aligned AES unit and the weight of the corresponding connection (the latter denoted with symbol )
| (9) |
| (10) |
SC inhibitory units Ia and Iv, that receive input from non-AES areas, also receive an inhibitory input from the SC inhibitory unit at the same location that is excited by the other modality (e.g., Ia inhibits Iv and vice-versa at the same location). This implements a WTA mechanism. Inputs are computed as follows ( denoting the strength of the inhibitory connection from the other interneuron):
| (11) |
| (12) |
The connections are not modified, and have a Gaussian disposition in strength:
| (13) |
where dx is the distance between neurons at positions i and j, and and σIK,NK are the maximum amplitude and the standard deviation of the Gaussian function.
The output of these inhibitory units is determined using Eq. 1 and 2 where s is Ha, Hv, Ia, and Iv, respectively.
The SC output units
SC output units receive three different types of inputs: excitatory inputs from ascending (Na, Nv) and descending (Ca, Cv) sensory areas; shunting inhibition from the related SC inhibitory populations (Ia, Iv, Ha, Hv); and input from other SC output units via lateral inhibitory connections.
The input derived from the descending sensory inputs is computed by summing the products of the relevant connection strengths and unit activation levels:
| (14) |
| (15) |
The input derived from the ascending sensory inputs is computed in the same manner. However, the total ascending input is also subject to a multiplicative/divisive (“shunting”) inhibition (as is the case in GABAa-mediated inhibition, see Koch 1998). As indicates the shunting inhibition originating from SC inhibitory population Iv, the shunting inhibition originating from SC inhibitory population Ia, and and the inhibitory influence of Hv and Ha, the following expression describes the net ascending input:
| (16) |
| (17) |
where the notational conventions are the same as in Eq. 13 and the inhibitory terms are defined as:
| (18) |
| (19) |
| (20) |
| (21) |
Note that the ascending inhibition arrives only from the neuron in the same spatial position whereas, as a consequence of training, descending inhibition can arrive from several neurons in different spatial positions.
The previous equations can be interpreted as follows: the ascending auditory inputs receive shunting inhibition from the visual ascending modality, while the ascending visual inputs receive inhibition from the auditory ascending modality. This implements the WTA competition between the two ascending channels. Both ascending channels are inhibited by both descending channels, so that descending inputs, when active, will overwhelm the ascending inputs.
Finally, each SC output neuron also receives lateral input from other SC neurons:
| (22) |
The net input to an SC output unit i is computed as the sum of all of these inputs:
| (23) |
Its output is computed from this input using Eq. 1 and 2 where s=Sm.
2.2 Learning rules
Stimulus exposure trials cause the connection strengths in the network to change based on Hebbian algorithms, where connections are strengthened if the projecting and receiving units are co-active. All connections are modifiable with the exception of the projections onto ascending inhibitory units (i.e., populations Ia and Iv) and lateral connections within sensory input regions, all of which are assumed to be mature at birth. Projections from AES are the most flexible (have the highest learning rate). In addition to the simple Hebbian associative/correlative rule, two additional rules are applied that reflect biological resource scarcity and stabilize the network. A post-synaptic gating rule restricts modifications to when the activity of the receiving unit is above a certain threshold, else it decays in strength. In addition, a saturation rule limits the magnitude of an individual connection to a maximum value and limits the sum of the magnitudes of connections received by an individual unit to a maximum value by normalizing the magnitudes by their sum.
For example, an excitatory connection from unit j in area k to unit i in area Sm is modified according to:
| (24) |
where αij and βij represent learning factors for potentiation and depression, respectively, []+ is a rectifying function with threshold 0, and U() represents the unitary step function (i.e., U(y) = 1 if y > 0, and U(y) = 0 if y < 0). This rule is applied after each exposure trial.
The second term on the right side of Eq. 24 represents Hebbian potentiation, where two thresholds (ϑi and ϑj) are used for the activity of the receiving and projecting units. According to the considerations developed above, synapses must saturate to upper values. This is obtained using the following expressions for the learning factor αij
| (25′) |
| (25″) |
where WTOTmax is the maximum value allowed for the sum of descending weights, Wmax is the maximum value allowed for an individual weight, WTOT is the sum of all descending excitatory weights received by the unit, and the different values for α0 are the maximum learning factors (i.e., the learning factor when the weights are at zero).
The third term on the right side of Eq. 24 is a forgetting factor, which resembles that used in unsupervised learning paradigms. A connection decreases its strength if the receiving unit is active and the projecting unit is not: the forgetting factor depends on the actual strength of the connection (or on the sum of connection strengths). Accordingly, the following expression can be used for the depressing component (where function U(Wij) avoids that an excitatory synapse becomes negative)
| (26′) |
| (26″) |
where β0 in Eq. 26″ is the learning factor when the connections strength is at one.
Similar rules (Eqs. 24, 25″ and 26″) are used for the inhibitory descending weights too (replacing with with k = Ha or Hv)
Lateral connections within the SC (reflecting consolidated excitatory/inhibitory interactions) use a modified gating rule: their strength is increased if the projecting and receiving unit activity levels exceed some threshold, but is decreased if the receiving unit’s activity is above threshold but the projecting unit’s activity below it. We have
| (27) |
where
| (28) |
| (29) |
where Lmin and Lmax are the saturation values allowed for each synapse, and and are the learning factors when Lij = 0.
2.3 Parameter assignment
Numerical parameter values for the simulations are given by Table 1 unless otherwise noted.
Table 1.
Parameter values
| Receptive Fields | |||||||||||
| s = Cv, Ca, Nv, Na | s = Cv, Nv | s = Ca, Na | |||||||||
|
|
1 |
|
1 (1.8°) |
|
1.5 (2.7°) | ||||||
| Neurons (s = Cv, Ca, Nv, Na) | |||||||||||
| τs | 3 ms | ϑ s | 20 | p s | 0.3 | ||||||
| Intra-area Synapses | |||||||||||
| AEV | Non-AEV | FAES | Non-FAES | ||||||||
|
|
5.4 |
|
1.2 |
|
5.4 |
|
3 | ||||
|
|
1.8 (3.24°) |
|
2.5 (4.5°) |
|
2.5 (4.5°) |
|
1.5 (2.7°) | ||||
|
|
18 |
|
1 |
|
15 |
|
3 | ||||
|
|
8 (14.4°) |
|
6 (10.8°) |
|
12 (21.6°) |
|
37.4 (67.3°) | ||||
| Superior Colliculus | |||||||||||
| Lmax | 0.1 |
|
0.0001 | Lmin | 7 |
|
0.007 | ||||
| Inter-area Excitatory Synapses | |||||||||||
|
|
15 |
|
14 | WTOT max | 40 | ϑ | 0.12 | ||||
|
|
0.033 |
|
0.033 |
|
0.031 |
|
0.031 | ||||
|
|
8 |
|
1.5 (2.7°) |
|
4 |
|
2 (3.6°) | ||||
|
|
5.8 |
|
2 (3.6°) |
|
2.8 |
|
20 (36°) | ||||
|
|
7.2 |
|
3.8 |
|
0.0048 0.0025 |
|
0.00067 0.00067 |
||||
| Interneurons (s = Hv, Ha, Iv, Ia) | |||||||||||
| τs | 3 ms | ϑ s | 3 | p s | 1 | ||||||
| Inter-area Inhibitory Synapses | |||||||||||
| Visual Interneurons (Hv, Iv) | Auditory Interneurons (Ha, Ia) | ||||||||||
| ϑ | 0.12 |
|
1 |
|
0.005 0.005 |
|
0.00067 0.00067 |
||||
|
|
33 |
|
33 | ||||||||
|
|
1 |
|
1 | ||||||||
Unit model
The time constants of individual units were given in accordance with those usually adopted for neuron membranes (a few milliseconds). The unit model’s sigmoidal characteristics were chosen to meet two criteria: 1) Units have negligible activity in the absence of stimulation; 2) there is a graduate transition from inhibition to saturation (saturation is conventionally set to 1). Inhibitory units use a more rapid transition; hence, even a moderate input activity can induce shunting inhibition, reflecting their generally higher firing rates (Koch 1998).
Ascending inputs
Parameters which describe the sensory input areas are consistent with those used previously (Cuppini et al. 2010; Magosso et al. 2008; Ursino et al. 2009), the critical feature being that a stimulus evoked a pattern of activity within each subregion that resembled a “Mexican hat” function. Projections from non-AES sources were initially organized to produce SC output unit RFs consistent with those observed at 4 weeks of age in cat SC: auditory RFs were very large (encompassing most of a hemisphere) and visual RFs were approximately 200% of the adult size (Wallace and Stein 1997). The strengths of these projections were initially set so that a strong single-stimulus input would produce moderate SC activation. The projections of the SC inhibitory units were set to implement a robust WTA between the different modalities. The learning rates for the ascending projection were set to be relatively slow to reflect the relative maturity of this projection in the initial state. The individual saturation levels were given to obtain a model behavior (in terms of RF size and amplitude of SC neuron responses) after AES deactivation that was similar to that found empirically (Alvarado et al. 2008; Fuentes-Santamaria et al. 2009; Jiang et al. 2002; Jiang et al. 2001; Jiang et al. 2007).
Descending inputs
Projections from AES were initially set to zero strength. Learning rate parameters for the AES projection strengths were set so that the excitatory synapses potentiated more quickly than the corresponding inhibitory synapses. This arrangement prevented the inhibitory AES synapses from blocking any non-AES activity well before the establishment of significant descending connections, which would otherwise prevent further modification. The forgetting factor of the AES-SC projection was set so that spuriously converging projections from different modalities would decay in the absence of matching experience with cross-modal stimuli. The population saturation value for the excitatory AES projection was given to fulfill two criteria: i) the response to a single stimulus in the mature circuitry would not produce a saturated response in the SC neuron; ii) converging descending synapses were reinforced when derived from input areas representing the center of the RFs, but were weakened if they were on the borders (RFs contracted during the training phase to reach the adult size as a consequence). The saturation values for the inhibitory projections from the AES-sensitive interneuron populations (Ha, Hv) ensured that even moderate AES activity after training would completely inhibit non-AES influence on the SC.
Lateral connections
Lateral projections within the SC were initially set to zero strength. Learning rate parameters for lateral projections within the SC were assigned to be slower than the descending projection. The saturation values for lateral synapses were set to implement inhibitory surrounds after training, in agreement with observed cross-modal suppression in single neurons (Meredith and Stein 1986).
3. RESULTS
The model begins in an immature state (corresponding to approximately 4 weeks postnatal) in which the descending connections from AEV and FAES and lateral connections in the SC are silent (Fig 1A), so that the only functioning inputs to SC output units are from non-AES sources and the related interneuron populations Iv and Ia. The excitatory projection from non-AES input units to SC units is wide and weak in strength, though connections onto inhibitory units are established and robust. Consequently, SC output unit RFs are large and response magnitudes are weak. Because the inhibitory populations receiving input from ascending sources mutually inhibit one another, a type of “winners-take-all” (WTA) competition takes place between the sensory channels when cross-modal stimuli are simulated, resulting in an SC output unit response that reflects only the more robust sensory input. In this way, SC output neurons in the immature state are multisensory but do not show multisensory integration capabilities.
The sensory experiences that drive maturation are simulated by repeated presentations of modality-specific and cross-modal stimuli to the input regions (100,000 “exposures” overall). To replicate the complexity of a natural environment, stimuli are simulated at different locations in space on different trials. The training statistics were set as follows: 10% only visual stimuli, 10% only auditory, and 80% visual and auditory spatially coincident cross-modal stimuli.
The response properties of several multisensory neurons were analyzed in different maturational epochs: before the training phase, during training (i.e. at different levels of SC maturation), and in the mature phase. Then, a sensitivity analysis on the main model parameters is performed, to reveal their role in the development phase and point out the robustness of the obtained results. Finally, the effect of different input statistics (percentage of cross-modal vs. modality-specific inputs) on the population multisensory properties is analysed, to point out the environmental effect. In an additional set of simulations, we tested two anomalous maturational (i.e., rearing) conditions: one in which the exposures were specific only to a single stimulus modality (which simulates dark-rearing), and another in which the cross-modal exposures were always precisely separated in space (which simulates animals reared in anomalous environments where cross-modal stimuli are spatially disparate).
3.1 Analysis of the maturation process
Immature Phase
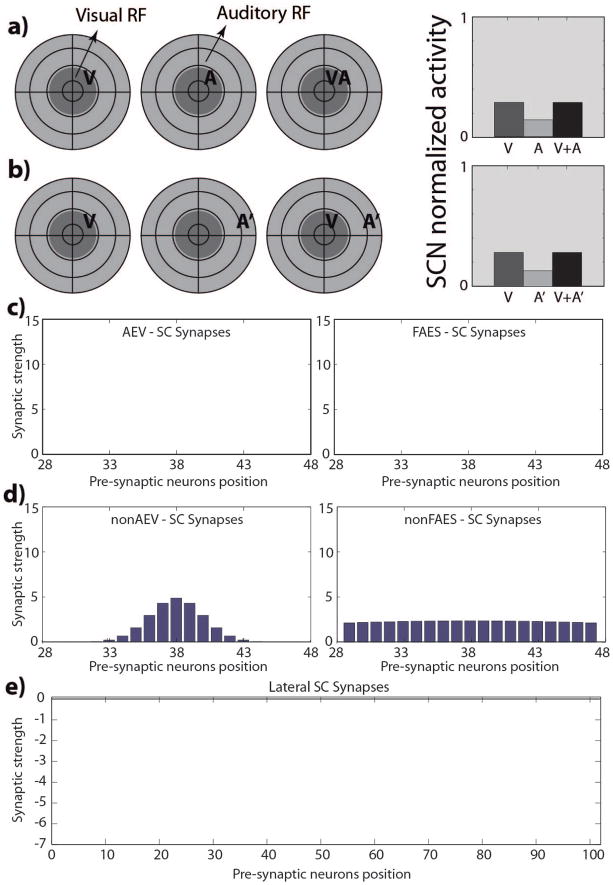
An initial set of simulations was performed to verify that SC output units produce sensory responses qualitatively similar to those obtained from real neurons in the cat 4 weeks after birth. The model was set to its initial state and presented with simulated visual, auditory, and visual-auditory stimulus combinations at different locations in space. Each SC output unit generated approximately the same response patterns due to the homogeneity in their initial conditions: they were overtly responsive to each of the sensory modalities (and were thus multisensory), but did not show the hallmark properties of multisensory integration. Spatially-concordant cross-modal stimuli generated responses no stronger than the most effective modality-specific component stimulus (regardless of intensity or dynamic range), and spatially-disparate cross-modal stimuli did not produce any inhibitory effect. Moreover, the units showed very large RFs and only modest sensory response magnitudes, which is in agreement with the empirical data (Wallace and Stein 2001; Wallace and Stein 1997). The model generated biologically-realistic responses in this phase largely because the ascending afferents are organized in a widespread but roughly topographic map (Fig. 2D); however, the descending projections (Fig. 2C) and lateral connections within the SC (Fig. 2E) were functionally inactive.
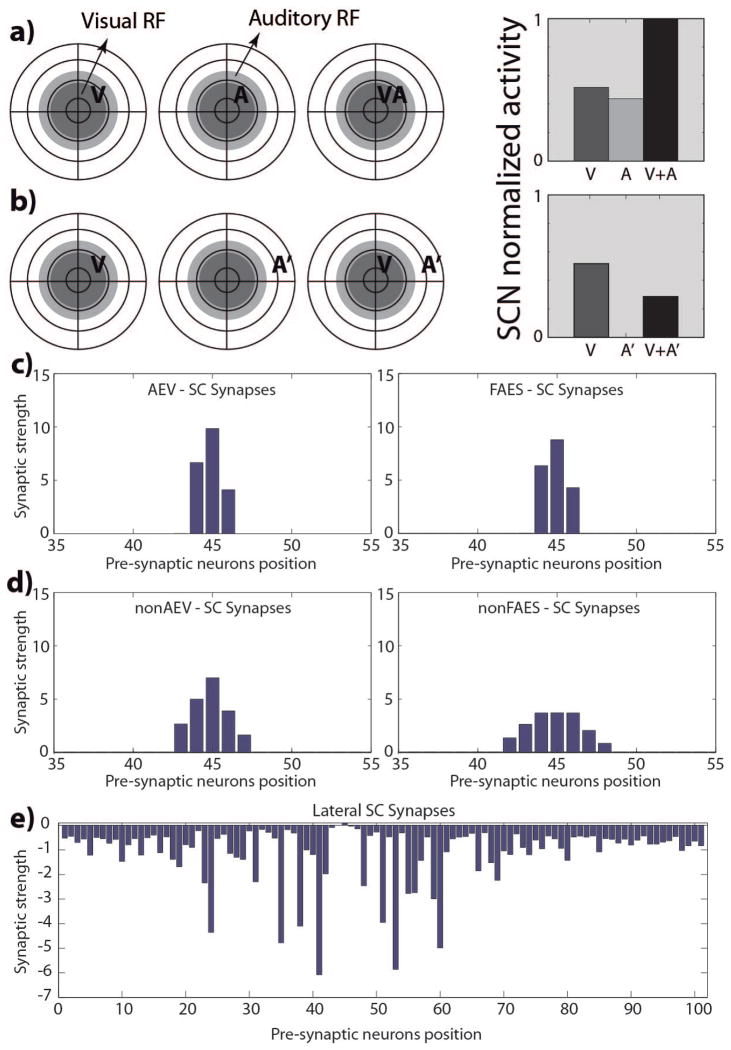
Fig. 2. SC responses and targeting synaptic strengths in the newborn.
Responses of a simulated immature SC neuron to different spatial configurations of modality-specific and cross-modal stimuli (a, b). The dark grey circles on the left represent qualitatively the visual RF of a SC neuron, while the light grey circles represent its auditory RF. We used this schematic representation to replicate that adopted by Stein and colleagues (see for example (Wallace and Stein 1997)) to facilitate the comparison between the simulated results and the data present in literature. The neuron is incapable of integrating its two cross-modal inputs and has responses equivalent to those of the stronger of the two. Figures 2.c and 2.d report the strengths of the incoming excitatory synapses that this SC immature neuron receives from the four unisensory input regions; in figures the x-axis represent the position of the pre-synaptic unisensory neurons, while the y-axis reports the synaptic strength of the connections. In this phase, the SC targeting synapses from AES subregions (panels c) are ineffective; on the contrary, the projections from non-AES input areas are diffuse and weak (panels d). Finally, in the neonatal condition, the SC doesn’t present any lateral interaction (fig. 2.e).
Maturation Phase
Experimental data show that real SC multisensory circuits adapt to the statistics of cross-modal experience, and beginning at about 4 weeks it is possible to find SC neurons that are not only multisensory but capable of multisensory integration (see Wallace and Stein 1997; Wallace and Stein 2000; Wallace and Stein 2001). This maturational profile of multisensory integration is a gradual process. The model replicated these results.
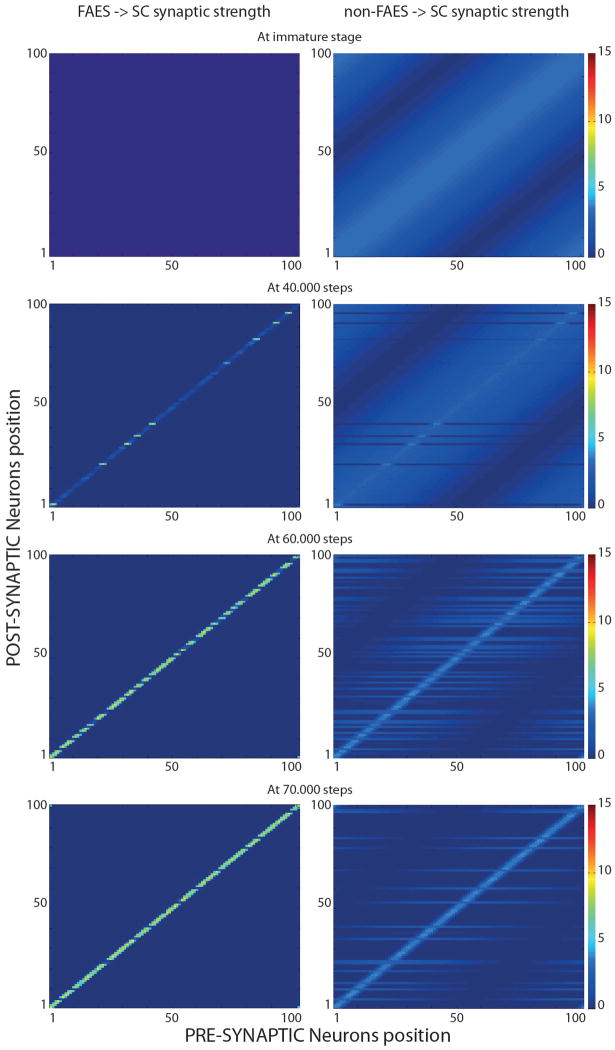
Fig. 3 provides four snapshots of the strengths of projections from auditory unisensory units to SC output units throughout this process (the visual weights change in a similar way). In each plot, the x-axis represents to the array of projecting units, the y-axis the array of receiving SC units, and the gray level represents the strength of the projection (lighter = stronger). The first integrating SC output units appear after roughly 40,000 exposures, and these units were the first to receive functionally active AES projections. The incidence of integrating output units gradually increased after this point. After 70,000 training exposures, just a few units are not able to integrate, and still presented immature response patterns. Interestingly, these units appear to never have developed significantly strong input from AES (such as neuron SCN24, see below), and still received widespread input from the ascending path (and therefore exhibit large RFs).
Fig. 3. SC targeting synapses in different phases of development.
In figures only FAES (left panels) and non-FAES synapses (right panels) are shown. AEV and non-AEV synapses exhibit similar development. In the initial condition (first row), non-AEV synapses are similar but narrower than non-FAES, while AEV synapses are inactive as FAES. X-axis and y-axis represent the position of the pre-synaptic and post-synaptic neuron respectively, while the grayscale denotes the strength of each synapse. Thus, each single row in a panel represents the synapses that target one specific SC neuron. In the immature stage (top row in the figure) the SC receives effective (but weak) synapses only from non-AES areas (specifically, non-FAES for auditory and non-AEV for visual inputs). These inputs provide the sole sensory drive to SC neurons. Connections from AES (i.e., AEV, visual area and FAES auditory area) are not effective, and the very large RFs of SC neurons, in the neonatal condition, reflect the diffuse nature of this projection. In an early stage of the development (after 40.000 steps, second row of panels in the figure), the model presented the first SC multisensory neurons with mature AES-SC synapses (light-grey stripes in the left figure), and pruned non-AES connections (right figure); these synaptic patterns led to a contraction in their RFs. These neurons resulted capable of integrating cross-modal stimuli. In an intermediate stage of the development (after 60.000 steps, third row in the figure), the simulated SC presented an increased number of integrative multisensory neurons, with similar synaptic patterns described above. In a late phase of development, there are just a few non-integrative multisensory neuron in the modeled SC, characterized by widespread projections from non-AES areas (light-grey stripes in the bottom right figure), and non-effective synapses from AES.
Adult-like Phase
The maturation phase is concluded after 100,000 simulated exposures of modality-specific and cross-modal stimuli. The network was then tested with the same evaluations conducted in the immature phase: modality-specific stimuli and their combinations when they were spatially concordant and spatially disparate. The network produced three types of SC output units: 80% were capable of both forms of multisensory integration (response enhancement and response depression); 18% of them were capable of only response enhancement; and 2% of them did not develop multisensory integrative capabilities, responding as if they were still in the immature developmental phase. We separately analyzed the performance of three different SC output units (SCN24, SCN38, and SCN45) representative of each of these three different outcomes. The strengths of all of the connections received by each unit are shown to identify their respective roles in the maturation process.
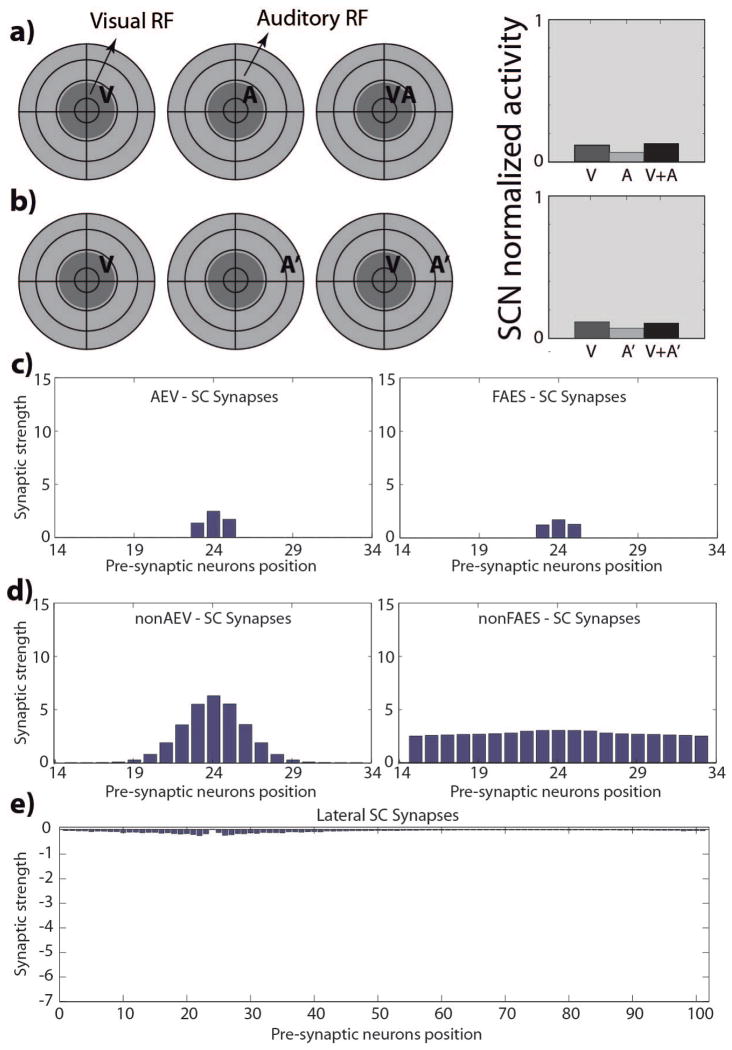
SCN24 (multisensory non-integrating)
Even after extensive cross-modal exposure, units in this category did not acquire multisensory integration capabilities despite retaining their multisensory nature (i.e., responding to more than one stimulus modality). Two cross-modal stimuli inside of their respective RFs did not evoke enhanced activity from these units compared to that evoked by the most effective modality-specific stimulus (Fig. 4A). Similarly, spatially disparate cross-modal stimuli did not evoke any response depression in these units (Fig. 4B). Finally, the responses elicited by the auditory stimuli in two different regions of space (compare responses in Fig. 4A and 4B), illustrate the substantial width of the auditory RF, which is still similar to that in the immature configuration. The reason for this result is that the projections from AES to the SC never potentiated (Fig. 4C), and as a consequence, neither they nor the non-AEV projections were refined (Fig. 4D), and so units in this category remained in their immature state. The lateral connections (Fig. 4E) were similarly not refined, thus explaining the lack of cross-modal depression.
Fig. 4. SCN24 responses and targeting synaptic strengths after development.
Responses of a simulated immature SC neuron, at the position 24 in the modeled SC area (SCN24), after 100.000 training steps, using the same stimulus configurations as used in Fig. 2(a, b). The neuron is incapable of integrating its two cross-modal inputs and has responses equivalent to those of the stronger of the two. The SC targeting synapses from AES subregions (panels c) are still too weak in this phase, as in the neonatal phase, to elicit an activity in the neuron. In figures the x-axis represents the position of the pre-synaptic unisensory neuron, while the y-axis reports the synaptic strength of the incoming connection. Also projections from non-AES input areas are in a neonatal fashion, diffuse but weak (figures 4.d), and the lateral synapses among SC neurons are still immature (fig. 4.e).
SCN38 (multisensory enhancement, but no multisensory depression)
This unit and other units of its type produce enhanced responses to spatially concordant pairings of visual-auditory stimuli (i.e., responses were greater than those to the most effective component stimulus), but did not show strong multisensory depression in response to spatially disparate cross-modal stimuli (the response was similar to the response to the within-RF stimulus alone, Fig. 5A–B), This contrasts with the response obtained when two spatially disparate stimuli belonging to the same modality were presented: in this configuration, strong (unisensory) depression results. This result parallels observations in the literature suggesting that multisensory and unisensory integration appear to obey different principles and have different contingencies, which were hypothesized to be due to differences in the underlying circuitry (Alvarado et al. 2009; Kadunce et al. 1997; Kadunce et al. 2001; Stein and Meredith 1993). In the model, these circuitry differences are explicit: pairs of within-modal stimuli interact within the unisensory afferent layers. In contrast, multisensory depression is primarily driven by the lateral connections between the SC output units, which do not properly mature in the case of SCN38 and similar units (Fig. 5F). However, the projections from AES units to the SC unit are strong and more precise in their distribution (Fig. 5D). The non-AES inputs also become more precise after training. As a consequence, the RFs shrink and align during maturation and SC output units generate enhanced responses to spatially concordant cross-modal stimuli.
Fig. 5. SCN38 responses and targeting synaptic strengths after development.
Responses of a simulated adult SC neuron, in the position 38 of the modeled SC area (SCN38), after 100.000 training steps. The neuron presents cross-modal enhancement (fig. 5.a), but, although it shows modality-specific depression (fig. 5.c), it doesn’t present cross-modal depression (fig. 5.b). In this phase the SC targeting synapses from AES subregions (panels d) are strong enough to drive the activity in the SC neuron and generate the multisensory integration. Projections from non-AES input areas are pruned in an adult-like condition and are stronger with respect to the newborn configuration (fig. 5.e). The overall amount of the lateral synapses of the SC targeting this neurons is still weak and this can be responsible for the lack of the cross-modal depression (fig. 5.f).
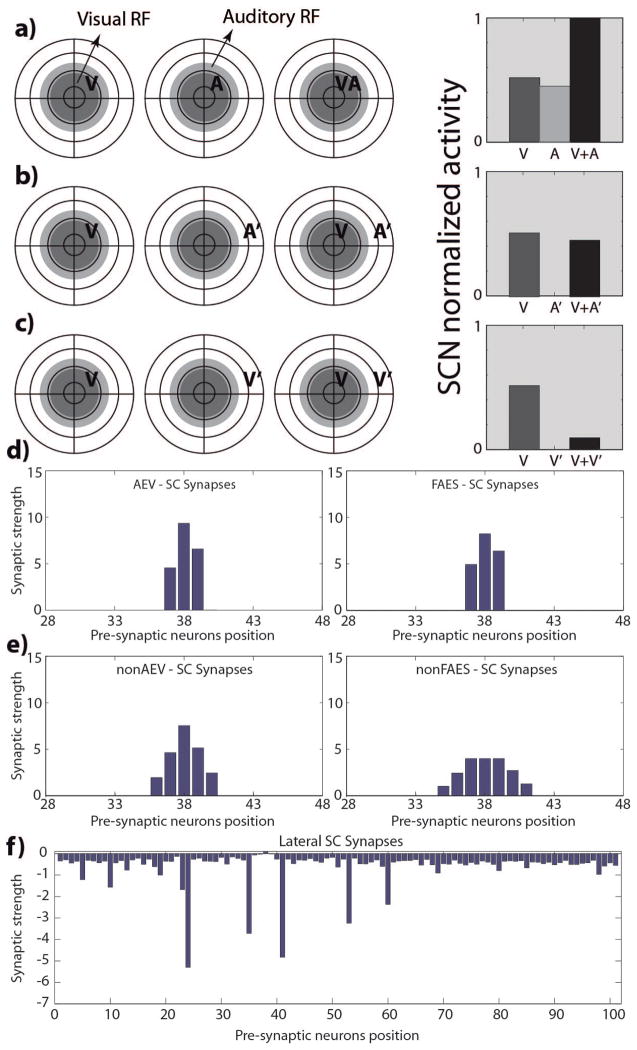
SCN45 (full multisensory integration capabilities)
The third type of SC output unit resulting from these simulations exhibits both multisensory enhancement and multisensory depression after the maturation phase (Fig. 6A–B). They also show within-modal depression for spatially disparate stimuli from the same modality. This response pattern is what is most typically observed in the SC (Kadunce et al. 1997; Meredith and Stein 1996; Stein and Meredith 1990; Stein and Meredith 1993). The difference between this outcome type and the others is that, not only have the AES projections become active and more refined, and paralleled by refinement in the non-AES projection, but also the lateral connections between the SC output units are developed (Fig. 6C–E). Projections from AES have become dominant, RFs have contracted, and are now aligned.
Fig. 6. SCN45 responses and targeting synaptic strengths after development.
Responses of a simulated adult SC neuron, in the position 45 of the modeled SC area (SCN45), after 100.000 training steps. The neuron presents cross-modal enhancement (fig. 6.a), and depression (fig. 6.b). In this phase the SC targeting synapses from AES subregions (panels c) are strong, and the projections from non-AES input areas are pruned in an adult-like condition (fig. 6.d). The lateral synapses in the SC are effective and generate the cross-modal depression (fig. 6.e).
Comparisons
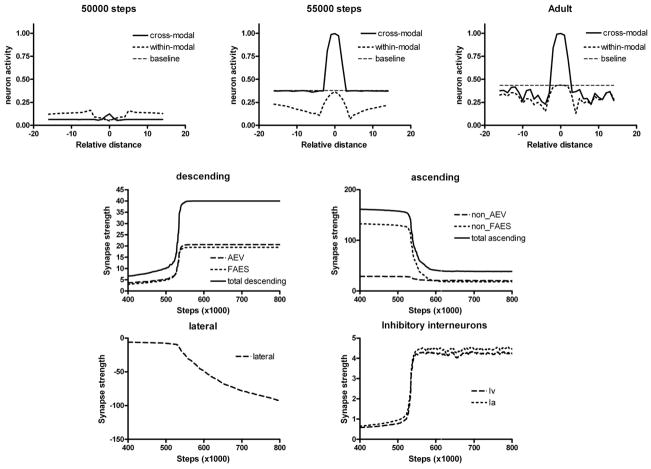
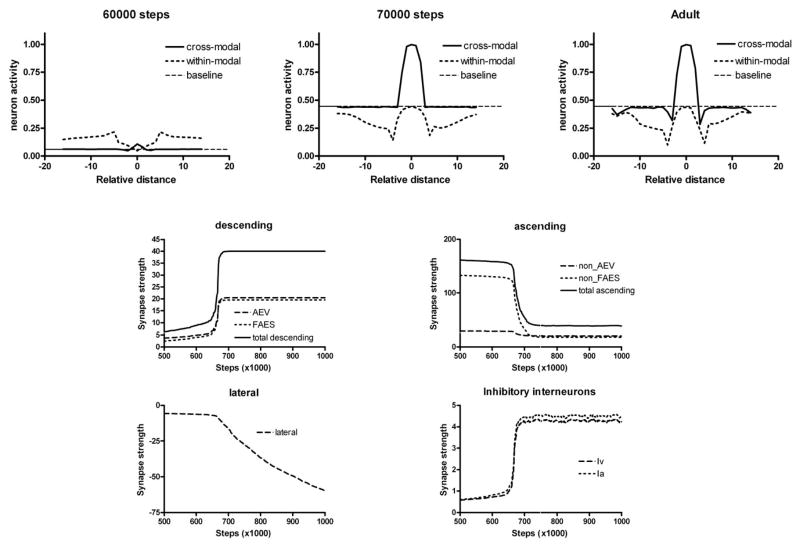
The developmental trajectories of SCN45 and SCN38 are detailed in Figs. 7 and 8, respectively. In the case of neuron SCN45, the AES projection potentiates slowly until a given value is reached, and then it quickly moves to saturation, as if there were two phases of development. Inhibitory projections driven by AES inputs show a delayed development but a similarly rapid change. As long as the AES inputs are weak (e.g., on training “step” 50000), the response of SCN45 to cross-modal and within-modal stimuli is poor and there is no evidence of integration. As soon as the AES inputs approach saturation (e.g., on step 55000), the unit shows strong multisensory enhancement and significant within-modal depression becomes evident, which originates from lateral inhibition in the unisensory input areas. However, at this maturation stage multisensory depression is still weak. It develops only later, when lateral connections within the SC become sufficiently negative (e.g., step > 70000). Fig. 8 shows that the maturation of SCN38 exhibits two main differences as compared to SCN45: multisensory integration develops only later (e.g., step 70000), and lateral connections remain insufficiently strong even after 100000 training steps.
Fig. 7. Maturation of SCN45 at different training steps.
The upper panels show the effect of two cross-modal and within-modal stimuli, at different spatial positions, on the neuron response. In all simulations, an auditory stimulus has been given at the center of the RF, and a second stimulus (either cross-modal or within modal) has been placed at different distances. The x-axis in the upper panels shows the distance between the two stimuli, while the y-axis is the activity of the neuron. Baseline refers to the neuron response to the central auditory stimulus given alone.
The bottom panels show the sum of all trained synapses entering the neuron (excitatory descending, excitatory ascending, lateral, inhibitory descending) at different training steps. It is worth noting that descending synapses start to increase abruptly after reaching a given threshold (approximately at step 52000), than rapidly assess at a saturation level. Ascending synapses decrease with training, while lateral synapses become negative, reflecting the predominance of inhibition. These synapses also exhibit the slower dynamics.
Fig. 8. Maturation of SCN38 at different training steps.
The meaning of panels is the same as in Figure 7. In this neuron, however, descending synapses develop later (approximately at step 65000) and the lateral synapses are still immature at the end, thus inducing just a poor cross-modal depression in the presence of strong within-modal depression.
Behaviour of a typical multisensory neuron
In this section, we summarize the behavior of a fully developed integrative neuron in the adult stage, to review the main characteristics of multisensory integration. It is worth noting that this behavior depends both on some characteristics present in the immature model (sigmoidal relationships, lateral synapses in unisensory areas) and some characteristics developed as a consequence of cross-modal inputs through Hebbian learning (descending synapses, lateral synapses in the SC, inhibition of the ascending path, refinement of RFs).
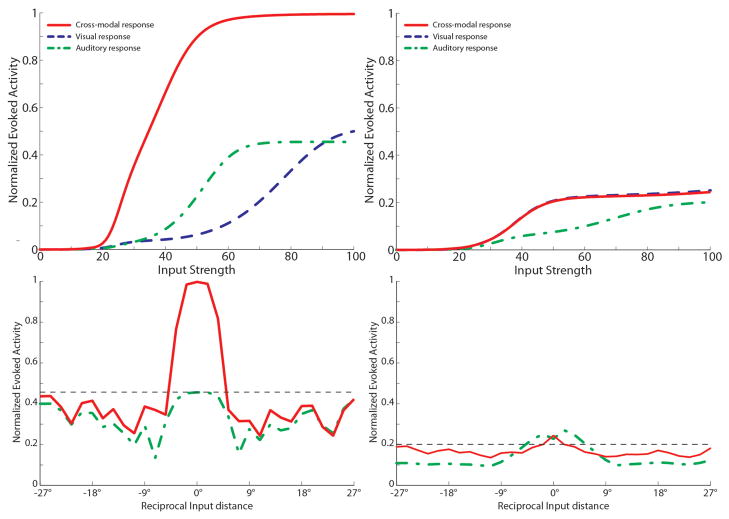
The behavior of a fully developed neuron is shown in Fig. 9. Here we show the response to different unisensory and paired cross modal inputs of different intensities (upper panels) and the response to within-modal and cross modal stimuli at different locations (bottom panels) in the intact network (left) and after elimination of the descending paths (bottom). The latter was simulated by setting the descending synapses at zero, a condition that mimics AES cortical deactivation (Jiang et al. 2006; Jiang et al. 2007).
Fig. 9. Behavior of a mature multisensory integrative neuron as function of AES cortex.
The figures show the activity of a SC neuron (in this case we used the SCN at position 47 in the network) in response to different inputs configurations, with AES active (left panels) and deactivated (right panels). In particular, here we present a neuron which has acquired both integrative capabilities during the development: cross-modal enhancement and multisensory depression. Dynamic Ranges (DRs) (upper figures). In all simulations the activity was assessed by stimulating the model with auditory (dash-dotted line), visual (dashed line) and multisensory (solid line) inputs at various intensities. The stimuli were presented in the center of the RF of the observed SC neuron. Note that with AES active, the simulated SC neuron shows multisensory enhancement in response to a cross-modal stimulation; if the AES is inhibited, the SC shows no multisensory integration, the unisensory responses are reduced by about 50% and the response to two cross-modal stimuli looks like the stronger unisensory one. Integration as a function of the position of two stimuli (lower panels). The figures show the response of the mature SC neuron to paired stimuli in different spatial configurations. Simulations are made by stimulating the model with an auditory (A) stimulus at the center of the RF of the observed SC neuron. The response elicited by this modality-specific stimulus (dashed thin lines) is then compared with those produced by coupling either a second auditory stimulus (dash-dotted lines) or a visual stimulus (solid lines) in different positions. The x axis displays the position of the second stimulus relative to the center of the RF. x = 0° means that both stimuli are at the center of the RF; increasing x means that the position of the second stimulus is increasingly farther from the RF. Results with AES active show: multisensory enhancement in the case of cross-modal stimulation inside the RF irrespective of the position of the two stimuli; no unisensory enhancement in case of a second within-modal stimulus inside the RF; multisensory and unisensory inhibition in the case of two stimuli far in space. In case of AES deactivated, the network shows the loss of multisensory enhancement in case of cross-modal stimulation inside the RF, and a slight inhibition in case of two stimuli of the same or different sensory modality far in space.
According to Fig. 9, multisensory integration is characterized by the presence of the following major properties: i) multisensoriality, i.e., the neuron exhibits a clear response to both visual and auditory stimuli; ii) enhancement, i.e., the response to two cross-modal stimuli is stronger than the response to each unisensory stimulus; iii) super-additivity, i.e., the response is greater than the sum of the individual unisensory responses; iv) inverse effectiveness: the percentage enhancement is maximal for mild stimuli and progressively decreases with stimuli of higher intensities; v) the dynamical range, defined as the difference between the maximal neural activity and the basal activity (i.e., activity with no inputs) is larger in case of cross-modal stimulation than within-modal stimulation (i.e., unisensory stimulation cannot induce a maximal activation of the SC neuron). vi) the neuronal response to a stimulus centered in the RF is affected by the presence of a second stimulus placed at a different position in space. More precisely, if the second stimulus is too far, no evident interference occurs. Conversely, at moderate distances a second cross-modal stimulus has a depressive effect.
The model can explain these properties through the following mechanisms: the presence of a sigmoidal characteristic in the unisensory neurons, which limits the within-modal dynamic range (property v); the presence of converging visual and auditory synapses from neurons in spatial register (produced by the Hebbian mechanism in presence of a sufficient statistics of cross-modal inputs) which explain both multisensory responses (property i) and enhancement (property ii); the presence of a sigmoidal relationship for SC neurons, which explain the inverse effectiveness effect (property iv) and the presence of a superadditive response at moderate intensities (property iii); the presence of lateral inhibitory synapses among SC neurons, learned through experience, which induce cross-modal suppression.
Finally, cortical deactivation eliminates most of the previous properties (except the first), making the SC behavior dependent only on the characteristics of the ascending path: multisensory enhancement and cross-modal suppression are lost, and the neuron behavior is similar to that in the immature phase, with just a reduced RF compared with childhood.
3.2 Sensitivity analysis on model parameters
To better understand the main mechanisms involved in the maturation process, we performed a sensitivity analysis, by using different patterns of parameters values in the simulation of the training period. In particular, we tested the influence of the different parameters both on the overall development of the network, specifically in terms of the speed of the network maturation, and on the emergent behaviors of the individual SC neurons at different phases of the training process.
The network showed a quite steady behavior to the variation of several parameters’ value. The main mechanism involved in the development is the reinforcement of the descending synapses. The faster the influence of AES cortex on the SC area is acquired, the sooner the network reaches its mature state. In this mechanism the population saturation value for the excitatory AES projection, WTOT max, can tune the speed of the process: greater values of WTOT max result in speeding up the maturation of the network. A similar effect, but with lesser effectiveness, is played by the learning rates for the AES projection strengths, and .
These three parameters are also responsible for the mature modality-specific dynamic ranges of the individual SC neurons: with higher WTOT max neurons can present higher dynamical ranges at the end of the training. The same effect can be obtained with higher learning rates for the AES projection strengths.
An important role is played by the maturation of the inhibitory mechanism realizes by the AES-sensitive interneuron populations (Ha, Hv): with a slow maturation of these projections (caused by weak learning rates, and ), the development of the network is quicker, because the excitatory effect of the non-AES neurons on the SC area is summed with the increasing effect of the developing AES projections. This results in a greater elicited activity in the SC area and, as a consequence of the learning algorithms, in a faster synaptic maturation in the network.
Finally, parameters driving the development of the ascending projections are critical just for the final strength of these projections, and mainly affect the responses of the SC neurons in case of deactivation of AES areas (i.e., in the conditions shown in Fig. 9 right panels), but do not affect the speed or the mature behavior of the network. The same influence is played by the parameters responsible for the maturation of lateral synapses among elements in the SC area: their learning rates can speed up the acquisition of the cross-modal depression, but this needs first the maturation of effective AES projections to begin, and so it takes place later during the maturation, once the network has already acquired the integrative properties.
Finally, the percentage of neurons developing multisensory integration remains substantially unaffected, being especially influenced by the statistics on the environment (see next section).
3.3 Statistics of cross-modal sensory experience determine the maturational outcome
In a separate set of simulations, we exposed the network to variations of stimuli and stimulus combinations to evaluate the model against extant data and to generate predictions for future experiments. Three variations were tested, and the maturational outcomes of the model were evaluated.
The ratio of multisensory/unisensory exposures
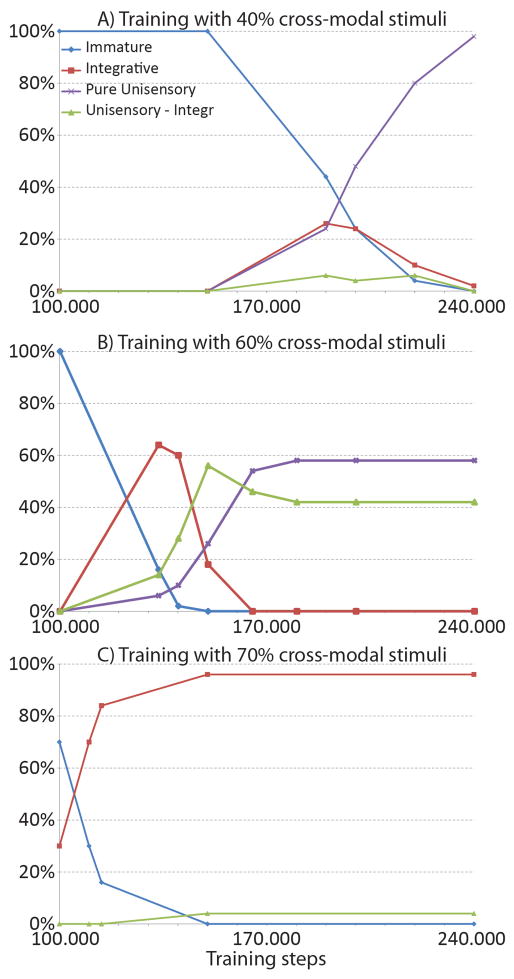
Our initial simulations used a ratio of 4/1 for multisensory/unisensory exposures (i.e., 80% of stimuli were cross-modal). The maturation process was then replicated by varying this value between 40% and 80%. Results are shown in Fig. 10. A relevant aspect is that, when the number of cross-modal inputs is too low, a significant number of unisensory neurons develop. In order to facilitate the analysis, neurons were subdivided into four main categories, on the basis of the response to individual stimuli, and paired cross-modal stimuli: immature, if they exhibit the same behaviour as in the immature stage (i.e., a weak multisensory response with no significant enhancement); purely unisensory if they responds significantly to just one modality; unisensory integrative, if they exhibit just one unisensory response, but some cross-modal enhancement; multisensory integrative, if they exhibit multisensory responses and a significant cross-modal enhancement. It is worth noting that only the first and fourth type was present in the final status at the end of the previous analysis. The latter class, in turn, can be further divided in neurons with cross-modal suppression or without cross modal suppression. Exemplary cases of neurons in the immature case and in the multisensory integrative cases have already been shown in Fig. 4, and in Figs. 5, 6 and 9, respectively. Exemplary cases of the neuron dynamic ranges for the two classes of unisensory neurons (with and without enhancement) are shown in Fig. 11.
Fig. 10. Development of emergent behaviors in the trained SC neurons as a function of the cross-modal input statistics.
Panels show the behaviors of the SC neurons in different phases of their maturation, in case of three trainings performed with different cross-modal input statistics. x-axis reports the training phases. y-axis shows the percentage of SC neurons showing a particular emergent behavior. Figure A) presents the sensory abilities of SC neurons in different development phases when the network is trained with just 40% of cross-modal stimuli. The network does not start its maturation since it has been stimulated by 150.000 inputs. Then the AES synapses become effective and the SC neurons begin to present cross-modal integrative capabilities. After about 200.000 training stimuli, immature, multisensory integrative, and unisensory SC neurons coexist in the network. As the training proceeds the multisensory integrative neurons evolve to unisensory, until a mature steady state is reached (at 240.000 stimuli) in which more than the 95% of the SC neurons are modality-specific, and just a few are multisensory. Figure B) presents the behaviors acquired by the SC neurons after a training with 60% of cross-modal inputs: here the network starts its maturation after 100.000 stimuli. As in figure A) in a first phase the network develops multisensory integrative (60%), unisensory (with and without integrative capabilities, 28% and 10% respectively) and still immature (2%) neurons. After 170.000 training stimuli, the network reaches a mature steady state in which there are only unisensory neurons (58% purely unisensory and 42% with integrative capabilities). Finally, Figure C) presents the abilities acquired if the SC is trained with 70% of cross-modal inputs: here the network reaches its maturation final state after about 150.000 stimuli. In this phase 96% of SC neurons are multisensory, while just 4% are unisensory. All of them show integrative capabilities.
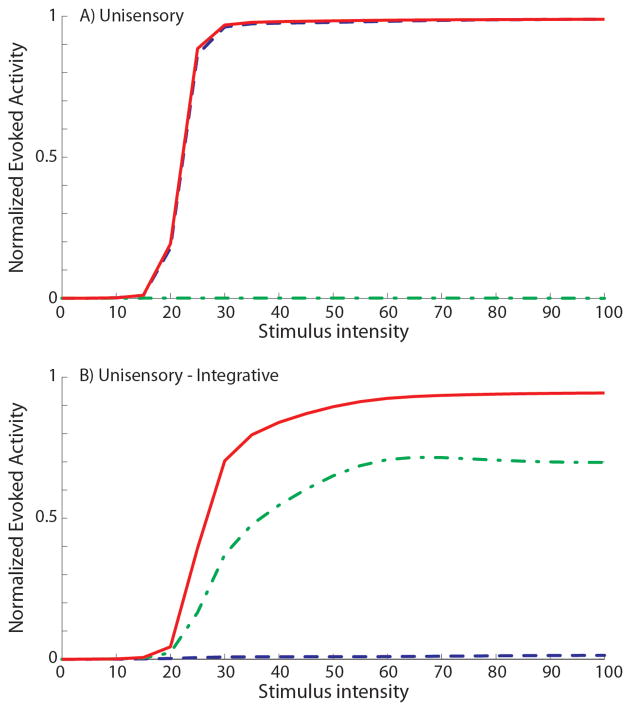
Fig. 11. New emergent behaviors in the mature neurons in case of trainings with low cross-modal input statistics.
The figures show the dynamic ranges of two SC neurons at the end of a simulated development in which the network has been trained with less than 60% cross-modal inputs. The upper panel reports the responses of a visual neuron, which does not show any integrative capability: a cross-modal stimulation elicits a response no stronger than the activity elicited by a visual stimulus. The lower panel shows the responses of a mature SC neuron which responds only to the auditory modality (visual inputs are almost ineffective), but when a visual stimulus is paired with an auditory one, the neuron presents a clear enhancement of its evoked activity. This neuron can be defined unisensory, but with integrative capabilities acquired along its maturation.
These tests confirm that the ratio of multisensory/unisensory exposures strongly affect the population of neurons. Two main factors emerge: first, the duration of the maturation phase strongly increases if the number of cross-modal input is reduced; second, if the number of cross-modal inputs is reduced below 65–70%, many neurons lose one of the two modalities and tend to become unisensory, although with a certain amount of enhancement. It is worth noting that many multisensory neurons appear in an intermediate maturation phase, but most of them subsequently lose one modality if the statistics of the training inputs exhibits an insufficient number of cross-modal stimuli.
Finally, when the percentage of cross-modal stimuli is higher than 70%, a large number of multisensory integrative neurons exhibit cross-modal depression (78% after a training period of 150.000 stimuli); this percentage falls to about 35% when the statistics of cross-modal inputs is reduced down to 40%. Moreover, in the last condition the number of multisensory neurons decreases with the training epochs; as a consequence, matured neurons drop also the ability to present cross-modal depression: the percentage is reduced down to 12% after 240.000 stimuli.
Modality-Specific Exposure
In these experiments we presented only modality-specific stimuli to the network, in trials that were either blocked or interleaved (i.e., never together). As result, the converging connections required for multisensory integration never develop. The reason is that, in the absence of exposure to cross-modal stimuli, projections derived from different modalities engage in a “push-pull” competition that leads to a stalemate; as a consequence, the descending projections never develop significantly and cannot assert their proper dominance over the ascending projections. Because of this competition, the modeled SC can develop multisensory units, but not multisensory integration capabilities. Similarly, these capabilities cannot develop in the model in the absence of experience. One aspect of these specific predictions has been tested and confirmed (Wallace et al. 2004).
Adaptation to anomalous cross-modal exposure
There was a weak topography present in the model’s initial state that reflects the biology of the neonatal SC, and it is believed that this topography is sharpened by spatiotemporally concordant cross-modal experiences typical of the normal environment. To evaluate the impact of an anomalous environment in this model, another set of simulations (beginning at the initial state) was conducted in which cross-modal exposure always simulated visual and auditory stimuli that were displaced by 40 units in the array. In the model this produced a maturational outcome in which many neurons showed misalignment of cross-modal RFs (see Figure 12), and in these cases, the optimal stimulus complex required to evoke multisensory integration was one in which the component stimuli were appropriately misaligned. The model also showed a slower development and a general decrease in the total number of neurons evidencing multisensory integration. After a training period (230.000 training stimuli) twice as long as normal, 42% of the multisensory neurons had misaligned RFs, and the vast majority (90%) of them were capable of both multisensory enhancement and depression. The remaining 58% of the neurons were not yet capable of integrating cross-modal stimuli. These findings matched well with the empirical literature describing the outcome of animals reared with spatially misaligned cross-modal stimuli (Wallace and Stein 2007). Again, this was due to AES inputs becoming dominant.
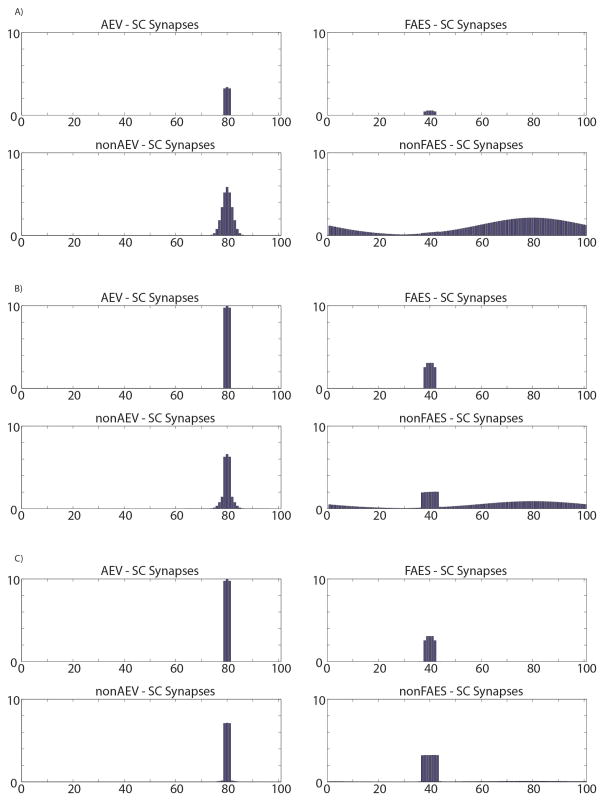
Fig. 12. SC targeting synapses in different phases of development with disparate cross-modal inputs.
The figure displays the maturation of synaptic connections between the four unisensory input areas and the neuron in position 80 in the SC area, as the result of a repeated exposure to two cross-modal inputs coincident in time, but not in space. The x-axis represents the position of the pre-synaptic unisensory neurons, while the y-axis reports the synaptic strength of the connections. In particular in this case the visual input is placed in the center of the corresponding RF, whereas the auditory inputs are placed in the RF of unit at position 40 (i.e., about 70° far from the corresponding visual inputs). Panel A) shows the synaptic strength in an early stage of this developmental process. The connections from AES regions are weak and the ascending projections still present an immature arrangement. In this phase the observed SC neuron is maximally responsive for visual and auditory inputs placed in the same position (position 80). Panel B) shows synapses in a late training phase. Finally, panel C) reports the final synaptic configuration. It’s worth noting that the center of the SC auditory RF is spatially shifted (in fact, the RF of the auditory neuron was placed at position 40 in the immature phase, but it is now centered at position 80), reflecting the stimulus position during the training period; as a consequence, the unisensory RFs (i.e. visual and auditory) are no longer overlapped.
4. DISCUSSION
Signals from different senses are integrated to improve performance and behavior so that animals can make the best use of the available information. How the neural architecture implements these computations is currently unknown. It is important to combine physiological research with modeling efforts to resolve this important hole in our knowledge. Here, the modeled system is the SC, whose circuitry, response properties, and behavioral links have been studied extensively.
Describing the operations of multisensory integration in the SC has been the focus of a number of recent models. The earliest focused on using information theory to compute the conditional probability (Anastasio et al. 2000; Anastasio and Patton 2003; Patton et al. 2002; Patton and Anastasio 2003) or the maximum likelihood (Colonius and Diederich 2004) that a target is present in the neuron’s RFs. More recent models focus on how excitatory and inhibitory interactions among multiple afferents are computed by a target neuron to yield multisensory integration (Rowland et al. 2007), and/or how the networks uses divisive normalization to compute the multisensory product (Ohshiro et al. 2011).
Although each of these models is effective in dealing with how multisensory integration takes place in the adult, none focus on how this capability is instantiated in this circuit. Multisensory integration is not the default state of the SC, as it is neither present in the neonate (Wallace and Stein 1997; Wallace and Stein 2001), nor in neonatal multisensory cortex (Wallace et al. 2006), and does not appear in the absence of experience with cross-modal cues (Wallace and Stein 2007; Yu et al. 2010). Not only must the fundamental neural scaffolding necessary for multisensory integration develop, but its organizational features must be refined during experience with cross-modal stimuli so that the principles guiding multisensory integration are appropriate for the environment in which it will be used (Yu et al. 2010). One of the compelling questions answered here is how sensory experience can transform the circuit from its immature state in which multisensory integration is lacking, to the adult stage in which it is robust.
The present study promotes a neural network model with several physiologically plausible assumptions that provide a basis for understanding the mechanisms underlying this maturational process: i) Early experience with cross-modal cues leads SC neurons to acquire multisensory enhancement capabilities as a consequence of the formation of descending excitatory synapses; ii) The neurons develop multisensory depression due to the formation of intrinsic lateral connections; iii) Synapses at the borders of the RFs of descending afferents remain weak, leading to the formation of narrow RFs in the SC; iv) Mature SC neurons lose some connections from non-AES regions because of the forgetting factor, and this reduces their RFs even in absence of input from AES; v) Because of the formation of descending inhibition that shunts ascending influences, SC multisensory responses become governed only by AES activity. The key concept is that the AES inputs, once active, “locks” neurons into a particular computational mode by dominating non-AES inputs.
It is important to note that the model shows that experience with cross-modal stimuli also leads to a synergy among converging afferents from the AES, that is critical for multisensory integration and closely parallels physiological findings (Alvarado et al. 2009). Experience with independent visual and auditory stimuli is not sufficient for this purpose, as simulated conditions in which the network receives only alternating modality-specific stimuli produce very weak descending projections that are not able to interact synergistically, and that are unable to mediate multisensory integration in SC neurons. The presence of a forgetting factor in the learning rule is critical, because it progressively reduces the strength of any inactive tectopetal inputs. A similar developmental failure of multisensory integration occurs in the model when the AES input is eliminated early in the training phase, an effect that parallels the results of early cortical lesions (Jiang et al. 2006).
The analysis of the network architecture and of the learning mechanisms allows the formulation of several testable predictions that should guide future physiological experiments. One of these concerns the speed of transition from the immature to the mature phase. The training rules adopted here depend on the activity of the SC output unit, and predict that during the initial developmental phase, training proceeds quite slowly. This is because descending synapses are still poorly formed, and the weak sensory responses of SC neurons primarily reflect ascending inputs. When descending connections achieve a functional threshold their target neurons become far more responsive to all external stimuli, dramatically accelerating learning in the circuit. The consequence of including saturation for connection strength is that, at maturity, the plasticity of the circuit is degraded and the rate of learning significantly slowed. Physiological experiments comparing the speed of acquiring multisensory integration capabilities at different maturational stages would provide a critical test of this prediction.
The model also assumes that multisensory enhancement and depression develop via two different mechanisms with different speeds. The former is linked to the maturational speed of AES projections and the inherent synergy among them resulting from the statistics of their cross-modal experience. This happens comparatively rapidly. The latter, however, depends on the functional development of intrinsic lateral inhibitory synapses, whereby neurons with distant RFs provide the stronger inhibitory inputs. Their maturational rates are slower. This leads to the prediction that multisensory depression appears later in maturation than multisensory enhancement. This remains to be determined physiologically.
Although the model predicts that SC neurons have a rapid transition from not-integrative to integrative states, the speed of this transition depends on the relative percentage of modality-specific and cross-modal stimuli they experience. Unisensory experiences in either modality reduce the strength of descending connections from the other modality, slowing this transition. Thus, in the unopposed presence of modality-specific auditory experience, such as would occur in dark rearing, the synaptic coupling of visual afferents would have been seriously weakened, and thereby precluding visual-auditory integration. A parallel condition would be expected of animals reared with compromised auditory experience. The relative vigor of visual (or auditory) responses after such rearing should be lower than normal, and the effect of manipulating the relative proportion of unisensory and cross-modal experience should be predictable.
The model predicts that repeatedly exposing animals to spatially disparate configurations of cross-modal stimuli should, over time, shift the RFs of SC neurons and thereby change their alignment, leading to more efficacious integration of spatially disparate stimuli consistent with the animal’s experience. This has already been noted in developing animals (see (Wallace and Stein 2007).
It should also be noted that the model predicts that GABA-initiated inhibitory mechanisms play a pivotal role in the maturation of the circuit. It is used by AES to suppress non-AES tectopetal sensory inputs, and in the absence of AES inputs, it is used by the stronger of the two non-AES tectopetal inputs to suppress the weaker. The model predicts that blocking the intrinsic GABAergic mechanisms through which non-AES inputs compete, would eliminate the normal effect of AES deactivation on multisensory integration. Whereas AES deactivation normally blocks SC multisensory integration (Alvarado et al. 2007; Alvarado et al. 2009; Jiang et al. 2001; Wallace and Stein 1994), this would no longer be possible once its mediating effect (i.e., intrinsic GABAergic inhibition) has been eliminated.
Despite the effectiveness of the model in explaining the major events leading to the maturation of SC multisensory integration, it has several limitations. The model does not explicitly represent the contributions of a cortico-collicular region neighbouring AES, the rostral portion of the lateral suprasylvian sulcus (rLS), which has been shown to modulate multisensory integration in a minority of adult SC neurons (Jiang et al. 2001). Furthermore, AES and rLS can substitute for one another when one is removed in the neonate (Jiang et al. 2006), suggesting that they have similar organizational features, developmental time courses, and experiential dependencies.
The model is also limited by the narrow set of the input statistics and the learning rates used here in the training paradigm. A greater number of alternative schedules are planned for the future, in which the relative percentage, disparity, and rate of sensory inputs are varied. Currently, the model dynamics are such that two stimuli must occur in very close temporal and spatial proximity to interact and to induce the maturation of multisensory integration. Although there is no empirical data regarding the impact of different cross-modal intervals and disparities on the maturation of multisensory integration, physiological data reveals that the spatial and temporal windows of integration are wider than tested here (Holmes and Spence 2005; Kadunce et al. 1997; Maruff et al. 1999; Meredith et al. 1987; Meredith and Stein 1996; Stein and Meredith 1990; Stein and Meredith 1993). It would be informative to examine how varying these factors affects the maturation of multisensory integration. Lastly, for simplicity it was assumed that all neonatal SC neurons had the same ascending synapses, the only difference being the nature and position of the stimuli presented in the training period. This is not anatomically likely, and the consequences of greater variations among neurons should be explored in the future.
Acknowledgments
Supported by NIH Grants NS036916 and EY016716.
Reference List
- Alvarado JC, Rowland BA, Stanford TR, Stein BE. A neural network model of multisensory integration also accounts for unisensory integration in superior colliculus. Brain Research. 2008;1242:13–23. doi: 10.1016/j.brainres.2008.03.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarado JC, Stanford TR, Rowland BA, Vaughan JW, Stein BE. Multisensory Integration in the Superior Colliculus Requires Synergy among Corticocollicular Inputs. J Neurosci. 2009;29:6580–6592. doi: 10.1523/JNEUROSCI.0525-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarado JC, Stanford TR, Vaughan JW, Stein BE. Cortex Mediates Multisensory But Not Unisensory Integration in Superior Colliculus. J Neurosci. 2007;27:12775–12786. doi: 10.1523/JNEUROSCI.3524-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anastasio TJ, Patton PE. A two-stage unsupervised learning algorithm reproduces multisensory enhancement in a neural network model of the corticotectal system. J Neurosci. 2003;23:6713–6727. doi: 10.1523/JNEUROSCI.23-17-06713.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anastasio TJ, Patton PE, Belkacem-Boussaid K. Using Bayes rule to model multisensory enhancement in the superior colliculus. Neural Comput. 2000;12:1165–1187. doi: 10.1162/089976600300015547. [DOI] [PubMed] [Google Scholar]
- Colonius H, Diederich A. Why aren’t all deep superior colliculus neurons multisensory? A Bayes’ ratio analysis. Cogn Affect Behav Neurosci. 2004;4:344–353. doi: 10.3758/cabn.4.3.344. [DOI] [PubMed] [Google Scholar]
- Cuppini C, Stein B, Rowland B, Magosso E, Ursino M. A computational study of multisensory maturation in the superior colliculus (SC) Experimental Brain Research. 2011:1–9. doi: 10.1007/s00221-011-2714-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuppini C, Ursino M, Magosso E, Rowland BA, Stein BE. An emergent model of multisensory integration in superior colliculus neurons. Frontiers in integrative neuroscience. 2010;4:1–15. doi: 10.3389/fnint.2010.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuentes-Santamaria V, Alvarado JC, McHaffie JG, Stein BE. Axon Morphologies and Convergence Patterns of Projections from Different Sensory-Specific Cortices of the Anterior Ectosylvian Sulcus onto Multisensory Neurons in the Cat Superior Colliculus. Cereb Cortex. 2009 doi: 10.1093/cercor/bhp060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes NP, Spence C. Multisensory Integration: Space, Time and Superadditivity. Current Biology. 2005;15:R762–R764. doi: 10.1016/j.cub.2005.08.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W, Jiang H, Stein BE. Two Corticotectal Areas Facilitate Multisensory Orientation Behavior. J Cogn Neurosci. 2002;14:1240–1255. doi: 10.1162/089892902760807230. [DOI] [PubMed] [Google Scholar]
- Jiang W, Wallace MT, Jiang H, Vaughan JW, Stein BE. Two Cortical Areas Mediate Multisensory Integration in Superior Colliculus Neurons. J Neurophysiol. 2001;85:506–522. doi: 10.1152/jn.2001.85.2.506. [DOI] [PubMed] [Google Scholar]
- Jiang W, Jiang H, Rowland BA, Stein BE. Multisensory Orientation Behavior Is Disrupted by Neonatal Cortical Ablation. Journal of Neurophysiology. 2007;97:557–562. doi: 10.1152/jn.00591.2006. [DOI] [PubMed] [Google Scholar]
- Jiang W, Jiang H, Stein BE. Neonatal Cortical Ablation Disrupts Multisensory Development in Superior Colliculus. Journal of Neurophysiology. 2006;95:1380–1396. doi: 10.1152/jn.00880.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadunce DC, Vaughan JW, Wallace MT, Benedek G, Stein BE. Mechanisms of Within- and Cross-Modality Suppression in the Superior Colliculus. J Neurophysiol. 1997;78:2834–2847. doi: 10.1152/jn.1997.78.6.2834. [DOI] [PubMed] [Google Scholar]
- Kadunce DC, Vaughan JW, Wallace MT, Stein BE. The Influence of Visual and Auditory Receptive Field Organization on Multisensory Integration in the Superior Colliculus. Exp Brain Res. 2001;139:303–310. doi: 10.1007/s002210100772. [DOI] [PubMed] [Google Scholar]
- Koch C. Biophysics of Computation: Information Processing in Single Neurons. Oxford University Press; New York: 1998. [Google Scholar]
- Magosso E, Cuppini C, Serino A, Di Pellegrino G, Ursino M. A theoretical study of multisensory integration in the superior colliculus by a neural network model. Neural Networks. 2008;21:817–829. doi: 10.1016/j.neunet.2008.06.003. [DOI] [PubMed] [Google Scholar]
- Maruff P, Yucel M, Danckert J, Stuart G, Currie J. Facilitation and inhibition arising from the exogenous orienting of covert attention depends on the temporal properties of spatial cues and targets. Neuropsychologia. 1999;37:731–744. doi: 10.1016/s0028-3932(98)00067-0. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Nemitz JW, Stein BE. Determinants of multisensory integration in superior colliculus neurons. I. Temporal factors. J Neurosci. 1987;7:3215–3229. doi: 10.1523/JNEUROSCI.07-10-03215.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Visual, Auditory, and Somatosensory Convergence on Cells in Superior Colliculus Results in Multisensory Integration. J Neurophysiol. 1986;56:640–662. doi: 10.1152/jn.1986.56.3.640. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Spatial determinants of multisensory integration in cat superior colliculus neurons. J Neurophysiol. 1996;75:1843–1857. doi: 10.1152/jn.1996.75.5.1843. [DOI] [PubMed] [Google Scholar]
- Ohshiro T, Angelaki DE, DeAngelis GC. A normalization model of multisensory integration. Nat Neurosci. 2011;14:775–782. doi: 10.1038/nn.2815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patton PE, Anastasio TJ. Modelling cross-modal enhancement and modality-specific suppression in multisensory neurons. Neural Comput. 2003;15:783–810. doi: 10.1162/08997660360581903. [DOI] [PubMed] [Google Scholar]
- Patton PE, Belkacem-Boussaid K, Anastasio TJ. Multimodality in the superior colliculus: an information theoretic analysis. Brain Res Cogn Brain Res. 2002;14:10–19. doi: 10.1016/s0926-6410(02)00057-5. [DOI] [PubMed] [Google Scholar]
- Rowland BA, Stanford TR, Stein BE. A model of the neural mechanisms underlying multisensory integration in the superior colliculus. Perception. 2007;36:1431–1443. doi: 10.1068/p5842. [DOI] [PubMed] [Google Scholar]
- Stein BE, Labos E, Kruger L. Sequence of changes in properties of neurons of superior colliculus of the kitten during maturation. Journal of Neurophysiology. 1973b;36:667–679. doi: 10.1152/jn.1973.36.4.667. [DOI] [PubMed] [Google Scholar]
- Stein BE, Labos E, Kruger L. Determinants of response latency in neurons of superior colliculus in kittens. Journal of Neurophysiology. 1973a;36:680–689. doi: 10.1152/jn.1973.36.4.680. [DOI] [PubMed] [Google Scholar]
- Stein BE, Meredith MA. Multisensory integration. Neural and behavioral solutions for dealing with stimuli from different sensory modalities. Annals of the New York Academy of Sciences. 1990;608:51–70. doi: 10.1111/j.1749-6632.1990.tb48891.x. [DOI] [PubMed] [Google Scholar]
- Stein BE, Meredith MA. The Merging of the Senses. MIT Press; Cambridge, MA: 1993. [Google Scholar]
- Ursino M, Cuppini C, Magosso E, Serino A, Di Pellegrino G. Multisensory integration in the superior colliculus: a neural network model. Journal of Computational Neuroscience. 2009;26:55–73. doi: 10.1007/s10827-008-0096-4. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Perrault TJ, Jr, Hairston WD, Stein BE. Visual Experience is Necessary for the Development of Multisensory Integration. J Neurosci. 2004;24:9580–9584. doi: 10.1523/JNEUROSCI.2535-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Sensory and Multisensory Responses in the Newborn Monkey Superior Colliculus. J Neurosci. 2001;21:8886–8894. doi: 10.1523/JNEUROSCI.21-22-08886.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Onset of Cross-Modal Synthesis in the Neonatal Superior Colliculus is Gated by the Development of Cortical Influences. Journal of Neurophysiology. 2000;83:3578–3582. doi: 10.1152/jn.2000.83.6.3578. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Cross-modal synthesis in the midbrain depends on input from cortex. Journal of Neurophysiology. 1994;71:429–432. doi: 10.1152/jn.1994.71.1.429. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Development of Multisensory Neurons and Multisensory Integration in Cat Superior Colliculus. J Neurosci. 1997;17:2429–2444. doi: 10.1523/JNEUROSCI.17-07-02429.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace MT, Carriere BN, Perrault TJ, Jr, Vaughan JW, Stein BE. The Development of Cortical Multisensory Integration. J Neurosci. 2006;26:11844–11849. doi: 10.1523/JNEUROSCI.3295-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Early Experience Determines How the Senses Will Interact. Journal of Neurophysiology. 2007;97:921–926. doi: 10.1152/jn.00497.2006. [DOI] [PubMed] [Google Scholar]
- Yu L, Rowland BA, Stein BE. Initiating the Development of Multisensory Integration by Manipulating Sensory Experience. The Journal of Neuroscience. 2010;30:4904–4913. doi: 10.1523/JNEUROSCI.5575-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]