Interleaved Variable Density Sampling with a Constrained Parallel Imaging Reconstruction for Dynamic Contrast-Enhanced MR Angiography

Abstract

For MR applications such as contrast-enhanced MR angiography (CE-MRA), it is desirable to achieve simultaneously high spatial and temporal resolution. The current clinical standard uses view sharing methods combined with parallel imaging; however this approach still provides limited spatial and temporal resolution. To improve on the clinical standard, we present an Interleaved Variable Density (IVD) sampling method that pseudorandomly undersamples each individual frame of a 3D Cartesian k_y-k_z plane combined with parallel imaging acceleration. From this data set, time-resolved images are reconstructed with a method that combines parallel imaging with a multiplicative constraint. Total acceleration factors on the order of 20 are achieved for CE-MRA of the lower extremities, and improvements in temporal fidelity of the depiction of the contrast bolus passage are demonstrated relative to the clinical standard.

INTRODUCTION

3D time-resolved MR angiography (MRA) is a widely used technique in clinic for the diagnosis of a variety of vascular disease (1). This technique often requires high spatial and temporal resolution to achieve better visualization of blood vessels as well as the ability to separate of arterial from venous phases. However, for applications that employ large sampling matrices, such as imaging the peripheral vasculature, the Nyquist criterion precludes the possibility of obtaining both goals simultaneously using conventional Fourier encoding techniques. Acquisition strategies that undersample k-space (with respect to the Nyquist criterion) and reconstruction algorithms that minimize artifacts are needed to advance the capabilities of MRI as a dynamic imaging modality.

To meet this need, several Cartesian acquisition methods, such as CAPR (2,3), TRIPPS (4), and random sampling (5), have been reported. CAPR and TRIPPS are similar approaches in that for every “time frame” that is reconstructed, the center of the phase-encoding plane (k_y-k_z plane) is fully sampled on the accelerated (CAPR) or original (TRIPPS) Cartesian grid, and the peripheral region is undersampled by collecting views either within radial sectors (CAPR) or along radial lines (TRIPPS). Over several time frames, the undersampled views are interleaved, producing an average k-t density in the periphery that is constant (CAPR) or falls off radially as approximately 1/k_r (TRIPPS). Random sampling is an alternative approach that can be customized to achieve more scattered views in the k_y-k_z plane with the corresponding artifacts less coherent in image space.

It is well understood that reconstructing undersampled k-space data leads to artifacts in image space. Reconstructing data from undersampled Cartesian acquisition methods in which views are grouped along radial sectors or lines, i.e. CAPR or TRIPPS, results in streak-like artifacts appearing in the images, similar to those observed when an undersampled radial stack of stars acquisition is reconstructed. However, reconstructing undersampled Cartesian data in which the views are randomly arranged results in less coherent, speckle-like image artifacts, rather than streaks (6). Several techniques have been developed to ameliorate the effects of undersampling. Temporal view-sharing methods (2,4,7) are techniques that are used to approximate high frequency data for a given time frame by using data from neighboring time frames prior to the image reconstruction of the selected time frame. However, these techniques may lead to compromises in the temporal resolution of the reconstructed images (8,9). Parallel imaging methods allow for acceleration of the data acquisition by regular undersampling, and use the coil sensitivity information to unfold the images in the reconstruction. Among these methods, the coil sensitivity information is used either explicitly (i.e. model-driven) such as SMASH(10), SENSE (11) and GEM (12), or implicitly (i.e. data-driven) such as AUTO-SMASH (13), VD-AUTO-SMASH (14) and GRAPPA (15). The combination of view-sharing and parallel imaging is able to improve the temporal resolution of dynamic MR imaging (2,3). Other reconstruction approaches to improve time-resolved imaging include model-based reconstruction methods (16,17) and constrained reconstruction methods including compressed sensing (5,18–20) and algorithms in the HYPR-like family (21–25). Compressed sensing requires that the reconstructed image be sparse in a known transformed domain, and HYPR methods have been demonstrated to be capable of suppressing radial undersampling artifacts while improving temporal fidelity during in-vivo studies (26).

We have recently proposed an Interleaved Variable Density (IVD) sampling method in which the 3D Cartesian k_y-k_z plane matrix is pseudorandomly sampled such that data from individual time frames are undersampled but when data from multiple time frames are combined a fully-sampled data set may be achieved (9). We also have proposed that incoherent artifacts caused by the pseudorandom undersampling may be suppressed by applying a multiplicative constraint similar to that used by the HYPR techniques (9,27). In this work, we present a novel technique that integrates parallel imaging (PI) with an IVD sampling method and the multiplicative constrained reconstruction, referred to here as IVD HYCR (HighlY constrained Cartesian Reconstruction). IVD HYCR uses the combined undersampling resulting from PI and IVD to allow total acceleration factors on the order of 20 relative to fully-sampled Cartesian imaging when applied to time-resolved contrast-enhanced peripheral vascular imaging.

THEORY

Sampling

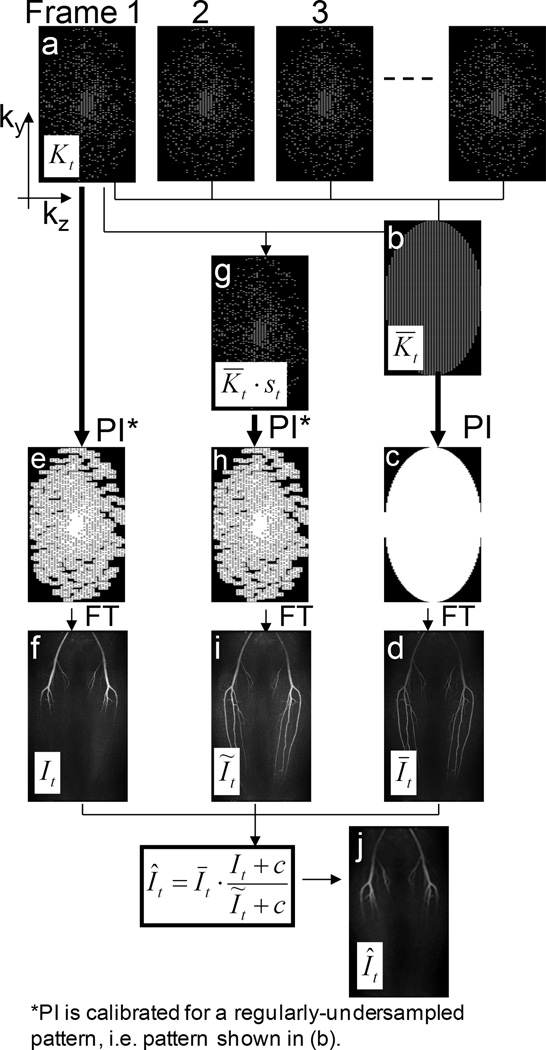
Let S(k_y,k_z) represent all view locations in the k_y-k_z (phase-encoding) plane that are sampled during the course of a 3D acquisition. Anticipating that a parallel-imaging reconstruction will be used, S(k_y,k_z) may have view spacing that violates the Nyquist criterion over the FOV to be imaged (in either or both phase encode directions), yielding a regularly-undersampled pattern as shown in Fig. 1(a). For the work shown here, a typical acceleration factor of 4 (2 × 2) was used. To further accelerate the acquisition, let s_t(k_y,k_z) be a single subset of these k-space locations sampled within the “time frame” t. This subset of views may be subsampled from S(k_y,k_z) in a pseudorandom fashion given by a pre-determined k-t density function, such as 1/k_r as shown in Fig. 1(b). Acceleration factors of 3–6 from the pseudorandom undersampling were empirically found to cause minimal incoherent undersampling artifacts producing a total acceleration factor in the range of 12–24 shown in Fig. 1(c). The pseudorandom subsampling patterns can be interleaved such that over N time frames, all sampling locations in S(k_y,k_z) are sampled at least once. The sampling pattern is calculated for each individual scan based on patient-specific FOV (i.e. k_y-k_z matrix size), parallel imaging factor along k_y and k_z directions, and the desired temporal resolution while maintaining the 1/k_r fall-off. This acquisition strategy is referred to as Interleaved Variable Density (IVD) sampling.

Figure 1.

(a) All view locations that are sampled during the course of an acquisition, with parallel imaging acceleration factor of 4. (b) A given k-t sampling density (1/k_r) over N time frames. (c) An example of the IVD sampling pattern for an individual frame with an additional acceleration of 4 (total acceleration of 16).

Reconstruction

In this section, we first assume that S(k_y,k_z) meets the Nyquist criterion (e.g. no parallel-imaging acceleration) and demonstrate the principles of the multiplicative constrained reconstruction. After that, the integration of parallel imaging is presented.

Let K_t(k_y,k_z) be the k-space data acquired at locations s_t(k_y,k_z) during a time frame t. If S(k_y,k_z) met the Nyquist criterion, then a Fourier transform of the K_t(k_y,k_z) would yield an image, I_t, albeit one with spatially blurring due to the variable sampling density and incoherent artifacts due to the unacquired “holes” left in k-space.

Let K̅_t(k_y,k_z) be the k-space data integrated over a sliding window of N frames. This integrated data set (one per time frame) also could be reconstructed using a Fourier transform to yield an image Ī_t, free of spatial blurring and incoherent artifacts, but temporally blurred due to integrating data over several time frames. It should be noted that the integration uses a density correction factor to account for the variable k-t sampling density.

Let K̃_t(k_y,k_z) be the subset of k-space points from the integrated data set corresponding to the same sampled locations given by s_t(k_y,k_z):

$${\tilde{K}}_t(k_y,k_z)={\overline{K}}_t(k_y,k_z)·s_t(k_y,k_z).$$ [1]

In this formulation, s_t(k_y,k_z) can be treated as the sampling function used to subsample K̅_t(k_y,k_z). A Fourier transform of these data yields an image Ĩ_t. It should be noted that both I_t and Ĩ_t have the same data sampling pattern s_t(k_y,k_z) and therefore have the same blurring and similar incoherent artifact due to the point spread function of s_t(k_y,k_z).

Finally, these three images (per time frame t) are combined in a multiplicative constrained reconstruction described by the following function:

$${\widehat{I}}_t={\overline{I}}_t·\frac{I_t+c}{{\tilde{I}}_t+c},$$ [2]

where c is a small regularization constant to avoid zero division. This operation has the effect of imposing the dynamic characteristics of I_t upon the spatially sharp and fully-sampled constraining image Ī_t. The undersampling artifacts that appear in I_t and Ĩ_t tend to cancel because they are derived from the same undersampling function, s_t(k_y,k_z). This multiplicative constraint is similar to the image-space variation of HYPR reconstruction described in (23), and similar to the “local reconstruction” variation of HYPR described in (22).

The integration of parallel imaging is achieved by applying a parallel imaging reconstruction method prior to the multiplicative constrained reconstruction. More specifically, to unfold the aliased images, a parallel imaging reconstruction method is applied to generate the images I_t, Ī_t and Ĩ_t prior to combining these into the final image Î_t. Unaliasing coefficients may be derived from a separate calibration scan or from data acquired during the acquisition. A diagram summarizing the proposed method with parallel imaging is shown in Fig. 2.

Figure 2.

Diagram for the Cartesian constrained parallel imaging reconstruction method. Step 1:(a,b) Data from a subset of all the time frames are combined, using a sliding window average to create a composite data set that has uniform undersampling on the 2 × 2 acceleration grid, K̅_t. (c) parallel imaging is used to synthesize the missing data points. (d) An FFT of these data produces the temporally-blurred, high spatial resolution, high SNR image, Ī_t. Step 2:(e) For data in each undersampled time frame K_t, parallel imaging is used to synthesize points off the 2 × 2 acceleration grid. (f) An FFT of these data produce the high temporal resolution, low spatial resolution, high SNR image I_t. Step 3:(g) The K̅_t are subsampled using the IVD pattern for that time frame t. (h) parallel imaging is used to synthesize points off the 2 × 2 acceleration grid. (i) An FFT of these data produce the image Ĩ_t. Step 4:(j) The final image Î_t is calculated using Eq. [2].

In the experiments presented here, all parallel imaging (PI) reconstructions were performed using ARC (GE Healthcare, Waukesha, WI, USA): proprietary software that employs an indirect calibration procedure (28) to generate unaliasing coefficients in k-space together with hybrid-space data synthesis, described in Ref. (29) as “Method 5”. The software was instructed to generate unaliasing coefficients for the regularly undersampled pattern S(k_y,k_z) (not s_t(k_y,k_z)), using data from a pre-contrast acquisition in which the center of k-space was fully sampled. In the synthesis phase, the software was instructed to apply these coefficients to data sets K_t, K̃_t and K̅_t. As demonstrated in the experiments below, applying parallel imaging in such a fashion suppresses coherent (parallel imaging) artifacts; the missing data propagates into the intermediate reconstructed images as incoherent artifacts, but such artifacts are largely suppressed in the final image by the constrained reconstruction (application of Eq. [2]).

MATERIALS AND METHODS

Contrast-enhanced MR angiography exams of the calf were performed on ten normal volunteers using 3T clinical MRI scanners (Signa HDx and Discovery MR750, GE Healthcare, Waukesha, WI, USA) with two different commercially available coils (8-channel and 32-channel Torso Arrays, GE Healthcare, Waukesha, WI, USA) to validate the proposed methods. The protocol was IRB approved and informed consent was obtained from all volunteers. A range of parallel imaging and IVD undersampling factors were investigated to determine parameters that yielded maximum spatial and temporal resolution while maintaining clinically acceptable image quality. Following this parameter optimization, two volunteers (referred to below as volunteer 1 and volunteer 2) were imaged to demonstrate the technique optimized for each of the two coils. The first experiment, using an 8-channel torso coil, demonstrates the process of integrating parallel imaging into the multiplicative constrained reconstruction, as well as the feasibility of the proposed method. The second experiment, using a 32-channel torso coil, was used to demonstrate the capability of improving the spatial resolution and SNR using the proposed method and a coil array with higher channel count.

Volunteer 1 was imaged using an 8-channel torso coil. A 15× acceleration factor was achieved: 4× parallel imaging acceleration (R = 2 along L/R and A/P directions) and 3.8× IVD acceleration. Acquisition parameters included: matrix size of 512 (freq) × 298 (phase) × 70 (slice) over an FOV of 480 (S/I) × 278 (L/R) × 126 (A/P) mm³ for a spatial resolution of 0.94 × 0.94 × 1.8 mm³ with 75% fractional readout (zero-filled in the reconstruction), BW= ±62.5kHz, and TR/TE= 5.6/2.0 ms. Twenty-four time frames, resolved at 7.7 seconds, were acquired over 3 minutes. In the reconstruction, a kernel of size W_x × W_y × W_z = 3 × 7 × 7 was used to determine the calibration coefficients for the parallel imaging reconstruction. The data were reconstructed in two ways for comparison. First, the data were processed using the proposed method with sliding window length of 9 frames for Ī_t. Second, the data were also reconstructed using view-sharing (nearest temporal-neighbor interpolation within a window length of 9 frames). In both methods, this temporal window was cropped for the first and last four frames.

Volunteer 2 was imaged using a 32-channel torso coil. A 23× acceleration factor was achieved: 4× parallel imaging (R = 2 along L/R and A/P directions) and 5.8× IVD. Acquisition parameters included: matrix size of 480 (freq) × 290 (phase) × 120 (slice) over an FOV of 480 (S/I) × 290 (L/R) × 120 (A/P) mm³ for an isotropic resolution of 1.0 mm³, 75% fractional readout (zero-filled in the reconstruction), BW= ±62.5kHz, TR/TE= 5.2/1.9 ms. Twenty-four time frames were resolved at 8.0 seconds. A kernel size of W_x × W_y × W_z = 3 × 5 × 5 was used for estimating the calibration coefficients for the parallel imaging reconstruction. As above, the data were reconstructed with the proposed method (11-frame sliding window for Ī_t), and also with a view-sharing (11-frame window) reconstruction. An ROI was placed on the popliteal trifurcation and the signal was measured within the ROI as a function of time and compared for the proposed reconstruction method vs. the view sharing approach. In addition, a zero-filled parallel imaging reconstruction (zero-filling followed by parallel imaging synthesis) was performed on the same data set to generate images for comparison. The zero-filled parallel imaging reconstruction used the weighting coefficients that were determined by a calibration for a regularly-undersampled pattern, i.e. S(k_y,k_z).

RESULTS

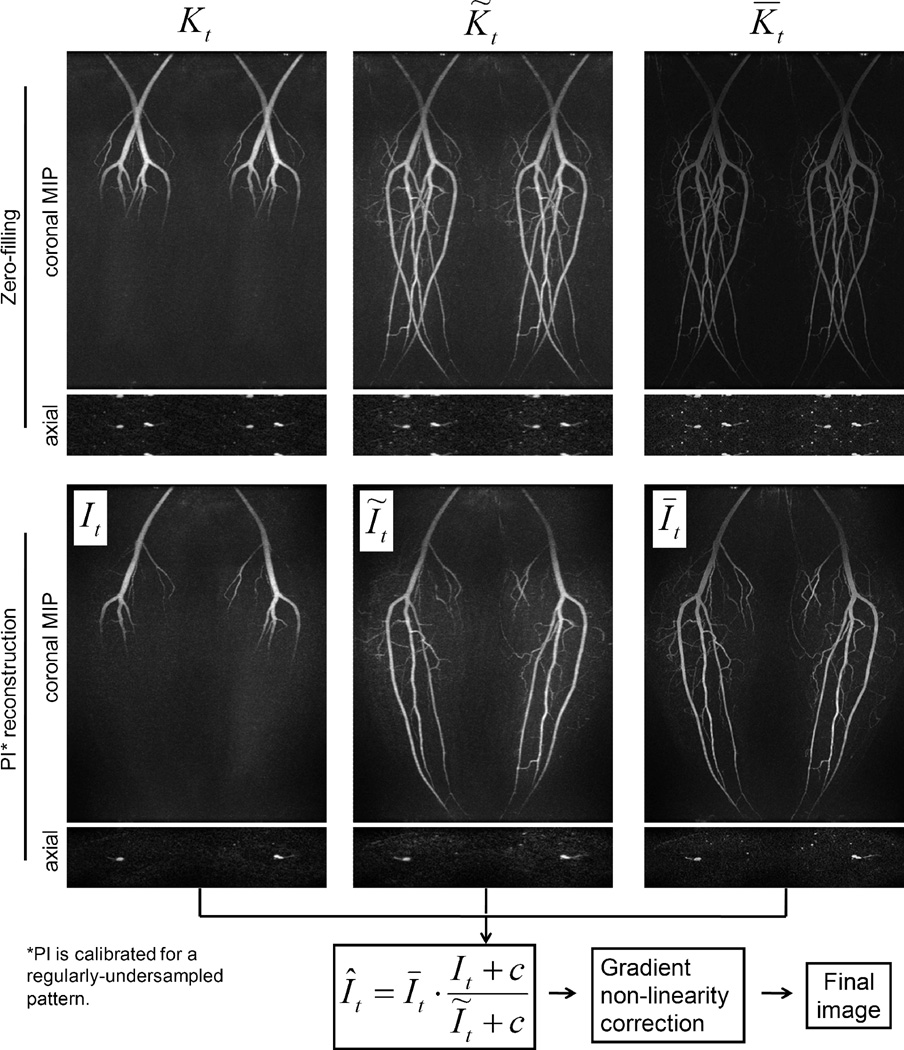
In order to demonstrate that the proposed reconstruction effectively removes coherent aliasing in intermediate images and incoherent aliasing in the final image, data from the first normal volunteer exam was used. Fig. 3, first row, shows the data sets K_t, K̃_t and K̅_t reconstructed with zero-filling FFT. The images exhibit coherent aliasing in an axial slice and coronal MIP. The second row shows the same data reconstructed with parallel imaging. These images are unaliased, although the images reconstructed from the IVD-undersampled data (columns 1 and 2) exhibit the expected blurring and incoherent artifacts. It is worth pointing out here that the image I_t is temporally resolved, i.e. only arteries in the superior half of the FOV were enhanced; the image Ī_t is sharp and free of spatial artifacts, but temporally blurred, i.e. arteries over the entire FOV were enhanced; the image Ĩ_t is derived from Ī_t using the same sampling function s_t(k_y,k_z), yielding similar spatial blurring and incoherent artifacts as in I_t. Finally, the application of the constrained reconstruction (Eq. [2]) is able to impose the accurate temporal dynamics of I_t onto the constraining image Ī_t, generating a final image Î_t of both high spatial and temporal resolution, shown in Fig. 4(a).

Figure 3.

Intermediate images in the proposed reconstruction method. Images in the first row are reconstructed using zero-filling and exhibit coherent aliasing artifacts due to the regular undersampling by parallel imaging. Images in the second row are reconstructed using parallel imaging calibrated for a regularly-undersampled pattern. These images do not have coherent aliasing (parallel imaging) artifacts, although images I_t and Ĩ_t exhibit expected spatial blurring and incoherent artifacts due to the IVD undersampling. However, these artifacts can be suppressed in the constrained reconstruction in the next step (bottom equation). Note that although images shown here are coil-combined (for demonstration purpose), the multiplicative constrained reconstruction is applied in a coil-by-coil basis (see Discussion). Also notice that the compensation for non-linear gradient effects is not applied to the intermediate images shown here; instead it is only applied to the image Î_t after the constrained reconstruction and coil combination.

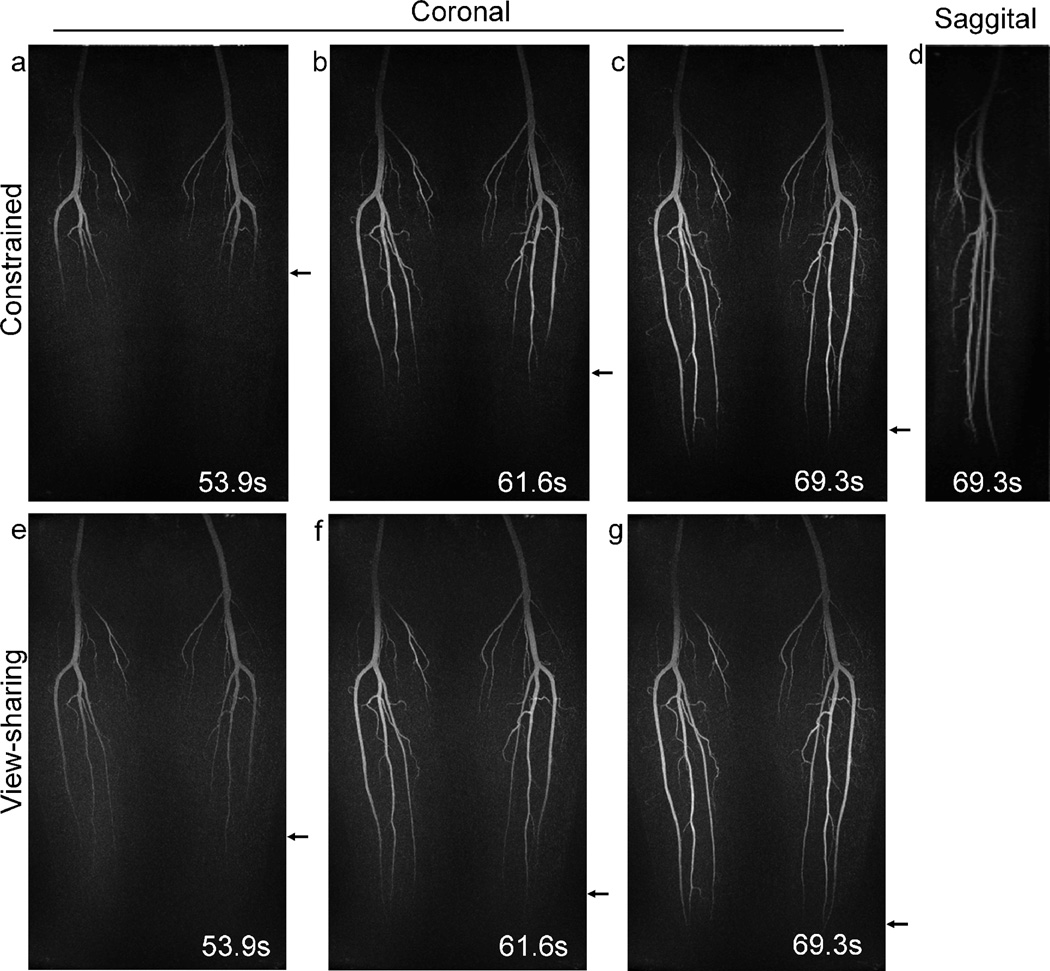
Figure 4.

Results obtained from volunteer 1. The constrained reconstruction method implemented in conjunction with parallel imaging shows better depiction of the progressive filling of the popliteal and tibial arteries than the view-sharing method, as indicated by the arrows. A sagittal reformat (d) of the constrained reconstruction image confirms that no aliasing is present.

Fig. 4 shows example time-frame images from the time-resolved exam of volunteer 1 acquired with the 8-channel coil. Coronal MIP images of three consecutive time frames demonstrate improved temporal depiction of the contrast bolus (Fig. 6(a–c) arrows). Sagittal reformats of the data for a single leg show improved visualization of small vessels (Fig. 6(d)). No aliasing artifacts due to parallel imaging undersampling are observed in the images. Images reconstructed with view-sharing are also provided for comparison (Fig. 6(e–g)). As shown by the arrows, the movement of the bolus from superior (top) to inferior (bottom) is better depicted in the constrained reconstruction. The temporal blurring effect of the view-sharing technique is typically manifested as early enhancement of the vessels, which can be best observed by comparing Fig. 4(a) and (e).

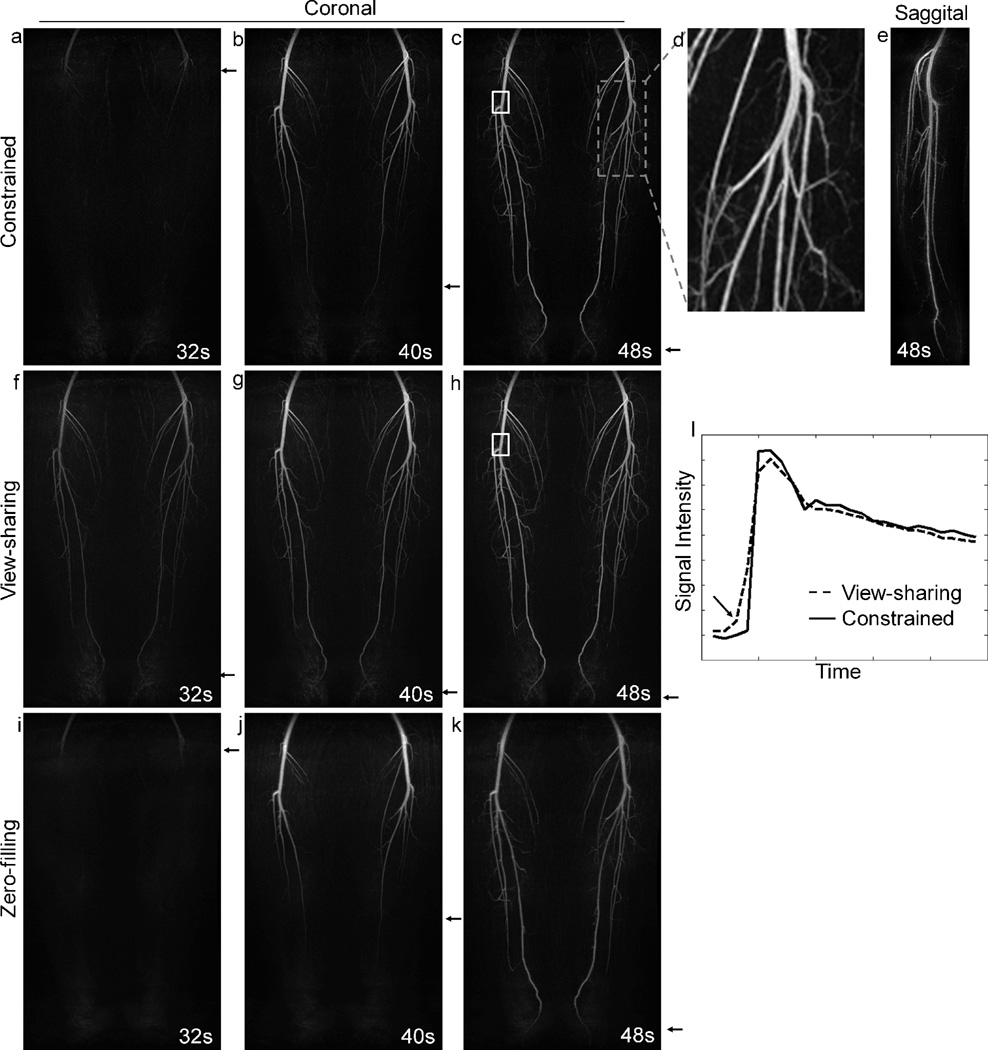
Higher resolution and image quality were achieved using the proposed method with a 32-channel phased array coil. Images acquired with decreased voxel size (isotropic spatial resolution) are shown in Fig. 5 for volunteer 2. Fig. 5(a–c) shows three consecutive arterial time frames produced using the proposed constrained reconstruction method. The high spatial resolution can be appreciated by observing an enlarged image of the gray dashed box (Fig. 5(d)), where small arteries are well visualized. A sagittal reformat (Fig. 5(e)) demonstrates the improved resolution in the slice-encoding dimension compared to Fig. 4(d). The view-sharing method (Fig. 5(f–h)) results in significant temporal blurring, as indicated by the arrows showing the leading edge of the contrast bolus. The images produced by zero-filling (Fig. 5(i–k)) suffer from spatial artifacts and blurring; however, since the zero-filling method does not employ any temporal interpolation, these images can be considered as temporally closest to the truth. As shown by the arrows, the constrained reconstruction provides more accurate temporal depiction of the filling arteries than the view-sharing method. This effect can be best appreciated by comparing Fig. 5(a), (f) and (i). In both the constrained reconstruction image (Fig. 5(a)) and the zero-filling image (Fig. 5(i)), only a small portion of the popliteal artery are enhanced at t = 32s; however, in the view-sharing (Fig. 5(f)), the arteries are enhanced over the entire FOV. The improved temporal fidelity is also demonstrated by plotting the signal within the selected ROI (white box in Fig. 5(c) and (h)) as a function of time as shown in Fig. 5(l). Fig. 5(l) compares the waveforms obtained from both the constrained reconstruction and view-sharing methods. As indicated by the arrow in Fig. 5(l), view-sharing causes a temporal blurring at the sharp uptake. It is worth noting that no apparent coherent aliasing (parallel imaging) artifacts are seen in the zero-filled images (Fig. 5(i–k)). This supports the previous results in Fig. 3, suggesting that coherent aliasing artifacts can be effectively removed by parallel imaging when it is calibrated for a 4-fold regularly-undersampled pattern and applied to the 23-fold undersampled data set.

Figure 5.

Results obtained from volunteer 2. (a–c) Coronal MIP images from the constrained reconstruction showing good depiction of the arteries filling with contrast material. (d) An enlarged image of the dashed box with small arteries well visualized. (e): sagittal reformat. (f–h) Same data set reconstructed using view-sharing method and parallel imaging. (i–k) Same data set reconstructed using zero-filled parallel imaging calibrated for a regularly-undersampled pattern. Note that no apparent coherent aliasing are present in these images. (l) Waveforms obtained from view-sharing and constrained reconstruction, with the former method causing temporal blurring indicated by the arrow.

DISCUSSION

In this work, a method for high acceleration that utilizes IVD Cartesian sampling, parallel imaging, and a constrained reconstruction was described and feasibility demonstrated in-vivo. The increased acceleration provided using this method can be utilized to improve spatial resolution and/or temporal resolution, depending on the specific clinical need. While all the studies presented in this work used moderate IVD undersampling factors of 4 to 5 to maintain minimal level of incoherent undersampling artifacts, it can be expected that increased temporal resolution may be achievable in other applications where the clinical need for very high temporal resolution may drive a different trade-off with spatial resolution (30,31).

When performing parameter optimization, a range of parallel imaging and IVD undersampmling factors was studied to understand the trade-offs between these two forms of acceleration. It was found that if parallel imaging is not used (i.e. R = 1), requiring a higher IVD undersampling factor, then residual undersampling artifacts in the final image was observed, manifesting when visualized as a time-series movie as “flashing” effect. With the 8-channel torso coil, a parallel imaging factor of 4 (2 along each direction) can be achieved with no apparent coherent aliasing artifacts. While keeping the total undersampling factor the same, the integration of parallel imaging can decrease the burden for the IVD undersampling, which results in a significant reduction of the flashing effect. Using a 32-channel coil, 1.0 mm isotropic resolution can be achieved because of the increased SNR from the higher channel count. More recent work (32) has demonstrated the feasibility of using parallel imaging R = 6 with this coil to achieve 1.0 mm isotropic resolution and temporal resolution of about 5 sec/frame, with total acceleration factor of about 36. Generally speaking, the maximum acceleration factors (parallel imaging factor and IVD factor) depend on the spatial-temporal sparsity of the specific application, coil used, and particular clinical requirements.

As demonstrated experimentally, parallel imaging can reconstruct highly undersampled data with coherent aliasing artifacts in intermediate images I_t and Ĩ_t significantly reduced. If one were to attempt to produce the highest quality image reconstructed from only the highly undersampled time frame data K_t, one might consider using a much larger kernel size and calibrating for the actual sampling pattern s_t(k_y,k_z), rather than the pattern of the integrated data S(k_y,k_z). We found that this results in much (100×) longer reconstruction times, and may suffer from noise amplification. Such an observation does not imply that the method proposed here is the optimal reconstruction of the data, but it does appear to be a practical solution for rapid reconstruction with good image quality.

Conceivably, Eq. [2] could be applied either before or after coil-combing processing. In this work, for each time frame t, intermediate images (I_t, Ī_t and Ĩ_t) were generated for each coil, and Eq. [2] was applied on a coil-by-coil basis followed by a sum-of-squares reconstruction (33). The reason for applying Eq. [2] prior to coil combination is that each coil image is sparser than the coil-combined image, and thus is better conditioned for the multiplicative constrained reconstruction.

It is also worth noting that the coil images I_t, Ī_t and Ĩ_t, are complex-valued. In applications such as CE-MRA, phase information is typically not needed. Therefore, one way to enforce real-positive constraint is to use the magnitude of these complex coil images. Alternatively, a low-resolution phase map can be obtained from Ī_t, and subsequently used to rephase all the images and enforce the real-positive constraint. The SNR of the final images reconstructed using the rephasing method was found to be better than the SNR of the final images reconstructed using the magnitude method, because in the former method, incoherent background noise from the imaginary channel is excluded. This rephasing method is essentially the noise reduction application of homodyne detection (34).

Due to the division operation, two types of regularization methods were included in the proposed method. First, in Eq. [2], a small constant c (usually chosen as 2% of the maximum value of Ī_t) may be added as a base-line shift in the image intensity to avoid zero division. Second, an empirically-chosen maximum value may be used to threshold the ratio image to further avoid noise amplification, prior to the multiplication with Ī_t. For all the calf studies in this work, the threshold value was chosen between 1.5 and 2. Other regularization methods to further reduce noise amplification will be investigated in future work.

The proposed constrained reconstruction (HYCR) can be considered as a Cartesian implementation of the HYPR technique (21–23), in which a time-averaged, high spatial resolution, high SNR image is multiplied by a lower spatial resolution, high SNR, temporally-resolved weighting image. The application of the HYPR principle to Cartesian-sampling was first proposed in Ref. (35); however that earlier work did not describe interleaved sampling or parallel imaging (it was targeted at combining a number of fully sampled data sets to improve SNR) and it applied the multiplicative constraint in hybrid space, not image space.

Besides Cartesian approaches, several non-Cartesian techniques have also been developed for time-resolved CE-MRA that aim to improve image quality by reducing coherent artifacts compared to undersampled Cartesian methods. These techniques include radial acquisition approaches, such as Stack-of-Stars (SOS) (36) and VIPR (7,37), and spiral acquisitions (38,39). However, for some applications such as peripheral run-off CE-MRA, Cartesian sampling trajectories offer some important advantages over non-Cartesian approaches. First, spin-warp phase-encoding (acquiring parallel lines of k-space along the readout direction) is very robust to k-space trajectory errors caused by gradient timing errors and eddy-currents. Second, parallel readout acquisitions permit establishment of a single frequency-encoding direction, which enables application of filters to limit aliasing of signal from outside the field of view (FOV), typically along the longest axis of the acquisition volume. Third, separable view spacing in the two phase-encoding directions enables scan times to be reduced by tailoring the FOV to the anatomy. Fourth, parallel imaging techniques for Cartesian acquisitions are more computationally efficient than similar parallel imaging reconstruction techniques for non-Cartesian acquisitions.

A number of previous studies that compared a constrained reconstruction to standard view-sharing techniques have been performed and reported (8,9,40). Keith et al. (8) and Busse et al. (9) used the concept of temporal point-spread-function (PSF) in numerical simulations, where the temporal input function was a step function. They both demonstrated that the constrained reconstructions provided superior temporal fidelity by better resolving rapidly occurring dynamic processes. These results are consistent with the in-vivo results reported here, which suggest a reduction in temporal blurring compared to the view-sharing reconstruction. It should be recognized that the relative performance of the proposed method and the view-sharing approach may also depend on spatial and temporal characteristics including vessel structures and contrast kinetics, which are application-dependent. Generally, the depiction of smaller vessels requires more high frequency data for accurate depiction and view-sharing methods are expected to produce more temporal blurring than the constrained method when applied to smaller vessels. It should also be noted that the optimal sampling pattern for constrained reconstruction and view-sharing reconstruction may be different. For example, we found that the 1/k_r density is optimal for the HYCR algorithm, while other sampling density functions may be optimal for view-sharing reconstruction in terms of minimizing the temporal footprint.

There are other reconstruction methods that can be used for dynamic MR imaging, such as k-t BLAST/SENSE (17) and compressed sensing (5). k-t BLAST/SENSE are model-based techniques that utilize a training data set to guide the reconstruction of the high resolution time frames, and have shown improved spatial and temporal resolution primarily in cardiac cine MRI, because the cardiac motion is approximately periodic and can be approximated with a few Fourier coefficients. However, such feature does not exist for CE-MRA. In contrast, the proposed method in this work generates a time-averaged composite image from the undersampled time frame, and thus does not require the acquisition of the training data set. Conventional compressed sensing methods explore the sparsity in the spatial domain, or transformed-spatial domain, as demonstrated in Fig. 9 in Ref. (5), but it may be time-consuming for time-resolved MRI with large matrix sizes. Differently, the proposed method in this work aims to explore the sparsity in the spatial-temporal domain, and preliminary results from other applications which involve spatially non-sparse images have been reported (25,41). In the mean time, there are some recent works on using compressed sensing framework to explore the sparsity in the spatial-temporal domain, such as k-t SPARSE (42) and k-t FOCUSS (43).

Iterative HYPR-like approaches can be employed to enforce data consistency, further improve temporal waveform fidelity and increase robustness to motion (24,44). The iterative formulation of Eq. [2] can be written as:

$${\widehat{I}}_t(n+1)={\widehat{I}}_t(n)\cdot \frac{I_t+c}{{\tilde{I}}_t(n)+c},$$ [3]

with the first image estimation being the composite image, i.e. Î_t(0) = Ī_t, and Ĩ_t(n) being the re-sampled Î_t(n) at location s_t(k_y,k_z). This iterative formulation has similarities to some expectation maximization algorithms, such as the Multiplicative Algebraic Reconstruction Technique (MART) (45) that was first developed for x-ray imaging.

CONCLUSION

In this work, a novel interleaved variable density Cartesian sampling method and an image reconstruction technique that combines a multiplicative constrained reconstruction with parallel imaging (IVD HYCR), was described. It was demonstrated in volunteers that the technique is capable of producing high spatial resolution and high SNR images while maintaining high temporal resolution in small, enhancing vessels. The proposed data acquisition and image reconstruction methods can also be applied to other areas where higher temporal resolution is needed.