Distinguishing Ordinal and Disordinal Interactions

Abstract

Re-parameterized regression models may enable tests of crucial theoretical predictions involving interactive effects of predictors that cannot be tested directly using standard approaches. First, we present a re-parameterized regression model for the linear X linear interaction of two quantitative predictors that yields point and interval estimates of one key parameter – the cross-over point of predicted values – and leaves certain other parameters unchanged. We explain how resulting parameter estimates provide direct evidence for distinguishing ordinal from disordinal interactions. We generalize the re-parameterized model to linear X qualitative interactions, where the qualitative variable may have two or three categories, and then describe how to modify the re-parameterized model to test moderating effects. To illustrate our new approach, we fit alternate models to social skills data on 438 participants in the NICHD Study of Early Child Care. The re-parameterized regression model had point and interval estimates of the cross-over point that fell near the mean on the continuous environment measure. The disordinal form of the interaction supported one theoretical model – differential susceptibility – over a competing model that predicted an ordinal interaction.

Methods for testing interactive effects of predictors using multiple regression analysis are widely known and used. Several excellent texts (e.g., Aiken & West, 1991; Cohen, Cohen, West, & Aiken, 2003) discuss how to test quantitative X quantitative, quantitative X qualitative, or qualitative X qualitative interactions. If a significant interaction is detected, follow-up analyses are typically required to characterize the nature of the interaction, such as whether the interaction is ordinal or disordinal. A re-parameterized regression model that distinguishes clearly between ordinal and disordinal interactions and obviates the need for involved follow-up calculations to determine point and interval estimates of key parameters would be a useful adjunct to standard approaches. Here we propose such an approach and illustrate it using data for gene by environment (GXE) interactions. Although we selected GXE data for the demonstration, the approach advocated herein is general in nature and thus is applicable to a wide range of research domains in which statistical interactions are evaluated using regression analysis.

After discussing briefly why our new approach may be of use, we show how a linear regression model with a linear X linear interaction of two predictors can be re-parameterized to estimate parameters that characterize the ordinal or disordinal nature of the interaction and then adapt this approach to qualitative X quantitative interactions. We also apply our approach to a set of relevant data to demonstrate the unique outcomes obtained using our modeling approach.

Statistical Interactions in Substantive Research

Our efforts here were motivated by the fact that researchers often formulate interaction hypotheses imprecisely. If interaction hypotheses are phrased non-specifically, misfit between theoretical formulations and trends in data may go unrecognized. If methods for testing specific interaction hypotheses were developed, researchers could be challenged to provide more detail regarding the expected form of interactions. Without clear predictions, no definitive evidence regarding confirmation or disconfirmation of theoretical predictions is generated, aside from statistical significance of the interaction effect. Indeed, researchers often present disordinal interaction plots that appear inconsistent with their theories, but theory-data mismatch is rarely, if ever, noted. Armed with clearer predictions, misfit between predictions and results might be more readily recognized, leading to the need to revise theories to accord better with data.

One limitation of most research investigating interaction effects is lack of detail regarding the predicted form of the interaction. Researchers could specify whether an ordinal or disordinal interaction is predicted. For example, educational researchers might want to estimate the age at which one early intervention treatment becomes more effective than another, so policy makers can tailor interventions to children of appropriate ages. Or, Lynn (1999) offered a controversial maturational theory of intellectual development that holds that earlier maturation in females will lead to higher performance relative to males on intelligence tests at early ages. But, by mid to late adolescence, males will begin to outperform females due to their later maturation and larger brain size. Research contexts such as these suggest that interactions should be disordinal, with a cross-over point at some point on age.

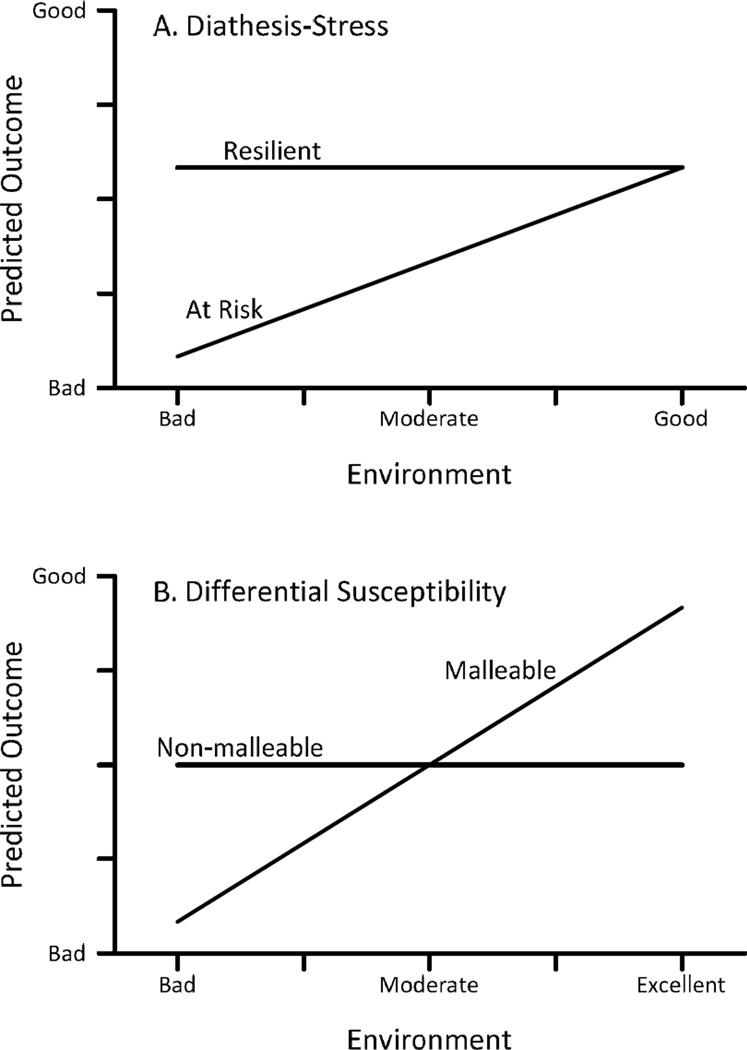
One domain in which specific forms of interaction differentiate theoretical positions is the study of GXE interactions. Many GXE studies(e.g., Caspi et al., 2002, 2003) are based on a diathesis-stress model of environmental action (Belsky et al., 2009). Under diathesis-stress (Zuckerman, 1999), individuals with a “ risk or vulnerability” gene are affected negatively by poor environments, whereas individuals with a different version of the same gene are relatively unaffected by environments. In the best environments, persons with differing polymorphisms may exhibit similar levels of behavior, but behavior of the groups diverges with worsening environmental conditions. Diathesis-stress therefore leads to prediction of a GXE interaction with the ordinal form shown in Figure 1A.

Figure 1.

Predicted outcomes of GXE interaction under (A) diathesis-stress, and (B) differential susceptibility.

Recently, two research teams advanced a different theoretical model, differential-susceptibility (Belsky, 1997, 2005; Boyce & Ellis, 2005; Ellis, Boyce, Belsky, Bakermans-Kranenburg & Van IJzendoorn, 2011). Differential-susceptibility also leads to prediction of a GXE interaction, but one disordinal in form. Under differential-susceptibility, persons carrying a so-called risk allele may simply be more malleable. From this perspective (and in accord with diathesis stress), persons with a putative high-risk allele should exhibit poorer outcomes in poor environments and similar outcomes to persons with a low-risk allele in average environments. However, the model suggests that, in very good environments, persons with a putative high-risk allele will show outcomes that are superior to persons with the low-risk allele. This theoretical conceptualization leads to prediction of the disordinal, or cross-over, interaction in Figure 1B. Thus, diathesis-stress and differential susceptibility theories make identical predictions about the differing slopes for the two gene allele groups; what distinguishes predictions under the two models is the location of the cross-over point (cf.Figure 1).

Methods for testing interactions reflecting differential susceptibility have been proposed (e.g., Belsky et al., 2007; Belsky & Pluess, 2009; Ellis et al., 2011) and applied to GXE data (e.g., Bakermans-Kranenburg, Van IJzendoorn, Pijlman, Mesman, & Juffer, 2008). Our goal is to develop a more direct test of competing predictions regarding the ordinal vs. disordinal nature of an interaction that is widely applicable across research domains, including GXE studies.

Regression Equations with a Linear X Linear Interaction

Standard Parameterizations

A linear regression model with a linear X linear interaction can be written as:

$$Y_i=B_0+B_1{X}_{1i}+B_2{X}_{2i}+B_3(X_{1i}·X_{2i})+E_i$$ (1)

where Y_i is the score of person i (i = 1, … , N) on the dependent variable, B₀ is the intercept, the B_j (j = 1, 2, 3) are regression weights for the three predictors, X_1i and X_2i are scores of person i on predictors X₁ and X₂, respectively, and, E_i is a stochastic error score. The third predictor in Equation 1 is the product of X_1i and X_2i and carries the interactive effects of X_1i and X2_i if the two lower-order effects (i. e., X_1i and X2_i) are included in the equation (cf.Cohen, 1978).¹

Equation 1 can be fit using raw scores on X₁ and X₂, but regression coefficients and standard errors for X₁ and X₂ can be rather volatile if the product term is in the equation. To reduce these problems, many experts (e.g., Cohen et al., 2003), recommend centering X₁ and X₂ at their respective means, leading to:

$$Y=B_0^{*}+B_1^{*}{X}_1^{*}+B_2^{*}{X}_2^{*}+B_3^{*}(X_1^{*}·X_2^{*})+E$$ (2)

where $X_1^{*}\text{and}{X}_2^{*}$ are sample-mean-centered versions of X₁ and X₂, respectively, asterisks on $B_0^{*}$ through $B_3^{*}$ indicate weights for mean-centered predictors, and other symbols were defined above. Sample-mean-centering often reduces correlations among predictors and leads to many interpretive advantages (see, e.g., Aiken & West, 1991; Cleary & Kessler 1982).

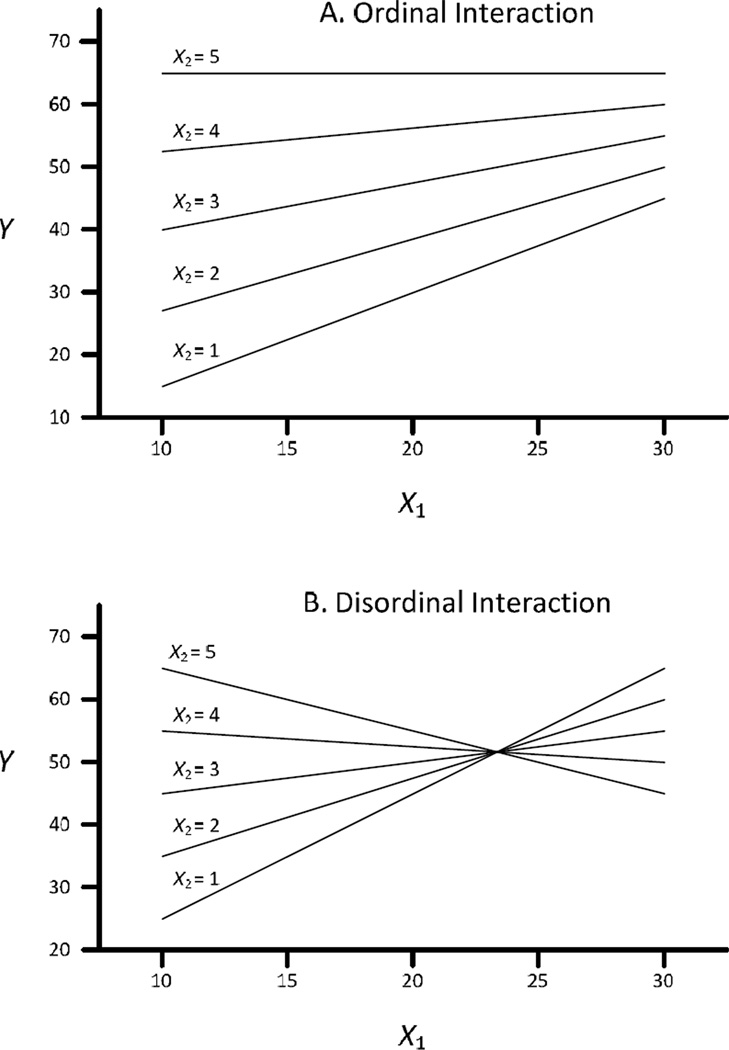
A linear X linear interaction effect of X₁ and X₂ on a quantitative outcome variable Y can assume various forms. But, one feature of all linear X linear interactions is that predicted values from the fitted equation for different values of X₂ converge to a single cross-over point at some point on X₁, if predicted values are projected onto the (Y, X₁) plane. Of course, predicted values for X₁ converge to a single cross-over point at some value of X₂ if predicted values are projected onto the(Y, X₂) plane.

Placement of the cross-over point has led researchers to distinguish between ordinal and disordinal interactions. In brief, an ordinal interaction has the cross-over of predicted values at the boundary (e.g., Figure 1A) or outside the range of observed values on X₁ in the study (e.g., Figure 2A), whereas a disordinal interaction contains a cross-over of predicted values within the observed range of values on X₁ as in Figures 1B and 2B. Therefore, the location of the cross-over point is central to differentiating the two forms of linear interaction.

Figure 2.

Plots of linear X linear interaction of two quantitative predictors X₁ and X₂: (A) ordinal interaction, and (B) disordinal interaction.

Consistent with Aiken and West (1991), we derived a point estimator for the cross-over point as follows: Select two values for X₂ (e.g., 0 and 1), insert one value for X₂ into the right side of Equation 1, insert the other value for X₂ into the right side of Equation 1, set the two equations to equality, and solve for X₁:

$$B_0+B_1{X}_1+B_2(0)+B_3(X_1·0)=B_0+B_1{X}_1+B_2(1)+B_3(X_1·1)$$ (3)

which, after a little algebra, yields:

$$X_1=-\frac{B_2}{B_3}=C$$ (4)

where C is a symbol for the cross-over point, and other symbols were defined above. An analog of Equation 4 can be obtained using mean-centered predictors. This solution is:

$$X_1^{*}=-\frac{B_2^{*}}{B_3^{*}}=C^{*}$$ (5)

which yields the cross-over point C* in a mean-centered metric. To calculate the cross-over point in the raw metric of X₁, one must add X̄₁ to each side of Equation 5, leading to:

$$X_1=-\frac{B_2^{*}}{B_3^{*}}+{\overline{X}}_1=C$$ (6)

where symbols in Equations 3–6 were defined previously (see Aiken & West, 1991, for details).

Re-parameterized Equation

Derivation of re-parameterized model

Centering a predictor at its sample mean is a choice, with many advantages (Aiken & West, 1991; Cleary & Kessler, 1982), but not the only choice. We decided to center X₁ at C, the cross-over point on X₁. This involved substituting (X₁ − C) in place of X₁ in Equation 1. To determine the expected value of Y (or Ŷ) when X₁ is at the cross-over point, we solved the following equation:

$$\mathrm{E}(Y_{X_1=C})=B_0+B_1(C)+B_2(\theta )+B_3(C·\theta )$$ (7)

where E( ) is the expected value operator, θ is any random value of X₂, and other symbols were defined above. Substituting Equation 4 into Equation 7 yields:

$$\mathrm{E}(Y_{X_1=C})=B_0+B_1(-\frac{B_2}{B_3})+B_2(\theta )+B_3(-\frac{B_2}{B_3}·\theta )$$ (8)

which simplifies to

$$\mathrm{E}(Y_{X_1=C})=B_0-\frac{B_1{B}_2}{B_3}=A_0$$ (9)

where A₀ represents the expected value of Y for X₁ = C, and other symbols were defined above.

Predicted values for varying values of X₂ are identical when X₁ = C, because predicted values fall at a single point for any value of X₂. We altered Equation 1 by replacing X₁ with (X₁ − C) and placing the new intercept (Equation 9) in the equation. In this model, B₂ becomes inestimable, because X₂ has no relation to Y at the cross-over point on X₁. The re-parameterized equation thus becomes:

$$Y_i=A_0+B_1(X_{1i}-C)+B_3((X_{1i}-C)·X_{2i})+E_i$$ (10)

where all symbols were defined previously. Equation 10 is a four-parameter equation because C is now a parameter to be estimated, with the same number of free parameters as Equations 1 and 2. Symbols for B₁ and B₃ remain the same as in Equation 1 because these coefficients are unchanged by re-centering X₁ at C. Equation 10 is a re-parameterization of Equation 1 (as shown in supplemental material²) and thus leads to identical predicted values when plotting interactions. We also note that, because of its form, Equation 10 must be estimated using a non-linear regression program, rather than a standard linear regression program.²

As shown above, a point estimate of the cross-over point C is simple to compute using Equations 1 and 4 or Equations 2 and 6, but an interval estimate is more difficult to compute. Using Equation 10, the SE of Ĉ can be used to calculate an interval estimate (e.g., a 95% CI); estimation of SEs of parameters in Equations 1, 2, and 10 is discussed in supplemental material.³

Regression Equations with Linear X Qualitative Interaction

The foregoing results hold for a linear X linear interaction of two quantitative predictors, but must be modified if one of the predictors is qualitative in nature. Here, we consider parameterizations with two-group and three-group qualitative variables.

Standard Parameterizations

Dichotomous grouping

If only two groups are used (e.g., low-risk vs. high-risk), the regression model is similar to Equation 1. Let X₁ represent the quantitative predictor, and D₂ a dummy variable (0 = group 1, and 1 = group 2). The standard regression model is:

$$Y_i=B_0+B_1{X}_{1i}+B_2{D}_{2i}+B_3(X_{1i}·D_{2i})+E_i$$ (11)

where D_2i is the score of person i on dummy variable D₂, the subscript 2 on D_2i is a reminder that group 2 has the unit value on the dummy variable, and other symbols were defined above.

A mean-centered version of Equation 11 can also be formulated as:

$$Y=B_0^{*}+B_1^{*}{X}_1^{*}+B_2^{*}{D}_2+B_3^{*}(X_1^{*}·D_2)+E$$ (12)

where asterisks on regression weights indicate they are for mean-centered predictors, and other symbols were defined above. Only the quantitative predictor X₁ was mean-centered; centering the dummy variable D₂ would lead to a less interpretable set of regression weights.

Ternary grouping

The standard parameterization of a regression model with a linear X qualitative interaction involving three groups on the latter variable is:

$$Y=B_0+B_1{X}_1+B_2{D}_2+B_3{D}_3+B_4(X_1·D_2)+B_5(X_1·D_3)+E$$ (13)

where D₂ and D₃ are dummy variables with unit values for persons in groups 2 and 3, respectively, and other symbols were defined above. In Equation 13, group 1 is the reference group, and D₂ and D₃ allow one to determine whether groups 2 and 3 differ from group 1 in mean level (or intercept) or in moderation with X₁. A mean-centered version of Equation 13 is:

$$Y=B_0^{*}+B_1^{*}{X}_1^{*}+B_2^{*}{D}_2+B_3^{*}{D}_3+B_4^{*}(X_1^{*}·D_2)+B_5^{*}(X_1^{*}·D_3)+E$$ (14)

where all symbols were defined above. Again, only the quantitative predictor was mean-centered, to retain interpretive advantages of regression coefficients for the dummy variables.

Model comparisons to test lower-level and interactive effects using Equations 13 or 14 are well known (cf. Cohen et al., 2003, pp. 308–316), so are not detailed here. But, Equations 11–14 are only as informative about the ordinal or disordinal nature of the interaction as was true of Equations 1 and 2. Modified versions of Equations 4 and 6 could be developed to estimate cross-over points for different groups, but SEs or CIs would still be unavailable for these estimates.

Re-parameterized Equation

Dichotomous grouping

A more directly informative understanding of a linear X qualitative interaction is obtained using the re-parameterized equation:

$$Y=A_0+B_1(X_1-C)+B_3((X_1-C)·D_2)+E$$ (15)

where all symbols were defined above. The following equation is an equivalent formulation:

$$Y:\{\begin{array}{c}\text{group}=1Y=A_0+B_1(X_1-C)+E\hfill \\ \text{group}=2Y=A_0+B_2(X_1-C)+E\hfill \end{array}$$ (16)

where B₁ and B₂ are slopes on X₁ for groups 1 and 2, respectively, and other symbols were defined above. Equations 15 and 16 lead to exactly the same R² as Equations 11 and 12. Thus, Equations 11, 12, 15, and 16 are equivalent regression models, with the same number of free parameters and the same R². But, Equations 15 and 16 have a unique advantage over Equations 11 or 12: the direct estimate for the cross-over point C and its SE. The difference between Equations 15 and 16 is the way in which the slope on X₁ for group 2 is represented. In Equation 15, B₃ is the difference between slopes on X₁ for groups 1 and 2, so the slope for group 2 must be calculated as B₁ + B₃; in Equation 16, B₂ is a direct estimate of the slope on X₁ for group 2.

Ternary grouping

If the qualitative variable represents the presence of three groups, one modified version of Equation 13 can be written as:

$$Y:\{\begin{array}{c}\text{group}=1Y=A_0+B_1(X_1-C)+E\hfill \\ \text{group}=2Y=A_0+B_2(X_1-C)+E\hfill \\ \text{group}=3Y=A_0+B_3(X_1-C)+E\hfill \end{array}$$ (17)

where B₁ through B₃ are regression slopes on X₁ for groups 1 through 3, respectively, and other terms were defined above. Equation 17 contains a single cross-over or convergence point C, so is a restricted re-parameterization of Equation 13. That is, Equation 17 has 5 free parameters, whereas Equation 13 has 6 free parameters. Several alterations could be made to Equation 17 to introduce an additional parameter; for example, one could fit the following model:

$$Y:\{\begin{array}{c}\text{group}=1Y=A_0+B_1(X_1-C_{12})+E\hfill \\ \text{group}=2Y=A_0+B_2(X_1-C_{12})+E\hfill \\ \text{group}=3Y=(A_0+B_1(C_{13}-C_{12}))+B_3(X_1-C_{13})+E\hfill \end{array}$$ (18)

where C₁₂ (labeled simply C in Equation 17) and are the points at which regression lines for groups 2 and 3, respectively, cross the line for group 1, and other symbols were defined above. With the additional parameter, Equation 18 has the same number of free parameters and R² as Equation 13. Thus, a nested-model test of the difference in R² for Equations 17 and 18 provides a 1 df test of the hypothesis that a single cross-over point holds for groups 1, 2, and 3.

Considerations Regarding Re-Parameterized Models

Assumptions Underlying Estimation of the Cross-Over Point

Using re-parameterized models to obtain interpretable point and interval estimates of C rests on standard assumptions for linear regression. Three important assumptions are (a) linearity of relations among variables, (b) equal measurement precision and equal intervals across the range of each variable, and (c) the observed range of X₁ corresponding closely to its population range. First, regarding linearity, the cross-over point might be estimated in biased fashion if a linear model were fit to data with a quadratic relation between X₁ and Y. Screening for nonlinearities in relations among variables would allow a researcher to evaluate the seriousness of this issue for data under consideration.

Second, the assumption about measurement precision and intervals at all points on a dimension is also of key importance. If this assumption were incorrect, point and interval estimates of the cross-over point could be biased. This concern is difficult to evaluate empirically, but must be borne in mind. Third, drawing firm conclusions about the ordinal or disordinal nature of the interaction presumes that the full population range on X₁ is observed in a study or at least considered. If range restriction on a predictor occurs, the range of values observed in a study is narrower than in the population. A cross-over point that falls outside the range of X₁ values observed in a study, but still falls within the population range of X₁ values, may require special care when characterizing the interaction as ordinal or disordinal.

Finally, we note that none of the three assumptions is unique to our re-parameterized equations, but all apply with equal force to the standard parameterizations of regression models when they are used to obtain point estimates of C.

Strengths and Weaknesses of Re-parameterized Equations

Some strengths and weaknesses of our re-parameterized models deserve mention. One strength, already noted, is the ready calculation of an interval estimate for the cross-over point. The SE that accompanies the point estimate of Ĉ allows one to calculate an interval estimate of Ĉ, enabling a more nuanced evaluation of the form of the interaction.

This strength leads, however, to a potential complication when interpreting results. Four outcomes of point and interval estimates might be considered: (a) disordinal interaction (i.e., Ĉ falling within the range of X₁), with the entire CI for Ĉ falling within the observed (or potential) range of X₁; (b) disordinal interaction, but with the CI for Ĉ falling partly outside the range of X₁; (c) ordinal interaction (i.e., Ĉ falling outside the range of X₁), but with the CI for Ĉ falling partly within the range of X₁; and (d) ordinal interaction, with the CI for Ĉ falling completely outside the range of X₁. Scenarios (a) and (d) allow clear interpretation: under (a), both point and interval estimates of Ĉ are consistent with the interaction being characterized as disordinal; under (d), both point and interval estimates of Ĉ are consistent with the interaction being characterized as ordinal. Scenarios (b) and (c) are more problematic for interpretation. Under (b), one might conclude that the interaction is disordinal in the sample, but an ordinal interaction in the population cannot be rejected. In turn, (c) might be rendered as an ordinal interaction in the sample, but a disordinal interaction in the population cannot be rejected. Note that these complications arise only with consideration of the CI of Ĉ. If a researcher used Equation 1 or 2 and calculated only the point estimate of Ĉ, the result would be an overly simplified interpretation of the ordinal or disordinal nature of the interaction.

A second strength of the re-parameterized equation is the potential for modifying an equation to test additional, specific hypotheses regarding parameters describing the interaction. For example, consider a dichotomous variable S (i.e., a dummy variable for Sex, coded 1 = male, 0 = female). Equation 10 could be modified in the following fashion:

$$Y=(A_0+A_{0s}S)+(B_1+B_{1s}S)(X_1-(C+C_{s}S))+(B_3+B_{3s}S)((X_1-(C+C_{s}S))·X_2)+E$$ (19)

where A₀ is the intercept for females, A_0s the intercept difference for males, B₁ is the slope of X₁ for females, B_1s the difference in X₁ slope for males, C is the cross-over point for females, C_s the difference in cross-over points for males, B₃ is the slope coefficient for the product term for females, and B_3s the difference in product term slope for males. One could test lower-order and interactive effects of Sex by altering Equations 1 or 2 (see Cohen et al., 2003, for details). The resulting equation would have 8 free parameters, just as Equation 19 does, and sex differences in the interaction would be embodied in coefficients. But, point estimates of the cross-over points for males and females still would not have SEs. In contrast, Equation 19 allows one to test specific hypotheses about sex differences in particular parameters, providing point and interval estimates of group differences on parameters that characterize the form of the interaction.

One possible weakness of re-parameterized models is the empirical identification of parameters for interactions with nil or small effect sizes. In the limit, if the interaction were completely absent, iterative fitting of model estimates would not converge and the estimate of the cross-over point Ĉ would be empirically unidentified and inestimable; if the interaction coefficient were a very small positive or negative value, the cross-over point Ĉ would be difficult to estimate and might tend to ±∞ with extremely large SE. Although some might view lack of convergence as a problem, it might be seen as a strength of the procedure, indicating that the interaction effect may be small or non-existent. Or, if a test of an interaction were significant using a standard model, lack of convergence of a re-parameterized model may not be due to an extremely small interaction effect (e.g., one or more outliers may lead to non-convergence), and the researcher should explore the data more fully to isolate the problem.

Empirical Example Using Data from the NICHD Child Care Study

To demonstrate the utility of the re-parameterized equation, we analyzed data from the NICHD Study of Early Child Care (NICHD-SECC). The NICHD-SECC was a 10-site study, with research sites across the United States (NICHD Early Child Care Research Network, 2005). A minimum of 100 participants was to be obtained at each site, and participating children and their mothers were enrolled in the study when children were one month of age.

Variables

We utilized data on child gene polymorphism, child sex, the quantitative variable of childcare quality, and the child outcome variable of social skills. The two-group gene categorization for this analysis was based onexon-3 VNTR in the dopamine D4 receptor gene (DRD4). Prior research (e.g., Bakermans-Kranenburg & van IJzendoorn, 2006; Belsky & Pluess, 2009) suggests that presence of a 7-repeat on DRD4 is a risk factor for many developmental outcomes. The dummy variable for DRD4 was coded as D₂ = 0 or 1 for absence or presence, respectively, of a 7-repeat. Of 438 participants with genotype data, 95 (22%) had the 7-repeat on DRD4, so constituted the high-risk/malleability group. The remaining 343 participants (78%) did not have the 7-repeat, so constituted the low-risk/malleability group. Child sex was coded as 0 = female, 1 = male; the sample was almost equally divided on sex (51.8% female).

The quantitative predictor was childcare quality, assessing more attentive, stimulating, and affectionate care and was derived from observational coding do neat five times between child ages of 6 and 54 months. Sample statistics on childcare quality were: M = 2.83, SD = 0.24, Mdn = 2.82, and range 2.10 – 3.38. Children with a DRD4 7-repeat (M = 2.87, SD = 0.24) did not differ significantly on childcare quality from children without a 7-repeat (M = 2.82, SD = 0.24), in either mean level, t (439) = 1.74, p = .08, or variability, F (345, 94) = 1.03, p = .87.

The outcome variable was teacher-reported social skills of children in grade 1, assessed with the Social Skills Rating System (Gresham & Elliott, 1990). Standardized scores revealed sample mean and standard deviation (M = 104.30, SD = 13.19) that were near population values, indicating that children in the sample were fairly representative of the population. Greater detail on all measures is available in NICHD Early Child Care Research Network (2005).

GXE Results

As discussed earlier, a nonlinear relation between X₁ and Y can lead to bias in estimating the cross-over point. As a preliminary analysis, we regressed Y on the linear, quadratic, and cubic trends of X₁ for each of the two groups. Using hierarchical testing, the quadratic and cubic trends had F-ratios of 0.13 and 0.02, respectively, for the DRD4 low-risk group, and F-ratios of 0.83 and 0.01, respectively, for the DRD4 high-risk group. These results suggest the absence of nonlinearities that might bias estimation of the cross-over point under a linear specification.

Standard equations

First, we fit Equation 11 with raw-scored predictors (see left part of Table 1). The X₁-by-group interaction was significant, B̂₃ = 17.51 (SE = 6.23), p < .006. The cross-over point was estimated as Ĉ = −(−47.95)/17.51=2.74, using Equation 4.

Table 1.

Results for Standard and Re-Parameterized Regression Models for Social Skills: Data from the NICHD Study

	Standard parameterization			Re-parameterized model
Par.	Raw score	Par.	Mean- centered	Par.	Crossover- centered	95% CI
B0	94.92 (8.11)	$B_0^{*}$	104.57 (0.68)	A0	104.30 (0.91)	[102.5, 106.0]
B1	3.41 (2.87)	$B_1^{*}$	3.41 (2.87)	B1	3.41 (2.87)	[−2.22, 9.05]
B2	−47.95 (17.9)	$B_2^{*}$	1.56 (1.48)	C	2.74 (0.09)	[2.55, 2.92]
B3	17.51 (6.23)	$B_3^{*}$	17.51 (6.23)	B2	20.92 (5.53)	[10.05, 31.80]

Note: Unless otherwise noted, tabled values are parameter estimates, with standard errors in parentheses. Column headings: Par. = parameter in regression equation, 95% CI = endpoints of 95% confidence interval enclosed in brackets. B₀ through B₃ are the intercept and three regression weights, respectively, using raw scored predictors; $B_0^{*}$ through $B_3^{*}$ are the intercept and three regression weights, respectively, using mean-centered predictors; and, for the re-parameterized equation (i.e., Equation 16), A₀ is the intercept, B₁ and B₂ are the slope coefficients for the effects of the cross-over centered X₁ for groups 1 and 2, respectively, and C is the cross-over point.

Then, we fit the mean-centered version of this equation, Equation 12, to the data (see middle section Table 1). The mean-centered equation gave the same estimate of the interaction effect and an identical estimate of cross-over point, Ĉ = (−(1.56)/17.51)+2.83 = 2.74, using Equation 6, as with raw-scored predictors. Thus, both raw-scored and mean-centered equations provided evidence that the interaction was disordinal, with a point estimate of C close to the sample mean on X₁, although lack of a SE for the cross-over point hinders full interpretation.

Re-parameterized equation

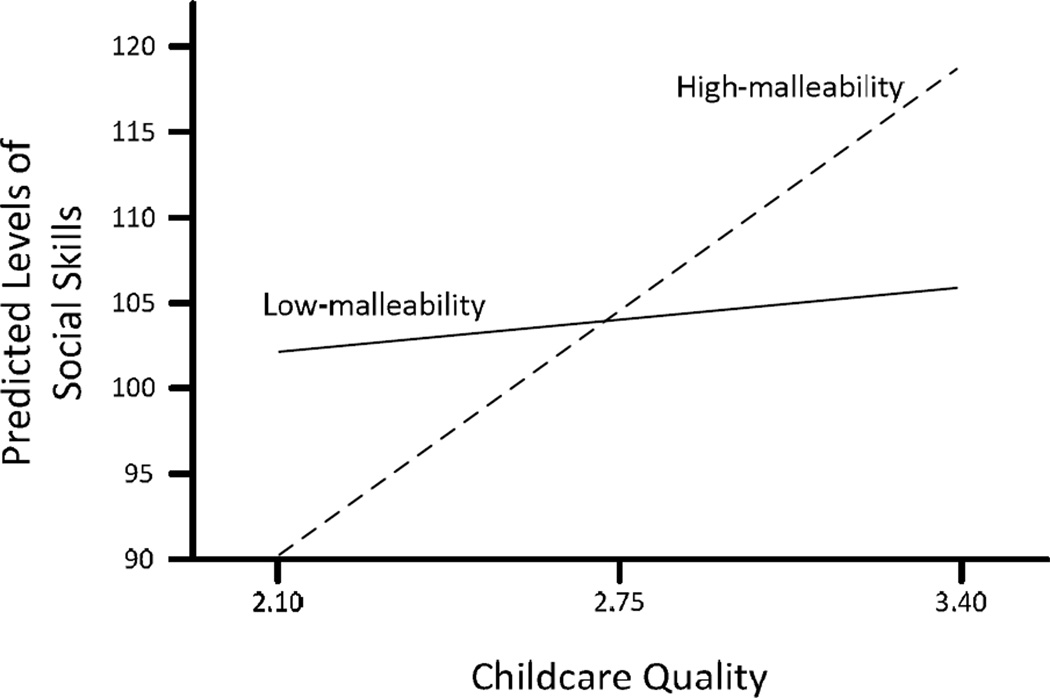
Next, we fit the re-parameterized Equation 16 to the data. Parameter estimates and their SEs and CIs are shown in the right side of Table 1. The point estimate of the cross-over point Ĉ, (SE = 0.09), 95% CI [2.55, 2.92], fell just below the sample mean on X₁ (M = 2.83). The lower limit of the CI for Ĉ fell 1.17 SD units below the sample mean of childcare quality and the upper limit fell 0.38 SD units above the sample mean, so the CI covers values in the middle of the range of X₁ in the sample. Thus, both point and interval estimates of the cross-over point support a conclusion that the interaction was disordinal, providing stronger support for differential-susceptibility model than for diathesis-stress.

A plot of predicted values of social skills for the two groups of children is shown in Figure 3. As predicted, childcare quality was non-significantly related to social skills for the low-malleability group, B̂₁ = 3.41 (SE = 2.87). In contrast, childcare quality was relatively strongly and significantly related to social skills for the high-malleability group, B̂₂ = 20.92 (SE = 5.53). Thus, at high levels of childcare quality, the high-malleability group had predicted levels of social skills that were higher than those for the low-malleability group; but, at low levels of childcare quality, the high-malleability group had lower predicted levels of social skills.

Figure 3.

Predicted levels of social skills for the low-malleability and high-malleability groups as a function of childcare quality.

In supplementary analyses, we also tested whether child sex moderated results shown in Table 1. That is, we modified Equation 16 to include the effect of Sex in a fashion analogous to that for Equation 19. Relative to females, males had a slightly lower estimated cross-over point, Ĉ_s = −0.12 (SE = 0.24), and a somewhat lower level of social skills at the cross-over point, Â_0s = −1.17 (SE = 1.84). Also, males were slightly less affected than females by child care in both the low-malleability, B̂_1s = −2.37 (SE = 5.77), and high-malleability groups, B̂_1s = −13.27 (SE = 11.10). But, none of these effects was statistically significant, as t-values ranged between |0.41| and |1.20| (all ps > .20). Although accepting the null hypothesis can be a risky gambit, the present data provide no evidence that results differed significantly by child sex.

Discussion

Our primary aim was to re-parameterize the standard linear regression model to allow clearer distinctions between ordinal and disordinal interactions. Researchers often hypothesize interactive effects of predictors in fairly nonspecific terms. In our opinion, researchers should be challenged to make stronger predictions about the form of an interaction, such as whether the interaction is ordinal or disordinal. If such a prediction were warranted, then a re-parameterized regression model that estimates explicitly the cross-over point of predicted values and its CI would enable stronger tests of the match between theoretical predictions and trends in data.

After presenting standard ways of parameterizing regression models with interaction effects, we derived a re-parameterized regression model for linear X linear interaction of two quantitative predictors. The most important benefit of a re-parameterized equation is the SE and associated CI of the estimated cross-over point Ĉ. Further, as stressed throughout, the CI of Ĉ allows a more informed evaluation of the ordinal vs. disordinal form of the interaction.

Our procedures apply to any theoretically-guided testing of interactions using regression analysis where the cross-over point is at issue. In the context of GXE interactions, some have argued that negative emotionality, a quantitative temperament factor, is a diathesis, whereas others see it as a more general malleability marker (Belsky, 1997, 2005; Belsky & Pluess, 2009; Boyce & Ellis, 2005; Ellis et al., 2011). Thus, a researcher could use quantitative measures of both the environment (X₁ = childcare quality) and a genetically-related factor (e.g., X₂ = negative emotionality) to test competing trends in linear X linear GXE interactions.

We extended the re-parameterization of the regression model to scenarios in which one of the interacting predictors is a categorical, or grouping, variable. If just two groups are present (e.g., low-risk vs. high-risk), only a single cross-over point is possible. If a ternary, or three-class, categorization into groups is used, alternate models can test whether a single cross-over point holds for all three groups or whether such a restriction should be rejected.

When we applied the standard and re-parameterized models to data on interactive effects of child-care quality and genotype (i.e., DRD4) on social skills, we found a significant GXE interaction. The disordinal form of the interaction was confirmed more strongly after fitting the re-parameterized model to the data by showing that both the point and interval estimates of the cross-over point Ĉ were clearly within the range of values observed on the environmental variable. Further, the slope for the high-malleability group (i.e., DRD4-7R) was significant and the slope for the low-malleability group was non-significant, and both of these results proved consistent with tenets of the differential-susceptibility model.

Our proposed re-parameterized regression approach rests on critical assumptions and has some potential weaknesses that accompany its clear strengths. The assumptions are not unique to the new methods we proposed here, but apply equally to use of standard approaches used to estimate the cross-over point in interactions. Moreover, assumptions should always be evaluated to the extent possible. Threats to the validity of conclusions using any statistical procedures, our re-parameterized models included, should always be investigated, and conclusions should be qualified if assumptions are not fully met. In our opinion, the benefits of our re-parameterized equations outweigh any potential drawbacks to their use and supplement in informative ways traditional approaches to testing interactions using regression methods.

Our major goal was to develop a re-parameterized regression model that captures one essential aspect of an interaction more informatively than do standard analytic approaches. If the ordinal vs. disordinal form of an interaction is crucial for distinguishing theoretical positions, our re-parameterized regression model yield more detailed information for evaluating the fit of data with theoretical predictions. With more useful tools for asking key questions, researchers can be challenged to provide more explicit hypotheses regarding predicted patterns in data. Confirming predicted patterns in data yields inductive support for the validity of a theory, but disconfirming predicted patterns points to the need to reconsider theory, measurements, or conditions to ferret out reasons for disconfirmation. Clearer predictions tested against data using more focused and definitive statistical models will provide clearer evidence regarding whether theoretical conjectures driving the research were confirmed or disconfirmed. We trust our re-parameterized equation will be yet one more tool for testing theoretical conjectures directly and strongly.