The Effect of Slice Thickness on the Assessment of Bone Defect Volumes by the Cavalieri Principle Using Cone Beam Computed Tomography

Abstract

The purpose of this study was to investigate the possible effects of section thickness on volume estimations obtained by cone beam computed tomography. Intraosseal cavities representing bone defects on vestibular sides of the two dry sheep mandibles were scanned by a cone beam computed tomography system. Consecutive sections at 0.2, 0.6, 1, 1.4, and 2.2 mm thickness were used to estimate the volumes of the cavities using the Cavalieri principle of stereological methods. Estimated volumes are then compared with the volumes obtained by the Archimedean principle. In 0.2-, 0.6-, and 1-mm-thick slices, the volumes estimated by the Cavalieri principle did not differ from the volumes by the Archimedean principle (p > 0.05). The 0.2 mm slice-thickness group had the highest asymptotic significance value (p = 0.6). Although the thinnest slice appears to provide the most accurate values, slice thickness up to 1 mm can be chosen for volume calculations on CBCT images.

Introduction

Cone beam computed tomography (CBCT) is a relatively new imaging technology in dentistry and is able to produce a three-dimensional dataset from the chosen region of the patient’s head with lower radiation doses than a medical computed tomography (CT) claimed by the authors [1–3]. As in CT and magnetic resonance imaging (MRI) scans, the basic image presentations for CBCT systems are views in axial, sagittal, and coronal planes. These image series on a chosen plane make the calculation of the volume of either an anatomic or pathologic structure possible using the Cavalieri principle [4]. Due to this principle, volume of an arbitrarily shaped object can be estimated in an unbiased manner from the product of the distance between planes and the sum of areas on systematic random sections through the object [5]. Since systems such as CT, MRI, and ultrasonography section imaging can obtain entire sets of two-dimensional slices through objects which are parallel to each other and separated by a known distance, they are used in the estimation of the volume of an object utilizing this method [6–9].

In literature, there are quantitative studies carried out on the use of CBCT systems and software in dental volumetric analysis [4, 10–17]; however, the effect of section thickness on the accuracy of the volume estimate obtained by using CBCT has not been researched in these studies.

The aim of this study is to analyze the effect of section thickness on volume estimation by applying the Cavalieri principle to CBCT images.

Materials and Methods

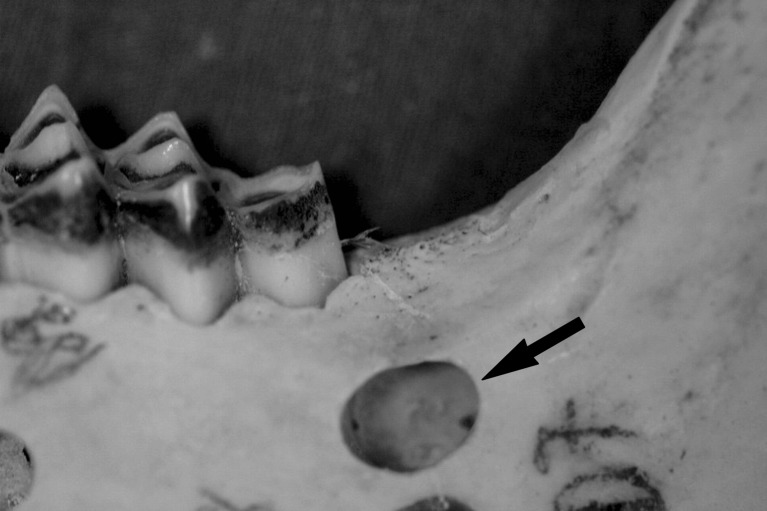
Two dry sheep mandibles were selected for the study. A total of six roughly spherical shaped intraosseal cavities representing bone defects were created on the vestibular side of the mandibles in various sizes, using a round-shaped tungsten carbide burr (Fig. 1). The vestibular boundaries of the cavities were determined with plaster casts before the preparation.

Fig. 1.

Intra-bony cavity representing a bone defect on the vestibular side of sheep mandible

The mandibles were scanned with a Kodak 9500 Cone Beam 3D System (Kodak Dental Systems, Carestream Health, Rochester, New York). Scans were performed with the following parameters: 9 × 15 cm field of view, 0.2 mm voxel size, 90 kV tube voltage, 10 mA tube current, and 10.8 s scan time. Tap water was used to simulate soft tissue. Volumetric data were reconstructed and sectioned in the coronal plane. Slices of 0.2 mm thickness with 0.8 mm interval, 0.6 mm thickness with 0.4 mm interval, and 1 mm thickness were obtained. Additionally, two thick section series with 1.4 and 2.2 mm thicknesses were taken to see the effect of thicker section on the estimated volume values.

The volume of each defect was estimated using the Cavalieri principle. The surface area of each section was measured via the planimetry method, using ImageJ software (National Institutes of Health, Bethesda, USA) (Fig. 2). Each measurement was performed three times by a single observer. The average of the three scores was used for calculation. The sum of the areas was used to estimate the volume using the following formula, which has been described in previous reports [7–9]:

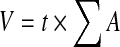where, t is the section thickness (including intervals) and ∑A is the total sectional area of the consecutive sections.

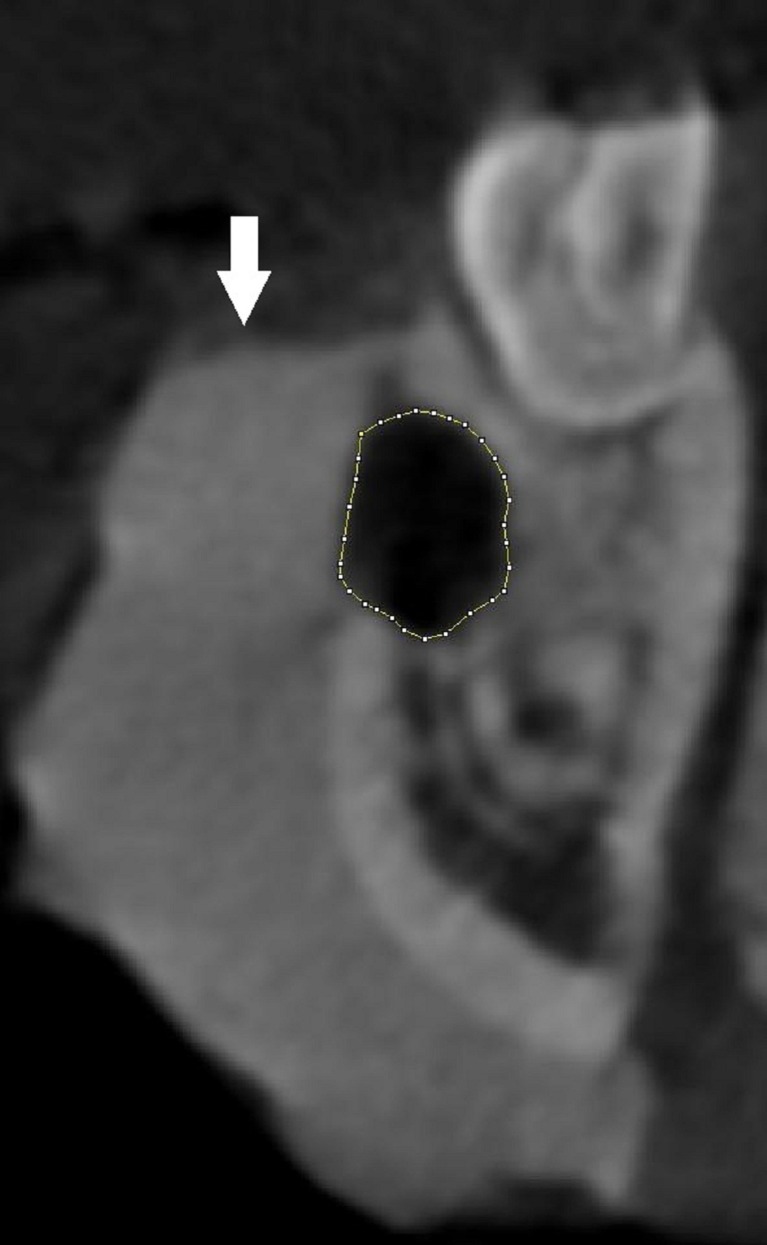
Fig. 2.

Appearance of bone defect on CBCT image. Borders of the defect were manually traced by image-J software. Arrow shows the plaster cast covering the vestibular surface of the bone

After the estimations were completed, intraosseal cavities were filled with low viscosity silicon impression material. After the polymerization, silicon impressions were immersed into a pycnometer filled with water, and the volumes were calculated using the density and weight of the water run-over, based on Archimedean principle. Measurements by the water displacement method were accepted as the actual volume values and served as gold standard [18–21].

The data were analyzed using SPSS, version 12 (Chicago, IL, USA). The Kendall’s W test was used to determine the possible statistically significant differences between the groups. Differences between groups were further analyzed by the Wilcoxon signed-rank test. All statistical tests were set at the 95 % confidence level (p < 0.05).

Results

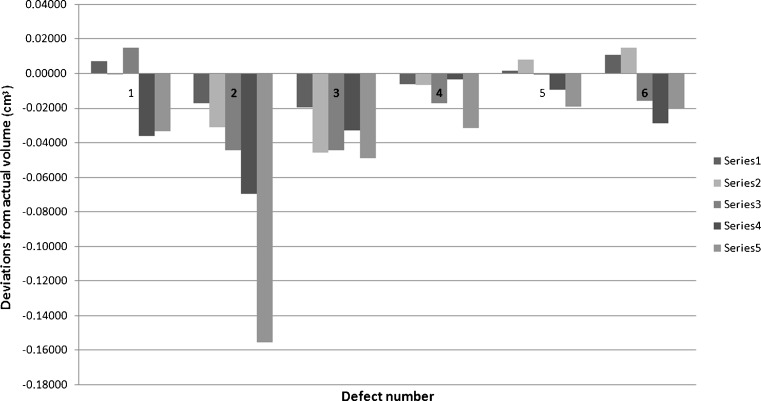
The results of the volume estimations using CBCT images and the actual volumes via pycnometer are shown in Table 1. The differences between the estimated volumes and the actual volumes were between 0.0003 and 0.1552 cm³ (Fig. 3). Although the most close volume estimation on CBCT images was for 1-mm-thick slices at defect number 5 with a 0.1 % deviation from the actual volume of the cavity, 0.2-mm-thick slices gave the most similar results in three of six defects. The results of the Kendall’s W test showed that there is statistically significant difference between volume estimations by Cavalieri principle and Archimedean principle, considering each slice thickness and pycnometer as independent judges and intraosseal cavities as objects (W = 0.571, p = 0.004). According to the results of statistical analysis of Wilcoxon signed-rank test, the estimated volumes for 0.2, 0.6, and 1 mm slice-thickness groups did not differ from the actual volumes of cavities while the estimations for 1.4 and 2.2 mm slice-thickness groups differed (Table 2).

Table 1.

Actual and estimated volumes of bone defects (cm³)

Defect no.	Actual	0.2 mm	0.6 mm	1 mm	1.4 mm	2.2 mm
1	0.155	0.1623	0.1546	0.1701	0.1190	0.1218
2	0.5657	0.5484	0.5349	0.5208	0.4961	0.4105
3	0.2412	0.2218	0.1954	0.197	0.2083	0.1925
4	0.1913	0.1853	0.1845	0.1743	0.1877	0.1597
5	0.2984	0.3001	0.3064	0.2981	0.2891	0.2792
6	0.2023	0.2129	0.2171	0.1866	0.1738	0.1821

Fig. 3.

A graphic showing the differences between the actual volumes and the estimated volumes in different slice thicknesses

Table 2.

Agreement of volume estimations obtained by Cavalieri principle on CBCT images and actual volumes based on the Archimedean principle (p > 0.05)

	0.2 mm − actual	0.6 mm − actual	1 mm − actual	1.4 mm − actual	2.2 mm − actual
Z	−0.524	−0.734	−1.782	−2.201	−2.201
Asymptotic significance (2-tailed)	0.600	0.463	0.075	0.028	0.028

Discussion

Bone defects of the jaws may be caused by various factors such as periapical infections, cysts, tumors, and periodontal disease. Panoramic and conventional projection radiographic applications may be performed for diagnosis and post-operative follow-ups of the defects. The amount of bone loss at the initial diagnosis, however, and the amount the bone gain at a certain time after the treatment can just be estimated as areas or lengths. For an assessment of volume gain or loss, a 3D imaging technique should be performed.

Medical literature does have studies showing that the CBCT technique is reliable for estimating volume. Agbaje et al. [10] compared volumes of the extraction sockets that they estimated from CBCT images with the values they got by using the Archimedean principle in their clinic, and they reported a good match between results. In 2009, Agbaje et al. [11] used CBCT in evaluation of the bone healing process by measuring volumetric changes of the extraction sockets in head and neck cancer patients undergoing radiotherapy after tooth extraction. Deguchi et al. [12] used CBCT to determine the volumes of the maxilla and mandible in subjects with skeletal Class I, Class II, and Class III malocclusions. Bayram et al. compared the mandibular condyle volume measurements done using the Cavalieri principle on CBCT images with physical volume measurements via Archimedean principle. They concluded that the Cavalieri principle is a valid tool for volume estimation of the mandibular condyle [13].There are also reports showing the use of CBCT in estimating the volume of teeth, pulp chamber, mandibular condyle, and upper airway volume [13–17]. In our previous study, we evaluated the accuracy of the volume assessment of the intraosseal defects using CBCT sections with a thickness of 0.2 mm. Our results showed that the obtained results did not differ from the actual volumes of bony defect [4]. However; none of these studies have included research on the effect of slice thickness on CBCT images.

Since the CBCT system we used can provide 0.2 mm as the thinnest slice, we defined slice thicknesses in this study as 0.2, 0.6, and 1 mm. An equal number of slices for each cavity was obtained by leaving 0.8 and 0.4 mm intervals between 0.2- and 0.6-mm-thick slices, respectively. Using this sampling procedure, we obtained slice series from the same point of the lesion with different section thicknesses. Additionally, we took the images with 1.4 and 2.2 mm thicknesses to see the effect of thicker sectioning. Our results did not show statistically significant differences between estimations from CBCT and actual volume achieved by water displacement up to 1 mm slice thickness.

In studies analyzing the effect of section thickness on volume estimations of organs or cavities by using CT images, authors reported underestimations of the volumes which were caused by increases in slice thickness [18, 19]. In our study, 1.4- and 2.2-mm-thick slices caused statistically significant underestimation problem. However, our study design was limited by relatively small sizes of the intraosseal cavities with a highest actual volume of 0.57 cm³. Thicker slices could be appropriate for larger defects.

In conclusion, volume assessments can be performed on CBCT images safely by using the Cavalieri principle. A slice thickness up to 1 mm can be chosen for volume estimation of intraosseal defects. Although thicker slices resulted in underestimation, further investigation is necessary on the relation between slice thickness and size of the intraosseal cavity.