Abstract
Fluorescent nucleic acid base analogues are important spectroscopic tools for understanding local structure and dynamics of DNA and RNA. We studied the orientations and magnitudes of the electric dipole transition moments (EDTMs) of 6-methyl isoxanthopterin (6-MI), a fluorescent analogue of guanine that has been particularly useful in biological studies. Using a combination of absorption spectroscopy, linear dichroism (LD) and quantum chemical calculations, we identified six electronic transitions that occur within the 25 000–50 000 cm−1 spectral range. Our results indicate that the two experimentally observed lowest-energy transitions, which occur at 29 687 cm−1 (337 nm) and 34 596 cm−1 (289 nm), are each polarized within the plane of the 6-MI base. A third in-plane polarized transition is experimentally observed at 47 547 cm−1 (210 nm). The theoretically predicted orientation of the lowest-energy transition moment agrees well with experiment. Based on these results, we constructed an exciton model to describe the absorption spectra of a 6-MI dinucleotide–substituted double-stranded DNA construct. This model is in good agreement with the experimental data. The orientations and intensities of the low-energy electronic transitions of 6-MI reported here should be useful for studying local conformations of DNA and RNA in biologically important complexes.
INTRODUCTION
Experiments that reveal the local conformations of nucleic acids and conformational transitions along a reaction pathway are needed to better understand the mechanisms of the various proteins and protein complexes that comprise the ‘macromolecular machines’ that manipulate genes and other elements of the DNA genome. The use of fluorescent nucleic acid analogue probes, in conjunction with well-chosen spectroscopic measurements, can help to reveal important information about local conformations at chosen sites within nucleic acid constructs, and thus the roles played by these specific structures in key steps of biologically important protein–nucleic acid reactions.
6-methyl isoxanthopterin (6-MI) is a fluorescent analogue of the natural nucleic acid base guanine. 6-MI absorbs light in the long wave ultraviolet (UV) regime at lower energies (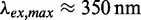 ) than do the canonical nucleic acid bases, and (unlike the natural bases) fluoresces with relatively high quantum yield (
) than do the canonical nucleic acid bases, and (unlike the natural bases) fluoresces with relatively high quantum yield (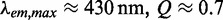 for the nucleoside in aqueous buffer) (1–9). The ability of 6-MI to form Watson–Crick base pairs with cytosine when it replaces guanine within a DNA or RNA strand, in addition to its low-energy spectral properties, makes it a useful spectroscopic site-selective probe of local base conformation and dynamics (3,10,11). As is seen for other fluorescent nucleic acid base analogues such as 2-aminopurine, pyrrolo-cytosine and tricyclic cytosine, the spectral properties of 6-MI can provide information about the local conformation and dynamics of nucleic acids (3,9,12–15). The extent of fluorescence quenching in 6-MI appears to be a measure of the degree of stacking between the site-specifically inserted base analogue probe and its flanking bases on the same oligonucleotide strand. It has recently also been demonstrated that the substitution of two sequential 6-MIs for adjacent guanines within DNA constructs results in exciton coupling between these ‘dimer’ probes characterized by distinguishing features in the near-UV absorption and circular dichroism (CD) spectra (3,11).
for the nucleoside in aqueous buffer) (1–9). The ability of 6-MI to form Watson–Crick base pairs with cytosine when it replaces guanine within a DNA or RNA strand, in addition to its low-energy spectral properties, makes it a useful spectroscopic site-selective probe of local base conformation and dynamics (3,10,11). As is seen for other fluorescent nucleic acid base analogues such as 2-aminopurine, pyrrolo-cytosine and tricyclic cytosine, the spectral properties of 6-MI can provide information about the local conformation and dynamics of nucleic acids (3,9,12–15). The extent of fluorescence quenching in 6-MI appears to be a measure of the degree of stacking between the site-specifically inserted base analogue probe and its flanking bases on the same oligonucleotide strand. It has recently also been demonstrated that the substitution of two sequential 6-MIs for adjacent guanines within DNA constructs results in exciton coupling between these ‘dimer’ probes characterized by distinguishing features in the near-UV absorption and circular dichroism (CD) spectra (3,11).
Exciton coupling is a spectroscopic phenomenon in which electronically interacting chromophores are excited collectively, with the electronic transition energies of the interacting components being split relative to those of the isolated molecules (16). The transition energies and intensities of the electronically coupled dimer are sensitive to the relative orientation and separation of the monomer subunits. Spectroscopic methods that are sensitive to exciton coupling, such as CD and 2D fluorescence spectroscopy (2D FS) (17–19), can detect changes in the conformation of an exciton-coupled dimer. Thus by exploiting the electronic properties of 6-MI dimer–substituted nucleic acids, local base-stacking conformations in various DNA (and RNA) constructs can be studied under physiological conditions (11).
To better understand the spectroscopic properties of 6-MI–substituted nucleic acids, it is important to characterize the electric dipole transition moments (EDTMs) of the isolated probe molecule. Interactions between the 6-MI chromophore and its local environment perturb the electronic excitation and relaxation pathways, which is the origin of the probe’s sensitivity to local macromolecular conformation. Knowledge of the directions and magnitudes of the EDTMs can be used to model the effects of nucleic acid structure on spectroscopic observables such as transition strengths, energies and optical activity. Of particular importance for biochemical studies is the ability to model the electronically coupled states of two adjacent 6-MI chromophores substituted at sites within an oligonucleotide construct that are functionally important in protein–nucleic acid complexes. Exciton coupling models have been used to elucidate local probe conformation in such constructs using CD spectroscopy (11,17). A combined analysis of linear spectroscopic measurements and 2D FS can provide more detailed information about the conformations of exciton-coupled chromophores than CD. For example, the conformation of a dimer of Mg-tetraphenylporphyrin suspended in a phospholipid bilayer membrane was recently determined using this approach (17,18).
In the present work, we describe experimental and theoretical investigations of the EDTMs of 6-MI. Although the photo-physical properties of 6-MI such as fluorescence parameters (1,7–9,20,21), absorption spectra (7,8,20,21), solvatochromism (8,20) and Stark spectra (8) have been the focus of previous experimental and theoretical studies, the directions and magnitudes of the EDTMs within the molecular frame have not been investigated experimentally. To determine transition polarizations and oscillator strengths, we performed UV absorbance and linear dichroism (LD) measurements on 6-MI nucleosides embedded in stretched poly(vinylalcohol) (PVA) films using an established approach developed by others (19,22–24). Comparison between our measurements and the results of quantum chemical calculations allowed us to characterize the lowest-energy transitions. Based on our assignments, we constructed an exciton coupling model to describe the absorption spectrum of 6-MI dinucleotide in B-form double-stranded (ds) DNA. The results are in good agreement with experimental data.
MATERIALS AND METHODS
Experimental procedures
Chemicals
6-methylisoxanthopterin riboside (r(6-MI)) was obtained from Fidelity Systems, Inc. and used without further purification. PVA (Mw = 85 000–124 000) was purchased from Sigma Aldrich and used as received. All organic solvents were spectrophotometric grade. Solution phase absorption spectra were measured using 13.2 μM r(6-MI) dissolved in 5 mM aqueous sodium phosphate buffer, pH 7.
Film preparation
A 9.1% (by weight) aqueous PVA solution was prepared by dissolving the polymer in nanopure water while heating to 95°C, and then allowing the solution to cool to room temperature. Sample solutions were prepared by combining 6 ml of the aqueous PVA solution with 1.33 ml of 0.45 mM r(6-MI) in methanol, and stirring the mixture for several minutes. A reference solution was prepared by following an identical procedure but withholding the r(6-MI). The sample and reference solutions were then placed under vacuum for 1 h in a desiccator that contained a small amount of water. The solutions were transferred to Eppendorf tubes and spun down in a centrifuge at 10 000 r.p.m. for 15 min to remove bubbles and non-dissolved PVA. Films were cast by pouring 3 ml of sample (or reference) solution into 2.5 × 2.5 × 0.5 cm3 wells, which were cut into paraffin wax molds supported on a glass sheet. The films were then allowed to dry for 2 days in an area free from dust and air currents. Films were stretched to 1.5× their original length while they were heated using a hot-air gun.
Spectroscopy
Solution phase absorption spectra were measured using a Cary 3E UV-visible spectrophotometer. LD and absorption spectra of PVA films were simultaneously measured using a Jasco CD spectrophotometer running in LD mode (Horiba Jobin-Yvon, J-720). Sample LD spectra were corrected for background from the PVA host material by subtracting the LD of a stretched reference film from that of the stretched sample films. Significant host absorption was observed in sample films at wavelengths below 250 nm. The reduced linear dichroism (LDr) spectra were calculated using the absorption spectrum of r(6-MI) in aqueous buffer, which was scaled so that the intensity of its lowest-energy absorption peak (where PVA absorption is negligible) matched that of r(6-MI) in the film.
Quantum chemical calculations for electronic excitation energies and electric dipole transition moments
Low-lying electronic excitation energies and EDTMs of small organic molecules can be predicted using modern quantum computational methods with reasonable accuracy (25–29). The computed excitation energies are typically accurate to within 0.2–0.4 eV (ca. 1600–3200 cm−1) for low-lying valence electronic excitations (25,26,29). The accuracy of computed EDTMs and oscillator strengths is less studied (28). However, the shapes of electronic absorption spectra predicted by quantum chemical methods tend to match experimental absorption spectra quite well, especially in their low-energy parts.
In this work, we use three well-established quantum chemical methods to perform ground-state geometry optimizations and to compute excitation energies and transition moments for the 10 lowest electronic excitations of N8-methyl-6-MI, namely approximate second-order coupled-cluster with resolution of the identity approximation (RICC2) (30,31) and density functional theory using the Becke 3-parameter hybrid (B3LYP) (32) and the ωB97 long-range corrected functional (33). Triple-zeta valence basis sets with two sets of polarization functions (TZVPP) (34) and corresponding auxiliary basis sets (35) were used throughout. The stabilities of the optimized ground-state structures were established by force constant calculations. Owing to pyramidalization of the NH2 group, the ground-state structure of N8-methyl-6-MI belongs to the C1 point group. RICC2 and B3LYP calculations were performed using the TURBOMOLE. program package (36). ωB97 calculations used the Q-Chem program (37).
Moments of inertia of r(6-MI) were computed using B3LYP-optimized ground-state structures (32). The resolution-of-the-identity approximation was used for the Coulomb energy (RI-J) (38). TZVPP basis sets were used along with corresponding auxiliary basis sets. To determine the lowest-energy conformation of r(6-MI), different conformations of the ribose ring and the glycosidic substituent were sampled by the Dreiding force field (39) and subsequently optimized using the B3LYP functional.
Theoretical considerations for linear dichroism measurements
LD experiments were performed on r(6-MI), in which the ribose sugar is covalently bound at the N8 position of the 6-MI free base (see Figure 1). Samples were prepared by suspending the nucleoside in PVA films. By applying a uniaxial strain to these films, a net alignment of the excitation transition moments was established (19,23,40,41). We performed LD measurements on both stretched and un-stretched PVA films.
Figure 1.
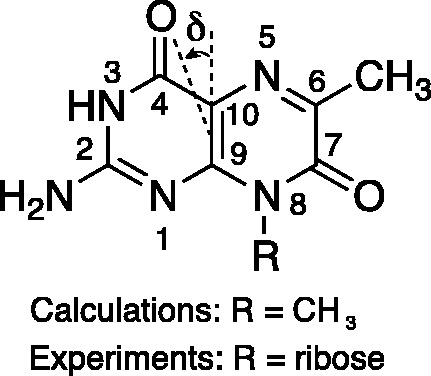
The structure of the fluorescent guanine analogue 6-MI is shown with the atomic numbering system used in this work. The in-plane angle δ is defined relative to the C9-C10 axis, as shown. For our LD measurements on the 6-MI nucleoside (r(6-MI)), the R-group was ribose. Quantum chemical calculations were carried out on the 8-methyl–substituted 6-MI.
LD is the difference between absorption of light polarized parallel and perpendicular to an orientation axis, which is defined as the direction of the uniaxial strain applied to the PVA films.
| (1) |
The absorption of each polarized component is proportional to the square of the projection of the transition moment vector onto the electric field vector. The extents to which the parallel and perpendicular transition moment projections differ—and hence, the magnitude of the LD signal—depends on both the orientation of the r(6-MI) transition moments and on how narrowly distributed the r(6-MI) orientations are in the film. The reduced linear dichroism (LDr) is defined as
| (2) |
where 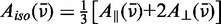 is the corresponding absorption of light in an isotropic sample. The quantity
is the corresponding absorption of light in an isotropic sample. The quantity 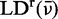 depends only on the orientations of the transition moments that absorb at frequency
depends only on the orientations of the transition moments that absorb at frequency  , and not on their strengths. For a purely polarized transition, the value of
, and not on their strengths. For a purely polarized transition, the value of 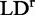 is expected to be constant across the absorption band.
is expected to be constant across the absorption band.
The distribution of r(6-MI) orientations in the film is specified by the Saupe orientation parameters 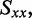
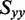 and
and 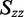 , where the z-axis is taken to be the uniaxial direction of the film (19). For a planar molecule with in-plane and out-of-plane transition polarizations, the x-axis is assumed to be perpendicular and the y- and z-axes are parallel to the molecular plane. The relationship between the value of
, where the z-axis is taken to be the uniaxial direction of the film (19). For a planar molecule with in-plane and out-of-plane transition polarizations, the x-axis is assumed to be perpendicular and the y- and z-axes are parallel to the molecular plane. The relationship between the value of 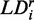 and the angle
and the angle 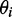 of the ith transition moment vector relative to the film orientation axis is given by
of the ith transition moment vector relative to the film orientation axis is given by
| (3) |
Ideally, the Saupe parameters would be determined in an independent experiment. For example, the infrared LD spectrum could be used, in principle, to solve Equation (3) for the Saupe parameters under the assumption that the molecule aligns with its longest axis parallel to the film stretch direction, and that the vibrational transition moments of the carbonyl groups can be clearly identified (22,24). Unfortunately, our attempts to measure the infrared LD spectrum of our samples were unsuccessful because the limited solubility of r(6-MI) resulted in insufficient signal intensity compared with background absorption by the PVA host material. We therefore followed an alternative approach to estimate the Saupe parameters by using the following relations, where 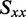 is the orientation parameter for the out-of-plane polarized x-axis (19,24).
is the orientation parameter for the out-of-plane polarized x-axis (19,24).
| (4) |
| (5) |
and
| (6) |
In the approach we followed, the value of 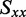 was estimated from the average of the LDr values corresponding to the out-of-plane polarized transitions. The values of
was estimated from the average of the LDr values corresponding to the out-of-plane polarized transitions. The values of 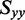 and
and 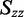 were estimated from the minimum and maximum LDr values, respectively, of in-plane polarized transitions. Equation (6) was used to calculate
were estimated from the minimum and maximum LDr values, respectively, of in-plane polarized transitions. Equation (6) was used to calculate 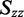 because a transition with positive LDr was not available from which to estimate it. The Saupe parameters were then used in Equation (3) to calculate the value of
because a transition with positive LDr was not available from which to estimate it. The Saupe parameters were then used in Equation (3) to calculate the value of 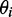 for the ith in-plane polarized electronic transition, which yielded two possible values of
for the ith in-plane polarized electronic transition, which yielded two possible values of 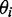 , one positive and one negative. We selected between these possibilities by comparison with the computational results. Finally, we used the computed ground-state geometry of r(6-MI) to calculate its minimum principal moment of inertia axis, which lies approximately along the longest axis of the molecule. This was assumed to lie parallel to the orientation axis of the stretched films. The angle
, one positive and one negative. We selected between these possibilities by comparison with the computational results. Finally, we used the computed ground-state geometry of r(6-MI) to calculate its minimum principal moment of inertia axis, which lies approximately along the longest axis of the molecule. This was assumed to lie parallel to the orientation axis of the stretched films. The angle 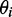 was then related to the angle
was then related to the angle 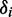 , which describes the orientation of the EDTM of the ith transition polarized in the plane of the molecule.
, which describes the orientation of the EDTM of the ith transition polarized in the plane of the molecule.
RESULTS
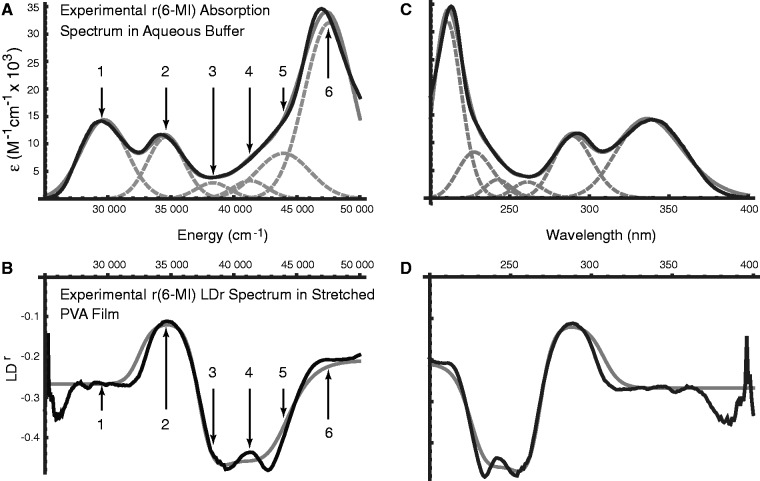
The absorption spectrum of r(6-MI) in aqueous buffer exhibited three major peaks centred at 29 687, 34 596 and 47 547 cm−1 (337, 289 and 210 nm), which we identify as peaks 1, 2 and 6, respectively (see Figure 2A). The absorption spectrum of r(6-MI) in PVA films exhibited the same features as in isotropic solution, although the highest-energy transition was obscured by background absorption of the PVA host material. The LD spectrum of r(6-MI) in un-stretched PVA films was weak. In stretched PVA films, the LD spectrum exhibited features at the same energies as in isotropic solution. However, as expected, the relative intensities of each absorptive feature in the stretched films deviated from those measured in isotropic solution. Four films were examined, and the analysis below was carried out using the average of two LD spectra of one representative film.
Figure 2.
(A) The experimental absorption spectrum of r(6-MI) in aqueous buffer (black) is shown in comparison with a fit (grey) of the data to the sum of six Gaussian functions (dashed grey). Transitions are numbered according to the same scheme as in Table 1. (B) The experimental LDr spectrum of r(6-MI) in the stretched PVA film (black) is shown in comparison with the calculated LDr spectrum (grey), which is based on the experimental transition moment orientations and intensities, energies and peak widths obtained from a simultaneous fit to the data shown in (A) and (B). (C) Plot (A), shown as a function of wavelength in nanometers. (D) Plot (B), shown as a function of wavelength in nanometers.
We constructed the experimental reduced linear dichroism (LDr) by dividing the LD obtained from the stretched PVA films by the absorption measured in aqueous buffer, according to Equation (2) (see Figure 2B). We chose to use the buffer solution spectrum rather than that of the un-stretched PVA films in Equation (2) because of the background absorption of the PVA at wavelengths shorter than 250 nm. On examination of the LDr, it was revealed that three additional transitions occur over the range 38 000–44 000 cm−1 (labeled as peaks 3, 4 and 5). These features were initially not evident from the experimental absorption spectrum because they were buried beneath the shoulder of the feature centred at 47 547 cm−1 (peak 6). We determined the values of LDr for each transition using the method of Thulstrup, Eggers, and Michl (TEM method) (42), which involves making linear combinations of the polarized spectra, 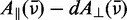 for different values of the reduction coefficient
for different values of the reduction coefficient 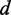 . The value
. The value 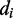 for which the ith spectral feature vanishes yields the corresponding value
for which the ith spectral feature vanishes yields the corresponding value 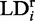 of the transition, according to
of the transition, according to
| (7) |
We performed a global numerical fitting analysis of the experimental absorption spectrum and the LDr spectrum, in which each of the six absorptive features was modelled as a Gaussian line shape with variable frequency, line width and intensity. This was accomplished by minimizing the target function described by Equation (8) with the aid of the nonlinear global optimization package KNITRO (43), where 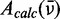 is given by Equation (9) and
is given by Equation (9) and 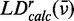 is given by Equation (10).
is given by Equation (10).
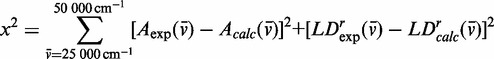 |
(8) |
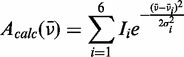 |
(9) |
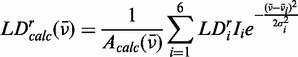 |
(10) |
This procedure yielded optimized parameters for each of the six transitions. We note that our results were independent of film preparation conditions (using methanol or dimethyl sulfoxide (DMSO) as the solvent for r(6-MI)) and independent of whether the film or solution absorption spectrum was used to calculate the LDr spectrum. The results of the fitting analysis are shown in Figure 2A and are listed in Table 1.
Table 1.
Results of global fitting of r(6-MI) absorption and LDr spectra
| Transition | ε (M−1 cm−1)a |
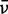 (cm−1)b (cm−1)b
|
λ (nm)c |
 (cm−1)d (cm−1)d
|
|---|---|---|---|---|
| 1 | 14 400 | 29 687 | 336.8 | 1815 |
| 2 | 11 200 | 34 596 | 289.1 | 1452 |
| 3 | 2900 | 38 327 | 260.9 | 1344 |
| 4 | 3300 | 41 282 | 242.2 | 1371 |
| 5 | 8300 | 43 923 | 227.7 | 2107 |
| 6 | 32 000 | 47 547 | 210.3 | 1952 |
aMolar extinction coefficient.
bCentre transition energy in wave numbers.
cCentre transition wavelength in nanometers.
dAbsorption line width.
We next compared the results of the quantum chemical calculations with those of the experimental absorption and LDr spectra (summarized in Table 2). We noted that there are significant differences between the LDr values of peaks 1, 2 and 6 and those of peaks 3, 4 and 5, despite the absorbance being weak in the region of the latter group, suggesting the presence of hidden weak transitions with significantly different orientations from the in-plane polarized transitions. The RICC2 results indicated the following progression in order of increasing energy; two strong in-plane polarized transitions, which we assigned to peaks 1 and 2 of the experimental spectra; four weak out-of-plane polarized transitions, of which only peaks 3, 4 and 5 could be identified in the data and a series of strong in-plane polarized transitions, of which experimental peak 6 was assigned to the lowest in energy. The data therefore matched the ordering of transitions found with the RICC2 method, provided that peaks 3, 4 and 5 were assigned to out-of-plane polarized transitions.
Table 2.
Computed and experimental electronic excitation parameters for 6-MI
| Tran. | RICC2 |
ωB97 |
Experimental |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
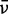 (cm−1)a (cm−1)a
|
fb | δ (°)c |
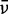 (cm−1) (cm−1) |
f | δ (°) |
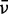 (cm−1) (cm−1) |
fd | δ1 (°)e | δ2 (°)f | ||||
| 1’ | 32 342 | 0.031 | 76 | 35 659 | 0.001 | oop | |||||||
| 1 | 32 410 | 0.28 | 76 | 36 372 | 0.35 | 73 | 29 687 | 0.28 | 66 | 88 | |||
| 2 | 37 756 | 0.12 | −22 | 41 287 | 0.15 | −28 | 34 596 | 0.18 | −61 | −69 | |||
| 3 | 40 115 | 0.0001 | oop | 45 028 | 0.0005 | oop | 38 327 | 0.042 | oop | oop | |||
| 4 | 42 372 | 0.0002 | oop | 45 981 | 0.0001 | oop | 41 282 | 0.049 | oop | oop | |||
| 5 | 42 592 | 0.0003 | oop | 50 796 | 0.0019 | oop | 43 923 | 0.19 | oop | oop | |||
| 5’ | 42 994 | 0.001 | oop | ||||||||||
| 6 | 45 158 | 0.16 | −49 | 52 816 | 0.51 | −61 | 47 547 | 0.68 | −66 | −78 | |||
aCentre transition energy in wave numbers.
bOscillator strength.
cAngle of in-plane polarized EDTM relative to C9-C10 axis in degrees (oop = out-of-plane).
dOscillator strength obtained by integrating the Gaussian functions given in Table 1.
eEDTM angle corresponding to orientation parameters obtained from orientation triangle.
fEDTM angle corresponding to orientation parameters obtained from Equation (5).
RICC2 predicts electronic excitation energies that are ca. 0.35 eV (ca. 2800 cm−1) too high for the strong peaks 1 and 2, consistent with previous benchmark studies (27). The accuracy of theoretical predictions for higher-lying electronic excited states is less certain. The excitation energy for peak 6 is underestimated by ca. 0.3 eV (ca. 2300 cm−1) by RICC2 compared with experiment. The ωB97 functional systematically overestimates the experimental excitation energies for the peaks 1–5 by ca. 0.81 eV (ca. 6800 cm−1), which is similar to the 0.5–0.6 eV error found in a recent benchmark study (28). The computed oscillator strengths of peaks 1 and 2 are in good agreement with experiment for both RICC2 and ωB97 methods. In comparison, the oscillator strength of peak 6 is considerably underestimated by RICC2 and is slightly underestimated by ωB97. These results suggest that peak 6 is likely to be prone to mixing with other high-lying excited states. As a result, the predicted excitation energies and transition moments are expected to be less accurate.
We estimated the value of 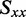 to be −0.157 according to Equation (4) and by using the average of the LDr values corresponding to peaks 3, 4 and 5. Of the remaining in-plane polarized transitions, peak 1 had the lowest value of LDr (−0.268), which was used in Equation (5) to place an upper limit on the value of
to be −0.157 according to Equation (4) and by using the average of the LDr values corresponding to peaks 3, 4 and 5. Of the remaining in-plane polarized transitions, peak 1 had the lowest value of LDr (−0.268), which was used in Equation (5) to place an upper limit on the value of 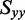 (
( −0.089). Because no transition was observed with a positive value of LDr, we estimated a lower limit on the value of
−0.089). Because no transition was observed with a positive value of LDr, we estimated a lower limit on the value of 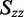 (
( 0.246) using Equation (6). A lower limit on the value of
0.246) using Equation (6). A lower limit on the value of 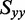 was estimated using the properties of an orientation triangle (see Figure 3) (19). The orientation triangle describes the relative magnitudes of the Saupe orientation parameters for molecules of different symmetries. Molecules with ideal rod-like symmetry are expected to fall along the lower side of the triangle, whereas molecules with ideal disk-like symmetry fall along the upper side of the triangle. Molecules of intermediate symmetries must fall within the boundaries of the triangle. Using the value we previously determined for
was estimated using the properties of an orientation triangle (see Figure 3) (19). The orientation triangle describes the relative magnitudes of the Saupe orientation parameters for molecules of different symmetries. Molecules with ideal rod-like symmetry are expected to fall along the lower side of the triangle, whereas molecules with ideal disk-like symmetry fall along the upper side of the triangle. Molecules of intermediate symmetries must fall within the boundaries of the triangle. Using the value we previously determined for 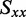 = −0.157, we note that the values of
= −0.157, we note that the values of 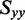 and
and 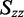 must fall on the line
must fall on the line 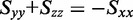 , as required to satisfy Equation (6). The intersection between this line and the boundary of the orientation triangle provides the lowest possible value of
, as required to satisfy Equation (6). The intersection between this line and the boundary of the orientation triangle provides the lowest possible value of 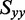 (=−0.157) and the highest possible value of
(=−0.157) and the highest possible value of 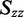 (=0.314) that are consistent with the experimental data. The absolute value of
(=0.314) that are consistent with the experimental data. The absolute value of 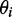 was then calculated for each transition using Equation (3). The order parameters and values of
was then calculated for each transition using Equation (3). The order parameters and values of 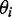 for in-plane polarized transitions 1, 2 and 6 obtained by this analysis are summarized in Table 3.
for in-plane polarized transitions 1, 2 and 6 obtained by this analysis are summarized in Table 3.
Figure 3.
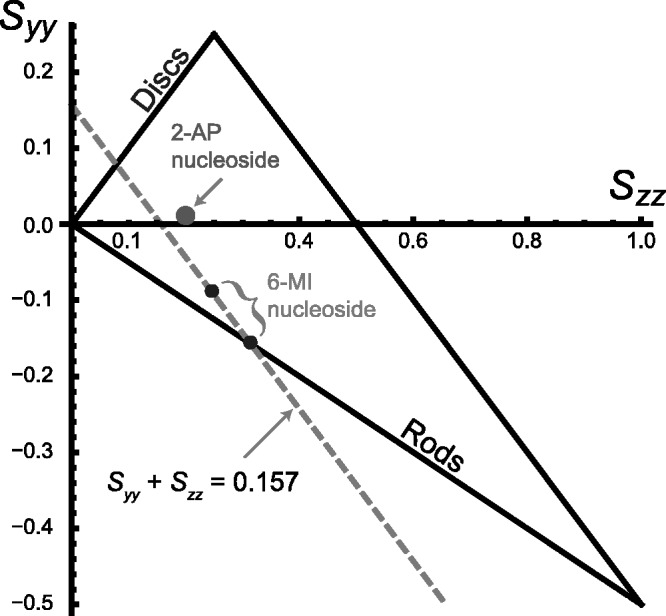
An orientation triangle for anisotropic molecules in stretched polymer films. The large dot specifies the in-plane orientation parameters obtained for 2-aminopurine nucleoside [24]. The upper small dot indicates the orientation parameters corresponding to the largest possible value of 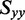 that is consistent with the experimental LDr data for r(6-MI). Because
that is consistent with the experimental LDr data for r(6-MI). Because 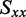 (=−0.157) is defined by the experimental LDrs of the out-of-plane polarized transitions, the values of
(=−0.157) is defined by the experimental LDrs of the out-of-plane polarized transitions, the values of  and
and 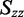 must fall on the line:
must fall on the line: 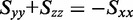 [see Equation (6)]. The intersection of this line (dashed grey) with the boundary of the orientation triangle (lower small dot) yields the smallest value of
[see Equation (6)]. The intersection of this line (dashed grey) with the boundary of the orientation triangle (lower small dot) yields the smallest value of 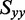 , and the largest value of
, and the largest value of 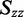 that are consistent with the experimental data.
that are consistent with the experimental data.
Table 3.
Experimental limits on orientation parameters and in-plane polarized EDTM angles
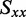 |
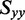 |
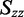 |
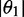 (°) (°) |
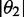 (°) (°) |
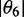 (°) (°) |
|
|---|---|---|---|---|---|---|
| Orientation triangle | −0.157 | −0.157 | 0.314 | 67.7 | 59.8 | 64.5 |
| Equation (5) | −0.157 | −0.089 | 0.246 | 90.0 | 67.0 | 75.9 |
We determined the minimum principal moment of inertia axis from B3LYP calculations of the optimized ground-state geometry of r(6-MI), finding that it lies roughly parallel to the glycosidic bond. By assuming that r(6-MI) orients with this axis parallel to the PVA film stretching direction, we converted the lab-frame angles 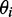 to the angles
to the angles 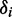 , which describe the orientations of in-plane polarized EDTMs relative to the C9-C10 axis (the two central carbons of the 6-MI base, see Figure 1). For each electronic transition, we obtained upper and lower bounds to the angles
, which describe the orientations of in-plane polarized EDTMs relative to the C9-C10 axis (the two central carbons of the 6-MI base, see Figure 1). For each electronic transition, we obtained upper and lower bounds to the angles 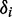 by estimating the range of orientation parameters, as described above (see Figure 4). The RICC2 prediction for the lowest-energy transition (peak 1) falls within the experimental limits, but this is not the case for the next two higher-energy in-plane polarized transitions (peaks 2 and 6). As discussed above, state mixing affects the computed orientations of higher-energy transition moments more than low-energy ones. However, we note that the prediction to peak 6 by the ωB97 method falls only 5° outside of the experimentally determined range, and the ordering of the transitions from ‘most y-polarized’ to ‘most z-polarized’ are in agreement between experiment and both RICC2 and ωB97 methods. Our experimental and computed results for the orientation of the EDTM of peak 1 are consistent with the orientation computed using the B3LYP functional and 6-311 + G(d,p) basis set in reference 8 (δ = 79°) (8).
by estimating the range of orientation parameters, as described above (see Figure 4). The RICC2 prediction for the lowest-energy transition (peak 1) falls within the experimental limits, but this is not the case for the next two higher-energy in-plane polarized transitions (peaks 2 and 6). As discussed above, state mixing affects the computed orientations of higher-energy transition moments more than low-energy ones. However, we note that the prediction to peak 6 by the ωB97 method falls only 5° outside of the experimentally determined range, and the ordering of the transitions from ‘most y-polarized’ to ‘most z-polarized’ are in agreement between experiment and both RICC2 and ωB97 methods. Our experimental and computed results for the orientation of the EDTM of peak 1 are consistent with the orientation computed using the B3LYP functional and 6-311 + G(d,p) basis set in reference 8 (δ = 79°) (8).
Figure 4.
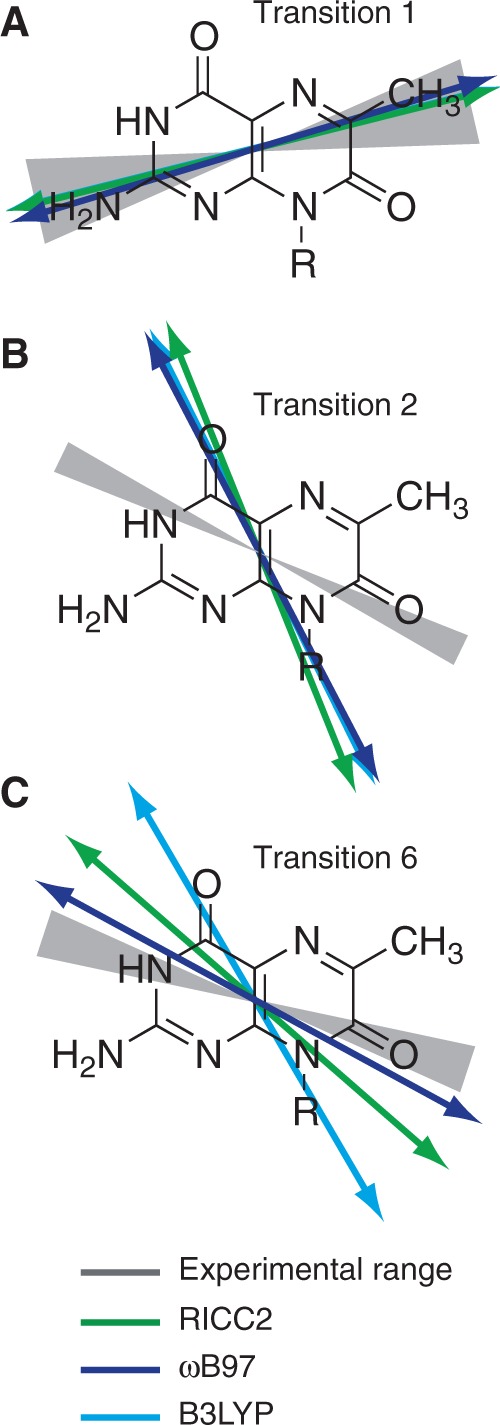
The results of experimental and calculated in-plane polarized EDTMs of 6-MI are shown. Grey hourglass regions indicate the range of EDTM orientations corresponding to the experimental limits for 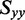 (indicated by upper and lower small dots in Figure 3). The green (RICC2), dark blue (ωB97) and light blue (B3LYP) arrows indicate the EDTMs obtained from calculations. (A) Transition 1; (B) Transition 2; (C) Transition 6.
(indicated by upper and lower small dots in Figure 3). The green (RICC2), dark blue (ωB97) and light blue (B3LYP) arrows indicate the EDTMs obtained from calculations. (A) Transition 1; (B) Transition 2; (C) Transition 6.
DISCUSSION
As mentioned in the Introduction to this article, 6-MI can be used as a fluorescent guanine analogue probe to study the local conformations of nucleic acids. A number of spectroscopic observables can yield qualitative information about local base environment, without detailed knowledge of the EDTMs in 6-MI. For example, 6-MI fluorescence intensity can indicate the extent of local base stacking in the nucleic acid or protein–nucleic acid complex being studied. Spectroscopic measurements that are sensitive to the exciton coupling between the adjacent 6-MI residues, such as CD and 2D FS, have the potential to provide more quantitative information about local base conformation, if we have accurate knowledge of the EDTMs.
In 6-MI dinucleotide–substituted DNA constructs, exciton coupling is sensitive to the magnitude, separation and relative orientation of the 6-MI EDTMs. In the point-dipole approximation (16), the exciton coupling between two 6-MI chromophores can be described using Equation (11), where 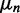 is the transition dipole of the nth [
is the transition dipole of the nth [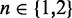 ] chromophore, R is the inter-chromophore centre-to-centre vector and
] chromophore, R is the inter-chromophore centre-to-centre vector and 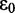 is the vacuum permittivity.
is the vacuum permittivity.
| (11) |
Thus, a determination of the coupling for specific conformations requires knowledge of the EDTM orientation within the 6-MI chromophore.
To test our determination of the lowest-energy EDTM of 6-MI, we modelled the exciton coupling between these transitions in a 6-MI di-probe–substituted dsDNA construct (3) (see Figure 5). The dipole strength 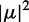 of the transition can be determined from the absorption spectrum of a mono-probe–substituted dsDNA construct, according to Equation (12).
of the transition can be determined from the absorption spectrum of a mono-probe–substituted dsDNA construct, according to Equation (12).
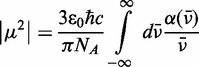 |
(12) |
Figure 5.
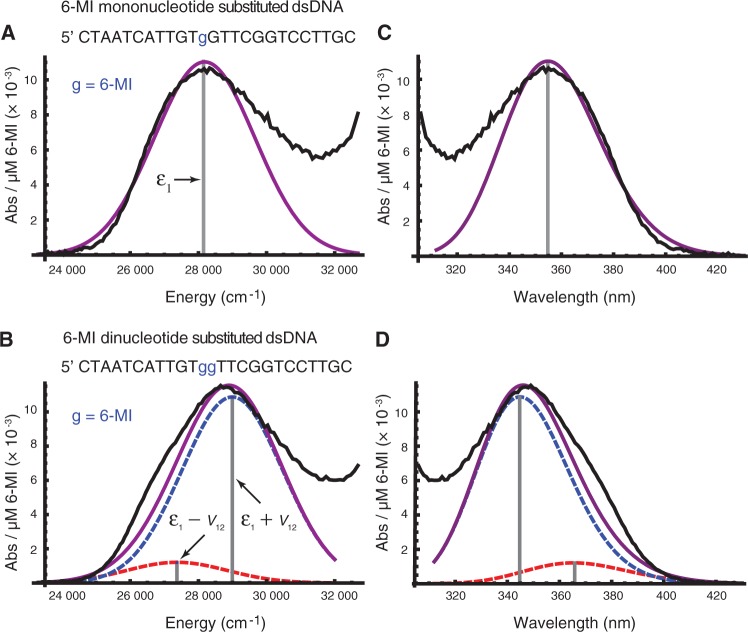
(A) A fit is shown of the low-energy region of the absorption spectrum of dsDNA containing one 6-MI base substitution (black) to a Gaussian (purple). The fit was optimized using only the 23 310–29 326 cm−1 region of the absorption spectrum to model only the lowest-energy 6-MI transition (transition 1 in our assignments), and to avoid effects from overlapping transitions in the native DNA bases. (B) The determined strength and orientation of the lowest-energy EDTM in 6-MI was used to calculate the coupling between adjacent 6-MIs expected for a B-form dsDNA structure. The spectrum of dsDNA containing two adjacent 6-MI residues (black) is shown along with the spectrum modelled using the calculated coupling and crystallographic structural parameters (purple, underlying exciton transitions in dashed blue and dashed red). The sequence of each 6-MI containing DNA strand is shown above its spectrum. The complimentary strand is not shown. (C) Plot (A), shown as a function of wavelength in nanometers. (D) Plot (B), shown as a function of wavelength in nanometers. Experimental data from reference 3.
Here, α is the absorption coefficient, 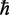 is Planck’s constant divided by
is Planck’s constant divided by  , c is the speed of light and NA is Avogadro’s number. The factor
, c is the speed of light and NA is Avogadro’s number. The factor 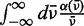 is the integrated optical line shape of the lowest-energy transition, measured in wave numbers and divided by its frequency. We fit the lowest-energy absorption peak of a 6-MI mono-probe–substituted dsDNA construct to a Gaussian line shape, as shown in Figure 5A. We thus determined the line width, intensity and transition energy of the 6-MI monomer probe within the dsDNA construct to be
is the integrated optical line shape of the lowest-energy transition, measured in wave numbers and divided by its frequency. We fit the lowest-energy absorption peak of a 6-MI mono-probe–substituted dsDNA construct to a Gaussian line shape, as shown in Figure 5A. We thus determined the line width, intensity and transition energy of the 6-MI monomer probe within the dsDNA construct to be 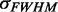 = 3480 cm−1, I = 0.011 absorbance units/μM 6-MI and
= 3480 cm−1, I = 0.011 absorbance units/μM 6-MI and 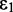 = 28 183 cm−1, respectively. Using Equation (12), we estimated the norm of the transition moment of the 6-MI monomer to be
= 28 183 cm−1, respectively. Using Equation (12), we estimated the norm of the transition moment of the 6-MI monomer to be 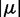 = 3.65 D. This is to be compared with a computed value of 4.27 D, which was obtained using the RICC2 method.
= 3.65 D. This is to be compared with a computed value of 4.27 D, which was obtained using the RICC2 method.
Using the values determined experimentally for the monomer transition energy and dipole strength, we calculated the absorption spectrum expected for the 6-MI dinucleotide–substituted B-form dsDNA construct (3) (see Figure 5B). These calculations assumed the in-plane orientation of the EDTM that we calculated using the RICC2 method (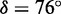 ), which falls within the boundaries established by our experiments. We further assumed that the coordinates of the two adjacent 6-MIs were the same as those of two guanines in B-form dsDNA, which we obtained from crystallographic data (protein data bank reference code 1BD1).
), which falls within the boundaries established by our experiments. We further assumed that the coordinates of the two adjacent 6-MIs were the same as those of two guanines in B-form dsDNA, which we obtained from crystallographic data (protein data bank reference code 1BD1).
Based on the exciton coupling model described above for the 6-MI dinucleotide dsDNA construct, we obtained values for the coupling V12 = 814 cm−1 and relative dipole angle 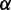 = 36.9°. The absorption spectrum of the di-probe DNA construct was calculated assuming that the exciton coupling between 6-MI residues leads to a splitting of the transition energies with
= 36.9°. The absorption spectrum of the di-probe DNA construct was calculated assuming that the exciton coupling between 6-MI residues leads to a splitting of the transition energies with 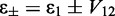 and intensities
and intensities 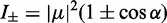 . Because the adjacent bases in duplex DNA adopt a face-to-face geometry, the sign of V12 is positive, such that the resulting spectrum exhibits a strong, blue-shifted transition and a weaker red-shifted transition, as shown in Figure 5B. We note that the agreement between the calculated and experimental spectra is excellent. For different possible values of the lowest-energy EDTM angle
. Because the adjacent bases in duplex DNA adopt a face-to-face geometry, the sign of V12 is positive, such that the resulting spectrum exhibits a strong, blue-shifted transition and a weaker red-shifted transition, as shown in Figure 5B. We note that the agreement between the calculated and experimental spectra is excellent. For different possible values of the lowest-energy EDTM angle 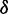 , the magnitude of the exciton coupling varies from 136 to 856 cm−1, and only values of
, the magnitude of the exciton coupling varies from 136 to 856 cm−1, and only values of 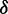 near our experimentally determined and computed values reproduce the observed shift in the absorption spectrum on addition of a second 6-MI residue.
near our experimentally determined and computed values reproduce the observed shift in the absorption spectrum on addition of a second 6-MI residue.
While the calculated spectrum shown in Figure 5B captures the observed blue shift of the absorption maximum, there is a significant low-energy shoulder in the experimental spectrum that is not reproduced by the exciton coupling model. The calculated spectrum has only a slight shoulder in this region owing to the presence of a weak red-shifted exciton transition. We note the presence of a similar shoulder in the absorption spectrum of the 6-MI mono-probe–substituted DNA construct, which represents a deviation of the monomer line shape from Gaussian. A similar shoulder is visible in the low-temperature absorption spectrum of r(6-MI) and is likely due to an underlying vibronic progression (8).
CONCLUSIONS
Using a combination of absorption and LD measurements of 6-MI in stretched PVA films, we identified six electronic transitions that occur within the spectral region between 25 000 and 50 000 cm−1. The range of possible orientations for each in-plane transition moment was determined experimentally. We performed quantum chemical calculations (RICC2 and ωB97) to predict (in order of increasing energy) two in-plane transitions, three weak out-of-plane polarized transitions and a strong in-plane polarized transition. We found that the orientation of the lowest-energy transition moment, which was predicted by both RICC2 and ωB97, agreed well with experiment. We compared the absorption spectra of two 6-MI–substituted dsDNA constructs, each labelled with just one or two adjacent 6-MI residues. We found that the strength and orientation of the lowest-energy EDTM determined in this work accurately predicts the experimentally observed blue shift in the absorption due to exciton coupling on addition of a second 6-MI residue. In future work, these results will be used to interpret in structural terms 2D FS spectra reflecting the conformations of site-specifically placed 6-MI probes in biologically active protein–nucleic acid complexes. For example, such studies have the potential to reveal valuable insights into the role of local base pair conformation and breathing fluctuations on the biochemical pathways that govern DNA replication and transcription.
FUNDING
Office of Naval Research [N00014-11-1-0193 to A.H.M.]; the National Science Foundation, Chemistry of Life Processes Program [CHE-1105272 to A.H.M.] and the National Institutes of Health [GM-15792 to P.H.v.H.]. Supported as part of the Center for Excitonics, an Energy Frontier Research Center funded by the US Department of Energy, Office of Basic Sciences [DE-SC0001088 to A.P.-O., D.R. and A.A.-G.]. Funding for open access charge: National Science Foundation.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
We thank Keira Roberts and Kristen Brewster, who were supported by the NSF sponsored Undergraduate Catalytic Outreach and Research Experiences (UCORE) program during the summer of 2011 at the University of Oregon, for their assistance in developing the PVA film preparation methods. We also acknowledge helpful experimental advice on PVA film measurements from Professor Bengt Nordén, Chalmers Institute, Goteburg, Sweden. P.H.v.H. is an American Cancer Society Research Professor of Chemistry.
REFERENCES
- 1.Driscoll SL, Hawkins ME, Balis FM, Pfeiderer W, Laws WR. Fluorescent properties of a new guanosine analog incorporated into small oligonucleotides. Biophys. J. 1997;73:3277–3286. doi: 10.1016/S0006-3495(97)78352-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hawkins ME, Pfleiderer W, Mazumder A, Pommier YG, Balis FM. Incorporation of a fluorescent guanosine analog into oligonucleotides and its application to a real time assay for the HIV-1 integrase 3′-processing reaction. Nucleic Acids Res. 1995;23:2872–2880. doi: 10.1093/nar/23.15.2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Datta K, Johnson NP, Villani G, Marcus AH, von Hippel PH. Characterization of the 6-methyl isoxanthopterin (6-MI) base analog dimer, a spectroscopic probe for monitoring guanine base conformations at specific sites in nucleic acids. Nucleic Acids Res. 2012;40:1191–1202. doi: 10.1093/nar/gkr858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hawkins ME. Fluorescent pteridine nucleoside analogs: a window on DNA interactions. Cell Biochem. Biophys. 2001;34:257–281. doi: 10.1385/CBB:34:2:257. [DOI] [PubMed] [Google Scholar]
- 5.Hawkins ME. Synthesis, purification and sample experiment for fluorescent pteridine-containing DNA: tools for studying DNA interactive systems. Nat. Protoc. 2007;2:1013–1021. doi: 10.1038/nprot.2007.150. [DOI] [PubMed] [Google Scholar]
- 6.Hawkins ME. Fluorescent pteridine probes for nucleic acid analysis. Methods Enzymol. 2008;450:201–231. doi: 10.1016/S0076-6879(08)03410-1. [DOI] [PubMed] [Google Scholar]
- 7.Narayanan M, Kodali G, Singh V, Xing Y, Hawkins ME, Stanley RJ. Differential fluorescence quenching of fluorescent nucleic acid base analogues by native nucleic acid monophosphates. J. Phys. Chem. B. 2010;114:5953–5963. doi: 10.1021/jp1011507. [DOI] [PubMed] [Google Scholar]
- 8.Kodali G, Narayanan M, Stanley RJ. Excited-state electronic properties of 6-methylisoxanthopterin (6-MI): an experimental and theoretical study. J. Phys. Chem. B. 2012;116:2981–2989. doi: 10.1021/jp2110083. [DOI] [PubMed] [Google Scholar]
- 9.Hawkins ME, Pfleiderer W, Balis FM, Porter D, Knutson JR. Fluorescent properties of pteridine nucleoside analogs as monomers and incorporated into oligonucleotides. Anal. Biochem. 1997;244:86–95. doi: 10.1006/abio.1996.9879. [DOI] [PubMed] [Google Scholar]
- 10.Augustyn KE, Wojtuszewski K, Hawkins ME, Knutson JR, Mukerji I. Examination of the premelting transition of DNA A-tracts using a fluorescent adenosine analogue. Biochemistry. 2006;45:5039–47. doi: 10.1021/bi0518343. [DOI] [PubMed] [Google Scholar]
- 11.Datta K, Johnson NP, von Hippel PH. DNA conformational changes at the primer-template junction regulate the fidelity of replication by DNA polymerase. Proc. Natl Acad. Sci. USA. 2010;107:17980–17985. doi: 10.1073/pnas.1012277107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wojtuszewski Poulin K, Smirnov AV, Hawkins ME, Balis FM, Knutson JR. Conformational heterogeneity and quasi-static self-quenching in DNA containing a fluorescent guanine analogue, 3MI or 6MI. Biochemistry. 2009;48:8861–8868. doi: 10.1021/bi9003414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wilhelmsson LM, Sandin P, Holmén A, Albinsson B, Lincoln P, Nordén B. Photophysical characterization of fluorescent DNA base analogue, tC. J. Phys. Chem. B. 2003;107:9094–9101. [Google Scholar]
- 14.Stengel G, Gill JP, Sandin P, Wilhelmsson LM, Albinsson B, Nordén B, Millar D. Conformational dynamics of DNA polymerase probed with a novel fluorescent DNA base analogue. Biochemistry. 2007;46:12289–12297. doi: 10.1021/bi700755m. [DOI] [PubMed] [Google Scholar]
- 15.Engman KC, Sandin P, Osborne S, Brown T, Billeter M, Lincoln P, Nordén B, Albinsson B, Wilhelmsson LM. DNA adopts normal B-form upon incorporation of highly fluorescent DNA base analogue tC: NMR structure and UV-Vis spectroscopy characterization. Nucleic Acids Res. 2004;32:5087–5095. doi: 10.1093/nar/gkh844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kasha M, Rawls HR, El-Bayoumi MA. The exciton model in molecular spectroscopy. Pure Appl. Chem. 1965;11:371–392. [Google Scholar]
- 17.Perdomo-Ortiz A, Widom JR, Lott GA, Aspuru-Guzik A, Marcus AH. Conformation and electronic population transfer in membrane-supported self-assembled porphyrin dimers by 2D fluorescence spectroscopy. J. Phys. Chem. B. 2012;116:10757–10770. doi: 10.1021/jp305916x. [DOI] [PubMed] [Google Scholar]
- 18.Lott GA, Perdomo-Ortiz A, Utterback JK, Widom JR, Aspuru-Guzik A, Marcus AH. Conformation of self-assembled porphyrin dimers in liposome vesicles by phase-modulation 2D fluorescence spectroscopy. Proc. Nat. Acad. Sci. USA. 2011;108:16521–16526. doi: 10.1073/pnas.1017308108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nordén B, Rodger A, Dafforn T. Linear Dicrhoism and Circular Dichroism: A Textbook on Polarized-Light Spectroscopy. Cambridge, UK: RSC Publishing; 2010. pp. 15–48, 141–210. [Google Scholar]
- 20.Seibert E, Alexander Ross JB, Osman R. Quantum mechanical investigation of the electronic structure and spectral properties of 6,8-Dimethylisoxanthopterin. Int. J. Quantum Chem. 2002;88:28–33. [Google Scholar]
- 21.Seibert E, Chin AS, Pfleiderer W, Hawkins ME, Laws WR, Osman R, Alexander Ross JB. pH-dependent spectroscopy and electronic structure of the guanine analogue 6,8-Dimethylisoxanthopterin. J. Phys. Chem. A. 2003;197:178–185. [Google Scholar]
- 22.Holmén A, Nordén B, Albinsson B. Electronic transition moments of 2-aminopurine. J. Am. Chem. Soc. 1997;119:3114–3121. [Google Scholar]
- 23.Michl J, Thulstrup EW. Spectroscopy With Polarized Light. New York: VCH Publishers; 1995. pp. 135–138. [Google Scholar]
- 24.Holmén A. Vibrational transition moments of aminopurine: stretched film IR linear dichroism measurements and DFT calculations. J. Phys. Chem. A. 1997;101:4361–4374. [Google Scholar]
- 25.Dreuw A, Head-Gordon M. Single-reference ab initio methods for the calculation of excited states of large molecules. Chem. Rev. 2005;105:4009–4037. doi: 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
- 26.Rappoport D, Hutter J. Fundamentals of time-dependent density functional theory. In: Marques MA, Maitra NT, Nogueira FM, Gross EKU, Rubio A, editors. Lecture Notes in Physics. Berlin/Heidelberg: Springer; 2012. pp. 317–336. [Google Scholar]
- 27.Schreiber M, Silva-Junior MR, Sauer SP, Thiel W. Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3. J. Chem. Phys. 2008;128:134110. doi: 10.1063/1.2889385. [DOI] [PubMed] [Google Scholar]
- 28.Jacqemin D, Perpète EA, Ciofini I, Adamo C. Assessment of the ωB97 family for excited-state calculations. Theor. Chem. Acc. 2010;128:127–136. [Google Scholar]
- 29.Caricato M, Trucks GW, Frisch MJ, Wiberg KB. Oscillator strength: how does TDDFT compare to EOM-CCSD? J. Chem. Theory Comput. 2011;7:456–466. doi: 10.1021/ct100662n. [DOI] [PubMed] [Google Scholar]
- 30.Hättig C, Weigend F. CC2 excitation energy calculations on large molecules using the resolution of the identity approximation. J. Chem. Phys. 2000;113:5154–5161. [Google Scholar]
- 31.Hättig C, Köhn A. Transition moments and excited-state first-order properties in the coupled-cluster model CC2 using the resolution-of-the-identity approximation. J. Chem. Phys. 2002;117:6939–6951. [Google Scholar]
- 32.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- 33.Chai J-D, Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008;128:084106. doi: 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- 34.Weigend F, Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 35.Weigend F, Häser MH, Patzelt R. Ahlrichs, RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998;294:143–152. [Google Scholar]
- 36. TURBOMOLE V6.3 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, cited TURBOMOLE GmbH, since 2007. http://www.turbomole.com.
- 37. Q-Chem. (2011) Version 4.0, Q-Chem, Inc., Pittsburgh, PA. http://www.q-chem.com.
- 38.Weigend F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006;8:1057–1065. doi: 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- 39.Mayo SL, Olafson BD, Goddard WA. DREIDING: a generic force field for molecular simulations. J. Phys. Chem. 1990;94:8897–8909. [Google Scholar]
- 40.Matsuoka Y, Nordén B. Linear dichroism studies of nucleic acid bases in stretched poly (vinyl alcohol) films. J. Phys. Chem. 1982;86:1378. [Google Scholar]
- 41.Natarajan LV, Robinson M, Blankenship RE. Linear dichroism of cyanine dyes in stretched polyvinyl alcohol films. J. Chem. Ed. 1983;60:241–243. [Google Scholar]
- 42.Michl J, Thulstrup EW, Eggers JH. Polarization spectra in stretched polymer sheets II. J. Phys. Chem. 1970;74:3868. [Google Scholar]
- 43.Byrd RH, Nocedal J, Waltz RA. KNITRO: an integrated package for nonlinear optimization. In: di Pillo G, Roma M, editors. Large-Scale Nonlinear Optimization. Springer-Verlag, New York; 2006. pp. 35–59. [Google Scholar]