Abstract
Common diseases such as endometriosis (ED), Alzheimer's disease (AD) and multiple sclerosis (MS) account for a significant proportion of the health care burden in many countries. Genome-wide association studies (GWASs) for these diseases have identified a number of individual genetic variants contributing to the risk of those diseases. However, the effect size for most variants is small and collectively the known variants explain only a small proportion of the estimated heritability. We used a linear mixed model to fit all single nucleotide polymorphisms (SNPs) simultaneously, and estimated genetic variances on the liability scale using SNPs from GWASs in unrelated individuals for these three diseases. For each of the three diseases, case and control samples were not all genotyped in the same laboratory. We demonstrate that a careful analysis can obtain robust estimates, but also that insufficient quality control (QC) of SNPs can lead to spurious results and that too stringent QC is likely to remove real genetic signals. Our estimates show that common SNPs on commercially available genotyping chips capture significant variation contributing to liability for all three diseases. The estimated proportion of total variation tagged by all SNPs was 0.26 (SE 0.04) for ED, 0.24 (SE 0.03) for AD and 0.30 (SE 0.03) for MS. Further, we partitioned the genetic variance explained into five categories by a minor allele frequency (MAF), by chromosomes and gene annotation. We provide strong evidence that a substantial proportion of variation in liability is explained by common SNPs, and thereby give insights into the genetic architecture of the diseases.
INTRODUCTION
Common diseases including coronary heart disease, cancer, mental disorders, chronic respiratory illnesses, inflammatory bowel disease and diabetes account for the greatest health care burden in many countries. Most of these common diseases are complex and the risk of diseases are influenced by multiple environmental and genetic factors. Identifying specific environmental risk factors and quantifying their contributions to disease risk are difficult. In contrast, studies show that genetic variation makes a substantial contribution to disease risk for many common diseases (1,2) and genome-wide association studies (GWASs) provide a powerful method to identify genetic risk factors contributing to common diseases. Many individual genetic variants contributing to disease risk for a range of diseases have been identified using these methods (3–5).
It is important to understand the genetic architecture of complex diseases to help develop better methods for diagnosis and treatment. The effect size for most variants is small and collectively the known variants explain only a small proportion of the estimated heritability for most diseases (3,6). This gap between the estimated heritability and the proportion of variation explained by known risk variants is generally referred to as ‘the missing heritability’ (7,8). The estimates of the significance of GWAS results must be corrected for the large number of tests and as a consequence, GWAS analyses control false positives at the expense of false negatives. Many other variants in linkage disequilibrium with single nucleotide polymorphisms (SNPs) on commercial genotyping chips could contribute to disease risk, but have not been identified as genome-wide significant. Yang et al. (2010) (9) demonstrated that approximately half of the heritability (45% of the phenotypic variance) of human height could be explained by considering all SNPs simultaneously in a linear model analysis. The results suggest that most of the heritability is not missing, but has not been detected in current GWAS data because the effect sizes for many variants are too small. Moreover, much of the remaining ‘missing’ heritability is likely to be due to incomplete linkage disequilibrium between causal variants and SNPs on the early commercial chips. Reduced linkage disequilibrium will occur if causal variants have a minor allele frequency (MAF) different from (typically lower than) genotyped SNPs (10).
The methods derived for quantitative traits have been adapted for case–control studies of disease using a linear mixed model, in which the estimates made on the observed binary scale are transformed to a scale of liability, whilst adjusting both for scale and for ascertainment (11). Theory and pedigree simulation suggest that the method is unbiased (11). We and others have applied the methods to a range of diseases, including schizophrenia (12), rheumatoid arthritis (13) and major depressive disorders (14). Genetic variation is estimated when case–case pairs and control–control pairs are, on average, more similar genome-wide than case–control pairs. However, application to binary traits has potential problems that do not arise for quantitative traits. Quality control (QC) of SNP genotype data and adjustment for possible population stratification are important because any artefact that causes genotypes of cases to be more similar to each other on average and controls to be more similar to other controls would be estimated and interpreted as ‘genetic’ variance.
In this study, we have applied methods to estimate and partition the proportion of variation attributable to causal variants in linkage disequilibrium with common SNPs by analysing data for endometriosis (ED), Alzheimer's disease (AD) and multiple sclerosis (MS); diseases associated with reproduction, aging and the immune system. We recently conducted a GWAS for ED using the same data as used here and reported the proportion of variation in ED risk explained by common SNPs (15). However, those estimates were not adjusted for ascertainment and scale, nor were they further partitioned.
Importantly for this study, for all three diseases case and control samples were not all genotyped in the same laboratory. We demonstrate that a careful analysis can obtain robust estimates, but also that insufficient QC of SNPs can lead to spurious results and too stringent QC is likely to remove real genetic signals.
RESULTS
Estimated genetic variance tagged by all SNPs
After our standard QC protocol, the proportion of variation in liability captured by all SNPs was estimated and ranged from 0.24 to 0.30 (Table 1). For ED, the estimated genetic variance proportional to the total variance on the liability scale was 0.26 (SE 0.04). The estimates for the other diseases were similar with the estimates on the liability scale of 0.24 (SE = 0.03) for AD and 0.30 (SE 0.03) for MS. The P-values for tests of the estimates being different from zero for all three diseases were highly significant (Table 1). The estimated genetic variances on the liability scale using genome-wide SNPs were lower than the heritability estimated from twin or family-based studies, but much higher than variance explained by genome-wide significant SNPs (Table 1). For AD, the proportion of variance in liability explained by a GWAS is relatively large (∼0.18) because of the very large effect of APOE (16,17).
Table 1.
Estimated heritability using genome-wide SNP data after the stringent QC
| Disease | Case/control | No. of SNPs |
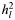 (SE)a (SE)a
|
P-value | Heritabilityb | GWASc |
|---|---|---|---|---|---|---|
| ED | 3154/6981 | 488 532 | 0.26 (0.04) | 3.62e-11 | ∼ 0.5 (38) | <0.01 (15) |
| AD | 3290/3849 | 499 757 | 0.24d (0.03) | 2.15e-15 | ∼ 0.76 (40) | 0.18d (16) |
| MS | 1604/1953 | 293 474 | 0.30e (0.03) | 7.15e-22 | 0.25–0.76 (46) | 0.06e (23) |
aEstimated genetic variance proportional to the total variance on the liability scale. bHeritability estimated from twin or family-based studies. cVariance explained by genome-wide significant SNPs. dOf this, ∼0.04 can be attributed to the APOE locus. eOf this ∼0.03 can be attributed to the MHC region.
Data were also analyzed after a more stringent QC protocol. There was a small decrease in the estimates of genetic variance and the P-values increased slightly (Supplementary Material, Table S4). These small changes showed that the estimates were robust and had stabilized given the QC protocols implemented. We used the two-locus test (18) and checked whether there were artefactual batch effects associated with the case–control status (Supplementary Material, Figs S1–S3). The results show that stringent QC and controlling for possible batch effects in genotyping between cases and controls made little difference to our estimates and there was no apparent inflation caused by genotyping artefacts between case and control samples across the three diseases (Supplementary Material, Figs S1–S3).
Genetic variance partitioned by MAF
In order to explore whether common causal variants are responsible for part of the variance explained by the SNPs, we undertook an analysis partitioning the variance tagged by SNPs into five components defined by MAF (Table 2). As expected, the sum of the five components was similar to the single SNP set analysis for each disorder. For ED, the estimated genetic variances for five components ranged from 0.03 to 0.08 (SE = 0.03–0.04) across the allele frequency range. The highest estimates were for the categories of MAFs from 0.2 to 0.4. Approximately 90% of the estimated genetic variance was explained by common SNPs of MAF > 0.1 (Table 2). For AD, the pattern of the estimated genetic variance fluctuated across the MAF categories, ranging from 0.0 for SNPs with MAFs 0.1–0.2 up to 0.08 for SNPs with low MAFs (<0.1) and MAFs between 0.3 and 0.4. A significant proportion of the genetic variance was explained by common SNPs with MAFs >0.2 (Table 2) (again reflecting APOE). Adjusting for APOE by fitting five tagging SNPs in APOE as covariates changed the partitioning results slightly (results not shown). For MS, the estimated genetic variances for five components ranged from 0.03 to 0.09 (SE = 0.02–0.03), and the distribution of the estimated genetic variance for MAF was similar to ED. A substantial proportion of genetic variance (90%) was due to common SNPs with MAFs >0.1.
Table 2.
Estimated proportion of variance on the liability scales explained by all SNPs and partitioned by SNP MAF
| MAF | ED |
AD |
MS |
|||
|---|---|---|---|---|---|---|
| No. of SNPs |
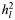 (SE) (SE) |
No. of SNPs |
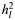 (SE) (SE) |
No. of SNPs |
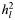 (SE) (SE) |
|
| <0.1 | 83034 | 0.03 (0.03) | 83002 | 0.08 (0.02) | 40360 | 0.03 (0.02) |
| 0.1–0.2 | 118571 | 0.03 (0.04) | 121780 | 0.00 (0.03) | 70550 | 0.08 (0.03) |
| 0.2–0.3 | 102261 | 0.07 (0.04) | 104937 | 0.06 (0.03) | 63876 | 0.07 (0.03) |
| 0.3–0.4 | 94183 | 0.08 (0.03) | 96610 | 0.08 (0.03) | 60243 | 0.09 (0.03) |
| 0.4–0.5 | 90483 | 0.05 (0.03) | 93428 | 0.02 (0.02) | 58445 | 0.03 (0.02) |
| Total | 488532 | 0.25 | 499757 | 0.25 | 293474 | 0.30 |
Genetic variance partitioned by chromosome
We performed two kinds of analyses which estimated the proportion of additive genetic variation contributed by individual chromosomes: one in which the similarity relationship matrix for each chromosome was fitted separately (one additive genetic variance component per analysis) and one in which we fitted 22 relationship matrices simultaneously (22 additive genetic variance components). The estimates from the joint analysis and those from each chromosomal analysis were similar (Supplementary Material, Figs S4–S6), and only the results from the joint analysis are presented in the main text (Fig. 1). The sum of estimates from the joint analysis was similar to the estimates from the analysis using all SNPs simultaneously in estimating relationships.
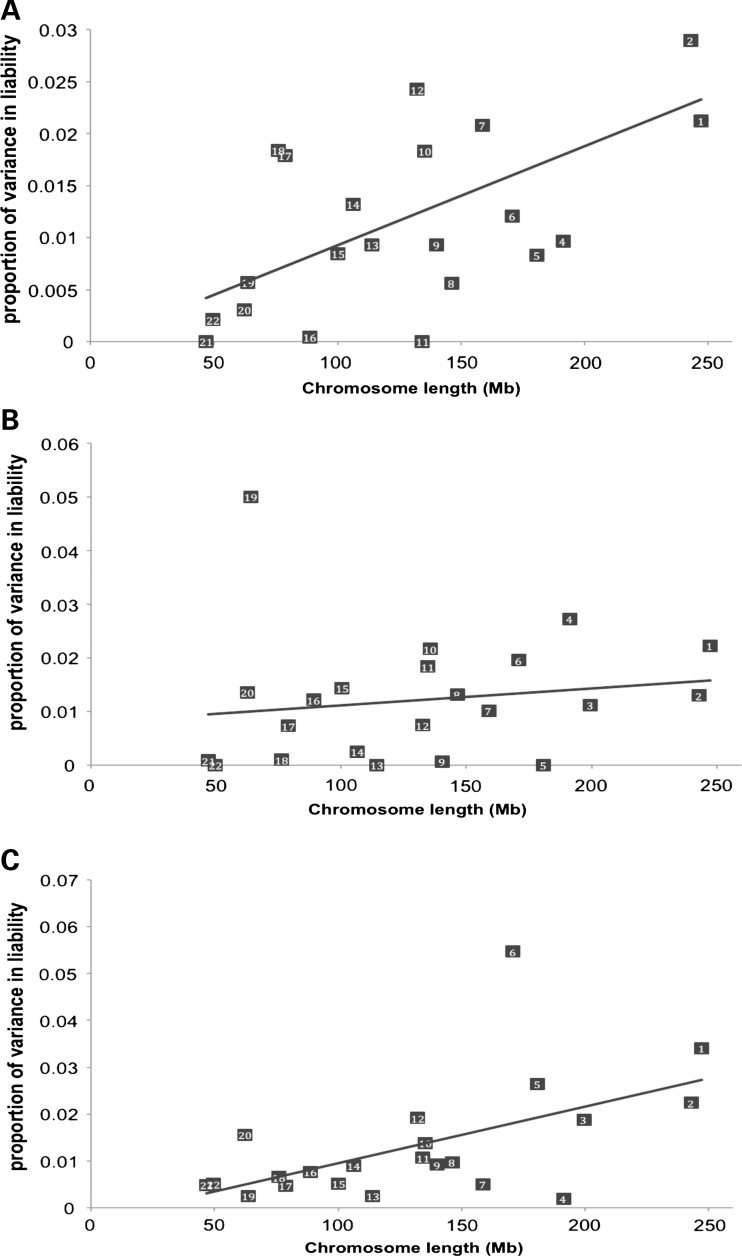
Figure 1.
Joint analysis for each chromosome for estimating the genetic variance using SNP data. (A) ED. y = −0.0002 + 0.00009x, R2 = 0.37, P = 0.003. (B) AD. y = 0.0081 + 0.00003x, R2 = 0.024, P = 0.49 and omitting chromosome 19, y = 0.00061 + 0.00007x, R2 = 0.25, P = 0.02. (C) MS. y = −0.002509 + 0.00012x, R2 = 0.31, P = 0.007 and omitting chromosome 6, y = 0.0014 + 0.0001x, R2 = 0.45, P = 0.0009.
The estimates of variance explained by each chromosome are linearly related to the length of the chromosome for ED (R2 = 0.59) (Fig. 1A) and for MS (R2 = 0.37) (Fig. 1C). However, for AD, there was no linear relationship between the estimates and the length of the chromosome, although the linear relationship became significant without the component due to chromosome 19 (R2 = 0.25) (Fig. 1B). These analyses quantify the total amount of additive genetic variation tagged by SNPs for each chromosome, and should be consistent with reported GWAS findings on either the same or other datasets. Accordingly, we observe a moderate deviation from the regression line for chromosome 7 for ED (Fig. 1A) and substantial deviations for chromosome 6 for MS (Fig. 1C) and chromosome 19 for AD (Fig. 1B), consistent with the reported GWAS signals at 7p, major histocompatibility complex (MHC) and APOE, respectively. We estimated the contribution of the APOE locus. We fitted the five most associated SNPs in the APOE region from the Harold et al. analysis (listed in their Table 1: rs2075650, rs157580, rs6859, rs8106922, rs405509) as covariates and found that the variance explained by chromosome 19 dropped from 5 to 1%. These analyses demonstrate that the APOE locus explains most of the variation for chromosome 19. We also used the weighted probit model (19) fitting the five SNPs in the APOE region, and obtained ∼4% of the total variance explained by the SNPs. For MS, we estimated the variance attributed to the MHC region from 29799095 to 33162954 bp in chromosome 6. The estimated proportion of variance in liability was ∼3% (Table 1).
Genetic variance partitioned based on SNP annotation
Partitioning the genetic variance explained by SNPs into two components by creating relationship matrices from SNPs located in genes and those not associated with annotated genes (Table 3) showed that the variance explained by SNPs associated with genes was equal to that explained by non-genic SNPs for ED (Table 3). The variance associated with annotated genes was greater than the proportion of the genome that they represent for AD and MS, but this excess variation was not significant (P = 0.12 for AD and 0.06 for MS). Further, we estimated the variance explained by specific genes related to the diseases (12), i.e. CNS+ (20) for AD, immune-related genes (21) for MS and genes annotated by terms related to ED using Gene2MeSH (22) for ED (Supplementary Material, Table S2). For MS, genetic variance was significantly enriched in immune-related genes (P = 0.001) (Supplementary Material, Table S2), consistent with the results from validated genome-wide significant SNPs (23). However, there was no enrichment of the CNS+ and ED-related genes for AD and ED, respectively.
Table 3.
Estimated proportion of variance on the liability scales explained by SNPs associated with annotated genes and SNPs not associated with annotated genes
| No. of SNPs | ∼Mb |
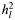 (SE) (SE) |
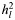 as % of total as % of total |
|
|---|---|---|---|---|
| ED | ||||
| Genesa | 253514 | 1370 (49%) | 0.13 (0.03) | 50% |
| Not in genes | 235018 | 1408 (51%) | 0.13 (0.03) | 50% |
| Total | 488532 | 2778 (100%) | 0.27 | |
| AD | ||||
| Genesa | 259031 | 1367 (49%) | 0.15 (0.03) | 62% |
| Not in genes | 240726 | 1412 (51%) | 0.09 (0.03) | 38% |
| Total | 499757 | 2779 (100%) | 0.24 | |
| MS | ||||
| genesa | 150499 | 1368 (49%) | 0.19 (0.03) | 62% |
| Not in genes | 142975 | 1409 (51%) | 0.11 (0.03) | 38% |
| Total | 293474 | 2777 (100%) | 0.30 | |
aSNPs were assigned to genes if they were positioned within 20kb from the boundary of a gene. The P-value for difference between the proportion of physical coverage and genetic variance of genic region is P = 0.785, 0.117 and 0.059 and for ED, AD and MS, respectively.
Control–control analyses
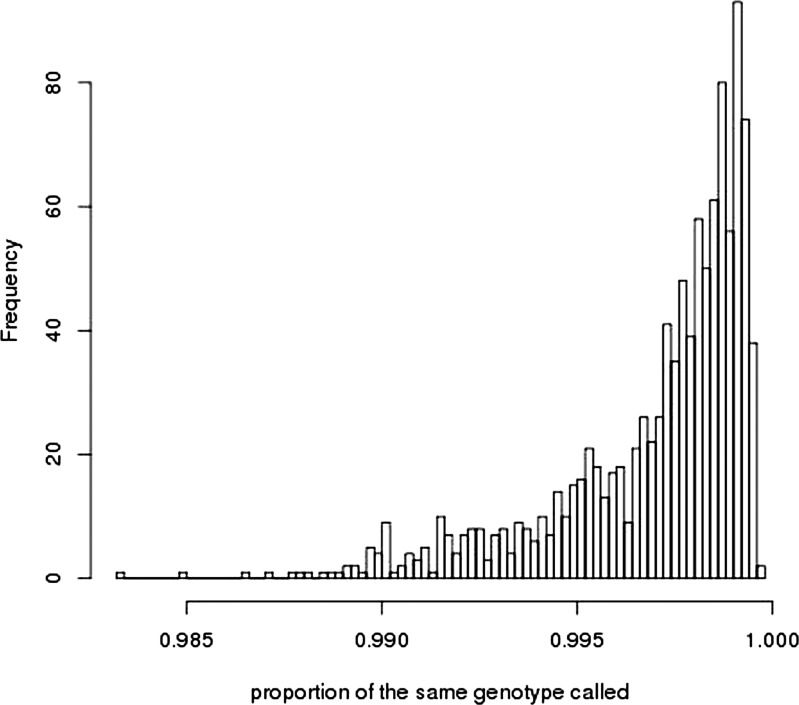
In extending the methods derived for quantitative traits to binary traits, we cautioned that any artefacts causing genotypes of cases to be more similar to each other on average, and genotypes of controls to be more similar to other controls would be estimated and interpreted as ‘genetic’ variance (11). For all three case–control samples analysed here, cases and controls were genotyped independently. To determine whether artefacts could explain the case–control results, we undertook analyses based on control–control comparisons, with results presented in Supplementary Material, Table S3. Under standard QC, five of the six control–control analyses showed estimates of ‘genetic’ variance significantly different from zero. After the most stringent QC, the estimates were not significant, except for the 1958/QIMR and the Oxford ED controls (OEC)/QIMR comparisons, where OEC are the Oxford ED Controls, a sample that overlaps in part with the 1958 sample (therefore, the 1958/QIMR and OEC/QIMR estimates are not independent). Although these results could reflect genuine population differences, subtle differences in genotyping and QC practices could generate differences in allele frequencies for SNPs across the entire genome. One known difference between the samples was that the genotypes for the OEC, 1958 and AD samples were called from the raw intensity data with the Illuminus (24) algorithm, whereas the QIMR genotypes were called with the GenCall (25) algorithm. The original intensity data were not available to us to allow direct investigation of the impact of genotype calling algorithm. However, the International Endogene consortium provided genotype data from a sample that partly overlapped with the1958 sample, for which genotypes had been called with the GenCall algorithm. To illustrate the problem more clearly, we constructed three independent UK control datasets: 1958A (the subset of the 1958 cohort for which the same individuals were called with both Illuminus and GenCall), 1958B (the subset of the 1958 cohort with genotypes called only with Illuminus) and OECX (the OEC controls called with Illuminus with any individuals featured in 1958A or 1958B removed). Analyses under standard QC show that point estimates of ‘genetic’ variance for 1958A/1958B and 1958A/OECX with 1958A genotypes called by Illuminus are small and non-significant, whereas the estimates when the 1958A genotypes were called with the GenCall algorithm are large and for 1958A/OECX are significantly different from zero (Table 4). The differences in genotype calling between the algorithms for the 1958A cohort are subtle, with 99.697% (SD 0.2539%) of genotypes called the same. The distribution of proportion of genotypes called the same over SNPs is given in Fig. 2, with allele frequencies per SNP plotted in Supplementary Material, Fig. S7. However, genotype calling algorithm does not solely contribute to the control–control results with the QIMR sample, since analyses of both 1958AI/QIMR and 1958AG/QIMR generates estimates of ‘genetic’ variance which are significantly different from zero. In these examples, the estimates of genetic variance become non-significant under the most stringent QC.
Table 4.
Impact of genotype calling algorithm on estimates of heritability from control–control samples
| Disease | Samples | No. of SNPs |
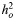 (SE) (SE) |
P-value |
|---|---|---|---|---|
| Standard QC | ||||
| 1958A (I)/1958B (I) | 1076/1576 | 492893 | 0.00 (0.13) | 1.00 |
| 1958A (G)/1958B (I) | 1076/1576 | 492893 | 0.20 (0.14) | 0.13 |
| 1958A (I)/OECX (I) | 1076/2565 | 473047 | 0.04 (0.10) | 0.66 |
| 1958A (G)/OECX (I) | 1076/2565 | 466005 | 0.48 (0.10) | 1.9e-06 |
| 1958A (I)/QIMR (G) | 1076/1836 | 488150 | 0.53 (0.12) | 4.7e-06 |
| 1958A (G)/QIMR (G) | 1076/1836 | 472019 | 0.64 (0.12) | 1.0e-07 |
| Most stringent QC | ||||
| 1958A (G)/OECX (I) | 1076/2565 | 313076 | 0.04 (0.10) | 0.68 |
| 1958A (I)/QIMR (G) | 1076/1836 | 397802 | 0.08 (0.12) | 0.48 |
| 1958A (G)/QIMR (G) | 1076/1836 | 337695 | 0.16 (0.12) | 0.20 |
The 1958 cohort was split into a sample (1958A) for which genotypes had been called with both Illuminus (I) and with GenCall (G) and into a sample only called with Illuminus (1958B). The OECX sample is the OEC control samples with 1958 cohort controls removed. In this way, 1958A, 1958B and OECX are three independent control samples.
Figure 2.
Histogram of the proportion of genotypes for each SNP that is called the same for the 1958A cohort called by the Illuminus or GenCall algorithm.
How do these control–control results impact on the interpretation of the case–control results? When the most stringent QC was applied to the case–control studies for ED, AD and MS, the estimates were reduced as expected (Supplementary Material, Table S4), because the most stringent QC used here is likely to exclude real genetic signals. Nevertheless, a significant proportion of genetic variation was retained for each dataset (∼60% of the estimates before this QC), and the P-value for the estimates were still highly significant. Furthermore, for AD and MS, the variance explained by SNPs in genes is significantly more expected by chance (Table 3), a result that is unlikely to be generated by genotyping artefacts. The results from the ED sample should be considered with more caution.
DISCUSSION
There has been considerable debate on the relative contribution of common and rare variants to the risk of common diseases (26,27). We have estimated genetic variances on the liability scale using SNPs from GWASs in unrelated individuals for three important diseases. Our estimates show that common SNPs on commercially available genotyping chips capture significant variation contributing to liability for all three diseases. The estimated proportion of total variation tagged by all SNPs was 0.26 (SE 0.04) for ED, 0.24 (SE 0.03) for AD and 0.30 (SE 0.03) for MS. These estimates are lower than those from twin or family-based studies, but substantially higher for ED and MS than the variance explained by genome-wide significant SNPs for each disease. The comparison of additive variance explained by all SNPs and the total genetic variation estimated from twin and family-based studies is not straightforward. However, the estimates from pedigree studies can be biased by non-additive genetic variation and by confounding with environmental factors (28,29), whereas our estimates are based on such distant relationships that such effect are expected to be negligible.
To consider the allele spectrum for the contribution of common variants to disease risk, we partitioned the variance explained into five categories by MAFs. For each disease, a substantial proportion of variation was explained by SNPs with MAFs between 0.2 and 0.4. Linkage disequilibrium between low frequency causal variants and common genotyped SNPs is low (30) and therefore, the observation that genotyped SNPs with MAFs >0.2 explains a substantial proportion of variation in liability points to underlying common causal variants that are in high LD with these genotyped SNPs (12). Using simulation, Lee et al. (12) showed that the estimated genetic variance for each MAF interval is likely proportional to the real genetic variance in each MAF interval (Supplementary Material, Table S6 in (12)), and those results are applicable here also. One might hypothesize that the reduced fertility and fecundity associated with both ED (31) and MS (32), but not AD (which has age on onset after reproductive years), could generate differences in the frequency distribution of risk alleles between the diseases. Our results present no support for this hypothesis. However, the large standard errors of the estimates of genetic variance associated with the genome and with the allelic spectrum mean that it is difficult to draw conclusions—much larger sample sizes and ideally a better coverage of low frequency variants would be needed to make stronger inference. In addition, the focus on the allelic spectrum of risk variants for a particular disease ignores the effect of those variants on other (unmeasured) traits and therefore, the net effect of the risk variants on fitness may be quite different from their apparent effects on a single disease. Therefore, in principle our results could be consistent with pleiotropy that is inevitable under a polygenic architecture of multiple complex traits (33).
We estimated the variance explained by each chromosome by a joint or separate analysis. When fitting one chromosome at a time, the variance attributable to the chromosome could include variance contributed by other chromosomes if there is LD between chromosomes as a consequence of population stratification (10,34). However, the inflation due to variance contributed by other chromosomes was negligible, i.e. the estimates from the joint and separate analyses were similar to each other (Supplementary Material, Figs S4–S6), consistent with the absence of population stratification (10).
There are now many case–control datasets available to researchers for analysis. In a number of these, genotyping was not performed on cases and controls in the same experiment. For example, researchers increasingly rely on shared controls from a repository or simply cannot afford to genotype both cases and controls. These experimental designs can lead to bias, for example due to technical artefacts or differences in calling algorithms. Subtle artificial allele frequency differences between cases and controls will make the cases appear to be more similar to each other than they are to the controls, and this could cause the estimation of spurious genetic variance (11). Here, we show that with careful and stringent QC steps, these potential problems can be overcome to a large extent. However, we did find differences between control cohorts (Table 4). Our results imply that differences in calling algorithms can contribute to spurious estimation of genetic variation. Therefore, caution should be applied when estimating genetic (co)variation from samples that were genotyped separately and we advocate careful attention to ensure that post-genotyping analysis procedures are the same across cases and controls. This potential for bias is much less severe for quantitative traits, because different cohorts are likely to have samples across the entire range of phenotypes.
In conclusion, we estimated additive genetic variation that is captured by the current generation of SNP arrays for three important diseases, and partitioned this variation according to chromosome, MAF, gene and pathway groups. We provide strong evidence that a substantial proportion of variation in liability is explained by common SNPs, and thereby, give insights into the genetic architecture of the diseases. Consistent with reports on other diseases (11,13), schizophrenia (12,35) and quantitative traits (9,10,36,37), these results point to a disease model where the cumulative effect of many risk variants, across a range of allele frequencies, together with environmental risk factors causes common disease.
MATERIALS AND METHODS
Data
Endometriosis
ED is a gynaecological disease where tissue that resembles endometrium is found growing on sites outside of the uterus, and affects 6–10% of women of reproductive age (38). Symptoms vary, but typically include severe menstrual pain, chronic pelvic pain, sub- or infertility and digestive system problems, all of which can have major impacts on the overall health and well-being of sufferers in addition to imposing significant annual costs on health care systems (39). A GWAS was conducted by the International Endogene Consortium with 2247 cases recruited at the Queensland Institute of Medical Research and 924 cases recruited at the University of Oxford (15). All cases had surgically confirmed disease and samples were genotyped on the Illumina Human670Quad BeadArray (15). Illumina Human610Quad control genotypes for QIMR cases were available for 1836 individuals in an adolescent twin study. The Oxford controls were 5190 UK population controls obtained from the Wellcome Trust Case Control Consortium (WTCCC2). These controls were genotyped with the Illumina Human1M-Duo array (15). The Wellcome Trust controls consist of the 1958 British Birth Cohort and from the National Blood Donors. Since the samples from the 1958 British Birth Cohort were also used in the analysis of the Alzheimer's GWAS, but not with perfect overlap, we refer to the controls used by the Oxford researchers as the OEC. For the ED analyses, the QIMR and Oxford samples were combined. Genotypes from Oxford cases and controls were called with the Illuminus (24) algorithm. Genotypes from the QIMR cases and controls were called with the GenCall (25) algorithm. Initial data for ED were 3171 cases and 7026 controls with 496733 SNPs.
Alzheimer's disease
The samples included 3333 cases and 1225 elderly screened controls genotyped at the Sanger Institute on the Illumina 610-quad chip after filtering a stringent QC process for which the details were described by Harold et al. (40). According to Harold et al. (33), ‘these samples were recruited by the Medical Research Council (MRC) Genetic Resource for AD (Cardiff University; Institute of Psychiatry, London; Cambridge University; Trinity College Dublin), the Alzheimer's Research Trust Collaboration (University of Nottingham; University of Manchester; University of Southampton; University of Bristol; Queen's University Belfast; the Oxford Project to Investigate Memory and Ageing, Oxford University); Washington University, St Louis, USA; MRC PRION Unit, University College London; London and the South East Region AD project (LASER-AD), University College London; Competence Network of Dementia and Department of Psychiatry, University of Bonn, Germany and the National Institute of Mental Health AD Genetics Initiative’ (40). Population controls of 2699 samples from a WTCCC2 1958 cohort (Illumina 1.2M) were additionally combined for analyses. Genotypes of cases and controls were called with the Illuminus (24) algorithm (40). Initial data for AD consisted of 3333 cases and 3924 controls with 529 205 SNPs, which were quality controlled again.
Multiple sclerosis
There were 1618 cases from the Australia and New Zealand (ANZ) cohort genotyped on the Illumina infinium Hap370CNV array and 1988 healthy US controls of Caucasian descent from Illumina iControlDB. According to the ANZGene Consortium (41), ‘Australian MS cases were self-identified volunteers recruited at centers located in Adelaide, Brisbane, Gold Coast, Hobart, Melbourne, Newcastle, Perth and Sydney. New Zealand MS cases were collected across the country as part of a recent national prevalence survey. Controls were provided by the Sanger Institute (Cambridge, UK)’. These samples passed careful QC as previously described (41) with genotypes called with the GenCall (25) algorithm (41). Initial data for MS included 1618 cases and 1988 controls with 293 631 SNPs.
Quality control (QC)
Standard QC
Standard QC steps were applied to protect against artefacts (11). SNPs with MAFs <0.01, missing rates >0.05 or P-value <0.0001 for the Hardy–Weinberg equilibrium test were excluded as were individuals with SNP missingness rates >0.01. We also excluded subjects so that no pair of individuals had a similarity relationship coefficient >0.05 (equivalent to about second-cousins). Sex chromosomes were excluded from the analysis. Supplementary Material, Table S1 shows how many cases and controls, and SNPs were excluded after the standard QC. After the standard QC process, the number of samples and SNPs used for estimating the genetic variance was 10135 individuals (3154 cases and 6981 controls) with 488532 SNPs for ED, 7139 individuals (3290 cases and 3849 controls) with 499 757 SNPs for AD and 3557 individuals (1604 cases and 1953 controls) with 293 474 SNPs for MS (Supplementary Material, Table S4).
Stringent QC
When two groups of samples are separately genotyped, batch effects may influence the estimated genetic variances that are systematically biased (11,18). Therefore, stringent QC was applied to check how robust the estimates were. For this test, SNPs for which P-values were <0.05 for the Hardy–Weinberg equilibrium and for missingness difference between two groups were excluded. We also applied a two-locus QC test (18) based on the difference in test statistic of association between single SNPs and pairs of SNPs, and diagnosed whether there were artefact batch effects. After this stringent QC, the number of SNPs was decreased although the number of samples was not changed (Supplementary Material, Table S1). The number of SNPs that remained was 416 816 SNPs for ED, 426 467 SNPs for AD and 261 309 SNPs for MS (Supplementary Material, Table S4).
Most stringent QC
In addition to the stringent QC, for some analyses we applied even more stringent QC that is most likely to remove the true signal as well as artefacts in the estimation of variance explained by SNPs. In this most stringent QC, we compared allele frequencies in each cohort with those from HapMap3 samples, and excluded SNPs having a significantly different frequency from HapMap3 (P < 0.003). Subsequently, we applied a two-locus QC step (18) to filter out problematic SNPs. In the process of the two-locus QC, we excluded SNPs that caused the joint two-SNP model to fit significantly better (P < 0.02) than expected from the two single SNP models (18), considering each of 20 flanking markers. In addition, we fitted the first 50 principal components estimated from the two control cohorts in the association model. The number of SNPs that remained was 391 913 for ED, 403 398 for AD and 248 980 for MS (Supplementary Material, Table S4).
Model
We estimated the variance in case–control status explained by all SNPs using a linear mixed model,
| (1) |
where y is a vector of case (=1) or control (=0) status on the observed scale, β is a vector for fixed effects of overall mean (intercept), and 10 ancestry principal components (for ED, cohort status, QIMR and Oxford, was additionally fitted as a fixed effect to adjust for possible artefactual batch effects), g is the vector of random additive genetic effects based on aggregate SNP information and e is a vector of random error effects. X is an incidence matrix for the fixed effects relating to individuals. The variance structure of phenotypic observations is
Where 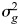 is the additive genetic variance tagged by the SNPs,
is the additive genetic variance tagged by the SNPs, 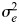 is the error variance, A is the genomic similarity relationship matrix estimated from SNP data and I is an identity matrix. The genomic similarity relationship for each pair of individuals is calculated as the sum of the products of SNP coefficients between two individuals scaled by the SNP heterozygosity (9).
is the error variance, A is the genomic similarity relationship matrix estimated from SNP data and I is an identity matrix. The genomic similarity relationship for each pair of individuals is calculated as the sum of the products of SNP coefficients between two individuals scaled by the SNP heterozygosity (9).
All variances are on the observed (0–1) scale, were estimated using restricted maximum likelihood (42–44) and were transformed to those on the liability scale as shown previously (11), assuming a disease prevalence (lifetime risk) of 8% for ED (15), 2% for AD (45) and 0.1% for MS (23).
Genome partitioning linear mixed model
We partitioned the variance explained by the SNPs in several ways using the linear model
| (2) |
where n is the number of subsets from any non-overlapping partitioning of SNPs; n = 22 for the joint analysis by chromosome and n = 5 for the analysis by MAF bin. We partitioned the variance by annotation n = 2, when SNPs were annotated as being in ‘genes’ or ‘not in genes’ where gene boundaries were±20 kb from 3′ and 5′ UTRs of each gene. Further, we annotated SNPs being in disorder-specific genes (Supplementary Material, Table S2). That is, SNPs were in genes if they were positioned within 50 kb from the boundary of ED-related genes (annotated by terms related to ED using Gene2MeSH (22)), CNS+ (one set comprised genes expressed preferentially in the brain compared with other tissues and the other three sets comprised genes annotated to be involved in neuronal activity, learning and synapses (20)) and immune-related genes (21) for ED, AD and MS, respectively.
Control–control analyses
Since for each disorder, cases and controls were genotyped separately, we were concerned that the estimated genetic variance could be biased due to artefacts, for example genotyping batch effects or differential genotype calling algorithms. The essential information on estimating genetic variation comes from the average genomic similarity of case–case, case–control and control–control groups, so any non-genetic effect that makes cases more similar to other cases and controls more similar to other controls will result in the estimated genetic variance that is spurious. To explore the possibility of artefacts, we applied a QC process that would control for most artefact batch effects and performed pseudo case–control studies on combinations of the control cohorts, by treating one of the controls cohorts as ‘cases’. As several of the control sets are overlapping, in order to clearly illustrate the impact of QC factors confounded with cohort, we constructed three independent UK control datasets: 1958A (the subset of the 1958 cohort for which the same individuals were called with both Illuminus, 1958AI, and GenCall, 1958AG), 1958BI (the subset of the 1958 cohort with genotypes called only with Illuminus) and OECXI (the OEC controls called with Illuminus with any individuals featured in 1958A or 1958B removed.
SUPPLEMENTARY MATERIAL
DATA AVAILABILITY
The University of Queensland authors accessed the data through formal requests to the three consortia. The QCed data will be returned to the consortia and can be accessed by other researchers for collaborative research by contacting the consortia: ANZGene, Endogene, GERAD1.
FUNDING
This work was supported by the Australian National Health and Medical Research Council (NHMRC) 1011506. P.M.V. (613601), N.R.W. (613602, 1011506), G.W.M. (619667), D.R.N. (339462 and 613674) were supported by the NHMRC Fellowships Scheme. N.R.W. (FT0991360) and D.R.N. (FT0991022) were supported by the ARC Future Fellowship schemes. K.T.Z. is supported by a Wellcome Trust Research Career Development Fellowship (WT085235/Z/08/Z). Funding to pay the Open Access publication charges for this article was provided by the NHMRC (1011506).
Supplementary Material
ACKNOWLEDGEMENTS
We thank Jian Yang for helpful discussions. This study makes use of data generated by the Wellcome Trust Case Control Consortium. A full list of the investigators who contributed to the generation of the data is available from www.wtccc.org.uk. Funding for the project was provided by the Wellcome Trust under award 076113.
Conflict of Interest statement. None declared.
REFERENCES
- 1.Boomsma D., Busjahn A., Peltonen L. Classical twin studies and beyond. Nat. Rev. Genet. 2002;3:872–882. doi: 10.1038/nrg932. doi:10.1038/nrg932. [DOI] [PubMed] [Google Scholar]
- 2.WTCCC. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. doi:10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Manolio T.A. Genomewide association studies and assessment of the risk of disease. N. Engl. J. Med. 2010;363:166–176. doi: 10.1056/NEJMra0905980. doi:10.1056/NEJMra0905980. [DOI] [PubMed] [Google Scholar]
- 4.Hindorff L.A., Sethupathy P., Junkins H.A., Ramos E.M., Mehta J.P., Collins F.S., Manolio T.A. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl Acad. Sci. USA. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. doi:10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Visscher P.M., Brown M.A., McCarthy M.I., Yang J. Five years of GWAS discovery. Am. J. Hum. Genet. 2012;90:7–24. doi: 10.1016/j.ajhg.2011.11.029. doi:10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Visscher P.M., Montgomery G.W. Genome-wide association studies and human disease. JAMA. 2009;302:2028–2029. doi: 10.1001/jama.2009.1643. doi:10.1001/jama.2009.1643. [DOI] [PubMed] [Google Scholar]
- 7.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J., McCarthy M.I., Ramos E.M., Cardon L.R., Chakravarti A., et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. doi:10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Maher B. Personal genomes: the case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. doi:10.1038/456018a. [DOI] [PubMed] [Google Scholar]
- 9.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W., et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42:565–569. doi: 10.1038/ng.608. doi:10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang J., Manolio T.A., Pasquale L.R., Boerwinkle E., Caporaso N., Cunningham J.M., de Andrade M., Feenstra B., Feingold E., Hayes M.G., et al. Genome partitioning of genetic variation for complex traits using common SNPs. Nat. Genet. 2011;43:519–525. doi: 10.1038/ng.823. doi:10.1038/ng.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee S.H., Wray N.R., Goddard M.E., Visscher P.M. Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 2011;88:294–305. doi: 10.1016/j.ajhg.2011.02.002. doi:10.1016/j.ajhg.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee S.H., DeCandia T.R., Ripke S., Yang J. Sullivan P.F., Goddard M.E., Keller M.C., et al., editors. Schizophrenia Psychiatric Genome-Wide Association Study Consortium (PGC-SCZ), International Schizophrenia Consortium (ISC), Molecular Genetics of Schizophrenia Collaboration (MGS) Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat. Genet. 2012;44:247–250. doi: 10.1038/ng.1108. doi:10.1038/ng.1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stahl E.A., Wegmann D., Trynka G., Gutierrez-Achury J., Do R., Voight B.F., Kraft P., Chen R., Kallberg H.J., Kurreeman F.A.S., et al. Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet. 2012;44:483–489. doi: 10.1038/ng.2232. doi:10.1038/ng.2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lubke G.H., Hottenga J.J., Walters R., Laurin C., de Geus E.J., Willemsen G., Smit J.H., Middeldorp C.M., Penninx B.W., Vink J.M., et al. Estimating the genetic variance of major depressive disorder due to all single nucleotide polymorphisms. Biol. Psychiatry. 2012;78:707–709. doi: 10.1016/j.biopsych.2012.03.011. doi:10.1016/j.biopsych.2012.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Painter J.N., Anderson C.A., Nyholt D.R., Macgregor S., Lin J., Lee S.H., Lambert A., Zhao Z.Z., Roseman F., Guo Q., et al. Genome-wide association study identifies a locus at 7p15.2 associated with endometriosis. Nat. Genet. 2011;43:51–54. doi: 10.1038/ng.731. doi:10.1038/ng.731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.So H.-C., Gui A.H.S., Cherny S.S., Sham P.C. Evaluating the heritability explained by known susceptibility variants: a survey of ten complex diseases. Genet. Epidemiol. 2011;35:310–317. doi: 10.1002/gepi.20579. doi:10.1002/gepi.20579. [DOI] [PubMed] [Google Scholar]
- 17.Corder E.H., Saunders A.M., Risch N.J., Strittmatter W.J., Schmechel D.E., Gaskell P.C., Rimmler J.B., Locke P.A., Conneally P.M., Schmader K.E., et al. Protective effect of apolipoprotein E type 2 allele for late onset Alzheimer disease. Nat. Genet. 1994;7:180–184. doi: 10.1038/ng0694-180. doi:10.1038/ng0694-180. [DOI] [PubMed] [Google Scholar]
- 18.Lee S.H., Nyholt D.R., Macgregor S., Henders A.K., Zondervan K.T., Montgomery G.W., Visscher P.M. A simple and fast two-locus quality control test to detect false positives due to batch effects in genome-wide association studies. Genet. Epidemiol. 2010;34:854–862. doi: 10.1002/gepi.20541. doi:10.1002/gepi.20541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee S.H., Goddard M.E., Wray N.R., Visscher P.M. A better coefficient of determination for genetic profile analysis. Genet. Epidemiol. 2012;36:214–224. doi: 10.1002/gepi.21614. doi:10.1002/gepi.21614. [DOI] [PubMed] [Google Scholar]
- 20.Raychaudhuri S., Korn J.M., McCarroll S.A., Altshuler D., Sklar P., Purcell S., Daly M.J., Int Schizophrenia C. Accurately assessing the risk of Schizophrenia conferred by rare copy-number variation affecting genes with brain function. Plos Genet. 2010;6:e1001097. doi: 10.1371/journal.pgen.1001097. doi:10.1371/journal.pgen.1001097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.The Immunology Database and Analysis Portal (IMMPORT) https://immport.niaid.n-ih.gov/immportWeb/queryref/immportgene/immportGeneList.do .
- 22.Gene Annotation with MeSH Terms. http://gene2mesh.ncibi.org/index.php .
- 23.The International Multiple Sclerosis Consortium, the Wellcome Trust Case Control Consortium 2. Genetic risk and a primary role for cell-mediated immune mechanisms in multiple sclerosis. Nature. 2011;476:214–219. doi: 10.1038/nature10251. doi:10.1038/nature10251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Teo Y.Y., Inouye M., Small K.S., Gwilliam R., Deloukas P., Kwiatkowski D.P., Clark T.G. A genotype calling algorithm for the Illumina BeadArray platform. Bioinformatics. 2007;23:2741–2746. doi: 10.1093/bioinformatics/btm443. doi:10.1093/bioinformatics/btm443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Weber J.L., Wong C. Mutation of human short tandem repeats. Hum. Mol. Genet. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. doi:10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]
- 26.Cirulli E.T., Goldstein D.B. Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nat. Rev. Genet. 2010;11:415–425. doi: 10.1038/nrg2779. doi:10.1038/nrg2779. [DOI] [PubMed] [Google Scholar]
- 27.McClellan J., King M.C. Genomic analysis of mental illness: a changing landscape. JAMA. 2010;303:2523–2524. doi: 10.1001/jama.2010.869. doi:10.1001/jama.2010.869. [DOI] [PubMed] [Google Scholar]
- 28.Visscher P.M., Hill W.G., Wray N.R. Heritability in the genomics era—concepts and misconceptions. Nat. Rev. Genet. 2008;9:255–266. doi: 10.1038/nrg2322. doi:10.1038/nrg2322. [DOI] [PubMed] [Google Scholar]
- 29.Lee S., Goddard M., Visscher P., van der Werf J. Using the realized relationship matrix to disentangle confounding factors for the estimation of genetic variance components of complex traits. Genet. Sel. Evol. 2010;42:22. doi: 10.1186/1297-9686-42-22. doi:10.1186/1297-9686-42-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wray N.R. Allele frequencies and the r2 measure of linkage disequilibrium: impact on design and interpretation of association studies. Twin Res. Hum. Genet. 2005;8:87–94. doi: 10.1375/1832427053738827. doi:10.1375/twin.8.2.87. [DOI] [PubMed] [Google Scholar]
- 31.Cramer D.W., Missmer S.A. The epidemiology of endometriosis. Ann. N. Y. Acad. Sci. 2002;955:11–22. doi: 10.1111/j.1749-6632.2002.tb02761.x. discussion 34-16, 396–406 doi:10.1111/j.1749-6632.2002.tb02761.x. [DOI] [PubMed] [Google Scholar]
- 32.Nielsen N.M., Jorgensen K.T., Stenager E., Jensen A., Pedersen B.V., Hjalgrim H., Kjaer S.K., Frisch M. Reproductive history and risk of multiple sclerosis. Epidemiology. 2011;22:546–552. doi: 10.1097/EDE.0b013e31821c7adc. doi:10.1097/EDE.0b013e31821c7adc. [DOI] [PubMed] [Google Scholar]
- 33.Turelli M., Barton N.H. Polygenic variation maintained by balancing selection: pleiotropy, sex-dependent allelic effects and G x E interactions. Genetics. 2004;166:1053–1079. doi: 10.1534/genetics.166.2.1053. doi:10.1534/genetics.166.2.1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Visscher P.M., Yang J., Goddard M.E. A commentary on ‘Common SNPs explain a large proportion of the heritability for human height’ by Yang et al. (2010) Twin Res. Hum. Genet. 2010;13:517–524. doi: 10.1375/twin.13.6.517. doi:10.1375/twin.13.6.517. [DOI] [PubMed] [Google Scholar]
- 35.Purcell S.M., Wray N.R., Stone J.L., Visscher P.M., O'Donovan M.C., Sullivan P.F., Sklar P. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Davies G., Tenesa A., Payton A., Yang J., Harris S.E., Liewald D., Ke X., Le Hellard S., Christoforou A., Luciano M., et al. Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Mol. Psychiatry. 2011;16:996–1005. doi: 10.1038/mp.2011.85. doi:10.1038/mp.2011.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Deary I.J., Yang J., Davies G., Harris S.E., Tenesa A., Liewald D., Luciano M., Lopez L.M., Gow A.J., Corley J., et al. Genetic contributions to stability and change in intelligence from childhood to old age. Nature. 2012;482:212–215. doi: 10.1038/nature10781. [DOI] [PubMed] [Google Scholar]
- 38.Montgomery G.W., Nyholt D.R., Zhao Z.Z., Treloar S.A., Painter J.N., Missmer S.A., Kennedy S.H., Zondervan K.T. The search for genes contributing to endometriosis risk. Hum. Reprod. Update. 2008;14:447–457. doi: 10.1093/humupd/dmn016. doi:10.1093/humupd/dmn016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gao X., Outley J., Botteman M., Spalding J., Simon J.A., Pashos C.L. Economic burden of endometriosis. Fertil. Steril. 2006;86:1561–1572. doi: 10.1016/j.fertnstert.2006.06.015. doi:10.1016/j.fertnstert.2006.06.015. [DOI] [PubMed] [Google Scholar]
- 40.Harold D., Abraham R., Hollingworth P., Sims R., Gerrish A., Hamshere M.L., Pahwa J.S., Moskvina V., Dowzell K., Williams A., et al. Genome-wide association study identifies variants at CLU and PICALM associated with Alzheimer's disease. Nat. Genet. 2009;41:1088–1093. doi: 10.1038/ng.440. doi:10.1038/ng.440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.The Australia and New Zealand Multiple Sclerosis Genetics Consortium. Genome-wide association study identifies new multiple sclerosis susceptibility loci on chromosomes 12 and 20. Nat. Genet. 2009;41:824–828. doi: 10.1038/ng.396. doi:10.1038/ng.396. [DOI] [PubMed] [Google Scholar]
- 42.Gilmour A.R., Gogel B.J., Cullis B.R., Thompson R. ASReml User Guide Release 2.0. Hemel Hempstead, UK: . VSN International; 2006. [Google Scholar]
- 43.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: A tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. doi:10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lee S.H., Van der Werf J.H.J. An efficient variance component approach implementing an average information REML suitable for combined LD and linkage mapping with a general complex pedigree. Genet. Sel. Evol. 2006;38:25–43. doi: 10.1186/1297-9686-38-1-25. doi:10.1186/1297-9686-38-1-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brookmeyer R., Gray S., Kawas C. Projections of Alzheimer's disease in the United States and the public health impact of delaying disease onset. Am. J. Public Health. 1998;88:1337–1342. doi: 10.2105/ajph.88.9.1337. doi:10.2105/AJPH.88.9.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hawkes C.H., Macgregor A.J. Twin studies and the heritability of MS: a conclusion. Mult. Scler. 2009;15:661–667. doi: 10.1177/1352458509104592. doi:10.1177/1352458509104592. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The University of Queensland authors accessed the data through formal requests to the three consortia. The QCed data will be returned to the consortia and can be accessed by other researchers for collaborative research by contacting the consortia: ANZGene, Endogene, GERAD1.