Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2012 Dec 5;110(2):131–137. doi: 10.1038/hdy.2012.80

The effects of inheritance in tetraploids on genetic diversity and population divergence

P G Meirmans 1,*, P H Van Tienderen 1
PMCID: PMC3554447  PMID: 23211786

Abstract

Polyploids are traditionally classified into allopolyploids and autopolyploids, based on their evolutionary origin and their disomic or multisomic mode of inheritance. Over the past decade it has become increasingly clear that there is a continuum between disomic and multisomic inheritance, with the rate of tetrasomy differing among species and among chromosomes within species. Here, we use a simple population genetic model to study the impact of the mode of inheritance on the genetic diversity and population divergence of tetraploids. We found that under almost strict disomic inheritance the tetraploid genome is divided into two separate subgenomes, such as found in classical allopolyploids. In those cases, assuming full tetrasomy in the analysis of polyploid genetic data will lead to an important bias in estimates of genetic diversity and population divergence. However, we found that even a low rate of allele exchange between the two subgenomes, at about one event per generation, is sufficient to homogenise the allele frequencies over the subgenomes, and the estimates become essentially unbiased. The inbreeding coefficient FIS can then be used to detect whether the estimates of diversity and divergence will be biased when full multisomy is assumed. Finally, we found that different summary statistics for measuring the strength of population differentiation are differentially affected by a deviation from full tetrasomy. Our model results provide several useful guidelines for the analysis of polyploid data, helping researchers to determine when their inferences are biased and which summary statistics to use.

Keywords: population structure, F-statistics, heterozygosity, segmental polyploids, disomy, multisomy

Introduction

Polyploidy is a widespread phenomenon with a tremendous influence on the genomic evolution of plants, animals and fungi. Traditionally, a distinction is made between allopolyploids and autopolyploids, with segmental allopolyploidy as an intermediate state (Stebbins, 1947; Ramsey and Schemske, 1998). Allopolyploidy is the union of distinct progenitor genomes, for example, following hybridisation between species. Autopolyploidy is the combination of genomes originating from a single species. This distinction affects the pairing and segregation of chromosomes during meiosis, where allopolyploids are traditionally thought to mostly form bivalents of homoeologs and autopolyploids mostly form multivalents. Although the distinction between allopolyploids and autopolyploids is useful from the perspective of their origin, it has become increasingly clear over the past decades that there is not a one-to-one link between the origin and the pattern of inheritance and chromosomal pairing (Ramsey and Schemske, 2002; Chester et al., 2012). In allopolyploids, there can be pairing, recombination and gene transfer between homoeologous chromosomes (Gaeta and Pires, 2009). Furthermore, the amount of divergence between the two progenitor genomes may vary among chromosomes; for example, depending on the presence of chromosomal rearrangements. Therefore, the rate at which pairings between homoeologs occur may differ strikingly among chromosomes (Chester et al., 2012). Furthermore, in polyploids, a process known as rediploidisation occurs: over time, there usually is an increase in the formation of bivalents, which can eventually lead to full disomic inheritance even in autopolyploids (Haufler and Soltis, 1986; Bowers et al., 2003). The rate of tetrasomy can be estimated based on segregation patterns of molecular markers in the offspring of polyploids (Diter et al., 1988; Mable and Bogart, 1995). Recently, Stift et al. (2008) developed a maximum likelihood approach that makes it easier to quantify the rate of tetrasomy. Applying their method to data from several polyploid species revealed that estimates of the rate of tetrasomy vary widely not only between species, but in segmental allopolyploids (Stebbins 1947) also within the genome of a single species (Stift et al., 2008; Kamiri et al., 2011). Variation in the rate of tetrasomy within a genome may be present in autotetraploids that are in an intermediate state of rediploidisation or in allotetraploids where the different progenitor genomes have different karyotypes or different numbers of chromosomes. In such cases some chromosomes may have a homoeolog, while other chromosomes do not.

The theoretical effects of polyploidy on genetic diversity have been studied to some extent (Haldane, 1930; Moody et al., 1993; Obbard et al., 2006). A population of autotetraploids contains twice the number of copies of each gene as a similar sized population of diploids. Therefore, they can harbour a larger amount of genetic diversity as there are more mutations and there is a lower impact of genetic drift. Polyploidy also has consequences for the population structure, as the same rate of migration of individuals between populations will lead to a lower degree of genetic differentiation in polyploids as compared with diploids. This is because a polyploid migrant will carry more gene copies than a diploid migrant, leading to more homogenisation among populations. The system of chromosome pairing and subsequent segregation in polyploids has an important role here as it changes the distribution of genetic variation. In the two extreme cases, the effects are clear, and the analysis of genetic data is relatively straightforward. Under strict disomic inheritance, the subgenomes should be analysed as independent loci. However, this requires that all alleles/markers can be attributed to the correct non-homologous locus, which can be difficult in practice and may require synteny information. Under strict multisomic inheritance, the whole genome can be analysed using the framework developed by Ronfort et al. (1998) as a set of loci with multiple alleles per locus in each individual, depending on the ploidy level. In most species, the exact pairing and segregation patterns are unknown and are studied using progeny arrays (Stift et al., 2008) or cytogenetic behaviour (Comai et al., 2003; Chester et al., 2012). When the segregation patterns are unknown, it is not clear to what extent an assumption of tetrasomy will bias analyses of genetic diversity and population differentiation, if in fact there is partial disomic inheritance.

Here, we use a simple population genetic simulation model to study genetic diversity and population differentiation in tetraploids. We focus on how much gene exchange between homoeologous subgenomes is needed to homogenise their allele frequencies to such an extent that there is no bias in analyses that assume full tetrasomy. For this, we define the rate of homoeologous allele exchange as the probability that an allele switches in affinity from one subgenome to the other. This could be due to a recombination event, gene conversion or chromosomal rearrangements. This rate varies from zero for strict disomy to one for strict tetrasomy, when the affinity is equal for all combinations. Specifically, we ask the following questions: what is the bias resulting from assuming full tetrasomy when in fact there is partial disomy? How are different summary statistics for genetic diversity and population divergence affected by the rate of gene exchange among sub genomes? Our simulations show that different summary statistics are differently affected when there is a deviation from full tetrasomy. The best overall performance was shown by the ρ-statistic (Ronfort et al., 1998), a ploidy-independent FST-analogue, whose value was mostly independent of the rate of tetrasomy. All other summary statistics showed large bias when tetrasomy was assumed and the species is in fact fully disomic. However, even for those summary statistics, in most cases a single exchange per generation is sufficient to homogenise the allele frequencies so that the assumption of full tetrasomy will not introduce any important bias in their results.

Materials and methods

The model

One population of a tetraploid species with size N is simulated that splits into two separate populations, each of the same size N. Migration takes place between these two populations at rate m per generation. A total of L marker loci is modelled with mutation following a K-alleles model with mutation rate μ. The segregation model of the tetraploid species is determined by the parameter Θ, ranging from strict disomic pairing of homologs (Θ=0) to the formation of multivalents or random bivalent pairing of chromosomes (Θ=1). There is no double reduction at loci. The species is hermaphroditic and mating at random, including a probability of selfing of 1/N. The model was written and run in the statistical language R; the code is available in Supplementary data.

The model is not individual-based, but simply keeps track of the allele frequencies in the two different subgenomes in the two populations. To this end, each locus is modelled as two integer vectors, each vector representing one of the diploid subgenomes of the tetraploid genome. The length of these vectors is determined by the maximum number of possible alleles at a locus K (a value of K=100 is used for all simulations). Each element in the vectors represents the number of copies of the corresponding allele that is present in the population. As the population size is fixed, the sum of the elements of each vector is always equal to 2N. In total, there are four such vectors in the model; for each of the two populations there are two vectors representing the subgenomes A and B.

Every generation, the drawing and union of gametes is simulated by making a random draw from these vectors, while allowing for allele exchange between the subgenomes, mutation, and migration. We do this by calculating, for each of the K alleles, its expected frequency in the next generation and then drawing random numbers from a multinomial distribution based on the expected frequencies. We perform this drawing separately for each subgenome and each population.

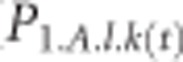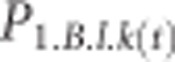For example, the expected frequency of allele k at locus l in subgenome A in population 1 in the next generation is first and foremost a function of the current frequency in subgenome A (Inline graphic) and, through allele exchange following tetrasomic inheritance, the current frequency in subgenome B (Inline graphic):

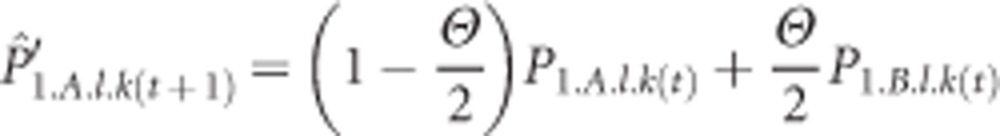graphic file with name hdy201280e3.jpg

In this equation, the parameter Θ defines the exchange of alleles between the two subgenomes, which is crucial in the model. For instance, a value Θ=0.01 means that the expected new frequency in the A subgenome is a weighted average of the frequency of the allele in the A and B subgenomes, the weights being 99.5% and 0.5%, respectively. Note that in this model Θ is a fixed parameter, and, furthermore, there is no tracking of alleles entering the subgenome pool; that is, no distinction is made between those that came from the A and B subgenomes. A very different, mechanistic model that could capture such differences and allow allele-specific changes in Θ is being developed in parallel to the current approach.

Mutation follows a K-alleles model with rate μ, where a mutation to all K possible allelic states is equally probable. For the used value of K=100, this closely resembles the infinite allele model that is the basis of most population genetic models. The used markers therefore represent multi-allelic markers such as allozymes, microsatellites, and, at lower mutation rates, also SNPs. We did not use a stepwise mutation model to specifically mimic microsatellites as the theoretical expectations are more easily derived under the infinite allele model. Furthermore, summary statistics that assume a stepwise mutation model, such as RST, already lose their validity when there is a low rate of non-stepwise mutations (Balloux et al., 2000). The mutation process changes the expected frequencies in the following way:

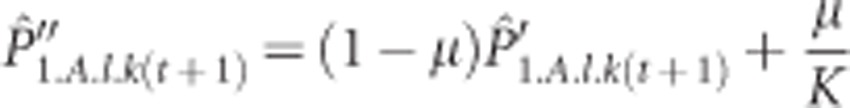graphic file with name hdy201280e4.jpg

Finally, migration takes place between the two populations. We wanted to be able to compare the values of the degree of population differentiation with the theoretical expectations given the migration rate m under a standard model with full tetrasomy. Therefore, migration follows the standard Island model (Wright 1931), where all migrants are assumed to form a common migrant pool and are then redistributed over the populations. As there are only two populations in our model, this means that only half of the individuals from the migrant pool are true migrants, whereas the other half are redistributed back to their population of origin. Implementing the migration in such a way gives us the complete expected frequency of the allele in the next generation:

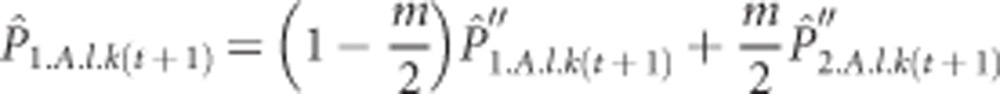graphic file with name hdy201280e5.jpg

In the initial phase, when there is only a single population, the simulation takes place without migration. This initial phase was run long enough to reach mutation-drift equilibrium and its length was set depending on the population size and the mutation rate, but lasted at least 10 000 generations. After the initial phase, the population was split into two populations, where each population was seeded with the same initial allele frequencies. These two populations were again run until equilibrium for at least 20 000 generations. As the different loci were completely independent of each other, they provide replicates of the simulation model. Therefore, the model was run only once with 1000 loci for each parameter combination.

During the simulations, several summary statistics were calculated to keep track of genetic diversity and population differentiation. The expected heterozygosities within populations (HS) and over all populations (HT) were calculated following Nei (1987). These were based on the known population allele frequencies, so we did not apply any correction for sample size. For these calculations, we combined the allele frequencies over the two subgenomes. This means that our analyses assumed full tetrasomy, mirroring the way in which polyploid data are often analysed when the segregation mode is unknown. The observed heterozygosity (HO) was calculated based on the concept of gametic heterozygosity (Moody et al., 1993): the heterozygosity observed when drawing random diploid gametes from individuals. As there is random mating in the model, any deviation of HO from HS is only determined by the differentiation between the two subgenomes, and the resulting degree of fixed heterozygosity. Therefore, HO can be calculated based on the allele frequencies within the two subgenomes without requiring any genotypic information:

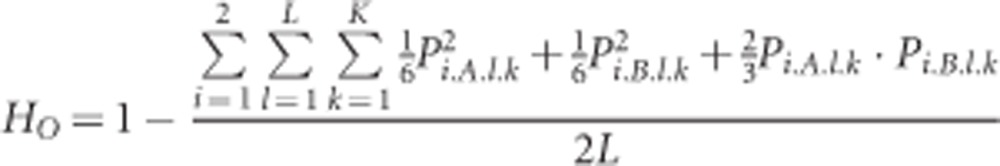graphic file with name hdy201280e6.jpg

After all generations were finished, a random sample of 100 individual genotypes was constructed from the allele frequencies and saved to a file. The programme Gℯ𝓃ℴD𝒾𝓋ℯ (Meirmans and Van Tienderen, 2004) was then used to calculate several additional summary statistics for genetic differentiation: ρ (Ronfort et al., 1998), F′ST (estimated using GST: Nei 1987), F′ST (Hedrick 2005; estimated using G″ST, Meirmans and Hedrick, 2011), and D (Jost, 2008; using the estimator Dest). This allowed us to test how these summary statistics were affected by deviations from the assumption of full tetrasomy.

Results

Approach to equilibrium

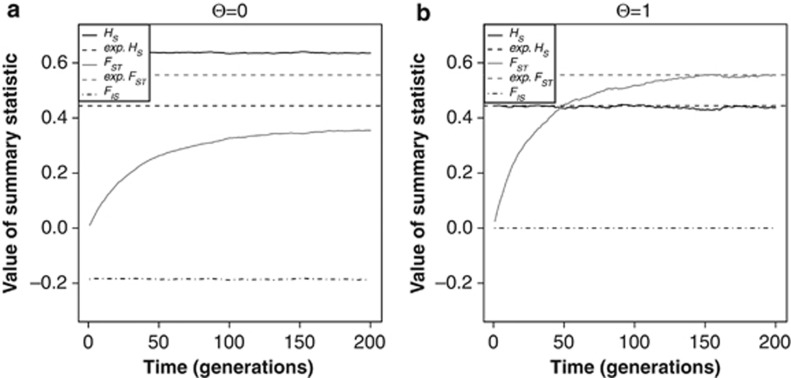
Assuming tetrasomy when a tetraploid species is in fact fully disomic will lead to large errors in the estimation of the genetic diversity and population differentiation. This effect is shown in Figure 1. Under full tetrasomy (Θ=1, Figure 1b), both HS and FST quickly reach equilibrium values that match the theoretical expectations (dotted lines). As there was random mating within the simulated populations, HO (not shown) is exactly the same as HS and therefore, FIS is equal to 0. However, under full disomy (Θ=0, Figure 1a) but assuming tetrasomic inheritance, the graph looks strikingly different. The equilibrium values of both HS and FST are far from their theoretical expectations: HS is much higher than expected; FST is much lower. There is significant deviation from Hardy–Weinberg equilibrium, as the disomic inheritance leads to fixed heterozygosity. Therefore, FIS has a negative value as HO (not shown) is much higher than HS.

Figure 1.

Figure 1

Open in a new tab

The expected heterozygosity HS and the inbreeding coefficients FIS and FST as a function of the number of generations since population divergence, for two values of the tetrasomy parameter Θ: (a) Θ=0, (b) Θ=1. N=1000, m=0, μ=0.0001, 1000 loci. The dotted lines show the theoretical expectations for HS and FST based on full tetrasomy.

The effect of changing Θ

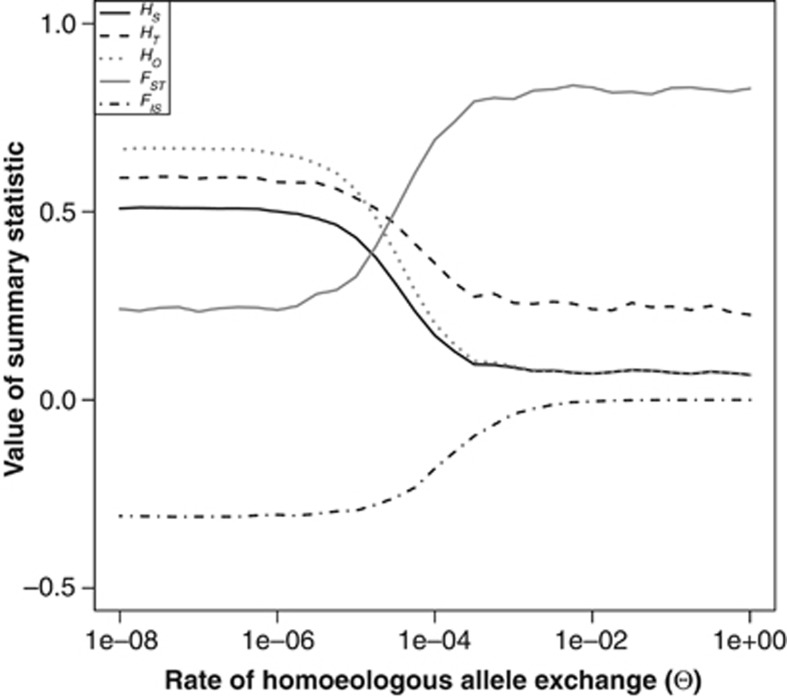
As the Θ parameter obviously has a large influence on basic population genetic summary statistics, it is of interest to ask how rare tetrasomy can be without biasing the analyses. We therefore ran the model with multiple values of Θ on a logarithmic scale from 10−8 to 1. Figure 2 shows that a small amount of allele exchange can homogenise the allele frequencies between the two subgenomes in such a way that there is very little bias in the estimation of the summary statistics. This is best shown by the value of FIS, which is close to zero for all values of Θ that are larger than 10−3. Only for very small values of Θ (<10−5) does the population essentially act like a fully disomic one. In between there is a relatively small transitional stage where the population is still out of Hardy–Weinberg equilibrium (negative FIS), but the two subgenomes are not completely differentiated from each other and still show some overlap in allele frequencies.

Figure 2.

Figure 2

Open in a new tab

The values of five different genetic summary statistics as a function of Θ, the rate of homoeologous allele exchange. N=1000, μ=0.00001, m=0. The results are averaged over 1000 loci.

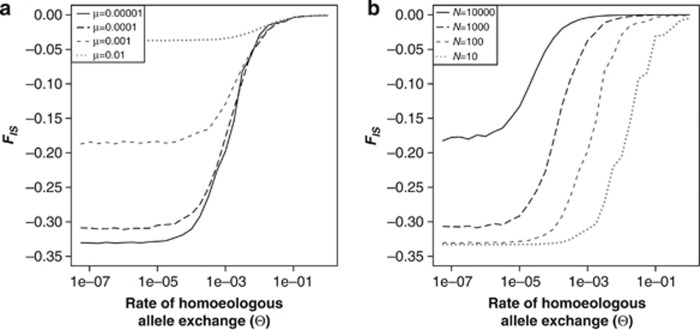
We also investigated how the effect of Θ depends on the other parameters in the model: the population size, the mutation rate and the migration rate. When changing mutation rate, while keeping the population size fixed, we see that the effect of Θ is largely obscured by the effect of mutation on the value of FIS (Figure 3a). Under disomy, the value of FIS is largely determined by the mutation rate. Under a low mutation rate, the two subgenomes each get fixed or nearly fixed for different alleles, and therefore there is fixed heterozygosity within the population. This gives a value of HS of 0.5, as there are two alleles at each locus (one for each subgenome) that are both present at an apparent frequency of 50%. Because of the fixed heterozygosity, the observed allelic heterozygosity is HO=0.66. This results in a minimum possible value of FIS under disomy of −0.33, which occurs with small Θ and a low mutation rate (Figure 3a). High mutation rates give a higher heterozygosity within each of the two subgenomes and therefore lead to FIS values that are closer to zero. Figure 3a also shows that the value of Θ at which a complete homogenisation of the subgenomes is achieved (that is, the point where FIS reaches zero) is mostly the same for all mutation rates. The only exception is at very high mutation rates where homogenisation is achieved at higher values of Θ than at low and moderate mutation rates. This effects is especially visible when the FIS values are scaled from 0 to 1 separately for every mutation rate (Supplementary Figure S1a).

Figure 3.

Figure 3

Open in a new tab

The effect of the rate of tetrasomy on the inbreeding coefficient FIS; (a) for different values of the mutation rate, keeping the population size fixed at N=100 (b) for different population sizes, keeping the mutation rate fixed at 0.00001. Other parameters: m=0, 1000 loci. See Supplementary Figure S1 for the same results scaled from 0 to 1 per series.

When the population size is changed, while keeping the mutation rate fixed, we see that this again has an influence on the value of FIS under disomy (Figure 3b). The population size also has a large effect on the rate of homogenisation of the two subgenomes. In this case, FIS seems to reach a value of zero approximately at a value of Θ of 1/N. From this we can postulate as a rule-of-thumb that if there is at least one event of allele exchange in the population per generation the bias in the estimates of genetic diversity and population differentiation will be minimal. When there is strict disomy and HS is low (that is, at small population sizes), FIS again reaches its minimum value of −0.33. When the population sizes are higher, and HS is higher, the value of FIS at disomy gets closer to zero (Figure 3b).

Comparison of summary statistics

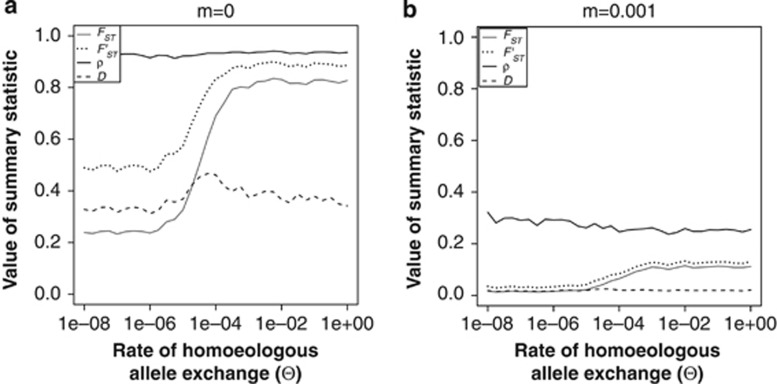
The four different summary statistics that we used to quantify the strength of the population divergence show marked differences in their response to Θ (Figure 4). Hedrick's (2005) standardisation of FST relative to its maximum given the amount of within-population diversity does not solve the bias in estimation of FST if tetrasomy is assumed when there is in fact disomy: F′ST is also underestimated when the rate of tetrasomy is low. In contrast, the ploidy-independent ρ-statistic (Ronfort et al., 1998) hardly shows any bias. When the two populations are completely isolated (m=0, Figure 4a) there is no apparent change in the value of ρ when Θ is changed. When there is a moderate level of migration between the two populations (m=0.001, Figure 4b), there is a slight decrease in the value of ρ with increasing Θ, but this is hard to distinguish from the sampling variance. Finally, Jost's (2008) D shows a rather erratic pattern. For m=0, the value of D is highest for intermediate values of Θ; for m=0.001, D does not respond to a change in Θ, but fails to detect any population structure, and has a value very close to zero.

Figure 4.

Figure 4

Open in a new tab

The effect of the rate of homoeologous allele exchange, Θ, on the value of different statistics for estimating population divergence; (a) for complete isolation between the two populations (m=0); (b) for a moderate rate of migration between the two populations (m=0.001).

Discussion

Infrequent allelic exchange among subgenomes is already similar to full tetrasomy

Our results confirm that the mode of inheritance in polyploids has important consequences for the analysis of their genetic diversity and population structure. Assuming tetrasomy when in fact there is full disomy will lead to an overestimation of the amount of within-population diversity (HS) and consequently to an underestimation of the amount of population divergence (as measured by FST). However, we found that these summary statistics are already essentially unbiased when there is a small amount of exchange between the subgenomes.

The distinction between allopolyploids and autopolyploids is currently seen as an oversimplification (Ramsey and Schemske, 2002; Chester et al., 2012), and in fact, there is a continuum between disomic and multisomic inheritance, with the rate of tetrasomy differing among species and among chromosomes within species (Stift et al., 2008; Kamiri et al., 2011; Chester et al., 2012). Our results indicate that this can affect estimates of genetic diversity and population divergence. Most importantly, our model showed that in tetraploids, some allele exchange among subgenomes in association with tetrasomy is sufficient to homogenise the allele frequencies between the two subgenomes to an extent that removes biases associated with strict disomy: approximately one exchange event per generation is enough. This is analogous to another rule-of-thumb from population genetics, namely that one migrant per generation is enough to prevent divergence of allele frequencies among populations (see Whitlock and McCauley 1999; Wang, 2004). In our case, the two subgenomes of the polyploids can be seen as two ‘populations' where the exchange events are the ‘migrations'.

The notion that two subgenomes in a tetraploid can be seen as two populations separated by migration means that standard simulation tools developed for diploids can also be used to simulate tetraploids. The programme ℳ𝒮 (Hudson, 2002) uses the coalescent to generate genetic samples from a Wright–Fisher neutral model. Using ℳ𝒮 to simulate a population of tetraploids as two populations of diploids gave results that were very similar to the results obtained from our own model (cf. Supplementary Figure S2 and Supplementary Figure S1b). However, there are some limitations to this approach. When tetrasomy events are modelled as migration between diploid populations, this means that there is no way left to simulate migration of tetraploids. Furthermore, even if such ‘diploid' simulation programmes allow for selfing, this cannot be used to simulate selfing in tetraploids. In practice, this means that tools to model diploids can only be used to simulate a single, randomly mating, population of polyploids. It is therefore preferable to develop modelling tools especially for polyploids. For example, for fully tetrasomic autotetraploids it has recently been shown that the standard coalescent can be used with a simple scaling of the population size (Arnold et al., 2012).

The inbreeding coefficient FIS may be used to detect whether there is an important impact of disomic inheritance. As disomy leads to fixed heterozygosity, strict disomy results in a negative value of FIS. Our results show that when the rate of tetrasomy is high enough to give FIS of zero, the estimates of HS and FST are also unbiased. However, the minimum possible value of FIS, reached under full disomy, is strongly determined by the mutation rate and the population size. When the mutation rate is low and/or the population size large, the minimum value of FIS is −0.33; this value increases with increasing mutation rate or decreasing population size. This means that for very high mutation rates and/or very small population sizes FIS may be close to zero even under full disomy. Therefore, under these conditions it is difficult to detect disomic inheritance using FIS. However, in these cases the bias in the estimation of HS and FST is minimal, as these values are then mostly determined by mutation rather than by other forces. Furthermore, the usefulness of FIS to detect disomy is reduced if there is non-random mating in populations. Both self-fertilisation and double reduction lead to an increase in homozygosity (Bever and Felber, 1992; Ronfort et al., 1998) and the value of FIS. This will counteract the effect of disomy on the value of FIS. Therefore, when the selfing rate is high and there is strict disomy there will be both fixed homozygosity within subgenomes and fixed heterozygosity among subgenomes.

Estimating population divergence

The different summary statistics to estimate the strength of the population divergence showed remarkable differences in their response to the rate of allele exchange. The statistic that was most robust to violations in assumptions was ρ (Ronfort et al., 1998), whose value was mostly independent of Θ. This is not unexpected as ρ was in fact developed to be independent both of the ploidy level and the amount of within-individual diversity; it is therefore also independent of the amount of selfing and double reduction. Although this statistic is not very widely used (but see Hardy and Vekemans, 2001; Meirmans et al., 2006), we recommend the use of ρ for any study of population structure in polyploids, especially when the exact mode of inheritance is unknown. However, it is important to realise that the interpretation of ρ is different than that of FST: ρ gives consistently higher values than FST (Ronfort et al., 1998). The value of ρ corresponds to the value that FST would have for a haploid species with the same population size and migration rate. As far as we are aware, there are only two programmes that allow the estimation of ρ from genetic marker data: S𝓅𝒶ℊℯ𝒹𝒾 (Hardy and Vekemans, 2002) and Gℯ𝓃ℴD𝒾𝓋ℯ (Meirmans and Van Tienderen, 2004).

Both the classic FST and the standardised F′ST are essentially unbiased when the rate of tetrasomy is high enough. This means that these statistics can also be used to measure the strength of the population divergence even if it is known that there is some deviation from full tetrasomy. For example, from genotyping progeny arrays of Rorippa amphibia, Stift et al. (2008) found for multiple microsatellite markers that the estimates of the rate of tetrasomy ranged from 0.59 to 0.96. R. amphibia is a widespread and common species and therefore will have a large effective population size. Assuming that the high rate of tetrasomy leads to frequent exchange of alleles, this means that the microsatellites used by Stift et al. (2008) can be used to estimate the genetic diversity (Luttikhuizen et al., 2007) and population structure of R. amphibia without bias.

In contrast with the other three summary statistics, D (Jost, 2008) showed rather erratic patterns and weak divergence among populations, even in the complete absence of migration. This behaviour stems from the long time that D needs to reach its equilibrium value (Ryman and Leimar, 2009; Meirmans and Hedrick 2011; Whitlock, 2011). In our simulations, the used number of generations (20 000) was not enough to reach equilibrium in the value of D even for the relatively small population size used (N=1000). Because of its prolonged period of non-equilibrium, we do not recommend the use of D for polyploids (see also Meirmans and Hedrick, 2011; Whitlock, 2011).

Model assumptions

There is a large number of computer programmes available for the simulation of population genetic scenarios (for example, Balloux, 2001; Neuenschwander et al., 2008; Meirmans, 2011). However, none of these programmes allow the simulation of polyploids. Rather than to develop a complex individual-based framework, we used a relatively simple population-based approach. Despite the simplicity of the model and its lack of features, it served its intended purpose and allowed us to answer our research questions. The advantages of our approach are that the calculations are straightforward and the model runs very fast. However, the trade-off is that some simplifying assumptions had to be made. As we did not keep track of individual genotypes, we could not incorporate self-fertilisation and double-reduction. This means that we could not assess the influence of the combination of disomy and selfing on the value of FIS. As selfing leads to a reduction in the effective population size, this means that for a given rate of tetrasomy there will be less homogenisation of the subgenomes under selfing than under random mating. The effect of double reduction will be similar since, like selfing, it leads to increased homozygosity (Haldane, 1930; Bever and Felber, 1992; Arnold et al., 2012).

Another important assumption of the model is that, coupled to a tetrasomy event, alleles that get transferred from one subgenome to the other immediately get incorporated into their new subgenome. This could be unrealistic if, after a chance tetrasomy event, the specific allele would still preferentially pair with its former subgenome. However, this does not invalidate our main results that a low rate of gene exchange is enough to homogenise the allele frequencies, as the Θ parameter should be seen as the rate of incorporation of alleles from one subgenome into the other, rather than the frequency of forming tetravalents. Such incorporation could occur through various mechanisms (Gaeta and Pires, 2009). Of course, this rate of incorporation will be lower than the observed rate of tetrasomy, depending on parameters like the level of divergence between the subgenomes and the rate of homoeologous recombination, gene conversion and chromosomal rearrangements. Our parameter Θ is therefore different from the rate of tetrasomy tau of Stift et al. (2008); our Θ does not only depend on tetrasomy, but also on the actual incorporation of the allele into the other subgenome.

As we used simulated data, we could use the exact population allele frequencies for the calculation of HO, HS, FST, and FIS. For real data this is not possible and the statistics are inferred from estimated allele frequencies in marker data. For polyploids, it can be hard to obtain the dosage of the alleles from, for instance, the band intensities (for example, Meirmans et al., 2006), especially for higher ploidy levels (Clark and Jaseniuk, 2011). This can lead to a bias in the estimation of allele frequencies and hence the degree of population differentiation. The problem with dosage is only present in partial heterozygotes, so that the extent of the bias will depend on the rate of tetrasomy. Several programmes are available that can help to prevent this bias by substituting the missing data in the calculations of summary statistics: Tℰ𝒯ℛ𝒜𝒮𝒜𝒯 (Markwith et al., 2006), F𝒟𝒜𝒮ℋ (Obbard et al. 2006), Tℰ𝒯ℛ𝒜 (Liao et al., 2008), A𝒯ℰ𝒯ℛ𝒜 (Van Puyvelde et al., 2010), P𝒪ℒ𝒴𝒮𝒜𝒯 (Clark and Jaseniuk, 2011), and the latest version of our programme Gℯ𝓃ℴD𝒾𝓋ℯ v. 2.0b23 (Meirmans & Van Tienderen 2004).

Guidelines for the analysis of polyploid data

The analysis of population genetic data for polyploids is more challenging than similar analyses for diploid data, due to a dearth of software and several complexities deriving from the nature of the polyploid data. Regarding the issues around the mode of inheritance of polyploids, the results from our model suggest several guidelines for the analysis of polyploid data. Although we only included tetraploids in our model, we believe our results may also be applicable to higher ploidy levels.

  • The assumption of tetrasomy may be valid in many cases, even when the inheritance is partly disomic. A low rate of incorporation of alleles from one subgenome into the other is generally enough to homogenise allele frequencies among the two subgenomes.

  • When random mating can be assumed within populations, F IS can be used for the detection of (partial) disomic inheritance. However, the usefulness of F IS for this purpose is reduced when the mutation rate is very high or the population size is very small.

  • The ρ-statistic can be used as an alternative to F ST that is independent of the ploidy level, the rate of double reduction, the selfing rate and the rate of tetrasomic inheritance. However, it is important to note that the interpretation of ρ is slightly different than that of F ST.

Data archiving

There were no data to deposit.

Acknowledgments

We would like to thank Brian Husband for the invitation to the conference that sparked this research and Barbara Mable for her comments on the paper and for her support as a guest editor of the special issue on polyploidy. Two anonymous reviewers provided valuable comments on the paper. This work was supported by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (838.06.042).

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Material
Click here for additional data file. (129KB, pdf)
Supplementary text, model source code in R
Click here for additional data file. (7.6KB, txt)

References

  1. Arnold B, Bomblies K, Wakeley J. Extending coalescent Theory to Autotetraploids. Genetics. 2012;192:195–204. doi: 10.1534/genetics.112.140582. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Balloux F. EASYPOP (Version 1.7): a computer program for population genetics simulations. J Hered. 2001;92:301–302. doi: 10.1093/jhered/92.3.301. [DOI] [PubMed] [Google Scholar]
  3. Balloux F, Brunner H, Lugon-Moulin N, Hausser J, Goudet J. Microsatellites can be misleading: an empirical and simulation study. Evolution. 2000;54:1414–1422. doi: 10.1111/j.0014-3820.2000.tb00573.x. [DOI] [PubMed] [Google Scholar]
  4. Bever JD, Felber F. The theoretical population genetics of autopolyploidy. Oxford Surv Evol Biol. 1992;8:185–217. [Google Scholar]
  5. Bowers JE, Chapman BA, Rong JK, Paterson AH. Unravelling angiosperm genome evolution by phylogenetic analysis of chromosomal duplication events. Nature. 2003;422:433–438. doi: 10.1038/nature01521. [DOI] [PubMed] [Google Scholar]
  6. Chester M, Gallagher J, Symonds V, Cruz Da Silva A, Mavrodiev E, Leitch A, et al. Extensive chromosomal variation in a recently formed natural allopolyploid species, Tragopogon miscellus (Asteraceae) Proc Natl Acad Sci USA. 2012;109:1176–1181. doi: 10.1073/pnas.1112041109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Clark L, Jasieniuk M. 𝒫𝒪ℒ𝒴𝒮𝒜𝒯: an R package for polyploid microsatellite analysis. Mol Ecol Res. 2011;11:562–566. doi: 10.1111/j.1755-0998.2011.02985.x. [DOI] [PubMed] [Google Scholar]
  8. Comai L, Tyagi AP, Lysak MA. FISH analysis of meiosis in Arabidopsis allopolyploids. Chromosome Res. 2003;11:217–226. doi: 10.1023/a:1022883709060. [DOI] [PubMed] [Google Scholar]
  9. Diter A, Guyomard R, Chourrout D. Gene segregation in induced tetraploid rainbow trout: genetic evidence of preferential pairing of homologous chromosomes. Genome. 1988;30:547–553. doi: 10.1139/g88-092. [DOI] [PubMed] [Google Scholar]
  10. Gaeta R, Pires JC. Homoeologous recombination in allopolyploids: the polyploid ratchet. New Phytol. 2009;186:18–28. doi: 10.1111/j.1469-8137.2009.03089.x. [DOI] [PubMed] [Google Scholar]
  11. Haldane JBS. Theoretical genetics of autopolyploids. J Genet. 1930;22:359–372. [Google Scholar]
  12. Hardy OJ, Vekemans X. Patterns of allozyme variation in diploid and tetraploid Centaurea jacea at different spatial scales. Evolution. 2001;55:943–954. doi: 10.1554/0014-3820(2001)055[0943:poavid]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  13. Hardy OJ, Vekemans X. SPAGEDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol Ecol Notes. 2002;2:618–620. [Google Scholar]
  14. Haufler CH, Soltis DE. Genetic evidence suggests that homosporous ferns with high chromosome numbers are diploid. Proc Nat Acad Sci USA. 1986;83:4389–4393. doi: 10.1073/pnas.83.12.4389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hedrick PW. A standardized genetic differentiation measure. Evolution. 2005;59:1633–1638. [PubMed] [Google Scholar]
  16. Hudson RR. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
  17. Jost L. GST and its relatives do not measure differentiation. Mol Ecol. 2008;17:4015–4026. doi: 10.1111/j.1365-294x.2008.03887.x. [DOI] [PubMed] [Google Scholar]
  18. Kamiri M, Stift M, Srairi I, Costantino G, Moussadik A, Hmyene A, et al. Evidence for non-disomic inheritance in a Citrus interspecific tetraploid somatic hybrid between C. reticulata and C. limon using SSR markers and cytogenetic analysis. Plant Cell Rep. 2011;30:1415–1425. doi: 10.1007/s00299-011-1050-x. [DOI] [PubMed] [Google Scholar]
  19. Liao W, Zhu B, Zeng Y, Zhang D. Tℰ𝒯ℛ𝒜: an improved program for population genetic analysis of allotetraploid microsatellite data. Mol Ecol Res. 2008;8:1260–1262. doi: 10.1111/j.1755-0998.2008.02198.x. [DOI] [PubMed] [Google Scholar]
  20. Luttikhuizen P, Stift M, Kuperus P, Van Tienderen P. Genetic diversity in diploid vs. tetraploid Rorippa amphibia (Brassicaceae) Mol Ecol. 2007;16:3544–3553. doi: 10.1111/j.1365-294X.2007.03411.x. [DOI] [PubMed] [Google Scholar]
  21. Mable BK, Bogart JP. Hybridization between tetraploid and diploid species of treefrogs (Genus Hyla) J Hered. 1995;86:432–440. doi: 10.1093/oxfordjournals.jhered.a111617. [DOI] [PubMed] [Google Scholar]
  22. Markwith SH, Stewart DJ, Dyer JL. Tℰ𝒯ℛ𝒜𝒮𝒜𝒯: a program for the population analysis of allotetraploid microsatellite data. Mol Ecol Notes. 2006;6:586–589. [Google Scholar]
  23. Meirmans PG, Hedrick P. Assessing population structure: FST and related measures. Mol Ecol Res. 2011;11:5–18. doi: 10.1111/j.1755-0998.2010.02927.x. [DOI] [PubMed] [Google Scholar]
  24. Meirmans PG, Van Tienderen PH. 𝒢ℰ𝒩𝒪𝒯𝒴𝒫ℰ and 𝒢ℰ𝒩𝒪𝒟ℐ𝒱ℰ: two programs for the analysis of genetic diversity of asexual organisms. Mol Ecol Notes. 2004;4:792–794. [Google Scholar]
  25. Meirmans PG, Den Nijs H, Van Tienderen PH. Male sterility in triploid dandelions: asexual females vs asexual hermaphrodites. Heredity. 2006;96:45–52. doi: 10.1038/sj.hdy.6800750. [DOI] [PubMed] [Google Scholar]
  26. Meirmans PG. Marlin, software to create, run, and analyse spatially realistic simulations. Mol Ecol Res. 2011;11:146–150. doi: 10.1111/j.1755-0998.2010.02888.x. [DOI] [PubMed] [Google Scholar]
  27. Moody ME, Mueller LD, Soltis DE. Genetic-variation and random drift in autotetraploid populations. Genetics. 1993;134:649–657. doi: 10.1093/genetics/134.2.649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Nei M. Molecular Evolutionary Genetics. Columbia University Press: New York; 1987. [Google Scholar]
  29. Neuenschwander S, Hospital F, Guillaume F, Goudet J. QuantiNemo: an individual-based program to simulate quantitative traits with explicit genetic architecture in a dynamic metapopulation. Bioinformatics. 2008;24:1552–1553. doi: 10.1093/bioinformatics/btn219. [DOI] [PubMed] [Google Scholar]
  30. Obbard DJ, Harris S, Pannell JR. Simple allelic-phenotype diversity and differentiation statistics for allopolyploids. Heredity. 2006;97:296–303. doi: 10.1038/sj.hdy.6800862. [DOI] [PubMed] [Google Scholar]
  31. Ramsey J, Schemske DW. Neopolyploidy in flowering plants. Ann Rev Ecol Syst. 2002;33:589–639. [Google Scholar]
  32. Ramsey J, Schemske DW. Pathways, mechanisms, and rates of polyploid formation in flowering plants. Ann Rev Ecol Syst. 1998;29:467–501. [Google Scholar]
  33. Ronfort JL, Jenczewski E, Bataillon T, Rousset F. Analysis of population structure in autotetraploid species. Genetics. 1998;150:921–930. doi: 10.1093/genetics/150.2.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ryman N, Leimar O. GST is still a useful measure of genetic differentiation - a comment on Jost's D. Mol Ecol. 2009;18:2084–2087. doi: 10.1111/j.1365-294X.2009.04187.x. [DOI] [PubMed] [Google Scholar]
  35. Stebbins GL. Types of polyploids: Their classification and significance. Adv Genet. 1947;1:403–429. doi: 10.1016/s0065-2660(08)60490-3. [DOI] [PubMed] [Google Scholar]
  36. Stift M, Berenos C, Kuperus P, Van Tienderen PH. Segregation models for disomic, tetrasomic and intermediate inheritance in tetraploids: a general procedure applied to Rorippa (yellow cress) microsatellite data. Genetics. 2008;179:2113–2123. doi: 10.1534/genetics.107.085027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Van Puyvelde K, Van Geert A, Triest L. A𝒯ℰ𝒯ℛ𝒜, a new software program to analyse tetraploid microsatellite data: comparison with Tℰ𝒯ℛ𝒜 and Tℰ𝒯ℛ𝒜𝒮𝒜𝒯. Mol Ecol Res. 2010;10:331–334. doi: 10.1111/j.1755-0998.2009.02748.x. [DOI] [PubMed] [Google Scholar]
  38. Wang JL. Application of the one-migrant-per-generation rule to conservation and management. Conserv Biol. 2004;18:332–343. [Google Scholar]
  39. Whitlock MC. G'ST and D do not replace FST. Mol Ecol. 2011;20:1083–1091. doi: 10.1111/j.1365-294X.2010.04996.x. [DOI] [PubMed] [Google Scholar]
  40. Whitlock MC, McCauley DE. Indirect measures of gene flow and migration: FST not equal to 1/(4Nm+1) Heredity. 1999;82:117–125. doi: 10.1038/sj.hdy.6884960. [DOI] [PubMed] [Google Scholar]
  41. Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
Click here for additional data file. (129KB, pdf)
Supplementary text, model source code in R
Click here for additional data file. (7.6KB, txt)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES