Absence of gene flow between diploids and hexaploids of Aster amellus at multiple spatial scales

Abstract

The potential for gene exchange across ploidy levels has long been recognized, but only a few studies have explored the rate of gene flow among different cytotypes. In addition, most of the existing knowledge comes from contact zones between diploids and tetraploids. The purpose of this paper was to investigate relationships between diploid and hexaploid individuals within the Aster amellus aggregate. A. amellus is known to occur in diploid and hexaploid cytotypes in Europe, with a complex contact zone in central Europe. Patterns of genetic diversity were investigated using seven microsatellite loci at three different spatial scales: (1) in the single known mixed-ploidy population; (2) in populations at the contact zone and (3) in a wider range of populations across Europe. The results show clear separation of the cytotypes at all three spatial scales. In addition, analysis of molecular variance strongly supported a model predicting a single origin of the hexaploids, with no or very limited gene flow between the cytotypes. Some hexaploid individuals found in the mixed-ploidy population, however, fell into the diploid cluster. This could suggest recurrent polyploid formation or occasional cross-pollination between cytotypes; however, there are strong post-zygotic breeding barriers between the two cytotypes, making the latter less plausible. Overall, the results suggest that the cytotypes could represent two cryptic species. Nevertheless, their formal separation is difficult as they cannot be distinguished morphologically, occupy very similar habitat conditions and have largely overlapping distribution ranges. These results show that polyploid complexes must be treated with caution as they can hide biological diversity and can have different adaptation potentials, evolving independently.

Introduction

Genome duplication has long been recognized as a major mechanism of sympatric speciation in flowering plants (Stebbins, 1950; Masterson, 1994; Soltis et al., 2009). As a result, species or species complexes consisting of several independent cytotypes have been documented in many families (for example, Buggs and Pannell, 2007; Halverson et al., 2008; Kloda et al., 2008; Trávníček et al., 2010; Münzbergová et al., 2011).

Understanding the mechanisms of structuring and maintaining these complexes, and their possible adaptations to novel environments requires detailed information on the frequency of gene flow and degree of isolation between the diploid and polyploid entities (Kloda et al., 2008; Symonds et al., 2010). In some cases, strong reproductive barriers may actually lead to the genesis of cryptic species (Soltis et al., 2007), while in other cases there may be substantial gene flow or shared ancestral variation among the cytotypes (Ramsey et al., 2008). Gene flow from diploid to polyploid species could have significant effects on the morphology and ecology of polyploids and affect both their coexistence at the contact zones and possible adaptations to novel environments (Stebbins, 1971; Chapman and Abbott, 2010). Even though the potential for gene exchange across ploidy levels has long been recognized (Stebbins, 1971; Levin, 1975; Chapman and Abbott, 2010), the knowledge on rate of gene flow among different cytotypes in natural systems is still rather limited (for example, Slotte et al., 2008; Chapman and Abbott, 2010; Fehlberg and Ferguson, 2012; Mráz et al., 2012).

Despite its importance, estimating rate of gene flow in polyploid complexes is strongly limited due to difficulties in allele dosage assessment and complex polysomic inheritance in polyploids (Stebbins, 1950, 1971; Clark and Jasieniuk, 2011). Recently, such estimates have been made easier by development of several software programs dealing with these issues (for example, POLYSAT—Clark and Jasieniuk, 2011, STRUCTURE—Falush et al., 2007 and so on).

A. amellus agg. is a widely distributed polymorphic species (Münzbergová et al., 2011). In Europe, this species is known to occur as diploid and hexaploid cytotypes, which are not distinguishable morphologically (Mandáková and Münzbergová, 2008), but form a largely diffuse contact zone across Poland, the Czech Republic, Slovakia, Austria and Romania (Castro et al., 2012). Despite growing in parapatry (except in one population; Castro et al. 2012), comparison of habitat requirements of the two cytotypes found no niche separation (Mandáková and Münzbergová, 2006) and each cytotype was able to grow on localities of the other cytotype (Raabová et al., 2008). Previous studies also indicated strong post-pollination breeding barriers between the two cytotypes (Castro et al., 2011).

The existence of diploid and hexaploid cytotypes growing in close proximity without the occurrence of an intermediate tetraploid cytotype and the absence of flowering triploids raises questions on the origin of the higher cytotype, as well as on the relationships between cytotypes. Triploid individuals, as a possible step towards hexaploids, have rarely been detected within the diploid populations and no hexaploid individuals have been detected in populations identified in the past as diploid (Castro et al., 2012). This suggests that the current distribution patterns are a result of secondary contact between cytotypes migrating from the center of their primary origin, most likely in south-eastern Europe or Asia (Münzbergová et al., 2011). However, additional primary contact zones could theoretically occur in other areas throughout the distribution range (Castro et al., 2012). Genetic relationships between diploid and hexaploid populations from the Czech Republic studied using allozymes indicated significant genetic separation between the two cytotypes (Mandáková and Münzbergová, 2008). The marker is, however, very conservative and low levels of genetic exchange between the cytotypes could thus remain undetected. Also, the previous sampling was spatially limited and did not include the single mixed-ploidy population detected so far.

The aim of this study was to assess relationships between the diploid and hexaploid cytotypes of A. amellus using highly variable microsatellite markers at three spatial scales: (1) within the single known mixed-ploidy population; (2) between pairs of diploid and hexaploid populations at the contact zone; and (3) between diploid and hexaploid individuals distributed across Europe. We used several alternative approaches to analyze the data and assessed if the different approaches provided comparable results and affected interpretation of patterns of gene flow among cytotypes.

Materials and methods

Study species

A. amellus L. (Asteraceae) is a polymorphic perennial herb growing in open xerothermic habitats. In Europe, its distribution area ranges from northern France to Lithuania, reaching Italy and Macedonia in the south, to the Black Sea, Caucasus and west Siberia outside Europe (Münzbergová et al., 2011). It has been suggested that A. amellus comprises three cytotypes: diploids (2n=2x=18), tetraploids (2n=4x=36), and hexaploids (2n=6x=54) (Münzbergová et al., 2011). However, only diploid and hexaploid cytotypes have been confirmed both in a large-scale screening of populations across Europe and in a literature survey (Münzbergová et al., 2011; Castro et al., 2012). Previous studies also show that the diploid and hexaploid cytotypes are not morphologically distinguishable (Mandáková and Münzbergová, 2008). In addition, we used allozyme analyses to compare the two cytotypes at the contact zone in the Czech Republic. Analyses of the data (presence/absence of the alleles) using principal component analyses (PCA), as well as a dendrogram based on Nei's genetic distances between populations constructed using Unweighted Pair Group Method with Arithmetic Mean (UPGMA) method of clustering clearly separated the two cytotypes. There were, however, very few unique alleles in each cytotype and all of these had very-low frequency. In addition, high frequency of unbalanced heterozygotes was found in the hexaploid banding patterns (Mandáková and Münzbergová, 2008). All this was used to conclude an autopolyploid origin for the hexaploids and that the contact zone is likely of secondary origin. The study of reproductive barriers between A. amellus cytotypes indicate that the absence of hybrids (tetraploids) in the field is mostly due to spatial segregation of diploids and hexaploids (Mandáková and Münzbergová, 2006; Castro et al., 2012) and to strong post-pollination barriers (Castro et al., 2011).

While a lot of previous knowledge has already been accumulated on the system, all the existing knowledge on genetic relationships between populations comes only from a small part of the contact zone, the Czech Republic, and was assessed using a very conservative marker, the allozymes.

Study populations

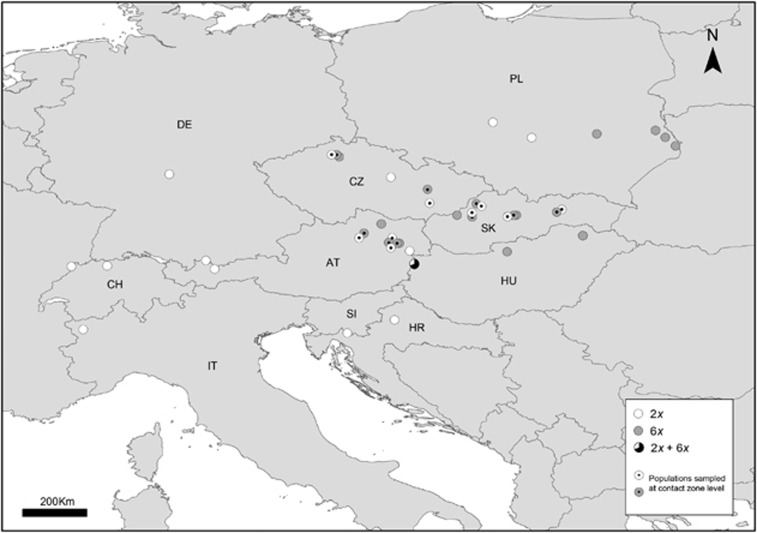
Genetic relationships between plants at a small spatial scale were studied in the Strebensdorf population (Austria), the only mixed-ploidy population that has been detected so far (Castro et al., 2012, Figure 1, Supplementary Information). In this population, every adult plant (both reproductive and vegetative plants) was labeled, its position recorded in a rectangular coordinate system, its DNA ploidy level measured using flow cytometry (Castro et al., 2012) and a sample for DNA analyses collected and stored in silica gel. In total, the sampling comprised 7 diploid and 61 hexaploid individuals.

Figure 1.

Location of the populations of Aster amellus studied. Cytotypes are represented by different colors: white circles-diploid (2x); grey circles-hexaploid (6x). The mixed population is represented by a pie diagram representing cytotype proportions (white-2x; black-6x). All locations were used in the large-scale spatial analyses; locations with dots represent the populations used in the intermediate spatial scale (contact zone). The population from Turkey (2x) is not displayed on the map. Country codes: AT, Austria; CH, Switzerland; CZ, Czech Republic; DE, Germany; HR, Croatia; HU, Hungary; IT, Italy; PL, Poland; SI, Slovenia; SK, Slovakia.

To detect genetic relationships at a larger spatial scale, nine pairs of diploid and hexaploid populations growing in close proximity (between 8 and 50 km apart, mean 14.4 km) and located across the contact zone in Austria, the Czech Republic and Slovakia were selected (Figure 1, Supplementary Information). Five plants were sampled from each population.

To analyze the data at the largest spatial scale, we selected 22 diploid and 22 hexaploid populations covering most of the European range (and a small part of Asia) of the species. We selected three plants per population for this analysis (Figure 1, Supplementary Information).

At all three spatial scales, two samples per plant were collected, one for ploidy assessment and the other for DNA analyses.

Microsatellite analyses

Total genomic DNA was extracted from dehydrated leaves and stored in silica gel using a sorbitol extraction method (Štorchová et al., 2000). Seven microsatellite loci were amplified: Aam.F58, Aam.A12, Aam.H231, Aam.B3, Aam.A415, Aam.J15 and Aam.G431 using specific primers for each region (Mayor and Naciri, 2007). Multiplex PCR reactions (Multiplex Mix) were designed combining microsatellites A12, A415, B3, F58 (Multiplex Mix 1) and J15, H231, G431 (Multiplex Mix 2). QIAGEN Multiplex PCR Master Mix (Qiagen, Hilden, Germany) containing HotStartTaq DNA polymerase (Lucigen, Middleton, WI, USA), a multiplex PCR buffer at 6 mℳ MgCl₂, deoxynucleotide triphosphates and a factor MP (Qiagen) that improves annealing and elongation were used. Initial Multiplex PCR reactions were designed for diploid and hexaploid individuals simultaneously. Afterwards, primer concentrations were adjusted separately for each cytotype for optimal and comparable electrophoretograms. Specifically, primer concentrations had to be increased for hexaploids because of the three times large genome, and thus higher total number of microsatellite sites.

Final Multiplex mix 1 PCR amplifications for diploids contained 5 μl QIAGEN Multiplex PCR Master Mix, 0.25 μl of A12, A415 and B3 primers and 0.35 μl of F58 primers (10 μℳ each in initial volume), 1.6 μl H₂O and 24 ng of DNA dissolved in 1.2 μl TE buffer. Final Multiplex mix 2 PCR amplifications for diploids contained 5 μl QIAGEN Multiplex PCR Master Mix, 0.25 μl of J15 and H231 primers and 0.35 μl of G431 primers (10 μℳ each in initial volume), 2.1 μl H₂O and 24 ng of DNA dissolved in 1.2 μl TE buffer. Final Multiplex mix 1 PCR amplifications for hexaploids contained 5 μl QIAGEN Multiplex PCR Master Mix, 0.25 μl of B3 primers, 0.35 μl of A12, A415 primers and 0.5 μl of F58 primers (10 μℳ each in initial volume), 0.9 μl H₂O and 24 ng of DNA dissolved in 1.2 μl TE buffer. Final Multiplex mix 2 PCR amplifications for hexaploids contained 5 μl QIAGEN Multiplex PCR Master Mix, 0.35 μl of J15, H231, G431 primers (10 μℳ each in initial volume), 1.7 μl H₂O and 24 ng DNA dissolved in 1.2 μl TE buffer were also added. An initial denaturation step at 95 °C for 15 min was followed by 35 cycles of denaturation (94 °C for 30 s), annealing (58 °C for 90 s) and extension (72 °C for 60 s) steps, and a final extension step at 60 °C for 30 min. A 1 μl aliquot of the PCR product was mixed with 11 μl of a 120: 1 solution of formamide and size standard GeneScan 500 LIZ (Life Technologies, Foster City, CA, USA). Fragment lengths were determined by capillary gel electrophoresis with an ABI 3130 Genetic Analyzer using Gene Mapper 4.0 (Life Technologies) and the peaks were scored manually.

To check the reproducibility of our microsatellite analyses, we selected three diploid and three hexaploid individuals, and repeated the microsatellite analyses of these in three independent runs for each individual. The results indicated 100% match in the results, suggesting that our microsatellite analyses are highly reproducible.

Data analyses

When scoring the data, for the hexaploids it was not possible to distinguish the exact number of copies for a given allele. Due to this, we worked only with the presence and absence of alleles.

The microsatellite results were used to calculate several genetic summary statistics for each of the three spatial scales studied, including total the number of alleles, observed (H_O) and expected heterozygosity (H_E), inbreeding coefficient (F_IS), and distribution of genetic diversity within and between cytotypes. The values of H_E and F_IS were calculated using SPAGeDi 1.2 (Hardy and Vekemans, 2002). s.e. of F_IS was obtained by jackknifing over loci.

Because of the unknown dosage of single alleles in the hexaploids, the H_E values for hexaploids are values of expected proportion of individuals bearing more than one allele and thus correspond to zygotic heterozygosity. This applies also for H_O values. Total gene diversity (H_T) was estimated as the H_E value for the whole data set, and the mean genetic diversity within populations (H_S) was calculated as the mean of the mean H_E value of all diploids in the data set, and mean H_E of all hexaploids in the data set. Genetic diversity among populations (D_ST) was calculated as D_ST=H_T—H_S. In case of the mixed population, the D_ST value represented differentiation between cytotypes within the single population.

To analyze relationships between the two cytotypes, we performed PCA using POLYSAT software (Clark and Jasieniuk, 2011). POLYSAT, running under the R platform, is a software program for analyzing autopolyploid and allopolyploid microsatellite data. It handles genotype data of any ploidy, including populations of mixed-ploidy, and assumes that the allele copy number is always ambiguous in partial heterozygotes. A pair-wise distance matrix between all samples was calculated using Bruvo distances (Bruvo et al., 2004), which takes distances between microsatellite alleles into account without the knowledge of allele copy number (Clark and Jasieniuk, 2011). The distance matrix was used as a correlation matrix needed for visualizing the results using PCA).

Differentiation between pairs of populations as a function of their geographic distance was assessed using two different measures of pair-wise between-population differentiation: the Bruvo distance calculated above and the Rho statistic (Ronfort et al., 1998). Rho is an inter class relatedness coefficient permitting comparison among ploidy levels and it was calculated using SPAGeDi at the intermediate and large spatial scale (it is not defined in the case of a single population). For Bruvo distances, we used the original data at the smallest spatial scale and population means at the intermediate and large spatial scales. In both cases, we calculated distances between diploid population pairs, hexaploid population pairs and inter-cytotype pairs. Isolation by distance was inspected through the regression of those values on the logarithm of geographic distance according to Hardy and Vekemans (2001). Statistical significance was tested using a Mantel test with 999 permutations. The Rho statistics was also used to compare the overall differentiation between populations within cytotypes and between cytotypes. In the case of the mixed population, the Rho value represented differentiation between cytotypes within the single population. Values of standard error of Rho were obtained by jackknifing over loci.

We also used STRUCTURE version 2.2 (Pritchard et al., 2000) to analyze the data. STRUCTURE is a Bayesian population assignment and inference software program widely used to detect population genetic structure (Kaeuffer et al., 2007). It implements algorithms accounting for genotypic uncertainty arising from copy number variation when the data includes polyploid cytotypes. Under the single-origin model, we would expect the K clusters identified by STRUCTURE to correspond to cytotypes, whereas under the multiple origins model we would expect clusters corresponding to sites. For each data set, we ran STRUCTURE using the admixture model and varying K values (up to the number of sub-populations) ranging from one to five at the small spatial scale and 10 at the medium and large spatial scales. Each run consisted of 100 000 burn-in iterations and 100 000 data collection iterations. Each value of K was evaluated using 20 independent Markov chain Monte Carlo replicates. We inferred the number of clusters following Pritchard et al. (2000), with posterior probabilities of K calculated assuming uniform priors on K and using for each K the maximum value of the probability of the data given K, ln Pr(X|K ), obtained over Markov chain Monte Carlo replicates (Halverson et al., 2008).

At the intermediate spatial scale we also tested two contrasting models explaining genetic relationships among cytotypes using analysis of molecular variance (AMOVA) (Excoffier et al., 1992), as implemented in GenAlEx 6 (Peakall and Smouse, 2006) by following the method described in Halverson et al. (2008). Specifically, we compared the single-origin model and a model with multiple origins of the cytotypes. The single-origin model proposes that the hexaploid cytotype arose only once from the diploid cytotype, and each cytotype currently represents a monophyletic lineage. This model also necessarily proposes that the origins of the polyploid cytotypes took place long enough ago for the resultant cytotypes to have spread across their modern range (Halverson et al., 2008). We tested this model by a hierarchical AMOVA model in which genotypes are nested within localities and localities within cytotypes. Alternatively, the strictest multiple origins model proposes that polyploid cytotypes have arisen repeatedly and independently (and perhaps recently) at each geographic location (Halverson et al., 2008). This hypothesis was tested using an AMOVA analysis in which genotypes were nested within cytotypes and these were nested within regions (pairs of nearby diploid and hexaploid populations). The preferred AMOVA model is that in which the higher stratum (cytotypes for the single-origin model or region for the multiple origins model) explains a greater component of total genetic variation (Halverson et al., 2008).

Results

The total number of alleles found across cytotypes ranged between 104 in the mixed-ploidy population and 179 at the largest spatial scale (Table 1). In all the three data sets, the number of alleles found in hexaploids exceeded the number found in the diploids (Table 1). The total number of alleles across cytotypes did not strongly exceed the number of alleles found in hexaploids, indicating relatively large overlap in identity of alleles between cytotypes. This large overlap in the identity of alleles was also confirmed by the relatively small D_ST values, which indicates relatively low differentiation between cytotypes when compared with total genetic diversity (H_T). Similarly, also the D_ST within populations was quite small compared with total genetic diversity within cytotypes (H_T) indicating large similarity between populations within cytotypes (Table 1).

Table 1. Summary characteristics describing genetic diversity assessed using microsatellites in the three data sets, in each case separately for diploids, hexaploids and for the total data set.

	Mixed-ploidy population			Contact zone			Europe
	2x	6x	Combined	2x	6x	Combined	2x	6x	Combined
TA	28	96	104	90	129	160	98	150	179
FIS (±s.e.)	−0.045±0.11	−0.232±0.12*	−0.0371±0.02s	−0.080±−0.11s	−0.099±0.02*	−0.002±0.05	−0.035±0.07	−0.154±0.03*	−0.013±0.003
HE	0.642	0.762	0.786	0.816	0.834	0.886	0.803	0.837	0.882
Ho	0.671	0.939	0.815	0.881	0.917	0.887	0.83	0.97	0.89
HT	NA	NA	0.786	0.816	0.834	0.886	0.803	0.837	0.882
Hs	NA	NA	0.702	0.753	0.827	0.825	0.697	0.815	0.820
DST	NA	NA	0.084	0.063	0.007	0.061	0.106	0.022	0.062
Rho (±s.e.)	NA	NA	0.511±0.07*	0.182±0.03*	0.115±0.03*	0.292±0.05*	0.257±0.03*	0.177±0.02*	0.347±0.03*
AMOVA
Among regions	NA	NA	NA	NA	NA	0%	NA	NA	NA
Among cytotypes	NA	NA	31%*	NA	NA	26%*	NA	NA	22%*
Among populations	NA	NA	NA	17%*	14%*	11%*	24%*	18%*	16%*
Within populations	NA	NA	69%*	83%*	86%*	63%*	76%*	82%*	62%*

Abbreviations: AMOVA, analysis of molecular variance; D_ST, genetic diversity among populations; F_IS, inbreeding coefficient; H_E, expected heterozygosity; Ho, observed heterozygosity; Hs, mean genetic diversity within populations; H_T, total gene diversity; NA, not applicable; TA, total number of alleles.

Values of F_IS and Rho, significantly deviating from 0, are marked by *. Also shown are the proportions of genetic variation in the data set at each hierarchical level as assessed by AMOVA; again those significantly deviating from 0 are marked by *. In the mixed-ploidy population, the ‘populations' in the table are groups of diploid and group of hexaploid individuals.

In spite of the relatively large overlap between cytotypes as indicated by D_ST values, the two cytotypes are significantly differentiated at all scales as indicated by Rho coefficient, which is significantly deviating from 0 in all cases. In addition, significant differentiation between cytotypes is also visible from AMOVA analyses (Table 1).

In all cases, the inbreeding coefficient (F_IS value) was negative. The values, however, significantly deviating from 0 only for the hexaploid cytotype, indicating strong heterozygote excess in the hexaploids (Table 1).

Mixed-ploidy population

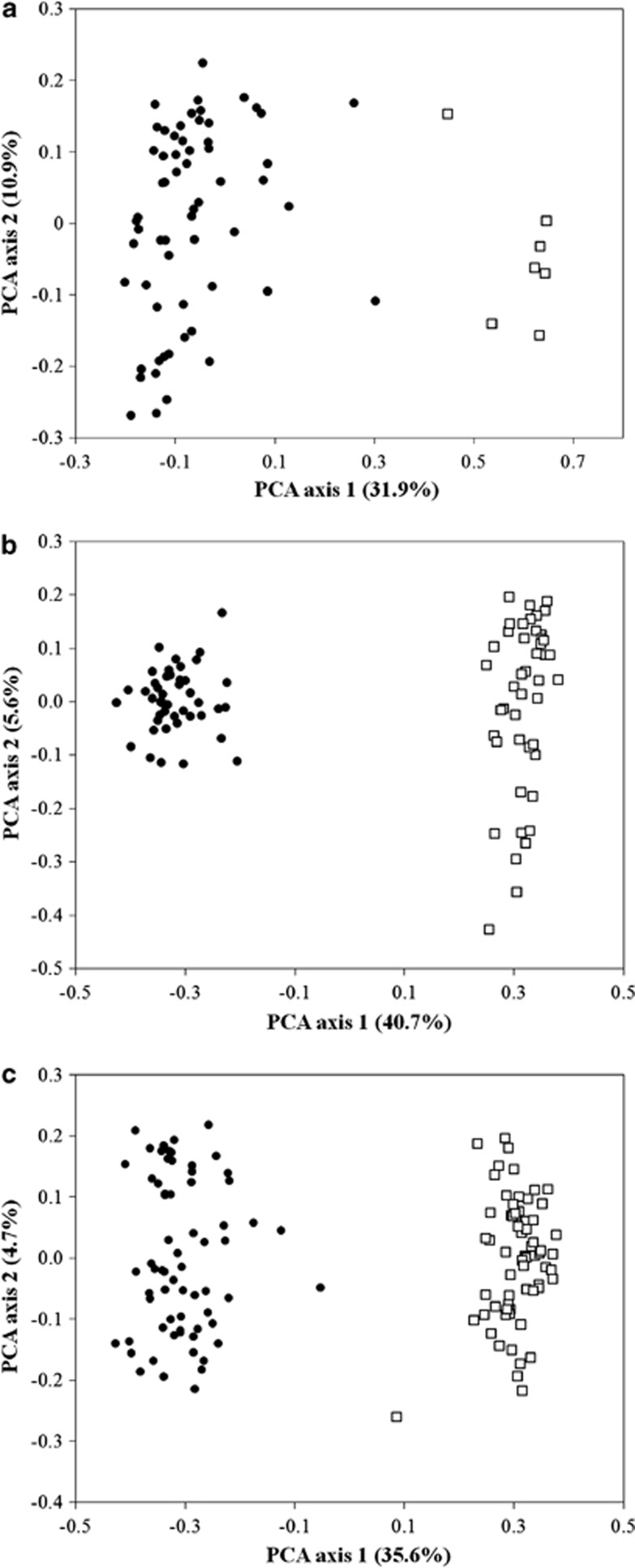
PCA analyses performed by POLYSAT clearly separated the two cytotypes into separate clusters along the first axis (Figure 2a). The first axis separating the cytotypes explained 31.9% of the total variation in the data set, while the second axis accounting for variation between individual plants within cytotypes explained only 10.9% of the total variation.

Figure 2.

PCAs using Bruvo distances performed in POLYSAT. (a) Mixed-ploidy population. (b) Contact zone between cytotypes. (c) Large spatial scale across Europe. Open squares indicate diploids, filled circles represent hexaploids. % of variance explained by each axis is provided within the figure.

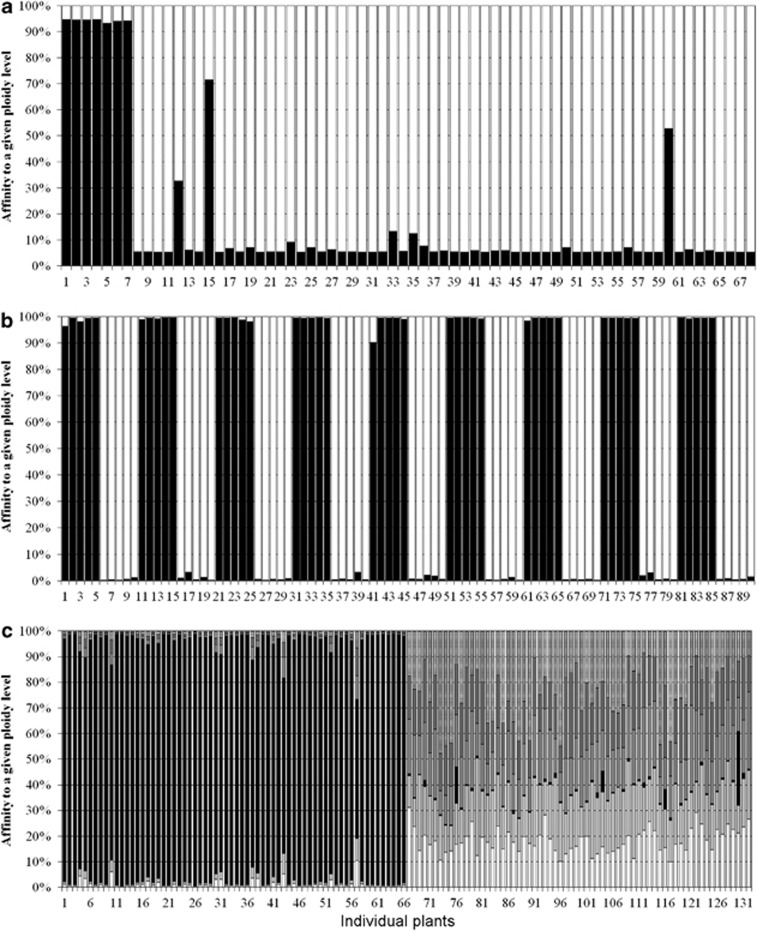
Similarly to the PCA, the analysis performed in STRUCTURE identified two clusters of individuals (K=2 having a posterior probability greater than 0.999 relative to other tested values of K; Table 2). All diploid individuals had >93% probability of falling into one of the clusters (mean±s.d., 94.1±0.5%). The assignment of all hexaploids into the second cluster was less certain (91.7±10.8%). Fifty-six hexaploid individuals had >90% probability of falling into the second cluster. However, the remaining five individuals had 88, 87, 67, 47 and 28% probability of falling into the cluster containing mostly hexaploids. Therefore, two of these had <50% chance to be a member of the cluster containing the diploids (Figure 3a). These five hexaploid individuals also can be seen as outliers in the PCA graph and represented the five hexaploid points closest to the diploid cluster (Figure 2a).

Table 2. Results of STRUCTURE analyses showing log-likelihood estimation of cluster number for K=1–5–(10).

Data set	K	1	2	3	4	5	6	7	8	9	10
Mixed-ploidy population	ln Pr(X|K)	−3511	−3393	−3817	−3632	−3513
	Δ ln-likelihood	−118	0	−424	−239	−120
	Posterior Pr(K)	<0.001	>0.999	<0.001	<0.001	<0.001
Contact zone	ln Pr(X|K)	−4479	−4081	−4131	−4185	−4200	−4284	−4378	−4293	−4328	−4412
	Δ ln-likelihood	−398	0	−49	−103	−119	−202	−297	−212	−247	−331
	Posterior Pr(K)	<0.001	>0.999	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
Europe	ln Pr(X|K)	−6594	−5979	−5985	−6166	−6154	−5896	−6363	−6270	−6195	−6197
	Δ ln-likelihood	−698	−83	−89	−270	−258	0	−467	−374	−299	−301
	Posterior Pr(K)	<0.001	<0.001	<0.001	<0.001	<0.001	>0.999	<0.001	<0.001	<0.001	<0.001

The results are shown for the small (mixed-ploidy population), intermediate (contact zone) and large (Europe) spatial scales. The favored K values are in bold

Figure 3.

Individual assignment based on Bayesian genotypic cluster analysis performed using STRUCTURE. Histograms demonstrate the proportion of each individual's genome that can be assigned to each of the clusters. (a) Mixed-ploidy population (individuals 1–7 are diploid, the remaining are hexaploid) at K=2. (b) Contact zone between cytotypes at K=2 (individuals are sorted by pairs of populations, the diploid population within each pair goes first; that is individuals 1–5 are diploids of pair 1, individuals 6–10 are hexaploids of pair 1, individuals 11–15 are diploids of pair 2). (c) Large spatial scale across Europe at K=6 (Individuals 1–66 are diploid, 67–132 are hexaploid).

There was significant isolation by distance among the hexaploid individuals, but not among the diploid individuals or between the diploid and hexaploid individual pairs based on Bruvo distances (Table 3).

Table 3. Correlation between pair-wise distances between populations measured using Rho coefficients and Bruvo distances, and the logarithm of the geographical distance.

	Mixed-ploidy population			Contact zone			Europe
	2x	6x	2x–6x	2x	6x	2x–6x	2x	6x	2x–6x
Rho
r	NA	NA	NA	0.04	0.46	0.04	0.06	0.15	0.03
p	NA	NA	NA	0.45	0.04	0.74	0.30	0.13	0.57
Bruvo
r	0.18	0.17	0.08	0.16	0.42	0.07	0.12	0.20	0.19
p	0.34	0.01	0.14	0.24	0.07	0.55	0.17	0.02	0.42

Abbreviation: NA, not applicable.

The calculations were done for diploid population pairs, hexaploid population pairs and diploid-hexaploid population pairs. Values significant at P⩽0.05 are in bold.

Multiple populations across the contact zone

Similarly to what occurred with the mixed-ploidy population, PCA performed using POLYSAT at the contact zone clearly separated the two cytotypes (Figure 2b). The first axis separating the two cytotypes explained 40.7% of the total variation in the data set. In contrast, the second axis representing variation between populations explained only 5.6% of the total variation in the data set. The variation between diploid populations was much higher than the variation between hexaploid populations.

STRUCTURE analysis also identified two clusters of individuals (K=2 having a posterior probability >0.99 relative to other tested values of K; Table 2), clearly separating the two cytotypes. All diploid individuals had >99±1.5% probability to fall into one of the clusters and all the hexaploids had more than 99±0.1% to fall into the other cluster (Figure 3b).

There was significant isolation by distance among hexaploid populations as assessed by the Rho coefficient and marginally significant isolation by distance as assessed by Bruvo distance (Table 3). There was no significant isolation by distance between diploid population pairs or between diploid and hexaploid population pairs based on either of the two distance measures (Table 3).

The AMOVA analyses comparing the single-origin polyploidy model and strict multiple origins polyploidy model clearly indicated that the single-origin model is superior to the multiple origin model. In the single-origin model, cytotype explained 26% of the total genetic variation and was highly significant. In contrast, the region in the multiple origins model explained 0% of the total variation and was not significant (Table 4). The variation between populations accounted for 11% of the variation in the data set (Table 1).

Table 4. AMOVA analyses at the intermediate spatial scale testing the (A) single-origin polyploidy model and (B) strict multiple origins polyploidy model.

Source of variation	d.f.	Sum of sq.	Percentage of variance	f	P
(A) Single-origin polyploidy model
Among cytotypes	1	206.267	26	0.266	0.001
Among localities w/in cytotypes	16	293.733	11	0.148	0.001
Individuals w/in localities	72	708.200	63	0.374	0.001
(B) Strict multiple origins polyploid model
Among regions	8	150.100	0	−0.148	1.000
Among cytotypes w/in regions	9	349.900	37	0.371	0.001
Individuals w/in localities	72	708.200	63	0.279	0.001

Values significant at P⩽0.05 are in bold.

Populations sampled across Europe

PCA analyses performed by POLYSAT at the largest spatial scale confirmed the clear separation between cytotypes (Figure 2c). The first axis separating the cytotypes explained 35.6% and the second axis capturing variation among populations explained 4.7% of the total variation in the data set. In contrast to the data at the contact zone, variation between populations in the diploid cytotype was comparable to variation between populations in the hexaploid cytotype.

STRUCTURE analysis at the largest spatial scale identified, in contrast to the two smaller scales, six clusters of individuals (K=6 having a posterior probability of >0.99 relative to other tested values of K; Table 2). Two spatial clusters were identified as the second most likely option. One of the clusters clearly corresponded to the diploids, while the other five clusters corresponded to the hexaploids. Most of the hexaploid individuals, however, appeared to be a mixture of all five types. (Figure 3c).

At the largest spatial scale there was significant isolation by distance only between hexaploid population pairs, detected using Bruvo distances (Table 3).

The AMOVA analyses partitioning variation among population and among cytotypes at the largest scale indicated that variation among cytotypes is slightly higher (22%) than variation among populations (16%, Table 1).

Discussion

The results obtained at the three spatial scales studied indicate relatively strong genetic separation between diploid and hexaploid cytotypes of A. amellus. This contrasts with many previous studies on diploid–polyploid systems, in which either frequent gene flow or broad shared ancestral polymorphisms among cytotypes has been reported (for example, Ramsey et al., 2008; Fehlberg and Ferguson, 2012). Thus, our results suggest that the two cytotypes are largely evolving independently (Soltis and Soltis, 1999) and could theoretically be viewed as two cryptic species (Soltis et al., 2007). Consequently, the two cytotypes are likely to follow different evolutionary trajectories and accumulate various divergent adaptations. In spite of this, their formal separation is difficult as they cannot be distinguished morphologically (Mandáková and Münzbergová, 2008), occupy very similar habitat conditions (Mandáková and Münzbergová, 2008) and have largely overlapping distribution ranges (Castro et al., 2012).

Strong separation among cytotypes was observed at all the three spatial scales. The relatively consistent results across the three spatial scale contrast with our expectations, based on the previous studies (for example, Hardy and Vekemans, 2001), that the strength of the separation between cytotypes will depend on spatial scale. This pattern, it means strong separation independent of scale, is probably due to the strong breeding barriers between the cytotypes (Castro et al., 2011) and very limited dispersal ability of the species (Münzbergová et al., 2011).

The test of the single versus multiple origin models at the intermediate spatial scale strongly supported the single-origin model, indicating that even at this scale, there is no or very limited gene flow between the cytotypes. On the basis of this we predict that the studied contact zone is of secondary origin, similarly to many contact zones between different cytotypes described in the literature (for example, Petit et al., 1999; Hardy and Vekemans, 2001).

In spite of the overwhelming evidence that the two cytotypes of A. amellus are separated, and that hexaploids are of single origin, there are also several lines of evidence suggesting that some hexaploid populations may have arisen in situ and thus that multiple origin could also occur in A. amellus. Specifically, occasional recurrent formation of hexaploid individuals in a diploid population followed by rapid reproductive isolation could explain the pattern. This is most clearly seen for the mixed population, in which several hexaploid individuals fell with high probability into a diploid cluster (as suggested by analyses in STRUCTURE and seen also in the PCA). Thus, it can be speculated that the hexaploid individuals might have originated in situ from the diploids and become established. The hexaploids could subsequently have become more abundant because of higher reproductive success in comparison with diploids (Castro et al., 2012) and the diploid cytotype (currently occurring as only seven mature plants at one edge of the population) is currently being excluded from the population (minority cytotype exclusion; Levin, 1975; Rodriguez, 1996). If this theory is correct, it could be confirmed by revisiting the population in several years and identifying changes in the proportion of the cytotypes. A similar scenario has been observed, for example, in Vicia cracca, where the diploid cytotype completely disappeared from several tetraploid populations (Trávníček et al., 2010). Alternatively, this pattern could also be a result of occasional cross-pollination, followed by introgression. Although such an explanation has been suggested repeatedly for other diploid–polyploid systems (for example, Slotte et al., 2006), we think it is quite unlikely in this system, due to strong post-pollination breeding barriers between the two cytotypes (Castro et al., 2011).

Multiple origins of higher ploidy levels has also been proposed repeatedly in various other polyploid aggregates (for example, Hardy and Vekemans, 2001; Segraves et al., 2002; Symonds et al., 2010) and multiple origins are commonly predicted even in secondary contact zones, such as the one observed in A. amellus. This suggests that repeated origins of a cytotype may be an important mechanism of diversification in many polyploid lineages, including A. amellus.

Isolation by distance was detected in the hexaploid cytotype at all the three scales but not for the diploid cytotypes or between cytotype pairs. This pattern is in agreement with theoretical expectations for polyploids, as hexaploid populations should experience lower genetic drift pressures due to polysomic inheritance and thus should be less divergent (for example, Moody et al., 1993; Ronfort et al., 1998, Mahy et al., 2000; Hardy and Vekemans, 2001). Our conclusion of lower differentiation between hexaploid populations compared with diploids is also apparent from lower D_ST values among the hexaploid populations. In contrast to our expectations, isolation by distance was similar across the three data sets and as above, this might be considered as the consequence of strong breeding barriers between the cytotypes (Castro et al., 2011) and very limited dispersal ability of the species (Münzbergová et al., 2011).

Overall, our results indicate that the two cytotypes represent two largely independent entities that could be viewed as two cryptic species, with the hexaploid being of autopolyploid origin. The relationships detected among the two cytotypes are largely comparable between the three spatial scales and between different techniques used to analyze the data. This suggests that our conclusions on the system are quite general and it can be expected that these two cytotype are undergoing largely independent evolutionary trajectories.

More generally, the results indicate that polyploidy can cause genetic divergence between populations of the same species, even in situations when the different cytotypes are morphologically very similar, have overlapped distribution ranges and similar habitat requirements. No or very-low gene flow between the cytotypes gives them a high potential for adaptations to novel environments. Thanks to this, the polyploid cytotypes may gain a large variation of novel properties that may prove as advantageous pre-adaptations in cases the species is transported to novel areas and thus increases its potential for colonization.

Data archiving

The data are available from the authors at zuzmun@natur.cuni.cz.

The authors declare no conflict of interests.