Abstract
Lung cancer is the leading cause of cancer-related deaths worldwide. Lack of early detection and limited options for targeted therapies are both contributing factors to the dismal statistics observed in lung cancer. Thus, advances in both of these areas are likely to lead to improved outcomes. MicroRNAs (miRs or miRNAs) represent a class of non-coding RNAs that have the capacity for gene regulation and may serve as both diagnostic and prognostic biomarkers in lung cancer. Abnormal expression patterns for several miRNAs have been identified in lung cancers. Specifically, let-7 and miR-9 are deregulated in both lung cancers and other solid malignancies. In this paper, we construct a mathematical model that integrates let-7 and miR-9 expression into a signaling pathway to generate an in silico model for the process of epithelial mesenchymal transition (EMT). Simulations of the model demonstrate that EGFR and Ras mutations in non-small cell lung cancers (NSCLC), which lead to the process of EMT, result in miR-9 upregulation and let-7 suppression, and this process is somewhat robust against random input into miR-9 and more strongly robust against random input into let-7. We elected to validate our model in vitro by testing the effects of EGFR inhibition on downstream MYC, miR-9 and let-7a expression. Interestingly, in an EGFR mutated lung cancer cell line, treatment with an EGFR inhibitor (Gefitinib) resulted in a concentration specific reduction in c-MYC and miR-9 expression while not changing let-7a expression. Our mathematical model explains the signaling link among EGFR, MYC, and miR-9, but not let-7. However, very little is presently known about factors that regulate let-7. It is quite possible that when such regulating factors become known and integrated into our model, they will further support our mathematical model.
Introduction
Lung cancer is the leading cause of cancer-related deaths worldwide. In the U.S. the number of new occurrences is approximately  annually, and the number of deaths is
annually, and the number of deaths is  , representing
, representing  of all cancer related deaths [1]. Lack of early detection and limited options for target therapies are both contributing factors to the dismal statistics observed in lung cancer. Thus, advances in both of these areas are likely to lead to improved outcomes.
of all cancer related deaths [1]. Lack of early detection and limited options for target therapies are both contributing factors to the dismal statistics observed in lung cancer. Thus, advances in both of these areas are likely to lead to improved outcomes.
microRNAs (miRs or miRNAs) represent a class of non-coding RNAs that have the capacity for gene regulation and may serve as diagnostic and prognostic biomarkers in lung cancer. Abnormal expression patterns for miRNAs have been identified in lung cancers. Specifically, let-7 and miR-9 are deregulated in both lung cancers and other solid malignancies. Takamizawa et al. (2004) and Nicoloso et al. (2009) demonstrated that let-7 is downregulated in non-small cell lung cancers (NSCLC) [2], [3]. Several investigators have shown that let-7 harbors tumor suppressive properties both in vitro and in vivo [4], [5]. Using microarray data, Yanaihara et al. (2006) reported that miR-9 was decreased in NSCLC [6], whereas Volinia et al. (2006) reported an increase in miR-9 expression [7]. More recently Crawford et al. (2009) reported increased expression of miR-9 in NSCLC [8], and Võsa et al. (2011) drew the same conclusion from their microarray data [9]. Recently, we have also independently analyzed  cases of NSCLC and compared miR-9 expression between tumors and adjacent uninvolved lung tissue. We found that in approximately
cases of NSCLC and compared miR-9 expression between tumors and adjacent uninvolved lung tissue. We found that in approximately  cases miR-9 was overexpressed in lung tumors; see Supplementary Material S1. A recent investigation showed that miR-9 contributes to metastatic potential in breast cancer in part by targeting components of epithelial mesenchymal transition (EMT) [10]. However, the role for miR-9 in the pathogenesis of lung cancer is less well understood. Mascaux et al. (2009) demonstrated an induction in miR-9 expression during bronchial squamous carcinogenesis [11].
cases miR-9 was overexpressed in lung tumors; see Supplementary Material S1. A recent investigation showed that miR-9 contributes to metastatic potential in breast cancer in part by targeting components of epithelial mesenchymal transition (EMT) [10]. However, the role for miR-9 in the pathogenesis of lung cancer is less well understood. Mascaux et al. (2009) demonstrated an induction in miR-9 expression during bronchial squamous carcinogenesis [11].
Given the fact that a single miRNA may regulate tens to hundreds of genes, understanding the importance of an individual miRNA in cancer biology can be challenging. This is further complicated by observations that the dysregulation of several miRNAs is often required to cause a given phenotype. To date, few models exist to elucidate the mechanisms by which multiple miRNAs contribute both individually and in tandem to promote tumor initiation and progression. Applying mathematical modeling to miRNA biology provides an opportunity to understand these complex relationships. In the current study, we have developed for the first time a mathematical model focusing on miRNAs (miR-9 and let-7) in the context of lung cancer as a model system; however, our model system could be applicable to miRNA biology in both malignant and benign diseases. For simplicity, we have integrated these miRNAs into a signaling pathway to generate an in silico model for the process of EMT. Herein, we include the EGF-EGFR complex and associated downstream signaling culminating in matrix metalloproteinase (MMP) expression. Other components of our pathway include SOS, Ras, ERK, MYC,E-Cadherin, miR-9, and let-7.
We have simulated the model under several scenarios of gene mutations that may lead to lung cancer and determined, in each scenario, that miR-9 was upregulated and let-7 downregulated. We have also shown that the process leading to EMT is somewhat robust against random input into miR-9 and more strongly robust against random input into let-7.
Results
Biological Background
Figure 1 A shows a signaling pathway involving miR-9, let-7, MYC, and EMT, while Figure 1 B is a simplified version that will be used in the mathematical model. miR-9 is upregulated in NSCLC. Although Yanaihara et al. (2006) reported a decrease of miR-9 using microarray data [6], several other papers, some more recent, reported an increase of miR-9 in NSCLC: Volinia et al. (2006) and Võsa et al. (2011) used microarray [7], [9], and Crawford et al. (2009) used PCR [8]. We have analyzed  cases of NSCLC with PCR and demonstrate miR-9 overexpression in lung tumors compared to adjacent uninvolved lung and present a representation of
cases of NSCLC with PCR and demonstrate miR-9 overexpression in lung tumors compared to adjacent uninvolved lung and present a representation of 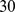 such cases; see Supplementary Material S1.
such cases; see Supplementary Material S1.
Figure 1. A signaling pathway for lung cancer.
A pathway from EGF-EGFR complex to MMP, which includes miR-9 and let-7, is given in (A) and a simplified pathway is shown in (B).
MYC controls many fundamental cellular processes, and aberrant MYC expression is known to be associated with cancer. For example, Frenzel et al. (2010) observed that MYC is usually activated in many cancers [12], and Aguda et al. (2008) showed how MYC can act as either an oncogene or tumor suppressor [13]. In lung cancer, MYC family oncogenes are amplified in both small-cell lung cancers (SCLC) and NSCLC [14], [15]. Moreover, c-MYC can induce metastasis in c-Raf mutant NSCLC [16].
Investigators have also identified a link between MYC and miRNAs that also play a significant role in cancer. Rinaldi et al. (2007) showed that both MYC and the miRNA cluster miR-17-92 are amplified in human mantle cell lymphoma [17]; Frenzel et al. (2010) described miR-9 as an oncogenic miRNA and let-7 as a tumor suppressor miRNA both of which are regulated by MYC [12]: MYC induces miR-9, which blocks tumor suppressor pathways, while MYC inhibits let-7, which blocks oncogenic pathways. Ma et al. (2010) found that miR-9 is driven by MYC, downregulates E-Cadherin, and induces metastasis in breast cancer [10]. Wolfer and Ramaswamy (2011) investigated the role of MYC in breast cancer metastasis using a signaling pathway that includes let-7, miR-9, E-Cadherin, and EMT [18].
Our proposed pathway is based on several lines of investigation. Similar to breast cancer, let-7 is downregulated in NSCLC [2], [3]. Takamizawa et al. (2004) demonstrated that reductions of let-7 as high as  occurred in tumors compared to uninvolved adjacent lung tissue [2]. In this same study, only
occurred in tumors compared to uninvolved adjacent lung tissue [2]. In this same study, only  cases had such reductions (
cases had such reductions ( ). However, more recent investigation by Inamura et al. (2007) demonstrated that among well-differentiated adenocarcinomas (
). However, more recent investigation by Inamura et al. (2007) demonstrated that among well-differentiated adenocarcinomas ( ), the reductions in let-7 family members were more modest (approximately
), the reductions in let-7 family members were more modest (approximately  ) [19]. Wang et al. (2011) asserted that c-MYC represses transcription of let-7 [20]. Johnson et al. (2005) and others showed that Ras is suppressed by let-7 [21]. Lee and Dutta (2007) suggested that let-7 represses HMGA-2 in a lung cancer cell [22], and Thuault et al. (2008) asserted that HMGA-2 causes EMT by activating Snail1 which in turn represses E-Cadherin [23]. E-Cadherin downregulates MMP in bronchial tumor cells [24]. Both E-Cadherin and MMP have been implicated as biomarkers in several solid malignancies including lung cancer. A recent investigation showed that elevated levels of MMP-9 in cases of NSCLC correlated with advanced stages and the presence of metastases [25]. In addition Rao et al. (2005) demonstrated in vitro and in vivo that adenoviral mediated gene transfer of MMP-9 could reduce lung cancer invasive capacity and formation of metastases [26]. Decreased E-Cadherin expression also appears to correlate with clinically more aggressive disease [27]–[29].
) [19]. Wang et al. (2011) asserted that c-MYC represses transcription of let-7 [20]. Johnson et al. (2005) and others showed that Ras is suppressed by let-7 [21]. Lee and Dutta (2007) suggested that let-7 represses HMGA-2 in a lung cancer cell [22], and Thuault et al. (2008) asserted that HMGA-2 causes EMT by activating Snail1 which in turn represses E-Cadherin [23]. E-Cadherin downregulates MMP in bronchial tumor cells [24]. Both E-Cadherin and MMP have been implicated as biomarkers in several solid malignancies including lung cancer. A recent investigation showed that elevated levels of MMP-9 in cases of NSCLC correlated with advanced stages and the presence of metastases [25]. In addition Rao et al. (2005) demonstrated in vitro and in vivo that adenoviral mediated gene transfer of MMP-9 could reduce lung cancer invasive capacity and formation of metastases [26]. Decreased E-Cadherin expression also appears to correlate with clinically more aggressive disease [27]–[29].
Roberts and Der (2007) used an EGFR-Ras-Raf-MEK-ERK pathway to explain that 10% of NSCLC arise from EGFR mutations and that 30% of NSCLC arise from mutations in Ras [30]. SOS is an intermediate between the EGF-EGFR complex and Ras [31], and is repressed through negative feedback by ERK [32], [33]. Huang et al. (2011) showed that ERK/MAPK in lung cancer activates c-MYC [34]. Figure 1 A provides a summary of the above lines of investigation. For the purposes of simplicity, we propose a simpler version in Figure 1 B which nevertheless encompasses the main features of Figure 1 A. We recognize that other signaling pathways are driven by the EGF-EGFR complex including PI3K/Akt which regulates cell survival. However, given our interest in miR-9 and let-7 as potential biomarkers, we have not included this pathway in our model.
Model Equations
We introduce a system of ordinary differential equations that describe a signaling pathway of EMT (represented by the level of MMP mRNA) induced by MYC through miR-9 and let-7 as shown in Figure 1 B. The differential equations  are based on Figure 1 B, and detailed explanations are given in Methods. Notation for species concentrations is given in Table 1.
are based on Figure 1 B, and detailed explanations are given in Methods. Notation for species concentrations is given in Table 1.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Table 1. Notation for species concentrations.
| Notation | Description |

|
EGF-EGFR complex (constant) |

|
active SOS concentration |

|
active Ras concentration |

|
active ERK concentration |

|
MYC protein concentration |

|
miR-9 concentration |

|
let-7 concentration |

|
E-Cadherin concentration |

|
MMP mRNA concentration |
The table gives notation for species concentrations that are used in the mathematical model.
Simulations
A large number of NSCLC cases arise from EGFR mutations [35], [36] or Ras mutations [37]. We assume that negative feedback of ERK to SOS may be disrupted in NSCLC. We describe these aberrations by increasing  , increasing
, increasing  , or decreasing
, or decreasing  , so that concentration level of EGF-EGFR complex increases, Ras is over-activated by SOS, or negative feedback of ERK to SOS is weakened. The following simulations demonstrate the effect of increase in
, so that concentration level of EGF-EGFR complex increases, Ras is over-activated by SOS, or negative feedback of ERK to SOS is weakened. The following simulations demonstrate the effect of increase in  and in
and in  and decrease in
and decrease in  on the increase in miR-9, let-7 and MMP.
on the increase in miR-9, let-7 and MMP.
Simulations of the model equations were performed using Matlab. We used an ode solver, ode15 s, to solve a system of ordinary differential equations numerically. To solve a system of stochastic differential equations with random inputs in miR-9 or let-7 numerically, we developed a code using an Euler scheme. All initial values are taken to be those of healthy normal cells, namely,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
If  increases as a result of mutations in EGFR, we expect an increase in miR-9 and a decrease in let-7 as indeed are observed in lung cancer. There will also be an increase in MMP mRNA signifying EMT and cell migration, which contributes to metastasis. Figure 2 shows the level of miR-9, let-7, and MMP at
increases as a result of mutations in EGFR, we expect an increase in miR-9 and a decrease in let-7 as indeed are observed in lung cancer. There will also be an increase in MMP mRNA signifying EMT and cell migration, which contributes to metastasis. Figure 2 shows the level of miR-9, let-7, and MMP at  as a function of
as a function of  : as
: as  increases, miR-9 and MMP mRNA concentrations increase and let-7 concentration decreases. For example, for
increases, miR-9 and MMP mRNA concentrations increase and let-7 concentration decreases. For example, for  , the level of miR-9 increases by
, the level of miR-9 increases by  -fold from
-fold from  to
to  and that of MMP mRNA concentration increases by
and that of MMP mRNA concentration increases by  -fold from
-fold from  to
to  compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by
compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by  -fold from
-fold from  to
to  .
.
Figure 2. Concentration changes of miR-9, let-7, and MMP mRNA with different values for.

 . The units on the vertical axes are in
. The units on the vertical axes are in  and the time is at
and the time is at  .
.
Figure 3 shows the effect of Ras mutations on the levels of miR-9, let-7, and MMP mRNA after  . Ras mutations are represented by an increase in
. Ras mutations are represented by an increase in  . We see that as
. We see that as  increases, so do the concentrations of miR-9 and MMP mRNA while let-7 concentration decreases. For example, for
increases, so do the concentrations of miR-9 and MMP mRNA while let-7 concentration decreases. For example, for  , the level of miR-9 concentration increases by
, the level of miR-9 concentration increases by  -fold from
-fold from  to
to  and that of MMP mRNA concentration increases by
and that of MMP mRNA concentration increases by  -fold from
-fold from  to
to  compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by
compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by  -fold from
-fold from  to
to  .
.
Figure 3. Concentration changes of miR-9, let-7, and MMP mRNA with different values for.

 . The units on the vertical axes are in
. The units on the vertical axes are in  and the time is at
and the time is at  .
.
When the negative feedback of ERK to SOS is weakened as a result of possible mutations in ERK, the parameter  in Eq. (1) is decreased. Figure 4 shows the effect of these mutations: as
in Eq. (1) is decreased. Figure 4 shows the effect of these mutations: as  decreases, the concentrations of miR-9 and MMP increase and that of let-7 decreases. For example, for
decreases, the concentrations of miR-9 and MMP increase and that of let-7 decreases. For example, for  , the level of miR-9 concentration increases by
, the level of miR-9 concentration increases by  -fold from
-fold from  to
to  and that of MMP mRNA concentration increases by
and that of MMP mRNA concentration increases by  -fold from
-fold from  to
to  compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by
compared to the level in healthy normal cells. On the other hand, the level of let-7 concentration decreases by  -fold from
-fold from  to
to  .
.
Figure 4. Concentration changes of miR-9, let-7, and MMP mRNA with different values for.

 . The units on the vertical axes are in
. The units on the vertical axes are in  and the time is at
and the time is at  .
.
In Figure 5, we simulate the time evolution of SOS, Ras, ERK, MYC, miR-9, let-7, E-Cadherin, and MMP mRNA over a period of  with
with  ; in Figure 6 the simulations are carried out for the longer period of
; in Figure 6 the simulations are carried out for the longer period of  . A comparison between the panels of the two figures shows that the dynamics of SOS, Ras, and ERK are very fast; MYC, miR-9, and let-7 change relatively slower, and MMP mRNA takes even longer to reach equilibrium. After
. A comparison between the panels of the two figures shows that the dynamics of SOS, Ras, and ERK are very fast; MYC, miR-9, and let-7 change relatively slower, and MMP mRNA takes even longer to reach equilibrium. After  minutes, SOS and Ras increased by
minutes, SOS and Ras increased by  -fold from
-fold from  to
to  and from
and from  to
to  , respectively; ERK and MYC increased by
, respectively; ERK and MYC increased by  -fold from
-fold from  to
to  and from
and from  to
to  , respectively; miR-9 increased by
, respectively; miR-9 increased by  -fold from
-fold from  to
to  ; MMP increased by
; MMP increased by 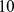 -fold from
-fold from  to
to  compared to their values in normal cells; let-7 decreased by
compared to their values in normal cells; let-7 decreased by  -fold from
-fold from  to
to  , and E-Cadherin decreased by
, and E-Cadherin decreased by  -fold from
-fold from  to
to  .
.
Figure 5. Simulation results for a cancer cell with EGFR mutations,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are in minutes.
and the units on the horizontal axes are in minutes.
Figure 6. Simulation results for a cancer cell with EGFR mutations,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are scaled in
and the units on the horizontal axes are scaled in  minutes.
minutes.
Figures 7 and 8 show similar simulations when  is increased to
is increased to  and Figures 9 and 10 show similar simulations when
and Figures 9 and 10 show similar simulations when  is decreased to
is decreased to  . In Figure 8, Ras increased by
. In Figure 8, Ras increased by  -fold from
-fold from  to
to  ; ERK and MYC increased by
; ERK and MYC increased by  -fold from
-fold from  to
to  and from
and from  to
to  , respectively; miR-9 increased by
, respectively; miR-9 increased by  -fold from
-fold from  to
to  ; MMP increased by
; MMP increased by  -fold from
-fold from  to
to  compared to their values in normal cells; SOS decreased by
compared to their values in normal cells; SOS decreased by  -fold from
-fold from  to
to  ; let-7 decreased by
; let-7 decreased by  -fold from
-fold from  to
to  , and E-Cadherin decreased by
, and E-Cadherin decreased by  -fold from
-fold from  to
to  . In Figure 10, concentration changes essentially in the same amount as in Figure 6.
. In Figure 10, concentration changes essentially in the same amount as in Figure 6.
Figure 7. Simulation results for a cancer cell with Ras mutations,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are in minutes.
and the units on the horizontal axes are in minutes.
Figure 8. Simulation results for a cancer cell with Ras mutations,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are scaled in
and the units on the horizontal axes are scaled in  minutes.
minutes.
Figure 9. Simulation results for a cancer cell with disruption in the negative feedback from ERK to SOS,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are in minutes.
and the units on the horizontal axes are in minutes.
Figure 10. Simulation results for a cancer cell with disruption in the negative feedback from ERK to SOS,
 . Time is from
. Time is from  to
to  ; initial values are those of a normal healthy cell; the units on the vertical axes are in
; initial values are those of a normal healthy cell; the units on the vertical axes are in  and the units on the horizontal axes are scaled in
and the units on the horizontal axes are scaled in  minutes.
minutes.
It would be interesting to study the effect of a ‘background’ on miR-9 and let-7, namely, the genes with whom these miRNAs interact. Such interactions however, are not reported in the literature. We therefore model such interactions by a random input. Figure 11 shows how random perturbations of miR-9 affect MMP (EMT). Setting  and
and  as given in Figure 2, miR-9 perturbed by random Gaussian input and MMP are shown in Figure 11 A–D and E–H, respectively (we added
as given in Figure 2, miR-9 perturbed by random Gaussian input and MMP are shown in Figure 11 A–D and E–H, respectively (we added  on the right-hand side of
on the right-hand side of  where
where  is a standard Brownian motion). Panels A/B and E/F in Figure 11 correspond to the case when miR-9 is perturbed by Gaussian input with
is a standard Brownian motion). Panels A/B and E/F in Figure 11 correspond to the case when miR-9 is perturbed by Gaussian input with  and Panels C/D and G/H in Figure 11 correspond to the case when we increase
and Panels C/D and G/H in Figure 11 correspond to the case when we increase  to
to  . In Panels B/D/F/H in Figure 11, we compare MMP concentration with random perturbations (red line) and without perturbations (green dotted line). Figure 12 shows similar results in the case of let-7 with
. In Panels B/D/F/H in Figure 11, we compare MMP concentration with random perturbations (red line) and without perturbations (green dotted line). Figure 12 shows similar results in the case of let-7 with  and
and  . Panels A/B and E/F in Figure 12 correspond to the case when let-7 is perturbed by Gaussian input with
. Panels A/B and E/F in Figure 12 correspond to the case when let-7 is perturbed by Gaussian input with  and Panels C/D and G/H in Figure 12 correspond to the case when we increase
and Panels C/D and G/H in Figure 12 correspond to the case when we increase  to
to  . Figures 13 and 14 show means (blue or red line) and standard deviations (black dotted line) from the means of miR-9, let-7, and MMP concentrations obtained from
. Figures 13 and 14 show means (blue or red line) and standard deviations (black dotted line) from the means of miR-9, let-7, and MMP concentrations obtained from  realizations of simulation with the same parameters in Figures 11 and 12. Simulation results in Figures 11-14 are obtained with fixed time step,
realizations of simulation with the same parameters in Figures 11 and 12. Simulation results in Figures 11-14 are obtained with fixed time step,  .
.
Figure 11. One sample path of miR-9 and MMP concentrations in time with random input in miR-9.
For (A–D)  and for (E–H)
and for (E–H)  . For (A, B, E, F)
. For (A, B, E, F)  and for (C, D, G, H)
and for (C, D, G, H)  . The units on the horizontal axes are scaled in
. The units on the horizontal axes are scaled in  minutes.
minutes.
Figure 12. One sample path of let-7 and MMP concentrations in time with random input in let-7.
For (A–D)  and for (E–H)
and for (E–H)  . For (A, B, E, F)
. For (A, B, E, F)  and for (C, D, G, H)
and for (C, D, G, H)  . The units on the horizontal axes are scaled in
. The units on the horizontal axes are scaled in  minutes.
minutes.
Figure 13. Mean concentrations of miR-9 and MMP and standard deviations from the means in time with random input in miR-9.
For (A–D)  and for (E–H)
and for (E–H)  . For (A, B, E, F)
. For (A, B, E, F)  and for (C, D, G, H)
and for (C, D, G, H)  . The units on the horizontal axes are scaled in
. The units on the horizontal axes are scaled in  minutes. The result is taken from
minutes. The result is taken from  realizations of simulation.
realizations of simulation.
Figure 14. Mean concentrations of let-7 and MMP and standard deviations from the means in time with random input in let-7.
For (A–D) 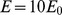 and for (E–H)
and for (E–H)  . For (A, B, E, F)
. For (A, B, E, F)  and for (C, D, G, H)
and for (C, D, G, H)  . The units on the horizontal axes are scaled in
. The units on the horizontal axes are scaled in  minutes. The result is taken from
minutes. The result is taken from  realizations of simulation.
realizations of simulation.
We conclude that mean MMP concentrations and standard deviations from the means are stable (robust) to small perturbations in miR-9, i.e. when  . However, when we increase
. However, when we increase  already to
already to  stability of standard deviations from the mean MMP concentration tends to break down as we see from Panels D/H in Figure 13; Panels D/H in Figure 11 show one sample path of unstable MMP concentration against miR-9 perturbation. On the other hand, mean MMP concentrations and standard deviations from the means are much more stable for let-7 perturbations with large
stability of standard deviations from the mean MMP concentration tends to break down as we see from Panels D/H in Figure 13; Panels D/H in Figure 11 show one sample path of unstable MMP concentration against miR-9 perturbation. On the other hand, mean MMP concentrations and standard deviations from the means are much more stable for let-7 perturbations with large  , and trajectories of means closely follow the trajectory of MMP without random input as shown in Figure 14; Figure 12 shows one sample path of MMP concentration against let-7 perturbation. Notice that we have taken
, and trajectories of means closely follow the trajectory of MMP without random input as shown in Figure 14; Figure 12 shows one sample path of MMP concentration against let-7 perturbation. Notice that we have taken  in Panels A/B/E/F and
in Panels A/B/E/F and  in Panels C/D/G/H. For let-7, if we take
in Panels C/D/G/H. For let-7, if we take  as small as
as small as  as we did in Panels C/D/G/H in Figure 11, standard deviations are very small and negligible (not shown here). The reason why MMP is more stable against random perturbations of let-7 than against miR-9 perturbations is that let-7 perturbations undergo damping by the negative feedbacks from let-7 to Ras and from ERK to SOS, as shown in Figure 1. Similar results (not shown here) hold when we vary
as we did in Panels C/D/G/H in Figure 11, standard deviations are very small and negligible (not shown here). The reason why MMP is more stable against random perturbations of let-7 than against miR-9 perturbations is that let-7 perturbations undergo damping by the negative feedbacks from let-7 to Ras and from ERK to SOS, as shown in Figure 1. Similar results (not shown here) hold when we vary  or
or  , instead of
, instead of  .
.
Sensitivity Analysis
Since we are focusing on miR-9 upregulation and let-7 downregulation as potential biomarkers for lung cancer, we wanted to determine how the quotient  of miR-9 divided by let-7 depends on the parameters of the model equations. We focused on the
of miR-9 divided by let-7 depends on the parameters of the model equations. We focused on the  parameters in Table 2 which are only estimations. We performed sensitivity analysis, employing the method of partial rank correlation coefficient (PRCC), using previously described program [38]. We let each of the
parameters in Table 2 which are only estimations. We performed sensitivity analysis, employing the method of partial rank correlation coefficient (PRCC), using previously described program [38]. We let each of the  parameters vary in the interval between
parameters vary in the interval between  of the estimated value and twice its estimated value. Using Latin Hypercube sampling method as in [38], we sampled each parameter from uniformly distributed intervals and ran
of the estimated value and twice its estimated value. Using Latin Hypercube sampling method as in [38], we sampled each parameter from uniformly distributed intervals and ran  realizations of simulation. Then, we transformed the sampled parameter values and the ratio
realizations of simulation. Then, we transformed the sampled parameter values and the ratio  between miR-9 and let-7 as computed in the simulation to rank values, and computed partial rank correlation coefficients. PRCC values of the estimated parameters and their ranges are presented in Table 3, and scatter plots of statistically significant parameters are shown in Figure 15.
between miR-9 and let-7 as computed in the simulation to rank values, and computed partial rank correlation coefficients. PRCC values of the estimated parameters and their ranges are presented in Table 3, and scatter plots of statistically significant parameters are shown in Figure 15.
Table 2. Summary of the parameter values.
| Name | Description | Value used | References |

|
concentration of EGF-EGFR complex |

|
[32] |
| (constant) | |||

|
total concentration of SOS |

|
[32] |

|
total concentration of Ras |

|
[32] |

|
total concentration of ERK |

|
[32] |

|
Steady-state concentration of active SOS |

|
estimated |

|
Steady-state concentration of active Ras |

|
estimated |

|
Steady-state concentration of active ERK |

|
estimated |

|
Steady-state concentration of MYC protein |

|
[41] |

|
Steady-state concentration of miR-9 |

|
estimated |

|
Steady-state concentration of let-7 |

|
[43] |

|
Steady-state concentration of E-Cadherin |

|
[47] |

|
Steady-state concentration of MMP mRNA |

|
[49] |

|
Saturation of inactive SOS on active SOS |

|
[32] |

|
Saturation of active SOS on inactive SOS |

|
[32] |

|
Saturation of inactive Ras on active Ras |

|
[32] |

|
Control of let-7 on Ras |

|
estimated |

|
Saturation of active Ras on inactive Ras |

|
[32] |

|
Saturation of inactive ERK on active ERK |

|
[32] |

|
Saturation of active ERK on inactive ERK |

|
[32] |
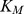
|
Saturation of MYC on miR-9 |

|
estimated |

|
Control of MYC on let-7 |

|
estimated |

|
Control of MYC on E-Cadherin |

|
estimated |

|
Control of E-Cadherin on MMP mRNA |

|
estimated |

|
Catalytic production rate of active SOS |

|
[32] |

|
Catalytic production rate of active Ras |

|
[32] |

|
Catalytic production rate of active ERK |

|
[32] |

|
Catalytic production rate of MYC |

|
estimated |

|
Catalytic production rate of miR-9 |

|
estimated |

|
Catalytic production rate of let-7 |

|
estimated |

|
Catalytic production rate of E-Cadherin |

|
estimated |

|
Catalytic production rate of MMP |

|
estimated |

|
Degradation rate of active SOS |

|
[32] |

|
Degradation rate of active Ras |

|
[32] |

|
Degradation rate of active ERK |

|
[32] |

|
Degradation rate of MYC protein |

|
[42] |

|
Degradation rate of miR-9 |

|
[45] |

|
Degradation rate of let-7 |

|
[46] |

|
Degradation rate of E-Cadherin |

|
[48] |

|
Degradation rate of MMP mRNA |

|
[51] |
The table summarizes all the parameter values of the model equations (1)–(8).
Table 3. Parameter ranges and partial rank correlation coefficient (PRCC) values.
| Parameter | Range | PRCC |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Statistically significant parameters are denoted as * (p-value ).
).
Figure 15. Scatter plots of rank transformed  with several rank transformed parameters.
with several rank transformed parameters.
Scatter plots are drawn for statistically significant parameters (p-value ); the units on the horizontal and vertical axes are scaled in
); the units on the horizontal and vertical axes are scaled in  ; time is at
; time is at  minutes and the result is taken from
minutes and the result is taken from  realizations of simulation.
realizations of simulation.
Among the  parameters,
parameters,  ,
,  ,
,  ,
,  ,
,  , and
, and  were statistically significant. The parameters
were statistically significant. The parameters  and
and  were strongly positively correlated with
were strongly positively correlated with  . This is natural; indeed
. This is natural; indeed  and
and  are production rates of MYC and miR-9. As we increase production rate of MYC, miR-9 concentration increases and let-7 concentration decreases. On the other hand,
are production rates of MYC and miR-9. As we increase production rate of MYC, miR-9 concentration increases and let-7 concentration decreases. On the other hand,  ,
,  , and
, and  were strongly negatively correlated to
were strongly negatively correlated to  . This is also to be expected. Indeed,
. This is also to be expected. Indeed,  is the production rate of let-7,
is the production rate of let-7,  is the saturation constant of MYC as source for miR-9, and
is the saturation constant of MYC as source for miR-9, and  is the control constant of MYC in the let-7 equation. Therefore, it is natural that
is the control constant of MYC in the let-7 equation. Therefore, it is natural that  would decrease as the parameters
would decrease as the parameters  ,
,  , and
, and  increase. When we ran
increase. When we ran  realizations of simulation, we obtained similar results.
realizations of simulation, we obtained similar results.
EGFR inhibition reduces both c-MYC and miR-9 in a concentration dependent manner
In an initial attempt to validate our mathematical model, we treated an EGFR mutant lung cancer cell line with several concentration of the clinically used EGFR inhibitor Gefitinib. We then assessed treated cells for miR-9, let-7a and c-MYC expression by QRT-PCR. As shown in Figure 16, we determined that while lower concentrations ( ) of Gefitinib caused a statistically significant reduction in both miR-9 and c-MYC, similar effects were not evident at higher concentrations of Gefitinib or in let-7a. These findings while they would need to be validated in other cell lines suggest the additional complexity of the effects EGFR inhibition on miRNA expression and that our mathematical model only partially predicts the biological links between EGFR, c-MYC and miRNA in lung cancer.
) of Gefitinib caused a statistically significant reduction in both miR-9 and c-MYC, similar effects were not evident at higher concentrations of Gefitinib or in let-7a. These findings while they would need to be validated in other cell lines suggest the additional complexity of the effects EGFR inhibition on miRNA expression and that our mathematical model only partially predicts the biological links between EGFR, c-MYC and miRNA in lung cancer.
Figure 16. QRT-PCR expression of miR-9, let-7a and c-MYC in HCC827 lung cancer cell lines treated with Gefitinib.

Statistical significance is defined as *p<0.05 in (A) and **p<0.01 in (C).
Discussion
Lung cancer is the leading cause of cancer-related deaths worldwide. The majority of cases are diagnosed at later stages thus limiting therapeutic options and contributing to poor outcome. As a result, investigators have sought to identify lung cancer specific biomarkers that may be utilized for early detection and to better understand the metastatic process. Such biomarkers may significantly improve prognosis and reduce mortality. In this paper, we have proposed a mathematical model that integrates the miRNAs let-7 and miR-9 into the process of EMT. miR-9 has been shown to be significantly upregulated and let-7 downregulated in NSCLC.
Based on the experimental literature, we introduced a signaling pathway from the EGF-EGFR complex to MMP expression which involves SOS, Ras, ERK, MYC, the miRNAs miR-9 and let-7, E-Cadherin, and MMP. Recent studies have demonstrated elevated MMP-9 in NSCLC [25], but for modeling purposes we have referred to MMP in a generic manner. Using an EGFR mutant lung cancer cell line, we showed that inhibition of EGFR leads to a reduction in miR-9 as well as c-MYC expression. However, the relationships between miR-9 and c-MYC were not consistent at higher concentrations of drug treatment. These findings support the complexity of the kinetics of miRNA and target gene relationships and highlight the inherent difficulties with modeling miRNA biology. Our findings suggest that higher concentrations of EGFR are likely to engage other regulators of miR-9 and/or c-MYC and that miR-9 may be under the regulatory control of additional genes beyond c-MYC.
We correspondingly developed a mathematical model including a system of differential equations and used the model to compute the level of miR-9 overexpression and let-7 downexpression in the setting of EGFR mutations and Ras mutations. We showed that such mutations upregulate the level of miR-9 and downregulate the level of let-7. The  -fold increase in miR-9 levels obtained in the simulations was consistent quantitatively with clinical data reported in human lung tumors (Supplementary Material S1). Our experiments with EGFR mutant lung cancer cells did not show any significant changes in let-7 suggesting that let-7 may also be regulated by other signaling networks. We investigated how random perturbations of let-7 and miR-9 affect MMP and concluded that MMP is more robust against let-7 perturbations than against miR-9 perturbations; this can be explained by the fact that let-7 perturbations undergo damping by the negative feedbacks from let-7 to Ras and from ERK to SOS.
-fold increase in miR-9 levels obtained in the simulations was consistent quantitatively with clinical data reported in human lung tumors (Supplementary Material S1). Our experiments with EGFR mutant lung cancer cells did not show any significant changes in let-7 suggesting that let-7 may also be regulated by other signaling networks. We investigated how random perturbations of let-7 and miR-9 affect MMP and concluded that MMP is more robust against let-7 perturbations than against miR-9 perturbations; this can be explained by the fact that let-7 perturbations undergo damping by the negative feedbacks from let-7 to Ras and from ERK to SOS.
To the best of our knowledge, the present paper is the first one that develops a model for lung cancer and miRNA in terms of differential equations. The model is based on a signaling pathway that includes miR-9 and let-7. Simulations of the model demonstrate how mutations that are detected in NSCLC include upregulation of miR-9 and downregulation of let-7. The mathematical model could be further extended by including additional signaling pathways, specifically involving let-7, that are associated with lung cancer. However, an important next step in this line of investigation is to determine how deregulation of miR-9 and let-7 may jointly contribute to lung cancer progression and may be used as reliable biomarkers. In order to address this challenge mathematically, additional clinical investigation will be required.
Methods
In this model, we assume that the EGF-EGFR complex is at steady state and set it as a constant. Brown et al. (2004) modeled EGFR signaling with negative feedback of ERK to SOS [32]. We simplified some parts of their model to obtain the equations for SOS, Ras, and ERK. We denote by  ,
,  , and
, and  the concentrations of active SOS, inactive SOS, and total SOS, respectively. Assuming that the total number of SOS is conserved, we have
the concentrations of active SOS, inactive SOS, and total SOS, respectively. Assuming that the total number of SOS is conserved, we have
| (9) |
We denote by  the activation rate of the inactive SOS and by
the activation rate of the inactive SOS and by  as the deactivation rate of the active SOS. Describing these conversions by the Michaelis-Menten kinetics, the governing equation for the concentration of the active SOS is given by
as the deactivation rate of the active SOS. Describing these conversions by the Michaelis-Menten kinetics, the governing equation for the concentration of the active SOS is given by
Using the fact that the EGF-EGFR complex activates SOS and that ERK represses active SOS, we replace  by
by  and
and  by
by  , and we get Eq. (1). Similarly, we describe conversions between active and inactive Ras and between active and inactive ERK using Michaelis-Menten kinetics, and derive Eqs. (2) and (3). Here, catalytic activation rates of Ras and ERK are proportional to active SOS and active Ras concentrations, respectively. In Eq. (2), repression by let-7 of the activation of Ras is described by an inhibition factor,
, and we get Eq. (1). Similarly, we describe conversions between active and inactive Ras and between active and inactive ERK using Michaelis-Menten kinetics, and derive Eqs. (2) and (3). Here, catalytic activation rates of Ras and ERK are proportional to active SOS and active Ras concentrations, respectively. In Eq. (2), repression by let-7 of the activation of Ras is described by an inhibition factor,  . In Eq. (4), production of MYC is proportional to active ERK concentration. In Eq. (5), activation of miR-9 by MYC is described by the fourth-order Hill function, since MYC is a transcription factor and miR-9 activation may involve several enzymatic steps. In Eq. (6), let-7 production is inhibited by MYC. In Eq. (7), E-Cadherin production is proportional to let-7 concentration and is inhibited by miR-9. Throughout Eqs. (4)–(7), degradation of species is described by linear mass action kinetics. Finally, in Eq. (8) MMP is produced at constant rate and is degraded by E-Cadherin.
. In Eq. (4), production of MYC is proportional to active ERK concentration. In Eq. (5), activation of miR-9 by MYC is described by the fourth-order Hill function, since MYC is a transcription factor and miR-9 activation may involve several enzymatic steps. In Eq. (6), let-7 production is inhibited by MYC. In Eq. (7), E-Cadherin production is proportional to let-7 concentration and is inhibited by miR-9. Throughout Eqs. (4)–(7), degradation of species is described by linear mass action kinetics. Finally, in Eq. (8) MMP is produced at constant rate and is degraded by E-Cadherin.
The parameters of Eqs. (1)–(8) are derived in the following subsections. Most of the parameters are taken from Brown et al. (2004) [32]. In their model, they have taken the initial concentrations of all active signaling species to be zero, and the initial concentrations of all inactive signaling species to be  except for MEK and ERK, whose concentrations were taken to be
except for MEK and ERK, whose concentrations were taken to be  . As for the EGF-EGFR complex concentration, Brown et al (2004) [32] assume it to be a variable but in our model, it is constant. This constant is chosen as the steady state concentration of the EGF-EGFR complex computed using their parameters.
. As for the EGF-EGFR complex concentration, Brown et al (2004) [32] assume it to be a variable but in our model, it is constant. This constant is chosen as the steady state concentration of the EGF-EGFR complex computed using their parameters.
Computation of 
We denote by  ,
,  , and
, and  the numbers of molecules of EGF, free EGFR, and EGF-EGFR complex, and by
the numbers of molecules of EGF, free EGFR, and EGF-EGFR complex, and by  and
and  the binding and unbinding rates for the EGF-EGFR complex. If
the binding and unbinding rates for the EGF-EGFR complex. If  is the total number of the EGFR molecules, then
is the total number of the EGFR molecules, then  . Assuming that binding and unbinding of EGF and EGFR are balanced at steady state, we have
. Assuming that binding and unbinding of EGF and EGFR are balanced at steady state, we have
which gives
| (10) |
According to Brown et al. (2004) [32],
and hence  . We shall determine
. We shall determine  by converting
by converting  into a unit of concentration. Lung cells size, however, vary up to
into a unit of concentration. Lung cells size, however, vary up to  -fold differences [39]. We therefore use an “average” cell size by taking it to be the HeLa cell.
-fold differences [39]. We therefore use an “average” cell size by taking it to be the HeLa cell.
Since EGF and EGFR are located on the cell surface, we need to compute the cell surface area; we assume that the cells have spherical shape with radius  . For HeLa cell, the total volume is
. For HeLa cell, the total volume is
 |
according to Fujioka et al. (2006) [40]. Hence  and its surface area is
and its surface area is
Converting the number of molecules of  into concentration on the cell surface, we compute steady-state concentration of EGF-EGFR complex as
into concentration on the cell surface, we compute steady-state concentration of EGF-EGFR complex as
 |
where  is the Avogadro's number,
is the Avogadro's number,  ;
;  is the amount of a substance that contains as many entities as there are atoms in
is the amount of a substance that contains as many entities as there are atoms in  of
of  , and
, and  is
is  molar concentration (per liter),
molar concentration (per liter),
Other parameters in the SOS equation
Let  and
and 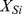 denote the numbers of active and inactive SOS molecules. According to Brown et al. (2004),
denote the numbers of active and inactive SOS molecules. According to Brown et al. (2004),
| (11) |
where P90Rsk is a p90 ribosomal s6 kinase that inactivates SOS, and  is the number of active P90Rsk molecules [32]. In that paper, parameters are given as
is the number of active P90Rsk molecules [32]. In that paper, parameters are given as  ,
,  ,
,  , and
, and  . Using these numbers, we determine our parameters by
. Using these numbers, we determine our parameters by
where  is the volume of the cytoplasm in a HeLa cell. The total number of molecules of active P90Rsk was taken to be
is the volume of the cytoplasm in a HeLa cell. The total number of molecules of active P90Rsk was taken to be  [32]. Since the initial concentration of ERK,
[32]. Since the initial concentration of ERK,  , corresponds to
, corresponds to  molecules, we get
molecules, we get
The initial concentration of SOS (all inactive) was  , which corresponds to
, which corresponds to  molecules. We convert this number to concentration using the volume of the cytoplasm in a HeLa cell,
molecules. We convert this number to concentration using the volume of the cytoplasm in a HeLa cell,
Parameters in the Ras equation
Let  and
and  denote the numbers of molecules of active and inactive Ras. From Brown et al. (2004),
denote the numbers of molecules of active and inactive Ras. From Brown et al. (2004),
| (12) |
where  and
and  denote the numbers of molecules of active SOS and active Ras-Gap [32]. In [32], parameters are given as
denote the numbers of molecules of active SOS and active Ras-Gap [32]. In [32], parameters are given as  ,
,  ,
,  , and
, and  . Also, the number of molecules of active Ras-Gap is treated as a constant equal to
. Also, the number of molecules of active Ras-Gap is treated as a constant equal to  . Accordingly, we determine our parameters by
. Accordingly, we determine our parameters by
For total Ras concentration, we convert the total number of Ras molecules in a cell obtained from [32] to concentration using the volume of the cytoplasm in a HeLa cell,
Parameters in the ERK equation
Let  and
and  denote the numbers of molecules of active and inactive ERK. Following Brown et al. (2004),
denote the numbers of molecules of active and inactive ERK. Following Brown et al. (2004),
| (13) |
where  and
and  denote the numbers of molecules of active MEK and active PP2A [32]. PP2A is protein phosphatase 2 which is an enzyme targeting proteins in oncogenic signaling pathways. In that paper, parameters are given as
denote the numbers of molecules of active MEK and active PP2A [32]. PP2A is protein phosphatase 2 which is an enzyme targeting proteins in oncogenic signaling pathways. In that paper, parameters are given as  ,
,  ,
,  , and
, and  ; the initial total numbers of molecules of MEK and Ras are given as
; the initial total numbers of molecules of MEK and Ras are given as  and
and  , and the number of molecules of active PP2A is treated as a constant equal to
, and the number of molecules of active PP2A is treated as a constant equal to  . Therefore, we determine our parameters by
. Therefore, we determine our parameters by
We convert the total number of ERK molecules, consisting of active and inactive ERK in a cell to concentration, using the volume of the cytoplasm in a HeLa cell, and set
Parameters in the MYC equation
Following Rudolph et al. (1999), there are  c-MYC proteins in the nucleus [41]. We convert this to concentration using the volume of the nucleus in a HeLa cell,
c-MYC proteins in the nucleus [41]. We convert this to concentration using the volume of the nucleus in a HeLa cell,  . Treating this concentration as the steady-state concentration of MYC, we get
. Treating this concentration as the steady-state concentration of MYC, we get
Half-life of c-MYC protein is 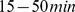 [42]. We take the half-life of c-MYC as
[42]. We take the half-life of c-MYC as  , and compute a degradation rate as
, and compute a degradation rate as
In steady state in Eq. (4),
| (14) |
where  is the steady-state concentration of ERK. To determine
is the steady-state concentration of ERK. To determine  , we first compute steady-state concentration of let-7. Following Lim et al. (2003), there are
, we first compute steady-state concentration of let-7. Following Lim et al. (2003), there are  let-7 molecules in a human HeLa cell [43], and we assume that this number is at steady state. We convert it to concentration by
let-7 molecules in a human HeLa cell [43], and we assume that this number is at steady state. We convert it to concentration by
We compute a solution of Eq. (1)–(3) for  ,
,  , and
, and  with
with  replaced by
replaced by  using Matlab, and obtain the steady-state concentration of ERK as
using Matlab, and obtain the steady-state concentration of ERK as  . From Eq. (14), we then get
. From Eq. (14), we then get
Parameters in the miR-9 equation
Since the miR-9 copy number in the normal lung cell is very small [44], we take the steady-state concentration of miR-9 to be  . Half-life of miR-9 in human brain tissue is
. Half-life of miR-9 in human brain tissue is  [45], which gives the degradation rate
[45], which gives the degradation rate  . In steady state in Eq. (5),
. In steady state in Eq. (5),
Based on the fact that miR-9 expression in the NSCLC tissues is about  times that of normal tissues (see Supplementary Material S1), we take
times that of normal tissues (see Supplementary Material S1), we take  to be very large, namely,
to be very large, namely,  . Then
. Then
Parameters in the let-7 equation
Half-life of let-7 after TAM treatment is  [46]. Accordingly, we take the degradation rate of
[46]. Accordingly, we take the degradation rate of  . Then, in steady state in Eq. (6),
. Then, in steady state in Eq. (6),
Taking  gives
gives
Parameters in the E-Cadherin equation
Using the total E-Cadherin concentration in Chaplain (2011) [47], we set steady-state concentration,  . Half-life of E-Cadherin is
. Half-life of E-Cadherin is  [48], so the degradation rate is
[48], so the degradation rate is  . In steady state in Eq. (7),
. In steady state in Eq. (7),
Taking 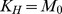 gives
gives
Parameters in the MMP mRNA equation
According to Safranek et al. (2009), the number of MMP-9 mRNA in human lung tissue is  [49]. Using the human lung tissue density of
[49]. Using the human lung tissue density of  [50], we compute the MMP mRNA concentration in steady state,
[50], we compute the MMP mRNA concentration in steady state,
 |
Half-life of MMP-9 mRNA is  [51], so the degradation rate is
[51], so the degradation rate is  . Using the steady state equation for MMP concentration,
. Using the steady state equation for MMP concentration,
and taking  , we get
, we get
Cell culture and drug treatment
For our experiments shown in Figure 16, we obtained the EGFR mutant lung cancer cell line (HCC827) (E746-A750 deletion) as a generous gift from our collaborator (Michela Garofalo, OSU). Cells were maintained in appropriate media. HCC827 cell lines were subsequently treated with Gefitinib (generous gift from Michela Garofalo, OSU) at concentrations of  ,
,  , and
, and  . Following
. Following  hours of exposure, cells were harvested for RNA and assessed for miR-9 (Assay ID# Hs000583), let-7a (Assay ID# Hs00377), c-MYC (Assay ID# Hs00153408_m1) (Applied Biosystems) by QRT-PCR. For miRNA assessment RNU48 was used as the endogenous control and for c-MYC GAPDH was used. Data is presented as fold difference based on
hours of exposure, cells were harvested for RNA and assessed for miR-9 (Assay ID# Hs000583), let-7a (Assay ID# Hs00377), c-MYC (Assay ID# Hs00153408_m1) (Applied Biosystems) by QRT-PCR. For miRNA assessment RNU48 was used as the endogenous control and for c-MYC GAPDH was used. Data is presented as fold difference based on  . Statistical analyses were performed using ANOVA with Tukey Post Hoc analysis.
. Statistical analyses were performed using ANOVA with Tukey Post Hoc analysis.
Supporting Information
Experimental results of miR-9 in lung tumor tissues. Experimental results using quantitative reverse transcription polymerase chain reaction and in situ hybridization for miR-9 are provided.
(PDF)
Funding Statement
This research has been supported in part by the Mathematical Biosciences Institute and the National Science Foundation under grant DMS 0931642 and by the National Cancer Institute under grant CA 150297. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Siegel R, Naishadham D, Jemal A (2012) Cancer statistics, 2012. CA: A Cancer Journal for Clinicians. [DOI] [PubMed]
- 2. Takamizawa J, Konishi H, Yanagisawa K, Tomida S, Osada H, et al. (2004) Reduced expression of the let-7 microRNAs in human lung cancers in association with shortened postoperative survival. Cancer Research 64: 3753. [DOI] [PubMed] [Google Scholar]
- 3. Nicoloso M, Spizzo R, Shimizu M, Rossi S, Calin G (2009) MicroRNAs-the micro steering wheel of tumour metastases. Nature Reviews Cancer 9: 293–302. [DOI] [PubMed] [Google Scholar]
- 4. Trang P, Medina P, Wiggins J, Ruffino L, Kelnar K, et al. (2009) Regression of murine lung tumors by the let-7 microRNA. Oncogene 29: 1580–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Trang P, Wiggins J, Daige C, Cho C, Omotola M, et al. (2011) Systemic delivery of tumor suppressor microrna mimics using a neutral lipid emulsion inhibits lung tumors in mice. Molecular Therapy 19: 1116–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Yanaihara N, Caplen N, Bowman E, Seike M, Kumamoto K, et al. (2006) Unique microRNA molecular profiles in lung cancer diagnosis and prognosis. Cancer Cell 9: 189–198. [DOI] [PubMed] [Google Scholar]
- 7. Volinia S, Calin G, Liu C, Ambs S, Cimmino A, et al. (2006) A microRNA expression signature of human solid tumors defines cancer gene targets. Proceedings of the National Academy of Sciences of the United States of America 103: 2257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Crawford M, Batte K, Yu L, Wu X, Nuovo G, et al. (2009) MicroRNA 133B targets pro-survival molecules MCL-1 and BCL2L2 in lung cancer. Biochemical and Biophysical Research Communications 388: 483–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Võsa U, Vooder T, Kolde R, Fischer K, Välk K, et al. (2011) Identification of miR-374a as a prognostic marker for survival in patients with early-stage nonsmall cell lung cancer. Genes, Chromosomes and Cancer [DOI] [PubMed] [Google Scholar]
- 10. Ma L, Young J, Prabhala H, Pan E, Mestdagh P, et al. (2010) miR-9, a MYC/MYCN-activated microRNA, regulates E-cadherin and cancer metastasis. Nature Cell Biology 12: 247–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mascaux C, Laes J, Anthoine G, Haller A, Ninane V, et al. (2009) Evolution of microRNA expression during human bronchial squamous carcinogenesis. European Respiratory Journal 33: 352. [DOI] [PubMed] [Google Scholar]
- 12. Frenzel A, Lovén J, Henriksson M (2010) Targeting MYC-regulated miRNAs to combat cancer. Genes & Cancer 1: 660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Aguda B, Kim Y, Piper-Hunter M, Friedman A, Marsh C (2008) MicroRNA regulation of a cancer network: consequences of the feedback loops involving miR-17-92, E2F, and Myc. Proceedings of the National Academy of Sciences of the United States of America 105: 19678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Yokota J, Wada M, Yoshida T, Noguchi M, Terasaki T, et al. (1988) Heterogeneity of lung cancer cells with respect to the amplification and rearrangement of myc family oncogenes. Oncogene 2: 607. [PubMed] [Google Scholar]
- 15. Broers J, Viallet J, Jensen S, Pass H, Travis W, et al. (1993) Expression of c-myc in progenitor cells of the bronchopulmonary epithelium and in a large number of non-small cell lung cancers. American Journal of Respiratory Cell and Molecular Biology 9: 33. [DOI] [PubMed] [Google Scholar]
- 16. Rapp U, Korn C, Ceteci F, Karreman C, Luetkenhaus K, et al. (2009) MYC is a metastasis gene for non-small-cell lung cancer. PLoS One 4: e6029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Rinaldi A, Poretti G, Kwee I, Zucca E, Catapano C, et al. (2007) Concomitant MYC and microRNA cluster miR-17-92 (C13orf25) amplification in human mantle cell lymphoma. Leukemia & Lymphoma 48: 410. [DOI] [PubMed] [Google Scholar]
- 18. Wolfer A, Ramaswamy S (2011) MYC and metastasis. Cancer Research 71: 2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Inamura K, Togashi Y, Nomura K, Ninomiya H, Hiramatsu M, et al. (2007) let-7 microRNA expression is reduced in bronchioloalveolar carcinoma, a non-invasive carcinoma, and is not correlated with prognosis. Lung Cancer 58: 392–396. [DOI] [PubMed] [Google Scholar]
- 20. Wang Z, Lin S, Li J, Xu Z, Yao H, et al. (2011) MYC protein inhibits transcription of the microRNA cluster MC-let-7a-1 – let-7d via noncanonical e-box. Journal of Biological Chemistry 286: 39703–39714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Johnson S, Grosshans H, Shingara J, Byrom M, Jarvis R, et al. (2005) RAS is regulated by the let-7 microRNA family. Cell 120: 635–647. [DOI] [PubMed] [Google Scholar]
- 22. Lee Y, Dutta A (2007) The tumor suppressor microRNA let-7 represses the HMGA2 oncogene. Genes & Development 21: 1025–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Thuault S, Tan E, Peinado H, Cano A, Heldin C, et al. (2008) HMGA2 and Smads co-regulate SNAIL1 expression during induction of epithelial-to-mesenchymal transition. Journal of Biological Chemistry 283: 33437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Nawrocki-Raby B, Gilles C, Polette M, Bruyneel E, Laronze J, et al. (2003) Upregulation of MMPs by soluble E-cadherin in human lung tumor cells. International Journal of Cancer 105: 790–795. [DOI] [PubMed] [Google Scholar]
- 25. Zheng S, Chang Y, Hodges K, Sun Y, Ma X, et al. (2010) Expression of KISS1 and MMP-9 in non-small cell lung cancer and their relations to metastasis and survival. Anticancer Research 30: 713–718. [PubMed] [Google Scholar]
- 26. Rao J, Gondi C, Chetty C, Chittivelu S, Joseph P, et al. (2005) Inhibition of invasion, angiogenesis, tumor growth, and metastasis by adenovirus-mediated transfer of antisense uPAR and MMP-9 in non–small cell lung cancer cells. Molecular Cancer Therapeutics 4: 1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Sulzer M, Leers M, van NOORD J, Bollen E, Theunissen P (1998) Reduced Ecadherin expression is associated with increased lymph node metastasis and unfa29 vorable prognosis in non-small cell lung cancer. American Journal of Respiratory and Critical Care Medicine 157: 1319–1323. [DOI] [PubMed] [Google Scholar]
- 28. Mitselou A, Batistatou A, Nakanishi Y, Hirohashi S, Vougiouklakis T, et al. (2010) Comparison of the dysadherin and E-cadherin expression in primary lung cancer and metastatic sites. Histology and Histopathology 25: 1257–1267. [DOI] [PubMed] [Google Scholar]
- 29. Saad A, Yeap B, Thunnissen F, Pinkus G, Pinkus J, et al. (2008) Immunohistochemical markers associated with brain metastases in patients with nonsmall cell lung carcinoma. Cancer 113: 2129–2138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Roberts P, Der C (2007) Targeting the Raf-MEK-ERK mitogen-activated protein kinase cascade for the treatment of cancer. Oncogene 26: 3291–3310. [DOI] [PubMed] [Google Scholar]
- 31. Zhao C, Du G, Skowronek K, Frohman M, Bar-Sagi D (2007) Phospholipase D2-generated phosphatidic acid couples EGFR stimulation to Ras activation by Sos. Nature Cell Biology 9: 707–712. [DOI] [PubMed] [Google Scholar]
- 32. Brown K, Hill C, Calero G, Myers C, Lee K, et al. (2004) The statistical mechanics of complex signaling networks: nerve growth factor signaling. Physical Biology 1: 184. [DOI] [PubMed] [Google Scholar]
- 33. Orton R, Adriaens M, Gormand A, Sturm O, Kolch W, et al. (2009) Computational modelling of cancerous mutations in the EGFR/ERK signalling pathway. BMC Systems Biology 3: 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Huang S, Ren X, Wang L, Zhang L, Wu X (2011) Lung-cancer chemoprevention by induction of synthetic lethality in mutant KRAS premalignant cells in vitro and in vivo. Cancer Prevention Research 4: 666. [DOI] [PubMed] [Google Scholar]
- 35. Zhang Z, Stiegler A, Boggon T, Kobayashi S, Halmos B (2010) EGFR-mutated lung cancer: a paradigm of molecular oncology. Oncotarget 1: 497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. da Cunha Santos G, Shepherd F, Tsao M (2011) EGFR mutations and lung cancer. Annual Review of Pathology: Mechanisms of Disease 6: 49–69. [DOI] [PubMed] [Google Scholar]
- 37. Adjei A (2001) Blocking oncogenic Ras signaling for cancer therapy. Journal of the National Cancer Institute 93: 1062–1074. [DOI] [PubMed] [Google Scholar]
- 38. Marino S, Hogue I, Ray C, Kirschner D (2008) A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of Theoretical Biology 254: 178–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Stone K, Mercer R, Gehr P, Stockstill B, Crapo J, et al. (1992) Allometric relationships of cell numbers and size in the mammalian lung. American Journal of Respiratory Cell and Molecular Biology 6: 235. [DOI] [PubMed] [Google Scholar]
- 40. Fujioka A, Terai K, Itoh R, Aoki K, Nakamura T, et al. (2006) Dynamics of the Ras/ERK MAPK cascade as monitored by fluorescent probes. Journal of Biological Chemistry 281: 8917–8926. [DOI] [PubMed] [Google Scholar]
- 41. Rudolph C, Adam G, Simm A (1999) Determination of copy number of c-Myc protein per cell by quantitative western blotting. Analytical Biochemistry 269: 66–71. [DOI] [PubMed] [Google Scholar]
- 42. Luscher B, Eisenman R (1988) c-myc and c-myb protein degradation: effect of metabolic inhibitors and heat shock. Molecular and Cellular Biology 8: 2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Lim L, Lau N, Weinstein E, Abdelhakim A, Yekta S, et al. (2003) The microRNAs of Caenorhabditis elegans. Genes & Development 17: 991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Liang Y, Ridzon D, Wong L, Chen C (2007) Characterization of microRNA expression profiles in normal human tissues. BMC Genomics 8: 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Sethi P, Lukiw W (2009) Micro-RNA abundance and stability in human brain: specific alterations in Alzheimer's disease temporal lobe neocortex. Neuroscience Letters 459: 100–104. [DOI] [PubMed] [Google Scholar]
- 46. Iliopoulos D, Hirsch H, Struhl K (2009) An epigenetic switch involving NF-κ B, Lin28, let-7 microRNA, and IL6 links inflammation to cell transformation. Cell 139: 693–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Chaplain M (2011) Multiscale mathematical modelling in biology and medicine. IMA Journal of Applied Mathematics 76: 371. [Google Scholar]
- 48. Fujita Y, Krause G, Scheffner M, Zechner D, Leddy H, et al. (2002) Hakai, a c-Cbl-like protein, ubiquitinates and induces endocytosis of the E-cadherin complex. Nature Cell Biology 4: 222–231. [DOI] [PubMed] [Google Scholar]
- 49. Safranek J, Pesta M, Holubec L, Kulda V, Dreslerova J, et al. (2009) Expression of MMP-7, MMP-9, TIMP-1 and TIMP-2 mRNA in lung tissue of patients with non-small cell lung cancer (NSCLC) and benign pulmonary disease. Anticancer Research 29: 2513. [PubMed] [Google Scholar]
- 50. Hopkins S, Henderson A, Levin D, Yamada K, Arai T, et al. (2007) Vertical gradients in regional lung density and perfusion in the supine human lung: the Slinky effect. Journal of Applied Physiology 103: 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Akool E, Kleinert H, Hamada F, Abdelwahab M, Forstermann U, et al. (2003) Nitric oxide increases the decay of matrix metalloproteinase 9 mRNA by inhibiting the expression of mRNA-stabilizing factor HuR. Molecular and Cellular Biology 23: 4901. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Experimental results of miR-9 in lung tumor tissues. Experimental results using quantitative reverse transcription polymerase chain reaction and in situ hybridization for miR-9 are provided.
(PDF)














