Fast and robust extraction of hippocampus from MR images for diagnostics of Alzheimer's disease

Abstract

Assessment of temporal lobe atrophy from magnetic resonance images is a part of clinical guidelines for the diagnosis of prodromal Alzheimer's disease. As hippocampus is known to be among the first areas affected by the disease, fast and robust definition of hippocampus volume would be of great importance in the clinical decision making. We propose a method for computing automatically the volume of hippocampus using a modified multi-atlas segmentation framework, including an improved initialization of the framework and the correction of partial volume effect. The method produced a high similarity index, 0.87, and correlation coefficient, 0.94, with semi-automatically generated segmentations. When comparing hippocampus volumes extracted from 1.5 T and 3 T images, the absolute value of the difference was low: 3.2% of the volume. The correct classification rate for Alzheimer's disease and cognitively normal cases was about 80% while the accuracy 65% was obtained for classifying stable and progressive mild cognitive impairment cases. The method was evaluated in three cohorts consisting altogether about 1000 cases, the main emphasis being in the analysis of the ADNI cohort. The computation time of the method is about 2 minutes on a standard laptop computer. The results show a clear potential for applying the method in clinical practice.

Introduction

In current guidelines (Dubois et al., 2007), the diagnostic criteria for probable Alzheimer's disease (AD) require a presence of both impairment in episodic memory and one supportive feature, either medial temporal lobe atrophy, abnormal cerebrospinal fluid (CSF) biomarker, specific pattern in PET or proven AD autosomal dominant mutation. In addition, the guidelines specify a list of exclusion criteria. Similar components can be found also from the recent EFNS guideline (Waldemar et al., 2007). The revision of criteria for AD, mild cognitive impairment (MCI) and preclinical AD is also ongoing and will include further emphasis on biomarkers and imaging.

In medial temporal lobe (MTL), the volume loss of hippocampi, entorhinal cortex and amygdala is a hallmark indicating AD. The guidelines (Dubois et al., 2007) suggest that the volume loss is “evidenced on MRI with qualitative ratings using visual scoring”. Qualitative and subjective ratings may, however, lead to different results between interpreters and the diagnosis made by even a single interpreter may vary when re-examining images. Therefore, there is a clear need for objective methods for the assessment of hippocampal volume. Although automated tools are developed actively in many research groups, the development of robust, accurate and fast automatic methods is a highly challenging problem and automatic methods are still very much lacking in clinical practice.

Several methods have been published for segmenting hippocampus (Chupin et al., 2009a,b; Fischl et al., 2002; Lötjönen et al., 2010; Morra et al., 2008; van der Lijn et al., 2008; Wolz et al., 2010a). All these methods segment the hippocampus as a whole although in reality it contains sub-structures. However, the accurate segmentation of these structures is difficult from most images currently available in clinical practice. We therefore concentrate in this work on the segmentation of the hippocampus as a single structure. One of the main objectives of this work is to develop tools for clinical decision making.

Although many published methods are promising, some space remains for interpretations, either in accuracy, robustness or computational speed. First, there is no real gold-standard for defining the accuracy of segmentation. Currently manual segmentations by clinical experts represent the clinical gold-standard for hippocampal segmentation. Therefore, if the difference between automatically and manually generated segmentations is equal to the difference between two manual segmentations, automatic segmentation is typically considered to have corresponding accuracy to the manual segmentation. There are numerous methods characterizing the accuracy of segmentations: differences in various overlap measures between manually and automatically generated segmentations, such as the Dice similarity index, recall and precision values, or distances between the surfaces of objects, or differences in the volumes of objects, or differences in the ability to classify a subject to a correct class or group. Classification accuracy is an important measure if the ultimate goal is to use a certain biomarker in diagnostics. Classification accuracy reflects the robustness of segmentation not segmentation accuracy as such. For example, if an automatic method is consistent but systematically overestimates the volume, i.e., the measure is biased, the accuracy of the segmentation is obviously decreased. This systematic and consistent error does not, however, affect classification accuracy or ability to detect statistical difference between two populations. A less robust or consistent algorithm introduces noise into measurements and thus makes the classification less accurate. In diagnostics, the consistency of segmentation is even more important than ensuring that segmentation is not biased. As there are different guidelines for manual segmentation of the hippocampus, even the clinical gold-standards are biased relative to each other; efforts for harmonizing these guidelines are ongoing (Boccardi et al., 2010). All these indicators may lead to conflicting interpretations making the evaluation of results sometimes cumbersome. Second, methods are often validated using a relatively small database or somehow constrained data, e.g., from a single site or using only a device from one manufacturer. A clear problem in the evaluation of the accuracy is a limited number of manually segmented cases available because producing a representative set of manual segmentations is a highly laborious task. These issues make the extensive evaluation of the robustness in real clinical conditions difficult. Third, the computation time of a segmentation method is not considered in many scientific publications although it is a relevant issue in clinical practice. Computation times of hours or the requirement of special computer facilities or a need for careful and laborious tuning of the parameters of the method decrease the feasibility of a method in the clinical setting. In summary, demonstrating the usefulness of a method for clinical practice is a laborious task and still often leaves some space for interpretations.

Atlas-based segmentation is a commonly used technique to segment image data. In atlas-based segmentation, an intensity template is registered non-rigidly to an unseen image and the resulting transformation is used to propagate tissue class or anatomical structure labels of the template into the space of the unseen image. The segmentation accuracy can be improved considerably by combining basic atlas-based segmentation with techniques from machine learning, e.g. classifier fusion (Heckemann et al., 2006; Klein et al., 2005; Rohlfing et al., 2004; Warfield et al., 2004). In this approach, several atlases from different subjects are registered to unseen data. The label that the majority of all warped labels predict for each voxel is used for the final segmentation of the unseen image. This multi-atlas segmentation was shown to produce the best segmentation accuracy for subcortical structures in a comparison study (Babalola et al., 2008). However, the major drawback of the multi-atlas segmentation is that it is computationally expensive. For example, van der Lijn et al. (2008) reported computation times of several hours for multi-atlas segmentation.

In (Lötjönen et al., 2010), we recently presented a method for fast and robust multi-atlas segmentation of volumetric image data. The tool was based on a fast non-rigid registration algorithm, use of atlas-selection and use of intensity information via graph-cut or expectation maximisation (EM) algorithms. The use of atlas selection and the use of intensity modeling improved significantly the segmentation accuracy. The computation time for segmenting the hippocampus was 3–4 minutes using an 8-core workstation. The computation time was clearly shorter than in many published methods and it is not a limiting factor in many applications anymore. However, even shorter computation time would make online segmentation more attractive in clinical practice and allow more freedom in planning clinical work-flows. Other requirements for clinical use include that no manual tuning of segmentation parameters should be needed, and complex and expensive computer facilities and maintenance should not be required. In this work, we propose two major methodological contributions to our previously published method: 1) use of an inter-mediate template space between unseen data and atlas spaces for speeding up the computation time, and 2) use of partial volume modeling in segmenting hippocampus for improving the classification accuracy.

In (Lötjönen et al., 2010), atlas selection was performed first: the unseen data and all atlases were registered non-rigidly to a template, and atlases being most similar to the unseen data were selected. Then, multi-atlas segmentation was applied: each of the selected atlases was registered separately non-rigidly to the unseen data and classifier fusion was performed. The innovation of our current work is that transformations computed in the atlas selection step are used to initialize the multiple transformations when registering atlases to unseen data. The process becomes much faster as only small tuning of the transformations from atlases to unseen data is needed. The intermediate template space, used in our atlas-selection step, has been previously utilized to speed-up and to improve the accuracy of non-rigid registration by Tang et al. (2010) using initialization based on principal component analysis and by Rohlfing et al. (2009) using subject-specific templates generated by a regression model.

The volume of the hippocampus is typically 1–3 ml in elderly subjects, including Alzheimer's disease cases. In a typical clinical setting, the voxel size of MR images is around 1×1×1 mm³ which means that hippocampus is presented only by 1000–3000 voxels. Up to 80–90% of these voxels are on the surface of the object which means that partial volume effect may affect dramatically the estimate of the volume. There are multiple approaches published for estimating the partial volume effects in the EM framework (Acosta et al., 2009; Shattuck et al., 2001; Tohka et al., 2004). In this work, we used the method proposed by Tohka et al. (2004).

In addition to the methodological contributions, we demonstrate using large data cohorts the performance of automatically computed hippocampus volumes 1) in diagnostics of Alzheimer's disease and 2) compared with semi-automatically generated volumes. Data from almost 1000 cases originating from three different patient cohorts are used. For comparison, only 60 cases were used in our previous paper (Lötjönen et al., 2010).

In this article, we first introduce a method utilizing the template space to speed up the computation and an approach for modeling the partial volume effect. Thereafter, the data used and experiments performed are described. Finally results are shown and discussed.

Materials and methods

Classification based on multi-atlas segmentation

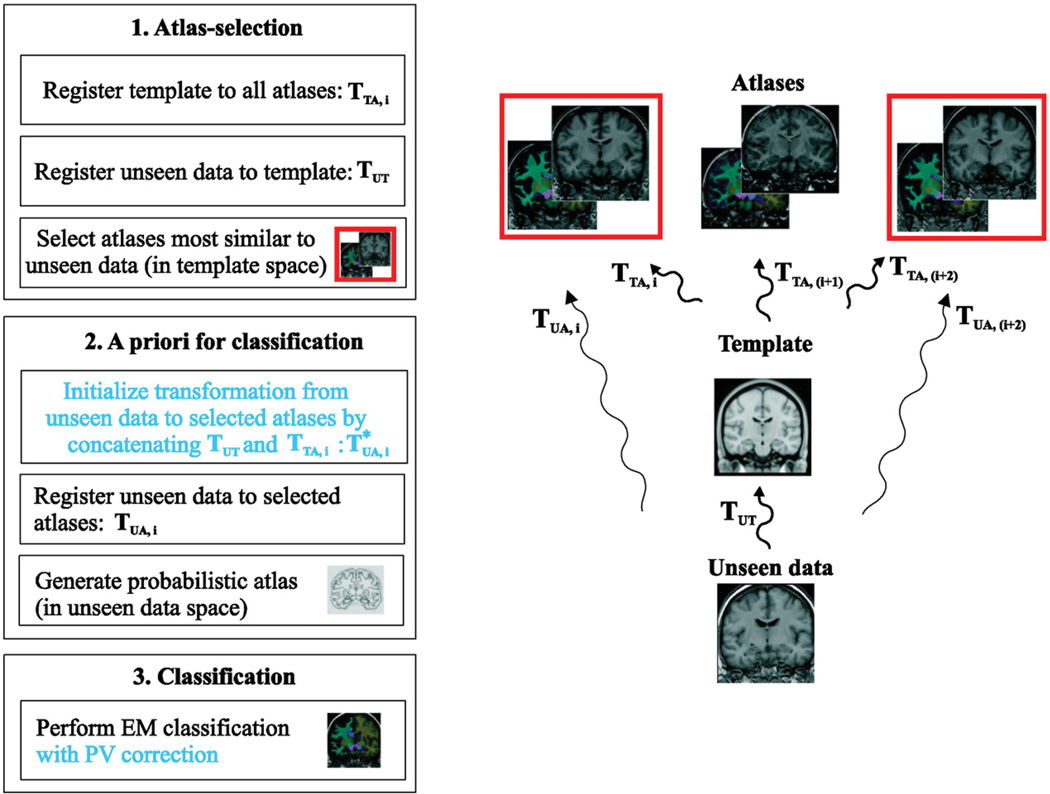
Fig. 1 summarizes our multi-atlas segmentation pipeline (Lötjönen et al., 2010) including also the contributions made in this work (indicated by the blue text). Step 1: Both unseen data and atlases are registered non-rigidly to a template. The atlases most similar to the unseen data, measured by normalized mutual information in the template space, are selected to be used in the next step. Step 2: Non-rigid transformations between the unseen data and the selected atlases are computed. Our contribution in this work is to initialize these transformations using the transformations computed in the step 1. After propagating the tissue labels of the selected atlases to the space of the unseen data using the transformations computed, tissue probabilities can be computed for each voxel of the unseen data leading to a probabilistic atlas. Step 3: We perform tissue classification using the standard EM classification framework (van Leemput et al., 1999). In the standard multi-atlas segmentation, the tissue class having the highest probability in a voxel is chosen producing the final segmentation. The use of the EM framework allows including statistical modeling of tissue intensities in addition to the use of a priori spatial information utilized in the standard multi-atlas segmentation. The modeling of tissue intensities improves the segmentation accuracy as shown in (Lötjönen et al., 2010). In this work we study, if the partial volume (PV) correction improves the estimate of the volume and produces better classification accuracy when used as a biomarker.

Fig. 1.

The segmentation pipeline showing also transformations between the unseen data, template and atlas spaces.

Initialization of transformations to atlases

In the standard multi-atlas segmentation, the unseen data (in unseen data space) is non-rigidly registered directly to each atlas (in atlas space), or vice versa producing the transformation T_UA. In this work, we propose to perform non-rigid registration via a separate template as an inter-mediate step between atlas and unseen data spaces. The approximation of the transformation unseen-to-atlas, T_UA, is generated by the concatenation of the transformations unseen-to-template T_UT and template-to-atlas, T_TA,i, (the parameter i indicates the index of an atlas):

$$T_{\mathit{\text{UA}},i}^{*}=T_{\mathit{\text{UT}}}°T_{\mathit{\text{TA}},i}.$$

As the transformations T_TA,i are independent on the unseen data, they can be pre-computed. The transformation T_UT is computed already during the atlas selection step (Fig. 1). Therefore, no extra registration steps are needed to generate ${\mathrm{T}}_{\text{UA},\mathrm{i}}^{*}$. Our non-rigid registration tool outputs a displacement vector for each voxel making the concatenation simple. Tri-linear interpolation is used in concatenating the displacement vectors.

The transformation ${\mathrm{T}}_{\text{UA},\mathrm{i}}^{*}$ is used as an initialization for the accurate transformation T_UA,i. Computing the T_UA,i is exactly similar to our multi-atlas segmentation protocol (Lötjönen et al., 2010) except that the computation of the transformation is not initialized by the identity transformation but by an already quite good approximation of the final transformation ${\mathrm{T}}_{\text{UA},\mathrm{i}}^{*}$. This means that much less iterations are needed in subsequent non-rigid registration as only small updates are required to the transformation.

Partial volume modeling

The expectation maximisation algorithm used is described in detail in Appendix A. In this work, we used the method proposed by Tohka et al. (2004) to estimate the amount of partial volume effect in each voxel. In addition to real tissue classes, hippocampus (HC), cerebrospinal fluid (CSF), gray-matter (GM) and white-matter (WM), mixed classes HC–CSF and HC–WMwere used in the EM classification. As the intensity values of the GM and HC are approximately equal, the class HC–GM was not used. The prior probabilities of mixed tissue classes were estimated as proposed in (Cardoso et al., 2009). After computing the probabilities for each tissue class using the EM classification, the proportion of the tissues in the mixed classes were estimated. The volume of HC was the sum of tissue proportions for HC in all voxels (proportion 1 for the real HC class) multiplied by the voxel size.

Image data

The experimental validation of the developed algorithms was performed using data from three cohorts. The descriptive statistical information of the cohorts is shown in Table 1.

Table 1.

Descriptive statistical information for the cohorts ADNI, Kuopio and GEHC. Abbreviations used: CN = cognitively normal, SMCI = stable mild cognitive impairment subject, PMCI = progressive mild cognitive impairment subject, AD = Alzheimer's disease subject, MMSE = mini mental state examination.

	ADNI				Kuopio		GEHC
	CN	SMCI	PMCI	AD	SMCI	PMCI	CN	MCI	AD
Sample size	216	216	155	189	64	42	25	20	27
Age	76.5 ± 5.1	75.6 ± 7.6	75.0 ± 7.0	76.0 ± 7.4	72.7 ± 4.7	71.3 ± 7.4	68.7 ± 7.6a	72.7 ± 7.1	69.6 ± 7.0
Females [%]	49	34	40	48	70	62	48	45	55
MMSE	29.1 ± 1.0	27.2 ± 1.8	26.7 ± 1.7	23.3 ± 2.0	24.6 ± 3.3	23.2 ± 3.3	29.4 ± 1.0	28.0 ± 0.9	23.3 ± 2.2

^aThe age is 68.7 ± 7.6 yrs for the elderly group (age>55 yrs, N = 15) and 37.9 ± 11.5 yrs for younger group (age<55 yrs, N = 10).

ADNI-cohort

The Alzheimer's Disease Neuroimaging Initiative (ADNI) was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The principle investigator of this initiative is Michael W. Weiner, M.D., VA Medical Center and University of California—San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the US and Canada. The initial goal of ADNI was to recruit 800 adults, aged 55 to 90 years, to participate in the research—approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years.

We studied T1-weighted 1.5 T and 3 T MR images from all 838 subjects of the ADNI database, http://www.loni.ucla.edu/ADNI. The ADNI consortium has classified data into three groups: Alzheimer's patients (AD), mild cognitive impairment (MCI) and cognitively normal (CN). This information was available for 776 cases. From these cases, we used 1.5 T images in 595 cases and 3 T images in 181 cases. A semi-automated segmentation of the hippocampus was provided by ADNI for 340 cases (297 images using 1.5 T and 43 images using 3 T). From these 340 cases, the classification information was available for 321 cases. We found 181 cases for which both 1.5 T and 3 T images were available and acquired within a short period. These images were used to verify the consistency of the algorithm, i.e., both 1.5 T and 3 T were segmented and the volumes were compared (a test–retest study). Finally, we compared the use of the hippocampus volumes in classification with atrophy rates computed using the method by Wolz et al. (2010b). We used 478 cases having both 12- and 24-months follow-up periods for computing the atrophy rates. For these reason, we defined ADNI sub-cohorts: N = 776, N = 478, N = 340, N = 321 and N = 181.

The semi-automated protocol is described in detail on the ADNI website: http://www.loni.ucla.edu/twiki/pub/ADNI/ADNIPostProc/UCSFMRI_Analysis.pdf. In summary, the protocol consists of three steps: 1) the user locates manually altogether 44 landmark points from hippocampi, 2) a commercially available high dimensional brain mapping tool (Medtronic Surgical Navigation Technologies, Louisville, CO, USA) is used to map a template brain with individual brains for producing hippocampal boundaries (Hsu et al., 2002), and 3) possible segmentation errors are corrected manually by an expert. Although the segmentation does not represent a real independent manual segmentation, the bias caused by automation has been minimized as the registration is driven by manually located landmarks and the result is finally manually checked. Because fully manual segmentation of large databases would be an extremely laborious task, the semi-automated results represent the best estimate of the ground truth currently available for the reasonable sized dataset (N = 340).

The images were acquired using MRI scanners from three different manufacturers (General Electric Healthcare (GE), Siemens Medical Solutions, Philips Medical Systems) and using a standardised acquisition protocol. Acquisition parameters on the SIEMENS scanner (parameters for other manufacturers differ slightly) were echo time (TE) of 3.924 ms, repetition time (TR) of 8.916 ms, inversion time (TI) of 1000 ms, flip angle 8°, to obtain 166 slices of 1.2-mm thickness with a 256×256 matrix. The size of the volumes were from 192×192×160 to 256×256×180 voxels with the voxel size from 0.9×0.9×1.2 mm to 1.3×1.3×1.2 mm.

The set of atlases used in this work consisted of 30 ADNI images. The set contained cases from AD, MCI and CN, 10 from each. One of the atlases was used as a template (76 years old female with AD diagnosis, MMSE = 26) in the atlas selection (Fig. 1). We tested different atlases and chose the atlas giving best results. The use of a mean shape atlas could improve further the results. As the atlases were a part of the ADNI cohort, a specific atlas was not used when it was the case being segmented, i.e., only 29 atlases were used for those cases. Five atlases were selected in the atlas selection.

In this work, we analyzed only baseline images, i.e., the first images acquired from a patient during the ADNI study. As ADNI is a longitudinal study, some MCI patients convert during the study to AD, denoted PMCI (progressive MCI), and the others remain non-converted, denoted as SMCI (stable MCI). The ability to classify correctly the PMCI and SMCI groups from the baseline data reflects the ability to predict the conversion which is clinically highly interesting. The mean time and its standard deviation from the baseline to the time point when the diagnosis was done, i.e., when the diagnosis flag in the ADNI database was changed, was 18.1±8.9 months. The follow-up time in the data used was 33.2±8.4 months.

Although ADNI is a large cohort including data from several clinical centers and data acquired by devices from different manufactures, we evaluated the robustness of the method using also two other cohorts: Kuopio and GEHC cohorts. These cohorts are independent on the ADNI, i.e., the ADNI acquisition protocol has not been followed.

Kuopio-cohort

Kuopio cohort included 106 MCI subjects pooled from population-based study databases gathered in the University of Kuopio (Kivipelto et al., 2001, Hänninen et al., 2002). MCI was diagnosed using the following criteria originally proposed by the Mayo Clinic Alzheimer's Disease Research Center (Petersen et al., 1995, Smith et al. 1996): (1) memory complaint by patient, family, or physician; (2) normal activities of daily living; (3) normal global cognitive function; (4) objective impairment in memory or in one other area of cognitive function as evident by scores >1.5 S.D. below the age-appropriate mean; (5) CDR score of 0.5; and (6) absence of dementia. As in the ADNI cohort, the MCI subjects who developed AD during the course of the follow-up were considered as PMCI subjects (N = 42) and those whose status remained stable or improved (i.e., those who were later diagnosed as controls) were considered having SMCI (N = 64).

All the MR images were acquired with two different 1.5 T MRI scanners in the Department of Clinical Radiology, Kuopio University Hospital (Julkunen et al., 2010). Two sets of imaging parameters were used with both scanners. In the first set, the parameters were: coronal slices with repetition time [TR] = 9.7 ms, echo time [TE] = 4.0 ms, flip angle = 12°, slice thickness = 2.0 mm, field of view = 240×240 mm, voxel volume = 1.9 mm³, matrix size = 256×256 and number of slices = 128. In the second set, the parameters were: axial slices with repetition time[TR] = 13.5 ms, echotime[TE] = 7.0 ms, flip angle = 12°, slice thickness = 1.5 mm, field of view = 240×240 mm, voxel volume = 1.3 mm³,matrix size = 256×256 and number of slices = 128. The cohort did not include manual segmentations. As the voxels were clearly anisotropic, we resampled the voxels to isotropic resolution using simple and fast trilinear interpolation.

GEHC-cohort

The GEHC cohort include of PET and MR data from the GEHC [18F] flutemetamol Phase II study (Vandenberghe et al., 2010). The study sample size was 27 clinical probable AD (MMSE 15–26, CDR 0.5–2), 20 amnestic MCI (MMSE 27–30, CDR 0–0.5) and 15 elderly CN (age>55 yrs) and 10 younger CN (age<55 yrs). For this work, we used only the MR data from this cohort. The MR images were obtained at four imaging sites using both 3 T and 1.5 T scanners. Imaging was performed using a 3D MPRAGE T1 weighted sequence with isotropic voxels not larger than 1 mm³. The actual imaging parameters varied slightly across the different scanners. The cohort did not include manual segmentations.

Evaluation tools

Because the Dice similarity index (SI) is one of the most widely used measures in assessing the performance of segmentation, it will be used in the comparison:

$$\mathit{\text{Similarity index }}(\mathit{\text{SI}})=2\frac{A\cap B}{A+B}$$

where A and B represent automatically and semi-automatically generated segmentations. The similarity index gives the value zero if the segmentations are not overlapping, and the value one for the perfect overlap. In addition, intra-class correlation coefficients between hippocampus volumes based on automatic and semi-automatic segmentations were computed.

When the consistency of the segmentations was studied, the test–retest variability (in %) was defined as:

$$v_{1.5-3}(\%)=100\frac{|V_{1.5}-V_3|}{(V_{1.5}+V_3)/2},$$

where V_1.5 and V₃ are the volumes of hippocampus computed from 1.5 T and 3 T images. In addition, the correlation coefficient between V_1.5 and V₃ was defined.

One way to evaluate segmentation indirectly is to study the performance of the volumes in classifying subjects to correct diagnostic groups (cognitively normal, stable MCI, progressive MCI or Alzheimer's disease patient; measured by the correct classification rate, CCR). More robust and accurate segmentation should perform better in classifying patients if a measure extracted from images is a good biomarker for detecting a disease. In the classification, we used the simplest possible linear classifier:

$$C={\beta }_0+{\beta }_1{F}_1,$$

where β_i is the weight of the feature (independent variable) F₁ (volume of hippocampus) and C represents a dependent variable used to predict the class, e.g. class AD if C≥0 and class CN if C<0. When building a linear classifier, the task is to define the weights β_i. Typically, they are obtained by solving the matrix equation β = F⁺C where the matrix F and the vector C consist of rows retrieved from data samples, i.e., feature values and class information of different cases, and the superscript ‘⁺’ indicates pseudo-inverse. A widely used extension of this approach is logistic regression, where the vector C is formulated as a probability measure. However, in the linear classifiers, the way to compute the pseudo-inverse of F affects the result and may lead to a sub-optimal classifier. Therefore, we chose a method where we define the weights β_i using an extensive search producing an optimal linear classifier, i.e., we tested all possible combinations of weights and chose the one producing the highest classification accuracy.

Separate training and test sets were chosen to avoid over-learning. We used 2/3 of cases in the training set to build the classifier and 1/3 of cases to test the correct classification rate (CCR). As two randomly chosen training and test sets may produce very different classification results, we repeated the selection 1000 times and computed different statistical measures (mean, standard deviation, confidence interval) for the results.

The statistically significant differences between groups were studied by Wilcoxon Rank Sum test for paired samples (Matlab R2009b, The MathWorks Inc, USA). The difference was considered statistically significant if p<0.05.

Results

ADNI cohort

Table 2 shows the similarity index and its standard deviation, the intra-class correlation coefficient of volumes and computation times for two computers: 8-core workstation (Intel Xeon E5420 @ 2.50 GHz) and dual-core laptop (Intel Core2 Duo P8600 @ 2.4 GHz). When compared with the accuracy between two different raters, reported in four publications, our method gives comparable results. The computation times are also on the range that is clinically acceptable.

Table 2.

Similarity index, correlation coefficient of volumes and computation times.

Hippocampus from MRI	Similarity index	Correlation of volumes	Time 8 cores	Time 2 cores
Proposed method (ADNI N = 340)	0.869 ± 0.035	0.94	1 min 25 s	1 min 59 s
Manual segmentation (inter-rater):
Morra, NeuroImage, et al., 2008 (N = 21)	0.85	0.71
van der Lijn, NeuroImage, et al., 2008 (N = 20)	0.86	0.83
Leung, NeuroImage, et al., 2010 (N = 15)	0.93	0.95
Niemann, Psych. Res, et al., 2000 (N = 20)	–	0.93

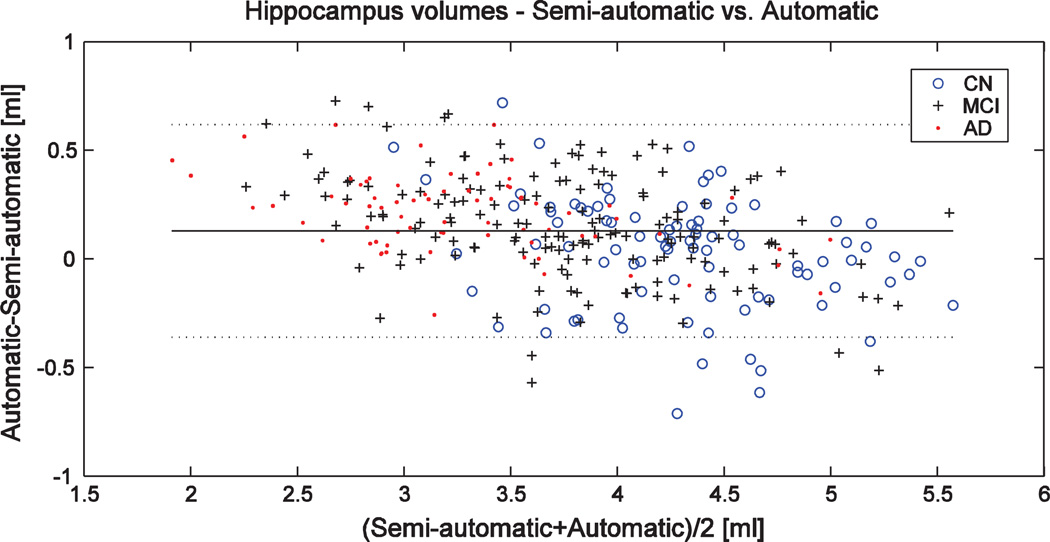
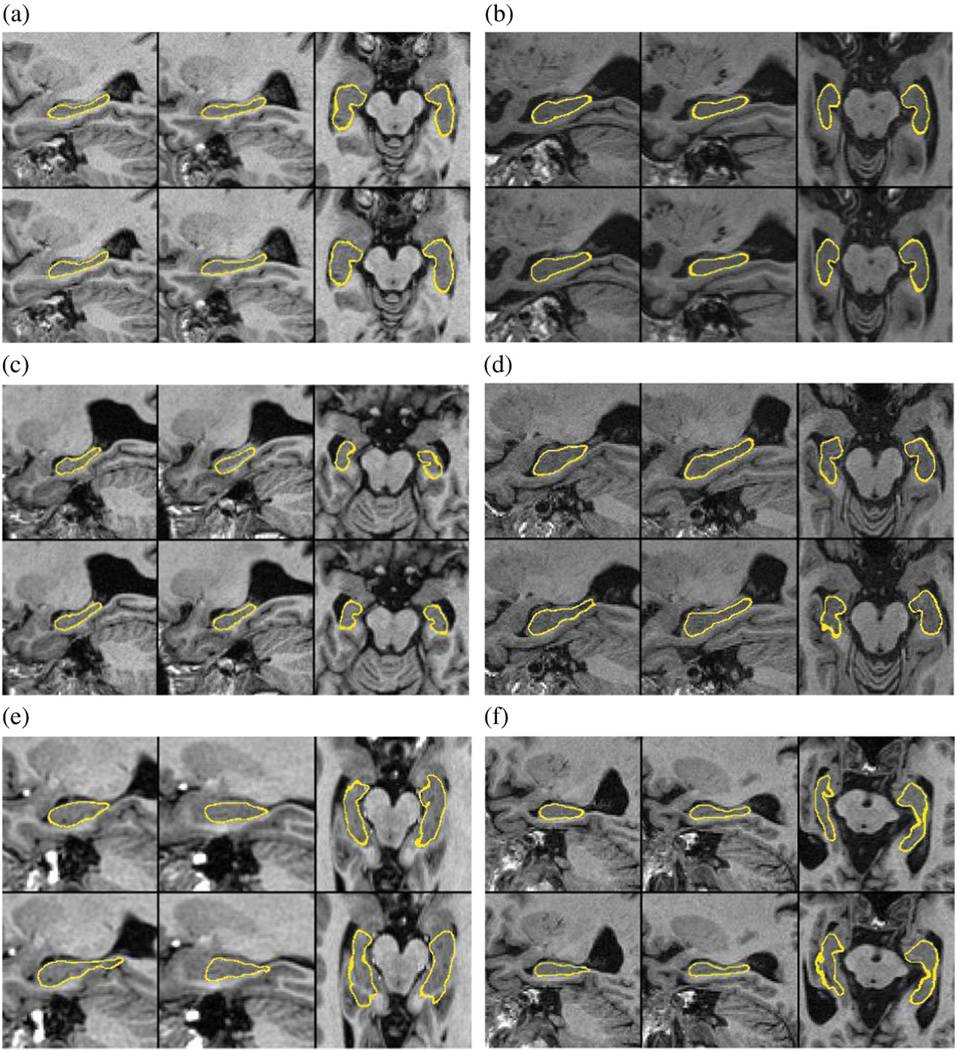
There is no threshold for the similarity index to define when segmentation failed but in general values over 0.7 can be considered good (Bartko, 1991). Using our method, 3.1% of segmentations had SI<0.8 and only 0.6% of segmentations produced SI<0.7 demonstrating the robustness of our method. Fig. 2 shows the Bland–Altman plot for semi-automatically and automatically defined volumes containing no clear outliers. Semi-automatic segmentations (N = 340) contained 297 images using 1.5 T and 43 images using 3 T. The similarity index computed separately for 1.5 T and 3 T images was 0.870 and 0.859, respectively (the difference is statistically significant). Fig. 3 shows both semi-automatic (top row) and automatic (bottom row) segmentations superimposed on the images for two cases having SI≈0.87 (a–b) and for four cases having the lowest SI values (c–f).

Fig. 2.

Bland–Altman plot for semi-automatically and automatically defined volumes in the ADNI N = 340 cohort. Horizontal lines show the mean ± 2*standard deviation.

Fig. 3.

Segmentation results of six cases from which the first two show one cognitively normal (a) and one AD case (b) with average segmentation accuracy (SI≈0.87) and the rest four (c–f) the cases with the lowest SI values from the cohort N = 340. The top and bottom rows show the semi-automatic and automatic, respectively, segmentations superimposed on the image. On the locations where the thickness of the yellow line is higher than a voxel, the surface and the image plane are partially parallel and the surface cross-sects several neighboring voxels. The left and right hippocampi are shown in a sagittal view and in a transaxial view for each case. The similarity index is reported both for the left and right sides, the volume of hippocampi when using semi-automatic and automatic segmentations (S/A), and the ADNI classification of the patient (C): a) SI(L/R) = 0.844/0.868, V(S/A) = 4.3/4.4 ml, C = CN, b) SI(L/R) = 0.852/0.892, V(S/A) = 3.1/3.5 ml, C = AD, c) SI(L/R) = 0.743/0.671, V(S/A) = 2.8/2.9 ml, C = PMCI, d) SI(L/R) = 0.702/0.817, V(S/A) = 4.5/4.5 ml, C = PMCI, e) SI(L/R) = 0.654/0.697, V(S/A) = 4.1/3.8 ml, C = not known, and f) SI(L/R) = 0.635/0.863, V(S/A) = 3.3/3.3 ml, C = not known.

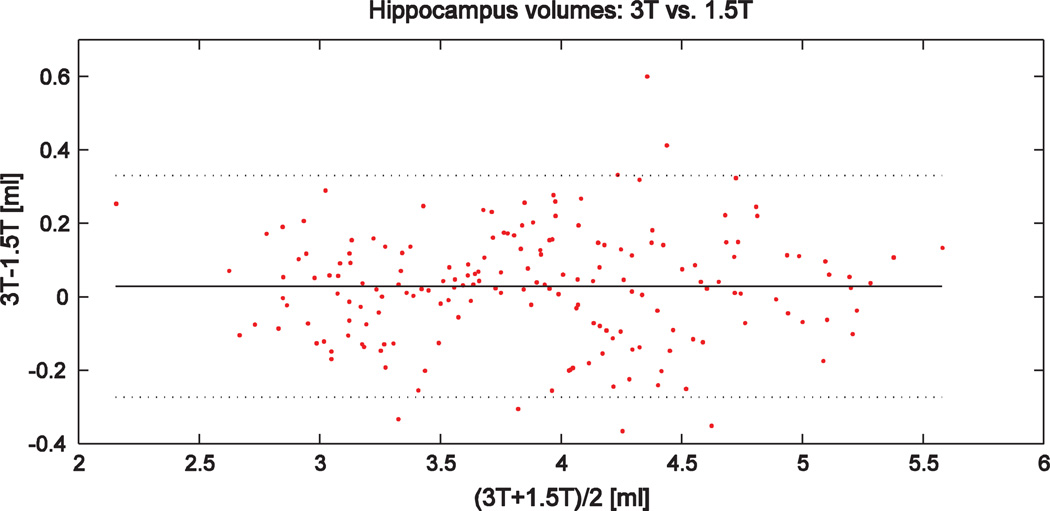
The test–retest variability v_1.5–3 between the hippocampus volumes segmented from 1.5 T and 3 T images (N = 181) was 4.23±10.7%. The results contained two outliers: the background of 3 T images was extremely noisy in those two cases and the affine registration between the template and the 3 T image failed when using a simple algorithm based on the maximization of normalized mutual information using a gradient descent optimization. When these two outliers were excluded from the results, the variability was 3.17±2.47%. The corresponding value for semi-automatic vs. automatic segmentations was 4.69±3.94%. The intra-class correlation coefficient between 1.5 T and 3 T volumes was 0.98. The Bland–Altman plot is shown in Fig. 4. These results demonstrate a high consistency of the segmentations.

Fig. 4.

Bland–Altman plot for hippocampus volumes computed using 1.5 T and 3 T images in the ADNI N = 181 cohort. Horizontal lines show the mean ± 2*standard deviation.

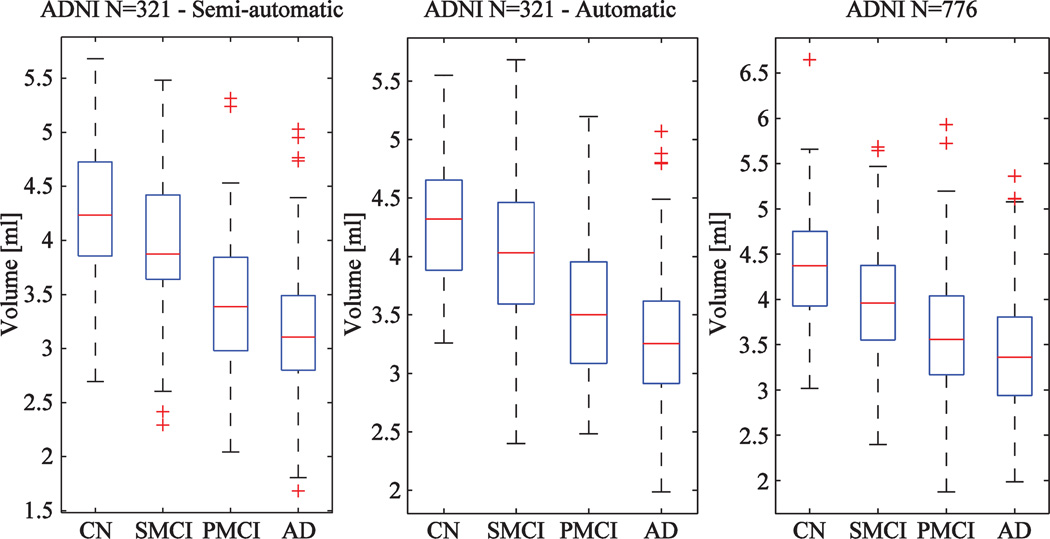
Fig. 5 shows the distributions of hippocampus volumes computed for the ADNI data. The plots on the left and on the center are for the ADNI N = 321 cohort when using semi-automatically and automatically generated segmentations, respectively. The distributions look very similar. The plot on the right shows the distribution for the whole ADNI N = 776 cohort.

Fig. 5.

Boxplots computed for volumes of hippocampus (CN = cognitively normal, SMCI = stable MCI-patient, PMCI-progressive MCI-patient and AD = Alzheimer's disease patient) using semi-automatic (left) and automatic (center) segmentations in the ADNI cohort N = 321 and automatic segmentations in the ADNI cohort N = 776 (right).

The mean classification accuracy and its standard deviation are shown for the cohorts N = 321 and N = 776 in Tables 3 and 4, respectively. When using semi-automatically segmented volumes (Table 3), the classification accuracies were 82.5% for the CN and AD groups and 71.4% for the SMCI and PMCI groups. The corresponding values for the automatic volumes were 83.4% and 64.9% which shows that semi-automatic volumes gave slightly lower classification rate for the CN–AD classification but higher for the SMCI–PMCI classification. The differences were statistically significant for all four columns in Table 3 when comparing semi-automatic and automatic segmentations. The results show also that partial volume correction improves the classification accuracy (difference statistically significant).

Table 3.

The mean classification rate (the highest value of the column in bold) and standard deviation for the ADNI N = 321 cohort using both semi-automatic and automatic segmentations with and without partial volume (PV) correction. The results are reported both for the training and test sets. The difference between semi-automatically and automatically (both with and without PV correction) generated volumes is statistically significant for all columns (not indicated in the table).

Classification rate	CN(N = 89)–AD(N = 82)		SMCI(N = 76)–PMCI (N = 75)
ADNI (N = 321)	Training set	Test set	Training set	Test set
Semi-automatic volumes	85.5 ± 1.9	82.5 ± 4.4	72.9 ± 2.5	71.4 ± 5.4
Automatic volumes — No PV	84.5 ± 2.0	82.1 ± 4.5	68.5 ± 2.5	63.7 ± 5.8
Automatic volumes — PV	84.7 ± 2.0*	83.4 ± 4.4*	68.9 ± 2.5*	64.9 ± 6.1*

The statistically significant difference with and without partial volume correction is shown by ‘*’.

Table 4.

The mean classification rate and standard deviation for the ADNI N = 776 cohort using automatic segmentations with and without partial volume (PV) correction. The results are reported both for the training and test sets.

Classification rate	CN(N = 216)–AD (N = 216)		SMCI(N = 155)–PMCI (N = 189)
ADNI (N = 776)	Training set	Test set	Training set	Test set
Automatic volumes — No PV	80.3 ± 1.4	79.1 ± 3.0	65.3 ± 1.6	62.4 ± 3.7
Automatic volumes — PV	80.6 ± 1.3*	79.7 ± 2.8*	65.4 ± 1.7*	63.3 ± 3.9*

The statistically significant difference is shown by ‘*’.

The remarkable difference in the classification rate of the SMCI and PMCI groups when using semi-automatically or automatically defined volumes requires detailed considerations (Table 3). The better quality of the semi-automatic segmentations in the ADNI cohort might explain the difference but we made an interesting finding which explains most of the difference. Inspecting more carefully the semi-automatic segmentations we noticed that the classification accuracy for the cases surrounding the optimal threshold (3.57 ml) was very high. For example, the classification accuracy was 93% for 15 cases closest to the optimal threshold (the cases were within the range 3.48–3.66 ml). By definition, the classification accuracy should be close to 50% near the threshold, i.e., equal to tossing a coin. The probability of classifying correctly at least 14 cases out of 15 cases randomly is 0.05%, being an extremely improbable event. We are not aware of all details by which semi-automatic segmentations were performed in ADNI but it seems probable that there is some mistake or a very improbable event has appeared. Table 5 shows results when the cases with semi-automatically defined hippocampus volumes between 3.48 and 3.66 ml were excluded. The difference between results computed using semi-automatically and automatically generated volumes becomes clearly smaller (the difference still statistically significant). We did not observe by visual inspection any systematic errors in automatic or semi-automatic segmentations that could explain this issue.

Table 5.

The mean classification rate and standard deviation for the ADNI N = 321 cohort using both semi-automatic and automatic segmentations. The columns 2 and 3 show the result for the original cohort (equal to Table 3) and the columns 4 and 5 when all cases with manually defined volume between 3.48 and 3.66 ml were excluded.

Classification rate	SMCI–PMCI		SMCI–PMCI
ADNI (N = 321)	Training set	Test set	Training set	Test set
	N = 106	N = 52	N = 96	N = 47
Semi-automatic volumes	72.9 ± 2.5	71.4 ± 5.4	71.6 ± 2.5	67.9 ± 5.4
Automatic volumes	68.9 ± 2.5	64.9 ± 6.1	69.9 ± 2.6	64.6 ± 6.1

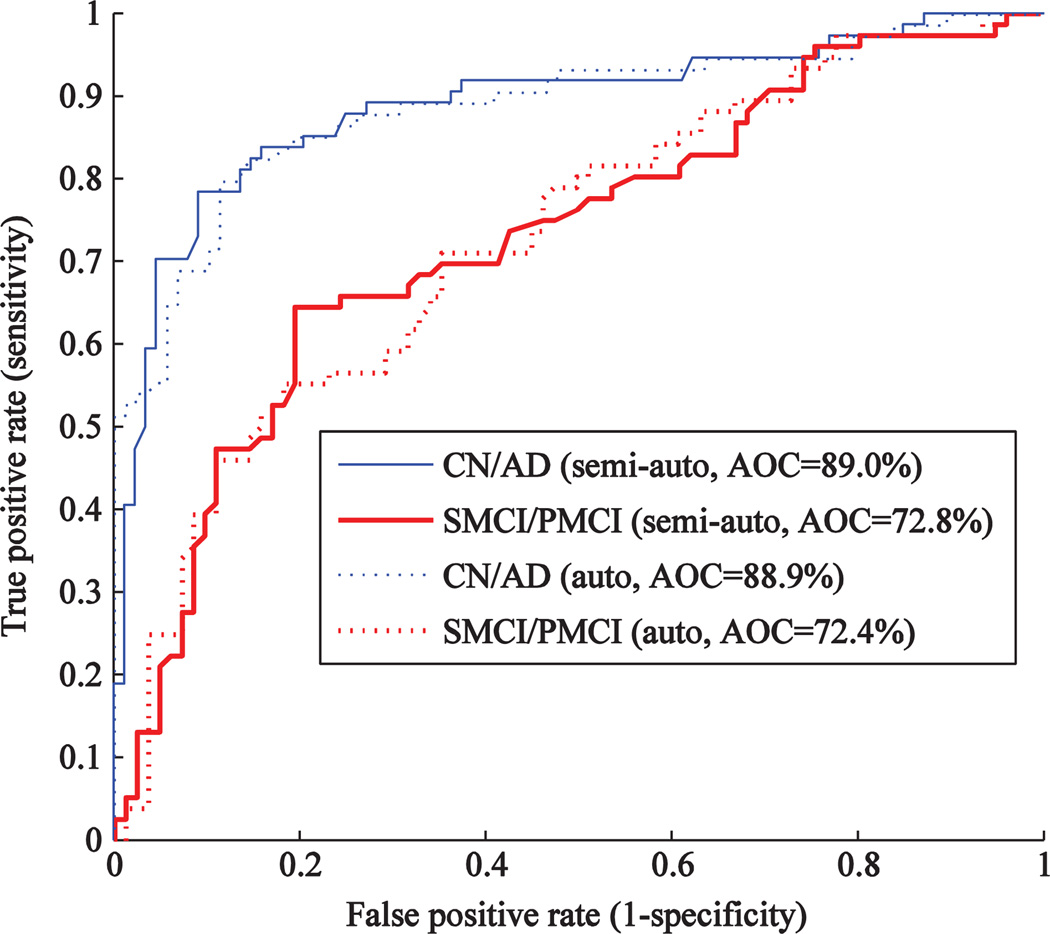
Fig. 6 shows the receiver operating characteristic (ROC) curve for the semi-automatic and automatic segmentations. The areas under the curve (AOC) are 89.0% and 88.9% for the classification CN-AD, and 72.8% and 72.4%, for the classification SMCI–PMCI, when using semi-automatic and automatic segmentations, respectively. These values indicate that the performance is very similar. The difference observed in Table 3 can be seen as a ‘hill’ in the middle of the SMCI–PMCI curves.

Fig. 6.

ROC-curve for the classification performance using semi-automatically and automatically generated volumes of hippocampus in the cohort N = 321.

We computed for comparison results using also our previous version (Lötjönen et al., 2010) for the cohort N = 340/321 (in the previous report N = 60). The similarity index was 0.872 (previous 0.885), the correlation coefficient was 0.95 (previous 0.94) and the classification accuracies were 84.4% (training set) and 80.2% (test set) for the CN and AD groups, and 68.6% (training set) and 63.4% (test set) for the SMCI and PMCI groups. The values are corresponding to the values reported in Tables 2 and 3. The computation time with a laptop computer was 4 min 24 s which is more than double compared with the approach proposed in this work.

We computed the hippocampus volumes for the ADNI cohort using the method presented in (Wolz et al., 2010a). In the ADNI (N = 321) cohort, the classification accuracy was 75.0% for the CN and AD groups, and 60.0% for the SMCI vs. PMCI groups, and the intra-class correlation coefficient was 0.88. The corresponding values in this work were 83.4%, 64.9% and 0.94, respectively (Tables 2 and 3). In the ADNI (N = 776) cohort, the classification accuracy was 71.6% for the CN and AD groups, and 60.0% for the SMCI and PMCI groups. The corresponding values in this work were 79.7% and 63.3%, respectively (Table 4). The improvements in classification accuracy achieved with the proposed method were statistically significant.

We compared the classification performance of the hippocampus volume from this work with the atrophy rates computed by the method proposed by Wolz et al. (2010b). The results are shown in Table 6. We used the ADNI cohort (N = 478) and computed atrophy rates using 12 months and 24 months follow-up period. The data with 24-months follow-up period produced clearly the best accuracy (difference statistically significant compared with the hippocampus volume and the 12-months follow-up). The hippocampus volume and the 12-months follow-up period produced comparable classification accuracies: the atrophy rate produced higher accuracy for the CN and AD groups whereas the hippocampus volume was better in the SMCI and PMCI groups for the test sets.

Table 6.

The classification rate for the ADNI (N = 478) cohort using the hippocampus volumes from this work and the atrophy rates from the work by Wolz et al. (2010b). The differences between all rows of each column are statistically significant.

Classification rate	C-AD		SMCI–PMCI
ADNI (N = 478)	Training set	Test set	Training set	Test set
	N = 171	N = 84	N = 149	N = 73
Hippocampus volume	80.9 ± 1.7	78.2 ± 3.7	63.1 ± 2.2	59.5 ± 5.1
Atrophy rate — 12 months	82.0 ± 1.7	79.6 ± 3.6	65.1 ± 1.9	58.6 ± 4.1
Atrophy rate — 12 months	89.0 ± 1.4	86.8 ± 3.0	67.3 ± 2.1	64.5 ± 4.8

Kuopio and GEHC cohorts

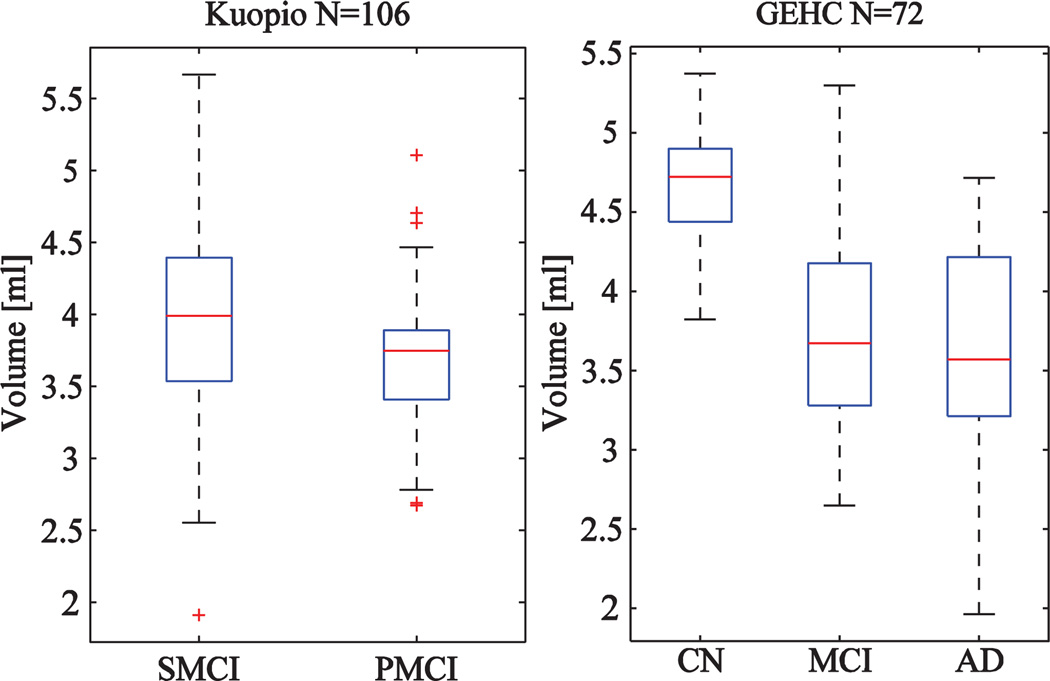
As Kuopio and GEHC cohorts do not include manual segmentations, the validation will be based only on the classification accuracy. Fig. 7 shows the distributions of hippocampus volumes in the Kuopio and GEHC cohorts. The classification accuracies are shown in Table 7. The 30 atlases from the ADNI cohort were used to make the multi-atlas segmentations. The accuracies correspond to results reported in Tables 3–5 demonstrating the robustness of the method also in different data.

Fig. 7.

Boxplots computed for volumes of hippocampus (CN = cognitively normal, SMCI = stable MCI-patient, PMCI-progressive MCI-patient and AD = Alzheimer's disease patient) using the Kuopio (N = 106) and GEHC (N = 72) cohorts.

Table 7.

The mean classification rate and standard deviation for the Kuopio (N = 106) cohort in the SMCI–PMCI classification and for the GEHC (N = 52) cohort in the CN–AD classification.

Classification rate	Training set	Test set
Kuopio (N = 106): SMCI–PMCI	69.4 ± 3.0	66.2 ± 7.6
GEHC (N = 52): CN–AD	86.1 ± 3.3	80.3 ± 7.9

Discussion

In this work, we proposed and validated a method for automatic segmentation of the hippocampus from MRI images. Our final objective is to develop a tool for helping decision making in real clinical conditions. A segmentation tool must be accurate, robust and fast enough to be attractive in clinical practice. Our preliminary analysis shows that it is possible to generate fully automatically segmentations where the accuracy corresponds to semi-automatic segmentation, and the computation time is two minutes in a standard laptop computer. The performance of the method was evaluated using data from three cohorts consisting of altogether about 1000 cases. The parameters of the method were not tuned between the cases.

The performance of the method was validated in four aspects. The first two performance measures were the overlap of automatically and semi-automatically generated segmentations (measured by the similarity index), and the similarity of automatically and semi-automatically defined hippocampus volumes (measured by the correlation coefficient). They require semi-automatic segmentations which were available for 340 cases, only in the ADNI cohort. The similarity index 0.87 and the intra-class correlation coefficient 0.94 (the Pearson correlation 0.96) obtained in our study correspond to inter-rater results produced in different studies (Table 2). The following values (SI = similarity index, r = correlation coefficient) have been reported for other automatic methods: SI = 0.87 (Chupin et al., 2009a), SI = 0.89, r = 0.83 (Collins and Pruessner, 2009), SI = 0.89 (Leung et al., 2010), SI = 0.89, r = 0.94 (Lötjönen et al., 2010), SI = 0.85, r = 0.71 (Morra et al., 2008), and SI = 0.85, r = 0.81 (van der Lijn et al., 2008). The magnitude of the values corresponds to ours but a detailed comparison is impossible as the datasets used are different.

The third measure evaluated the consistency of segmentations using 1.5 T and 3 T images from 181 cases. The test–retest variability was 3.2% without two outliers (4.2% with outliers) and the intra-class correlation coefficient was 0.98 which indicates the good consistency of the method even for different strengths of magnetic field.

The fourth approach evaluated the performance in classifying subjects to correct diagnostic groups. Chupin et al. (2009b) reported recently classification accuracy of 76% for CN–AD (N = 311) and 65% for SMCI–PMCI (N = 294). Using our automatic tool for the ADNI cohort N = 321, the correct classification rates were 83% and 65% for CN–AD and SMCI–PMCI classifications, respectively. The corresponding values for semi-automatic segmentations were 83% and 71%. However, we demonstrated an improbable distribution of volumes computed semi-automatically for the SMCI and PMCI cases near the classification border. When this bias was removed, the classification accuracy decreased to 68% but the value is still higher by 3% units than in the automatic method. There are two obvious explanations to the difference. First, semi-automatic segmentations in ADNI are just highly consistent and of good quality — not reached by the automatic method. However, we are not aware of details of the segmentation protocol and whether the accuracy corresponds to the inter-rater variability reported in other studies (Table 2). Second, the size of the dataset is still relatively limited (training set 96 cases and test set 47 cases) causing inaccuracies to CCR values. The estimate of the mean CCR was relatively precise as the standard error computed for 1000 repetitions is small: the mean CCR was 64.2–65.0% (95%–confidence interval). However, the variability of the CCR values was high: CCR values varied between 53 and 77% (95%-confidence interval). This means that using a different subset from the ADNI or a totally different dataset might produce clearly different results. Even using the whole ADNI, i.e., 371 SMCI and PMCI cases from which 249 cases in the training set and 122 cases in the test set, the CCR values varied still between 56 and 71% (95%-confidence interval). In other words, if we had a dataset of 371 cases and we divided it randomly to training and validation (test) sets, as done typically in life-science studies, we could obtain any CCR value between 56% and 71% with a reasonable probability. Therefore, the size of the database hinders certainly the final conclusions. In addition, the classification results of SMCI and PMCI groups will change in future when the follow-up time gets longer and more cases convert from the SMCI to the PMCI group. When this study was performed, the follow-up time was on average 33.2±8.4 months which is still a relatively short time period in the context of Alzheimer's disease.

In the PredictAD project (www.predictad.eu), we are developing a software tool for decision support using heterogeneous patient data (clinical, imaging and electrophysiological data) including also tools for image segmentation (Mattila et al., 2010). Our objective is that when a clinician is inspecting the patient data, she/he could analyze also images online without long waiting times and especially a need for reserving another session just for studying segmentation results. As Alzheimer's disease is not an acute disease, the requirement of fast computation is related mostly to clinical usability: fast methods make simple and fluent clinical work-flows easier to implement. The computation time may not be of importance for the productivity and efficiency at patient visits in a memory clinic but can be an issue in a neuroradiology department with several thousand studies per year. Despite the computation time requirement, the segmentation accuracy and robustness are the most important requirements in the clinical diagnostics. The computation time could be also an issue, e.g., in time-critical brain surgery. In that context, the hippocampus is not a highly interesting structure but as our framework is fully generic it can be used to segment also other brain structures, as done, for example, in (Lötjönen et al. 2010).

This work made two technological contributions. First, we proposed to use a separate template space between the patient data and atlas for initializing the transformation from the atlas to patient data. This approach allowed clear improvements in the computation time and made it possible to segment images in less than two minutes. Second, the need for the inclusion of partial volume correction is intuitively clear especially for small objects, such as, the hippocampus. Our results show that the partial volume correction improves the classification accuracy (difference statistically significant). Although the improvement is only about 0.5–1% units, it is worth using as the extra computation time needed is only a few seconds. On the other hand, the correlation coefficients of volumes between semi-automatic and automatic (without and with PV correction) were very similar (difference 0.001). As semi-automatic segmentations are not real gold standards and are not performed in sub-voxel accuracy, there is no clear reason to expect higher correlation for PV corrected volumes. The similarity indices were not compared as the computation of the index between binary and fuzzy segmentations has not been defined.

Differences in the classification accuracies between semi-automatic and automatic segmentations were statistically significant. Semi-automatic segmentation performed better in the SMCI–PMCI classification and automatic segmentation in the CN-AD classification. However, this result requires careful interpretations. The statistical analysis is performed for 1000 CCR estimates produced by 1000 randomly selected training and test sets. As the number of samples is high, even tiny and possibly clinically non-relevant differences become statistically significant. In addition, the difference is shown only for the used subset of the ADNI. As described above, the result could be clearly different if a different dataset was used. For example, Table 6 shows results which can be explained by this reasoning: atrophy rate over 12-months performed better than the hippocampus volume in the training set of the SMCI and PMCI groups while the hippocampus volume was better in the test set.

Current diagnostic criteria (Dubois et al., 2007; Waldemar et al., 2007) for probable Azheimer's disease suggest estimating the atrophy of the brain from MRI images. As hippocampus is known to be among the first areas affected by the disease, automatic measurement of its volume is clinically interesting. In this work, we demonstrated that the accurate and robust computation of the volume is possible automatically in a clinically acceptable time. Our results indicated a good correspondence in semi-automatically and automatically generated segmentation accuracies although some space for discussions remained especially when analyzing the classification accuracies. The variability in the data was just too high even we used larger databases than used in most previous studies. As a conclusion, the results were promising but they must be confirmed with more cases in clinical conditions.

Appendix A. Expectation maximisation formulation

The labeling f of the image I minimizing an energy functional was searched:

$$f=\mathit{\text{arg }}\underset{f}{\mathit{\text{min }}}{E}_{\mathit{\text{intensity}}}(f)+\alpha E_{\mathit{\text{priorS}}}(f)+\beta E_{\mathit{\text{priorR}}}(f),$$

where E_intensity measures the likelihood that observed intensities are from specific classes and E_priorS and E_priorR (see definitions below) describe the prior knowledge of class labels. Different values for the parameters α and β were tested: in this work the values α = 1 and β = 0.1 were used. The segmentation accuracy was not, however, very sensitive to the parameter values.

The intensity of each structure k was assumed to have a Gaussian density function, described by the mean μ and standard deviation σ:

$$E_{\mathit{\text{intensity}}}=-{\displaystyle \sum _{p\in I}}\text{ln}p(I_p|f_p=k),$$

where

$$p(I_p|f_p=k)=\frac{1}{\sqrt{2\mathrm{\pi }}{\mathrm{\sigma }}_k}{e}^{-\frac{{(I_p-{\mathrm{\mu }}_k)}^2}{2{\mathrm{\sigma }}_k^2}}.$$

The parameters μ_k and σ_k were estimated from the target volume by weighting each voxel with the spatial prior probability that it belongs to the class k. Following van der Lijn et al. (2008), our spatial prior probabilities are obtained from a subject-specific probabilistic atlas built from the labels obtained from multi-atlas segmentation (Heckemann et al., 2006). With multiple (N) label maps f ^j, the prior probability for a voxel p of its label being the label from the structure (class) k is therefore:

$$p(f_p=k)=\frac{1}{N}{\displaystyle \sum _{j=1,‥,N}}\{\begin{array}{c}1,{\mathit{\text{iff}}}_p^j=k\hfill \\ 0,{\mathit{\text{iff}}}_p^j\ne k\hfill \end{array}.$$

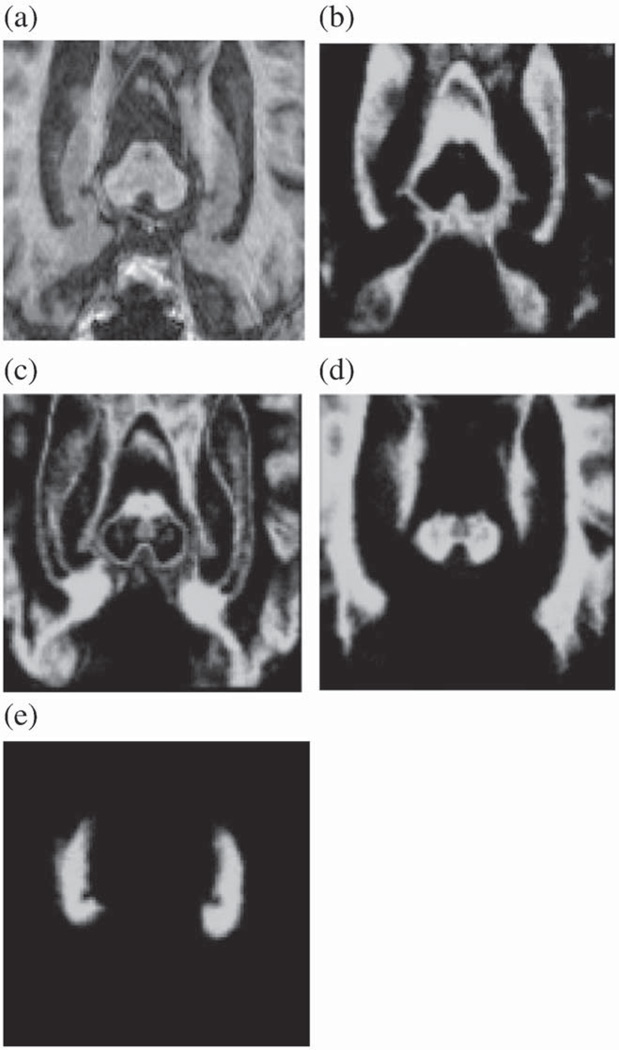
Fig. 8. shows the spatial prior probability maps computed for CSF, gray-matter, white-matter and hippocampus. In this work, the hippocampus was modeled using only one Gaussian distribution expecting homogeneous signal from the structure. In reality, the hippocampus contains substructures which become visible in high-quality images. Different spatial priors could be defined in that case for these substructures. However, we demonstrated that the proposed method produces satisfactory results for both 1.5 T and 3 T images used in the typical current clinical settings.

Fig. 8.

Probabilistic atlases used as spatial priors in the expectation maximization segmentation: a) original MR image, and the probabilistic atlas of b) CSF, c) gray-matter, d) white-matter and e) hippocampus.

The prior energy consisted of two components: spatial prior and regularity prior. The spatial prior was defined as follows:

$$E_{\mathit{\text{priorS}}}=-{\displaystyle \sum _{p\in I}}\text{ln}p(f_p=k).$$

The regularity prior, based on Markov Random Fields, was defined for keeping the structures smooth. The formulation described in (Tohka et al., 2004) was used:

$$E_{\mathit{\text{priorR}}}={\displaystyle \sum _{p\in I}}{\displaystyle \sum _{q\in N_p}}\frac{a_{\mathit{\text{pq}}}}{d(p,q)},$$

where N_p is the 6-neighborhood around voxel p, d(p,q) is the distance between centers of voxels p and q (in 6-neighborhood always 1), and

$$a_{\mathit{\text{pq}}}=\{\begin{array}{cc}-2\hfill & f_p=f_q\hfill \\ -1\hfill & f_p\text{ and }{f}_q\text{ share a component}\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}$$

The classification algorithm used was as follows (Lötjönen et al., 2010):

1. Estimate model parameters mean μ and standard deviation σ (maximisation step of the EM algorithm, M-step).

2. For each voxel p∈Ι, define classes f in the 6-neighborhood including also voxel p.

3. Classify voxel p to a class from f according to the maximum a posterior probability (expectation step of the EM algorithm, E-step).

4. Iterate until the segmentation does not change.