Electrokinetic confinement of axonal growth for dynamically configurable neural networks

Abstract

Axons in the developing nervous system are directed via guidance cues, whose expression varies both spatially and temporally, to create functional neural circuits. Existing methods to create patterns of neural connectivity in vitro use only static geometries, and are unable to dynamically alter the guidance cues imparted on the cells. We introduce the use of AC electrokinetics to dynamically control axonal growth in cultured rat hippocampal neurons. We find that the application of modest voltages at frequencies on the order of 10⁵ Hz can cause developing axons to be stopped adjacent to the electrodes while axons away from the electric fields exhibit uninhibited growth. By switching electrodes on or off, we can reversibly inhibit or permit axon passage across the electrodes. Our models suggest that dielectrophoresis is the causative AC electrokinetic effect. We make use of our dynamic control over axon elongation to create an axon-diode via an axon-lock system that consists of a pair of electrode `gates' that either permit or prevent axons from passing through. Finally, we developed a neural circuit consisting of three populations of neurons, separated by three axon-locks to demonstrate the assembly of a functional, engineered neural network. Action potential recordings demonstrate that the AC electrokinetic effect does not harm axons, and Ca²⁺ imaging demonstrated the unidirectional nature of the synaptic connections. AC electrokinetic confinement of axonal growth has potential for creating configurable, directional neural networks.

Introduction

Over the past few decades, neuroscientists have developed numerous methods that can manipulate, direct, and enhance the intrinsic axonal growth process. Approaches include the use of micropatterned topographical structures [1, 2], patterns of adhesion-promoting molecules or guidance cues [3, 4], mechanical forces [5, 6] or light-based guidance [7, 8]. These techniques have led to the fabrication of in vitro devices capable of guiding axons along a predetermined path, with applications for quantitative studies in neurite outgrowth [9], neural signalling [10], and the creation of engineered, oriented in vitro neural networks [11].

These methods typically employ a `static', pre-fabricated pattern of features to spatially control neural outgrowth. However, developing axons in vivo are subject to guidance cues that vary both spatially and temporally [12]. For example, early axons from retinal ganglion cells in Xenopus larvae decussate at the optic chiasm to form contralateral connections, but some later axons are repelled from the midline due to heightened ephrin-B expression and do not cross [13]. Studying and manipulating such processes requires methods that can provide both temporal and spatial control over neural development by switching the state of regions between outgrowth permissive to restrictive. Currently, optical methods can achieve temporal control of axon outgrowth by moving the laser spot, which attracts the developing growth cone [8], but these methods are not readily scalable for creating networks for large numbers of axons across large distances.

Here we demonstrate dynamic control of axonal outgrowth by using AC electric fields to guide axons from rat hippocampal neurons in vitro. AC electric fields can induce electrokinetic forces including dielectrophoresis (DEP), AC electroosmosis, and electrothermal flows. Of these, DEP has previously been applied to manipulate a wide range of particles and cells [14, 15, 16], including neurons [17], most commonly to confine cell bodies in predetermined locations. Heida et al. [18, 19] extensively studied the influence of DEP on neuron development and showed that neurons remain viable after field exposure. In vitro devices were presented [20, 21] to position neuron somata in a grid, and were subsequently cultured for several days until a neuronal network was formed. When coupled with micro electrode arrays (MEAs), these devices provided a scalable platform to study neuronal networks [22, 23]. Importantly, all these devices controlled the positioning of the cell body, not of the neurite outgrowth; axon guidance has not been demonstrated using AC electrokinetic forces.

DC electric fields have been used to guide neuronal growth, where growth cones turn toward the cathode [24, 25], but the risk of electrolysis at the electrodes limits its applications [26, 27]. Non-uniform AC electric-fields can overcome this issue because the high frequencies can minimize harmful electrochemical reactions [28].

Using non-uniform AC electric fields, we demonstrate reversible growth cone arrest upon application of an AC field, develop a quantitative model for the phenomenon, and show that guided axons can transmit action potentials. Finally, we present a dynamically configurable axon-lock microfluidic system that is capable of creating unidirectional connections between multiple neuronal populations.

Results and Discussion

“Stop and go” electrokinetic effect on axonal growth

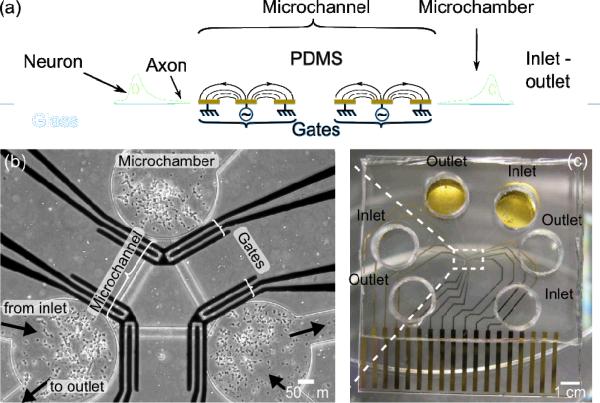
To determine if AC electrokinetic forces could affect axonal growth, we developed a microfluidic platform based on an axon isolation device developed by Talor [29], which is composed of two wide microfluidic chambers, in one of which neurons are cultured (Fig 1). The two chambers are connected by an array of parallel microchannels that constrain axonal outgrowth to one dimension. To enable the application of AC fields within the microchannels, the microfluidic platform is bonded to glass that has been prepatterned with interdigitated gold electrodes (15 μm width spaced by 15 μm). By bonding the glass and PDMS such that the electrodes run perpendicular to the microchannels, we can apply AC electrokinetic forces that act parallel to the channel to block the one-dimensional axon growth.

Fig. 1.

Microfluidic neuronal electrokinetic platform. (a) An illustrated cross section of the device. (b) An image of neurons growing in the device at 4 DIV. (c) A photograph showing the 4-well fluidic interface and the electric interface.

Upon adding neurons to the culture chamber, extensive neurite outgrowth occurred by 4 days in vitro (DIV), with many neurites entering the microchannels (Fig 1b).

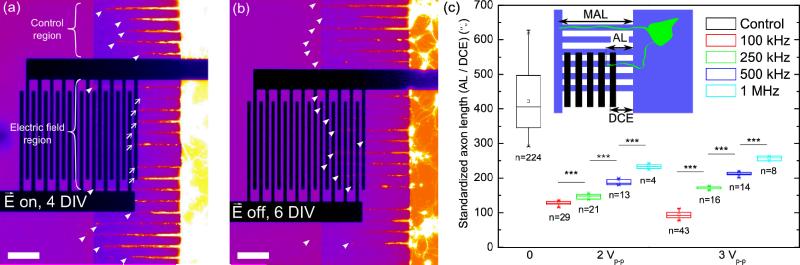
We next applied AC signals to the electrodes and monitored axon growth. In microchannels that were not crossed with electrodes, axons grew through the length of the microchannel (Fig 2a–b). However, axons in microchannels with electrodes stopped growing at the electrodes (Fig 2a) when the field was applied. Once the field was turned off, axons resumed their growth through the microchannel (Fig 2b), indicating that they remained viable. To quantify the effect that AC fields have on axonal growth, we varied both the frequency and the voltage amplitude of the AC signal after application for 7 days in vitro. We limited frequencies to the range of 100 kHz – 1 MHz and voltages to a range of 0–3 V_p-p to avoid significant temperature rise (ΔT~σV² /k, where σ is the medium electrical conductivity and k its thermal conductivity [30], here ΔT~7 °C in cell culture media at maximum voltage) or electrolysis in the high-conductivity hippocampal culture medium (measured at σ_m = 0.98 ± 0.08 S/m). We found that both the frequency and voltage of the AC signal had a significant effect on the axon length, with lower frequencies causing greater inhibition of axon outgrowth (Fig 2c) at a given voltage.

Fig.2.

(a): Fluorescent falsed-colored image of axonal growth in microchannels with perpendicular interdigitated electrodes at 4 DIV. Neurons are infected with tubulin-GFP baculovirus for live-cell visualization purposes. Closed arrowheads denote an axon in a control region without electrodes that grows through the microchannel. Open arrowheads denote an axon in a microchannel with electrodes that is stopped at the electrode edge. f=100 kHz and V_p-p=2 V. Scale bar is 150 μm (b): Fluorescent falsed-colored image of axonal growth at 6 DIV after application of the electric field for 4 DIV. Closed arrowhead denotes the end of an axon. (c): Standardized axon length after 7 days culture in the chipwith voltage ON. (***: p<0.001). n refers to the number of axons measured over two independent replicate experiments.

All the frequency and voltage values resulted in significantly shorter axons than the control (V = 0) (p < 0.005). Moreover, increasing the voltage from 2 to 3 V_p-p for AC signals above 100 kHz does not significantly affect the neurite length (p > 0.5). We did observe a decrease in axon length when switching from 2–3V at 100 kHz (p < 0.001). Also, measurements of the axon length versus time at the optimum blocking parameters (Fig. S1) show that axon elongation after removal of the AC voltage occurs within less than 1 day whereas new axons take ca. 3 days to reach the electrodes, strongly suggesting that the elongating axons observed upon removal of the axon block are from axons that were previously blocked and not new dendrites coming from the cell body compartment. Applying voltages more than 3.5 V_p-p caused cell death within 1–2 days after the application of the electric field. Measurements using the temperature-sensitive fluorophore Rhodamine B [31, 32] showed that the average temperature around the electrodes increased with voltage and reached levels known to induce heat shock and cell death between 3 and 4 V_p-p (~50 °C at 4 V) as shown by Hisanaga et al [33], suggesting that the observed cell death above 3.5 V is due to temperature rises as a result of Joule heating (Fig. S2).

Overall, our results demonstrate that AC electric fields are capable of stopping axonal outgrowth in a voltage- and frequency-dependent manner.

Modelling of the electrokinetic effect on the growth cone

We can discern the mechanism of the effect by determining which types of AC electrokinetic phenomena are consistent with the results in Fig 2b. We thus modelled the different AC electrokinetic forces acting on the growth cone.

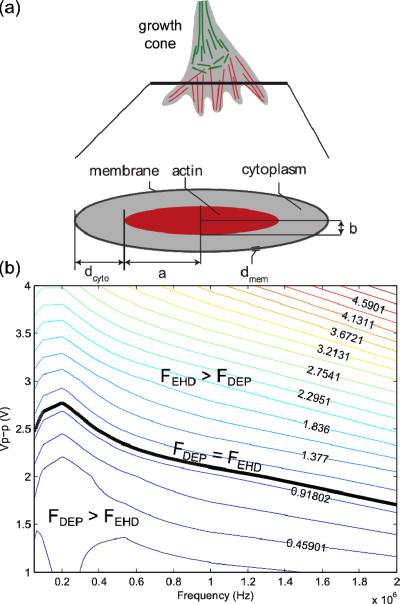
The growth cone is ellipsoidally shaped near a glass surface [34], connected to an axon that is 10 times smaller to its width [35], and a large fraction of it is comprised of actin filaments that coordinate its growth [36, 37]. We hence modelled the growth cone as a core-shell oblate object composed of three shells (Fig 3a): (1)- an actin layer (width a = 2 μm, height b = 200 nm), (2)- a cytoplasm layer (homogenous height d_cyt = 300 nm) and (3)- the cell membrane (homogenous height d_mem = 10 nm). The characteristic lengths of this objects are a₁=b+d_mem and a₂=a₃=a+d_cyto+d_mem. This polarizable object is exposed to 3 forces [38]: AC electroosmosis (ACEO) and electrothermal effect (ETE), that are electro-hydrodynamical forces acting on pure fluid (i.e., in the absence of particles) and dielectrophoresis (DEP) that is acts on the growth cone itself.

Fig. 3.

(a) Growth cone model used in our analysis. (b) Modelled ratio between DEP and EHD forces on the growth cone.

ACEO refers to the flow generated near the electrodes surfaces when AC signals are applied [39]. It is a frequency-dependent flow that is maximal at the frequency at which the product of the tangential electric field and the induced double-layer charge reaches a maximum. Following the traditional method to model co-planar electrodes ACEO [40], the time-average ACEO velocity (⟨u_ACEO⟩) on the electrode is given by

$$\begin{array}{c}\hfill \langle u_{\mathit{ACEO}}\rangle =\frac{1}{8}\frac{{∊}_m{V}_0^2}{{\sigma }_{m}r}\frac{{\Omega }_{\mathit{ACEO}}^2}{{(1+{\Omega }_{\mathit{ACEO}}^2)}^2}\hfill \\ \hfill \text{with}{\Omega }_{\mathit{ACEO}}=\frac{\pi }{2}\frac{r}{{\lambda }_2}\frac{{∊}_m}{{\sigma }_m}\omega \hfill \end{array}$$ (1)

where Ω_ACEO is the non-dimensional frequency, ε_m is the permittivity of the media, σ_m is the media conductivity, V₀ is the potential applied on the electrodes, r is the polar coordinate where the force is evaluated (here r is set to the half-length of the growth cone), λ_d the Debye length of the electrolyte/electrode interface and ω the frequency of the AC signal.

Second, an electrothermal flow can be induced when an electric field is applied in the media and causes Joule heating. For non-uniform fields (as is the case here), there will be spatial variation in heat generation, which leads to spatial variation in heat generation, which leads to spatial gradients in the local permittivity and conductivity, which are acted upon by the electric field to induce a bulk fluid flow. The time-averaged velocity ⟨u_ETE⟩ is [30]

$$\begin{array}{c}\hfill \langle u_{\mathit{ETE}}\rangle =\frac{\ln \left(2\frac{a_1}{a_2}\right)-1}{2{\pi }^{4}k{\eta }_m{a}_1}\frac{{∊}_m{\sigma }_m{V_0}^4}{r^3}\left(1-\frac{2\theta }{\pi }\right)\prod \left(\omega \right)\hfill \\ \hfill \text{with}\prod \left(\omega \right)=\frac{\alpha -\beta }{1+{\left(\omega {\tau }_m\right)}^2}-\frac{\alpha }{2}\hfill \end{array}$$ (2)

where η_m is the media viscosity, k is the media thermal conductivity, (r,θ) is the polar coordinate where the force is evaluated, τ_m the media relaxation time given as τ_m=ε_m/σ_m, α=−0.4% K⁻¹ and β=2% K⁻¹ [30]. The factor Π does not vary over the range of frequencies we apply for our medium conductivity and has a constant value of −0.022.

The ACEO and ETE velocities sum to give a global net EHD velocity ⟨u_EHD⟩ that is converted to a force ⟨u_EHD⟩ acting on the growth cone via the ellipsoidal friction factor at steady state regime [40].

$$\langle F_{\mathit{EHD}}\rangle =f.\langle u_{\mathit{EHD}}\rangle =f.(\langle u_{\mathit{ACEO}}\rangle +\langle u_{\mathit{ETE}}\rangle )$$ (3)

where

$$f=\frac{4\pi {\eta }_m{a}_1}{\ln \left(2\frac{a_1}{a_2}\right)-1}$$

The third force is the DEP force. Using the same approach as Castellarnau [41], for an oblate spheroid in a co-planar electrode configuration, we extrapolate the n-th order of the DEP force acting on the growth cone is given as

$$\langle F_{\mathit{DEP}}\rangle =\frac{32}{3}{a}_1{a}_2{a}_3{∊}_m\frac{{V_0}^2}{d^3}e-\frac{\pi r}{d}Re\left[\mathit{CMF}\right(\omega \left)\right]$$

With

$$Re\left[\mathit{CMF}\right(\omega \left)\right]=\sum _{i=1}^3\frac{1}{3}\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{n{\epsilon }_m^{\ast }+A_i(n+1)({\epsilon }_p^{\ast }-{\epsilon }_m^{\ast })}$$ (4)

where d is the distance between the electrodes (in our setup d=15 μm), A_i is a component of the depolarization factor along any one of the three axes of the ellipsoid, and are the complex permittivities of the inner and of the outer compartment of the i layer, respectively and n the order of the multipole. The Clausius-Mossotti factor (CMF) captures the frequency dependence of the force [42] and is represented for a wide range of frequency and for several media conductivity on Fig S3. The dielectric properties of each layer were extracted from literature for actin [43], neuron cytoplasm and membrane [44]. Since the field strength varies greatly over the growth cone dimensions, we consider higher order moments of the Clausius-Mossotti factor (Fig S3b) as introduced by Jones and Washizu (1994) up to n=4. We find that the contribution to the overall DEP force of these higher-order multipoles is much smaller (~10⁵ times smaller) than that of the classical dipole contribution. These higher-order forces, as our results and literature [45, 46] have shown, repel the object and so add constructively to the DEP force, and thus are consistent with our findings that the DEP force is larger than the EHD forces at our operating conditions. Moreover, this model does not take into account deviations in the DEP force due to proximity of the growth cone with the glass surface. However, Lynch et al. [47] measured the DEP force of red blood cells attached to a glass surface and found that the forces were in good agreement with the classical core-shell isolated-particle model. We can therefore assume the same behavior for growth cones in our system.

Since all forces are frequency and voltage dependent, we plot the relative magnitude of induced EHD and DEP forces across a range of frequencies and voltage amplitudes (Fig 3b) and the absolute values of those forces are plotted on Fig S4. DEP forces and EDH flow both act cooperatively to repulse the growth cone from the electrodes. The resulting model provides robust information about trends and order of magnitudes of the forces exerted on the growth cone. The EHD Force has an almost-constant response across the 200 kHz – 1 MHz frequency range, whereas the DEP force magnitude is strongly frequency dependent (Fig S3b). We find that the DEP force is larger than EHD forces at low voltages ($\widetilde{<}$ 2.70 V_p-p) where heating is minimal. In terms of frequency, EHD becomes more significant at frequencies above ~250 kHz because the magnitude of the CMF of the growth cone (and thus the DEP force) decreases at f > 100 kHz.

Examining our axon blockage data (Fig 2b), we find that lower frequencies (f < 250 kHz) resulted in the smallest axon lengths, and is where the DEP/EHD ratio is largest (Fig 3b). Similarly, the model shows a decrease in the magnitude of the DEP force at higher frequencies (f > 250 kHz), while experimentally we observed increasing axon lengths—and thus smaller electrokinetic effect—when raising frequencies. Moreover, the model shows that the DEP/EHD ratio decreases with increasing voltage at a given frequency, while the experiments show increasing axon length with increasing voltage at all frequencies except 100 kHz. Interestingly, this lowest frequency may correspond to the peak in the DEP/EHD versus frequency plot (Fig 3b), where the DEP force is stronger than EHD over a large voltage range. Thus, the trends in our quantitative axonal length data (Fig 2b) are most consistent with a mechanism whereby the developing axon is acted upon by a DEP force. With our model and the values of the parameters, we found that the maximum DEP force that is exerted on the growth is ~66 pN (Fig S4), which is in the same order of magnitude of the pulling force exerted by the growth cone of spinal commissural neuron axons in vitro, and the force exerted by Netrin-1 to cause growth cone attraction [48].

We stress that our AC electrokinetic model is not definitive, but provides insight into the potential process that drives inhibition of axonal growth from high-strength AC electric fields. Alternative mechanisms could act intracellularly, such as through field-induced actin polarization [49, 50], and are an intriguing avenue for future research.

Axon diodes: Axon-lock system triggered by AC fields

We next sought to exploit the dynamic nature of electrokinetic axon blocking to enable unidirectional growth of axons, and thus the creation of an axon diode. The axon diode uses two sets of electrodes that act like gates in a lock to enable axons from only one side to grow across (Fig 4a). The device is a three-microchamber chip, arranged as an equilateral triangle, with each microchamber having its own inlet and outlet reservoirs (Fig 4b) that interface with 6 wells for solution transfer (Fig 4c). Each microchamber is connected to the other one through microchannels in which only the axons can grow (height ~ 3 μm). Each microchannel has two axon `gates' formed by placing two sets of electrodes (ground-AC-ground), at each end of the microchannel (Fig 4b).

Fig. 4.

(a) Side-view schematic of axon diode. (b–c) Images of axon diode chip showing three microchambers and electrodes.

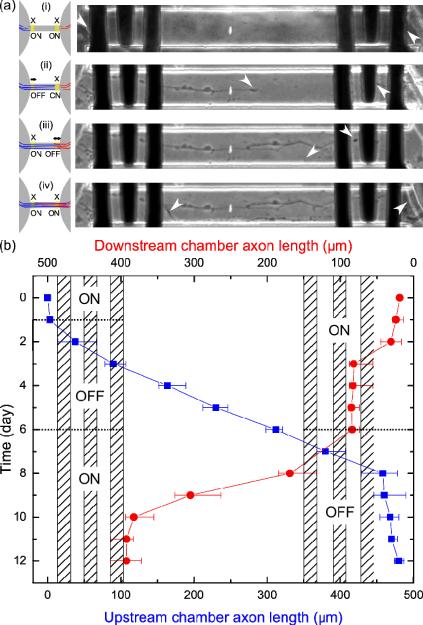
To create an axon diode, the gates that connect each pair of microchambers are opened and closed in a dynamic manner. When its AC voltage is turned off, the gate is open and the axons are free to grow beyond the electrodes. When the AC signal is turned on, the gate is closed and the axons cannot proceed across the gate. The parameters of the AC signal applied to close a gate are set to f = 100 kHz and V = 3 V _p-p, as these were found to be most effective at blocking neurite outgrowth (Fig 2b).

We demonstrated the diode functionality by first plating neurons in each of the three microchambers with the gates initially closed (the AC voltage is applied) (Fig 5a–i). After 24 hours, one of the two gates in a microchannel are opened (the AC voltage is switched off), allowing axons from one microchamber, which we will term `upstream' microchamber, to extend axons into the microchannel (Fig 5 a–ii), while axons in the opposite `downstream' microchamber, remain blocked by the closed gate. The directionality of the neuronal connection is defined by which gate is opened first, with axons passing only from upstream to downstream microchambers. Once axons have extended beyond the open gate, the state of the two gates is reversed: the initially open gate is closed and the previously closed gate is opened (Fig 5a–iii). In doing so, upstream axons in the microchannel will extend beyond the second gate and establish connections with the downstrean neuron population. Since the first gate is now closed, axons from the downstrean microchamber are unable to migrate to the upstream microchamber and will be trapped in the microchannels or remain in the downstream microchamber. Finally, both gates are closed to prevent any further axons from migrating through the microchannel (Fig 5a–iv). The lengths of axons (n=12) from upstream to downstream microchambers have been measured during this process (Fig 5b). It can be seen that the axon did not pass across the activated electrodes as long as the field was turned on. Moreover, the growth cone did not turn back from the activated electrodes (standard deviation of the growth cone medium position diminished with time). When the gate opened, the axon growth process continued at a rate of 42 ± 7 μm / day which is significantly slower (relative error of 41 %) compared with the observed growth rate in the middle of the channel (72 ± 10 μm / day). This could be explained by the time for the growth cone to explore the surface that was previously inaccessible because of the electric field. Finally, the downstream axon stays in front of the upstream gate without passing through once that gate is turned on. We call this specific spatio-temporal application of the electrokinetic axon blockage the “axon-lock system”.

Fig. 5.

(a): Schematic (left) and phase images (right) of the axon-lock system where growth cones are pinpointed by an oriented white arrow. The middle of the channel is highlighted by a white spot. (i) Both gates closed, no axons enter microchannel. (ii) Left gate opened, and a single axon enters from the left. (iii) Left gate closed and right gate opened. (iv) Once the first axon passes completely beyond the gate, both gates are closed. (b) Measured lengths of axons migrating from the upstream microchamber (blue) and the downstream microchamber (red) along with the activation timing of the left and right gates.

Formation of directional neuronal networks

Next, using our axon-lock system, we demonstrate the construction of functional axon diodes. Axon diodes have been developed and used in vitro to mimic the directionality of neuronal path guidance in vivo. Directionality is critical for regenerating axons to create proper connections after peripheral nerve injury and during development [51]. A few in vitro systems are capable of creating directional connections. Taylor et al. extended their initial microfluidic system to create auto-synapses [52] and Peyrin et al. modified the same initial system to create mechanical constraints on growing axons to induce directional growth [53]. Feinerman et al. patterned a chain of triangles of adhesive protein to permit axon passage in only one direction and create an axon diode [11]. AC electrokinetic effects have the advantage of reconfigurability because the electric field can be turned on and off at will. Thus, the capacity to dynamically lock or release the growth of a developing axon has exciting potential for the creation of neuronal networks. In particular, selective growth of axons in neural guidance conduits could improve routing of axons to their targets and prevent mis-sprouting of axons and inappropriate innervation.

To generate neural networks using multiple axon diodes, we dynamically opened and closed electrode gates to direct axons such that chamber `A' was connected in one direction with chamber `B', and chamber `B' was connected in one direction with chamber `C', whereas chamber `C' was not connected in either direction to chamber `A' (Fig 6a).

Fig. 6.

(a) Fluorescent false-colored image of a 12 DIV neuronal network configured by the axon-lock system. The plain arrows represent the direction of the diode. (b) Action potential recording, showing the stimulation signal (black) and the downstream recorded signals (colored). (c) False-colored fluorescent images of Oregon Green BAPTA 1-stained neurons when stimulating each sub-population of neurons in turn (denoted by +KCl). Scale bar is 50 μm

We first examined the functionality of axons that passed through an active gate to verify that the AC electric field does not damage the axons' ability to generate and propagate action potentials (APs). To make action potential measurements, we re-purposed the gate electrodes as stimulating and recording electrodes to monitor AP propagation in axons that passed through the diode. The first set of electrodes was used as stimulating electrodes and the second set as recording electrodes.

Fig 6b shows action potential readings from a set of axons that had passed through one of the axon-locks. When each stimulating pulse was applied, an AP was recorded further along an axon that passed through the entire diode, establishing that the axon-lock system does not interfere with AP generation or propagation.

We then determined whether the synapses of the directional network were active. We used Oregon Green BAPTA 1 staining to visualize Ca⁺⁺ fluxes elicited when action potentials were induced with KCl addition. KCl stimulation was confined to a single microchamber by selectively pressurizing the other outer reservoirs (Fig S6). When KCl was added to chamber `A', depolarization was observed in all three chambers (Fig 6c, left), whereas addition of KCl to chamber `B' only elicited Ca⁺⁺ oscillations in chambers `B' and `C' (Fig 6c, middle), and addition of KCl to chamber `C' only induced oscillations in chamber `C' (Fig 6c, right). These results demonstrate that chamber `A' was connected to chamber `B' and to chamber `C' (Fig 6c, left), and further that functional synapses were able to transfer signals from neurons originating in chamber `A' to those in chamber `C', via chamber B. Additionally, the observation that stimulating chamber `B' induces Ca⁺⁺ oscillations in chamber `C' (Fig 6c, middle) but stimulating chamber `C' does not induce Ca⁺⁺ oscillations in chamber `B' (Fig 6c, right) demonstrates that the two chambers are directionally connected by the axon diode Overall, these results demonstrate the ability to create directionally connected networks of hippocampal neurons in our axon-lock system.

Conclusions

In this study, we determined that AC electrokinetic forces can influence axonal growth. Using a platform that constrains axonal growth to one dimension, we showed that AC electrokinetic forces are capable of stopping the axonal growth of rat hippocampal neurons.

Comparison of quantitative experiments and modelling pointed to dielectrophoresis as the causative force. We then introduced the concept of dynamic construction of neuronal networks by an axon-lock system that uses axon diodes to induce directional growth of axons from one chamber to another, and showed that axons that pass through axon lock are viable and capable of action potential propagation. The dynamic nature of axon diodes opens up a number of applications ranging from development neuroscience to peripheral nerve injury regenerative devices.

Materials and methods

Microfabrication of electrokinetic devices and preparation for neuron plating

The microfluidic chip was fabricated on a 150-mm glass wafer. Following a standard photolithography step, a 10/100 nm Ti/Au bi-layer was e-beam deposited and a lift-off in acetone revealed the electrodes. The wafer was then diesawed to obtain individual chips. The microchannels comprise two types of components: high channels (100 μm) for cell injection and shallow channels (3 μm in height) for axon growth. They were molded from a SU-8 (Microchem) master that was fabricated with a two-step lithography process with thin (SU-8 2005) thick (SU8-2050) resists. Microchannels were then molded with degassed and cured PDMS (9:1 mass ratio with curing agent, Sylgard 184, Dow Corning). We then used plastic masters as future molds for our final PDMS replicates [54]. The microgrooves were manually aligned under a binocular after air plasma exposure (2 minutes) and immersion in methanol (5 minutes) [55, 27]. The assembled chip was cured at 100 °C for 30 minutes.

Two different microfluidic chips were constructed in this way. The first (Fig 1) was a two-compartment chip made of rectangular microchannels (length: 4000 μm; width: 500 μm; height: 100 μm) separated by arrays of microgrooves (length: 450 μm; width: 5 μm; height: 3 μm). The second chip (Fig 4) was a three-compartment chip made of 5-mm punched inlet and outlet reservoirs connected to three microchambers (diameter: 500 μm, height: 100 μm) placed in an equilateral triangle. Each reservoir was connected to the other through microchannels (length: 450 μm; width: 50 μm; height: 3 μm). The microchannels were coated with 0.1 mg/mL poly-l-lysine (Sigma Aldrich) for 24 hours in an incubator. The channels were then rinsed 3 times with deionized (DI) water and coated with 20 ug/mL laminin (Sigma Aldrich) for 2 hours. The channels were washed again 3 times with DI water and washed and filled 3 times with Neurobasal-B27 containing 2 mM glutamine and 100 U/ml penicillin/streptomycin (hippocampal culture medium). The microfluidic chips were placed in an incubator until use.

Dissection and cell culture

All animal work was approved by the MIT Committee of Animal Care and Division of Comparative Medicine, and abided by institutional, state, and federal guidelines for animal welfare. Hippocampi were harvested from E18 Sprague Dawley rats (Charles River Laboratories,), and digested in ice-cold Hank's balanced salt solution (HBSS), buffered with 10mM HEPES, pH 7.3. The tissue was digested by a 30 min incubation in 2 ml of HEPES buffered HBSS containing 20 U/ml of papain (Worthington Biochem.), 1 mM EDTA and 1 mM L-cysteine. Next, the tissue was rinsed three times with 8 ml of hippocampal culture medium. The cells were gently triturated in 1 ml of hippocampal culture medium, counted with a hemocytometer, and flowed into the device. The cells were maintained at 37 C, 5% CO2.

Neuron seeding in device

Before seeding, the reservoir of the microfluidic chip was emptied without removing the media from the microchannel. For each inlet reservoir, 4 μL of high density (> 8 10⁶ cells/mL) dissociated neuron solution was placed near the entrance of the microchannel. The chip was returned to the incubator for 5 minutes in order to let the neurons adhere on the coated glass and the seeding process was repeated 3 times to achieve a high cell density. At the end, the input and output reservoir were quickly filled with hippocampal culture medium and chips were returned to incubator.

Neuron transfection

24 hours after plating, neurons were transfected with a tubulin-GFP baculovirus (Tubulin-GFP Bacmam 2.0 virus, Life Technologies) in a ratio 2 uL of virus for 10⁴ cells, as indicated by the distributor. Cells were then imaged in fluorescence after 16 hours of incubation.

Image acquisition

Images were acquired with an Axiovert 200M (Zeiss) fitted with a cooled CCD camera LaVision ImagerQE (LaVision) and a automated stage Ludl MAC 5000 (Ludl). The microscope was controlled with Metamorph software (Molecular Devices) and images were analysed using ImageJ and Matlab (The Mathworks) software.

In vitro platform to apply AC electric signals inside the incubator

AC signals were applied to the microelectrodes via a custom platform that was placed inside the incubator (Fig S5). The microfluidic chips were aligned and inserted into a Zero Insertion Force (ZIF) [55] connector that was linked to an Arduino homemade printed-circuit-board stack. The stack was composed of 3 boards, a master Arduino board, a direct digital synthesis (DDS)-generated AC signal board, and a routing board. The DDS board (based on the DDS-60 Daughtercard, Midnight Design Solution) was able to generate an AC signal in the range of 0–60 MHz and 0–10 V_p-p. The routing board (using an ADG333ABR switch, Analog Devices and 74HC595 shift registers, Texas Instruments) was able to reroute and maintain the AC signal to one or more electrodes. A Raspberry Pi minicomputer, which was connected to the Arduino by USB, piloted the entire stack. A web server was installed on the Rasberry Pi so that the frequency and the voltage for each electrode could be remotely changed via a web browser in real time. More details of the platform are given in the supplementary information.

Axon length measurements

All the grooves were photographed under epifluorescence and the length of the axon was measured with Matlab. The imaging algorithm consists of first enhancing contrast and brightness, then binarizing the image (threshold value manually optimized for each image), then applying a Hough transformation and finally measuring the gap between the channel edge and the end of the axon. For each voltage and frequency, we defined the standardized axon length as the ratio of the distance between the observed axon length (AL on Fig 2a) and the distance between the edge of the channel and the first electrode (DCE on Fig 2b). For the axon-lock system, the axon lengths were measured with the same algorithm than previously. When the growth cone was hidden by the electrodes, the position was assumed to be the middle of the electrode itself with an error of the electrode width.

Neuronal network stimulation

The neurons were stained with Oregon green BAPTA1 (Life Technologies) for 1 hour and washed with medium. To stimulate only one sub-population, 20 uL of a 90 mM KCl solution was injected in the inlet of one microchamber only. The reservoirs of the other population of the neurons were filled with 50 uL of medium each, thus creating a pressure differential between chambers to prevent KCl from flowing out of the injected microchamber. The details of this fluidic flow compartmentalization are given in supplementary information.

Action potential recording

Action potentials were recorded through the microelectrodes themselves in the axon-lock triangle chip. Microelectrodes from the same microchannel were connected as stimulation and as recording electrodes via the ZIF module. A pulse generator (TTi) was linked to a current converter (Isolator-10, Axon Instruments) then to the stimulation electrodes. The recording electrodes were linked to a lock-in amplifier (×10⁴ gain, ISO-80, World Precision Instruments) and to a PC oscilloscope (PicoScope, PC oscilloscope software). The signals were then exported into Matlab and temporally synchronized.

Statistical analysis

For axon stoppage analysis, differences were addressed by an unpaired Student's t-test from two independent experiments in which each experimental condition was performed in duplicate. For all analysis: *p-value < 0.05; **p-value < 0.01; ***p-value < 0.001.