Systems Biology of Complex Symptom Profiles: Capturing Interactivity across Behavior, Brain and Immune Regulation

Abstract

As our thinking about the basic principles of biology and medicine continue to evolve, the importance of context and regulatory interaction is becoming increasingly obvious. Biochemical and physiological components do not exist in isolation but instead are part of a tightly integrated network of interacting elements that ensure robustness and support the emergence of complex behavior. This integration permeates all levels of biology from gene regulation, to immune cell signaling, to coordinated patterns of neuronal activity and the resulting psychosocial interaction. Systems biology is an emerging branch of science that sits as a translational catalyst at the interface of the life and computational sciences. While there is no universally accepted definition of systems biology, we attempt to provide an overview of some the basic unifying concepts and current efforts in the field as they apply to illnesses where brain and subsequent behavior are a chief component, for example autism, schizophrenia, depression, and others. Methods in this field currently constitute a broad mosaic that stretches across multiple scales of biology and physiological compartments. While this work by no means constitutes an exhaustive list of all these methods, this work highlights the principal sub-disciplines presently driving the field as well as future directions of progress.

1. Introduction

The prevalence of behavioral and psychiatric disorders is increasing, and with it the cost to society. Currently, 5.4 million Americans have Alzheimer’s disease requiring $200 billion in care, with the prevalence of this disease expected to double by 2050 (Alzheimer’s Association, 2012). Autism now affects 1 in 88 children (Wingate et al., 2012) at an estimated annual cost of $60 billion (Järbrink and Knapp, 2001). An even more poorly understood illness, Chronic Fatigue Syndrome/ myalgic encephalopathy (CFS/ME), is estimated to affect 800,000 Americans and cost the US economy approximately $9.1 billion in lost productivity and up to $24 billion dollars in health care expenditures annually (Jason et al., 2008). Clearly, the individual suffering, loss of social function, and economic cost caused by these conditions present a significant societal burden, however resolution of these illnesses is anything but simple. In a clinical setting, the classification of behavioral and psychiatric disorders remains one of the foremost challenges (Bousman and Everall, 2011). Individuals with the same disorder often present with a broad constellation of symptoms. Likewise individuals presenting with the same symptom profile may be suffering from disparate diseases. This biological complexity creates significant challenges for standard illness classification frameworks such as the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV) (American Psychiatric Assoc., 1994) and the International Classification of Diseases (ICD-10) (World Health Org., 1992). Discovery of the molecular features that underlie these pathologies is desperately needed however in many if not most cases no single marker or identifiable lesion has been found that reliably supports screening and diagnosis of these conditions.

Reductionist approaches have and continue to serve us well on several fronts however the very breadth of symptoms and their inter-dependency pose significant challenges to this piece-wise approach. In illnesses where dysfunction spans across several of the body’s main systems the issue of breadth of coverage is critical if we are to examine markers in the proper biological context. The rise of “omic” research (genomic, proteomic, metabolomic etc…) has lead to a rapid increase in our ability to collect and store much more comprehensive snapshots of biological processes. Indeed more data can now be collected on a single process in a year, than has been gathered over the course of scientific history (Chuang, Hofree and Ideker, 2010). Yet despite the growing mass of data describing genotypic variation, transcription, translation, and enzymatic biochemistry, little is known of how these elements give rise to disease and their behavioral symptoms. Clearly breadth is not sufficient and it may well be perceived as overwhelming by most, leaving us data rich and knowledge poor. However is omic data as high-dimensional as it appears? Biological markers are not expressed independently but instead manifest according to patterns that arise at least in part from the critical property of robust design.

A first contributor to biological robustness is partial redundancy of the components themselves. For example genes with overlapping functions will be able to compensate for one another. A second source of robustness has its origin in the interactions linking components with distinct but complementary functions. These interactions are dictated by the structure of the overarching regulatory network (Barabási et al., 2011). At a given point in time, the end result is that the number of fundamental processes regulating the changes observed in broad sets of markers will typically be much smaller than the list of parts. Feala et al., (2012) estimate that the number of controllers in a typical biological network will be less than 10% of the total regulatory targets. Importantly, this active subset in a much larger network will change over time giving rise to complex dynamic behavior (Hanel et al., 2012). Understanding these system-wide relationships, how they evolve over time and the emergent behaviors they support is essential if we are to formulate and test clinical hypotheses in any but the simplest of pathologies. This is the aim of systems biology as we define it in this work. With this in mind, our aim in this review was not to be inclusive, but rather to provide a representative overview of the various dimensions of systems biology and the challenges faced with an emphasis on applications in the realm of behavioral medicine.

2. Interaction: the connective fabric of biology and emergent behavior

The nature of biology is that of a holistic system. Like words in a language, the actions and effects of biological components are dependent on the context within which they occur. Systems biology in its simplest form can be described as an integrative science. Fundamentally it is directed at the identification of organizing principles that govern the context-specific emergence of function from the interactions that occur between constituent parts (Broderick and Rubin, 2006; Chuang, Hofree and Ideker, 2010). Our current understanding suggests that many of these principles appear to be conserved across scales of biology. An important and popular example is the small-world or scale-free topology of biological networks whereby the number of highly connected nodes decreases according to a power law. This typically results in sparsely connected networks that are governed by a small number of highly influential nodes. This pattern of interactivity is a defining feature of network architecture; one that reaches from the regulation of genes within a cell to the social interaction between individuals (Barabási, 2009). Indeed this applies broadly to network nodes representing the concentration of an individual mRNA species to the activity an individual cell phone subscriber and where associations between nodes can represent a chemical bond or a telephone conversation. This pattern of interactivity is a defining feature of network architecture; one that reaches from the regulation of genes within a cell to the social interaction between individuals (Barabási, 2009). It is important at this point to distinguish clearly between scale-free topology of anatomical and biochemical association networks and scale invariance with respect to temporal dynamics. These are essentially independent properties that must not be mutually confused. Interestingly it is now well established that intrinsic brain activity is arrhythmic and manifests scale-free temporal dynamics, where the contribution or power at a specific frequency decreases according to a power law at rest (Ciuciu et al., 2012). Deviation from this bias towards persistent long-term associations occurs during certain tasks but has also been observed at rest in conditions such as Alzheimer’s disease (Maxim et al., 2005).

With interactivity being so pervasive in biology it follows that a physiological disturbance cannot be fully understood in terms of localized components alone, but must also be realized in the context of the entire system. The vast majority of research in the area of behavioral and psychiatric disorders has focused on the brain. However, to effectively address the growing epidemic of “brain diseases” the metabolic, nutritional, and environmental influences that exert effects on the brain must also be considered (Hyman, 2007). It is from this very interactivity and its fluidity in biology that complex behavior emerges. The first obvious examples of this phenomenon can be found in the generation of organ structure and function from cell interaction during embryological development (Setty et al., 2011). This is not limited to the emergence of structure but extends to complex dynamic behavior. Indeed it can be shown mathematically that interactivity between even a small number of components can lead to the existence of multiple regulatory modes. Examples of complex dynamic behavior include the emergent and context-dependent selection of cell fate (Hanel et al., 2012), immune cell population dynamics (Almeida et al., 2012) and bifurcation in immune response (Reynolds et al., 2006). Perhaps more complex still is the concept of emergence of consciousness from the large-scale interaction of neurons (Greenfield and Collins, 2005). Though we are increasingly aware of the relevance of these properties of biological systems to illness pathology their use in practice remains limited and focused primarily on the integration of elements that co-exist at the same scale, within specific physiological compartments and systems.

3. Linking parts within scales and compartments of biology

A natural consequence of interactivity and regulation is that biological markers will present in specific patterns of expression that reflect the underlying recruitment and instantiation of an active regulatory structure. Examining the structure of these co-expression patterns has the potential to enhance our diagnostic resolution by enforcing context (de la Fuente A., 2010). This was recognized early in the social and behavioral sciences where extensions of classical statistics were applied to identify symptom constructs. For example Schröder et al. (1992) applied common factor analysis (CFA) to isolate and describe patterns of symptom association and their relation to neuro-imaging results in the establishment of sub-types of schizophrenia. More recently similar statistical methods have been used to identify constructs that distinguish patient sub-groups based on clinical presentation in a complex and poorly understood illness: chronic fatigue syndrome/ myalgic encephalomyelitis (CFS/ME) (Aslakson et al., 2006). Methods such as these that are based on singular value decomposition (SVD) essentially capture patterns of linear correlation between markers that exist at distinct levels of resolution and that can be superimposed to reconstruct the original data. Another related method, independent component analysis (ICA), was applied recently to construct inter-regional networks of brain activity serving as cerebral correlates of cognitive deficits in schizophrenia (Nygård et al., 2012). Association networks can also be constructed using more sophisticated and sensitive measures of similarity. For example information theoretic measures such as mutual information (MI) have been used to map non-linear associations between transcription factors and their mediators in the context of oncogenesis (Sumazin et al., 2011) and schizophrenia (Torkamani et al., 2010). An important caveat to this remains the multiplicity of active regulatory configurations that can lead to similar if not identical symptom presentation. It might be more appropriate therefore to refer to families of biomarker association networks and the properties these networks might share when discussing diagnostic applications or illness fingerprinting.

Though informative, the analysis of associations existing at rest does not make it possible to infer the direction of flow of regulatory information. To make use of such cause and effect relationships one can first draw on known biochemical dependencies such as those encoded in pathway databases like Ingenuity Pathway (Ingenuity Systems, www.ingenuity.com) or the NCI/Nature Pathway Interaction Database (PID) (Schaefer et al., 2009). For example Guo et al. (2010) used regulatory associations documented in the Ingenuity Pathways database to identified feed-forward elements in the microRNA-transcription factor (miRNA-TF) regulatory networks that were enriched in schizophrenia. The limiting factor in this approach remains coverage of the actual regulatory network of interest. It is safe to say that a significant number of regulatory associations remain to be discovered. In these cases temporal precedence must be used as a proxy to infer causality. Empirical linear autoregressive models have been applied to describe the evolution of EEG recordings from patients in a minimally conscious state (MCS) from patients with severe neurocognitive disorders (SND) that show some signs of awareness (Pollonini et al., 2010). More recently the same approach has been applied to study the directed networks that emerge in traumatic brain injury (TBI)(Leon-Carrion et al., 2012). These examples represent an important step forward in that we are now examining illness in the context of altered regulatory circuitry. More ambitious and detailed models are now being constructed that extend the identification of the type of input-output associations to more complex model forms such as formal Hill kinetics (Schmidt et al., 2011). Similarly, added regulatory structure is also being applied to this analysis by re-organizing these networks into assemblies of formal feedback and feed-forward control elements or motifs (Alon, 2007). With few exceptions, the majority of these analyses is conducted at the level of the genome, the proteome or between coarsely defined anatomical compartments. Moreover, topological architecture is being compared between networks constructed for a priori defined clinical groups with the aim being one of identifying illness-specific network features such as local changes in connectivity and the appearance of hub transcripts or proteins (Fuite, Vernon and Broderick, 2008a). This is a static analysis and there is little if any direct consideration of the subsequent dynamical modes supporting the emergence and exacerbation of symptoms, be they sustained or episodic in illnesses such as multiple sclerosis (Vergelli et al., 2001) and chronic fatigue syndrome (Aschbacher et al., 2012). Even directed graphs that encode this dynamic information are still compared in terms of their structure, for example motif frequency, rather than the dynamics of information flow that they describe (Frankenstein, Alon and Cohen, 2006).

4. From connectivity to complex behavior and alternate homeostatic programs

Connectivity drives emergent behavior and vice versa. Indeed even without information regarding the kinetics of the processes in question Mendoza and Xenarios (2006) have shown that number and type of stable homeostatic states available to a regulatory system can be identified based on connectivity alone. This is an important result linking network structure to dynamic behavior. It is especially meaningful when one considers that the availability of dynamic parameters values describing in vivo kinetics is extremely limited however we have a much more substantial knowledge base of the regulatory connectivity from basic biochemistry and physiology (vasculature, innervation patterns, etc…). This analysis has been applied to understanding the dynamic properties of T helper (Th) cell immune regulation and is now being applied at a broader scale by our team to investigate the multi-stability of immune-neuroendocrine interaction as it applies to Gulf War Illness (GWI), building on previous work (Broderick et al., 2011). Though connectivity is a powerful determinant of system dynamics, the kinetic parameters are still required if one is to resolve behavior at so-called saddle points that separate regions of homeostatic stability (attractors). At the very least relative rates are required to obtain a realistic description of the transition states and the paths available to recover from a disturbance or migrate to an alternate homeostasis.

Such formal rate equation models were pioneered in early work on the dynamics of immune response to infection, giving rise to a new field called mathematical immunology (Perelson, 2002). Cytokines interact with neurons (Dustin, 2012) to produce a constellation of signs and symptoms known as ’sickness behavior’ (Tracey, 2010). Inflammation itself affects multiple behaviors including sleep, pain, appetite, cognition (learning and memory, or even chemo-brain), and plays a significant role in diseases such as depression, autism and schizophrenia (Khansari and Sperlagh, 2012). A basic understanding of the complex inner-workings of the immune system moves us one step closer to integrating sickness behavior symptoms with what we know about physiology. Using a simple continuous model of effector cell, self and pathogen interactions, Segal and Bar-Or (1999) captured key fundamental properties of immune feedback dynamics and demonstrated how multiple, potentially conflicting, goals are managed over time to favor the most appropriate response to a pathogen. More recently Reynolds et al. (2006) include immune response to cortisol to describe the effects of ant-inflammatory signaling on the geometry of stable homeostatic attractors during infection and sepsis. Investigations such as these draw on a rich foundation of differential equation methodology where the molecules, cells, etc… are distributed in space as an uninterrupted field and the changes in their concentration across time are assumed continuous in nature. While this framework is a powerful tool for exploring biological complexity there are limits to representing biology as dilute, well-mixed continuous systems. These large-scale population dynamics emerge from the collective behavior of individual cells enacting, what has been modeled by some as a discrete decisional logic. For example, spatial competition for antigen presentation in the thymus was demonstrated to be a key factor in T cell development using a discrete model (Efroni, Harel and Cohen, 2007). Only by using mathematical agents to represent individual cells was it possible to identify this effect; a result that was hiding beyond the resolution of continuous field equations. The property of emergent complexity is especially relevant to understanding the physiological mechanisms and events that drive the appearance of behavior. As with T cell development the emergence of human behavioral patterns will almost certainly lie beyond the grasp of field equations.

In much the same way, populations of neurons and their activity have been summarized over regions of the basal ganglia-thalamocortical system by sets of mean field equations and have successfully captured many of the key electrophysiological correlates of Parkinson’s disease (PD) (van Albada et al., 2009). More recently still, a lumped model of the continuous dynamics of superficial and deep pyramidal cells in the neocortex has been used to explore stable dynamic modes in this system and rapid transition (bifurcation) between these modes as they might relate to the onset of epileptic episodes (Visser et al., 2012). However, because of the nature of the brain as a biological compartment (tissue versus circulatory media) and the availability of spatial as well as temporal data, dynamic models of this organ have evolved methodologically along a different path. Perceived from the outset as computational engine, models of the brain have been inspired strongly by electrical circuit theory. Networks of logical switches, oscillators and other circuit-like components represented as nonlinear rate equations were used in early models to describe neural dynamics such as those responsible for odor recognition and discrimination (Skarda and Freeman, 1987). Increases in high-performance computing power have made it possible to create large-scale networks of interacting discrete agents. For example, Kumar et al., (2011) simulated a network of 3,000 leaky-integrate-and-fire (LIF) model neurons, of which 1,000 excitatory neurons were assigned to the sub-thalamic nucleus (STN) population and the remaining 2,000 inhibitory neurons to the globus pallidus external (GPe) population, and realistically modeled the effects of dopamine loss in Parkinson’s disease on firing rate.

Models of these systems extend inward to the level of intracellular pathway networks, biochemical reaction kinetics and even molecular binding; exchanging broad but coarse coverage of cellular processes for very detailed but focused descriptions. At one end of the spectrum, large-scale methods are being developed to recover organism-wide metabolic regulatory reaction kinetics (Schmidt et al., 2011) from experimental data. At the opposing end of the spectrum, Craddock et al., (2012) used computational molecular dynamics combined with pharmacokinetic modeling to describe β-amyloid-induced alterations in zinc concentration and its potential effects on neuronal microtubule stability and the molecular dynamics of cognition in Alzheimer’s disease. Similarly detailed representations of immune signal transduction have been constructed showing the importance of the cytoskeleton in sequestering excess inhibitors, therefore regulating steady-state and feedback behavior of NF-κB activation (Pogson et al., 2008). A more comprehensive review of these different methods and their application to models of the immune system is presented in Kim et al. (2009).

5. Bridging across systems from molecule to phenotype

Though informative in their own right, these model systems remain for the most part separated by scale in both time and space (Ridgway et al., 2006) as well as by physiological compartments. Efforts to integrate vertically across scales from molecular biology to function and behavior face several challenges and remain limited at present. Genetic studies have shown that functionally related causative genes support similar clinical phenotypes, be it through expression of a single protein or an entire network of protein interactions. On this basis, integrative methods are being developed to consolidate human protein–protein interactions, disease phenotype similarities, and known gene–phenotype associations to elucidate the genotype-phenotype interplay. One such method, the prioritization and complex elucidation (PRINCE) algorithm, works to infer novel causal genes via a prioritization function, which integrates protein-protein interaction (PPI) information with a disease similarity metric to score the strength-of-association of proteins with a disease of interest (Vanunu et al., 2010). Application of this algorithm to Alzheimer’s disease inferred the major genes previously associated with the disease and several novel candidates not previously identified, suggesting avenues for further research. This class of methods allows for the identification of causative genes from pre-existing phenotypic information. However, the reverse is also true. Using a bi-random walk (BiRW) algorithm, phenotype-gene association network patterns in circular bigraph format have been utilized to yield the associations between disease phenotypes and genes (Xie, Hwang and Kuang, 2012). This method identifies and quantifies an enrichment of “behavior”, “synaptic transmission”, and “transmission of nerve impulse” by the causative genes of psychiatric diseases. Similarly, in a bioinformatics-based study metadata was collected from genome-wide association studies (GWAS), genome-wide copy number variation (CNV) studies, linkage analyses, low-scale genetic association studies, expression profiling and other low-scale experimental studies and used in a scoring and ranking approach to select a core ensemble of 434 high-confidence genes associated with Autism (Xu et al., 2012). The genes identified corresponded to pathways that included neuroactive ligand-receptor interaction, synapse transmission and axon guidance; highly relevant processes. Methods such as these are capable of linking the genome to the phenome, identifying potential causal genes for specific phenotypic symptoms where previous genetic information is unknown. Conversely, where the genetic markers for behavioral and psychiatric disorders are known these methods serve to identify key areas where causal genes may affect behavior, albeit the resolution is vague. Though useful in supporting biomarker discovery, these methods produce relatively coarse associative models. Because of their generic structure and the significant gap in biological scale separating gene from behavioral trait these methods yield little of the illness mechanisms and how best to intervene therapeutically. To gain a more complete insight into how genetic changes promote illness mechanisms and affect brain function another level of understanding must be integrated into the framework.

A truly integrative model would adhere to the hierarchy and structure of biology and formally represent the intermediate levels of regulation. Vertical integration is an exercise in abstraction or progressive coarse-graining and can be directed from known biology in a top-down fashion or inferred from data using basic organizing principles in a bottom-up approach (Figure 1). The practical implications of this integration are several-fold. First, the concurrent profiling of marker expression across levels of biology provides an internal validation for each of these assays. For example, strong correlation linking changes in protein expression with changes in transcript abundance would help support the validity of both measurements. Second, a study of the path linking immune cell transcript abundance with changes in cell populations, the expression of signaling proteins and ultimately symptom exacerbation might help one distinguish between processes central to an illness and those that might be more peripheral or secondary. Useful as it may be, the true underlying biological structure is often unknown and must be inferred. A host of statistical methods have evolved from network theory with the objective of indentifying modular assemblies with potential functional bias in large-scale co-expression networks. Based primarily on the distribution of network connections, Winden et al. (2011) recently identified gene co-expression modules in transcriptomic data from an animal model of temporal node epilepsy. One of these module contained genes upregulated in the epileptogenic region, including multiple epileptogenicity candidate genes, and was found to be involved the protection of glial cells against oxidative stress. We have applied a similar approach, adjusting formally for network size and prior probability of occurrence, to isolate functionally related immune signaling modules from cytokine profiling of patients with chronic fatigue syndrome (Broderick et al., 2010) (Figure 2). More recently efforts have been made to enrich these data driven methods by guiding the search for functional modules using motifs based on feed-forward and feedback control elements. Yeger-Lotem et al., (2004) found that cellular regulation in yeast may be governed by assemblies of small network motifs, in particular a two-protein motif defining a mixed-feedback loop involving both transcription– regulation and protein-protein interaction. Methods such as these introduce structure in the form of generic features and remain exploratory in nature. That is after all their intended role. Unfortunately these purely data-driven methods continue to be used even when knowledge of the underlying physiology and biochemistry exists.

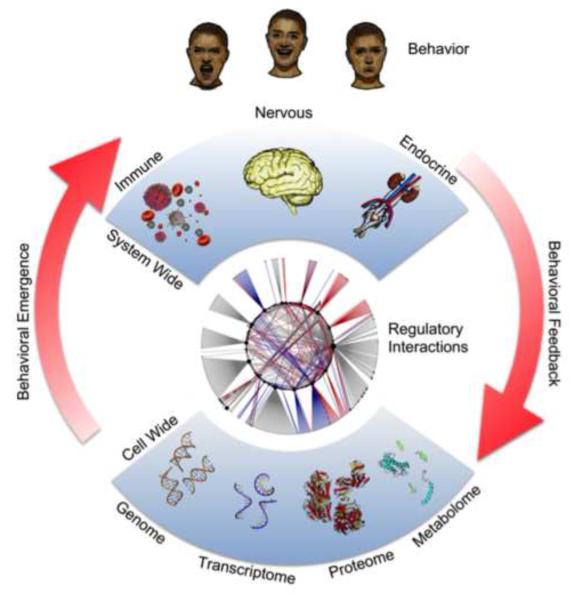
Figure 1. A science of integration and emergence.

High throughput technologies are now available to produce comprehensive molecular profiles of the genome, the transcriptome, the proteome and the metabolome (metabolites). Systems biology provides a framework to model and infer molecular interactions and their organization into pathways, and subsequently into signaling networks at the cellular, tissue and organ system levels (endocrine, brain/nervous and immune systems). Interactions among these body systems give rise to phenotypic changes that correlate with observable pathologies (top) such as sickness behavior, depression, etc…. Likewise, modifications to behavior as a result of external stressors can modulate the balance of cellular and intracellular signaling.

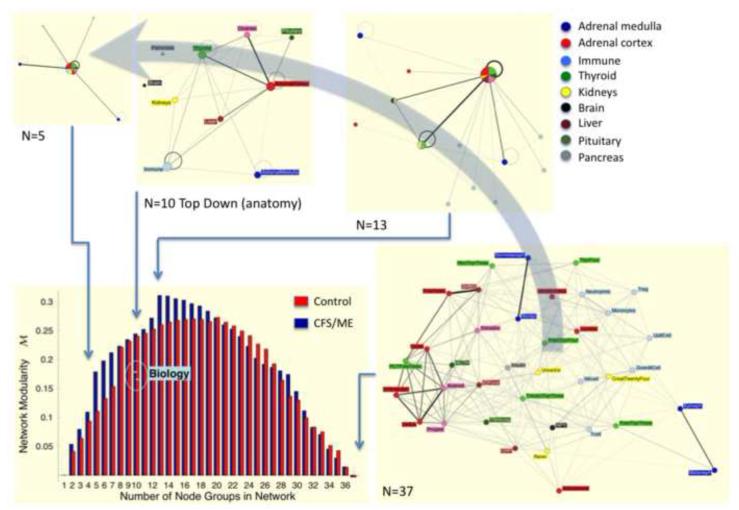
Figure 2. Emergent and fluid modularity of biology.

Networks were constructed for linking N=37 markers of immune and neuroendocrine status in patients with chronic fatigue syndrome (CFS) and in healthy control subjects. Inferring coherent modules on the basis of network topology (network modularity M) (Broderick et al., 2010), cohesive modules were found that formed coarse networks of N=13 and N=5 aggregate nodes in CFS. In contrast only one coarse network of N=8 aggregate nodes was found in healthy controls. This aligned with a top-down aggregation of N=10 organ-specific nodes based on known anatomical annotation (Fuite, Vernon and Broderick, 2008a, b).

In many cases a first step in exploiting existing knowledge of the system may consist of simply enforcing anatomical structure. Honey et al. (2007) proposed a computational approach that relates the features of measured spontaneous cortical dynamics to the underlying anatomical connectivity. Their model captured nonlinear neuronal dynamics spanning large-scale interregional connections of the macaque neocortex, yielding new insight into structure-function relations at multiple temporal scales in the brain. In a similar fashion Efroni et al. (2007) developed a novel approach for the analysis of gene expression data that exploits our current knowledge of pathway topology and biochemical function. The latter estimate discrete activation states for individual genes from expression data and project these onto the regulatory logic of known pathways to produce a relative estimate of pathway activation. Translation into discrete logic is a powerful avenue now being used by many as a framework for traversing scale and incorporating additional biological structure in computational models.

As processes are aggregated at higher scales a model inevitably extends beyond the limits of the biological components initially under consideration to adjacent interacting systems. Integrating vertically requires concurrent horizontal integration. For example the nervous, endocrine and immune system are tightly coupled and constitute what many have called an overarching regulatory super-system (Figure 1). The hypothalamic-pituitary-adrenal (HPA) axis occupies a central position at the interface of these three systems. It is one of the principal and better-known information trunks by which behavior mediates biology (Antoni et al., 2006) and biology mediates behavior (Kelley and Dantzer, 2011). Although connectivity of this axis across systems is well-documented mathematical models of the HPA axis continue to focus solely on the feedback of cortisol to the hypothalamus and pituitary (Vinther, Andersen and Ottesen, 2011). Simple models such as these have nonetheless served to demonstrate the potential association between altered HPA regulatory dynamics and behavioral pathology in chronic fatigue syndrome and fibromyalgia (Aschbacher et al., 2012). As the HPA axis does not operate in isolation, aggregating the effects of interaction with adjacent systems, in particular the immune system, leads to the loss of mechanistic understanding and limits insight into specific avenues for intervention to only general and abstract statements. In addition, important aspects of the dynamic behavior are obscured. In our current efforts we are finding that the inclusion of even coarse models of the adjacent immune and sex hormone axis reveal stable modes of homeostatic regulation with characteristics that align with chronic symptoms in Gulf War Illness and chronic fatigue syndrome. Even the inclusion of glucocorticoid receptor dynamics has shown alignment of clinical data with bifurcation of HPA dynamics in PTSD and depression (Sriram, Rodriguez-Fernandez and Doyle, 2012). In fairness, a limiting factor in these efforts is our recent and still growing knowledge of the avenues of interaction between the brain and the immune and endocrine systems (Dustin, 2012). Certainly the availability of kinetic parameters describing these interactions will continue to be limited even as our understanding of the molecular biochemistry of signaling grows. This is the case for many if not the majority of human physiological processes at this time.

6. Synopsis and future perspectives

Unlocking the fundamental molecular mechanisms of measureable symptoms can propel our understanding of the brain-body connection in its entirety, and potentially offer a substantial advance in the diagnosis and treatment of behavioral and psychiatric disorders. While, many of these diseases are highly heritable, progress in decisively determining the genetic changes associated with specific symptoms has been slow. A major obstacle has been the inherent difficulty in identifying behavioral measures that are concisely defined, yet compatible with high-throughput genetic association studies. Yet this is not the only difficulty. As our understanding of biology continues to grow, so does our appreciation of the critical importance of context, interaction and the dynamics of regulation. The behavior that emerges from these regulatory interactions can only be observed by collecting the parts to create a broader more comprehensive view. Systems biology is by definition an integrative science. It seeks to uncover the basic organizing principles that direct the emergence of complex behavior from the interactions between component parts. This integration is not without its challenges as biological processes are separated across multiple scales of time and spatial resolution as well as across physiological compartments. For these reasons, most current models encompass small to moderate scales of physiology. Moreover the association of molecular and cellular models with organism level pathologies is done almost solely through stratification of patient cohorts and their assignment to discrete clinical classes. Indeed in clinical psychiatry, the most daunting challenge consists in the translation of system-wide relationships amongst biological components into cognitive behavior, where cognition itself is a property that emerges from indirectly linked organizational hierarchies that can and do evolve over time (Greenfield and Collins, 2005). Nonetheless these models and the methods with which they are constructed continue to evolve, as does our computing power. This progress will only be further catalyzed by the development of frameworks that combine multiple mathematical formalisms, each optimally supporting the level of biological knowledge available to describe a specific sub-system at a specific scale (Figure 3). Formal methods exist to aggregate the collective dynamics of populations of discrete cells into local field equations producing significant gains in computational tractability (Raghib, Levin and Kevrekidis, 2010). Such field equations can be further abstracted and expressed as a time-delayed regulatory logic (Mendoza and Xenarios, 2006) to reconcile intracellular signaling, metabolic, and regulatory networks across time scales (Lee et al., 2008). The drive to seamlessly combine these and other methods into a comprehensive but computationally efficient framework is perhaps the biggest challenge in the field currently but may also deliver the largest rewards (Dada and Mendes, 2011).

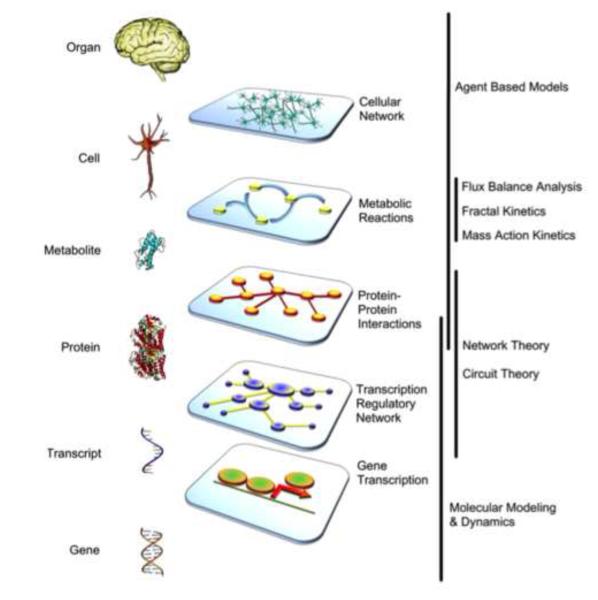
Figure 3. A mosaic of model forms.

As biological processes build upon one another from the molecular to the cellular, from organs to organ systems, the degree of resolution necessary to support a realistic representation of the biology will be optimally supported by different mathematical formalisms. These will range from molecular dynamics models (MD), which capture chemical binding with atomic resolution, to agent-based models (ABM) where mathematical automata can be used to represent populations of cells (e.g. embryogenesis) or even populations of individuals (epidemiological simulations).

Research Highlight.

Integrative systems biology is becoming a key enabler in understanding complex illnesses of the nervous, endocrine and immune systems where context is critical.