Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2012 Nov 15;7(2):405–416. doi: 10.1038/ismej.2012.117

Strain-specific functional and numerical responses are required to evaluate impacts on predator–prey dynamics

Zhou Yang 1,2,*, Chris D Lowe 2, Will Crowther 2, Andy Fenton 2, Phillip C Watts 2, David J S Montagnes 2,*
PMCID: PMC3555124  PMID: 23151643

Abstract

We use strains recently collected from the field to establish cultures; then, through laboratory studies we investigate how among strain variation in protozoan ingestion and growth rates influences population dynamics and intraspecific competition. We focused on the impact of changing temperature because of its well-established effects on protozoan rates and its ecological relevance, from daily fluctuations to climate change. We show, first, that there is considerable inter-strain variability in thermal sensitivity of maximum growth rate, revealing distinct differences among multiple strains of our model species Oxyrrhis marina. We then intensively examined two representative strains that exhibit distinctly different thermal responses and parameterised the influence of temperature on their functional and numerical responses. Finally, we assessed how these responses alter predator–prey population dynamics. We do this first considering a standard approach, which assumes that functional and numerical responses are directly coupled, and then compare these results with a novel framework that incorporates both functional and numerical responses in a fully parameterised model. We conclude that: (i) including functional diversity of protozoa at the sub-species level will alter model predictions and (ii) including directly measured, independent functional and numerical responses in a model can provide a more realistic account of predator–prey dynamics.

Keywords: functional response, numerical response, model protozoa, Oxyrrhis marina, temperature

Introduction

Protozoa (phagotrophic microbial eukaryotes) are key components of terrestrial and aquatic ecosystems (Bonkowski, 2004; Calbet, 2008). Both in natural and experimental systems, protozoa respond rapidly to increases in prey abundance, with short-term increases in numbers composed of one or a few similar species that potentially drive predator–prey cycles (Montagnes, 1996; Begun et al., 2004). Furthermore, ambient temperature interacts with prey abundance to alter protozoan rate processes (for example, ingestion, growth, gross growth efficiency, predator–prey dynamics; see Weisse et al., 2002; Atkinson et al., 2003; Montagnes et al., 2003; Kimmance et al., 2006). This interaction will also alter predator–prey bloom dynamics. Finally, not only do protozoa exhibit species-specific responses, there are good indications that strain-specific responses occur and will significantly alter population dynamics. Thus, there is a need to assess the effects of prey, temperature and predator strain on protozoan population dynamics. Here we use the model protozoa Oxyrrhis marina (Montagnes et al., 2011) to address two fundamental, and we suggest inexorably linked, issues associated with improving protozoan population models: (i) the influence of temperature on strain-specific responses and its impact on population dynamics and (ii) the structure of population models that examine protozoan-based predator–prey dynamics. Both of these topics are expanded on below.

Intraspecific variation

Intraspecific variation has, to date, received insufficient attention with regards to community ecology, including predator–prey dynamics (Violle et al., 2012). Predicting natural population dynamics can be complicated by the presence of competing strains, each with a distinct phenotype (for example, growth rates, competitive abilities and thermal optima). Thus, model predictions based on the responses of single strains are likely to have limited relevance to many natural, multi-strain systems. However, despite the growing recognition of genetic and phenotypic variation between protozoan populations (for example, Weisse and Montagnes, 1998; Lowe et al., 2005, 2010; Gächter and Weisse, 2006), we are unaware of any explorations of how environmental perturbations, such as temperature shifts, alter population dynamics of phenotypically distinct strains of the same species or the outcome of competition between them.

Trait-based models are now beginning to provide a means to incorporate variation into natural dynamics (for example, Le Quéré et al., 2005; Bruggeman and Kooijman, 2007; Follows et al., 2007; Violle et al., 2012). This direction offers an assessment of taxonomic variation that may alter population structure, as one strain replaces another (for example, Parmesan, 2006; Carroll, 2007). To date, however, the exploration of models using multiple functional groups (represented by taxa) has primarily focused on autotrophic protist (that is, prey) responses, although there has been some exploration of variable predator responses (for example, Tirok et al., 2011). Here, we indicate that multiple strain responses naturally exist for our model predator species and then examine how they might alter population dynamics, both in isolation and under competition, by comparing two strains in detail. We do this using an approach that simultaneously evaluates both the functional and numerical responses of the predator and how they are affected by a single environmental variable (that is, temperature).

Functional and numerical responses

Typically, many modern day population and ecosystem models, although highly sophisticated, are ultimately based on the original Lotka–Volterra (LV) models developed nearly 100 years ago. In particular, these models (both the original versions and their modern day counterparts) make the assumption that the numerical response (predator growth rate vs prey abundance) is directly proportional to its functional response (ingestion rate vs prey abundance). Specifically, these models rely on an experimentally parameterised functional response and derive the numerical response by imposing a constant conversion efficiency on the functional response (see Turchin, 2003). Rarely is it recognised that functional and numerical responses can qualitatively differ in shape, reflecting a variable conversion efficiency with food concentration (for a detailed microbial-based review and analysis of this see Fenton et al., 2010). Further complicating the situation, models rarely appreciate that both functional and numerical responses can be uniquely altered by external factors (for example, temperature: Kimmance et al., 2006; Montagnes et al., 2008).

To illustrate the problems associated with the standard approach described above, consider the case where two predator populations (for example, strains of the same species) exhibited similar functional responses but have different numerical responses. Logic dictated by the LV-based approach (that is, directly basing the numerical response on the observed functional response, with a constant conversion efficiency) would suggest that the two strains respond similarly (that is, typically, in the absence of data, a single conversion efficiency would be applied to all strains of a single species); there is no scope in this framework to recognise and include the different numerical responses (which could result from variable conversion efficiency). In reality, as these two strains exhibit different numerical responses, following logic outlined by Tilman (1982), the strain with the lowest growth requirement for a limiting resource (that is, the one able to maintain positive growth at the lowest resource concentration) will have the competitive advantage. Here, we present a case where, under some conditions (that is, varying temperature), the functional responses of different strains are not significantly distinguishable, and following the above logic, this would imply no difference between the strains response to prey abundance. We then reveal how combining independently derived functional and numerical responses leads to a very different conclusion (that is, one strain drives the other to extinction).

Summary of direction

Initially, and critically, we illustrate the importance of this issue of strain variation by revealing that several naturally occurring strains of our model species differ in thermal sensitivities; temperature was chosen as an environmental treatment because of its well-established effect on microbial rates and its ecological relevance, from daily fluctuations to climate change. We then intensively focus on two strains that exhibit distinctly different thermal responses. For these two strains, we examine the influence of temperature on their functional and numerical responses. Finally, we consider how these responses alter predicted predator–prey population dynamics under two simulated scenarios: first, by exploring the standard LV-based approach of deriving the numerical response directly from the functional response, and second by applying a more flexible framework that explicitly incorporates independent functional and numerical responses in a fully parameterised model.

Materials and methods

Study organisms

The autotrophic flagellate Dunaliella primolecta, Butcher (CCAP, Dunstaffnage, Scotland) was maintained in 32 PSU (practical salinity units) artificial seawater (Ultramarine synthetic sea salt, UK) enriched with F/2 marine water enrichment solution (Sigma-Aldrich, Dorset, UK) and exposed to 24-h irradiance at ∼50 μmol photons m−2 s−1. We collected 10 strains of O. marina Dujardin (following methods outlined in Lowe et al., 2011b) that were maintained on D. primolecta (Table 1). Note although that two of these may, in fact, be a different species of Oxyrrhis; following recent work by Lowe et al., (2011a) strains 356_Mal01 and 30_Pos01 may be Oxyrrhis maritima.

Table 1. Strain designation and locations of isolation of O. marina.

Strain Location Country Lat Long
45_BOG01 (OB) Bogense Denmark 55° 34′ 14.16″ 10° 5′ 2.76″
39_NAP01 Naples Italy 40° 47′ 49.94″ 14° 11′ 53.88″
30_POS01 Posithonia Greece 37° 40′ 39.95″ 24° 03′08.79″
CCMP1788a St Maarten Caribbean 18° 1′ 40.80″ −63° 3′ 10.80″
44_PLY01 Plymouth UK 50° 21′ 47.52″ −4° 8′ 20.76″
34_BAR01 Barcelona Spain 41°23′44.97″ 2°12′34.97″
351_FAR01 (OF) Algarve Portugal 37° 1′ 1.1″ −7° 59′ 35.5″
82_KOR01b Kunsan Korea 35° 58′ 48.00″ 126° 41′ 60.00″
44_STA01 Scotland (E) UK 56° 20′ 31.56″ −2° 47′ 20.04″
356_Mal01 Bahar ic Caghaq Malta 35° 56′ 24.36″ 14° 27′ 23.40″
Open in a new tab
a

From the Provasoli–Guillard National Centre for Culture of Marine Phytoplankton, West Boothbay Harbour, ME, USA; Table 1.

b

Kindly provided by Hae Jin Jeong, School of Earth and Environmental Science College of Natural Sciences, Seoul National University, Korea.

Temperature responses across strains

Both O. marina and D. primolecta were maintained at 10 °C, 20 °C, 26 °C and 30±1 °C, in batch cultures under the conditions outlined above; for each temperature n=3. Before estimating O. marina growth rate, D. primolecta was acclimated (5 days) to the experimental conditions; O. marina was then inoculated into prey cultures and acclimated under the same constant conditions (3 days). Cultures (50 ml plastic tubes) were gently mixed to maintain cells in suspension, and D. primolecta abundance was maintained at levels that would result in maximum growth rates (that is, exponentially growing prey >5 × 105 ml−1; see Kimmance et al., 2006 and our Results section) by adding an excess of prey. Growth rate was calculated, over the exponential growth phase, as the slope of ln abundance vs time over 48 h (measured at 0, 24 and 48 h).

To test the hypothesis that variation between strains occurred in their temperature responses, two-way analysis of variance (α=0.05) was performed to test for strain–temperature interactions. Further post hoc tests to examine where differences occurred were not performed, as the purpose of this broad analysis was to indicate that variation exists; that is, to contextualise the need for further focused work, rather than to examine specific pairwise comparisons. The only exception to this was a t-test on two strains that are the focus of the remainder of this study (see Results section).

Temperature responses of two strains

The temperature response data (Figure 1) were used to select two strains that exhibited different responses at 20 °C and 26 °C (351_FAR01 and 45_BOG01, Figure 1, Table 1, henceforth abbreviated to OF and OB, respectively); these strains were chosen based on their unique attributes, rather than considering the wider geographical location they were isolated from, as it is likely that many protists (and specifically O. marina) are widely dispersed and the local environment will act as a selective force (for example, see Watts et al., 2011). They were studied in detail in batch cultures to: (1) evaluate if maximum growth rates or the functional response alone would be appropriate predictors of strain differences and (2) obtain parameterise responses to be incorporated into a predator–prey population model to further assess strain responses.

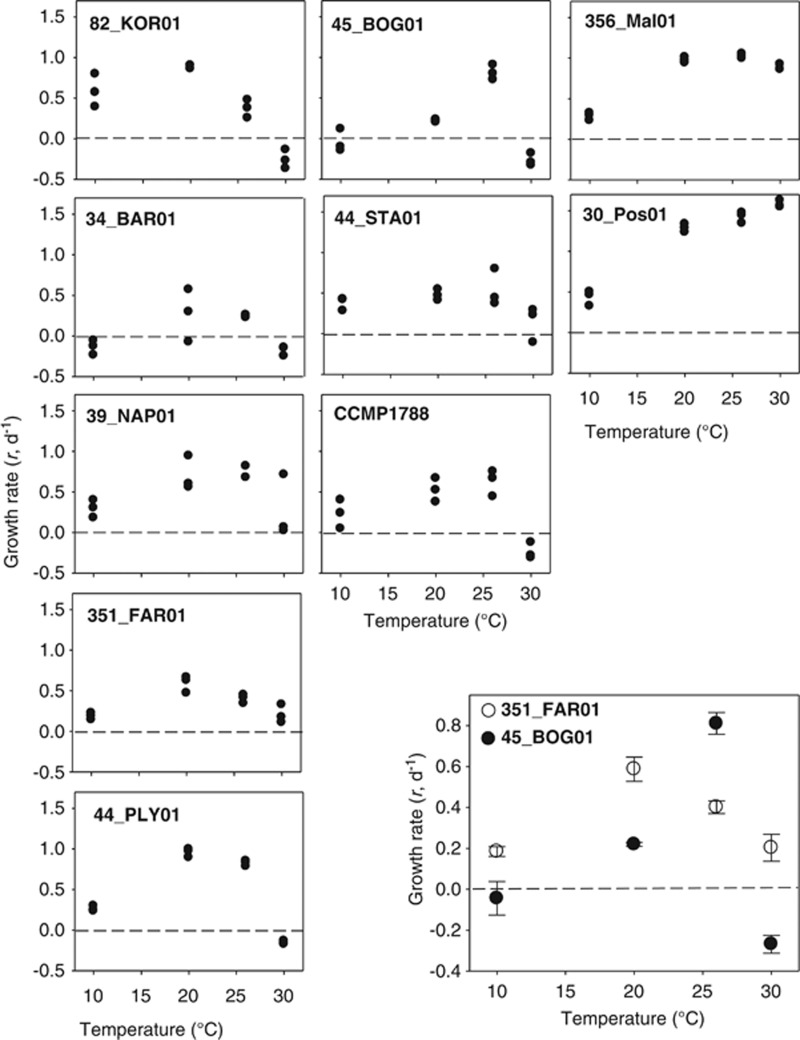
Figure 1.

Figure 1

Open in a new tab

Thermal responses: specific growth rate responses of 10 Oxyrrhis strains to four temperatures. See Table 1 for information on strains. The dashed horizontal line in each panel shows net zero growth. Three replicate measurements were made at each temperature (indicated by solid dots). The inset at the bottom right is provided as a comparison of two strains (OB, OF) that are used in later sections of this work; in this case mean estimates are presented, with error bars being 1 s.e.

D. primolecta growth response

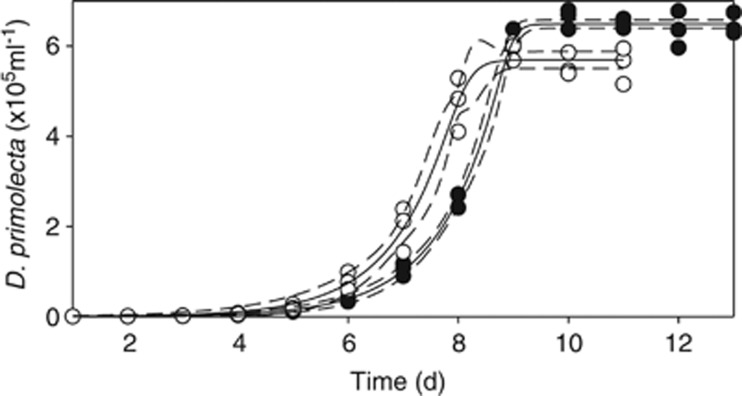
To fully parameterise the predator–prey model, logistic growth parameters for D. primolecta (that is, P, the prey) were determined at 20 °C and 26 °C. Triplicate cultures were maintained under the constant conditions described above, at 20 °C and 26 °C. Before experiments, cultures were acclimated (5 days); then change in population abundance was measured over 15 days. Theta-logistic growth curves (Equations 1 and 2; Sibly et al., 2005) were fit to the data, at each temperature, to determine the carrying capacity (K, prey ml−1), shape parameter (θ) and maximum growth rate (μ, day−1). Specifically, the solution of Equation (1) (that is, Equation 2) was fit to the responses of prey abundance (Pt) vs time (t), using the Marquardt–Levenberg algorithm (SigmaPlot, V 11, Systat Software Inc., San Jose, CA, USA) to obtain estimates of K, μ and θ (see Table 2).

Table 2. Parameters values, s.e., adjusted R2, and F- and P-values for equations predicting at 20 °C and 26 °C: D. primolecta theta-logistic growth Equation (1); functional responses Equation (3) for the two O. marina strains (OB, OF); and numerical responses Equation (4) for the two O. marina strains.

Parameters Value s.e. Adjusted R2 (F-value, P-value)
D. primolecta theta-logistic growth Equation (1)
 20 °C
  K (prey ml−1) 648 650 4520 0.997
  μ (day−1) 0.942 0.069 (4593, <0.0001)
  θ 9.62 5.46  
       
 26 °C
  K (prey ml−1) 569 070 9148 0.989
  μ (day−1) 0.963 0.165 (936, <0.0001)
  θ 5.84 7.37  
       
O. marina strain OB ingestion rate Equation (3)
 20 °C
  Imax (prey predator−1 day−1) 102 18.0 0.849
  k1 (prey ml−1) 378 130 122 630 (282, <0.0001)
       
 26 °C     0.873
  Imax (prey predator−1 day−1) 246 40.0 (458, <0.0001)
  k1 (prey ml−1) 339 740 167 580  
       
O. marina strain OF ingestion rate Equation (3)
 20 °C      
  Imax (prey predator−1 day−1) 317 46.0 0.849
  k1 (prey ml−1) 538 970 135 490 (4650, <0.0001)
       
 26 °C     0.873
  Imax (prey predator−1 day−1) 285 65.0 (302, <0.0001)
  k1 (prey ml−1) 437 280 167 580  
       
O. marina strain OB growth rate Equation (4)
 20 °C
  rmax (day−1) 0.50 0.07 0.600
  P′ (prey ml−1) 3850 1010 (35, <0.0001)
  k2 (prey ml−1) 7650 3020  
       
 26 °C     0.600
  rmax (day−1) 0.67 0.07 (35, <0.0001)
  P′ (prey ml−1) 1710 270  
  k2 (prey ml−1) 2160 640  
       
O. marina strain OF growth rate Equation (4)
 20 °C
  rmax (day−1) 0.80 0.06 0.700
  P′ (prey ml−1) 1810 400 (35, <0.0001)
  k2 (prey ml−1) 4440 1850  
       
 26 °C     0.700
  rmax (day−1) 0.50 0.05 (50, <0.0001)
  P′ (prey ml−1) 3420 550  
  k2 (prey ml−1) 5920 1460  
Open in a new tab
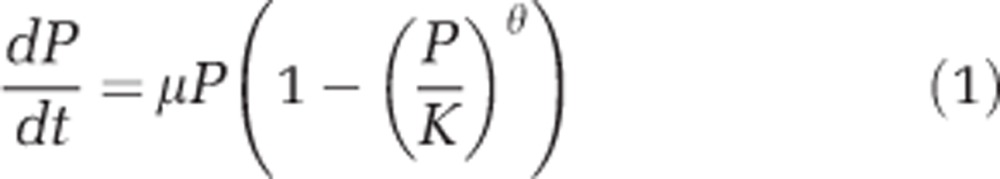graphic file with name ismej2012117e1.jpg
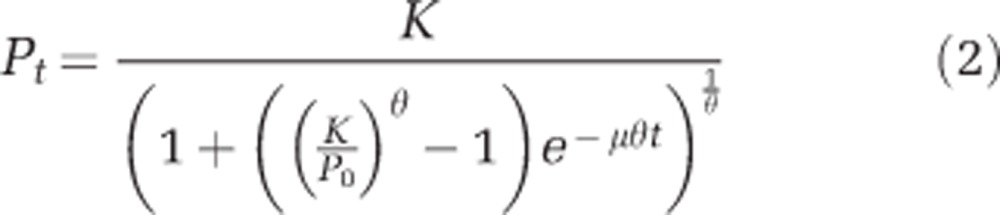graphic file with name ismej2012117e2.jpg

O. marina response to prey and temperature

O. marina was acclimated (2 days) to constant experimental prey levels (with more measurements at low levels; see Montagnes and Berges, 2004) at 20 °C and 26 °C, under the conditions described above (see D. primolecta growth response). Prey treatment levels ranged from near zero to where prey growth reached stationary phase (as determined experimentally, see Results section); such high levels of prey (similar to D. primolecta) can occur in coastal waters where O. marina exists (for example, Begun et al., 2004). Controls for prey growth, without O. marina, were conducted at constant prey and light levels, identical to the O. marina prey treatments. All cultures were maintained for 24 h at each temperature, after which prey and O. marina numbers were determined.

Ingestion rate of O. marina (prey predator−1 day−1) was determined from changes in prey abundance in control containers (without O. marina) compared with experimental containers (with predators), following well-established methods that account for changes in both predator and prey abundance over the incubation (for example, Heinbokel, 1978; Kimmance et al., 2006). Specific growth rate of O. marina (r, day−1) was determined as described above (Temperature responses across strains).

Developing response equations

Following standard practices for data that clearly follow a rectangular hyperbolic response (for example, Heinbokel, 1978; Berges et al., 1994; Montagnes et al., 2008), predator ingestion rate (I, prey predator−1 day−1) was modelled to vary with prey concentration (P, prey ml−1), following the Holling Type II function (Equation 3), where Imax and k1 are constants. Predator-specific growth rate (r, day−1) was modelled to follow a similar rectangular hyperbolic response (Equation 4), but with a non-zero intercept (P′, prey ml−1), assuming a basal metabolic rate, where rmax and k2 are constants with relevance to biological mechanisms (see Fenton et al., 2010).

graphic file with name ismej2012117e3.jpg
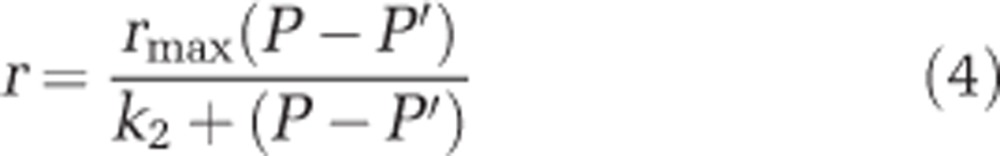graphic file with name ismej2012117e4.jpg

Equations 3 and 4, respectively, were fit to the numerical and functional response data, at each temperature, using the Marquardt–Levenberg algorithm, which is appropriate for such data (Berges et al., 1994). Adjusted R2 values for the responses, P- and F-statistics for the regression, and standard errors of the estimates are presented as indications of their goodness of fit. Comparisons of responses were performed using Bonferroni-corrected t-tests (Sokal and Rohlf, 1995) on response parameters. This was conducted by applying pooled standard errors obtained from the non-linear curve fitting (Table 2) and for determining the degrees of freedom the sample size was equal to the lowest values used in any comparison. For all tests α=0.05.

The influence of temperature on strain population dynamics

To explore the extent to which temperature-induced strain differences alter (i) population dynamics and (ii) competition between two O. marina strains, a model was constructed. Here we used the independent responses at each temperature (20 °C and 26 °C) for D. primolecta (P) and the two O. marina strains OF and OB (Table 1): D. primolecta grew following Equation 1 and was preyed upon by populations of the two strains of O. marina (OB, OF), based on their functional responses (Equation 3); O. marina (OB, OF) growth rates were prey dependent and were negative, because of starvation, below threshold levels (Equation 4). We applied an additive model of exploitative competition, such that each predator strain acted independently of the other, and the only interaction between predators was indirect, via the limiting prey resource. This is the simplest model of two consumers competing for an explicitly modelled resource and the most appropriate starting point in the absence of data to inform more sophisticated relationships. Equations (5, 6, 7) describe the model:

graphic file with name ismej2012117e5.jpg
graphic file with name ismej2012117e6.jpg
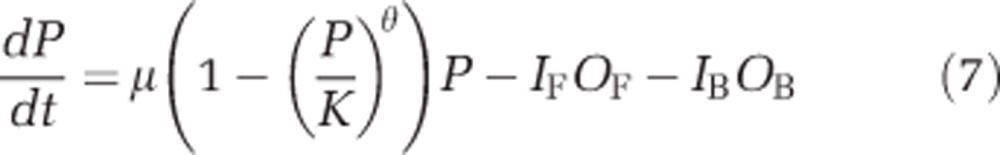graphic file with name ismej2012117e7.jpg

where OF and OB are the abundance of the two strains; rF and rB are the prey-dependent growth rates of the two strains Equation (4); IF and IB are the prey-dependent ingestion rates of the two strains Equation (3); P is prey abundance; μ is the specific growth rate of the prey; K is the prey carrying capacity; and θ is the shape parameter of the logistic growth curve Equation (1).

Results

Temperature responses across strains

Growth rates of O. marina strains ranged between −0.37 and 1.63 day−1, generally increasing with temperatures between 10 °C and 20 °C; at 10 °C and 30 °C growth was low or negative (Figure 1). There was significant variation between strains in their temperature responses (that is, significant interactions between temperature and strain; two-way analysis of variance, α=0.05), both quantitatively, in terms of maximum and minimum growth rates and temperatures of peak growth and qualitatively, in terms of the overall shapes of the growth responses with temperature (Figure 1). These data indicate substantial variation in the thermal growth responses of O. marina, sampled from a range of locations (Table 1). Recognising these differences in thermal responses, the remainder of this study focused on two example strains, 45_BOG01 and 351_FAR01 (OB and OF, respectively), which exhibited significantly different responses at 20 °C and 26 °C (t-test, α=0.05; inset, Figure 1).

D. primolecta logistic growth response

D. primolecta exhibited a theta-logistic growth response Equation (1) at 20 °C and 26 °C (Figure 2, Table 2). The carrying capacity was significantly higher at 20 °C, but neither growth rate (μ) nor θ were significantly affected by temperature (t-test, α=0.05).

Figure 2.

Figure 2

Open in a new tab

The theta-logistic growth curve of D. primolecta at 20 °C (•) and 26 °C (○). Points represent measurements. Lines represent the fit to the data following Equation (2); dashed lines represent the 95% confidence interval; for the parameters and their error estimates of this fit see Table 2.

O. marina functional and numerical responses

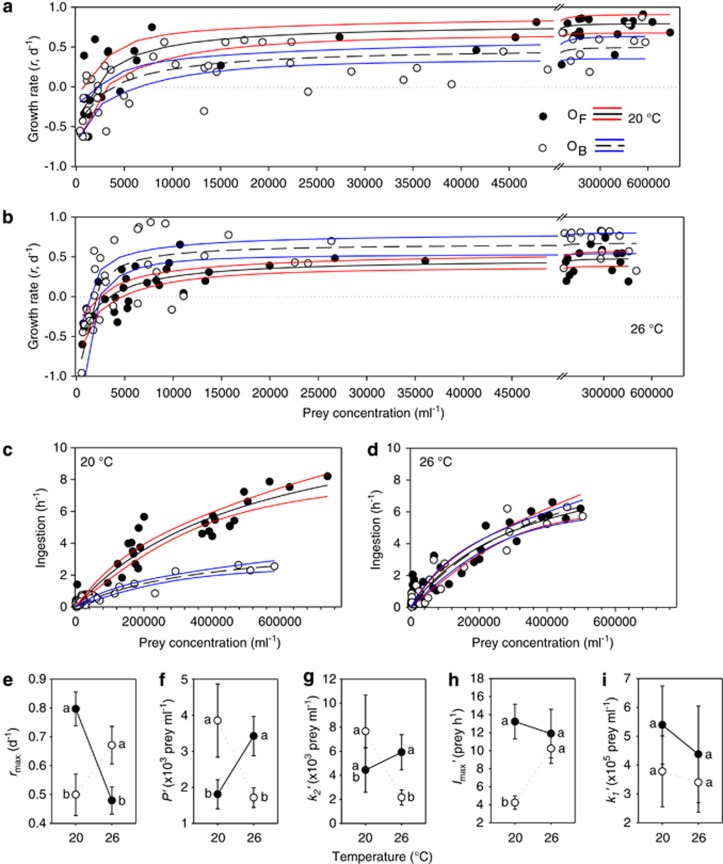
For both O. marina strains (OB, OF), ingestion followed a type II functional response, at both 20 °C and 26 °C, although neither reached saturation over the observed prey range at either temperature (Figures 3a and d). The functional responses of OF and OB were not significantly different at 26 °C, and these did not differ from the OF response at 20 °C. In contrast, the maximum ingestion rate for OB was significantly lower than that of all other treatments (Figures 3h and i). In all cases, the standard errors, P- and F-statistics for the regression, and adjusted R2 values indicate that Equation (3) was a very good representation of the data (Table 2).

Figure 3.

Figure 3

Open in a new tab

Numerical (a, b) and functional (c, d) responses of strains OF (∘) and OB (•) of O. marina. Points represent measurements. Solid and dashed lines on a–d represent the fit of Equation (3) (c, d) or Equation (4) (a, b) to the data. Coloured lines represent 95% confidence intervals of the fit line. For details of significance of the fit of the response and the parameters and their error estimates see Table 2. (e–i): parameter estimates (error bars=1 s.e.) for Equation (3) (h, i) and Equation (4) (e–g). Lines on e–i link measurements on the same strain. Symbols with the same letters (‘a', ‘b') indicate parameters that were not significantly different (see Materials and methods section).

For both OB and OF, growth followed a rectangular hyperbolic numerical response Equation (4) at 20 °C and 26 °C, with both strains approaching an asymptote at high prey levels, at both temperatures (Figures 3a and b). There were significant differences between the numerical response parameters for the two strains, at the two temperatures (Figures 3e–g). In terms of maximum growth rate and the threshold prey concentration, the two strains had virtually reversed responses at the two temperatures (Figures 3a–f). However, the k2-value Equation (4), reflecting the initial curvature of the response, did not follow this pattern (Figure 3g); the significant changes in k2 values imposed subtle (but as will be seen below important) changes to survival at low prey concentrations. The standard errors and adjusted R2 values indicate that Equation (4) was a good representation of the data (Table 2).

Model results

As indicated in the Introduction and Materials and methods Equations (5, 6, 7), we explored whether predator–prey dynamics would differ between stains. However, we first assessed how sensitive our predictions were to the modelling framework used, as the outcome of this analysis impacted our evaluation of strain differences.

If competition is evaluated following a standard LV-based approach (where the numerical response is derived from the functional response by assuming a constant conversion efficiency; Turchin 2003), it is apparent that at 20 °C, strain OF would outcompete strain OB; this is because OF has a significantly higher maximum ingestion rate, at all prey concentrations (Figures 3c and h), and therefore, because of the assumption of constant conversion efficiency, it also has a significantly higher growth rate. In contrast, at 26 °C, where there was no significant difference in the functional responses between OB and OF (Figures 3d, h and i), a competitive advantage of one strain would not be predicted by the functional response alone; rather it might be governed by strain differences in conversion efficiency, a parameter that we lack unless growth rate is also determined (see Fenton et al., 2010). We support this analysis based on visual observation of the functional responses by placing the functional responses into a Rosenzweig–MacArthur predator–prey model with constant assimilation efficiency and mortality rate (see online Supplement).

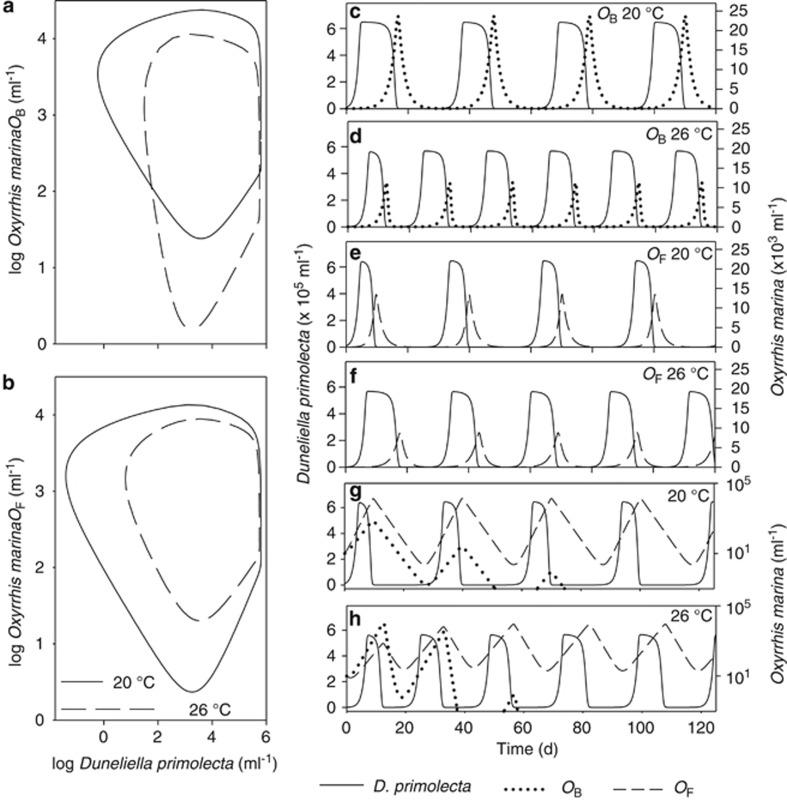
To reveal the importance of independently estimating predator growth rate across a range of prey abundances (that is, the numerical response), we then applied the Independent Response approach Equations (5, 6, 7), advocated by Fenton et al. (2010). When both the parameterised functional and numerical responses were included in the model Equations (3 and 4), stable predator–prey cycles occurred for strains OB and OF on their own at 20 °C and 26 °C (Figures 4a–f). The periods of both OB and OF cycles were ∼30 days at 20 °C and ∼20 days at 26 °C, respectively (Figures 4c–f). The highest maximum abundance of the predator occurred at 20 °C for OB, and the lowest maximum abundance occurred for OF at 26 °C. OF depressed prey ∼10 times lower than OB (Figures 4a and b) at both temperatures. Critically, temperature influenced the relationship between the predator and prey in unique ways (Figures 4a and b). Hence, temperature shifts, over the range examined, altered the quantitative dynamics (that is, peak-trough levels and periodicity) of the two strains in isolation.

Figure 4.

Figure 4

Open in a new tab

Model results for simulations with strains of O. marina (OF or OB, Table 1) and D. primolecta. (a, b) Phase plots for OB and OF, respectively. (c–f) Time-series for the two strains on their own with prey, at the two temperatures to illustrate period lengths and amplitudes. (g, h) Time-series for the two strains combined, at the two temperatures, to illustrate period lengths and amplitudes, the persistence of OF, and the rapid extinction of strain OB. Simulations for prey+one predator strain were initiated at a range of D. primolecta and O. marina abundances, all of which converged on single cycles (a, b). Simulations with prey+OB+OF also all converged on single predator–prey cycles, as OB became extinct; to illustrate this, time-series were presented that were initiated at 103 ml−1 D. primolecta and 103 ml−1 O. marina (g, h).

When the two strains were combined in the model OF survived, and OB became extinct at both temperatures (Figures 4g and h). This finding was robust over a wide range of combinations of initial predators and prey densities.

Discussion

This work combines an initial survey of naturally occurring strains (Table 1), the determination of functional and numerical responses, and application of a novel approach (see Fenton et al., 2010) to model formulation and parameterisation to illustrate how protozoan strain differences may alter the outcome of population models. From this we suggest that: (i) including functional diversity of protozoa at the sub-species (that is, strain) level can alter model predictions (and hence ecosystem dynamics where protozoa are important) and (ii) including directly measured, independent functional and numerical responses in models can provide a more realistic account of predator–prey dynamics.

Functional diversity

We found that strains of the model protozoa O. marina display variable growth rate responses to temperature and thus cannot be considered the same in an ecophysiological or modelling context (although it is possible that some of this variation is related to cryptic speciation within Oxyrrhis; Lowe et al., 2011a). O. marina has a global distribution, has been isolated from a wide range of locations (Lowe et al., 2010; Watts et al., 2011), and is used to parameterise a range of ecological models (reviewed by Davidson et al., 2011). Consequently, in terms of modelling protozoan population dynamics, our results suggest that the general application of parameters obtained from unspecified strains of this species (or poorly characterised species of the genus) would be inappropriate.

Our work supports the growing awareness of intraspecific variation in responses to environmental factors; for example, distinct thermal responses occur for isolates of the freshwater ciliate Urotricha farcta (Weisse and Montagnes, 1998), the globally distributed soil-ciliate Meseres corlissi (Gächter and Weisse, 2006) and the autotrophic flagellate Isochrysis galbana (Sayegh et al., 2007), and there are salinity–strain interactions for O. marina (Lowe et al., 2005). Accordingly, we recognise a need to quantify the impact of such strain differences using model systems; in the next section, we focus on two strains of O. marina to illustrate how this issue can be approached in a broader context.

Multiple predator responses

The magnitude of strain differences in the functional and numerical responses observed here are as great as those that can occur between different protozoan species (for example, Montagnes, 1996). It may seem that the scatter of our data is high, but it is typical for estimates of functional and numerical responses of protozoa (for example, Kimmance et al., 2006), and by performing many measurements across the prey range, especially with a focus on lower prey abundances, it is possible to obtain powerful, average estimates of parameters associated with the functional and numerical responses (Montagnes and Berges, 2004). Following this procedure, we have established functional and numerical responses that reveal significant differences in their parameters (Figure 3). A main implication from these data is that although simple parameters such as maximal growth rate may be useful and appropriate criteria for recognising strain diversity (Figure 1), they are unlikely to distinguish differences in a more dynamic, ecological context. Given the importance of temperature as a key environmental driver of ecological dynamics, we specifically explored its influence on strain dynamics.

Following predicted long-term increases (3–6 °C over the next century; Houghton, 2005), temperature of small water bodies, such as ponds and shallow estuaries will rise; specifically, the latter is where prey that are suitable food for O. marina occur at levels up to 106–107 ml−1, and O. marina can be abundant (>100 ml−1), occasionally reaching 105 ml−1 (Johnson et al., 2003; Begun et al., 2004). Furthermore, the intensity and frequency of short-term temperature variations because of global warming will increase (Houghton, 2005), and short-term warming events caused by other environmental processes, ranging from the North Atlantic Oscillation to seasonal effects, will alter the temperature of isolated water bodies (for example, Gerten and Adrian, 2000). Consequently, environments where taxa, such as our model protozoa, are abundant will be affected by temperature change. In a tri-trophic model (flagellate-ciliate-Daphnia), Montagnes et al. (2008) proposed that short-term temperature fluctuations would impact carbon flux in small fresh water bodies; in fact, they suggested that small temperature shifts could virtually block trophic coupling. Similarly, in our system, for both O. marina strains there were temperature-induced differences in the predator–prey dynamics (that is, changes in amplitude and frequency of cycles, Figure 3) that would manifest themselves in changes in carbon-flux through the food web. However, as is the case for most models, Montagnes et al. (2008) only parameterised their tri-trophic model with responses from single strains, and it is clear from our work that data from a single strain of predator may be inappropriate. Clearly, adding other species to the model or using parameters from a different species could alter the outcome, but equally the addition of other strains or including a single but different strain (as indicated in a general sense by Figure 1 and illustrated in detail by Figure 3) would alter predictions of carbon-flux, possibly stabilising the system and reducing the impact of temperature changes but alternatively extending the range of responses and increasing instability. A recent, novel approach to modelling (to date, focused on phytoplankton as prey and some predators) is to include a suite of responses, making models more robust; that is, the broad-ranged multi-species or multi-functional group approach (Le Quéré et al., 2005; Bruggeman and Kooijman, 2007; Follows et al., 2007; Tirok et al., 2011). Our data on this one predator–prey model system support the need to extend this approach to the protozoan component of such models.

Including functional and numerical responses in models

This study strongly supports the need to independently parameterise functional and numerical responses, rather than extrapolating the numerical response from the functional response, as is typically done in most models based on the original LV structure (Turchin, 2003). First, the functional responses for the two strains (Figures 3c and d) have a distinctly different shape from the numerical response (Figures 3a and b), providing strong evidence for a change in conversion efficiency with prey abundance; this discredits inferences that the numerical response should be based directly on the functional response (for detailed proof of these concepts see Fenton et al., 2010). Second, the thermal sensitivity of the numerical responses differed between strains, especially at low prey levels (Figures 3a, b).

Protozoa, such as O. marina, also lend themselves to act as model organisms for the wider evaluation of competition; for example, microcosm experiments can empirically assess competitive abilities and the subsequent change in biodiversity in response to temperature (for example, Petchey et al., 1999). However, employing laboratory techniques to empirically examine competition between morphologically identical strains, as we have here, is less tractable, as they cannot be distinguished. Consequently, we used a theoretical approach, parameterised from lab experiments, to assess how a temperature shift might alter dynamics when two strains are placed in identical environments.

OB and OF, independently, produce distinct predator–prey cycles at 20 °C and 26 °C, demonstrating that both would survive independently across a landscape over that temperature range. As indicated in the Results section (and in our online Supplement), if a traditional modelling approach (based only on the functional responses and a constant conversion efficiency) was applied to our data, we would predict that OF had the competitive advantage at 20 °C; following the same logic we could not identify a competitive advantage for either at 26 °C (that is, where the functional responses were not significantly different, Figures 3d, h and i). However, in our Independent Response model, when the two strains were combined using independently derived functional and numerical responses, OB was driven to extinction over days to weeks (Figures 4g and h), regardless of the ambient temperature.

The competitive ability of OF over OB is also apparent in the phase plots (Figure 4a and b), as OF drives the prey an order of magnitude lower than OB. These results derive from different abilities to survive at low prey levels, revealed by the numerical responses, which have different shapes (Figures 3f and g). In general, this principle of comparing numerical responses to explain the outcome of competition is not new: the species (or strain) with the lowest growth requirement for a limiting resource will have the competitive advantage (Tilman, 1982). However, as most population and ecosystem models rely on functional responses to establish numerical responses (by applying a constant conversion efficiency), and as shown above, the functional and numerical responses can differ in shape, there is a fundamental flaw in this logic. Consequently, we argue that, when possible, both functional and numerical responses should be obtained independently, or alternatively a well-parameterised variable conversion efficiency should be included (see Fenton et al., 2010; Minter et al., 2011; Montagnes and Fenton, 2012).

Conclusions

To encompass potential variation in ecosystem models, there is a growing effort to include response diversity, within trophic categories (for example, Le Quéré et al., 2005; Follows et al., 2007; Violle et al., 2012). Using a model protozoa, we support a growing concern that predator strain differences may need to be considered; we do this by first revealing the potential scope of the issue, across strains (Figure 1) and then providing a detailed example of how differences might alter predator–prey population dynamics. Clearly, such variation in responses requires further investigation before sweeping generalities are made, and this should ultimately include comparing model predictions with microcosm incubations (once means are developed to distinguish between virtually identical clones). However, the responses we present here are indicative of the potential influences of strain differences, and from our work, which builds on studies that recognise strain differences, we recommend that such response variation continues to be considered. We also recommend that a range of predator responses be included in trait-based models and that where only a single predator is included, sensitivity analysis be applied to embrace potential variation due that observed for strains.

Of more general concern, we have indicated that the standard method of modelling, using only a functional response and assuming a constant conversion efficiency to obtain the numerical response, could result in different conclusions from models where independently derived functional and numerical responses are included (for example, when assimilation is allowed to vary within the model; see Fenton et al., 2010). This supports the conclusions of Kimmance et al. (2006) who indicated, also using O. marina, that temperature-dependent gross growth efficiency has non-intuitive interactions with prey abundance. Consequently, we strongly recommend that modelling efforts on population dynamics of microbial eukaryotes, at the very least, consider variable assimilation efficiency and that laboratory studies should be directed at parameterising such responses.

Acknowledgments

This research was partially supported by the National Natural Science Foundation of China (31270504) and The Priority Academic Program Development of Jiangsu Higher Education Institutions, both awarded to ZY and a UK NERC grant (NE/F005237/1) awarded to PCW, CDL and DJSM. We thank the three referees for their constructive comments on the manuscript.

Footnotes

Supplementary Information accompanies the paper on The ISME Journal website (http://www.nature.com/ismej)

Supplementary Material

Supplementary Information
Click here for additional data file. (67KB, doc)

References

  1. Atkinson D, Ciotti BJ, Montagnes DJS. Protists decrease in size linearly with temperature: ca. 2.5 °C−1. Proc R Soc Lond B Biol Sci. 2003;270:2605–2611. doi: 10.1098/rspb.2003.2538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Begun AA, Orlova TY, Selina MS. A ‘Bloom' in the water of Amursky Bay (Sea of Japan) caused by the dinoflagellate Oxyrrhis marina Dujardin, 1841. Russ J Mar Biol. 2004;30:51–55. [Google Scholar]
  3. Berges JA, Montagnes DJS, Hurd CL, Harrison PJ. Fitting ecological and physiological data to rectangular hyperbolae: a comparison of methods using Monte Carlo simulations. Mar Ecol Prog Ser. 1994;114:175–183. [Google Scholar]
  4. Bonkowski M. Protozoa and plant growth: the microbial loop in soil revisited. New Phytol. 2004;162:617–631. doi: 10.1111/j.1469-8137.2004.01066.x. [DOI] [PubMed] [Google Scholar]
  5. Bruggeman J, Kooijman SALM. A biodiversity-inspired approach to aquatic ecosystem modelling. Limnol Oceanogr. 2007;52:1533–1544. [Google Scholar]
  6. Calbet A. The trophic roles of microzooplankton in marine systems. ICES J Mar Sci. 2008;65:325–331. [Google Scholar]
  7. Carroll SP, Hendry AP, Reznick DN, Fox CW. Evolution on ecological time-scales. Funct Ecol. 2007;21:387–393. [Google Scholar]
  8. Davidson K, Sayegh F, Montagnes DJS. Oxyrrhis marina based models as a tool to interpret protozoan population dynamics. J Plankton Res. 2011;33:651–663. [Google Scholar]
  9. Fenton A, Spencer M, Montagnes DJS. Parameterising variable assimilation efficiency in predator-prey. Oikos. 2010;119:1000–1010. [Google Scholar]
  10. Follows MJ, Dutkiewicz S, Grant S, Chisholm SW. Emergent biogeography of microbial communities in a model ocean. Science. 2007;315:1843–1846. doi: 10.1126/science.1138544. [DOI] [PubMed] [Google Scholar]
  11. Gächter E, Weisse T. Local adaptation among geographically distant clones of the cosmopolitan freshwater ciliate Meseres corlissi. I. Temperature response. Aquat Microb Ecol. 2006;45:291–300. [Google Scholar]
  12. Gerten D, Adrian R. Climate-driven changes in spring plankton dynamics and the sensitivity of shallow polymictic lakes to the North Atlantic oscillation. Limnol Oceanogr. 2000;45:1058–1066. [Google Scholar]
  13. Heinbokel JF. Studies on the functional role of tintinnids in the southern California Bight. 1. Grazing and growth rates in laboratory cultures. Mar Biol. 1978;47:177–189. [Google Scholar]
  14. Houghton J. Global warming. Rep Prog Phys. 2005;68:1343–1403. [Google Scholar]
  15. Johnson MD, Rome M, Stoecker DK. Microzooplankton grazing on Prorocentrum minimum and Karlodinium micrum in Chesapeake Bay. Limnol Oceanogr. 2003;48:238–248. [Google Scholar]
  16. Kimmance S, Atkinson D, Montagnes DJS. Do temperature—food interactions matter? Responses of production and its components in the model heterotrophic flagellate Oxyrrhis marina. Aquat Microb Ecol. 2006;42:63–73. [Google Scholar]
  17. Le Quéré C, Harrison SP, Prentice IC, Buitenhuis ET, Aumont O, Bopp L, et al. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Global Change Biol. 2005;11:2016–2040. [Google Scholar]
  18. Lowe C, Day A, Kemp S, Montagnes DJS. There are high levels of functional and genetic diversity in Oxyrrhis marina. J Eukaryot Microbiol. 2005;52:250–257. doi: 10.1111/j.1550-7408.2005.00034.x. [DOI] [PubMed] [Google Scholar]
  19. Lowe CD, Montagnes DJS, Martin LE, Watts P. Patterns of genetic diversity in the marine heterotrophic flagellate Oxyrrhis marina (Alveolata:Dinophyceae) Protist. 2010;161:212–221. doi: 10.1016/j.protis.2009.11.003. [DOI] [PubMed] [Google Scholar]
  20. Lowe CD, Keeling P, Martin LE, Slamovits CH, Watts PC, Montages DJS. Who is Oxyrrhis marina? Morphological and phylogenetic studies on an unusual dinoflagellate. J Plankton Res. 2011a;33:555–567. [Google Scholar]
  21. Lowe CD, Martin LE, Roberts EC, Watts PC, Wooton EC, Montagnes DJS. Collection, isolation, and culturing strategies for Oxyrrhis marina. J Plankton Res. 2011b;33:569–578. [Google Scholar]
  22. Minter EJ, Fenton A, Cooper J, Montagnes DJS. Prey-dependent mortality rate: a critical parameter in microbial models. Microl Ecol. 2011;62:144–161. doi: 10.1007/s00248-011-9836-5. [DOI] [PubMed] [Google Scholar]
  23. Montagnes DJS. Growth responses of planktonic ciliates in the genera Strobilidium and Strombidium. Mar Ecol Prog Ser. 1996;130:241–254. [Google Scholar]
  24. Montagnes DJS, Fenton A. Prey-abundance affects zooplankton assimilation efficiency and the outcome of biogeochemical models. Ecol Modelling. 2012;243:1–7. [Google Scholar]
  25. Montagnes DJS, Berges JA. Determining parameters of the numerical response. Microb Ecol. 2004;48:139–144. doi: 10.1007/s00248-003-9000-y. [DOI] [PubMed] [Google Scholar]
  26. Montagnes DJS, Kimmance SA, Atkinson D. Using Q10: can growth rates increase linearly with temperature. Aquat Microb Ecol. 2003;32:307–313. [Google Scholar]
  27. Montagnes DJS, Morgan G, Bissinger JE, Atkinson D, Weisse T. Short-term temperature change may impact freshwater carbon flux: a microbial perspective. Global Change Biol. 2008;14:2810–2822. [Google Scholar]
  28. Montagnes DJS, Lowe CD, Roberts EC, Breckels MN, Boakes DE, Davidson K, et al. An introduction to the special issue: Oxyrrhis marina, a model organism. J Plankton Res. 2011;33:549–567. [Google Scholar]
  29. Parmesan C. Ecological and evolutionary responses to recent climate change. Ann Rev Ecol Syst. 2006;37:637–669. [Google Scholar]
  30. Petchey OL, Phearson PT, Casey TM, Morin PJ. Environmental warming alters food-web structure and ecosystem function. Nature. 1999;402:69–72. [Google Scholar]
  31. Sayegh FAQ, Radi N, Montagnes DJS. Do strain differences in microalgae alter their relative quality as a food for the rotifer Brachionus plicatilis. Aquaculture. 2007;273:665–678. [Google Scholar]
  32. Sibly RM, Barker D, Denham MC, Hone J, Pagel M. On the regulation of populations of mammals, birds, fish and insects. Science. 2005;309:607–610. doi: 10.1126/science.1110760. [DOI] [PubMed] [Google Scholar]
  33. Sokal RR, Rohlf FJ.1995Biometry3rd ednFreeman: New York, USA; 887 [Google Scholar]
  34. Tilman D. Resource Competition and Community Structure. Princeton University Press: Princeton; 1982. p. 296. [PubMed] [Google Scholar]
  35. Tirok K, Bauer B, Wirtz K, Gaedke U. Predator-prey dynamics driven by feedback between functionally diverse trophic levels. PLoS ONE. 2011;6:e27357. doi: 10.1371/journal.pone.0027357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Turchin P. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton University Press: Princeton NJ; 2003. [Google Scholar]
  37. Violle C, Enquist BJ, McGill BJ, Jiang L, Albert CH, Hulshof C, et al. The return of the variance: intraspecific variability in community ecology. Trends Ecol Evol. 2012;27:244–252. doi: 10.1016/j.tree.2011.11.014. [DOI] [PubMed] [Google Scholar]
  38. Watts PC, Martin LE, Kimmance SE, Montagnes DJS, Lowe CD. The distribution of Oxyrrhis marina—a global wanderer or poorly characterised endemic. J Plankton Res. 2011;33:579–589. [Google Scholar]
  39. Weisse T, Montagnes DJS. Effect of temperature on inter and intraspecific isolates of Urotricha (Prostomatida, Ciliophora) Aquat Microb Ecol. 1998;15:285–291. [Google Scholar]
  40. Weisse T, Stadler P, Lindström ES, Kimmance SA, Montagnes DJS. Interactive effect of temperature and food concentration on growth rate: a test case using the small freshwater ciliate Urotricha farcta. Limnol Oceanogr. 2002;47:1447–1455. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (67KB, doc)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES