Toward practicing privacy

Abstract

Private data analysis—the useful analysis of confidential data—requires a rigorous and practicable definition of privacy. Differential privacy, an emerging standard, is the subject of intensive investigation in several diverse research communities. We review the definition, explain its motivation, and discuss some of the challenges to bringing this concept to practice.

The sanitization pipe dream

In the sanitization pipe dream, a magical procedure is applied to a database full of useful but sensitive information. The result is an ‘anonymized’ or even ‘synthetic’ database that ‘looks just like’ a real database for the purposes of data analysis, but which maintains the privacy of everyone in the original database. The dream is seductive: the implications of success are enormous and the problem appears simple. However, time and again, both in the real world and in the scientific literature, sanitization fails to protect privacy. Some failures are so famous they have short names: ‘Governor Weld,’¹ ‘AOL debacle,’² ‘Netflix Prize,’³ and ‘GWAS allele frequencies.’^{4 5} Some are more technical, such as the composition attacks that can be launched against -anonymity, -diversity, and -invariance,⁶ when two different, but overlapping, databases undergo independent sanitization procedures.

The mathematical reality is that anything yielding ‘overly accurate’ answers to ‘too many’ questions is, in fact, blatantly non-private: suppose we are given a database of rows, where each row is the data of a single patient, and each row contains, among other data, a bit indicating the patient's HIV status. Suppose further that we require a sanitization that yields answers to questions of the following type: a subset of the database is selected via a combination of attributes, for example, ‘over 5 feet tall and under 140 pounds’ or ‘smokes one pack of cigarettes each day’ⁱ and the query is, ‘How many people in the subset are HIV-positive?’ How accurate can the answers to these counting queries be, while providing even minimal privacy? Perhaps not accurate at all! Any sanitization ensuring that answers to all possible counting queries are within error permits a reconstruction of the private bits that is correct on all but at most rows.⁷ For example, if the data set contains rows, and answers to all counting queries can be estimated to within an error of at most , then the reconstruction will be correct to within . If the estimations were correct to within , then reconstruction would be correct on all but rows, an overall error rate of at most , no matter how weakly the secret bit is correlated to the other attributes.

Formally, blatant non-privacy is defined to be achieved when the adversary can generate a reconstruction that is correct in all but entries of the database, where the notation ‘’ denotes any function that grows more slowly than for every constant as goes to infinity. The theorem says that if the noise is always then the system is blatantly non-private.ⁱⁱ

Clearly, the unqualified sanitization pipe dream is problematic: sanitization is supposed to give relatively accurate answers to all questions, but any object that does so will compromise privacy. Even on-line databases, which receive and respond to questions, and only provide relatively accurate answersⁱⁱⁱ to most of the questions actually asked (see the online supplementary appendix for further details), risk blatant non-privacy after only a linear number of random queries.^7–9 To avoid the blatant non-privacy of the reconstruction attacks, the number of accurate answers must be curtailed; to preserve privacy, utility must inevitably be sacrificed.

This suggests two questions: (1) How do we ensure privacy even for few queries?^iv and (2) Is there a mathematically rigorous notion of privacy that enables us to argue formally about the degree of risk in a sequence of queries?

Differential privacy is such a definition; differentially private techniques guarantee privacy while often permitting accurate answers; and the goal of algorithmic research in differential privacy is precisely to postpone the inevitable for as long as possible. Looking ahead, and focusing, for the sake of concreteness, on counting queries, the theoretical work on differential privacy exposes a delicate balance between the degree of privacy loss, number of queries, and degree of accuracy (ie, the distribution on errors).

On the primacy of definitions

Differential privacy is inspired by the developments in cryptography of the 1970s and 1980s. ‘Pre-modern’ cryptography witnessed cycles of ‘propose-break-propose-again.’ In these cycles, an implementation of a cryptographic primitive, say, a cryptosystem (a method for encrypting and decrypting messages), would be proposed. Next, someone would break the cryptosystem, either in theory or in practice. It would then be ‘fixed’—until the ‘fixed’ version was broken, and so the cycle would go.

Among the stunning contributions of Goldwasser et al^{10 11} was an understanding of the importance of definitions. What are the properties we want from a cryptosystem? What does it mean for an adversary to break the cryptosystem, that is, what is the goal of the adversary? And what is the power of the adversary: what are its computational resources; to what information does it have access? Having defined the goals and (it is hoped, realistically) bounded the capabilities of the adversary, the cryptographer then proposes a cryptosystem and rigorously proves its security, formally arguing that no adversary with the stated resources can break the system.^v This methodology converts a break of the implementation into a break of the definition. That is, a break exposes a weakness in the stated requirements of a cryptosystem. This leads to a strictly stronger set of requirements. Even if the process repeats, the series of increasingly strong definitions converts the propose-break-propose-again cycle into a path of progress.

Sometimes a proposed definition can be too strong. This is argued by proving that no implementation can exist. In this case, the definition must be weakened or altered (or the requirements declared unachievable). As we will see, this is what happened with one natural approach to defining privacy for statistical databases—what we have been calling privacy-preserving data analysis.

A natural suggestion for defining privacy in data analysis is a suitably weakened version of the cryptographic notion of semantic security. In cryptography this says that the encryption of a message leaks no information that cannot be learned without access to the ciphertext.¹¹ In the context of privacy-preserving databases we might hope to ensure that anything that can be learned about a member of the database via a privacy-preserving database should also be learnable without access to the database. And indeed, 5 years before the invention of semantic security, the statistician Tore Dalenius framed exactly this goal for private data analysis.¹²

Unfortunately, Dalenius’ goal provably cannot be achieved.^{13 14} The intuition for this can be captured in three sentences: A Martian has the (erroneous) prior belief that every Earthling has two left feet. The database teaches that almost every Earthling has exactly one left foot and one right foot. Now the Martian with access to the statistical database knows something about the first author of this note that cannot be learned by a Martian without access to the database.

Databases that teach

The impossibility of Dalenius’ goal relies on the fact that the privacy-preserving database is useful. If the database said nothing, or produced only random noise unrelated to the data, then privacy would be absolute, but such databases are, of course, completely uninteresting. To clarify the significance of this point we consider the following parable.

A statistical database teaches that smoking causes cancer. The insurance premiums of Smoker S rise (Smoker S is harmed). But, learning that smoking causes cancer is the whole point of databases of this type: Smoker S enrolls in a smoking cessation program (Smoker S is helped).

The important observation about the parable is that the insurance premiums of Smoker S rise whether or not he is in the database. That is, Smoker S is harmed (and later helped) by the teachings of the database. Since the purpose of the database—public health, medical data mining—is laudable, the goal in differential privacy is to limit the harms to the teachings, and to have no additional risk of harm incurred by deciding to participate in the data set. Speaking informally, differential privacy says that the outcome of any analysis is essentially equally likely, independent of whether any individual joins, or refrains from joining, the data set. Here, the probability space is over the coin flips of the algorithm (which the algorithm implementors, ie, the ‘good guys,’ control). The guarantee holds for all individuals simultaneously, so the definition simultaneously protects all members of the database.

An important strength of the definition is that any differentially private algorithm, which we call a mechanism, is differentially private based on its own merits. That is, it remains differentially private independent of what any privacy adversary knows, now or in the future, and to which other databases the adversary may have access, now or in the future. Thus, differentially private mechanisms hide the presence or absence of any individual even in the face of linkage attacks, such as the Governor Weld, AOL, Netflix Prize, and GWAS attacks mentioned earlier. For the same reason, differential privacy protects an individual even when all the data of every other individual in the database are known to the adversary.

Formal definition of differential privacy

A database is modeled as a collection of rows, with each row containing the data of a different individual. Differential privacy will ensure that the ability of an adversary to inflict harm (or good, for that matter)—of any sort, to any set of people—should be essentially the same, independent of whether any individual opts in to, or opts out of, the dataset. This is done indirectly, simultaneously addressing all possible forms of harm and good, by focusing on the probability of any given output of a privacy mechanism and how this probability can change with the addition or deletion of any one person. Thus, we concentrate on pairs of databases differing only in one row, meaning one is a subset of the other and the larger database contains just one additional row. (Sometimes it is easier to think about pairs of databases of the same size, say, , in which case they agree on rows but one person in has been replaced, in , by someone else.) We will allow our mechanisms to flip coins; such algorithms are said to be randomized.

Definition 3.1^{14 15} A randomized mechanism gives -differential privacy if for all data sets and differing on at most one row, and all ,

where the probability space in each case is over the coin flips of .

In other words, consider any possible set of outputs that the mechanism might produce. Then the probability that the mechanism produces an output in is essentially the same—specifically, to within an factor on any pair of adjacent databases. (When .) This means that, from the output produced by , it is hard to tell whether the database is which, say, contains the reader's data, or the adjacent database , which does not contain the reader's data. The intuition is: if the adversary can't even tell whether or not the database contains the reader's data, then the adversary can't learn anything sui generis about the reader's data.

Properties of differential privacy

Differential privacy offers several benefits beyond immunity to auxiliary information.

Addresses arbitrary risks

Differential privacy ensures that even if the participant removed her data from the data set, no outputs (and thus consequences of outputs) would become significantly more or less likely. For example, if the database were to be consulted by an insurance provider before deciding whether or not to insure a given individual, then the presence or absence of any individual's data in the database will not significantly affect her chance of receiving coverage. Protection against arbitrary risks is, of course, a much stronger promise than the often-stated goal in sanitization of protection against re-identification. And so it should be! Suppose that in a given night every elderly patient admitted to the hospital is diagnosed with one of tachycardia, influenza, broken arm, and panic attack. Given the medical encounter data from this night, without re-identifying anything, an adversary could still learn that an elderly neighbor was taken to the emergency room (the ambulance was observed) with one of these four complaints (and moreover she seems fine the next day, ruling out influenza and broken arm).

Worst-case guarantees

Differential privacy is a worst-case, rather than average-case, guarantee. That means it protects privacy even on ‘unusual’ databases and databases that do not conform to (possibly erroneous) assumptions about the distribution from which the rows are learned. Thus, differential privacy provides protection for outliers, even if they are strangely numerous—independent of whether this apparent strangeness is just ‘the luck of the draw’ or in fact arises because the algorithm designer's expectations are simply wrong.^vi

Quantification of privacy loss

Privacy loss is quantified by the maximum, over all , and all adjacent databases , of the ratio

1

In particular, -differential privacy ensures that this privacy loss is bounded by . This quantification permits comparison of algorithms: given two algorithms with the same degree of accuracy (quality of responses), which one incurs smaller privacy loss? Or, given two algorithms with the same bound on privacy loss, which permits the more accurate responses? Sometimes a little thought can lead to a much more accurate algorithm with the same bound on privacy loss; therefore, the failure of a specific -differentially private algorithm to deliver a desired degree of accuracy does not mean that differential privacy is inconsistent with accuracy.

Automatic and oblivious composition

Given two differentially private databases, where one is -differentially private and the other is -differentially private, a simple composition theorem shows that the cumulative risk endured by participating in (or opting out of) both databases is at worst -differentially private.¹⁵ This is true even if the curators of the two databases are mutually unaware and make no effort to coordinate their responses. In fact, a more sophisticated composition analysis shows that the composition of mechanisms, each of which is -differentially private, is, for all , at most -differentially private. (-differential privacy says that with probability the privacy loss is bounded by .)¹⁷ When , this replacing of by roughly can represent very large savings, translating into much improved accuracy.

Group privacy

Differential privacy automatically yields group privacy: any -differentially private algorithm is automatically -differentially private for any group of size ; that is, it hides the presence or absence of all groups of size , but the quality of the hiding is only .

Building complex algorithms from primitives

The quantitative, rather than binary, nature of differential privacy enables the analysis of the cumulative privacy loss of complex algorithms constructed from differentially private primitives, or ‘subroutines.’

Measuring utility

There is no special definition of utility for differentially private algorithms. For example, if we wish to achieve -differential privacy for a single counting query, and we choose to use the Laplace mechanism described in the ‘Differentially private algorithms’ section below, then the distribution on the (signed) error is given by the Laplace distribution with parameter , which has mean zero, variance , and probability density function . If we build a differentially private estimation procedure, for example, an M-estimator,^{18 19} we prove theorems about the probability distribution of the ( or , say) errors, as a function of (in addition to any other parameters, such as size of the data set and confidence requirements).^{15 19 20} If we use a differentially private algorithm to build a classifier, we can prove theorems about its classification accuracy or its sample complexity, again as a function of together with the usual parameters.²¹ If we use a differentially private algorithm to learn a distribution, we can evaluate the output in terms of its KL divergence from the true distribution or the empirical distribution, as a function of and the other usual parameters.^{22 23}

Differing intellectual traditions

The medical informatics and theoretical computer science communities have very differing intellectual traditions. We highlight some differences that we have observed between the perspectives of the differential privacy researchers and some other works on privacy in the literature. The online supplementary appendix contains an expanded version of this section.

Defense against leveraging attacks

An attacker with partial information about an individual can leverage this information to learn more details. Knowing the dates of hospital visits of a neighbor or co-worker, or the medications taken by a parent or a lover, enables a leveraging attack against a medical database. To researchers approaching privacy from a cryptographic perspective, failure to protect against leveraging attacks is unthinkable.

Learning distributions is the whole point

Learning distributions and correlations between publicly observable and hidden attributes is the raison d’être of data analysis.^vii The view that it is necessarily a privacy violation to learn the underlying distribution from which a database is drawn^{25 26} appears to the differential privacy researchers to be at odds with the concept of privacy-preserving data analysis—what are the utility goals in this view?

Re-identification is not the issue

We have argued that preventing re-identification does not ensure privacy (see the ‘Formal definition of differential privacy’ section). In addition, the focus on re-identification does not address privacy compromises that can result from the release of statistics (of which reconstruction attacks are an extreme case).

‘Who would do that?’

Some papers in the (non-differential) privacy literature outline assumptions about the adversary's motivation and skill, namely that it is safe to assume relatively low levels for both. However, there will always be snake oil salesmen who prey on the fear and desperation of the sick. Blackmail and exploitation of despair will provide economic motives for compromising the privacy of medical information, and we can expect sophisticated attacks. ‘PhD-level research,’ said Udi Manber, a former professor of computer science, commenting on spammers’ techniques, when he was CEO of Amazon subsidiary A9.²⁷

The assumption of an adversarial world

All users of the database are considered adversarial, and they are assumed to conspire. There are two reasons for this. In a truly on-line system, such as the American Fact Finder,^viii there is no control over who may pose questions to the data, or the extent to which apparently different people, say, with different IP addresses, are in fact the same person. Second, the mathematics of information disclosure are complicated, and even well-intentioned data analysts can publish results that, upon careful study, compromise privacy. So even two truly different users can, with the best of intentions, publish results that, when taken together, could compromise privacy. A general technical solution is to view all users as part of a giant adversary.

A corollary of the adversarial view yields one of the most controversial aspects of differential privacy: the analyst is not given access to raw data. Even a well-intentioned analyst may inadvertently compromise an individual's privacy simply in the choice of statistic to be released; the data of a single outlier can cause the analyst to behave differently. Analysts find this aspect very difficult to accept, and ongoing work is beginning to address this problem for the special case in which the analyst is trusted to adhere to a protocol.²⁸

Differentially private algorithms

Privacy by process

Randomized response is a technique developed in the social sciences to evaluate the frequency of embarrassing or even illegal behaviors.²⁹ Let XYZ be such an activity. Faced with the query, ‘Did you XYZ last night?’ the respondent is instructed to perform the following steps:

1. Flip a coin.

2. If tails, then respond truthfully.

3. If heads, then flip a second coin and respond ‘Yes’ if heads and ‘No’ if tails.

The intuition behind randomized response is that it provides ‘plausible deniability’: a response of, say, ‘Yes,’ may have been offered because the first and second coin flips were both heads, which occurs with probability . In other words, privacy is obtained by process. There are no ‘good’ or ‘bad’ responses; the process by which the responses are obtained affects how they may legitimately be interpreted. Randomized response thwarts the reconstruction attacks described in the ‘The sanitization pipe dream’ section because a constant, randomly selected, fraction of the inputs are replaced by random values.

Claim 5.1

Randomized response is -differentially private.^ix

Proof

The proof is a simple case analysis. Details are in the online supplementary appendix.

Differential privacy is ‘closed under post-processing,’ meaning that if a statistic is produced via an -differentially private method, then any computation on the released statistic has no further cost to privacy. Thus, if a data curator creates a database by obtaining randomized responses from, say, respondents, the curator can release any statistic computed from these responses, with no further privacy cost. In particular, the curator can release an estimate of the fraction who XYZ ed last night () from the fraction who replied ‘Yes’ () via the formula

while maintaining -differential privacy.

A general method

We now turn to the computation of arbitrary statistics on arbitrarily complex data, showing that the addition of random noise drawn from a carefully chosen distribution ensures differential privacy: if the analysts wishes to learn where is some statistic and is the database, the curator can choose a random value, say , whose distribution depends only on and , and can respond with . This process (it is a process because it involves the generation of a random value) will be -differentially private.

Recall that the goal of the random noise is to hide the presence or absence of a single individual, so what matters is how much, in the worst case, an individual's data can change the statistic. For one-dimensional statistics (counting queries, medians, and so on) this difference is measured in absolute value . For higher dimensional queries, such as regression analyses, we use the so-called norm of the difference, defined by

where is the dimension of the query.

Definition 5.2

(L₁ Sensitivity) For , the sensitivity of is

2

for all differing in at most one row.

The Laplace mechanism.

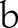The Laplace distribution with parameter , denoted , has density function ; that is, the probability of choosing a value falls off exponentially in the absolute value . The variance of the distribution is , so its SD is ; we say it is scaled to . Taking we have that the density at is proportional to . This distribution has highest density at (good for accuracy), and for any such that the density at is at most times the density at . The distribution gets flatter as increases. This makes sense, since large means that the data of one person can make a big difference in the outcome of the statistic, and therefore there is more to hide. Finally, the distribution gets flatter as decreases. This is correct: smaller means better privacy, so the noise density should be less ‘peaked’ at and change more gradually as the magnitude of the noise increases.

A fundamental technique for achieving differential privacy is to add appropriately scaled Laplacian noise to the result of a computation. Again, the curator performs the desired computation, generates noise, and reports the result. The data are not perturbed. The correct distribution for the noise is the Laplace distribution, where the parameter depends on the sensitivity (higher sensitivity will mean larger expected noise magnitude) and the privacy goal (smaller will mean larger expected noise magnitude).

Theorem 5.3¹⁵ For , the mechanism that adds independently generated noise with distribution to each of the output terms is -differentially private .

Let us focus on the case . The sensitivity of a counting query, such as ‘How many people in the database are suitable for the ABC patient study?’ is 1, so by Theorem 5.3 it suffices to add noise drawn from to ensure -differential privacy for this query. If it suffices to add noise with SD . Note that this expected error is much better than the expected error with randomized response, which is , so the Laplace mechanism is better than randomized response for this purpose.

If instead we want privacy loss then we would add noise with variance . In general, the sensitivity of counting queries is at most . So, taking , the simple composition theorem tells us that adding noise with expected magnitude is sufficient. For this is about 14; for it would be about . However, for large we can begin to use some of the more advanced techniques to analyze composition, reducing the factor of to roughly . These techniques give errors approaching the lower bounds on noise needed to avoid reconstruction attacks.

A major thread of research has addressed handling truly huge—exponential in the size of the database—numbers of counting or even arbitrary low-sensitivity queries, while still providing reasonably accurate answers.^{17 30–35x}

In the online supplementary appendix we discuss two computations for which Theorem 5.3 yields surprisingly small expected error: histogram release and finding a popular value. Both problems seem to require many counts, but a more careful analysis shows sensitivity , and hence may be addressed with low distortion.

The privacy budget

We have defined the privacy loss quantity, and noted that loss is cumulative. Indeed a strength of differential privacy is that it enables analysis of this cumulative loss. We can therefore set a privacy budget for a database and the curator can keep track of the privacy loss incurred since the beginning of the database operation. This is publicly computable, since it depends only on the queries asked and the value of used for each query; it does not depend on the database itself. This raises the policy question, ‘How should the privacy budget be set?’ The mathematics allows us to makes statements of the form:

If every database consumes a total privacy budget of then, with probability at least , any individual whose data are included in at most databases will incur a cumulative lifetime privacy loss of , where the probability space is over the coin flips of the algorithms run by the differentially private database algorithms.^xi

Were we able to get the statistical accuracy we desired with such protective individual databases, that is, with (which, as of this writing, we typically are not!), and were we to determine that is a reasonable upper bound on the total number of databases in which an individual would participate in his/her lifetime, then these numbers would seem like a fine choice: the semantics of the calculation are that the entire sequence of outputs produced by databases ever containing data of the individual, would be at most a factor of more or less likely were the data of this individual to have been included in none of the databases. Do the semantics cover what we want? Are we too demanding? For example, should we consider only the cumulative effects of, say, 100 or even just 50 databases? Should we consider much larger cumulative lifetime losses?

The differential privacy literature does not distinguish between degrees of social sensitivity of data: enjoying Mozart is treated as equally deserving of privacy as being in therapy. Setting differently for different types of data, or even different types of queries against data, may make sense, but these are policy questions that the math does not attempt to address.^xii

Differential privacy protects against arbitrary risks; specifically, via the parameter it controls the change in risk occurring as a consequence of joining or refraining from joining a dataset. However, what constitutes an acceptable rise in risk may vary according to the nature of the risk, or the initial probability of the risk. For example, if the probability of a ‘bad’ outcome is exceedingly low, say, , then an increase by a factor of 10, or even 1000, might be acceptable. Thus, the policy choice for for a given data set may depend on how the database is to be used. Caveat emptor: beware of mission creep (and see Dwork et al³⁶)!

If policy dictates that different types of data and/or databases should be protected by different choices of , say for music databases and for medical databases, and so on, then it will become even harder to interpret theorems about the cumulative loss being bounded by a function of the 's.

Toward practicing privacy

Differential privacy was motivated by a desire to utilize data for the public good, while simultaneously protecting the privacy of individual data contributors. The hope is that, to paraphrase Alfred Kinsey, better privacy means better data.

The initial positive results that ultimately led to the development of differential privacy (and that we now understand to provide -differential privacy for negligibly small ) were designed for internet-scale databases, where reconstruction attacks requiring (or even ) queries, each requiring roughly time to process, are infeasible because is so huge.³⁷ In this realm, the error introduced for protecting privacy in counting queries is much smaller than the sampling error, and privacy is obtained ‘for free,’ even against an almost linear number of queries. Moreover, counting queries provide a powerful computational interface, and many standard data mining tasks can be carried out by an appropriately chosen set of counting queries.³⁸

Inspired by this paradigm at least two groups have produced programming platforms^{39 40} enforcing differentially private access to data. This permits programmers with no understanding of differential privacy or the privacy budget to carry out data analytics in a differentially private manner.

Translating an approach designed for internet-scale data sets to data sets of modest size is extremely challenging, and yet substantial progress has been made; see, for example, the experimental results in Hardt et al²² on several data sets: an epidemiological study of car factory workers (1841 records, six attributes per record), a genetic study of barley powdery mildew isolates (70 records, six attributes), data relating household characteristics (665 records, eight attributes), and the National Long Term Care Survey (21 574 records, 16 attributes).

As with many things, special-purpose solutions may be of higher quality than general solutions. Thus, the Laplace mechanism is a general solution for real-valued or vector-valued functions, but the so-called objective perturbation methods have yielded better results (lower error, smaller sample complexity) for certain techniques in machine learning such as logistic regression.²¹ More typically, researchers in differentially private algorithms produce complex algorithms involving many differentially private steps (some of which may use any of the Laplace mechanism, the Gaussian mechanism (ie, addition of Gaussian noise, which yields -differential privacy), the exponential mechanism,⁴¹ the propose-test-release paradigm,¹⁸ sample and aggregate,⁴² etc, as computational primitives). The goal is always to improve utility beyond that obtained with naive application of the Laplace mechanism.

As of this writing, there is no magic differential privacy bullet, and finding methods for any particular analytical problem or sequence of computational steps that yield good utility on data sets of moderate size can be very difficult. By engaging with researchers in differential privacy the medical informatics community can and should influence the research agenda of this dynamic and talented community.