Simulating the effect of slab features on vapor intrusion of crack entry

Abstract

In vapor intrusion screening models, a most widely employed assumption in simulating the entry of contaminant into a building is that of a crack in the building foundation slab. Some modelers employed a perimeter crack hypothesis while others chose not to identify the crack type. However, few studies have systematically investigated the influence on vapor intrusion predictions of slab crack features, such as the shape and distribution of slab cracks and related to this overall building foundation footprint size. In this paper, predictions from a three-dimensional model of vapor intrusion are used to compare the contaminant mass flow rates into buildings with different foundation slab crack features. The simulations show that the contaminant mass flow rate into the building does not change much for different assumed slab crack shapes and locations, and the foundation footprint size does not play a significant role in determining contaminant mass flow rate through a unit area of crack. Moreover, the simulation helped reveal the distribution of subslab contaminant soil vapor concentration beneath the foundation, and the results suggest that in most cases involving no biodegradation, the variation in subslab concentration should not exceed an order of magnitude, and is often significantly less than this.

1. Introduction

In any vapor intrusion study, one of the most important issues is how the contaminant soil vapor enters a building of interest. This issue cannot be avoided for research no matter with focus on soil vapor transport [1–7], indoor air concentration [8–11] or both [12–18]. Two general hypotheses have been used in the analysis of the process. One is to assume that contaminants enter through a permeable concrete slab [8–9, 18], and the other involves assuming existence of a crack or cracks in the slab as the main entry pathway for soil vapor [1–7, 12–14, 19–21]. The use of the former is limited, largely due to the generally accepted low permeability of the typical concrete slab, while the latter was developed for radon intrusion studies, and later widely employed in chemical vapor intrusion studies [22–24]. One example of its use involves the application of Nazaroff’s equation [25], to calculate soil gas flow rate into a perimeter crack of a building, e.g. in the Johnson-Ettinger (J-E) model [12].

Though the crack concept has also been used in many more detailed studies beyond the J-E model, e.g. Abreu and Johnson’s three-dimension (3-D) CFD numerical model [1–3], the Brown 3-D CFD model [4–7, 14] and some case studies [26], most of these studies in vapor intrusion focused on the influence of environmental factors such as soil characteristics and contaminant source separation and distribution, and only a few of them considered the details of crack features on predictions. In Abreu’s thesis [2], the “center crack” scenario was simulated in a study of biodegradation effects, and it showed that the crack location can play a significant role in cases involving high biodegradation rate constants. Another important issue is the variation with position of subslab contaminant soil vapor concentration and how this might influence entry rates into a building. The question that this poses is whether taking monitoring data from one or two subslab sample points is sufficient to fully describe the necessary subslab near-crack concentration used in predicting contaminant entry rates?

Equation (1) shows the relationship between contaminant mass flow rate into a structure and indoor air concentration [12].

$$c_{in}\approx \frac{J_{ck}}{Q_b{A}_e}$$ (1)

Where c_in is the indoor air contaminant concentration [M/L³], J_ck is the contaminant mass flow rate into the building [M/T], Q_b is the volume of the enclosed space [L³/T] and A_e is the air exchange rate [1/T].

In this study, contaminant mass flow rate, rather than indoor air concentration, is used as the index of vapor intrusion risk, as suggested elsewhere [6, 14]. In equation (1), both Q_b and A_e are in practice often difficult to identify or measure, and will cause uncertainties in predicted c_in. As an alternative, J_ck the contaminant mass entry rate, can be obtained directly from 3-D numerical models. This merely postpones the problem of establishing Q_b and A_e to another point in the visual risk assessment based on c_in, but it more explicitly highlights the problem, and also allows comparing the potential for the vapor intrusion impacts in different structures without getting tied up in issues of idiosyncratic building operation.

2. The 3-D Numerical Model

The full 3-D model examined here is essentially that presented earlier by this group [4–7,14], and partly validated by previous study. The case of interest here is the steady-state “base case” discussed in the earlier studies, i.e., a single structure built atop an otherwise flat, open field, underlain by a homogeneous soil that stretches from the ground surface to a water table which serves as an infinite source of the contaminant vapor of interest.

Figure 1 presents a diagram of the base case situation, while Figure 2 shows different hypothetical crack shapes and distribution in the foundation slab. Table 1 shows the various parameters assumed in the modeling work. The model equations solved here are those shown in previous publications by our group [4–7, 14].

FIGURE 1.

Cross sectional view and boundary conditions of the model domain and house with a foundation crack

FIGURE 2.

Plan view of the location of the crack in the foundation of slab: (a) Perimeter Crack; (b) Center Crack; (c) Center Hole (The crack area in three cases is the same.)

TABLE 1.

Input parameters used in the 3-D simulations (unless otherwise noted in the figures and table)

Building/foundation parameters	Contaminant vapor source properties
Domain cross section size: 24 m × 24 m or 50 m × 50 m (for the foundation footprint size 20 m × 20 m)	Contaminant: TCE
	Diffusivity of TCE in crack (Dck): 7.4 ×10−6 m2/s
Foundation foot print: 5 m × 5 m, 10 m × 10 m, or 20 m × 20 m.	Effective diffusivity of TCE in soil (Deff): 1.04 ×10−6 m2/s
Depth of foundation (df): 0.1 m or 2 m	Soil gas flow properties
Crack/foundation slab thickness (dck): 0.152 m	Viscosity of air/soil gas (μg): 1.8648 ×10−5 kg/m/s
Crack width (wck): 0.005 m	Density of air/soil gas (ρg): 1.1614kg/m3
Depth to groundwater/source (ds) 3, 5, 8, 11, 14, or 18 m bgs	Soil permeability (k): 10−10, 10−11, 10−12, 10−13 or 10−14
3-D Finite Element Analysis Parameters	m2
Size of the grid elements: 0.001 m – 1 m	Total soil porosity (ϕt): 0.35
Number of elements: 200k – 1,000k	Soil porosity filled with gas (ϕg): 0.296

Effective soil diffusivity is in reality correlated with soil permeability [27]. However, in this paper we chose to assume a constant soil diffusivity to keep the comparison clearer as the small possible variation in dry soil diffusivity does not make a large difference in the results, as also noted in our previous research [4–7, 14]. Permeability can show significant variability with soil type and moisture content, but this is not a focus of this paper, which is concerned with the influence of the foundation crack characteristics.

Briefly, the 3-D modeling approach used here solves Darcy’s Law to obtain soil gas advection profiles, and then solves the contaminant gas diffusion-advection equation subject to the soil gas advection velocity profiles obtained from solving Darcy’s law. Again, details of the modeling procedure have been presented elsewhere [4–7, 14].

The governing equation of non-compressible soil gas flow in steady state is [14]:

$$q=-\frac{k}{{\mu }_g}\mathit{\nabla }p$$ (2)

Where q is the Soil gas velocity (L/T), k is the soil permeability (L²), μ_g is viscosity of soil gas (M/L/T) and p is the pressure of soil gas (M/L/T²).

And the general governing equation for convection and diffusion of non-biodegradable contaminant in soil is [14]

$$J_T=qc-D_{eff}\mathit{\nabla }c$$ (3)

Where J_T is Bulk mass flux of contaminant (M/L²/T), c is the concentration of chemical in soil gas (M/L³) and D_eff is the effective soil diffusivity (L²/T).

The entry rate of contaminant into the house is given by [12]

$$J_{ck}=\frac{\frac{Q_s{c}_{ck}}{A_{ck}}\mathit{\text{exp}}\left(\frac{Q_s{d}_{ck}}{D^{ck}{A}_{ck}}\right)}{\mathit{\text{exp}}(\frac{Q_s{d}_{ck}}{D^{ck}{A}_{ck}})-1}$$ (4)

Where c_ck is the subslab concentration (M/L³), A_ck is the crack area (L²) and J_ck is the bulk mass flux of chemical throughout the crack (M/L²/T)).

3. Results and discussion

3.1 The influence of crack configurations

The indoor air contaminant concentration is a key indicator of indoor air quality of enclosed space, and it is determined by contaminant entry rate J_ck and indoor air exchange rate. The latter is only influenced by building operation conditions, while the first is a result of both convection and diffusion. For scenarios with the same crack configuration it is the soil gas flow rate into a building that mainly determines the order of magnitude of contaminant mass entry rate, as near-crack subslab contaminant concentration does not typically vary much with location (and indoor air contaminant concentration is negligible compared to subslab crack concentration). The latter is true for a wide range of scenarios, because diffusion dominates the soil gas concentration profile, and convection is always too weak to affect the profile far from the crack.

Figure 3 shows typical steady state contaminant concentration profile plots for a building with a basement and a building built atop a slab-on-grade. The cases here involve the different assumptions of crack type, discussed below. The contour lines are for contaminant concentration normalized to vapor concentration at the groundwater source. They show the well-established upward-sucking of high concentration zones beneath the foundation. This is attributed to the foundation acting as a diffusion barrier, and is a common feature of all such modeling results [1–7]. Note that the variation of concentration with position beneath the building is relatively modest.

FIGURE 3.

The normalized contaminant soil vapor concentration profile of simulations with 10⁻¹¹ m² soil permeability, 10m X 10m foundation footprint and 8m source depth: (a) basement with perimeter crack; (b) slab-on-grade with perimeter crack; (c) basement with center hole; (d) slab-on-grade with center hole; (e) basement with center crack; (f) slab-on-grade with center crack.

Results for the soil gas entry flow rate for three different crack types and two foundation types are summarized in Figure 4. It should be emphasized that this is total soil gas entry rate and not contaminant entry rate, which is considered below. Note that the center hole and center crack curves for basement and slab cases fall atop one another.

FIGURE 4.

The influence of crack types on soil gas flow rate into a house for the cases with 2m (basement) and 0.1 m (slab-on-grade) foundation depth and foundation footprint size of 10 m × 10 m (PC, CH and CC indicate cracks of “Perimeter Crack”, “Center Hole” and “Center Crack” types; “base” refers basement and “slab” to slab-on-grade; k indicates soil permeability)

In Figure 4, the soil gas flow rate is the highest for a building with a “perimeter crack”, and smallest for a building with a “center hole”. This difference arises from the difference in the distance between the crack and the atmosphere in these two cases. This distance defines the pressure gradient that drives the gas flow. The difference in the soil gas flow rate Q_s is about one order of magnitude between these two cases. The building foundation type (slab-on-grade or basement) has the largest influence on soil gas flow rate in simulations involving a “perimeter crack”, while for the other two types of cracks the effect of foundation type is not significant. Generally, the choice of crack type can induce at most one order of magnitude difference in predicted soil gas entry rate, and foundation type (basement or slab-on-grade) does not matter much, except as noted.

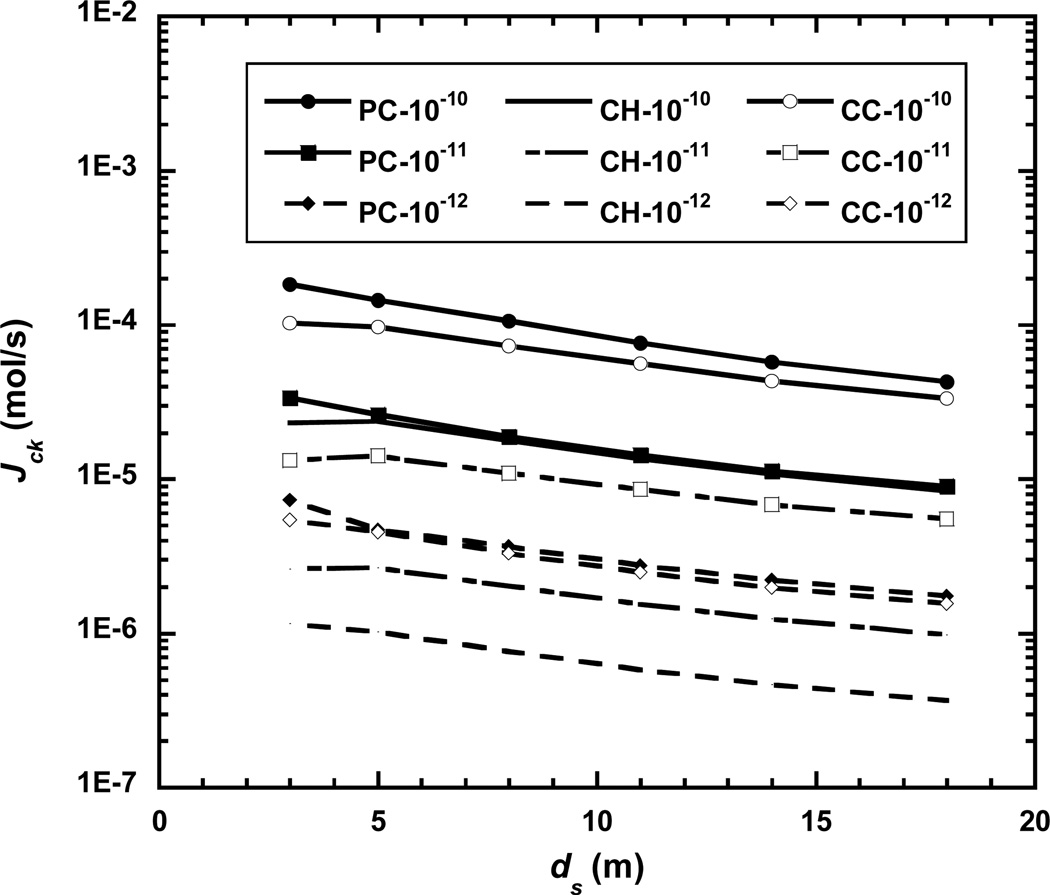
The simulation results in Figure 5 and 6 show the contaminant mass flow rate into the subject building for cases with different crack types, foundation types and soil permeabilities for different contaminant source depths. Equation (2) was used to calculate the indicated values of J_ck, using the valves of Q_s as illustrated in Figure 4 and the relevant subslab concentration at the crack (which is obtained from results such as in Figure 3). Figure 5 and 6 are plotted to show the influence of groundwater source depth, in addition to crack type and soil permeability. This variable is seen to have modest effect on the results. The contaminant mass flow rate into the house is determined by both soil gas flow rate and contaminant subslab crack concentration in these high permeability cases (shown as 10⁻¹⁰-10⁻¹² m² soil permeability) and mainly by contaminant subslab crack concentrations for low permeability cases (not shown, but 10⁻¹⁴ m² permeability). This is because in this latter case contaminant entry building can only occur via diffusion through the crack.

FIGURE 5.

The influence of crack types and sol permeability on contaminant mass entry rate for the cases with 2m foundation depth and building footprint size of 10 m × 10 m (PC, CH and CC indicate cracks of “Perimeter Crack”, “Center Hole” and “Center Crack” types. d_s indicates the depth of a groundwater contaminant source, below ground surface)

FIGURE 6.

The influence of crack types and soil permeability on contaminant mass entry rate for the cases with 0.1m depth foundation, i.e. slab-on-grade with footprint size as 10 m × 10 m (PC, CH and CC indicate cracks of “Perimeter Crack”, “Center Hole” and “Center Crack” types. d_s indicates the depth of a groundwater contaminant source, below ground surface)

For cases with high soil permeabilities, such as all those shown in Figure 5 and 6, the subslab crack concentration is relatively lowest adjacent to perimeter cracks due to their edge location nearest the atmospheric sink outside the building footprint. For “center hole” cases, advection into the building is weak as noted above, and diffusion plays a more significant role in contaminant entry. This results in a “sink effect” at the crack, which means the subslab concentration right at the “center hole” crack is lower than that of the surrounding subslab area. Without such a hole, contaminant concentration will always be highest under the center of the slab. For cases involving a center crack, the soil gas entry rate decreases along length of the crack from the edge to the center of the foundation slab. This is again attributable to the increase in lateral separation distance of the depressurized house interior from the surrounding atmosphere in going from edge to center. The diffusion “sink effect” is not as significant in this case which is more similar to the perimeter crack case, so the subslab contaminant concentration profile is also similar to that in the case of a perimeter crack. The product of local contaminant concentration and soil gas entry rate for the center crack case results in an almost equivalent contaminant mass entry rate to that for the perimeter crack cases, which again exceed those of “center hole” cases.

As the soil permeability decreases, diffusion becomes the process limiting contaminant entry since soil gas flow rate becomes unimportant in determining contaminant mass entry rate for all cases. Contaminant mass flow rate into a perimeter crack is greatly decreased in the absence of advection. The influence of low soil permeability in the “center crack” cases is not as significant as in the “perimeter crack” cases because soil gas entry rate does not contribute as much as in the “perimeter crack” cases. The predicted subslab concentration of the “center crack” cases decreases only a little due to the diffusion “sink effect”. The contaminant mass entry rate of the “center hole” cases is least affected by low permeability since advection already does not play a big role in this instance.

Generally, the contaminant mass entry rate decreases for all three crack types as advection decreases with reduced soil permeability, and in the “center crack” and “center hole” cases, the subslab crack concentration also decreases due to a the diffusion “sink effect”.

All the differences of contaminant mass entry rate found for different crack types for the cases of Figure 5 and 6 are within an order of magnitude of one another. In other words, making the assumption of a perimeter crack in describing the vapor intrusion situation does not influence the results much, as compared with assuming other cracks of similar area. Moreover, it can be seen that assuming a perimeter crack is a relatively conservative assumption, generally giving the highest mass entry rate due to strong convection, except in the case of slab-on-grade construction and relatively high soil permeability.

3.2 The influence of foundation footprint size

Figure 7 and 8 show the influence on contaminant mass entry rate through the unit area of a perimeter crack as a function of foundation size for basement and slab-on-grade cases, respectively.

FIGURE 7.

The influence of foundation footprint size on contaminant mass entry rate through unit perimeter crack area for the cases with 2m depth foundation (basement) (10m-10⁻¹⁰ m² means the building footprint size is 10m X 10m and soil permeability is 10⁻¹⁰ m²)

FIGURE 8.

The influence of foundation footprint size on contaminant mass entry rate through unit perimeter crack area for the cases with 0.1m depth foundation (slab-on-grade) (10m-10⁻¹⁰ m² means the building footprint size is 10m X 10m and soil permeability is 10⁻¹⁰ m²)

The soil gas flow rate through a unit area of perimeter crack for a certain soil permeability is determined by the pressure difference between that at the crack and atmosphere, and the separation distance from the open atmospheric surface surrounding the building and the crack. The crack pressure is only determined by the situation inside the building, while atmospheric pressure is the same for foundations of difference sizes. The flow at the crack also depends on foundation depth from the open ground surface.

Since the soil gas entry rate per unit crack area does not depend on foundation size for the “perimeter crack” cases, the similar contaminant mass entry rate per unit crack area for three different building foundation sizes indicates that the subslab crack contaminant soil vapor concentration varies little with foundation size. This is why there are clusters of curves for different soil permeabilities (soil gas flow is proportional to permeability for a given pressure difference), but in which the effect of foundation size is seen to be small (see Figure 7 and 8).

3.3 The influence of soil vapor diffusivity in the crack

Figure 9 and 10 show the influence of in-crack contaminant diffusivity on subslab contaminant concentration and mass entry rate. The effective diffusivities of contaminant in soil (1.04X10⁻⁶ m²/s) and in air (7.4X10⁻⁶ m²/s) were used as different limiting cases, since both assumptions have been used in the literature.

FIGURE 9.

The influence of crack diffusivity on contaminant subslab crack concentration for different contaminant source depths, with 2m depth foundation (basement) (S and G indicates that the effective diffusivity in the crack is assumed to be the effective diffusivity in soil (S) or air (G). 10⁻¹¹ refers to the soil permeability.)

FIGURE 10.

The influence of crack diffusivity on contaminant mass entry rate through unit perimeter crack area for the cases with 2m depth foundation (S and G indicates that the effective diffusivity in the crack is assumed to be the effective diffusivity in soil (S) or air (G). 10⁻¹¹ refers to the soil permeability.)

For cases with high soil permeability, such as 10⁻¹⁰ and 10⁻¹¹m², convection dominates the flux through the crack, and the diffusivity in the crack is not important in determining the contaminant flow rate through the crack. The contaminant concentration boundary condition at the crack is independent of the crack diffusivity, as is the contaminant concentration profile in the soil.

For cases with low soil permeability, less than 10⁻¹²m², diffusion dominates the flux through the crack. As the crack size is small compared to the overall domain of interest, the influence of the crack is limited as far as determining the contaminant concentration profile anywhere but near the crack. Figure 9 shows that the difference in contaminant subslab concentration caused by changing crack diffusivity is not significant. In other words, the contaminant mass entry rate is only determined by the crack diffusivity itself since all other conditions remain the same. Source depth is seen to be a far more important factor in determining subslab concentration than is any assumption regarding permeability.

3.4 The variation of subslab concentration

For vapor intrusion site investigation, subslab sampling location is always a concern. How much does the sample position influence observed contaminant subslab soil vapor concentration? Some VI models [12–13] employ the subslab perimeter crack contaminant concentration to calculate contaminant mass entry rate, using Nazaroff’s equation [25] to estimate soil gas entry rate. But in practice, it is generally not possible to examine the subslab soil vapor concentration at the entrance of any particular crack. Of course the Johnson-Ettinger model does not allow for any subslab variation in concentration because it is a one-dimensional model.

Figure 3 and 11 show the cross-sectional soil gas contaminant concentration profiles for both basement and slab-on-grade foundations, for different crack types and an assumed soil permeability of 10⁻¹¹ and 10⁻¹³ m², respectively. The first thing these figures suggest is that the crack type does not have much influence on subslab concentration distribution. Since, (indoor air is relatively clean compared to the soil gas,) the subslab crack contaminant concentration is always a bit lower than that of its immediate surroundings. The so called “sink effect” becomes more obvious for cases with low permeability as noted above. But in general, because this “sink effect” is limited by the crack size. What mainly determines the concentration profile under the slab is the blocking effect of the foundation slab on contaminant diffusion. Second, the subslab concentration contour shapes for the two cases of slab-on-grade and basement are quite similar, except that the normalized subslab concentration for a basement is about 0.1–0.2 larger than that of a slab-on grade for the same horizontal location. The reason is quite obvious; the subslab locations in the slab-on-grade case are closer to the atmospheric sink around the building. Figure 3 and 11 also suggest that for buildings with a typical 10m X 10m footprint size, the normalized contaminant subslab concentration range is 0.3–0.7 for basement cases and 0.1–0.5 for slab-on-grade cases. It should be noted that such limited ranges of variation will lead to only comparable variations in indoor air contaminant concentration (where only even correct order of magnitude estimates are still typically sought).

FIGURE 11.

The normalized contaminant soil vapor concentration profile of simulations with 10⁻¹³ m² soil permeability, 10m X 10m foundation footprint and 8m source depth: (a) basement with perimeter crack; (b) slab-on-grade with perimeter crack; (c) basement with center hole; (d) slab-on-grade with center hole; (e) basement with center crack; (f) slab-on-grade with center crack.

Figure 12 and 13 present the influence on subslab concentration of increasing foundation slab size for different soil permeabilities. Both figures show that the peak subslab concentration at the middle increases as the foundation size increases. For basement cases, the subslab concentration can for large structures reach values almost as high as the source soil vapor concentration, since it becomes progressively more difficult for the contaminant soil vapor to diffuse from the middle as the foundation size increases. These two figures also suggest that soil permeabilities play an insignificant role in determining subslab contaminant concentration profile.

FIGURE 12.

The normalized contaminant soil vapor concentration profile of simulations with 10⁻¹¹ m² soil permeability, perimeter crack and 8m source depth: (a) 5m X 5m basement; (b) 10m X 10m basement; (c) 20m X 20m basement; (d) 5m X 5m slab-on-grade; (e) 10m X 10m slab-on-grade; (f) 20m X 20m slab-on-grade.

FIGURE 13.

The normalized contaminant soil vapor concentration profile of simulations with 10⁻¹³ m² soil permeability, perimeter crack and 8m source depth: (a) 5m X 5m basement; (b) 10m X 10m basement; (c) 20m X 20m basement; (d) 5m X 5m slab-on-grade; (e) 10m X 10m slab-on-grade; (f) 20m X 20m slab-on-grade.

Except for something like the sink effect of a large hole in the slab, the subslab concentration increases as the sampling location approaches the center of the foundation slab. On the other hand, the limit of the subslab concentration at the edge of the foundation slab is zero, since the foundation slab edge approaches the open atmosphere. Overall, though subslab concentrations typically are predicted to fall in a range of 0.1 to 1 [28]. In other words, it is possible to conclude that the difference in subslab concentrations attributable to the location of subslab soil vapor sample points should be within an order of magnitude, and often much closer. Larger variations than this strongly suggest some other type of inhomogenously in the subslab (e.g. ventilation).

4. Conclusions

This paper presents 3-D simulations of vapor intrusion scenarios with different building foundation slab features. Three types of crack, e.g. perimeter crack, center crack and center hole, were simulated to examine the influence of vapor intrusion entry pathway. The simulation results show that soil gas flow rate can be influenced by crack configuration, but the contaminant mass entry rate, which determines the indoor air contaminant concentration, does not vary much, no more than one order of magnitude. Leaving aside the scenario of a center hole, the crack scenarios offer much closer than order of magnitude agreement. The simulations in this study provide support for the application of models that employ various crack descriptions. The location and the shape of an actual crack in the foundation slab (as opposed to a hole) is not important for determining contaminant mass flow rate into the building. This means it is safe to apply a model employing a perimeter crack assumption since other assumptions do not change this very much and assumption of a hole in the center leads to lower entry rate predictions. The foundation size affects neither the subslab perimeter crack concentration nor the contaminant entry rates much, as long as the overall crack area is constant. It is the overall area of cracks that is the key parameter. For an infinite homogenously distributed groundwater source, the subslab concentration (normalized to source vapor concentration) is predicted to range from lowest at the foundation edge to highest in the middle of the slab, and in most cases would fall in the range 0.1–1 [1, 14]. This means that the subslab sampling position should not make more than a comparable difference in observed contaminant concentrations. Again, for any particular scenario (e.g. basements), the variation in subslab concentration is much less than an order of magnitude. It is the large slab on grade scenarios that offer the greatest variation in subslab concentrations. All the above discussions are based on the assumption of homogenous source distribution.

Highlights.

• We simulate vapor intrusion scenarios with different slab features

• The results show slab features play insignificant role in vapor intrusion

• Perimeter crack can be used as a typical entry pathway in vapor intrusion models

• The sampling position of subslab soil gas concentration is not important