Tomographic sensing and localization of fluorescently labeled circulating cells in mice in vivo

Abstract

Sensing and enumeration of specific types of circulating cells in small animals is an important problem in many areas of biomedical research. Microscopy-based fluorescence in vivo flow cytometry methods have been developed previously, but these are typically limited to sampling of very small blood volumes, so that very rare circulating cells may escape detection. Recently, we described the development of a ‘diffuse fluorescence flow cytometer’ (DFFC) that allows sampling of much larger blood vessels and therefore circulating blood volumes in the hindlimb, forelimb or tail of a mouse. In this work, we extend this concept by developing and validating a method to tomographically localize circulating fluorescently labeled cells in the cross section of a tissue simulating optical flow phantom and mouse limb. This was achieved using two modulated light sources and an array of six fiber-coupled detectors that allowed rapid, high-sensitivity acquisition of full tomographic data sets at 10 Hz. These were reconstructed into two-dimensional cross-sectional images using Monte Carlo models of light propagation and the randomized algebraic reconstruction technique. We were able to obtain continuous images of moving cells in the sample cross section with 0.5 mm accuracy or better. We first demonstrated this concept in limb-mimicking optical flow photons with up to four flow channels, and then in the tails of mice with fluorescently labeled multiple myeloma cells. This approach increases the overall diagnostic utility of our DFFC instrument.

Introduction

Sensing and enumeration of specific types of circulating cells in small animals is an important problem in many areas of biomedical research. For example, obtaining an accurate count of circulating cells is frequently required in pre-clinical studies of the immune system and the metastatic spread of cancer (Steeg and Theodorescu 2008, Gupta et al 2005, Lang et al 2009, Smerage and Hayes 2008, Dawood and Cristofanilli 2007, Lo Celso et al 2009). Normally, this is achieved by drawing relatively small (~100 μL) blood samples which are analyzed at a later time using flow cytometry, hemocytometry and more recently with microfluidic devices (Shapiro 1995, Nagrath et al 2007, Huang et al 2008, Russom et al 2008, Cheng et al 2007). These approaches are generally limited since blood samples represent a small fraction of the total blood volume of the animal, so that rare cells may escape detection. Further, since samples are drawn typically only once per day, obtaining circulation kinetics is challenging (Hoff 2000). To address these limitations, in vivo flow cytometry (IVFC) techniques have been developed to allow continuous, non-invasive sensing of fluorescently labeled cells (Georgakoudi et al 2004). Typically this involves illumination of a small blood vessel in the ear (Novak et al 2004) or retina (Alt et al 2007) of a mouse and confocal detection of emitted fluorescence from individual cells. Similarly, two photon microscopy (Boutrus et al 2007), fiber-delivered intravascular (Chang et al 2010) and photoacoustic (Nedosekin et al 2011, Galanzha et al 2009) IVFC approaches have also subsequently been developed. While extremely useful, these IVFC approaches are limited by the relatively small sampling blood volume (of the order of μL min⁻¹) so that the lower sensitivity limit of detection is about 10³–10⁴ cells in circulation, making detection of very rare cells below this threshold challenging.

In an effort to address this limitation in sensitivity, we recently reported the development of a diffuse fluorescence flow cytometry (DFFC) instrument that used mesoscopic-scale (~3 mm pathlength) illumination and detection of fluorescent light from a limb (e.g. forelimb, hindlimb or tail) of a mouse using a high-sensitivity fiber-optic detection ring (Zettergren et al 2012). The key advantage of this approach is improved detection sensitivity, since it utilizes illumination of relatively large blood vessels with high flow rates from 0.2 to 0.5 mL min⁻¹ (Wagner et al 2004). This allows sampling of large blood volumes so that in principle the entire blood volume of the mouse can be sampled in less than 10 min. We demonstrated that the DFFC instrument was capable of detecting calibrated (cell-simulating) fluorescent microspheres and fluorescently labeled multiple myeloma (MM) cells both in limb-mimicking optical flow phantoms and in mice in vivo. Furthermore, we showed that the device could detect cells at concentrations lower than 100 cells mL⁻¹ at linear flow speeds up to 15 cm s⁻¹ with very high sensitivity. As such, the approach is of potentially high diagnostic value for researchers studying, for example, early-stage metastatic development of cancer and hematological malignancies such as MM.

However, we noted that the DFFC device did not provide information on the location of the moving cell in the cross section of the sample (limb), thereby limiting the diagnostic potential of the device. For example, we showed that without spatial data the DFFC could produce overcounting errors, since fluorescent signals (i.e. ‘spikes’) from individual cells would be double-counted, e.g. if they traveled twice through the field of view of the instrument on the return trip through the vasculature. Hence, the ability to obtain tomographic localization of the cell would yield important information to minimize this and increase the accuracy of the DFFC approach.

In this paper, we extend our previous work by developing a diffuse fluorescence tomographic imaging algorithm and demonstrating its operation in flow phantoms in vitro and in mice in vivo. This required modification of the DFFC instrument so that it now uses two sequentially illuminated laser sources and six detector channels. It was possible to coarsely localize the cross-sectional position of microspheres or cells by analyzing the relative amplitudes of the spikes detected on each channel using Monte Carlo (MC) models of photon propagation and the randomized algebraic reconstruction technique (r-ART). As we discuss, the primary technical challenge was the rapid, high-sensitivity optical scanning of the mouse limb so that full data sets (and therefore cross-sectional images) could be obtained at 10 Hz. This approach was validated first using fluorescent microspheres in multi-channel optical flow phantoms, and then tested in nude mice with circulating MM cells. This technique adds significant utility to our DFFC system since it allows, for example, determination of the cell count rate in a particular region on the limb (and corresponding group of blood vessels) rather than the entire instrument field of view. Furthermore, to our knowledge, this type of fast-scanning, transient diffuse fluorescence tomography on circulating fluorescently-labeled cells has never been described previously and may be applicable to other rapid sensing and imaging problems at similar physical scales.

Methods and materials

Instrument description and data acquisition

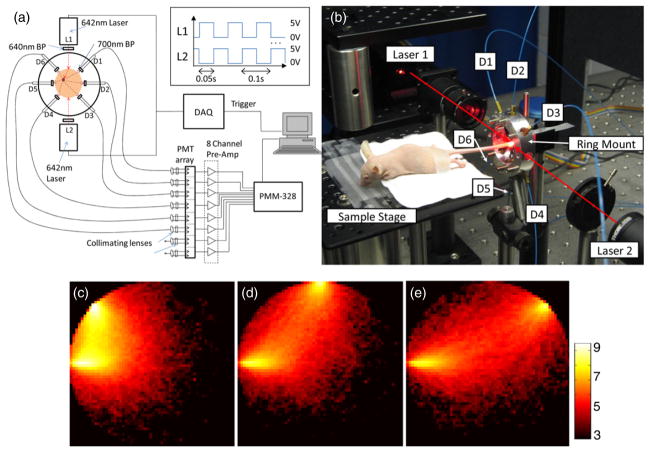
A schematic diagram of the modified diffuse fluorescence flow cytometer (DFFC) is shown in figure 1(a) along with a photograph of the instrument during in vivo operation (figure 1(b)). The sample—either a flow phantom model or mouse limb—was held in the center of the custom-designed ring and illuminated on opposite sides by two 642 nm solid-state modulateable lasers (DL640-050-O, CrystaLaser Inc., Reno, NV). Each laser was passed through a 640 nm ‘cleanup’ excitation filter with a 10 nm bandpass (Z640/10 ×, Chroma Technology, Rockingham, VT) before reaching the sample. In contrast to our previous work where only one illumination source was used, the two lasers were modulated at 10 Hz with a duty cycle of 50% and opposite phase as illustrated in the inset of figure 1(a). This modulation was controlled using two output channels of a multi-function data acquisition card (DAQ; NI-USB-6251, National Instruments, Austin, TX). The average power at the sample for both lasers was 7.5 mW with a spot size of 1 mm in diameter.

Figure 1.

(a) Schematic of the DFFC instrument showing the two-laser modulated illumination scheme (inset). (b) Photograph of the DFFC during in vivo operation. The positions of the six detectors and two light sources are indicated. Three example computed sensitivity functions (c)–(e) between the first laser and detectors 1–3, plotted on a logarithmic scale for clarity.

Fluorescence signals from the sample were collected with the six detector fibers arranged circularly around the ring as shown. Custom cut 2 mm × 3 mm 700 nm emission filters with a 50 nm bandpass (ET700/50, Chroma Technology, Rockingham, VT) were placed at the end of each detection fiber to reject laser light and background auto-fluorescence from the sample as well as auto-fluorescence from the fibers themselves. The fibers were then terminated on a custom filter housing with collimating lenses and a second set of 700 nm bandpass filters (Chroma) before reaching an eight-channel, multi-anode photo-multiplier tube (PMT; H9530–01, Hamamatsu Photonics, Japan). Output signals from the PMT array were then passed through a 1.6 GHz eight-channel preamp with 26 dB gain (HFAM-26dB-10, Boston Electronics, Brookline, MA) and then into an eight-channel multi-channel scalar (MCS) photon counting card (PMM-328, Boston Electronics). The instrument was controlled with a personal computer (NIXSYS Open Systems, Santa Ana, CA).

During experiments, photon count data were captured with the PMM-328 software (Boston Electronics). The cards were configured so that photon counting threshold for each channel was −100 mV with a sampling rate of 100 samples s⁻¹. For each sample ‘run’, we collected 7500 data samples so that the acquisition time was 75 s. Experimental runs could then be repeated an arbitrary number of times to allow for continuous data collection, and data from separate runs were concatenated during post-experimental signal processing. The start of each data acquisition cycle was triggered on the rising edge of laser 1 so that the lasers and MCS sampling times were synchronized. Since each data channel recorded signals when the lasers were sequentially illuminating, it was also necessary to parse the data after acquisition to generate 12 separate measurements for each of the source–detector pair combinations. This step was performed using custom-written code in MATLAB (The Mathworks, Natick, MA).

Optical flow phantom design

To test the tomographic image reconstruction capabilities of our instrument, we first used limb-mimicking optical flow phantoms and fluorescent calibrated cell-simulating flow cytometry microspheres as we have done previously (Zettergren et al 2012). We developed a set of flow phantoms with similar size, optical properties, flow speeds and autofluorescence of a mouse limb (e.g. forelimb, hindlimb or tail). Phantoms were made from a polyester resin material (Casting Craft, Fields Landing, CA) with titanium oxide (TiO₂; Sigma-Aldrich Inc., St Louis, MO) and India Ink (Higgins Ink, Bellwood, IL) added to control the optical properties (Baeten et al 2007). In all cases, phantoms were made with absorption coefficient μ_a = 0.1 cm⁻¹ and reduced scattering coefficient μ′_s = 15 cm⁻¹, which are in the range of optical properties of biological tissue at NIR wavelengths quoted in the literature (Niedre et al 2006). The resin was placed in a 3 mm diameter cylindrical mold before hardening with one or more lengths of 250 μm diameter microbore Tygon tubing (TGY-010-C, Small Parts, Inc., Seattle, WA) passed through to simulate the presence of large blood vessels.

To test the tomographic imaging capabilities of the DFFC instrument, we developed optical flow phantoms with increasing complexity of 1, 2 or 4 lengths of Tygon tubing embedded, i.e. to simulate the presence of multiple blood vessels in a mouse limb. For ‘single-tube’ flow phantoms, a length of tubing was passed either close to the edge of the phantom to simulate a superficial blood vessel or close to the center to simulate a deeper seated blood vessel (N = 4 for each). ‘Double-tube’ flow phantoms were made (N = 4) by embedding a single length of tubing that was passed along one edge of the phantom, then looped approximately 1 cm from the end and passed back through the resin a second time before hardening. As such, each microsphere would pass through the DFFC field of view twice on the return trip through the phantom. Finally, we constructed set of ‘quadruple-tube’ phantoms where two separate strands of Tygon tubing were passed through the phantom twice each in a loop, thereby creating four separate flow channels (N = 4). As we discuss, these were meant to mimic the major blood vessels in the tail of a mouse.

Data collection, optical flow phantoms

To simulate fluorescently labeled cells, we used commercially available flow cytometry calibration microspheres (PeakFlow Claret, P-24670, Invitrogen, Carlsbad, CA) with an absorption peak near 645 nm and an emission peak near 695 nm. We have shown in our previous work that these spheres have similar size and fluorescence intensity to Vybrant-DiD labeled MM cells (which were used in vivo testing). Before each experiment, microspheres were diluted and suspended in a phosphate buffered saline solution at a final concentration of approximately 10³ spheres mL⁻¹. This concentration was chosen so that only a single microsphere was in the DFFC field of view during essentially all of the acquisition period. Microsphere suspensions were sonicated (2510, Branson Ultrasonics Corp., Danbury, CT) for 5 min before running through the DFFC to prevent self-aggregation and clumping.

Each optical flow phantom was placed in the center of the tomographic ring and was marked to obtain an initial reference orientation of 0°. The Tygon tubing embedded in the phantom was then connected to a 30-gauge insulin syringe (Easy Touch, Loveland, OH) containing a suspension of cell simulating microspheres. Suspensions were then passed through the flow phantom using a microsyringe pump (70–2209, Harvard Apparatus, Holliston, MA). Except where noted, a constant linear flow speed of 1 cm s⁻¹ was used since it is similar to the upper limit of blood flow speeds reported in mouse tail veins (Wagner et al 2004). After data acquisition, the phantom was then rotated to different orientations with respect to the reference—specifically, 90°, 180°, 270° and 315°—and data collection was repeated. In the case of the ‘quadruple-tube’ phantoms, two syringes were connected (to each of the two strands of Tygon tubing) so that microspheres were flowing through all flow channels simultaneously. After DFFC imaging, phantoms were cleaved along their cross section at the imaging point with a fine razor blade. White-light photographs of the cross section were than taken with a custom-built imager, composed of an Andor IXON camera (DU-885K-CS0, Andor Technology, South Windsor, CT) with a 2 × objective (NT59-875, Edmund Optics, Barrington, NJ). The location of the mark was noted during imaging so that these cross-sectional images could be compared to our tomographic image reconstructions to assess the accuracy of our approach.

Cell culture and fluorescent labeling

MM cells were used for in vivo testing of our DFFC tomographic imaging approach since we used them previously in both in vitro and in vivo studies (20). MM cells have also been used extensively in microscopy-based IVFC studies by others previously (Azab et al 2009, Alsayed et al 2007). The cells were cultured and then harvested using Trypsin and spun down at 400G and re-suspended in RPMI with 0.1% bovine serum albumin at a concentration of 10⁶ cells mL⁻¹. Cells were dyed using a final concentration of 1 μmol L⁻¹ of Vybrant-DiD and incubated for 30 min at 37 °C. At the end of the incubation process, FBS was added (2% of total volume) to prevent cell clumping during centrifuging. Cells were centrifuged as before and washed, once with RPMI with FBS to remove any free DiD in suspension, and again with RPMI only. They were then resuspended for injection.

In vivo testing

All mice were handled in accordance with Northeastern University’s Division of Laboratory Animal Medicine policies on animal care. Nude (nu/nu) mice first were anesthetized using a cocktail of ketamine (100 mg kg⁻¹) and xylazine (5 mg kg⁻¹) injected i.p. The mice were then placed on a heated, adjustable platform with the tail passing through the center of the detector ring, oriented so that the ventral artery (VA) was directly illuminated by the first laser and the dorsal vein (DV) was directly illuminated by the second laser (i.e. with the mouse lying on its left side). The diameter of the tail in this position was approximately 3 mm. The tail was secured lightly on each end to minimize motion artifacts due to breathing, but not tight enough to restrict blood flow. The mouse was also secured to the platform with medical tape to further reduce motion artifacts. A 100 μL bolus containing a total of 10⁵ fluorescently labeled MM cells was injected retro-orbitally and DFFC data were collected for approximately 20 min after injection. Retro-orbital injections were used so as not to disrupt blood flow in the tail (as in tail vein injections) and since it allowed continuous acquisition of data before, during and immediately following the injection. Experiments were repeated on three animals, and unlabeled cells were also injected as a control (N = 3).

Fluorescence tomographic image reconstruction

Following data collection, tomographic image reconstructions were performed using custom-written MATLAB code. The data were first parsed into 12 different channels, corresponding to each of the (two) source and (six) detector pairs. Data were then re-summed into 0.1 s time bins, so that the overall effective sampling rate was 10 Hz. The intensities were calibrated for the (minor) differences in channel sensitivity. The mean background was then subtracted from each detection channel to remove dc background signals. This was achieved by subtracting the mean the signal from a moving 10 s window from each data point; this was empirically found to effectively remove dc drift at low concentrations of microspheres and cells.

Two-dimensional axial slice images of the phantom or tail cross section were then generated for each time point using an approach commonly used in fluorescence-mediated tomography (FMT) (Hielscher 2005, Ntziachristos et al 2002, Milstein et al 2003, Niedre and Ntziachristos 2010). Fluorescence information along the length of the tail could not be obtained using our scanning geometry and was therefore considered constant along the lateral direction inside the axial slice. Specifically, a linear matrix equation of the form W · x = b was formed for each 0.1 s time point. Here, b was the vector of 12 measurements collected during each sample interval (time point). In FMT the instrument ‘weight functions’ W are frequently calculated using the diffusion approximation to the Boltzmann transport equation (Jacques and Pogue 2008); however, since in this case the tissue volumes were very small (3 mm diameter) these were computed using a MC simulation. For this, we used modified MC code that was based on the publically available code on the Oregon Medical Laser Center (Wang et al 1995) website as we have described previously (Valim et al 2010). Herein, the 3 mm diameter medium was simulated with a 0.25 × 0.25 pixel size. The following optical properties were assumed: scattering coefficient μ_s = 150 cm⁻¹, anisotropy constant g = 0.9 and absorption coefficient μ_a = 0.1 cm⁻¹. The number and path of photons emerging from the medium from an incident pencil beam at the detector locations were logged. In each case, 1 billion photons were tracked which required about 72 h of computation time on a 3.2 GHz dual-core PC running Linux. Example weight functions between the first laser and detectors 1–3 are shown in figures 1(c)–(e), respectively.

To solve this system of equations and obtain a fluorescence image, the 3 mm diameter cross-sectional tissue volume was discretized into a 250 μm grid. The fluorescence concentration at each point in the cross section x was then calculated at each time point using the r-ART (Gaudette et al 2000, Intes et al 2002). r-ART is an iterative, regularized inverse algorithm commonly used for solving systems of equations of this form. For these experiments, a regularization parameter of λ = 0.25 was used. A total of 25 iterations were performed since further iterations resulted in no observable changes to the reconstruction. The choice of r-ART for computation of the inverse problem was somewhat arbitrary but was used here since it (i) is frequently used for FMT imaging, (ii) computes rapidly and (iii) allows the solution to be constrained to non-negative values.

Here, we note three specific points related to fluorescence tomographic image reconstruction problem that are unique to the present case. First, our approach implicitly assumed that the location of the moving fluorescently labeled cell or microsphere did not change significantly in the 0.1 s time interval. Second, we assumed that all fluorescent light that emerged at the edge of the limb adjacent to each detector was detected, i.e. we did not model light collection effects of the fibers and ignored the propagation of the light in the free space between the detectors and the limb. Third, we note that the inverse problem here is highly underdetermined, i.e. we obtain 144 unknown fluorescence concentrations with the use of only 12 equations (source–detector measurements). These issues are discussed in more detail below, but as we demonstrate, despite these simplifications our approach yielded image reconstructions with good accuracy.

Results

Single-tube flow phantoms

As an initial test of the tomographic reconstruction capability of the DFFC instrument, a set of flow phantoms embedded with single strands of Tygon tubing were fabricated and tested. Example background-subtracted measured photon counts on the six detectors as a function of time when the first laser (‘laser 1’) was illuminating the sample are shown in figures 2(a)–(f). An analogous data set was also simultaneously collected when laser 2 was illuminating the sample (not shown for brevity). When a fluorescent microsphere passed through the instrument field of view, a transient ‘spike’ was recorded on all channels. In this particular experiment, the flow tube of the phantom was oriented toward the bottom of the detector ring so that the tube was physically closest to detector 5. The difference in signal amplitude between each channel (i.e. the ‘spike heights’) is evident, i.e. the signals from detectors 4–6 were the largest in magnitude. This difference in inter-channel signal intensity provided the basis for our ability to reconstruct cross-sectional fluorscence images.

Figure 2.

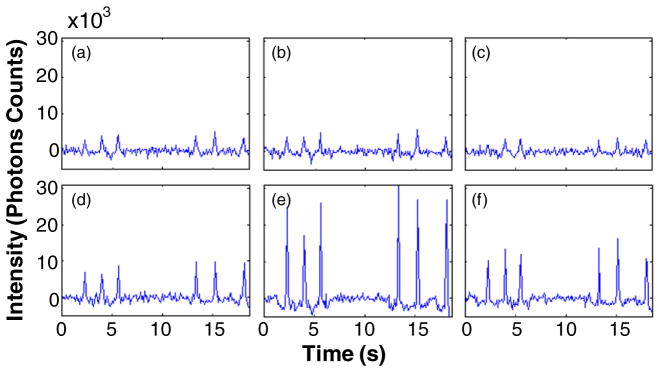
Example data acquired on each of the six detector channels (a)–(f) when a flow phantom with a single embedded tube was imaged. The tube was closest to detector D5 (e) where the largest spikes were observed. All flow phantoms were 3 mm in diameter.

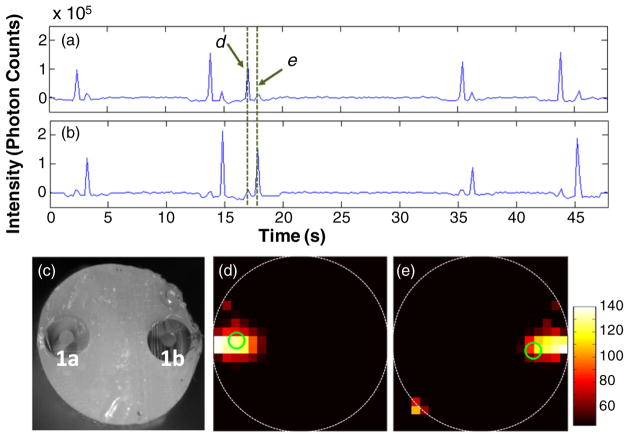
These data were next reconstructed using the approach described above. An example image obtained from a single fluorescent microsphere (spike), along with the white-light cross-sectional image of the phantom, is shown in figures 3(a) and (b), respectively. As shown, the microsphere was reconstructed in a location close to the physical location of the Tygon tube. Although in principle the spheres should have reconstructed as point objects, unsurprisingly the algorithm yielded images with a slightly extended (blurry) shape with a full-width-at-half-maximum (FWHM) diameter of about 0.5 mm. For clarity, the location of the centroid of the reconstruction is indicated with a green circle in figure 3(b) (and all reconstructions that follow). Similar measurements and reconstructions were performed when the same phantom was rotated counterclockwise through 90°, 180°, 270° and 135° Example image reconstructions for each of these orientations, along with white-light cross-sectional photographs, are shown in figures 3(c)–(j), respectively. In all cases the fluorescent microspheres were reconstructed in the approximate location of the tubing. In the particular case where the tube was oriented at 135° (i.e. closest to detector 1) the object was reconstructed as a more elongated source along the diagonal; however, the centroid of the reconstructed object corresponded well to the location of the tube. We analyzed the error in the position of the reconstruction centroid and the true position of the flow tube for 350 spikes at multiple orientations. For superficially located tubes, the mean error was 0.2 ± 0.1 mm. The technique was also found to be robust in that the reconstructed position was consistent between individual spikes for each experiment; an example of this for the 270° orientation is shown in supplemental video 1 available at stacks.iop.org/PMB/57/4627/mmedia. The reconstructed signal amplitudes varied by a factor of 2–3 from sphere to sphere, both due to variations in sphere brightness and variation in flow speeds in the parabolic flow profile as we have noted previously (Zettergren et al 2012).

Figure 3.

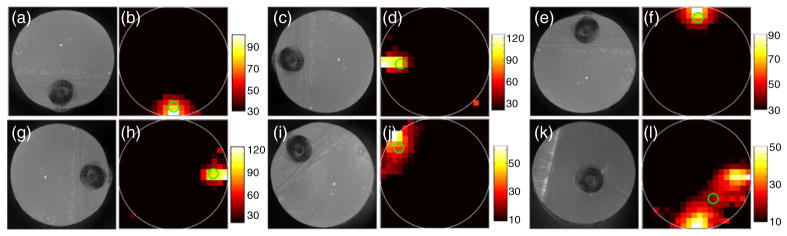
Example white-light images of phantom cross sections ((a), (c), (e), (g), (i), (k)) as well as fluorescence reconstructions of circulating microspheres ((b), (d), (f), (h), (j), (l)) when a flow phantom with a single embedded Tygon tube was oriented at 0° (bottom), 90°, 180°, 270°, 135° and inset 315°, respectively (see the text for details). The centroid of each reconstruction is marked with a green circle. An example reconstructed data set when the flow phantom was oriented at 270° is shown in supplemental video 1 available at stacks.iop.org/PMB/57/4627/mmedia.

As a test of the DFFC’s ability to resolve depth information, we conducted another set of experiments where the Tygon tubing was more centrally located in the phantom cross section. An example reconstruction where the tube was closest to the bottom right edge is shown in figure 3(k), along with the reconstructed image as shown in figure 3(l). In this case, the algorithm reconstructed a significantly more distributed source, the centroid of which was at the correct ‘clock position’ of the tube but at more superficial depth than the true position. We consistently observed this effect when imaging deep-seated flow tubes, i.e. the reconstruction algorithm produced images that were surface-biased. Our analysis showed that this resulted in a larger mean error between centroid and true position of 0.5 ± 0.2 mm (averaged over 200 spikes in multiple orientations). As we discuss in more detail below, this was most likely due to the rapidly acquired small data sets and the underdetermined nature of the reconstruction problem. Overall, the accuracy of our instrument is comparable to previously reported diffuse optical tomography and FMT imaging systems relative to the physical scale of the axial slice under consideration, i.e. 10–20% of the imaging scale (Wang and Wu 2007). We anticipate that alternate designs—for example, utilizing larger numbers of source and detector pairs—will improve on this limitation in the future. However, most large blood vessels of interest are located superficially (e.g. in the tail) so this limitation is generally acceptable for this application.

Double-tube flow phantoms

A similar series of tests were conducted with double-tube flow phantoms that used a single length of Tygon tubing looped twice through the resin material. Figures 4(a) and (b) show sample data sets from a phantom where two tubes were positioned on opposite sides of the phantom, close to the left and right edges. These data are the sum of the background-subtracted data from all six channels when lasers 1 and 2 were illuminating the sample, respectively. A cross-sectional image of the cleaved phantom (obtained after DFFC data acquisition) is shown in figure 4(c). Fluorescent spikes were detected in pairs separated by about 3 s, since each microsphere passed twice through the DFFC field of view, i.e. first along the left side and then right side of the phantom. In this case, the detected fluorescence amplitude for the first spike was significantly larger when laser 1 was illuminating the phantom (since it was directly illuminating the left flow tube) compared to laser 2, and the opposite was true for the second spike. Example reconstructed fluorescence images for two spikes (indicated by the arrows in figures 4(a) and (b)) are shown in figures 4(d) and (e), corresponding to the approximate locations of the left and right tubes. It is extremely unlikely that two microspheres passed through the instrument field of view in opposite tubes at the same time given the very low concentration used here (10³ mL⁻¹). However, we simulated this case in silico and determined that in principle our reconstruction algorithm would resolve at least two targets, although with lower resolution than with single targets. As noted, we intend to use our instrument at very low concentrations of circulating cells (<10⁴), so that this would be an equally unlikely case in vivo. Similar data were acquired when the same phantom was rotated 90° counterclockwise so that the tubes were close to the bottom and top edges of the phantom. As above, the spikes were detected in pairs, but the amplitude of the sum of the detected spikes was approximately the same when either laser was illuminating the sample (since the tubes were approximately equally far from the laser). Example data, along with a video of a reconstructed sequence from this experiment, are shown in supplemental video 2 available at stacks.iop.org/PMB/57/4627/mmedia.

Figure 4.

Example acquired data, summed from all detector channels during illumination of the sample by the first (a) and second (b) lasers. The phantom was embedded with a length of Tygon tubing first along the left and then the right side of the phantom, (c) a white-light cross-sectional image of the flow phantom and (d)–(e) example fluorescence reconstructions when a microsphere was traveling through the left and right flow channel, respectively. The centroid of each reconstruction is marked with a green circle.

Quadruple-tube flow phantoms

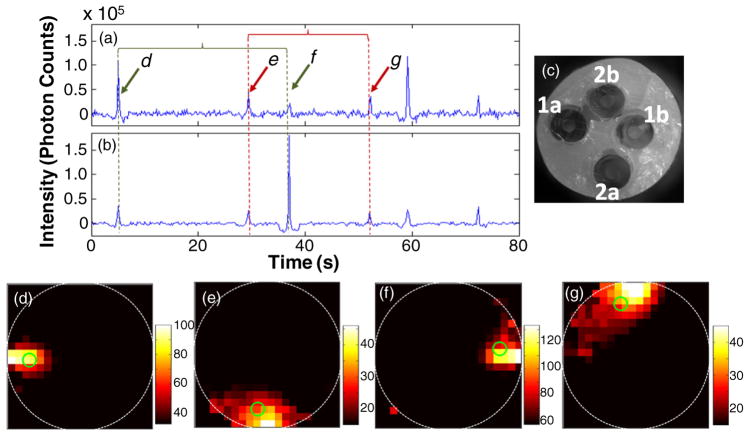
We next performed a series of experiments using phantoms with four flow channels; these were embedded with two separate lengths of Tygon tubing that were looped twice each through the resin material. Although difficult to fabricate, we attempt to make flow phantoms that had approximately evenly spaced flow channels, with one close to each of the top, bottom, left and right edges. The rationale here was that these would mimic the location of the four major blood vessels in the mouse tail, i.e. the ventral artery, lateral and dorsal tail veins (Cook 1965). Figures 5(a) and (b) show the sum of the detected signal on all six channels when each laser was illuminating the sample. The locations of the four flow channels—denoted as tubes 1a, 1b, 2a and 2b—in the phantom cross section are shown in the figure 6(c). Again, the fluorescent spikes were detected in pairs as microsphere passed through the field of view twice on its return trip through either tube. Example image reconstructions for each of the four flow channels are shown in figures 5(d)–(g). We note that lower flow rates (1 mm s⁻¹) were used for these experiments; as such, the inter-spike arrival times were about ten times longer than in the case of the double-tube phantoms. A video showing additional example reconstructed data from this experiment is shown in supplemental video 3 available at stacks.iop.org/PMB/57/4627/mmedia. Taken together, the experiments shown in the preceding sections demonstrate the ability of the DFFC instrument and image reconstruction algorithm to localize fluorescent microspheres with 0.5 mm or better accuracy in multiple locations in the phantom cross section.

Figure 5.

Example data acquired when the first (a) and second (b) lasers were illuminating a flow phantom. As shown in the white-light cross-sectional image (c), this phantom was fabricated with two tubes embedded, the first approximately along the left and then right edges of the phantom (labeled 1a and 1b) and the second along the bottom and top edges (2a and 2b). Example fluorescence reconstructions (d)–(g) when a microsphere was traveling through each of the four flow channels. The centroid of each reconstruction is marked with a green circle. Example reconstructed data set for this flow phantom is shown in supplemental video 3 available at stacks.iop.org/PMB/57/4627/mmedia.

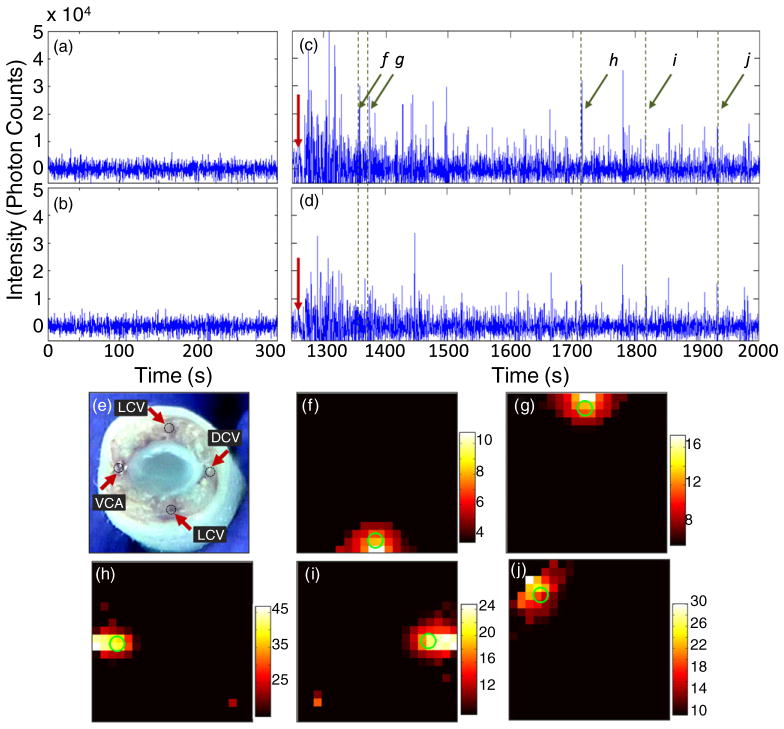
Figure 6.

Data acquired for uninjected mice ((a),(b)) and for a mouse where 10⁵ Vybrant-DiD labeled MM cells were injected retro-orbitally ((c),(d)) when the first ((a),(c)) and second ((b),(d)) lasers were illuminating the tail of a nude mouse. The red arrows in (c),(d) indicate the time of injection. A cross-sectional image of the tail of a mouse (obtained post-mortem) (e), indicating the position of the major blood vessels including the VA, LV and DV. The diameter was about 3 mm. For these experiments, the mouse was placed on its side, so that laser 1 directly illuminated the VA. Example reconstructions of circulating cells, corresponding to spikes detected at (f) 1350, (g) 1371, (h) 1714, (i) 1819 and (j) 1939 s. As above, the centroid of each reconstruction is marked with a green circle.

In vivo tomography

Finally, we tested the tomographic imaging abilities of the DFFC instrument in nude mice with retro-orbitally injected MM cells. Example background-subtracted data acquired prior to injection (control animal) when lasers 1 and 2 were illuminating the tail are shown in figures 6(a) and (b), respectively. As is evident, no spikes were present in the signal. A bolus of 10⁵ MM cells was then retro-orbitally injected into the mouse as shown in figures 6(c) and (d) (the red arrow indicates the time of injection). Example data were collected for 15 min after injection, and a large number of spikes were measured. As we reported previously (Zettergren et al 2012), a significant dc background was also observed immediately following the injection (subtracted here for clarity), corresponding to the bolus of the relatively large number of labeled MM cells. A cross-sectional white-light image of the tail (obtained after euthanizing the animal following injection of methylene blue) is shown in figure 6(e), indicating the location of the ventral artery (VA), lateral veins (LV) and dorsal veins (DV). As noted above, the mouse was placed on its left side during these experiments, so that the VA (normally on the bottom side on the tail) was facing laser 1. Example reconstructed images for five selected spikes are shown in figures 6(f)–(j). As shown, about two-thirds of the cells were reconstructed in approximately the left, right, top and bottom edges of the tail cross section (figures 6(f)–(i)), and the remainder of the cells were reconstructed at intermittent angles as in figure 6(j), presumably corresponding to smaller blood vessels in the field of view. Unfortunately, it was impossible to directly verify the accuracy of our image reconstructions following each experiment, i.e. since the cells were constantly in motion. However, it is interesting to note that these four positions correspond to the approximate anatomical locations of the major blood vessels in the tail of the mouse (figure 6(e)) (Cook 1965), although given the ~0.2 mm accuracy of the system for superficial sources we note that co-localization with the blood vessels cannot be explicitly confirmed. Since the cells were newly injected, it is reasonable to surmise that most of them were circulating through the major blood vessels. In addition, the average measured spike width was approximately 0.4 s (FWHM). We previously characterized the relationship between the FWHM of detected spikes as a function of flow speeds (Zettergren et al 2012) through our 0.7 mm instrument field of view. From these data, we estimate that the fluorescent spikes corresponded to a flow speed of approximately 0.3 cm s⁻¹. Since the animal was under general anesthesia, this implies that the cells were moving in large, relatively fast moving blood vessels. Finally, our studies in flow phantoms showed that the DFFC system is capable of accurately distinguishing between multiple circulating targets, further supporting the accuracy of our in vivo results.

Discussion

As we have noted, the primary challenge in obtaining accurate tomographic cross-sectional images was the rapid, transient and weak fluorescent signals that were measured from circulating cells. Nearly all cells remained in the instrument field of view for less than 1 s, so that long acquisition times or complicated tomographic illumination and detection schemes—common in most FMT imaging—were simply not feasible (Hielscher 2005). Furthermore, the weak fluorescent signals from single cells made detection extremely difficult (if not impossible) using a high-density multi-element detector array such as a CCD camera, so a few, discrete PMT detectors were selected for our design. This design led to sparse fluorescence tomographic data sets with 12 source and detector pairs, as opposed to hundreds or thousands as is typical in FMT imaging. Furthermore, we made two important simplifying assumptions in performing our image reconstructions: (i) the position of the cells did not change significantly in one acquisition cycle and (ii) the light emerging at the edge of the phantom or tail was measured by the adjacent detector (ignoring light propagation in free space between them). For the former assumption, our in vivo data indicate that this is a reasonable assumption. However, it would also be possible to obtain data sets at faster rates, simply by increasing the modulation rate of the two lasers, although correspondingly smaller fluorescence signals would be obtained. For the latter assumption, this greatly simplified the computation of the instrument weight functions.

Nevertheless, as we have demonstrated we were able to localize the cross-sectional position of fluorescent microspheres with a mean error of 0.2–0.5 mm in a limb-mimicking optical flow phantom, depending on the depth of the flow channel. As we have noted, our results indicate that the reconstruction algorithm produced images that were generally biased toward the surface of the phantom. Therefore, a centrally located or slightly inset flow channels were difficult to distinguish. However, we note that in all cases investigated the fluorescent object was reconstructed on the correct ‘clock position’. We have performed a number of in silico experiments that indicate that it would be possible to further improve imaging resolution through the use of alternate source and detector configurations. For example, our simulations indicate that simply by replacing our two-source and six-detector configuration with a four-source and four-detector configuration would improve the depth-sensing accuracy. Adding more source–detector pairs would further increase the accuracy accordingly. However, the use of more sources and detectors would require careful instrument design, i.e. in order to physically position the sources and optodes around the sample.

Finally, we demonstrated successful operation of our DFFC tomographic imaging approach in the tails of mice in vivo. As we have shown, detected fluorescent spikes could be reliably reconstructed; however, it was extremely difficult (if not impossible) to know the correct ‘ground truth’ solution, i.e. since the actual location of the circulating cell was unknown, and the transient nature of the cell movement did not allow post-experiment verification with an alternate fluorescence imaging modality. We have attempted to minimize this uncertainty first by extensively testing and validating our instrument and imaging algorithms in flow phantoms. Second, as we have noted, the reconstructed images implied that most of the cells were moving in one of the four ‘compass points’ in the cross section. These corresponded to the approximate location of the major blood vessels in the tail, i.e. the anterior and posterior tail veins and the anterior artery. In other words, the reconstructed images were reasonable based on a priori knowledge of the tail anatomy. We also note that the sensitivity of the DFFC approach relies on the underlying assumption that one cell is in the relatively large field of view at a time, so that at high cell concentrations (i.e. higher than ~10⁴ cells in circulation in a mouse) count inaccuracies may result and alternate techniques such as microscopy-based IVFC are therefore more appropriate. Nevertheless, this approach allows us to determine, for example, the cell count rate in a particular region of the tail (as opposed to an overall count rate in the limb) with the intention of minimizing double-counting of cells. We are currently studying the accuracy of cell clearance kinetics with our system compared to microscopy-based IVFC using a number of in vivo circulating cell models.

In summary, we have developed and demonstrated operation of a new approach for reconstructing the location of circulating fluorescently labeled cells in the cross section of a mouse limb. The 0.5 mm or better accuracy demonstrated here is sufficient for, for example, distinguishing major blood vessels in the tail, but could potentially be further refined, particularly with respect to depth discrimination. For example, we plan to refine the image using a priori structural information of the mouse limb, i.e. since the location of the major blood vessels is known with some accuracy in advance. We are also exploring sparse image reconstruction approaches since—assuming that only one cell is in the DFFC field of view at a time—it is known a priori that the reconstructed fluorescent image should be a single point object with zero background. Finally, we will explore the possibility of adding extra light sources or detectors to increase the size of tomographic data sets. In principle, this will allow better localization of the fluorescent cells in the instrument cross section.