A pillar-based microfilter for isolation of white blood cells on elastomeric substrate

Abstract

Our goal is to design, fabricate, and characterize a pillar-based microfluidic device for size-based separation of human blood cells on an elastomeric substrate with application in the low-cost rapid prototyping of lab-chip devices. The single inlet single outlet device is using parallel U-shape arrays of pillars with cutoff size of 5.5 μm for trapping white blood cells (WBCs) in a pillar chamber with internal dead-volume of less than 1.0 μl. The microstructures are designed to limit the elastomeric deformation against fluid pressures. Numerical analysis showed that at maximum pressure loss of 15 kPa which is lower than the device conformal bonding strength, the pillar elastomeric deformation is less than 5% for flow rates of up to 1.0 ml min⁻¹. Molding technique was employed for device prototyping using polyurethane methacrylate (PUMA) resin and polydimethylsiloxane (PDMS) mold. Characterization of the dual-layer device with beads and blood samples is performed. Tests with blood injection showed that ∼18%–25% of WBCs are trapped and ∼84%–89% of red blood cells (RBCs) are passed at flow rates of 15–50 μl min⁻¹ with a slight decrease of WBCs trap and improve of the RBCs pass at higher flow rates. Similar results were obtained by separation of mixed microspheres of different size injected at flow rates of up to 400 μl min⁻¹. Tests with blood samples stained by fluorescent gel demonstrated that the WBCs are accumulated in the arrays of pillars that later end up to blockage of the device. Filtration results of using elastomeric substrate present a good consistency with the trend of separation efficiencies of the similar silicon-based filters.

INTRODUCTION

Microfluidic devices intended for human blood cell separation prior to genomic analysis present advantages over the conventional laboratory techniques in terms of down-sizing, integration, portability, small volume of sample usage, and low-cost fabrication.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} To access the genomic information, deoxyribonucleic acid (DNA) must be extracted and purified from blood which exists in the white cells.^{1, 11, 12, 13, 14, 15, 16} It is just enough to have about 10% of the WBCs of ∼1 μl of blood sample isolated from contamination of most of the RBCs.^{17, 18}

Blood has three main categories of cells. Leukocytes or white cells are nearly spherical with diameters larger than 6–10 μm and concentration of 0.4–1.1 × 10⁷ cells ml⁻¹. Erythrocytes or red cells are biconcave with diameters between 6 and 8 μm, 1.8–2.8 μm thickness, and concentration of 4.2–5.4 × 10⁹ cells ml⁻¹. Platelets are 1–3 μm in diameter and concentration of 2.1–5.0 × 10⁸ cells ml⁻¹. Plasma is considered as the blood fluid with particles smaller than 0.5 μm.¹⁹

Blood cells can be separated using non-inertial forces and concepts such as magnetic bead immunoassay,¹⁰ dielectric properties,^{20, 21, 22, 23, 24} optical force,²⁵ magnetic,²⁶ electrohydrodynamic,²⁷ or acoustic^{28, 29, 30, 31, 32} as active separation strategies. The non-inertial forces may have some unexpected physiological effects on the blood component properties which are unsuitable for the downstream application of the separated products. These techniques add to the complexity of the microfluidic devices and normally run at very low flow rates.^{33, 34, 35, 36, 37, 38, 39, 40, 41, 42}

The difference in size and shape of the cells is exploited in simple and passive separation ways in which they do not involve external forces but rely purely on the interaction of the blood with internal geometries of microfluidic devices. The passive hydrodynamic separation of the cells needs specific design of the microchannels and normally is effective at limited and low flow rates.^{9, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57} The pore-based or slit-based passive devices have simple mechanical design and can function in a wide range of flow rates. WBCs are flexible and can deform to pass through 7 μm pores. The RBCs are also very flexible and can fold or align to cross the filter opening of ∼3–4 μm.⁵⁸ A perfect blood microfilter is able to trap all WBCs and pass all RBCs continuously without loss of separation efficiency at different flow rates and cell concentration. In the design cycle of a mechanical filter, reducing of pressure loss, blood dead volume, and cell sedimentation should be considered along with the simplicity and adaptability with other microfluidic elements.^{16, 58}

Silicon for its good properties is suitable for microfluidic device production. However, silicon has complicated and expensive fabrication process that makes it unsuitable for rapid prototyping purpose. Silicon-based microfilters present pore geometries as small as submicron and do not deform easily under typical microfluidic pressures.^{16, 58, 59, 60, 61, 62} So far, cell-free plasma has been prepared using microfilter with an opening size of less than 1 μm.^{43, 55, 63} Many designs applied based on crossflow with weir-based pores in a tortuous channel,^{55, 64} or in straight channels under capillary action,⁴⁴ and less frequently by involving microposts in crossflow plasma filtration,⁴³ or implementing membranes.^{50, 65} Using tortuous channel instead of straight ones results in loss of pressure and separation efficiency due to the back flow at the curvature segments of microchannel.⁶⁶ Isolation of WBCs requires microfilters with an opening size of ∼3.5 μm. Some efforts on silicon-based filters have been on pillar-based designs in a crossflow⁶⁴ or normalflow⁴ and reports on using weir-type filter designs.^{11, 64} It has been reported that pillar-based filter demonstrates a better separation performance than weir type or membrane.⁵⁸ Arrays of silicon microposts have been reported in fractionation of blood components using deterministic lateral displacement.^{45, 67}

Fabrications using polymers rely mostly on different low-cost techniques.⁶⁸ PDMS as an elastomeric polymer is suitable for rapid prototyping of microfluidic devices. This polymer has the desirable properties of optical transparency and high elasticity which assists in the easy mold release. Its low rigidity causes significant deformation of the microstructures under pressure.^{14, 61, 69, 70, 71} PDMS has been used in plasma separation by size-exclusion in a crossflow channel,⁷² by simple bifurcation microchannel,⁶³ isolation of WBCs,^{73, 74} and WBCs/RBCs⁷⁵ using laminar flow in microchannels. Moreover, a diffusive filter has been developed for blood leukocytes depletion using PDMS micro-sieve.⁵³

This paper is aimed at first, introducing a simple pillar-based filter that can demonstrate a comparable efficiency to other pillar-based designs in isolation of WBCs from undiluted blood. Second, presenting a methodology to adapt the design parameters to elastomeric substrate properties for the low-cost rapid prototyping purpose. The main substrate is polyurethane methacrylate (Code 1205, Polydiam, UK) previously characterized for rapid prototyping of microfluidic devices by the authors of the present work.⁶² A soft mold is needed for effective and easy replication of several copies of the device structure layer from PUMA resin needed in the present work and PDMS is the best choice. In terms of general properties such as low modulus of elasticity, PUMA is similar to PDMS, therefore, the current research could be conducted on either substrate. But the shorter curing time for PUMA which needs about 2–3 min using a standard UV system is an advantage over the PDMS which needs about 1–2 h to complete curing in oven or on a hot plate. The device is characterized using solid fluorescent microspheres and blood cells representing biological samples. Fabricated device is able to isolate part of the injected WBCs from most of the RBCs. The results of the present work are applicable in researches such as on-chip biological studies of the trapped cells using low-cost and rapid methods.

THEORETICAL

Design parameters and constraints

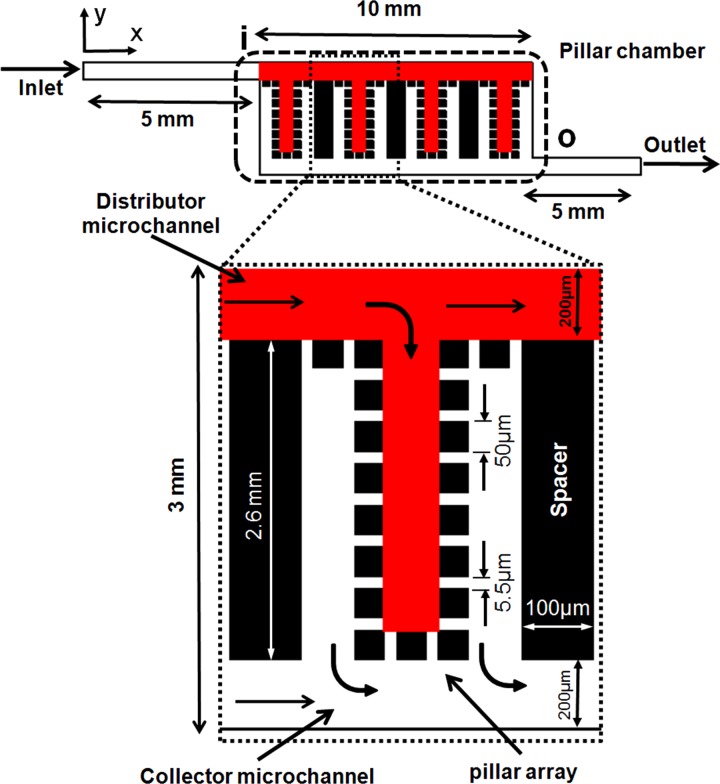
Fig. 1 shows a schematic layout of the proposed microfluidic filter. Blood is pumped into the device via inlet port, enters the filtration zone at the section “i,” and leaves it at the section “o”. Outlet port is for collecting the components of blood pass the filter. A rectangular chamber is employed to house the pillar arrays. In the upstream of the pillar chamber, the main microchannel distributes the fluidic flow to uniform and parallel branches. In each branch, an U-shape array of pillars considered for cell isolation. On the downstream side of the pillar chamber, another microchannel collects the filtered sample and directs it to outlet. The channel branching has three advantages of (1) reducing the overall device pressure loss or hydraulic resistance according to Kirchhoff's law for parallel flow channels compared to a single long channel,⁷⁶ (2) using parallel channel instead of one continuous tortuous prevents filtration performance loss to the backflow in the curved segments as reported in the literature,⁶⁶ and (3) reducing the footprint area of the device compared to long and straight channels.

Figure 1.

Schematic of the filtration device.

There are very limited guidelines in the literature on how to design micropillar-based filters for blood cell separation. Here, a simple strategy is used based on the parameters such as blood sample volume, cell size, and material structural considerations in the design process. The whole blood is introduced into arrays of regularly spaced micropillars with gaps of ∼5.5 μm defined by the rule of $2.5\mu \mathrm{m}<gap<6.5\mu \mathrm{m}$, which allow most of the RBCs and other small cells pass through and some of the WBCs get trapped. The gap size must be larger than RBCs thickness and smaller than the smallest WBCs diameter. Depth of microchannels is set at ∼50 μm uniformly all over the structure to large WBCs (monocytes diameter is ∼24 μm) free flowing or rotation with less rubbing against PUMA surface. The cross section of the pillars is considered square instead of circular⁶⁴ to enable better reliability of the gap size and for better maintaining the consistency between the design and the microfabrication. The slanted pillars or gaps with respect to the mainstream direction help improving performance in the crossflow silicon-based filters as reported in the literature⁵⁸ but elastomeric substrate can result in extreme deformation of sharp edges under fluidic pressure. High aspect ratio (height/width) elastomeric pillars or posts (AR > 5) bend easily under structural weight or fluidic pressure.⁷⁷ To reduce the effects of PUMA low modulus of elasticity (∼1.35 MPa), aspect ratio of each single pillar considered effectively low about 1.0. Then, by having the depth of microchannels and the presumed pillar AR, the pillar cross section dimensions are calculated as ∼50 μm × 50 μm.

The elastomeric PUMA is a material with very low stiffness similar to PDMS.⁶² Using too wide channels (height to width ratio < 0.05) can cause sagging of the top layer under its own weight or excessive flow pressure.⁷⁷ The main channel widths are considered 200 μm (AR ∼ 4) and low enough to be in the safe margin⁷⁷ and the branch channels set at 50 μm (AR ∼ 1). The length of pillar chamber is selectively set at 10.0 mm and the width of it is 3.0 mm calculated based on total internal volume of ∼1.5 μl. In a pillar chamber with the dimensions as explained, there will be just enough room for totally 27 U-shape arrays separated by solid low AR spacers of thickness 100 μm (AR ∼ 0.5) and 100 micropillars per array.

Modeling and simulation

Computational fluid dynamics analysis (CFD) was performed on a geometrical model of the filtration device using finite element method (FEM) by COMSOL Multiphysics software. A two-dimensional model of the device was constructed and the computational domain was meshed by the free triangular elements. The 2D steady-state incompressible laminar flow Navier-Stokes equations (i.e., continuity and momentum) were solved to approximate the velocity and pressure fields of the microfluidic flow. The blood is best approximated with a non-Newtonian model of the blood viscosity changes in the channels where the cells have to deform under fluidic pressure. For simplifying the numerical modeling, the simulation assumes a particle-free fluid and Newtonian flow that is best represented by water.

A no-slip boundary condition was set on the microchannel's internal surfaces. At the outlet, the boundary condition was considered as 0 Pa gauge pressure. A constant velocity profile was imposed on the inlet surface corresponding to constant flow rate. By varying the velocity magnitude at the inlet, the simulation was carried out in conditions such as 100 μl min⁻¹ as a low flow rate and 1000 μl min⁻¹ as a high flow rate corresponding to the maximum velocities of ∼0.25 m s⁻¹ and ∼2.5 m s⁻¹, respectively. The input parameters used in the present numerical simulation included 998 kg m⁻³ for water density and 0.001 Ns m⁻² for viscosity. The pressure and velocity magnitudes were normalized with the respected values at the section “i” of the pillar chamber.

EXPERIMENTAL

Microfabrication

The rapid prototyping process was performed by molding of PUMA resin as the main substrate. A glass photomask was manufactured for pattern transfer on a 3 in. silicon wafer (diameter thickness 450 μm, type P (100)). The silicon was anisotropically etched by deep reactive-ion etching (DRIE) (see Fig. 2a). The etched silicon was used in the molding process as positive master for producing soft PDMS negative mold. The silicon master was silanized with anti-sticking reagent (TDF-silane, UCT, USA) in a desiccator overnight. By pouring degassed PDMS mixture resin on the mold and curing at 75 °C for at least 2 h, a PDMS negative mold was made and peeled off from the master (see Fig. 2b). The PDMS soft mold was employed for making several copies of the structure layer of the filtration device by the UV-molding with PUMA resin (see Fig. 2c). Lastly, PUMA resin was dispensed on the PDMS mold without silanization, degassed in the vacuum chamber, and then covered with a transparent cover to prevent oxygen inhibition of the cross-linking during UV-exposure. The cured PDMS does not stick to the PUMA resin; therefore, peeling the cured PUMA from the PDMS mold was done without difficulty. Sealing layer of the microchannels was fabricated using PUMA according to the process previously explained in detail.⁶² The fluidic interconnection was of the type of embedded barbed sleeve interconnect presented for PUMA for its superior performance.⁶² The structure layer and the seal layer were bonded together conformally. For the range of operations of the present experiment, conformal bonding provides enough strength against fluidic pressures.

Figure 2.

Fabrication process of the filtration device. (a) SEM image of the fabricated silicon master, (b) SEM image of the PDMS mold, (c) SEM image of the PUMA microstructure, (d) device fabricated from fully PUMA.

Setup and preparatory tests

The single inlet single outlet fabricated device (see Fig. 2d) was connected to a syringe pump and controller (TS-1 A, LongerPump, china). The PTFE tubing (0.022 × 0.042 in, ColeParmer) was inserted into the Tygon tubes (1/32 in. i.d., 3/32 in. o.d., ColeParmer) of the device fluidic interconnects and was used for pumping of sample to the inlet port of the device and transfer of separated components from the device outlet port to the 2 ml collection tube. Some of the experiments were performed under an upright optical microscope (BA400 Epi-Fluorescent, motic) for detail investigation of the filtration process. The images and videos were captured by a camera installed on the eyepiece body tube of the microscope (Dino-Lite, AM423B Dino-Eye).

The blood sample was obtained from a healthy volunteer at the medical clinic of the National University of Malaysia. The blood was drawn by a syringe needle and collected in a purple BD vacutainer contains EDTA (the potassium salt, or K₂EDTA) anticoagulant and was immediately stored at the 4 °C until the experiments were performed. The phosphate buffered saline solution was prepared by dissolving a tablet of the phosphate buffered saline (PBS) (Sigma-Aldrich) in a 200 ml of distilled water. To better observe the filtration process and differentiate between the white and the red blood cells, SYBR Green I (Sigma Aldrich) as a nucleic acid fluorescent stain was employed. The gel was diluted in the ratio of ∼1/10 000 with PBS, then the blood sample was diluted in the solution with equal volumes followed by incubation at room temperature for ∼30 min. The blood was transferred into a 500 μl glass syringe (Luer Tip, 500 μl, Hamilton) with tips 23 G and was driven by syringe pump at constant flow rates. Prior to running the experiments, PBS was pumped into the device for 2 min. Pumping of the sample was continued until the device blockage by the trapped cells was observed visually. Injection of the sample was stopped once the device interlayer bonding initiates failing due to overloading. The test run at each case and flow rate was repeated three times, and the results were averaged.

Experiments for visualization of the separation phenomenon and characterization were conducted with fluorescent polymer microspheres. Two types of internally dyed beads packaged as aqueous suspensions were purchased from Thermo Scientific. The microspheres with a diameter of 9.9 μm (Fluoro-Max, Green Fluorescent, 1% solid) were to represent the white cells and with a diameter of 3.2 μm (Fluoro-Max, Red Fluorescent, 1% solid) were to represent the red cells as they have comparable dimensions except that the red cells are deformable and have biconcave discoid form. The density of the microspheres is 1.05 g cm⁻³ while it is 1.025 g cm⁻³ for blood plasma and 1125 g cm⁻³ for blood cells. In the same volume from both red and green microsphere, number of red beads are ∼30 times of the green beads calculated according to the 1% solid (volume/volume) of the suspension supplied by manufacturer. In the blood, white cells are less than the red cells with a ratio of about 1 to ∼700. To have a similarity in the ratio of the red to green microspheres with the ratio of the RBCs to WBCs, 1 μl of green microspheres was mixed with ∼23 μl of reds. The images of the microspheres were obtained using B-2 E/C filter cube for green fluorescent channel and G-2 E/C filter cube for the red fluorescent channel.

Swelling and pressure induced pillar deformation

Deformation of the elastomeric microstructures under pressure induced by fluidic flow or swelling effect as reported elsewhere in the literature⁷⁰ is important for that it disturbs the pillar gap uniformity in the arrays. Effect of fluidic pressure is significant compared to the swelling of the PUMA with water which is low as reported previously for the short time exposure to samples such as blood which has properties similar to water.⁶²

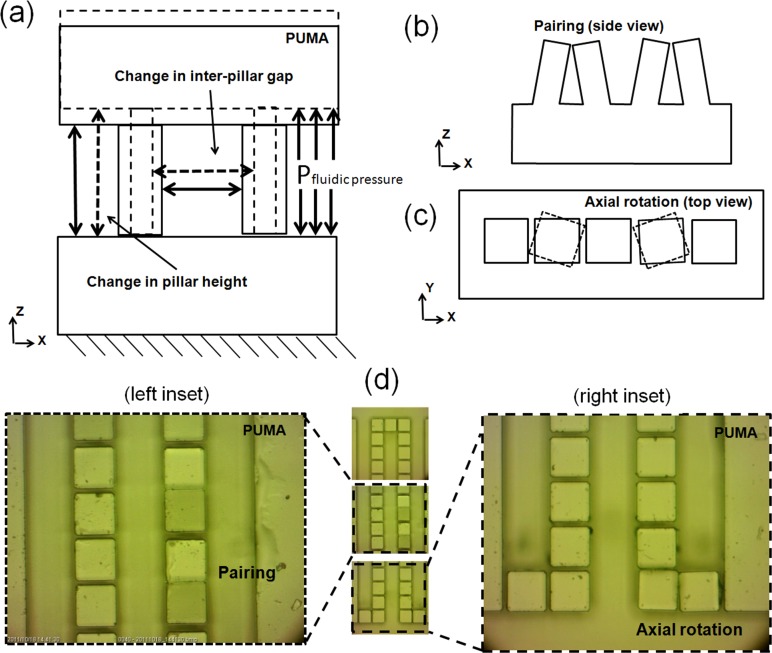
One of the modes of the structure deformations is the elongation according to the Hook's law defined by $\sigma =E{\epsilon }_a$, where σ is tensile stress (here is fluidic pressure P), E is the PUMA modules of elasticity (∼1.35 MPa), and ${\epsilon }_a$ is the pillar axial strain defined by $\Delta H/H$ (H is initially 50 μm) (see Fig. 3a). Elongation of a pillar under fluidic pressure causes its width contraction according to Poisson effect and therefore increases the pillars gap size (initially is 5.5 μm). The Poisson ratio is defined by $\nu =-{\epsilon }_l/{\epsilon }_a$, where ${\epsilon }_l$ is the pillar lateral strain and ν is ∼0.5 for rubbers. At high pressures, increase of gap size can be considerable and causes the performance degradation or device failure even before bonding failure.

Figure 3.

Deformation modes of the pillars. (a) Schematic of the pillars stretching under fluidic pressure, (b) schematic of pillars pairing effect, (c) schematic of pillars axial rotation, (d) optical microscopy image of the U-shape array of pillars. Pairing of two neighboring pillars (left inset) and angular distortion of corner pillar (right inset).

The high aspect ratio gaps (depth/ width) intensify the pillars buckling or pairing effect due to the capillary force and gravity in which the tips of the neighbor pillars tend to adhere⁷⁸ as shown in Figs. 3b, 3d. The pairing effect degrades the performance of the device by altering the uniformity of the pillar gap size. The size of the gaps may increase to twofold of the initial magnitude or may reduce to zero. This phenomenon may occur locally or widely throughout the filtration zone. This mode of deformation is constrained here by designing low aspect ratio pillars (height/width) of about 1.0. The fluidic flow pressure can also originate the local bonding failure and creates distortions in PUMA microstructures, such as axial rotation of pillar (see Figs. 3c, 3d). To avoid this unwanted effect, the internal pressure imposed on the device must be limited considerably below the bonding failure threshold which is ∼100 kPa in conformal bonding.⁶²

Postrun analysis

The number of cells and microspheres except for the trapped ones are measured off-chip before and after filtration. Two techniques are employed for this purpose. The blood cells are counted using the standard cell counter machine (Beckman Coulter). The microspheres are counted using the particle counter Plugin of ImageJ software. Microspheres suspensions of ∼1 μl are spread on a microscope glass slide and the images are captured under a fluorescent microscope. The images are analyzed by ImageJ for particle counting. The number of trapped cells/microspheres is calculated by having the counts of recovered and supplied cells/microspheres. Then, the device is evaluated for efficiencies of separation for blood and microspheres suspension samples. For instance, the microfilter efficiency of trapping WBCs is obtained by the cell count ratio of the trapped and supplied WBCs. Similarly, the efficiency for passing RBCs was calculated by the cell count ratio of the recovered and supplied RBCs.

RESULTS AND DISCUSSION

Simulation analysis

Fig. 4 shows the velocity vectors of the fluidic flow at the intersection of the pillar arrays and distributor channel. The vectors are colored by magnitude of the normal component of the local velocity vectors. The positive or negative sign gives the upward or downward direction of the vector. The red color with a positive sign in the colormap shows the upward vector and the blue color with negative sign stands for the downward velocity vector component. Two cases of low flow rate (100 μl/min) and high flow rate (1000 μl/min) are considered. At the entries to the pillar arrays, the velocity vectors accelerate by the change in magnitude and direction. In Figs. 4a, 4b, 4c, we see that at flow rates of 100 μl min⁻¹, the velocity vectors turn the corners gently at all points of the upstream flow between UL and UR. The magnitude of the normal component of the velocity vectors in the colormap is 0.04 to −0.05 m s⁻¹ throughout the flow field. Besides, the colormap of the velocity vectors shows that the velocity magnitude in U-shape array at the UM position is slightly less than the similar magnitudes in the positions UL and UR. This difference in the magnitude of the velocity vectors has been also reflected in the corresponding pressure change along the upstream side as graphed in Figure 5. Generally, at low flow rates, the distribution of the fluidic flow of the main channel between different U-shape arrays is considered uniform without recirculation zones. At flow rate of 1000 μl min⁻¹, it is noticeable from the velocity vectors of Figs. 4d, 4e that strong recirculation zones exist in some area in the flow field. The colormaps in Figs. 4d, 4e, 4f show that the normal component of the velocity has a range of 0.14 to −0.91 m s⁻¹ in the flow field and the corresponding value in the last branch in Fig. 4f (−0.7 m s⁻¹) is higher than other two in Figs. 4d, 4e (−0.2 m s⁻¹). The recirculation of the velocity vectors appeared in the first pillar array (location UL) as shown in Fig. 4d, also visible in the center pillar array (location UM) as shown in Fig. 4e, but no recirculation in the last array as shown in Fig. 4f. The adverse effect of this phenomenon is decreasing of the fluidic flow into pillar arrays with recirculation, which causes non-uniform flow rate distribution. Subsequent to partial flow blockage of the first few pillar arrays due to recirculation condition, the fluidic flow toward the end section of the filter is increased which in turn will increase the local velocities in that area as it is noticeable in Fig. 4f.

Figure 4.

Velocity vectors at the branch points colored by magnitude of the normal components of the local velocities. The positive or negative signs indicate that the velocity components have upward or downward directions. (a)-(c) Smooth direction change of the velocity at the first (UL), center (UM), and the last U-shape arrays of pillars (UR) at a flow rate of 100 μl/min. (d)-(e) Recirculation flow at the first and the center branch points at a flow rate of 1000 μl/min. (f) Velocity vectors at the last U-shape array of pillars.

Figure 5.

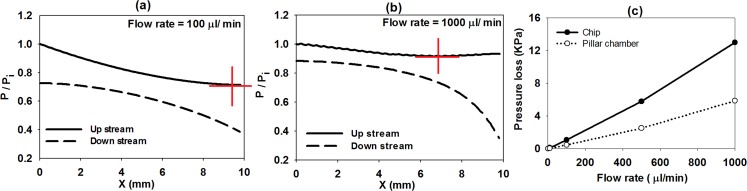
[(a), (b)] Normalized pressure of the upstream and downstream side of the pillar chamber at different flow rates. (c) Pressure loss of the chip and isolated pillar chamber at different fluidic flow rates.

Figs. 5a, 5b plot the pressure change along the upstream (distributor channel) and downstream (collector channel) of the pillar chamber. The trend of pressure difference between the upstream and the downstream is very similar at flow rate of 100 μl min⁻¹ and below it. This is the flow range where it is expected to have a relatively uniform distribution of flow between pillar arrays. At high flow rates as it is in case of 1000 μl/min, we learned that the pressure difference at the left section of the filter is uniform while at the right section has a diverging trend. This is one of the adverse effects of the blockage of the pillar arrays at high flow rates as described previously. The flow in the present device is pressure-driven and high pressure difference causes high flow rates. Another consequence of the high pressure difference would be the higher mechanical forces on the cells which can increase the possibility of cell rupture during testing of blood samples. If the pressure changes along the downstream channel considered, it can be seen that at low and high flow rates the pressure has a reducing trend due to the friction effect. Inspecting pressure change along the distributor channel at flow rate of 100 μl/min has a normal trend of declining due to friction loss from 1.0 (normalized local pressure with respect to the pressure at “i”) to a minimum point marked by a red cross followed by a slight pressure rise due to the stagnation condition of the channel flow when it comes to rest on the end wall of the distributor channel and causes a higher velocity drop and slightly pressure recovery to about 0.8 (refer to bernolli's principle). At a flow rate of 1000 μl min⁻¹, the trend of pressure is similar to the low flow rate with a difference that the minimum point has shifted to the left and up due to the existing of recirculation zones. This means that at high flow rates, the fluidic pressure is built up toward the right section of the filter and causes the fluidic velocity highly increases in the last few pillar arrays as described in Fig. 4.

Fig. 5c graphs the total pressure loss at different flow rates. The pressure loss is compared for two cases of the isolated pillar chamber (dotted line) and the microfluidic chip as a whole from the inlet to the outlet port (solid line) (connecting channel from inlet to “i” + the pillar chamber + connecting channel from “o” to filter outlet) as depicted in Fig. 1. The pressure loss of the whole chip is approximately twice the pressure loss in the isolated filter chamber. The maximum pressure loss in the chip is less than 15 kPa at a flow rate of 1 ml min⁻¹ which is tolerable by the PUMA conformal bonding strength.⁶² At this level of the internal pressure, calculated elongation of the PUMA pillar height based on the Hook's Law is ∼0.55 μm and corresponding increase of the pillar gap size is ∼0.28 μm which gives ∼5% increment. At maximum internal pressure of 100 kPa which is the threshold of bonding failure, the increase of the PUMA pillar gap size is ∼1.85 μm which gives ∼33% increment. This increment in the gap size due to the high internal pressure leads to substantial reduction of filtration efficiencies in the elastomeric devices. In the real experiments, any local clogging in one of the pillar arrays may increase the pressure loss in overall. Spreading the clogging or blockage effect (not simulated here) to another pillar array increases the internal pressure of the device above the bonding strength limit which will end up to bonding failure at low flow rates much less than the amounts predicted using CFD.

Testing with fluorescent microspheres

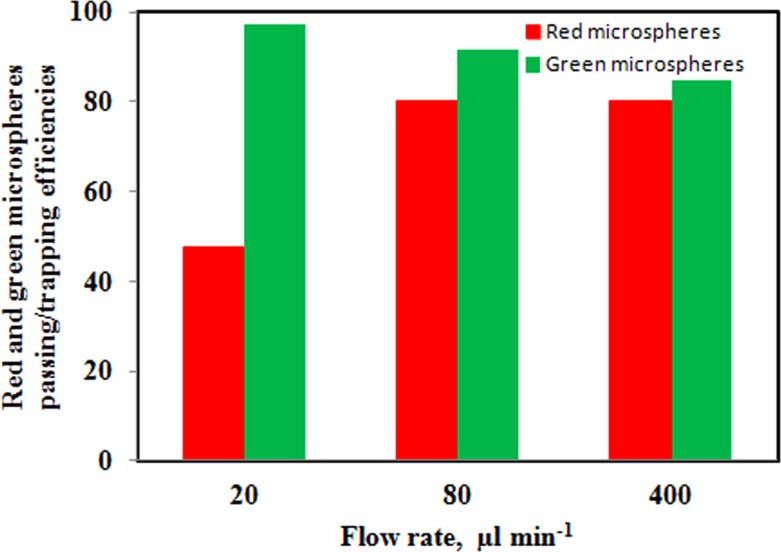
Results of separation test of mixed green and red microspheres are summarized in the bar charts in Fig. 6. The trapping efficiency of green microspheres at different flow rates is given by green bars. By increasing flow rate from 20 to 400 μl min⁻¹, the trapping efficiency is declining from ∼97% to ∼85%. The reduction in trapping efficiency is due to the higher fluidic pressure on the trapped microspheres at higher flow rates as well as an increment in the gap size as described earlier. The red bars show the passing efficiency of red microspheres. By increasing flow rate, more fluidic pressure has caused more red microspheres pass through the filter and the passing efficiency increase from ∼48% to ∼80%. At a flow rate of 20 μm min⁻¹, it was expected that the red microspheres passing efficiency to be higher than 48% because of bead diameter (3.2 μm) is much smaller than the gap size (5.5 μm). At flow rates of 80 μm min⁻¹ and above, there was a considerable increase in the efficiency of more than 80% which suggests that there is a role for velocity magnitude on the level of efficiency. In fact, the small beads tendency to deposit onto the channels might be one reason of low passing efficiency at very low flow rates and another reason is the polymer bead adhesion to elastomeric pillars or microchannel surface.

Figure 6.

Efficiencies of trapping green fluorescent microspheres (green bars) and passing red fluorescent microspheres (red bars) from the microsphere suspensions in the filtration device.

In the test with the mixed microspheres, initially, the red microspheres are expected to pass through the filter while the green microspheres get trapped. Continuous injection causes the accumulation of the red beads behind the trapped green beads which ends up to the full blockage of the filter. Fig. 7 shows the fluorescent photos of the accumulated microspheres in a pillar array in the middle of pillar chamber. The mode in which a pillar array is blocked by accumulation of the microspheres is shown here. At the gap site, the green microspheres block the way first (Fig. 7a) followed by the red microspheres accumulation behind them (Fig. 7b). The local clogging spreads downstream in the pillar array and causes partial jamming of the beads in the channel that ends up later to filter full blockage (Fig. 7c). We also noticed that the end part of each pillar array may remain empty from the microspheres due to the blockage of the channels near to the branch points and the entrapped bubbles which were difficult to expel at short test periods. These effects reduce the effective filtration volume of the device.

Figure 7.

Microscopic photos of clogging a pillar array in the middle of the pillar chamber under test with mixed green and red fluorescent microspheres. (a) Green fluorescent emission, (b) red fluorescent emission, (c) bright field illumination.

In the present filter design, the nominal capacity of the pillar chamber is ∼0.3 μl that is the red zone in Fig. 1. In the microsphere mixture, the red and green solid beads constitute ∼1% and the DI water is ∼99% of the total volume. If we consider 100% efficiency of trapping the greens and passing of the red beads, the capacity volume is enough for filtration of ∼30 μl of the suspension. Injection of this amount of sample to the device at flow rates of 20-400 μl min⁻¹ takes less than 1.5 min.

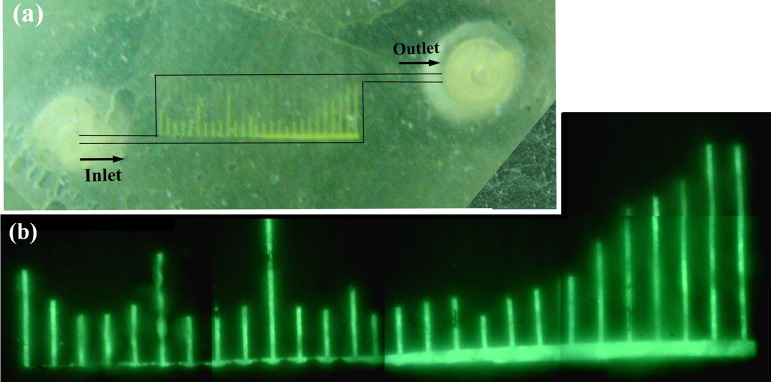
The FEM has predicted strong recirculation zones at flow rates of 1.0 ml min⁻¹. A test was arranged with the red fluorescent bead suspension to observe the recirculation at an injection flow rate of 1.0 ml min⁻¹. This test was not successful in capturing video of the fast moving beads. The beads were detectable to camera only when they were settled on the polymer surface or had a very low velocities. The velocity magnitude in the recirculation zone of the first branch channel is about 0–50 cm s⁻¹ according to CFD results at a flow rate of 1.0 ml min⁻¹ which is too high to be detected by the employed camera. Additional test was conducted by injection of green fluorescent bead suspension until filter blockage. The pattern of the clogging as can be seen in Fig. 8 shows that the last few branch channels are full of the trapped beads while the others are semi-filled. Comparing the trend of pressure difference between upstream and downstream of the pillar chamber (Fig. 5b) and pattern of the branch channel blockage reveals a similarity between them that is interpreted as indirect evidence of the recirculation zones in the flow field.

Figure 8.

Filtration test of green fluorescent microspheres injection at flow rate of 1.0 ml. (a) Optical photo of the device, (b) microscopy image of the pillar chamber under green fluorescent emission.

Testing with whole blood samples

The bar charts of Fig. 9 summarize the WBCs trapping and RBCs passing efficiency results. In Fig. 9a, the chart shows that there is a slight reduction in the WBCs trapping efficiency from ∼0.25 to ∼0.18 by increasing flow rate from 15 to 50 μl min⁻¹. This trend is explained by the fact that increasing the flow rate imposes more fluidic pressure on the trapped cells and deformability of cells and elastomeric filter under pressure that causes more WBCs pass the pillars. The passing efficiency for RBCs has a trend of increasing from ∼84% to ∼89% for flow rates of 15–50 μl min⁻¹. This effect can be explained by the fact that the cut-off size of the filter (∼5.5 μm) is considerably larger than the thickness of the red cells (<3.0 μm). The RBCs are foldable so that they can fold or align with the narrow gaps to pass the filter while their diameter is bigger than the pillar gap.

Figure 9.

Efficiency of blood cell separation at different flow rates. (a) Trapping efficiency of WBCs and passing efficiency of RBCs. (b) Trapping efficiencies of monocytes, lymphocytes, and granulocytes.

Another data extracted from the reports of off-chip automatic cell counting are trapping efficiencies based on different categories of white cells. Fig. 9b presents the trapping efficiencies for monocytes, lymphocytes, and granulocytes. The monocytes are the largest among all leukocytes (12–24 μm in diameter) and therefore have the highest trapping efficiency of ∼35% with almost a constant trend. For lymphocytes and granulocytes, the trapping efficiency is declining from ∼30% to ∼20% of lymphocytes and ∼20% to ∼15% for granulocytes by increasing flow rates from 15 to 50 μl min⁻¹. This effect can be explained by deformability of these two categories of leukocytes and smaller overall diameters compared to monocytes.

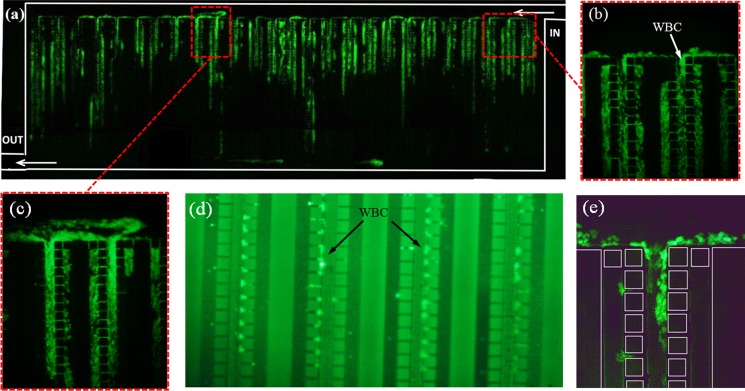
Fig. 10 shows photos of the filter under blood separation test stained with fluorescent gel and at low flow rate of 15 μl min⁻¹. The image of filtration area (Fig. 10a) has been prepared by stitching together different images captured at the same running condition. In Fig. 10a, stained white cells settled on the surfaces of whole pillar arrays can be seen. The cells have been squeezed and jammed under fluidic pressure while the deformability makes the individual cells in this area not distinguishable easily. Meanwhile, traces of stained cells which might have been burst are noticeable. Cell rupture under severe pressure may occur in any stage of the experimental works before or after injection to the microdevice. Figs. 10b, 10c illustrate the accumulation of white cells before and after pillar arrays. The undiluted blood cells injected at low flow rates have low moving velocities around the pillar gaps. These cells have a tendency to adhere and accumulate onto the polymer surface before pillar array or after passing it as described earlier in the case of microspheres. The low speed condition after the pillars is illustrated by the short velocity vectors in the simulation results in Fig. 4. In Figs. 10d, 10e, individual WBCs retained or while passing the pillars are noticeable.

Figure 10.

Microscopic photos of trapping of WBCs stained with SYBR green and under green fluorescent emission. (a) The whole pillar chamber, (b) image of a pillar array near to pillar chamber IN, (c) image of a pillar array in the middle of the chamber, (d) image of the middle section of the pillar arrays and the trapped white cells, (e) additional image of WBCs trapped in the flow in a pillar array.

Comparison with the pillar-based and other separation techniques

Different pillar filters and non-filtration separation techniques are listed for comparison in Tables 1, TABLE II.. Dilution of blood with PBS by a ratio of at least 10 times has been applied before injection as a way of improvement of separation efficiency in most of the reported research. In the present work, the blood was injected without dilution. Although it may cause early filter clogging or rapid degradation of the separation performance, but the benefit of using undiluted blood is shorter process time.

TABLE I.

Summary of the important parameters in separation of whole blood cells using pillar-based techniques.

Number and filter type	Dilution ratio	Total pore area (mm2)	Flow rate (μl min−1)	Capacity (μl)	Number of pillars	Cut-off size (μm)	RBCs pass efficiency	WBCs trap efficiency	Substrate
1) Crossflow64	0, 100	1.177	2.5–10	Unlimited	∼6038	6.5	45%, 85.3%	8%	Silicon
2) Present research	0	0.74	15–50	4	2700	5.5	∼84%–89%	∼ 18%–25%	PUMA
3) Crossflow58	200	12.67	20	>1.5	∼36 200	3.5	60%–95%	70%–95%	Silicon
4) Normalflow58	200	0.474	20	1.5	∼1355	3.5	20%–55%	70%–95%	Silicon
5) Normalflow4	100	0.187	35	1	667	3.5	…	…	Silicon
6) Crossflow53	0	0.05	5–12	…	500	2.5	25%–50%	60%–97%	PDMS

TABLE II.

Summary of the important parameters in separation of blood cells using non-filtration techniques.

Number and separation technique	Dilution ratio	Flow rate (μl min−1)	Plasma separation	Platelets separation	RBCs separation	WBCs separation
1) Dielectrophoresis41	∼15	2.5	…	95%	…	…
2) Hydrodynamic80	∼10	20	…	Ratio of WBCs to RBCs increased 29 folds
3) Streamline-based54	∼100–1000	∼0.6–1.0	…	…	…	97%
4) Bifurcation law63, 65	∼10	0.17	15–25%	…	…	…
5) Membrane68	0	10	22%	…	…	…
6) Dielectrophoresis20	0	∼0.1	…	98.8%	…	…
7) Magnetophoresis81	20	∼8.3–11.7	…	…	95%	…
8) Aqueous two-phase system74	…	1		Ratio of WBCs to RBCs increased 9.13 folds
9) Asymmetric pinched flow fractionation79	50	0.33	…	…	80%	…

Number of pillars, cut-off size, and total pore area are geometrical parameters with effects on the overall performance. The filters in the Table TABLE I. are tabulated according to reducing the cut-off size. In all filters in Table TABLE I., increasing cut-off size as the major parameter increases RBCs average passing efficiency and reduces WBCs average trapping efficiency and vice versa. Increasing the number of pillar gaps by increasing the number of pillars increases the total pore area. The higher pore area increases the filtration capacity without effect on the separation efficiencies.

The capacity of the filters in Table TABLE I. is defined as the amount of blood sample that can be processed. Filtration up to capacity causes highly accumulation of WBCs and RBSs. At this condition, maintaining a constant flow rate will increase the internal pressure higher than the bonding threshold which causes device failure. Nominal filter capacity is a function of the internal volume of the device before the pillars and pore area but the actual capacity also depends on the efficiencies of the trapping WBCs and passing RBCs. In blood, the red cells constitute ∼45% and the plasma is ∼55% of the total volume. The Buffy coat which includes the white cells and platelets forms less than 1% of the volume. Therefore, even 100% efficiency of trapping WBCs is ∼0.01 μl per μl of blood. The nominal capacity of the filter under test is ∼0.3 μl. The capacity volume is enough for filtration of ∼30 μl of blood sample giving that separation efficiencies are 100% but in fact, the passing RBCs efficiency is ∼85% will reduce the actual capacity to ∼4 μl in the best condition.

The maximum flow rates for blood cell separation in Tables TABLE I. and TABLE II. are reported below 50 μl min⁻¹ considerably lower than 400 μl min⁻¹ reported in this work for microspheres separation. The reason for low flow rates in blood injection is the high volume of erythrocytes in blood and the fact that the cells are highly deformable compared to the microspheres. Accumulation of the cells leaves very low space for the cells to rotate or move around, and also the WBCs and RBCs can be lysed under high flow rates or fluidic pressures. Tables TABLE I. and TABLE II. explain that the blood flow rate in the pillar-based techniques is higher than that in most of the non-filtration methods due to the fact that the non-filtration devices are effective in very low flow rates.

The RBCs passing efficiency in the present work is ∼84%–89%(average ∼86.5) for flow rates of 15–50 μl min⁻¹ that is higher than the average values of RBCs passing efficiencies reported for filter number 3–6 in Table TABLE I. and non-filtration methods such as asymmetric pinched flow fractionation.⁷⁹ The cut-off size of the present filter is ∼5.5 μm that allows most of the RBCs pass through easily as well as the WBCs with relatively low trapping efficiency of 18%–25% (average ∼21.5). This amount is higher than 8% trapping efficiency for filter No. 1 with cut-off size of 6.5 μm but lower than WBCs trapping efficiency for filters No. 3–6. These results explain that the efficiencies of the separation obtained in the present work agree well with the trend of the variation of the efficiencies versus cut-off size.

Almost all the fabricated pillar-based filters reported in Table TABLE I. have the silicon as the main substrate with tall pillars (heights ∼20–100 μm) and high aspect ratio posts (>2) except the filter No. 6 which is a PDMS-based with very short (height ∼ 2.5 μm) and low aspect ratio (<<1) posts. Using high aspect ratio structures on silicon substrate is a common practice but in the case of elastomeric materials, special considerations are necessary in the design process similar the present research.

CONCLUSION

Our findings through the performed analysis and test suggest as follows:

First, the elastomeric substrates such as PUMA and PDMS are effective in rapid prototyping of pillar-based microfluidic devices through simple molding technique. By appropriate design of the device, excessive deformation of the pillars and microstructures under fluidic pressure which is the major concern of the elastomeric substrates is limited to negligible or low level. The pillar arrays and high aspect ratio gaps remain almost consistent and uniform during low flow rate separation experiments.

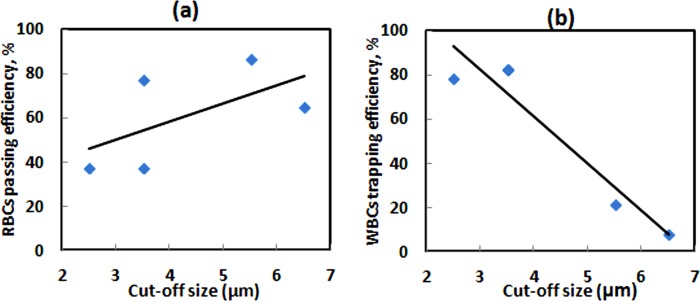
Second, blood filtration results of the fabricated device are comparable to silicon-based microfilters reported in the literature. The cut-off size of the pillar array is a determining parameter for cell and bead separation efficiencies. A large cut-off size gives WBCs of high purity from RBCs contamination but low concentration. Figs. 11a, 11b have been prepared using average efficiencies in Table TABLE I. as a guide for selecting a suitable pillar cut-off size to match the future applications.

Figure 11.

Separation efficiencies of pillar-based filter function of cut-off size. (a) Red blood cells passing efficiency, (b) white blood cells trapping efficiency.

The presented design can be integrated with other downstream microfluidic components such as microchannels with optimization of the dimensions. The percentage of the cell loss in the device needs to be determined for the applications where the cell viability is important. The cell adhesion to polymer surface is an important factor that needs further investigations.