Abstract
Brightness induction refers to a class of visual illusions where the perceived intensity of a region of space is influenced by the luminance of surrounding regions. These illusions are significant because they provide insight into the neural organization and processing strategies employed by the visual system. The nature of these processing strategies, however, has long been debated. Here we investigate the spatial characteristics of grating induction as a function of the distance from the inducing field edge to evaluate the viability of various competing models. In particular multiscale spatial filtering models and homogeneous filling-in models make very different predictions in regard to the magnitude of induction as a function of this distance. Filling-in explanations predict that the brightness/lightness of the filled-in region will be homogeneous, whereas multiscale filtering predicts a fall-off in induction magnitude with distance from the inducing field edge. Induction magnitude was measured using a narrow probe version of the quadrature-phase motion-cancellation paradigm (Blakeslee & McCourt, 2011) and a point-by-point brightness matching paradigm (McCourt, 1994; Blakeslee & McCourt, 1997; 1999). Both techniques reveal a decrease in the magnitude of induction with increasing distance from the inducing edge. A homogeneous filling-in mechanism cannot explain the induced structure in the test fields of these stimuli. The results argue strongly against filling-in mechanisms as well as against any mechanism that posits that induction is homogeneous. The structure of the induction is, however, well accounted for by the multiscale filtering (ODOG) model of Blakeslee and McCourt (1999). These results support models of brightness/lightness, such as filtering models, which preserve these gradients of induction.
Keywords: Brightness induction, grating induction, cancelation, point-by-point brightness matching, filling-in, multiscale filtering, quadrature motion
1) Introduction
Brightness/lightness induction effects refer to a class of visual illusions in which the perceived intensity of a region is modulated by the luminance of surrounding regions. These illusions are of interest because of the information they reveal regarding processing strategies within the visual system. The exact nature of these processing strategies, however, has long been debated and remains contentious. Kingdom (2011) provides a recent and comprehensive review of models of brightness and lightness perception and summarizes some of the controversies surrounding them. Most relevant to the current study is the debate regarding the mechanism responsible for simultaneous brightness/lightness contrast (simultaneous contrast) and its many variants. Simultaneous contrast is an effect in which a gray patch on a dark background looks brighter/lighter than an equivalent gray patch on a light background. Mach (1865, in Ratliff, 1965) and Hering (1874; 1964) advocated a “low-level” account of simultaneous contrast based on reciprocal interactions between elements in the visual system. This view was later represented by early models of lateral inhibitory interactions such as those performed by the center-surround receptive fields of cells in the retina and LGN of cats and primates (for reviews see: Heinemann, 1972; Kingdom & Moulden, 1988; Jameson & Hurvich, 1989; Fiorentini et al., 1990; Kingdom, 1997; 2003; 2011; Fiorentini, 2003) and is today represented by multiscale filtering models such as the ODOG model (Blakeslee & McCourt, 1999; Robinson, Hammond & de Sa, 2007), as well as by models relying on filling-in (Grossberg & Todorovic, 1988; Rossi & Paradiso, 2003; Rudd, 2010). Filling-in models differ from multiscale filter models, like the ODOG model, in that the brightness/lightness of the test patch or surface is determined by information extracted by relatively high-frequency filters (small receptive fields) at the edges of the patch or at multiple edges within the stimulus (Rudd, 2010). This information is then thought to be actively filled-in (isomorphic theory) or assigned (symbolic theory) to the entire enclosed area (Cornsweet & Teller, 1965; Gerrits & Vendrik, 1970; Grossberg & Todorovic, 1988; Fiorentini et al., 1990; Paradiso & Nakayama, 1991; Rossi & Paradiso, 1996; 2003; Paradiso & Hahn, 1996; Kingdom & Moulden, 1988; Grossberg, 2003; Rudd & Zemach, 2004; Grossberg & Hong, 2006; Komatsu, 2006; Rudd, 2010; Kingdom, 2011). Helmholtz (1866; 1962), on the other hand, emphasized the importance of “unconscious inference” in producing the simultaneous contrast effect. According to Helmholtz the test patch on the white background is interpreted to be under more intense illumination than the test patch on the black background. However, since the two gray test patches reflect the same amount of light the visual system “unconsciously infers” that the more highly illuminated test patch must possess a lower reflectance, thereby resulting in its perception as lower in brightness/lightness. This “higher-level” account is revisited in current models based on a variety of factors such as mid-level junction analysis (Adelson, 2000), Gestalt grouping (Gilchrist, 2006), and perceptual inferences about depth, shape, illumination, reflectance, and transparency (Gilchrist et al., 1999; Adelson, 2000; Logvinenko & Ross, 2005; Gilchrist, 2006; Bressan, 2006; Anderson & Winawer, 2008). Helmholtz's ideas are also closely echoed by proponents of the “empirical” approach that replaces the idea of “unconscious inference” with the idea that percepts arise in proportion to their respective frequencies of occurrence in the past experiences of both the species and the individual observer (Purves, Williams, Nundy & Lotto, 2004).
In grating induction a sinusoidal inducing grating produces a large-magnitude spatial brightness/lightness variation (i.e., a sinusoidal grating) in an extended homogeneous test field (Figure 1). Grating induction (McCourt, 1982) has been shown to be closely related, if not identical in all but the stimulus used to produce it, to the classical simultaneous contrast effect (Blakeslee & McCourt, 1997). Blakeslee and McCourt (1997) examined point-by-point matching profiles for a series of stimuli in which test field width transitioned smoothly from the two test patch configuration of simultaneous contrast to the single elongated test field of the grating induction configuration. These matching profiles revealed that horizontal induced structure was present in the test fields of all of these stimuli (i.e., none of the test fields appeared homogeneous) and that both the structure and magnitude of induction were parsimoniously accounted for by the output of a multiscale difference-of-Gaussians (DOG) filtering model. Using this same matching technique, Blakeslee and McCourt (1999) later showed that induction was not homogeneous in the test fields of White stimuli as well. The addition of orientation selectivity and response normalization to the DOG model, creating the oriented DOG (ODOG) model, extended the model to account for anisotropic effects such as the White effect.
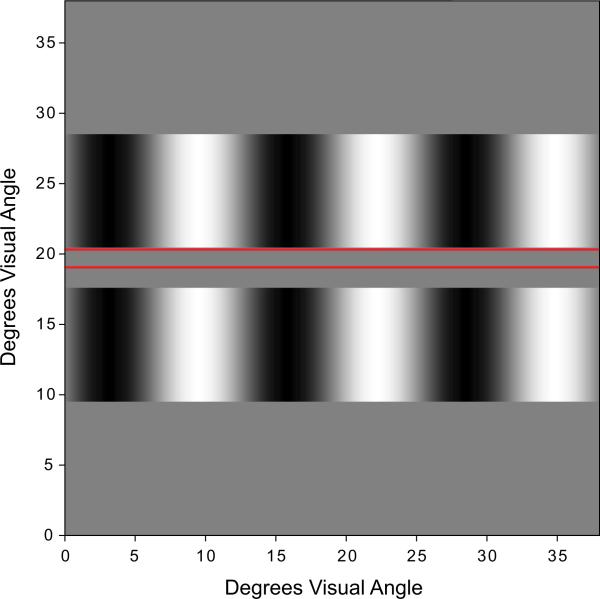
Fig. 1.
Schematic illustrating the size and position of the probe (red lines) relative to the grating induction stimulus when the probe was positioned near the center or edge of a 3° test field. The thickness of the red lines illustrates the probe grating height (0.2°).
That induction in the test fields of these stimuli is not homogeneous is of theoretical importance because of the difficulty of explaining this fact using currently popular (non-filtering based) models of brightness/lightness perception. Only the ODOG model and other closely related models relying on spatial filtering (Blakeslee & McCourt, 1999; Robinson, Hammond & de Sa, 2007) can explain these induced brightness/lightness gradients. Other older brightness/lightness effects commonly acknowledged to possess gradient structure and posing the same difficulty for non-filter based models (but see Geier & Hudak, 2011) include Mach bands (Mach, 1865; in Ratliff, 1965), the Chevreul illusion (Chevreul, 1861; Geier & Hudak, 2011), the Hermann grid illusion (Hermann, 1870; Spillmann, 1994), and linear gradient induction (Shapley & Reid, 1985; Moulden & Kingdom, 1991; Kingdom, 1999; Blakeslee & McCourt, 2005).
Here we investigate the spatial characteristics of grating induction as a function of the distance from the inducing field edge in an effort to further evaluate the viability of the various competing models. In particular multiscale spatial filtering models such as the ODOG and related models (Blakeslee & McCourt, 1997; 1999; Robinson et al, 2007) and filling-in models (Grossberg & Todorovic, 1988; Rossi & Paradiso, 2003; Komatsu, 2006) make very different predictions in regard to the magnitude of induction as a function of this distance. Filling-in explanations predict that the brightness/lightness of the filled-in region will be homogeneous, whereas multiscale filtering predicts a fall-off of induction magnitude with distance from the inducing field edge. A narrow probe version of the quadrature-phase motion-cancellation paradigm (Blakeslee & McCourt, 2011) and a point-by-point brightness matching paradigm (McCourt, 1994; Blakeslee & McCourt, 1997; 1999) are used to measure the magnitude of induction.
2. Materials and methods
The authors (BXB & MEM) and six naïve observers (MMM, LML, AMZ, JJW, APH, KXM) participated in the experiments. All observers possessed normal or corrected-to-normal vision. Each participant provided informed consent and the experimental protocol was approved by the NDSU Institutional Review Board.
Stimuli were presented on a 22” Mitsubishi DiamondPro (model 2070) CRT display at a frame refresh rate of 140 Hz. Stimuli were generated and presented using MATLAB routines to control a Cambridge Research Systems ViSaGe system (14-bit intensity resolution per channel). Gamma linearization was accomplished via look-up tables following photometric calibration. Display format was 1024 (w) × 768 (h) pixels. Viewing distance was 57 cm resulting in a stimulus field that was 40° in width and 30° in height. Individual pixels measured 0.039° × 0.039°. Mean display luminance was 53 cd/m2.
In order to study the properties of induction as a function of the distance from the test/inducing field edge, a narrow probe version of the quadrature phase motion cancellation technique (Blakeslee & McCourt, 2011) as well as a static point-by-point matching technique (McCourt, 1994; Blakeslee & McCourt, 1997; 1999) were used to measure the magnitude of grating induction. The quadrature procedures differed from earlier studies only in that the added luminance (quadrature) grating was restricted to a narrow strip that occupied only a small vertical extent (0.2°) of the test field. It thus served as a probe to measure the magnitude of induction as a function of its position within the test field (Fig. 1).
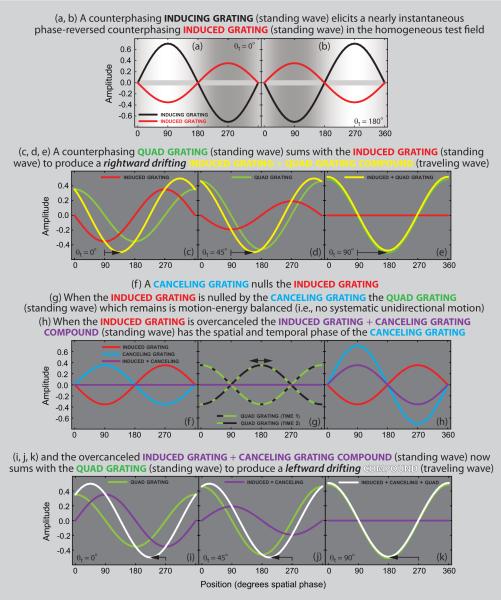
In the quadrature-phase motion cancelation technique a counterphasing inducing grating (standing wave) [Figure 2a, b (black line)] produces a nearly instantaneous phase-reversed counterphasing induced grating (standing wave) [Fig. 2a, b (red line)] in the homogeneous test field of a grating induction display (Blakeslee & McCourt, 1997; 2008; McCourt, 1982; 1994). A counterphasing quadrature grating (standing wave in 90° spatial and temporal phase relative to the induced grating) [Fig. 2c–e (green line)] sums with the induced grating (standing wave) [Fig. 2c–e (red line)] to produce a rightward drifting induced + quadrature grating compound (traveling wave) [Fig. 2c–e (yellow line)] to which the visual system is extremely sensitive (Blakeslee & McCourt, 2008). In order to measure the magnitude of induction the temporal phase of the quadrature grating is held constant at 90° phase relative to the induced grating. A second luminance grating is added to the test field. This second “canceling” grating [Fig. 2f, h (blue line)] possesses the same spatial and temporal frequency as the induced grating, but is 180° out of spatial phase with it. The canceling grating is added to the test field at a number of contrast levels, using the method of constant stimuli. When canceling grating contrast is less than induced grating contrast (i.e., when the induced grating is under-canceled) the compound grating possesses the spatial and temporal phase of the induced grating. It therefore combines with the quadrature grating to produce a rightward moving traveling wave just as in the case where no canceling grating is present [Fig. 2c–e (yellow line)]. When canceling grating contrast exceeds induced grating contrast (i.e., when the induced grating is over-canceled) the compound grating possesses the spatial and temporal phase of the canceling grating [Fig. 2h (purple line)]. This compound combines with the quadrature grating to produce a leftward moving traveling wave [Fig. 2i–k (white line)]. When canceling grating contrast equals induced grating contrast the sum is zero (i.e., the induced grating is nulled) [Fig. 2f, g (purple line)]. The motion energy of the counterphasing quadrature grating which remains is left/right balanced (i.e., a standing wave) [Fig. 2g (green/black lines)] yielding a 50:50 proportion of left/right motion judgments in a forced-choice motion direction discrimination task.
Fig. 2.
In the quadrature-phase motion technique a counterphasing inducing grating (standing wave) [a, b (black line)] produces a nearly instantaneous phase-reversed counterphasing induced grating (standing wave) [a, b (red line)] in the homogeneous test field of a grating induction display. A counterphasing quadrature grating (standing wave in 90° spatial and temporal phase relative to the induced grating) [c–e (green line)] sums with the induced grating (standing wave) [c–e (red line)] to produce a rightward drifting induced-plus-quadrature grating compound (traveling wave) [c–e (yellow line)] to which the visual system is extremely sensitive. The temporal phase of the quadrature grating can be varied to measure the phase (time) lag of induction. To measure the magnitude of induction the temporal phase of the quadrature grating is held constant at 90° phase relative to the induced grating, and a second luminance grating is added to the test field. This second “canceling” grating [f, h (blue line)] possesses the same spatial and temporal frequency as the induced grating, but is 180° out of spatial phase with it. The canceling grating is added to the test field at a number of contrast levels, using the method of constant stimuli. When canceling grating contrast is less than induced grating contrast (i.e., when the induced grating is under-canceled) the compound grating possesses the spatial and temporal phase of the induced grating. It therefore combines with the quadrature grating to produce a rightward moving traveling wave just as in the case where no canceling grating is present [c–e (yellow line)]. When canceling grating contrast exceeds induced grating contrast (i.e., when the induced grating is over-canceled) the compound grating now possesses the spatial and temporal phase of the canceling grating [h (purple line)]. This compound combines with the quadrature grating to produce a leftward moving traveling wave [i–k (white line)]. When canceling grating contrast equals induced grating contrast the sum is zero (i.e., the induced grating is nulled) [f, g (purple line)]. The motion energy of the counterphasing quadrature grating which remains is left/right balanced (i.e., a standing wave) [g (green/black lines)] yielding a 50:50 proportion of left/right motion judgments in a forced-choice motion direction discrimination task.
In preliminary measurements we determined that motion signals in grating compounds remained strong even for large mismatches of quadrature and induced grating contrast. Quadrature grating contrast was therefore held at 0.50 for the 1500 ms inspection interval rather than ramped between 0 and 0.50 as in previous experiments (Blakeslee & McCourt, 2008; Blakeslee & McCourt, 2011).
Quadrature motion magnitude experiments
Inducing grating spatial frequency was 0.025 c/d (1 cycle/screen). Inducing gratings were counterphased at 4 Hz for a 3° test field height condition and at 1 Hz for a 3° and a 9° height condition. The psychophysical task was a forced-choice “left” versus “right” motion judgment of the induced + quadrature probe grating + canceling grating compound in the test field. The contrast of the canceling grating, which filled the test field, was varied from −15% to 100%, where negative contrast signifies a spatial phase reversal of the canceling grating such that it augments rather than cancels the induced grating. Canceling grating contrast was constant over the 1500 ms duration of stimulus presentation. Separate blocks of trials were run for the various combinations of temporal frequency and test field height (4 Hz, 3°; 1 Hz, 3°; 1Hz, 9°). Each block presented 10–15 levels of canceling contrast (randomly interleaved) for each combination of temporal frequency and test field height. Subjects completed between 10 and 20 blocks per condition.
Point-by-point matching experiments
Induction magnitude was also measured using a static point-by-point matching technique. The inducing stimulus was modified from that in the quadrature-phase motion cancellation experiment in that it was restricted to the left three quarters of the display (30°). Spatial frequency was increased to 0.033 c/d such that the inducing grating still consisted of one full cycle. The right ¼ (10°) of the display contained a homogenous field (set to the mean luminance) and a small rectangular matching patch (0.3° h × 0.7° w) on a checkerboard background (0.9° h × 1.35° w). Check contrast was 0.30 and check size was 0.15° × 0.15°. The vertical position of the matching patch and checkerboard varied from trial to trial and cued the subject as to which part of the test field was to be matched. The horizontal location to be matched was constant and cued by a low contrast pointer. Observers were instructed to adjust the matching patch to match the brightness of the test field at the corresponding vertical location. To avoid any confusion observers were specifically told that brightness matching required them to “adjust the matching patch to match the intensity or amount of light coming from the indicated test patch area ignoring, as much as possible, other areas of the display”. Observers made 10–15 matches per location for each of three test field heights (3°, 6°, & 9°). Matches were obtained for both the maximum and minimum phases of the inducing grating. On each matching trial the initial luminance of the matching patch was randomized. Observers controlled subsequent increments or decrements in matching patch luminance via button presses. Each button press caused a luminance change of 1% relative to the maximum luminance (107 cd/m2).
3) Results
Quadrature motion magnitude experiments
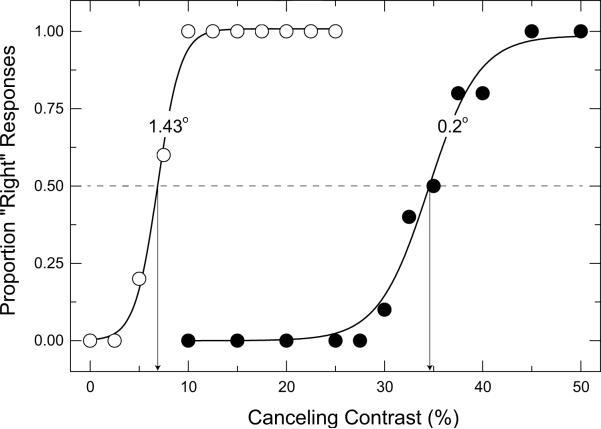
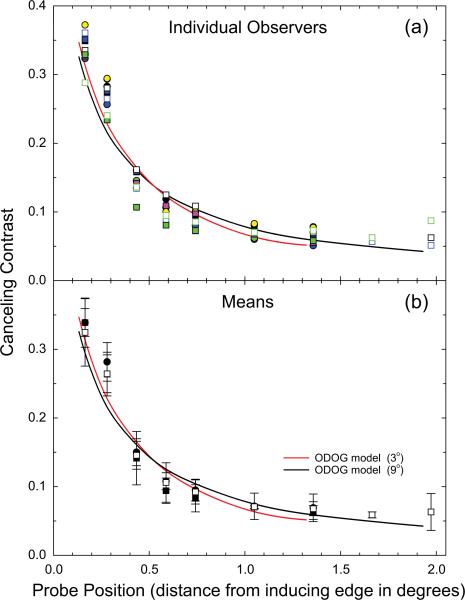
Psychometric data were fitted with a two-parameter (midpoint and slope) cumulative-normal function using a maximum-likelihood criterion. The fitted midpoint parameter corresponds to the contrast of the canceling grating yielding 50% “right” motion responses and was taken as a measure of grating induction magnitude. Figure 3 shows an example of fitted psychometric data for one observer. Induction magnitude results from four observers appear in Figure. 4, which plots canceling contrast as a function of probe position. The symbols in Fig. 4(a) plot the results from the individual observers (indicated by color) for the 4 Hz, 3° test field height (filled circles); 1 Hz, 3° test field height (filled squares) and 1 Hz, 9° test field height (open squares) conditions. The symbols in Fig. 4(b) plot the means and 95% confidence intervals for these four observers for the same conditions: 4 Hz, test field 3° (filled circles); 1 Hz, test field 3° (filled squares); 1 Hz, test field 9° (open squares). The individual and mean data clearly indicate that the magnitude of induction decreases with increasing distance from the inducing field edge for both 3° and 9° test field heights. For both test field heights, mean cancelling contrast similarly decreased from a value of 0.35 at the inducing edge to an asymptotic value of approximately 0.07 over a distance of 1.5°. These results are inconsistent with a filling-in mechanism that predicts, given sufficient time, a brightness/lightness percept of homogeneous magnitude throughout the test field. The results are, however, consistent with multiscale filtering by a finite set of filters such as that proposed by Blakeslee and McCourt (1999). This model has been described in detail elsewhere (Blakeslee & McCourt, 1999; 2004). The best fit predictions of the ODOG model for the 3° and 9° conditions are indicated in Fig. 4 by the solid red and black lines respectively. The model predictions are a good fit to the data. Overall the model accounts for 95% of the overall variance in the mean magnitude of induction found with distance from the inducing field edge.
Fig. 3.
Example psychometric functions from two probe locations (open symbols, 1.43° from the test field edge; filled symbols, 0.20° from the test field edge) are shown for one observer (BXB) in the quadrature-phase motion cancelation experiment. The 0.025 c/d inducing grating was counterphased at 1 Hz and test field height was 3°.
Fig. 4.
Canceling contrast plotted as a function of distance from the inducing field edge measured using the quadrature-phase motion cancelation technique. The symbols in panel (a) plot the results from the four individual observers (indicated by color) for the 4 Hz, 3° test field height (filled circles); 1 Hz, 3° test field height (filled squares) and 1 Hz, 9° test field height (open squares) conditions. The symbols in panel (b) plot the means and 95% confidence intervals for these four observers for the same conditions: 4 Hz, test field 3° (filled circles); 1 Hz, test field 3° (filled squares); 1 Hz, test field 9° (open squares). The individual and mean data clearly indicate that the magnitude of induction decreases with increasing distance from the test/inducing field edge for both 3° and 9° test field heights. The best fit predictions of the ODOG model (Blakeslee & McCourt, 1999) for the 3° and 9° conditions are indicated by the red and black lines, respectively, in both panels and account for 95% of the overall variance.
Matching magnitude experiments
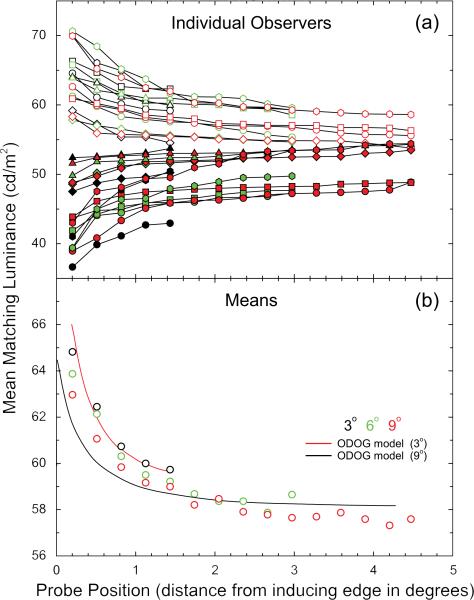
For each of six observers, Figure 5(a) plots matching luminance for test field heights of 3° (black symbols), 6° (green symbols) and 9° (red symbols) as a function of distance from the inducing field edge. Matches were obtained for both the maximum (filled symbols) and minimum (open symbols) inducing grating phase. Individual observers are indicated by symbol shape. Despite individual differences in absolute induction magnitude, all subjects show a decrease in induction strength with increasing distance from the inducing field edge. In Fig. 5(b) the minimum inducing grating phase data are collapsed across observers and plotted as means along with the linear best fit predictions of the ODOG model for the 3° and 9° conditions. The model predictions are a good fit to the data accounting for 95% of the overall variance in the mean magnitude of induction found with distance from the inducing field edge.
Fig. 5.
Matching luminance as a function of distance from the inducing field edge is plotted separately for five observers (indicated by symbol shape) in panel (a). Matches were obtained for test field heights of 3° (black symbols), 6° (green symbols) and 9° (red symbols) at both the maximum (filled symbols) and minimum (open symbols) inducing grating phase. All subjects show a decrease in the magnitude of induction as a function of the distance from the inducing field edge, despite individual differences in overall induction magnitude. In panel (b) the minimum inducing grating phase data are collapsed across observers and plotted as means along with the linear best fit predictions of the ODOG model for the 3° and 9° conditions. The model predictions are a good fit to the data accounting for 95% of the overall variance in the mean magnitude of induction found with distance from the inducing field edge.
4. Discussion
A decrease in the magnitude of induction with distance from the inducing edge was found in the present experiments using both a quadrature phase motion cancellation technique as well as a point-by-point static matching technique. These results complement prior point-by-point brightness matching data for grating induction, simultaneous contrast, and White stimuli that revealed the horizontal (as opposed to the vertical) induced structure in the test fields of these stimuli (Blakeslee & McCourt, 1997; 1999). In addition, the results confirm recent behavioral and fMRI evidence (Pereverzeva & Murray, 2008) that the magnitude of induction declines with distance from the inducing field edge of static central disks in which the disk surround was modulated at 1 Hz. The induced structure observed in all of these studies argues strongly against homogeneous filling-in mechanisms as well as against any mechanism, including most of the non-filter based mechanisms discussed in the Introduction, that posit that induction is homogeneous. The structured induction, however, is well accounted for by the ODOG model of Blakeslee and McCourt (1999) and supports any models of brightness/lightness that preserve these gradients of induction.
The arguments against a homogeneous filling-in mechanism are also consistent with and supported by earlier findings for grating induction stimuli obtained with the quadrature phase motion technique using full-field probes (Blakeslee & McCourt, 2008). Blakeslee and McCourt (2008) found that the temporal response of induced brightness differed from that of a real luminance grating by a very small temporal phase (< 0.016 cycle) or time (<1 ms) lag, and remained constant across wide variations of temporal frequency (2 – 24 Hz) and test field height (0.5° – 9°). The findings that the phase (time) lag of induction did not vary with test field height and that induction was present even at 24 Hz, argued against a slow filling-in explanation for brightness induction in grating induction stimuli. This conclusion has been further supported by investigations of induction magnitude in simultaneous contrast stimuli using very brief stimulus presentations (Robinson & de Sa, 2008; Kaneko & Murakami, 2012). Unlike earlier studies of simultaneous contrast indicating that induction was a slow process with a cut-off frequency between 2.5 and 5 Hz (DeValois, Webster, DeValois & Lingelbach, 1986; Rossi & Paradiso, 1996), these studies found that brightness induction was strongest at short presentation durations and declined in magnitude with increasing duration. The shortest presentation interval was 58 ms in the Robinson and de Sa (2008) study and 10 ms in the investigation by Kaneko and Murakami (2012). These results are inconsistent with the idea that brightness induction depends on a slow filling-in process; however, as noted by Robinson and de Sa (2008) they do not rule out a fast filling-in mechanism (Komatsu, 2006). The vertical spatial structure measured in the test fields of grating induction stimuli in the present study, and the horizontal structure measured in grating induction, simultaneous contrast, and White stimuli in previous studies (Blakeslee & McCourt, 1997; 1999), however, argue against homogenous filling-in at any speed as the mechanism responsible for these induced effects.
In the face of this evidence one might reasonably ask why it is so often the case that induction is assumed to be homogeneous. Interestingly, Heinemann (1972) addressed this same question with regard to the brightness variations that occur in physically uniform fields. He suggested that “subjects can use different criteria when assessing the brightness of an extended field. For, example, they may base their judgment on the brightness at the edges, or at the center, or on the average brightness in the field.” To illustrate this point Heinemann (1972) cited a study by Davidson (1968) in which subjects were briefly presented a strip of uniform luminance somewhat greater than the luminance of the background. When asked, the subjects reported that the strip was uniform in brightness. When this same strip was presented as one of a series of patterns and subjects were asked to indicate whether the center or the edge of each strip was darker, however, the center of the uniform strip was always reported to be darker. In other words, the criterion for what an observer reports as homogeneous can be influenced by the question posed or the task given. By this reasoning the grating induction stimulus configuration is a very effective one for revealing structured induction, at least in the horizontal direction, as is, for example, the Chevreul illusion discussed earlier. The brightness gradients in the vertical direction of the grating induction stimulus and in other induction stimuli such as the White effect or the classical simultaneous contrast effect are, however, more subtle resulting in their description as homogeneous or structured depending on the question or task.
Brightness induction is measured as a function of distance.
The magnitude of induction decreases with distance from the inducing field edge.
These results are inconsistent with a homogeneous filling-in mechanism.
The structure of induction is well accounted for by multiscale filtering models.
Acknowledgments
This work was supported by grants R01 EY014015 (BB) and NIH P20 GM103505 (MEM). The National Institute for General Medical Sciences (NIGMS), and the National Eye Institute (NEI) are components of the National Institutes of Health (NIH). The contents of this report are solely the responsibility of the authors and do not necessarily reflect the official views of the NIH, NIGMS or NEI. The authors thank Huanzhong (Dan) Gu for programming assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Commercial relationships: none.
REFERENCES
- Adelson EH. Lightness perception and lightness illusions. In: Gazzaniga M, editor. The New Cognitive Neurosciences. 2nd ed. MIT Press; Cambridge, MA: 2000. pp. 339–351. [Google Scholar]
- Anderson BL, Winawer J. Layered image representations and the computation of surface lightness. Journal of Vision. 2008;8(7):18, 1–22. doi: 10.1167/8.7.18. http://www.journalofvision.org/content/8/7/18, doi:10.1167/8.7.18. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. Similar mechanisms underlie simultaneous brightness contrast and grating induction. Vision Research. 1997;37:2849–2869. doi: 10.1016/s0042-6989(97)00086-2. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A multiscale spatial filtering account of the White effect, simultaneous brightness contrast and grating induction. Vision Research. 1999;39:4361–4377. doi: 10.1016/s0042-6989(99)00119-4. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A unified theory of brightness contrast and assimilation incorporating oriented multiscale spatial filtering and contrast normalization. Vision Research. 2004;44:2483–2503. doi: 10.1016/j.visres.2004.05.015. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A multiscale filtering explanation of gradient induction and remote brightness induction effects: A reply to Logvinenko (2003) Perception. 2005;34:793–802. doi: 10.1068/p5303x. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. Nearly instantaneous brightness induction. Journal of Vision. 2008;8(2):15, 1–8. doi: 10.1167/8.2.15. http://journalofvision.org/8/2/15/, doi:10.1167/8.2.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. Spatiotemporal analysis of brightness induction. Vision Research. 2011;51:1872–1879. doi: 10.1016/j.visres.2011.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressan P. The place of white in a world of grays: A double-anchoring theory of lightness perception. Psychological Review. 2006;113:526–553. doi: 10.1037/0033-295X.113.3.526. [DOI] [PubMed] [Google Scholar]
- Chevreul ME. In: The laws of contrast of colour: And their application to the arts. Spanton John., translator. Routledge, Warne & Routledge; London: 1861. [Google Scholar]
- Cornsweet TN, Teller D. Relation of increment thresholds to brightness and luminance. Journal of the Optical Society of America. 1965;55:1303–1308. doi: 10.1364/josa.55.001303. [DOI] [PubMed] [Google Scholar]
- Davidson ML. Perturbation approach to spatial brightness interaction in human vision. Journal of the Optical Society of America. 1968;58:1300–1309. doi: 10.1364/josa.58.001300. [DOI] [PubMed] [Google Scholar]
- DeValois RL, Webster MA, DeValois KK, Lingelbach B. Temporal properties of brightness and color induction. Vision Research. 1986;26:887–897. doi: 10.1016/0042-6989(86)90147-1. [DOI] [PubMed] [Google Scholar]
- Fiorentini A, Baumgartner G, Magnussen S, Schiller PH, Thomas JP. The perception of brightness and darkness: relations to neuronal receptive fields. In: Spillmann L, Werner JS, editors. Visual Perception: The Neurophysiological Foundations. Academic Press; San Diego: 1990. [Google Scholar]
- Fiorentini A. Brightness and lightness. In: Chalupa Leo M., L. M., Werner JS., editors. The Visual Neurosciences. MIT Press; Cambridge: 2003. [Google Scholar]
- Geier J, Hudak M. Changing the Chevreul illusion by a background luminance ramp: Lateral inhibition fails at its traditional stronghold – A psychophysical refutation. PLoS ONE. 2011;6(10):e26062. doi: 10.1371/journal.pone.0026062. doi:10.1371/journal.pone.0026062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrits HJM, Vendrik AJH. Simultaneous contrast, filling-in process and information processing in man's visual system. Experimental Brain Research. 1970;11:411–430. doi: 10.1007/BF00237914. [DOI] [PubMed] [Google Scholar]
- Gilchrist A, Kossyfidis C, Bonato F, Agostini T, Cataliotti J, Li X, Spehar B, Annan V, Economou E. An anchoring theory of lightness perception. Psychological Review. 1999;106:795–834. doi: 10.1037/0033-295x.106.4.795. [DOI] [PubMed] [Google Scholar]
- Gilchrist AL. Seeing black and white. Oxford University Press; New York: 2006. [Google Scholar]
- Grossberg S. Filling-in the forms: Surface and boundary interactions in visual cortex. In: Pessoa L, DeWeerd P, editors. Filling-in: From Perceptual Completion to Cortical Reorganization. Oxford University Press; New York: 2003. [Google Scholar]
- Grossberg S, Hong S. A neural model of surface perception: Lightness, anchoring, and filling-in. Spatial Vision. 2006;19:2–4. 263–321. doi: 10.1163/156856806776923399. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Todorovic D. Neural dynamics of 1-D and 2-D brightness perception: A unified model of classical and recent phenomena. Perception and Psychophysics. 1988;43:241–277. doi: 10.3758/bf03207869. [DOI] [PubMed] [Google Scholar]
- Heinemann EG. Simultaneous brightness induction. In: Jameson DH, L.M., editors. Handbook of Sensory Physiology. VII/4. Springer; Berlin: 1972. pp. 147–169. [Google Scholar]
- Helmholtz H. von. In: Treatise on physiological optics (Vol. II) Southall JPL, translator. Dover Publications; New York: 1866; 1962. pp. 264–301. Vol. II originally published in 1866. [Google Scholar]
- Hering . Outlines of a theory of light sense. Harvard University Press; Cambridge MA: 1874; 1964. originally published in 1874. [Google Scholar]
- Hermann L. Eine erscheinung simultanen contrastes. Pflügers Archiv für die gesamte Physiologie. 1870;3:13–15. [Google Scholar]
- Jameson D, Hurvich LM. Essay concerning color constancy. Annual Review of Psychology. 1989;40:1–22. doi: 10.1146/annurev.ps.40.020189.000245. [DOI] [PubMed] [Google Scholar]
- Kaneko S, Murakami I. Flashed stimulation produces strong simultaneous brightness and color contrast. Journal of Vision. 2012;12(12):1, 1–18. doi: 10.1167/12.12.1. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA. Lightness, brightness and transparency: A quarter century of new ideas, captivating demonstrations and unrelenting controversy. Vision Research. 2011;51:652–673. doi: 10.1016/j.visres.2010.09.012. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA. Levels of brightness perception. In: Harris L, Jenkin M, editors. Levels of Perception. Springer; New York: 2003. pp. 47–72. [Google Scholar]
- Kingdom FAA. Simultaneous contrast: The legacies of Hering and Helmholtz. Perception. 1997;26:673–677. doi: 10.1068/p260673. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA. Old wine in new bottles? Some thoughts on Logvinenko's “Lightness induction revisited.”. Perception. 1999;28:929–934. doi: 10.1068/p2808ed. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA, Moulden B. Border effects on brightness: A review of findings, models and issues. Spatial Vision. 1988;3:225–262. doi: 10.1163/156856888x00140. [DOI] [PubMed] [Google Scholar]
- Komatsu H. The neural mechanisms of perceptual filling-in. Nature Reviews Neuroscience. 2006;7:220–231. doi: 10.1038/nrn1869. [DOI] [PubMed] [Google Scholar]
- Logvinenko AD, Ross DA. Adelson's tile and snake illusions: A Helmholtzian type of simultaneous lightness contrast. Spatial Vision. 2005;18:25–72. doi: 10.1163/1568568052801627. [DOI] [PubMed] [Google Scholar]
- McCourt ME. A spatial frequency dependent grating-induction effect. Vision Research. 1982;22:119–134. doi: 10.1016/0042-6989(82)90173-0. [DOI] [PubMed] [Google Scholar]
- McCourt ME. Grating induction: A new explanation for stationary visual phantoms. Vision Research. 1994;34:1609–1618. doi: 10.1016/0042-6989(94)90118-x. [DOI] [PubMed] [Google Scholar]
- McCourt ME, Blakeslee B. A contrast matching analysis of grating induction and suprathreshold contrast perception. Journal of the Optical Society of America A. 1994;11:14–24. doi: 10.1364/josaa.11.000014. [DOI] [PubMed] [Google Scholar]
- Moulden B, Kingdom FAA. The local border mechanism in grating induction. Vision Research. 1991;31:1999–2008. doi: 10.1016/0042-6989(91)90194-a. [DOI] [PubMed] [Google Scholar]
- Paradiso MA, Hahn S. Filling-in percepts produced by luminance modulation. Vision Research. 1996;36:2657–2663. doi: 10.1016/0042-6989(96)00033-8. [DOI] [PubMed] [Google Scholar]
- Paradiso MA, Nakayama K. Brightness perception and filling-in. Vision Research. 1991;31:1221–1236. doi: 10.1016/0042-6989(91)90047-9. [DOI] [PubMed] [Google Scholar]
- Pereverzeva M, Murray SO. Neural activity in human V1 correlates with dynamic lightness induction. Journal of Vision. 2008;8(15):8, 1–10. doi: 10.1167/8.15.8. [DOI] [PubMed] [Google Scholar]
- Purves D, Williams SM, Nundy S, Lotto RB. Perceiving the intensity of light. Psychological Review. 2004;111(1):142–158. doi: 10.1037/0033-295X.111.1.142. [DOI] [PubMed] [Google Scholar]
- Ratliff F. Holden-Day Series in Psychology. Holden-Day, Inc.; San Francisco: 1965. Mach Bands: Quantitative studies on neural networks in the retina. [Google Scholar]
- Robinson AE, de Sa VR. Brief presentations reveal the temporal dynamics of brightness induction and White's Illusion. Vision Research. 2008;48:2370–2381. doi: 10.1016/j.visres.2008.07.023. [DOI] [PubMed] [Google Scholar]
- Robinson AE, Hammond PS, de Sa VR. Explaining brightness illusions using spatial filtering and local response normalization. Vision Research. 2007;47:1631–1644. doi: 10.1016/j.visres.2007.02.017. [DOI] [PubMed] [Google Scholar]
- Rossi AF, Paradiso MA. Temporal limits of brightness induction and mechanisms of brightness perception. Vision Research. 1996;36:1391–1398. doi: 10.1016/0042-6989(95)00206-5. [DOI] [PubMed] [Google Scholar]
- Rossi AF, Paradiso MA. Surface completion: Psychophysical and neurophysiological studies of brightness. In: Pessoa L, DeWeerd P, editors. Filling-in: From Perceptual Completion to Cortical Reorganization. Oxford University Press; New York: 2003. [Google Scholar]
- Rudd ME. How attention and contrast gain control interact to regulate lightness contrast and assimilation: A computational neural model. Journal of Vision. 2010;10(14):40, 1–37. doi: 10.1167/10.14.40. [DOI] [PubMed] [Google Scholar]
- Rudd ME, Zemach IK. Quantitative properties of achromatic color induction: An edge integration analysis. Vision Research. 2004;44:971–981. doi: 10.1016/j.visres.2003.12.004. [DOI] [PubMed] [Google Scholar]
- Shapley R, Reid RC. Contrast and assimilation in the perception of brightness. Proceedings of the National Academy of Sciences, USA. 1985;82:5983–5986. doi: 10.1073/pnas.82.17.5983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spillmann L. The Hermann grid illusion: a tool for studying human perceptive field organization. Perception. 1994;23:691–708. doi: 10.1068/p230691. [DOI] [PubMed] [Google Scholar]