A Simulation Based Analysis of Motor Unit Number Index (MUNIX) Technique Using Motoneuron Pool and Surface Electromyogram Models

Abstract

Motor unit number index (MUNIX) measurement has recently achieved increasing attention as a tool to evaluate the progression of motoneuron diseases. In our current study, the sensitivity of the MUNIX technique to changes in motoneuron and muscle properties was explored by a simulation approach utilizing variations on published motoneuron pool and surface electromyogram (EMG) models. Our simulation results indicate that, when keeping motoneuron pool and muscle parameters unchanged and varying the input motor unit numbers to the model, then MUNIX estimates can appropriately characterize changes in motor unit numbers. Such MUNIX estimates are not sensitive to different motor unit recruitment and rate coding strategies used in the model. Furthermore, alterations in motor unit control properties do not have a significant effect on the MUNIX estimates. Neither adjustment of the motor unit recruitment range nor reduction of the motor unit firing rates jeopardizes the MUNIX estimates. The MUNIX estimates closely correlate with the maximum M wave amplitude. However, if we reduce the amplitude of each motor unit action potential rather than simply reduce motor unit number, then MUNIX estimates substantially underestimate the motor unit numbers in the muscle. These findings suggest that the current MUNIX definition is most suitable for motoneuron diseases that demonstrate secondary evidence of muscle fiber reinnervation. In this regard, when MUNIX is applied, it is of much importance to examine a parallel measurement of motor unit size index (MUSIX), defined as the ratio of the maximum M wave amplitude to the MUNIX. However, there are potential limitations in the application of the MUNIX methods in atrophied muscle, where it is unclear whether the atrophy is accompanied by loss of motor units or loss of muscle fiber size.

I. Introduction

Since the introduction of the motor unit number estimation (MUNE) method in 1971 [1], the technique and its various modifications have been used to detect motoneuron loss, and to measure disease progression in amyotrophic lateral sclerosis (ALS) and other neuromuscular disorders (see reviews [2–4]). The MUNE methods involve estimates of single motor unit action potential (MUAP) size, using either incremental electrical nerve stimulation or spike triggered averaging techniques, both potentially laborious and time-consuming. A recently developed technique uses the compound muscle action potential (CMAP) or the maximum M wave and surface electromyography (EMG) interference patterns recorded during voluntary muscle contraction to derive an index associated with the number of motor units in a muscle [5]. This method, called motor unit number index (MUNIX), offers several practical benefits compared with the MUNE techniques because it is easy and quick to perform, and induces minimal discomfort. The MUNIX method has been used to quantitatively assess motoneuron loss in ALS patients [5]. Recently, the method has attracted increasing applications for tracking disease progression of ALS, and for assessing motor unit loss in other neurological illnesses [6–16].

As an index measurement, the MUNIX does not provide an absolute count of the motor units in a muscle. Instead, it aims to provide a value that is proportional to the motor unit numbers in a muscle. Therefore, its applications have always been focused on examining motor unit number alterations by comparing different muscles (e.g., neurologically intact and disease state muscles), or the same muscles over time in a longitudinal study. Although the validity of MUNIX for revealing such alterations has been demonstrated in earlier experimental studies, there is a lack of systematic analysis that quantifies the sensitivity of the MUNIX measurement with respect to the actual motor unit number changes in a muscle. In particular, the MUNIX values are estimated from a mathematical model that relies on voluntary surface EMG signals, while the content of the voluntary surface EMG is very complex, and is dependent on a variety of factors, both muscular and neural.

For example, muscles impaired by neuromuscular disorders may experience muscle atrophy, manifested as a loss of muscle cross-sectional area. This area loss could be a result of motor unit loss, or shrinkage of individual muscle fibers comprising the motor units. Moreover, motor unit control properties are often profoundly affected. For example, data from patients with neurological disorders have shown that motor unit firing rates are reduced and recruitment thresholds are compressed during active force generation, potentially constraining voluntary EMG generation [17–19]. However, we do not know to what extent the muscle fiber and motor unit control property changes may also alter MUNIX estimates.

It follows that a systematic assessment of MUNIX performance is needed for assessment of motor unit number changes in a muscle. Of particular interest is how motor unit structure and neural control properties in diseased muscles may influence the MUNIX estimates. This information is important if we are to extract appropriate physiological or diagnostic information from MUNIX measurement. Accordingly, the objective of this study was to perform a systematic assessment of MUNIX methods using simulations of the motoneuron pool and the surface EMG [20]. Such simulation models have been used in the past to investigate the impact of changes in motoneuron pool or muscle properties on force and EMG output, and to assess the overall validity of motor unit analysis methods [21–30]. A simulation approach was used in this study to quantify the impact of different factors contributing to MUNIX estimates, especially those measures that are difficult to collect experimentally. The outcomes of our simulation analyses of the MUNIX estimates, examined with respect to changes in motor unit properties, could provide valuable information to enable an appropriate interpretation of the experimental MUNIX measurement.

II. Method

A. Overall Model Description

Surface EMG signals were simulated using a motoneuron pool model and a surface EMG model [20]. The motoneuron pool model transfers the excitation command (a given steady-state level of synaptic excitation) to motoneuron firing rate. The surface EMG model starts from the simulation of motor unit action potentials (MUAPs), to MUAP trains, and finally to surface EMG signal. Throughout the simulation, the model parameters were assigned according to the reported properties of the first dorsal interosseous (FDI) muscle [31–32].

B. Motoneuron Pool Model

The input and output properties of the motoneuron pool were simulated. The motoneuron threshold distribution was modeled as an exponential of the form [20]:

$$\mathit{RTE}(i)=e^{a·i}$$ (1)

$$a=(ln\mathit{RR})/n$$ (2)

where RTE is recruitment threshold excitation, i is an index identifying the motoneuron, and a is a coefficient used to establish a range of threshold values; ln is the natural logarithm, RR is the range of recruitment thresholds desired, and n is the total number of neurons. By this means, many neurons were assigned low thresholds while relatively few neurons were assigned high thresholds. A motoneuron remained inactive as long as the excitatory drive was less than the neuron’s assigned recruitment threshold value.

The firing rate of a motoneuron was modeled to increase linearly with excitatory drive above the recruitment threshold excitation. The minimum firing rate was set at 8 Hz for every motoneuron. The inter-spike interval of the motor unit firing was modeled as a random process with a Gaussian probability distribution function [33]. The standard deviation of the inter-spike interval was fixed for all motor units at 15% of the mean inter-spike interval. We included 120 motor units in the model (n = 120). The motor unit recruitment range was assigned to be up till 40% excitation [34].

The precise motor unit firing rate distribution that occurs for different motor units in vivo is still unknown. Justification of different opinions of this unresolved issue is beyond the scope of this paper. Accordingly, three types of motor unit firing rate strategies were used in the simulation based on experimental observations.

The first type modeled an “onion-skin” pattern of the motor unit firing rates observed from the voluntary contractions, i.e. the peak firing rate of a motor unit was inversely proportional to its recruitment threshold [34–37]. In this strategy, the slope of the excitatory drive-firing rate relation was set to be the same for all motoneurons. For the second type of motor unit firing rate strategy, the slope of the excitatory drive-firing rate relation of the motoneuron increased with the recruitment threshold, i.e., the firing rate of later recruited motor units increased faster than early recruited ones. All the motor units finally reached the same peak firing rate at the maximum excitation [38]. For the third type of motor unit firing rate strategy, the slope of the excitatory drive-firing rate relation was also set to be the same for all motoneurons. However, peak firing rates were linked to the mechanical properties of motor units, i.e., large rapidly contracting units were assigned higher peak firing rates than those with lower force recruitment thresholds and with small twitches and slow contraction times [39–41].

C. Surface EMG Simulation

The surface EMG signal is comprised of the sum of MUAPs from different motor units. The first order Hermite-Rodriguez (HR1) functions were selected to represent surface MUAPs, as described by earlier investigators [42–45]. Due to the wide distribution of the motor unit muscle fibers throughout the FDI muscle, all the motor units may be viewed as being at similar depth, which results in similar duration of the recorded surface MUAPs [32]. Therefore, the MUAPs from different motor units were assigned the same duration (~12 ms). MUAP peak-to-peak amplitude was assigned based on its linear relation proportional to twitch force. Thus, the MUAP was simulated to vary over a wide range (100 fold) and was linked to the motor unit recruitment threshold, such that the first recruited motor unit had a MUAP of 1 arbitrary unit (au), and the last recruited motor unit had a MUAP of 100 au.

To assess the MUNIX, surface EMG signals were derived in response to 14 steady-state excitation levels. The duration of each simulation period for each level of excitation was 3 s. The maximum M wave amplitude was calculated by linear summation of MUAPs from all motor units in the pool. To facilitate MUNIX calculation, the amplitude of the negative phase of the maximum M wave simulated from the default model parameters was set to be equivalent to 15 mV.

D. MUNIX Calculation

The simulated maximum M wave and the different levels of surface interference pattern (SIP) EMG were used to compute the MUNIX [5]. The “ideal case motor unit count (ICMUC)” was first calculated:

$$\mathit{ICMUC}=\frac{M_p{S}_a}{M_a{S}_p}$$ (3)

where M_p and M_a represent the maximum M wave power and area, while S_p and S_a represent SIP power and area. Regression analysis was then used to define the relationship between SIP area and ICMUC by the following formula:

$$\mathit{ICMUC}=\beta {(S_a)}^{\alpha }$$ (4)

The parameters β and α obtained from the regression were used to compute the MUNIX [5]:

$$\mathit{MUNIX}=\beta {(20)}^{\alpha }$$ (5)

E. MUNIX Evaluation by Varying Model Parameters

To investigate the sensitivity of the MUNIX to changes in motoneuron and muscle properties, four parameters describing such properties were specifically investigated. These parameters include the number of motor units contained in the muscle, motor unit recruitment range, motor unit firing rates, and the MUAP amplitude.

Each parameter describing these properties was adjusted, and the variation of the MUNIX with this parameter was investigated systematically. The motor unit size index (MUSIX), defined as the ratio of the maximum M wave amplitude to the MUNIX [7], was also examined. Each time when one parameter was adjusted, the other parameters remained the same as their initial assignments.

We acknowledge that even with identical motor unit firing rate assignment, the output of the model may vary slightly since a random process was involved in determination of the firing time of each action potential of a motor unit [33]. Therefore, for each simulation condition, 20 trials of surface EMG signals were simulated to obtain the average MUNIX estimates.

III. Results

A. MUNIX Calculation

Figure 1 demonstrates an example of a MUNIX calculation from simulated surface EMG signals, using the first motor unit firing rate strategy (the one demonstrates “onion skin” pattern). Figure1a is the maximum M wave and figure 1b shows different levels of surface EMG signals, derived using the default model parameters, when the level of excitation was set to different values respectively. As would be anticipated, the EMG outputs increased with the excitation level. Figure 1c shows the relation between the SIP area and the ICMUC, which demonstrates an excellent fit with the mathematical model used for MUNIX calculation (the solid line representing exponential fitting).

Fig. 1.

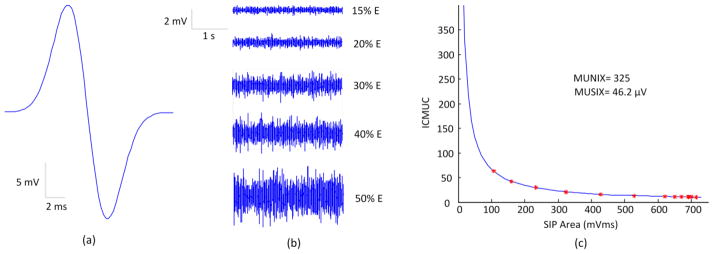
Demonstration of the MUNIX calculation from simulated signals. (a) Simulated maximum M wave; (b) Simulated surface EMG signals at different excitation (E) levels; (c) The exponential curve fitting used to calculate the MUNIX value.

We found that the other different motor unit firing rate strategies did not significantly influence the MUNIX estimates. Thus, in presenting the results we chose only one motor unit firing rate strategy (in which the later recruited motor units attained higher peak firing rates) to schematically demonstrate the sensitivity of the MUNIX with respect to each simulated motor unit property change. The results from the three motor unit firing rate strategies are summarized in Table 1.

Table 1.

The adjustment of the model parameters and the resultant MUNIX estimates for three motor unit firing strategies. For the column of peak firing rates (Hz), the numbers in the parentheses represent the peak firing rates used for the second strategy, where all the motor units reached the same peak firing rate. For each simulation condition, the mean value of the MUSIX estimates was also provided in the square brackets.

	Motor unit number	Recruitment range (%E)	Peak firing rate (Hz)	MUAP amplitude	MUNIX [mean MUSIX(μV)]
					Strategy 1	Strategy 2	Strategy 3
Default	120	40%	23–52 (40)	A	332±10 [45.2]	330±10 [45.5]	332±14 [45.2]
Motor unit number	90	40%	23–52 (40)	A	250±9 [46.2]	247±12 [46.7]	247±8 [46.7]
	60	40%	23–52 (40)	A	161±6 [46.9]	160±7 [47.2]	161±5 [46.9]
	30	40%	23–52 (40)	A	72±3 [54.2]	71±3 [54.9]	71±2 [54.9]
Recruitment range	120	20%	23–52 (40)	A	324±17 [46.3]	321±16 [46.7]	320±16 [46.9]
	120	60%	23–52 (40)	A	334±9 [44.9]	337±11 [44.5]	336±14 [44.6]
	120	80%	23–52 (40)	A	341±13 [44.0]	339±9 [44.2]	340±9 [44.1]
Peak firing rate	120	40%	18–40 (35)	A	332±10 [45.2]	330±13 [45.5]	335±11 [44.8]
	120	40%	15–30 (25)	A	333±12 [45.0]	333±10 [45.0]	335±8 [44.8]
	120	40%	13–20 (15)	A	333±12 [45.0]	332±10 [45.2]	337±15 [44.5]
MUAP amplitude	120	40%	23–52 (40)	0.75A	247±9 [46.3]	250±8 [45.7]	245±8 [46.6]
	120	40%	23–52 (40)	0.50A	167±6 [44.3]	167±5 [44.3]	165±5 [44.8]
	120	40%	23–52 (40)	0.25A	85±2 [44.4]	85±2 [44.4]	85±2 [44.4]

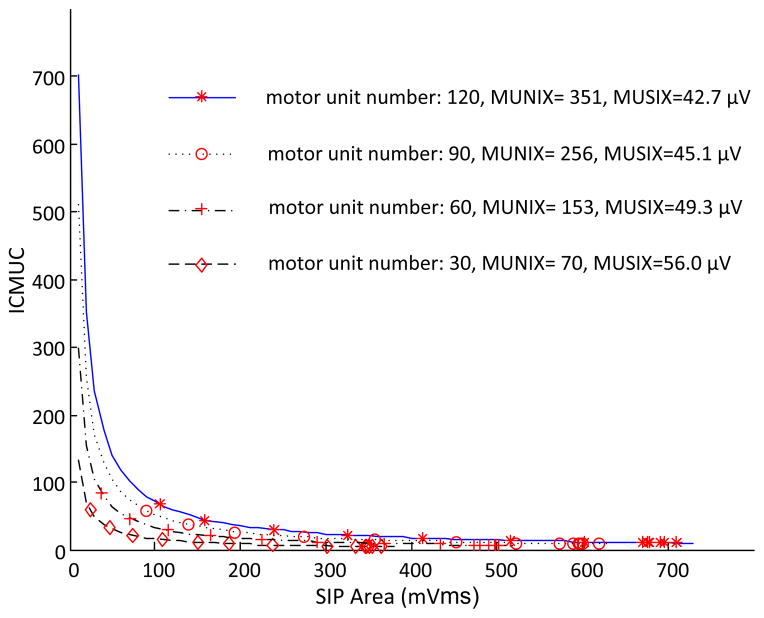
B. Effects of Adjusting Motor Unit Number

The motor unit number was adjusted from the default assignment 120 to be 90, 60 and 30 respectively. As figure 2 shows, we found that with the relatively small numbers of motor units used for the simulation, the estimated MUNIX value was also relatively small. Furthermore, the motor unit reduction ratio was close to the MUNIX reduction ratio. In addition, we found the MUSIX estimate slightly increased with reduction of the motor unit number, primarily due to the MUAP amplitude distribution used in the simulation.

Fig. 2.

A comparison of MUNIX and MUSIX estimates when different numbers of motor units were used for the simulation.

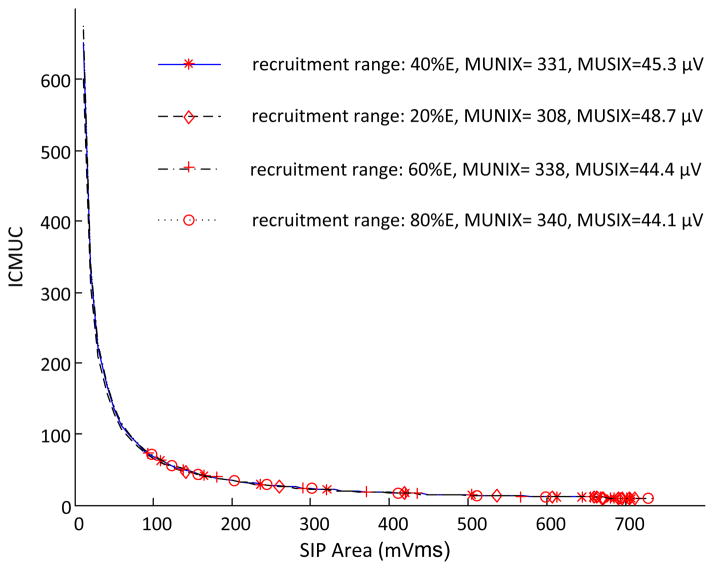
C. Effects of Changing Motor Unit Recruitment Range

The motor unit recruitment range was adjusted from 40% excitation to be 20%, 60% and 80% excitation with respect to the injected current, respectively. With different motor unit recruitment ranges, similar exponential fittings were obtained for the relation between the ICMUC and the SIP area (figure 3). Thus, the MUNIX and MUSIX values did not vary significantly with the changing motor unit recruitment range.

Fig. 3.

A comparison of MUNIX and MUSIX estimates when different motor unit recruitment ranges were used for the simulation.

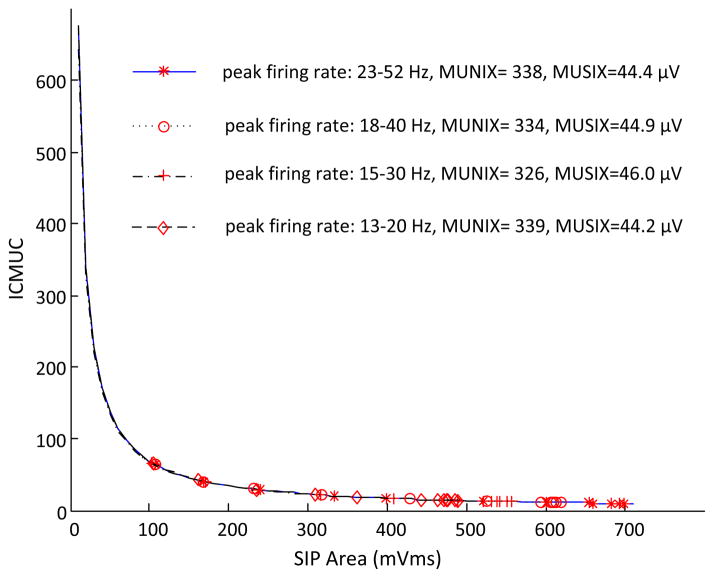
D. Effect of Reductions in Motor Unit Firing Rate

For the first (“onion skin” pattern) and third (progressive rate increase with higher threshold) motor unit firing strategies, the peak firing rates for slow and fast motor units were adjusted from 23–52 Hz to be 18–40 Hz, 15–30 Hz and 13–20 Hz, respectively. Peak firing rates for all the motor units in the second strategy were adjusted from 40 Hz to 35 Hz, 25 Hz, and 15 Hz, respectively. As with our findings regarding motor unit recruitment range changes, exponential fittings for the relation between the ICMUC and the SIP area did not vary significantly with different motor unit firing rates (figure 4). Thus, the MUNIX and MUSIX estimates were not sensitive to the motor unit firing rate changes.

Fig. 4.

A comparison of MUNIX and MUSIX estimates when different motor unit peak firing rates were used for the simulation.

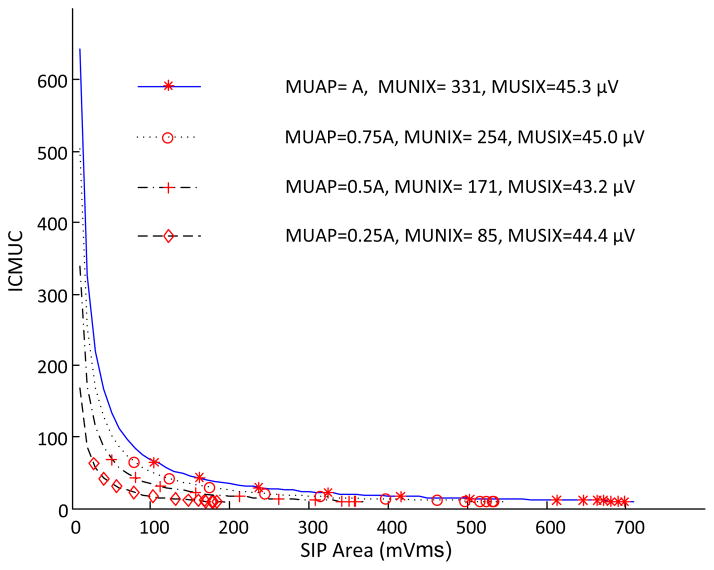
E. Effects of Decrease in MUAP Amplitude

For each motor unit, its MUAP amplitude was adjusted from the default assignment A to 0.75A, 0.50A, and 0.25A, respectively. As figure 5 shows, different exponential fittings were evident with reduced MUAP amplitude in the simulation. We observed that with reduced MUAP amplitude, the MUNIX values tended to systematically underestimate the motor unit number in the muscle, while the MUSIX estimates remained almost unchanged. The MUNIX reduction ratio was close to the MUAP amplitude reduction ratio.

Fig. 5.

A comparison of MUNIX and MUSIX estimates when different MUAP amplitude assignments were used for the simulation.

Table 1 summarizes the MUNIX estimates with respect to each of the four examined motor unit properties. For each condition, the MUNIX was averaged from 20 trials of simulation. The results from three different motor unit recruitment and rate coding strategies are all included in the table, which demonstrate that the MUNIX estimates are not sensitive to variations in such strategies. We found that if varying the input motor unit numbers to the model while keeping the other motoneuron pool and muscle parameters unchanged, then MUNIX estimates can appropriately characterize changes in motor unit numbers. Furthermore, reduction of motor unit firing rates or alteration in motor unit recruitment range does not have a significant effect on the MUNIX or MUSIX estimates.

Last but not the least, from the table we also observed that if we reduce the amplitude of each MUAP rather than simply reduce motor unit number, then MUNIX estimates fail to appropriately estimate the motor unit numbers. Indeed, the MUNIX measurements substantially underestimate the motor unit numbers in the muscle, and the ratio of such underestimation closely correlates with the ratio of MUAP amplitude reduction. It is noted that similar MUSIX estimates were obtained with different ratios of MUAP amplitude reduction.

IV. Discussion

A. Interpretation of the Simulation Results

The sensitivity of MUNIX estimates to different motor unit property changes was examined in this study. First, our simulation results indicate that if the number of motor units is reduced in a muscle, the MUNIX estimates can appropriately reflect such a reduction. Furthermore, the ratio of the motor unit reduction can be approximately reflected by the amount of MUNIX changes. From definition, computation of MUNIX is based on exponential curve fitting using the relation between the SIP area and the ICMUC, which is derived from the power and area of the maximum M wave and a specific level of voluntary surface EMG signals (Equation 3). In an ideal case that assumes all the MUAPs would be the same and no phase cancellation would occur, the ICMUC equals the actual motor unit number in the muscle. When the number of motor units in a muscle is reduced, the maximum M wave and voluntary surface EMG signals will both be reduced. However, as demonstrated in the simulation, for a given level of SIP, reduced maximum M wave amplitude resulted in relatively low ICMUC values. Therefore, the derived relation between the SIP area and the ICMUC was different, with different maximum M waves. The estimated MUNIX was a reflection of the altered relation and correlated well with the actual motor unit number.

On the other hand, varying recruitment threshold and peak firing rate assignment does not influence the maximum M wave, while the maximum voluntary EMG decreases with lower motor unit firing rates, or slightly changes with adjustment of the motor unit recruitment range. However, for a given level of SIP, the ICMUC values are similar. It follows that the points used for exponential curve fitting for the relation between the SIP area and the ICMUC are similar. Thus the MUNIX estimates do not show a significant change.

To simulate muscle atrophy that arises primarily from muscle fiber size changes rather than motor unit loss, each MUAP was assigned reduced amplitude. In such a case, both the maximum M wave and voluntary surface EMG signals are reduced at the same ratio. From definition of the ICMUC (Equation 3), if the maximum M wave and SIP signals have the same reduction ratio, the ICMUC values will not change. However, the x-axis values (i.e. SIP area) of the points used for the exponential curve fitting are different while the y-axis values (i.e. ICMUC) remain the same. More specifically, with reduced MUAP amplitude, the SIP area will be smaller to reach the same ICMUC values. This dramatically changes the exponential curve fitting, so the MUNIX calculation is also influenced.

To sum up, our simulation indicates that MUNIX is strongly related to the change in the maximum M wave amplitude, which is consistent to the findings of a recent preliminary study that simulated the MUNIX estimates with emphasis on muscle fiber reinnervation after motoneuron loss [46]. The study suggested that MUNIX closely correlates with the maximum M wave. Although the MUNIX may not ideally detect the motoneuron loss with the compensate muscle fiber reinnervation process, it follows motoneuron loss somewhat better than the maximum M wave [46].

In our simulation three motor unit firing rate strategies were used. Although the precise motor unit firing rate strategy is still a matter of debate, and may vary with different muscle types, we show that the MUNIX calculation is not sensitive to different motor unit firing rate strategies. This is probably because motor unit firing rate strategy is not a critical factor in determining the global surface EMG, as described in a previous study [27].

B. Implications for Interpretation of Experimental MUNIX Results

The current simulation study provides valuable information for experimental interpretation of MUNIX values. Previous studies have reported motor unit control property changes in motoneuron diseases or neurological disorders such as ALS, stroke and spinal cord injury [17–19]. Our simulation results indicate that these factors will not bias the MUNIX estimates. However, MUNIX estimates need to be interpreted with caution if muscle fiber atrophy occurs in the muscle. In a previous study [6], we have compared the MUNIX values between the paretic and contralateral muscles of stroke subjects and found that the maximum M wave amplitude and MUNIX values were significantly lower in paretic muscles than in contralateral muscles. These findings are consistent to previous studies using traditional MUNE methods based on incremental nerve stimulations [47–51]. However, by solely relying on MUNIX estimates, we should interpret with caution whether or to how much extent these findings provide further electrophysiological evidence of spinal motoneuron involvement following a stroke. Our simulation results suggest that the muscle fiber size change due to disuse of the muscle may also contribute to the significant MUNIX drop in paretic muscles. To support the concept of motoneuron degeneration after a brain lesion, other measurements may be necessary, either to evaluate the mechanisms causing muscle atrophy, or to assess whether there are signs for muscle fiber denervation/reinnervation subsequent to motoneuron loss, thus providing additional evidence of motoneuron degeneration. The latter can be performed by examining the motor unit size index (MUSIX) defined as the ratio of the maximum M wave amplitude to the MUNIX [7]. Reduction of MUNIX in combination with enlarged MUSIX can provide more secure evidence of loss of spinal motoneurons or motor units. Conversely, reduction of MUNIX without significant MUSIX changes may imply either decrease in muscle fiber size, or loss of motor unit without the compensatory muscle fiber reinnervation process. In this regard, MUNIX measurement is most suitable for motoneuron diseases that demonstrate signs of reinnervation. However, there are potential limitations for applications of the MUNIX method in myopathies or in atrophied muscle, where the neural or muscular origins of the atrophy are not clear.

C. Model Limitation

A simulation approach is useful in exploring the mechanisms of change in the MUNIX values that are difficult to address experimentally. Though, it is acknowledged that, as routinely is the case for a simulation research, limitations exist when building the models. For example, motor unit synchrony has been reported to occur frequently during voluntary contractions in several different limb muscles [52]. Our motoneuron pool model did not include motor unit synchrony. To promote simplicity of surface EMG simulations, we used a HR function to represent the basic shape of surface MUAPs. Although there may be a slight difference between the real MUAPs and the HR function, we assumed that such a difference would not have significant effects on the overall surface EMG. The amplitude of MUAP was modeled to be linearly proportional to the motor unit twitch amplitude. However, as was the case for the motor unit firing rate strategy, the MUAP-twitch relation is also a matter of debate [27]. For assignment of the MUAP duration, a constant value was used for different types of motor units, assuming that the muscle fibers of a motor unit were widely scattered throughout the whole muscle, and the fiber diameter of the small and big motor units are similar. All these assumptions were used to simplify the used model. There may be possible variations from the ideal model parameter assignment that may have an effect on the surface EMG signals. Nonetheless, the findings from the sensitivity analysis provided by this study still offer valuable guidance in predicting the trend of changes in the MUNIX estimates, with variation in different motor unit properties.

In conclusion, by systematically varying the input parameters to the motoneuron pool and surface EMG models, we have been able to explore the impact of different factors on the MUNIX measurement. We found that if the number of motor units changes in a muscle while the other parameters remain the same, MUNIX estimates can approximately track such motor unit number changes. With adjustment of the motor unit recruitment range or reduction of motor unit firing rates, the MUNIX estimates are not significantly influenced. However, decrease in MUAP amplitude may significantly reduce the MUNIX estimates, thus substantially underestimating the motor unit number in a muscle. These results from our current simulations, coupled with the previous simulation study on the effects of muscle fiber reinnervation [46], add new insights allowing appropriate interpretation of the fundamental MUNIX calculation, and provide clues that may help us understand the abnormal MUNIX estimates observed in pathological conditions.

Biographies

Xiaoyan Li received her B.S. degree in Electrical Engineering from Anhui University, and M.S. degree in Biomedical Engineering from University of Science and Technology of China, both in Hefei, China. She obtained her second M.S. degree in Computer Sciences from Loyola University Chicago in 2002, and her Ph.D. degree in Bioengineering from the University of Illinois at Chicago (UIC) in 2008. Later she was a Postdoctoral Research Fellow in Institute for Neural Computation of the University of California at San Diego (UCSD), CA, and in Department of Physical Medicine and Rehabilitation of Northwestern University, Chicago, IL, respectively. Currently she is a Research Associate at the Sensory Motor Performance Program of the Rehabilitation Institute of Chicago, IL. Her research interests focus on motor control, neurological disorders and rehabilitation.

William Zev Rymer received the M.B.B.S. degree from Melbourne University, Melbourne, Australia, in 1962, and the Ph.D. degree in neurophysiology from Monash University, Melbourne, in 1973. After residency training in internal medicine and neurology, he returned to graduate training. After postdoctoral training at the National Institutes of Health and Johns Hopkins University Medical School, Baltimore, MD, he became an Assistant Professor of neurosurgery and physiology at the State University of New York in 1976. He became an Assistant Professor in 1978 at Northwestern University Medical School, Chicago, IL, an Associate Professor in 1981, and a Professor in 1987. He now holds the John G. Searle Chair in Rehabilitation Research and is Vice President for Research at the Rehabilitation Institute of Chicago, IL, and President of the Rehabilitation Institute Research Corporation, Chicago, IL. He is also Director of the Sensory Motor Performance Program, Rehabilitation Institute of Chicago and the Medical Biomechanics Program at Northwestern University Medical School.

Ping Zhou (S’01–M’05–SM’07) received the B.S. degree in electrical engineering and the M.S. degree in biomedical engineering from the University of Science and Technology of China, Hefei, China, in 1995 and 1999, respectively, and the Ph.D. degree in biomedical engineering from Northwestern University, Evanston, IL, in 2004. His Ph.D. dissertation project was performed as part of the Sensory Motor Performance Program (SMPP), Rehabilitation Institute of Chicago, Chicago, USA.

From 2004 to 2006, he was a Research Associate in the Neural Engineering Center for Artificial Limbs (NECAL), Rehabilitation Institute of Chicago. After that he has been a Research Scientist in NECAL and later in SMPP at the Rehabilitation Institute of Chicago. He has been an Adjunct Assistant Professor since 2006 in the Department of Physical Medicine and Rehabilitation, Northwestern University, Chicago, USA, and a Professor since 2012 in the Institute of Biomedical Engineering, University of Science and Technology of China, Hefei, China. His current research interests include biomedical signal (in particular, EMG) processing, spinal motor neuron/motor unit pathophysiology in neurologic disorders, noninvasive electrodiagnosis of neuromuscular diseases, computational modeling of neuromuscular systems, myoelectric prosthesis control, and assistive devices.