Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jan 27.
Published in final edited form as: Psychol Sci. 2012 Mar 6;23(4):419–426. doi: 10.1177/0956797611429798

Comparison of Distortion of Probability information in Decision under Risk and an equivalent Visual Task

Craig Glaser 1, Laurence T Maloney 1,2, Julia Trommershäuser 2, Pascal Mamassian 3
PMCID: PMC3556465  NIHMSID: NIHMS430723  PMID: 22395127

Abstract

Decision makers typically overweight small probabilities and underweight large. However, there are recent reports that, when probability is presented in relative frequency form, this typical pattern reverses. We tested this hypothesis, comparing decision making in two decision tasks, in which probability was either stated numerically or conveyed through a visual representation. In the visual task, participants chose between firing a ‘stochastic bullet’ at a large target for a small reward or at a small target for a large reward. Participants’ knowledge of probability in the visual task was the results of extensive practice firing bullets at targets. In the classical numerical task, they chose between pairs of lotteries with probabilities and rewards matched to those in the visual task. We found that participants had significantly different probability weight functions in the two tasks but the pattern for the visual task was the typical, not the reversed, pattern.

Keywords: decision making under risk, probability, probability weight, experience

Introduction

Decisions share a formal structure. There are possible outcomes O1, O2,···, On, only one of which will occur. There are possible actions that affect the probabilities p1,···, pn of obtaining corresponding outcomes. Each choice of action is in effect a lottery (p1, O1; p2, O2; ···, pn, On). In decision making under risk, the participant chooses between lotteries where both outcomes and probabilities are explicitly given, e.g. (0.2,$200;0.8,$0).

Expected utility theory (EUT, Bernoulli, 1738/1954) is a normative model of decision under risk. Each outcome Oi in a lottery L is assigned a numerical “utility” U(Oi) and the expected utility of the lottery is,

EU(L)=∑i=1npiU(Oi) (1)

The EUT decision maker chooses the lottery with the highest expected utility.

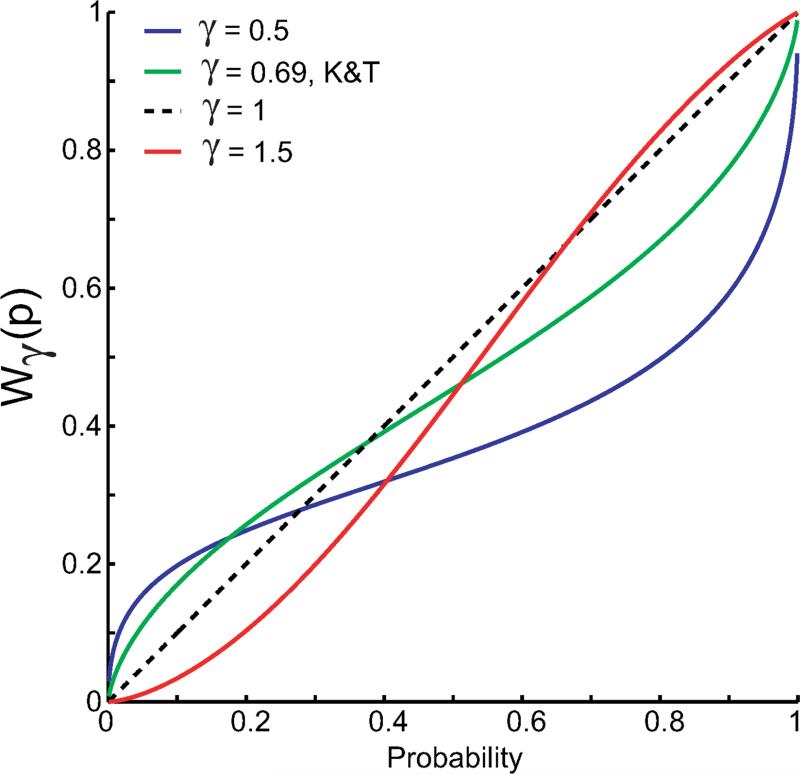
Human decision makers typically depart from the predictions of EUT by overweighting small probabilities and underweighting large (Allais, 1953; Kahneman & Tversky, 1979; Luce, 2000). This distortion of probability is captured by a probability weighting function Wγ(p). In Figure 1 we show three instances of a particular model of the probability weighting function with one free parameter γ due to Tversky & Kahneman (1992). The green curve is based on data observed in one condition of an experiment they report. For values of γ < 1 small probabilities are overweighted, large probabilities underweighted, the typical pattern observed in decision under risk experiments.

Figure 1. Probability weighting function.

Figure 1

Open in a new tab

The shape of the probability weighting function Wγ (p) is controlled by a single parameter γ > 0 . The function Wγ (p) = p is a straight line for γ = 1, i.e. probability is undistorted. When γ < 1, the probability weights assigned to smaller probabilities are higher than the probabilities and the probability weights assigned to larger probabilities are lower. The opposite pattern emerges when γ > 1.

For many of the decisions we make, we are not given explicit specifications of probability in numerical form. Often we have only the remembered relative frequency of events across time. The relative frequency of events is arguably the predominant if not sole source of information for non-human animals (Stephens & Krebs, 1986).

Recently researchers have examined whether the source of probability information in a decision task affects the decisions we make (Erev, Ert, Roth, Haruvvy, et al., 2010; Fox & Hadar, 2006; Hadar & Fox, 2009; Hau, Pleskac & Hertwig, 2010; Hertwig, Barron, Weber & Erev, 2004; Rakow, Demes & Newell, 2008; Ungemach, Chater & Stewart, 2009; Wu, Delgado & Maloney, 2009, 2011). Wu, Delgado & Maloney (2009, 2011) compared human decision making under risk in a classical decision task (“decision from description”) and a mathematically equivalent choice between “motor lotteries”. A motor lottery consisted of a speeded reaching task to a rectangular target. If the participant hit the target, he or she earned a reward (and otherwise received nothing) and the size of the rectangle determined the probability of success.

Wu et al. (2009, 2011) found that, while participants choosing between lotteries in classical form tended to overweight small probabilities and underweight large, the same participants, when presented with the equivalent motor decision task, showed the reverse pattern, underweighting small, and overweighting large. The red curve with γ > 1 in Figure 1 illustrates this second pattern. The same participants in a classical decision making task with probabilities explicitly given had the expected pattern of probability distortion with γ < 1.

Ungemach, Chater & Stewart (2009) reported patterned differences in use of probability in comparison of a classical decision task and a matched decision task in which probability information was obtained through sampling. In the classical decision task participants chose between lotteries which were presented in numerical form. In the sampling condition, participants sampled each of two events 40 times by pressing keys. Ungemach et al found that participants’ choices were consistent with underweighting smaller probabilities and overweighting large, i.e. γ > 1 in Figure 1. In the classical decision task, they found the typical overweighting of small probabilities and underweighting of large γ < 1.

Both Wu et al (2009, 2011) and Ungemach et al (2009) verified that participants’ estimates of the frequency of motor success or success in sampling were close to accurate.

A natural conjecture is that, whenever probability is based on observed or remembered frequency, the use of probability in decision making will exhibit the reversed pattern (γ > 1).

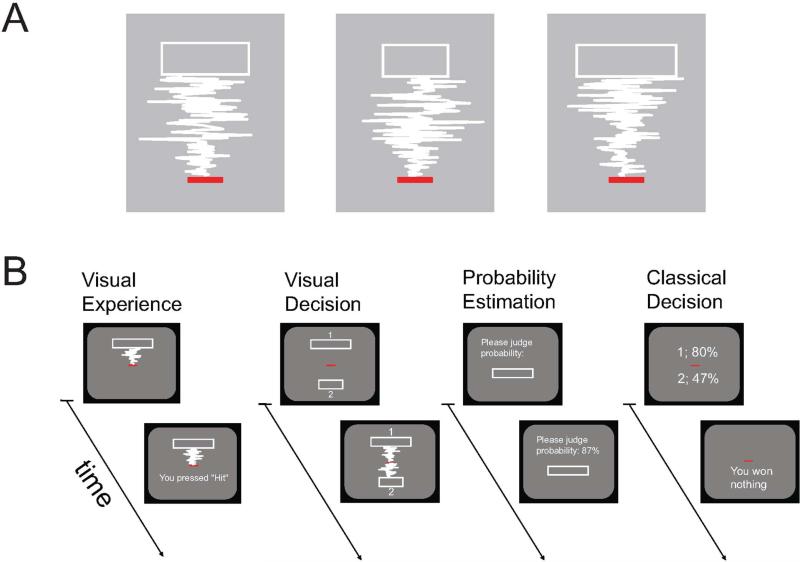
Here we test this conjecture by comparing decision making with probabilities learned through sampling a large number of random visual events and decision making with probabilities explicitly stated. The random visual event was the outcome of a Gaussian “stochastic bullet” aimed at a rectangular target. The path of the stochastic bullet was a Gaussian random walk resembling a lightning bolt. We varied the probability that the bullet would hit the rectangular target by varying the width of the rectangle. Figure 2A gives an example of three possible realizations of the stochastic bullet aimed at three rectangles varying in width. In the example, the bullet “hits” two times out of three.

Figure 2. Visual decision task.

Figure 2

Open in a new tab

A) Realizations of the visual stochastic process. During the visual decision task participants viewed a visual random event that signaled probability. A stochastic bullet moved from an initial location upward toward a target (rectangle outlined in white) along a Gaussian random walk trajectory. The participant judged whether the bullet hit the rectangle which is the case for two of the three realizations shown here. The stochastic path is shown here in white; in the actual experiment the path was not visible except for the instantaneous position of the moving bullet. The width of the rectangle determined the probability of hitting the rectangle. B) Conditions and Procedure. 1) Visual Experience Phase. In each trial of the experience phase, the participant observed the random walk from the screen center upward to the lower edge of the target rectangle. The target was always displayed in the upper half of the screen, centered above the shooter. The width of the rectangle varied randomly from trial to trial. Participants were instructed to judge whether the bullet hit the reward line (the edge of the target region). Each participant judged 300 experience trials. 2) Visual Decision Phase. In each trial of the visual decision task, participants chose between two target rectangles that differed in size. Both rectangles were displayed one above and one below the screen center. The larger target rectangle always carried a value of $1, the smaller target a value of $2. Following the participant's choice, the random walk was elicited twice, first towards the selected target rectangle, then towards the non-selected target rectangle. If the random walk hit within the target rectangle, the trial was considered to be a win. The size of the larger target rectangle was held fixed at 6 different sizes corresponding to probabilities (.1 .2 .4 .6 .8 .9); the size of the smaller target rectangle ($2) was adjusted across successive trials using an adaptive staircase procedure to estimate the ratio at which the participant was indifferent. 3) Probability Estimation Phase. In each trial of the estimation phase, participants were presented with target rectangles of different sizes. Participants provided a number between 0 and 100 that indicated their estimate of the probability with which the bullet had hit the target rectangle of this particular size. The estimation phase of the experiment consisted of 120 trials. 4) Classical Decision Phase. In each trial of the decision phase, participants chose between pairs of numerical lotteries equivalent to the visual lotteries of the visual decision phase. The lotteries were stated in text format and displayed above and below the screen center at the same location where the rectangles were placed in the visual decision phase. Each lottery was represented as a pair of numbers, a dollar value ($1 or $2) indicating the possible outcome of this lottery and a probability of that outcome probability (presented as frequency, ‘%’). Like the visual decision phase, the classical decision phase consisted of 396 trials.

In summary, we focused on human performance with large samples. Moreover, the number of practice and decision trials was fixed in advance by the experimenter and was not under the control of the participant. (cf. Fox & Hadar 2006; Ungemach, Chater & Stewart, 2009).

We illustrate the visual decision task in Figure 2B. There are two rectangles differing in width with monetary rewards assigned to either of the two targets. The participants choose whether to bet on the bullet hitting the upper target or hitting the lower. In the example, a hit on the smaller rectangle will earn $2 while a hit on the larger rectangle, though more likely, will earn only $1. In Figure 2B we illustrate the classical decision task, a decision between two lotteries that differ in probability and outcome.

In the first phase of the experiment, the participant viewed 300 realizations of the stochastic bullet aimed at rectangles of different sizes and could potentially learn the mapping between rectangle width and the probability with which the stochastic bullet will hit the target.

We estimated probability weighting functions in both decision making tasks (Figure 2), for each participant individually. Following Wu et al (2009, 2011) and Ungemach et al (2009) we also asked participants to directly estimate the frequency of visual events on a numerical scale. That is, they were shown a bullet and rectangle and asked to estimate the probability of a hit. We compared these three estimates of probability/frequency to test whether (1) the source of probability information affects the probability weighting function and (2) whether any differences in the probability weight function in the two decision tasks can be attributed to a simple misperception of the frequency of visual events.

We found large, patterned differences between the probability weighting functions for the two decision tasks with the probability weighting functions based on random visual events exhibiting greater distortion. Participants typically overweighted small probabilities and underweighted large probabilities in the visual task in contrast to the patterns of probability weight distortion found by Ungemach et al (2009) and Wu et al (2009, 2011). We also found that participants’ estimates of the relative frequency of events were close to veridical and could not explain their use of probability in visual decision making.

Methods

Apparatus

Participants were seated in a dimly lit room in front of a monitor (1280 × 1024 pixel at 60 HZ; 1 pixel = 0.026 mm). We recorded responses by means of a computer keyboard mounted on a table centered in front of the monitor. The experiment was run using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) on a Pentium IV Dell Precision workstation.

Participants

12 NYU undergraduate students participated in this experiment. All were unaware of the purpose of the experiment and all were paid for their participation. All participants had normal or corrected to normal vision. Participants were paid for their time and also received a bonus based on their performance paid at the end of the experiment.

Stimuli

The stochastic bullet

The participant observed a bullet that followed a visible random walk from the screen center upward (or downward) to a horizontal reward line (Figure 2). The center of the screen was marked by a small figure we refer to as the shooter. The random walk consisted of a series of N = 101 line segments connecting a series of points, beginning at the shooter and ending at the reward line. In the visual decision task described below, the shooter could shoot the bullet upward or downward. We describe the construction of the stimulus for a bullet traveling upward.

The vertical coordinates of the successive points increased by 1/Nth of the vertical distance from the screen center to the lower edge of the target rectangle so that the last point fell somewhere on the line containing the lower edge of the target rectangle. The horizontal coordinate of each point was displaced by a random offset from that of the previous point. The offsets were independent, drawn from a Gaussian (normal) distribution with mean 0 and variance σB2∕N, so that the distribution of bullet arrival points on the reward line was Gaussian (c,σB2) where c denotes the horizontal coordinate of the center of the rectangle. Three realizations of the random walk are shown in Figure 2. The distribution from which the random walk was drawn was held constant throughout the experiment with σB = 30mm corresponding to 3.6 degrees of visual angle (DVA).

The target rectangle

The lower edge of the target rectangle rested on the reward line, centered directly above the shooter. The probability p of hitting a rectangle of width w with the stochastic bullet is,

p[hit]=∫−w∕2w∕2ϕ(x;0,σB2)dx (2)

where ϕ(x;μ, σ2) denotes the Gaussian probability density function with location parameter μ and variance σ2 and w denotes the width of the rectangle. The mapping from w to p is invertible. Given any specified probability p we can compute the corresponding w.

Experimental design

The experiment consisted of five phases. The first four are illustrated in Figure 2B. Each participant completed all five phases in the order we describe next.

1. Experience phase

The purpose of the experience phase was to familiarize the participant with the mapping between the width of the rectangle and the probability that the stochastic bullet would hit the target. A single target was always displayed in the upper half of the screen, centered above the shooter. The width of the rectangle varied randomly from trial to trial.

On each trial of the experience phase, the participant observed the random walk from the screen center upward to the lower edge of the target rectangle. The participant's task was to judge whether the bullet hit the reward line within the target region and respond by key press. Participants were told the correct response after every trial. Each participant judged 300 trials with rectangles whose widths varied across the same range as in the visual decision task.

2. Visual decision phase

In this phase, participants chose between two target rectangles, one displayed above, one below the screen center. Once the participant had selected a target, the stochastic bullet was fired twice, first at the selected target rectangle, next at the non-selected target rectangle. Hitting the larger target rectangle always corresponded to winning $1, hitting the smaller, to winning $2. The larger rectangle was randomly placed above or below the shooter with equal probability.

The larger target rectangles ($1) were fixed at one of six sizes corresponding to probabilities (.1 .2 .4 .6 .8 .9); the size of the smaller target rectangle ($2) was adjusted across 33 successive trials using an adaptive staircase procedure (Leek, 2001). The values assigned to both regions were fixed throughout a session of 396 trials (v1 = $2 / v2 = $1). We varied the width of the target with value v2 from trial to trial to estimate probability p2 such that the participant was indifferent between (p1, v1) and (p2, v2). The participants had no control over the stopping rule. All staircases were run for a fixed number of trials.

At the end of the experiment, three trials were randomly selected and the participant was paid the outcome of those three trials. The participant was informed of this payment method at the beginning of the visual decision session.

3. Estimation phase

The purpose of the estimation phase was to test the participant's knowledge about the bullet's hit probability for target rectangles of different sizes. During this phase of the experiment, the participant was presented with target rectangles of different sizes and typed in a number between 0 and 100 as an estimate of the probability (in percent form) with which the bullet had hit the target rectangle of this particular size. The size of the target was determined by randomly selecting a probability between 10 and 90, turning it into a width (in mm) and then presenting it visually to the participant. No feedback was given. This phase of the experiment consisted of 120 trials.

4. Classical decision phase

In this phase of the experiment, participants chose between pairs of lotteries presented in numerical form equivalent to the visual lotteries of the visual decision phase (Figure 2B). The probability of winning the lower $1-outcome was held fixed at the same level as in the visual decision task (.1 .2 .4 .6 .8 .9). The classical decision phase consisted of 396 trials. Matching the conditions of the visual task, the choice with the smaller outcome ($1) was fixed at one of probabilities (.1 .2 .4 .6 .8 .9), stated in frequencies on the screen; the probability assigned to the higher outcome ($2) was adjusted across 33 successive trials using an adaptive staircase procedure (Leek, 2001). The values assigned to both regions remained fixed throughout the session of 396 trials. We varied the probability assigned to the higher outcome ($2) from trial to trial to estimate the probability p2 such that the participant was indifferent between (p1, v1) and (p2, v2).

5. Payoff phase

Participants were paid for their participation and received an additional bonus, depending on the outcome of three classical lottery trials and three visual lottery trials selected at random. We “replayed” the actual random walk that had previously occurred on each of the randomly chosen visual lottery trials and then paid participants according to their winnings. These payoffs occurred only after all data was collected and the experiment was otherwise complete.

Probability weighting and value functions

We characterized human performance in each phase by fitting performance to a parametric model, Kahneman & Tversky's Prospect Theory (Kahneman & Tversky, 1979). The lotteries we consider have only one non-zero monetary outcome that is always a gain. For simplicity, we omit zero outcomes in specifying lotteries (p, v). For pairs of lotteries with two fixed values, as in our experiment Prospect Theory coincides with the extension of Prospect Theory (Cumulative Prospect Theory) proposed by Tversky & Kahneman (1992; Quiggins, 1982, 1993; theory; Luce, 2000).

The participants chose between L1 = (p1, v1) and L2 = (p2, v2). We assume that participants first assign a prospect value to each lottery

π(Li)=Wγ(pi)Vα(vi),i=1,2 (3)

where Wγ (p) is a probability weighting function and Vα (v) a utility function for gains. We assume that the participant computes the decision variable

Δ=π(L1)−π(L2)+ε (4)

where ε is a Gaussian random variable with mean 0 and decision variance σD2. The participant chooses the lottery L1 if Δ > 0 and otherwise the lottery L2.

Because our outcomes are non-negative, we can model the utility function by the power function

Vα(v)=vα (5)

with one parameter α > 0. We model the probability weighting function by probability as probability weighting function with a single parameter γ,

Wγ(p)=pγ[pγ+(1−p)γ]1∕γ. (6)

Examples of Wγ (p) are shown in Figure 1.

There are competing models for how decision makers weight probability (Prelec, 1998; Gonzalez & Wu, 1999; Tversky & Kahneman, 1992) but they provide very similar fits to data (see Luce, 2000, Section 3.4). We are using Vα and wγ (p) to capture and compare performance across experimental phases.

On every trial there are only two non-zero outcomes, $1 and $2. If v1 is always $1 and v2 is always $2, then the comparison of lotteries,

Wγ(p1)Vα(v1)>Wγ(p2)Vα(v2)⇔ChooseL1elseL2 (7)

is equivalent to

Wγ(p1)Wγ(p2)>C⇔ChooseL1elseL2 (8)

where C = Vα (v2)/Vα(v1). The three parameters γ, C and σD characterized each participant's performance.

Analysis & Results

In each experimental condition and for each participant, and estimated parameters by maximum likelihood (Mood, Graybill & Boes, 1974). We combined data across the six probability conditions (.1, .2, .4, .6, .8, .9), a total of 396 trials The resulting estimates of γ, C, σD for the visual decision task are denoted γkv, Ckv and σD,kv with k = 1,···, 12 indexing the 12 participants. We also obtained the maximum log likelihood of each fit, λkv which we will use in testing hypotheses as described below. We similarly fit the data for the classical decision phase, obtaining estimates of γ, C, σD denoted γkc, Ckc, and σD,kc with k = 1,···, 12 and corresponding maximum log likelihoods, λkv.

Last we fit the data from the estimation phase by the method of least squares to obtain estimates γke with k = 1,···, 12 as well as the estimated standard error of the residuals, σke. The data are estimates Ek,j of probability (on a percentage scale) by the kth participant on the jth trial of the estimation task. The true probability that the bullet would hit the target on the jth trial of the estimation task is denoted pj. We fit the γke by minimizing,

∑j=1NE[Ek,j−100βkwγke(pj)]2. (9)

Note that we fit an additional parameter βk that captures any tendency on the participant's part to compress or expand the response scale.

Distortion of probability weight functions

In all three conditions, we found large individual differences in the γ-estimates, indicating that the extent to which probability information was distorted varied across participants. In the visual task, individual γ-estimates varied between 0.31 and 1 (median 0.725). In the classical decision task, individual γ-estimates ranged from 0.28 and 2 (median 1.05). In the estimation task, we found large individual differences in γ-estimates with values across participants that ranged from 0.36 to 1.55 (median 1.08).

Visual and classical decision tasks

The estimates for γkc, γkv, γke for each participant, k = 1,···, 12, are summarized in Figure 3A. The large individual differences for the classical decision task are typical of those found when participants’ data are fit individually (see discussion in Luce, 2000, Section 3.4). The mean 1.01 (median 1.05) is not significantly different from 1 (t(11)=0.103; p = 0.459); the values are evenly distributed around 1. In contrast, all values of γkv are less than 1 with mean value 0.721 (median 0.725). The difference is significant (t(11) = -4.323; p = 0.0012). Figure 3B shows boxplots indicating mean and confidence intervals for visual and classical decision task, for pooled parameter estimates specifying the probability weight function (pooled across 12 participants). The parameter estimates differed significantly for the visual and classical decision task for 8 of the 12 participants (log-likelihood-ratio-test, p=.05).

Figure 3. Results.

Figure 3

Open in a new tab

A. Parameter estimates specifying the probability weight function (separate estimates for each of 12 participants for each of the three phases of the experiment). B. Boxplots of γ, the parameter specifying the probability weight function, in the three phases of the experiment.

We believe that the lack of probability weighting (on average) in the classical decision session is due to the feedback which participants received on each trial. Decision makers faced with a series of decisions tend to move closer to maximum expected gain (see Redelmeier & Tversky, 1992; Wakker, Thaler & Tversky, 1997; Thaler & Johnson, 1990). Studies of risky decision find that participants are closer to maximizing expected gain for small stakes (Camerer, 1992; Holt & Laury, 2002; Thaler & Johnson, 1990; Wedell & Böckenholt, 1994).Similar results are found for motor tasks analogous to decision making (Trommershäuser, Maloney & Landy, 2003a,b; 2008).

We also tested whether γv and covary. Do participants with larger values of γc tend to have larger values of γv and vice versa (positive correlation)? We computed the correlation of γkv and γkc across participants. We find that participants did not show a significant correlation between visual decision γv and classical decision γc (r = -0.17, p = 0.61). We thus conclude that probability weight functions in the two decision tasks are different across participants with the probability weight function for the visual task more distorted.

Estimation task

We found large individual differences in γke with values across participants that ranged from 0.36 to 1.55 with mean 1.07 (median 1.08). Estimates of the scaling parameter βk ranged from 0.63 to 2.3 with a mean of 1.07 (median .94). The values of γke from the estimation task have mean 1.07 (median 1.08) and are not significantly different from 1 (t(11) = 0.563; p =0.585). On average, participants’ estimates of the frequency that the bullet would hit the target were little distorted.

Probability estimates and the visual decision task

We considered whether the observed distortions in probability weight could be due to misperception of the frequency with which the stochastic bullet hit targets of different widths. We first tested the hypothesis that γv = γe and rejected this hypothesis (t(11)=-3.256; p=0.008). We further tested whether γv was positively correlated with γe. The resulting correlation was r = 0.55 only marginally significantly different from 0 (p=0.066). This outcome is consistent with previous work comparing estimates and use of probability in decisions under risk or uncertainty (Ungemach et al, 2009; Wu et al, 2009, 2011).

Distortion of value functions

The CPT value function for gains is controlled by a single parameter α which we reduced to a single parameter C above. The estimates for each participant in the visual and classical decision tasks are denoted Ckv, Ckc, k = 1,···, 12, respectively. The values of Ckv have mean 1.338 (median 1.230) and the values of Ckc, mean 1.425 (median 1.255). The ratio of rewards was 2:1 and a value of C = 2 would indicate that participants made decisions consistent with expected value. We tested this possibility by a t-test and rejected it for Ckv (t(11)= -7.1832; p < 0.0001) and for Ckc (t(11) = -3.367; p = 0.006). In both decision conditions our estimates of their use of value were compressive as is typically the case for lotteries with non-negative outcomes (Tversky & Kahneman, 1992).

We finally tested whether participants treated information about reward similarly in the two decision conditions. We compared Ckv, Ckc using a paired sample t-test and found no significant difference (t(11)=-0.773; p = 0.456). Moreover, Ckv and Ckc were significantly correlated (r = 0.789; p = 0.002). These results are consistent with the conclusion that participants represented value similarly in the two decision conditions.

Conclusion

Ungemach et al. (2009) and Wu et al. (2009, 2011) compared human performance in classical decision making with information about probability and outcomes was explicitly given to performance in a matched decision task where knowledge of probability was obtained by observing or sampling stochastic events. Ungemach et al and Wu et al both found that decision makers in the classical task typically overweighted small probabilities and underweighted large. In contrast, they found the opposite pattern for the matched task based on relative frequency, suggesting that the shape of the probability weighting function changes markedly when probability is obtained in the form of relative frequency of events.

We tested this conjecture by comparing performance in a classical decision task with performance in a visual decision task. Participants practiced firing bullets at rectangles several hundred times. In this visual decision task the participant chose between firing a bullet at a larger, easier to hit rectangle for $1 or a smaller, harder to hit rectangle for $2. We varied the widths of the rectangles from trial-to-trial and the objective probabilities of success in the visual task and the classical task were matched, trial-by-trial.

We rejected the conjecture. In the visual task the values γv were all less than 1, indicating that participants typically overweighted small probabilities and underweighted large, the opposite of the pattern found by Ungemach et al (2009) and Wu et al (2009, 2011). Our results echo those of Gonzalez & Wu (1999) who discuss differences in the shape of the probability weight function across tasks and individuals.

We find that they do not, even after 300 practice trials and 396 decision trials. Sample size alone is not sufficient to account for differences in human choice in decisions from description and decision from sampling.”

In summary, we compared performance in a decision from description task and a decision from sampling task where the source of uncertainty was a stochastic visual event. We found that, even after many trials, participants’ probability weighting functions for description and sampling were significantly different and those from sampling showed marked overweighting of small probabilities, underweighting of large. Even with probabilities estimated as the frequency of large numbers of visual events observers do not maximize expected utility.

The task we consider is representative of a large class of everyday tasks where we learn about the stochastic outcomes of events by observing, a quintessential form of decision from experience. We might expect that, with hundreds of trials of training and decision, human performance would move toward choices maximizing expected utility. It does not.

Acknowledgments

JT was supported by Heisenberg Fellowship (DFG Grant TR528/2-1), LTM, by NIH/NEI EY019889, PM, by a Chair of Excellence from the French Ministry of Research.

References

  1. Allais M. Le comportement de l'homme rationnel devant le risque: Critique des postulats et axiomes de l'école Américaine (The behavior of a rational agent in the face of risk: Critique of the postulates and axioms of the American school). Econometrica. 1953;21(4):503–546. [Google Scholar]
  2. Bernoulli D. Exposition of a new theory on the measurement of risk. Econometrica. 1738/1954;22:23–36. [Google Scholar]
  3. Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
  4. Camerer CF. Recent tests of generalizations of expected utility theory. In: Edwards W, editor. Utility Theories: Measurement, and Applications. Springer; New York: 1992. pp. 207–251. [Google Scholar]
  5. Camerer CF, Hogarth RM. The effects of financial incentives in experiments: A review and capital-labor-production framework. Journal of Risk and Uncertainty. 1999;19:7–42. [Google Scholar]
  6. Erev I, Ert E, Roth AE, Haruvvy E, Herzog SM, Hau R, Hertwig R, Stewart T, West R, Lebiere A Choice Prediction Competition: Choices from Experience and from Description. Journal of Behavioral Decision Making. 2010;23:15–47. [Google Scholar]
  7. Fox CR, Hadar L. Decisions from experience = sampling error + prospect theory: Reconsidering Hertwig, Barron, Weber & Erev (2004). Judgm Decis Mak. 2006;1(2):159–161. [Google Scholar]
  8. Gonzalez R, Wu G. On the shape of the probability weighting function. Cognitive Psychology. 1999;38(1):129–166. doi: 10.1006/cogp.1998.0710. [DOI] [PubMed] [Google Scholar]
  9. Hau R, Pleskac, Hertwig R. Decisions From Experience and Statistical Probabilities: Why They Trigger Different Choices Than a Priori Probabilities. Journal of Behavioral Decision Making. 2010;23:48–68. [Google Scholar]
  10. Hadar L, Fox CR. Information asymmetry in decision from description version decision from experience. Judgment and Decision Making. 2009;4(4):317–325. [Google Scholar]
  11. Hertwig R, Barron G, Weber EU, Erev I. Decisions from experience and the effect of rare events in risky decision. Psychol. Sci. 2004;15:534–349. doi: 10.1111/j.0956-7976.2004.00715.x. [DOI] [PubMed] [Google Scholar]
  12. Holt C, Laury S. Risk aversion and incentive effects. Am. Econ. Rev. 2002;92:1644–1655. [Google Scholar]
  13. Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk. Econometrica. 1979;47:263–292. [Google Scholar]
  14. Leek MJ. Adaptive procedures in psychophysical research. Perception & Psychophysics. 2001;63:1279–1292. doi: 10.3758/bf03194543. [DOI] [PubMed] [Google Scholar]
  15. Luce RD. Utility of gains and losses: Measurement-theoretical and experimental approaches. Lawrence Erlbaum; London: 2000. [Google Scholar]
  16. Mood A, Graybill FA, Boes DC. Introduction to the theory of statistics. 3rd Edition McGraw-Hill; New York: 1974. [Google Scholar]
  17. Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat Vis. 1997;10(4):437–442. [PubMed] [Google Scholar]
  18. Prelec D. The probability weighting function. Econometrica. 1998;60:497–528. [Google Scholar]
  19. Quiggin J. A theory of anticipated utility. Journal of Economic Behavior and Organization. 1982;3(4):323–43. [Google Scholar]
  20. Quiggin J. Generalized expected utility theory; the rank-dependent model. Kluwer Academic Publishers; Boston: 1993. [Google Scholar]
  21. Rakow T, Demes KA, Newell BR. Biased samples not mode presentation: re-examining the apparent underweighting of rare events in experienced-based choice. Organizational Behavior and Human Decision Processes. 2008;106:168–179. [Google Scholar]
  22. Redelmeier DA, Tversky A. On the framing of multiple prospects. Psychol. Sci. 1992;3:191–193. [Google Scholar]
  23. Stephens DW, Krebs JR. Foraging theory. Princeton University Press; Princeton, NJ: 1986. [Google Scholar]
  24. Thaler R, Johnson EJ. Gambling with the house money and trying to break even: The effects of prior outcomes on risky decision. Manage. Sci. 1990;36:643–660. [Google Scholar]
  25. Trommershäuser J, Maloney LT, Landy MS. Statistical decision theory and trade-offs in the control of motor response. Spat. Vis. 2003a;16:255–275. doi: 10.1163/156856803322467527. [DOI] [PubMed] [Google Scholar]
  26. Trommershäuser J, Maloney LT, Landy MS. Statistical decision theory and the selection of rapid, goal-directed movements. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2003b;20(7):1419–33. doi: 10.1364/josaa.20.001419. [DOI] [PubMed] [Google Scholar]
  27. Trommershäuser J, Maloney LT, Landy MS. Decision making, movement planning, and statistical decision theory. Trends Cognitive Sciences. 2008;12:291–297. doi: 10.1016/j.tics.2008.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tversky A, Kahneman D. Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 1992;5:297–323. [Google Scholar]
  29. Ungemach C, Chater N, Stewart N. Are probabilities overweighted or underweighted when rare outcomes are experienced (rarely)? Psychological Science. 2009;20:473–479. doi: 10.1111/j.1467-9280.2009.02319.x. [DOI] [PubMed] [Google Scholar]
  30. Wakker PP, Thaler RH, Tversky A. Probabilistic insurance. J. Risk Uncertain. 1997;15:7–28. [Google Scholar]
  31. Wedell DH, Böckenholt U. Contemplating single versus multiple encounters of a risky prospect. The American Journal of Psychology. 1994;107:499–518. [Google Scholar]
  32. Wu S-W, Delgado M, Maloney LT. Economic decision-making compared to an equivalent motor task. Proceedings of the National Academy of Sciences, USA. 2009;106(15):6088–6093. doi: 10.1073/pnas.0900102106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wu S-W, Delgado MR, Maloney LT. The neural correlates of subjective utility of monetary outcome and probability weight in economic and in motor decision under risk. Journal of Neuroscience. 2011;31:8822–8831. doi: 10.1523/JNEUROSCI.0540-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES