Overview of Admixture Mapping

Abstract

Admixture mapping is a powerful method of gene mapping for diseases or traits that show differential risk by ancestry. Admixture mapping has been applied most often to African Americans who trace ancestry to Europeans and West Africans. Recent developments in admixture mapping include improvements in methods to take advantage of higher densities of genetic variants as well as extensions to admixed populations with three or more ancestral populations, such as Latino Americans. In this unit, I outline the key concepts of admixture mapping. I describe several approaches for inferring local ancestry and provide strategies for performing admixture mapping depending on the study design. Finally, I compare and contrast linkage analysis, association analysis, and admixture mapping, with an emphasis on integrating admixture mapping and association testing.

INTRODUCTION

The goal of this unit is to inform the reader on best practices for mapping complex diseases using admixture mapping. The basic idea of admixture mapping has been around for several decades (Rife, 1954) but the data and methods required to perform well powered analysis at the genome-wide level have been available for only the last decade (Patterson et al., 2004; Smith et al., 2004). Since 2004, rapid advancements in technology have led to large increases in the density of genotyped markers, which in turn have led to rapidly evolving statistical techniques and improved power to detect disease susceptibility or quantitative trait loci.

Many of the considerations described in (UNITS 1.9, 1.12, 1.14, 1.17, 1.18, 1.22) for other gene mapping approaches also apply to admixture mapping. As with other gene mapping techniques, admixture mapping is sensitive to ill-defined phenotypes, confounders, unknown inheritance patterns, and potential interactions between genetic and environmental risk factors. Admixture mapping offers similar potential insight into biology, etiology, prevention, and treatment. However, admixture mapping has special data requirements and the choice of phenotype to study deserves extra attention. Perhaps the most important difference between admixture mapping and other gene mapping techniques is that admixture mapping is poised to directly contribute to the understanding of health disparities because it is specifically designed to address differential risk by ancestry.

KEY CONCEPTS

Phenotype

A phenotype is an observable characteristic of an individual. A phenotype reflects the individual’s genetics, environment, and interactions between and within genetics and environment. In gene mapping experiments, phenotypes are broadly categorized into diseases and traits. Diseases are typically measured in terms of cases and controls status and are therefore represented by binary variables. Traits are typically quantitative and are therefore represented by continuous variables. A Mendelian phenotype is one for which the underlying genotype can be predicted given a phenotypic value. In contrast, a complex phenotype does not show such simple patterns of inheritance (Units 1.4, 1.9). Complex phenotypes are generally oligogenic (i.e., involving a few genes) or polygenic (i.e., involving many genes) and multifactorial. The distribution of phenotypes can vary by ancestry, e.g., autoimmune diseases such as multiple sclerosis tend to be more common in individuals of European ancestry whereas other diseases such as prostate cancer, kidney disease, and hypertension tend to be more common in individuals of African ancestry (Smith et al., 2004). It is important to recognize that admixture mapping does not assume that risk is evenly distributed across genetic loci. It is also important to recognize that it is generally unknown how much differential risk by ancestry is due to genetic vs. environmental risk factors. Thus, the absence of differential risk by ancestry does not guarantee that admixture mapping will fail and the presence of differential risk by ancestry does not guarantee that admixture mapping will succeed.

Locus

For the purposes of this Unit, a locus is defined as a region in the genome; a locus correlated with a disease is called a disease susceptibility locus whereas a locus correlated with a trait is called a quantitative trait locus.

Admixture

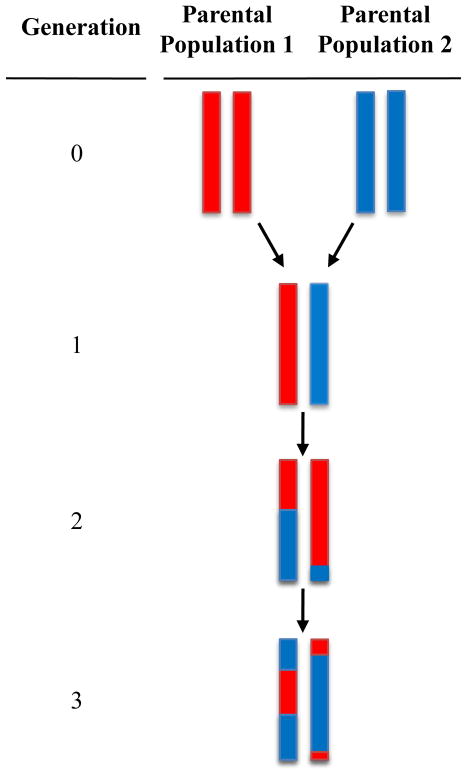
Admixture occurs when individuals from two or more previously isolated populations interbreed (Figure 1). The previously isolated populations are referred to as ancestral or parental and the newly formed population is referred to as admixed. In non-human species, the same process is often referred to as hybridization. Admixed or hybrid individuals have mixed ancestry. Admixture mapping is a method for capitalizing on recent admixture to correlate ancestry at genetic loci with a phenotype.

Figure 1.

The admixture process. After two generations of interbreeding between previously isolated parental populations, chromosomes in admixed individuals are mosaics of ancestry.

Most genetic variance is shared between populations but allele frequencies can vary, sometimes substantially so. For example, the null Duffy antigen has frequencies of ~100% in West African populations and ~0% in populations outside of Africa. Admixture mapping is designed to locate genetic loci with excess ancestry with respect to the phenotype, based on the assumption that causal variants leading to increased risk or trait values occur more frequently on chromosomal segments inherited from the ancestral population that has higher disease risk or larger average trait values.

Linkage analysis (Units 1.4, 1.9) directly measures recombination over a limited number of generations, which limits its resolution to an interval of ~10 cM. Such intervals can potentially contain hundreds of genes. In contrast, association mapping (Units 1.12, 1.17, 1.18, 1.20) indirectly measures recombination across many generations back to the most recent common ancestor of the entire sample. Consequently, association mapping allows for localization of signals typically down to 0.1 to 0.01 cM. Admixture mapping originally worked best for recent admixture, approximately <20 generations. Currently, the availability of improved methods and larger data sets allow for investigation of admixture dating back to <100 generations. Thus, resolution of admixture mapping is better than that of linkage analysis but not as good as association analysis.

STRATEGIC APPROACHES

Data requirements for admixture mapping include genotype data for samples from the admixed and ancestral populations. The original methods were based on a minimal number of markers ascertained to differ widely in frequency across the ancestral populations (Smith et al., 2004). These markers, known as ancestry-informative markers or AIMs, were ascertained by using one of several measures of population differentiation (Rosenberg et al., 2003). The two most widely used measures of population differentiation were delta, the difference in allele frequencies between the parental populations, and F_ST, the ratio of observed variance in allele frequencies to the variance in allele frequencies expected in the absence of population structure.

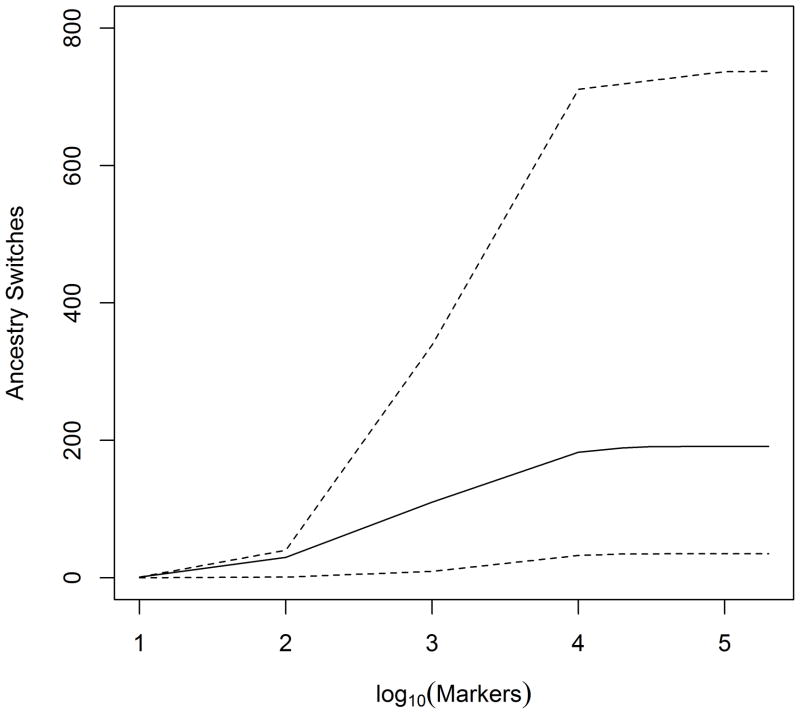
Although dense sets of markers are collectively more informative about ancestry, a methodological requirement for independent markers and the cost of de novo genotyping kept the number of markers used in admixture mapping in the low thousands. Current methods have relaxed the requirement for independent markers. In conjunction with less expensive genotyping by genome-wide microarrays (Units 1.20, 2.9, 2.11) or whole genome sequencing (Units 18.2, 18.4), admixture mapping can now use all of the available genotype data, resulting in improved power to detect disease susceptibility or trait loci. As another consequence, it is no longer necessary to measure population differentiation as a precursor to admixture mapping. For admixed African Americans (for whom admixture began ~8 generations ago), approximately 50,000 random markers are required to detect all ancestry switches, ranging from ~39,000 random markers up to ~160,000 random markers (Figure 2). As the number of generations since admixture began increases, more markers are required to detect all ancestry switches because recombination events accumulate linearly with the number of generations. Consequently, roughly twice as many markers are required to detect all ancestry switches for Latino Americans (for whom admixture began ~16 generations ago) as for African Americans.

Figure 2.

Marker density to detect all ancestry switches. The number of ancestry switches detected as a function of marker density for an individual with the median number (n = 191, solid line) or most extreme numbers (n = 35 or 737, dashed lines) of ancestry switches among 1,976 African Americans (Adeyemo et al., 2009). For admixed African Americans, high-throughput genotyping of approximately 1 million markers using commercially available microarrays is more than sufficient to extract all of the information on local ancestry.

Inferring Local Ancestry

Ancestry at any given locus, known as local ancestry, is unobservable and therefore has to be inferred. Ideally, at a fully informative marker, the allele frequency in one parental population is zero and the frequency of the same allele in the other parental population is one. In this scenario, inference of ancestry at that marker for any individual in the sample is deterministic. Unfortunately, there are very few such markers across the human genome. In the more common situation that multiple alleles are present in each parental population, inference of local ancestry is probabilistic.

Sophisticated algorithms based on hidden Markov models have been developed to infer ancestry probabilistically. The basic task is to infer the location of every ancestral switch, which is a recombination event that transitions from a haplotype from one parental population to a haplotype from another parental population. One class of such algorithms relies on reference allele frequencies for each of the parental populations. Software employing this class of algorithms includes LAMP (Sankararaman et al., 2008). The other class of such algorithms relies on reference haplotypes for each of the parental populations. The latter class, exemplified by HAPMIX (Price et al., 2009) and PCADMIX (Henn et al., 2012), is generally more sensitive than the former, which can be good or bad depending on the quality of the reference data. The latter requires larger reference data sets because larger sample sizes are required to capture haplotypic diversity than to estimate allele frequencies. A limited number of reference haplotypes can lead to inaccurate ancestry inference in genomic regions with high haplotypic diversity, such as the major histocompatibility complex (MHC) on chromosome 6. On the other hand, using reference haplotypes rather than allele frequencies makes it possible to combine ancestry inference with imputation of untyped markers. Currently, the most accurate software for local ancestry inference for unrelated individuals is LAMP-LD and for nuclear trios is LAMP-HAP (Baran et al., 2012).

An additional requirement of admixture mapping is a genetic map. The genetic map provides the hidden Markov model with local recombination rates, which informs the likelihood of a recombination event at a given locus, which in turn informs the likelihood of an ancestry switch at that locus. There are currently two genetic maps that are useful for admixture mapping. One map is specific for African Americans (Hinch et al., 2011). The other map is combined over multiple continental populations and is therefore generic (http://mathgen.stats.ox.ac.uk/impute/ALL_1000G_phase1integrated_v3_impute.tgz).

The choice of external reference data is critical. The reference samples typically serve as proxies for the true ancestral populations, given that we generally do not have historical samples of the true ancestral populations. For admixed African Americans, the HapMap or 1000 Genomes CEU and YRI samples perform quite well. First, the number of generations since admixture began in the history of admixed African Americans is sufficiently small so that allele frequencies in the CEU and YRI samples have not experienced much random genetic drift. Consequently, the CEU and YRI samples provide very good estimates of historical allele frequencies. Second, genetic variance between the CEU and YRI samples exceeds genetic variance between the various ancestral African ethnic groups collectively representing African ancestry or between the various ancestral European ethnic groups collectively representing European ancestry. Consequently, we can reasonably infer whether a chromosomal segment represents African or European ancestry, but it would be incorrect, for example, to infer that African ancestry in admixed African Americans solely derives from the Yoruba.

In the absence of reference data representing the parental populations, it is still possible to detect admixture because allele frequencies in admixed populations reflect the allele frequencies in the parental populations linearly weighted by the parental population’s contribution to ancestry. With reference data, detection of admixture is more powerful and labeling of populations is possible

Principal components analysis of genome-wide genotype data is widely used to detect population structure. Assuming no residual structure, admixture among K ancestral populations will be reflected by the top K-1 principal components, with or without reference data. When using genome-wide genotype data, these principal components correlate very strongly with global ancestry, which is the genome-wide average of the local ancestries. To infer local ancestry, local principal components must be used (Qin et al., 2010). Methods using this approach are currently underdeveloped relative to the approaches based on hidden Markov models described above.

Testing Local Ancestry

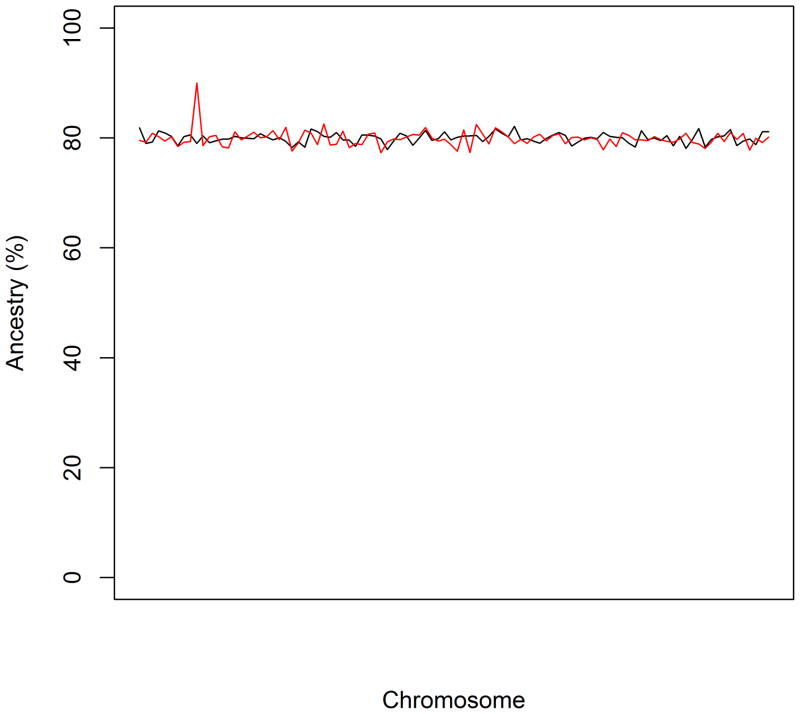
Admixture mapping is simply a test of the local ancestry-phenotype correlation. Such a test can be performed in a number of ways (Hoggart et al., 2004; Montana and Pritchard, 2004; Patterson et al., 2004). One test is a case-only statistic that is based on comparing local ancestry with global ancestry. The case-only statistic is based on the assumptions that there is no systematic deviation of ancestry in cases vs. controls, i.e., there is no confounding due to population stratification, and that controls contribute only noise to the estimation of ancestral allele frequencies. A second test is a case-control statistic that is based on excess ancestry in cases but not in controls (Figure 3). The case-control statistic does not rely on either of the two assumptions of the case-only statistic and therefore yields a more robust test.

Figure 3.

Detecting excess ancestry at a disease locus. The black line represents local ancestry among controls and the red line represents local ancestry among cases. Excess local ancestry in cases but not in controls suggests the presence of a disease locus.

Admixture mapping can be performed using likelihood ratio tests or regression. The preferred method is to use generalized linear models as they allow for many different phenotypic distributions, such as binary data, continuous data, count data, and ordinal data. For example, logistic regression is used with binary (case-control) data and linear regression is used with continuous data (quantitative traits). Generalized linear models readily allow for inclusion of covariates, interaction terms, and other model extensions without requiring specialized statistical software (Redden et al., 2006; Shriner et al., 2011a).

Estimating the Testing Burden of Genome-Wide Admixture Mapping

Genome-wide admixture mapping requires multiple comparisons and correcting for this is required to maintain control of the false positive error rate. The genome-wide significance level should account for the correlation of ancestry between markers, analogous to how the genome-wide significance level in association studies should account for the correlation of genotype between markers (i.e., linkage disequilibrium). The first analytical solution to this issue was developed for sparse maps of (nearly) uncorrelated AIMs (Sha et al., 2006). More recently, a more general solution based on autocorrelation was developed for dense maps of (correlated) random markers (Shriner et al., 2011b). Both of these solutions are data-dependent and therefore automatically account for the generally unknown population history of admixture. Therefore, these solutions are generically useful for admixture analysis, regardless of the number of ancestral populations, the number of generations since admixture began, or the rate of gene flow.

Replication and Follow-Up

Admixture mapping is fundamentally a statistical procedure, like linkage analysis or association testing. Consequently, replication of a finding in an independent data set is required (see UNIT 1.9). Also, follow-up studies for admixture peaks are very similar in design to follow-up studies for linkage peaks (see UNIT 1.9). When fine-mapping an admixture signal, the underlying causal variant (or variants) must display allele frequency differences and/or effect size differences, to generate the differential risk by ancestry detected by admixture mapping.

Joint Ancestry and Association Testing

A recent development in analysis of admixed individuals is a class of tests designed to jointly assess admixture and association. Joint testing offers two main advantages: power to detect disease susceptibility loci or trait loci is increased and association testing provides resolution to help localize admixture signals. For related individuals, the transmission-disequilibrium test can be performed separately with local ancestry and with genotype and the results combined into a single chi-squared test (Tang et al., 2010). For unrelated individuals, two tests have been devised to date. One combines the ancestry and genotype data into a single test and evaluates the test at a significance level appropriate for association testing (Pasaniuc et al., 2011). The other test first assesses ancestry, calibrated at a significance level appropriate for admixture mapping, and then updates the probabilities that the locus affects the phenotype with the genotype data, now calibrated at a significance level appropriate for association testing (Shriner et al., 2011b).

COMMENTARY

Admixture mapping and association studies are complementary. Admixture mapping is a test of the local ancestry-phenotype correlation, whereas association studies test the genotype-phenotype correlation. Admixture mapping is premised on population differentiation between the ancestral populations, whereas association studies are premised on similar allele frequencies across ancestries. Observed genotypes are conditional on unobserved but inferable local ancestry. That is, genotype and local ancestry are correlated, but conditioning genotype on local ancestry in association testing controls confounding due to population stratification.

As long as populations interbreed, admixture mapping will be a relevant gene mapping technique. The first applications of admixture mapping were to African Americans, for which the ancestral Europeans and West Africans genetically differ at the inter-continental level. Other examples of admixed populations for which the parental populations differ at the intercontinental level include Ashkenazi Jews (Eastern European and Middle Eastern ancestry), Australian Aboriginals (Aboriginal and European ancestry), Pacific Islanders (European and Polynesian ancestry), and Uyghurs (Asian and European ancestry) (Winkler et al., 2010). More generally, admixture mapping is relevant for two or more ancestral populations. For example, Hispanics are three-way admixed individuals, with ancestry derived in various proportions from Africans, Amerindians, and Europeans. The South African Coloureds are thought to represent five-way admixture of Bantu-speaking Africans, Europeans, Indians, Khoisan, and Southeast Asians. It is also possible to analyze admixture between more closely related ancestral populations (Shriner et al., 2011a).

CONCLUSIONS

Many phenotypes show population-specific effects, but whether such effects reflect environment or genetics remains largely unknown. For the proportion of phenotypic variance that is genetic, admixture mapping is a powerful technique for mapping genes conferring differential risk. Generalized linear models provide a highly flexible way to perform admixture mapping using widely available statistical software. The basic requirements for admixture mapping are genotype and phenotype data (including covariates as desired) from the admixed sample, genotype data for the parental populations (or proxies thereof), and a genetic map. The currently recommended software to infer ancestry is LAMP-LD if the sample consists of unrelated individuals or LAMP-HAP for nuclear trios. Dense panels of random markers provide better coverage of ancestry switches than do sparse panels of ancestry-informative markers. Given that high-throughput genotyping of dense panels via commercial chips is now cheaper than low-throughput genotyping of sparse panels, it is cost-effective to acquire high-density genotype or sequence data that can serve double-duty in ancestry inference and association mapping. The main limitation for admixture mapping is the availability of reference data for the parental populations for admixed samples other than African Americans. New methodologies will continue to be developed as populations with increasingly complex admixed histories are studied.