Abstract
Purpose
To quantify the extent to which a clinically significant prostate cancer mortality reduction due screening could have been masked by control arm screening (contamination) in the Prostate, Lung, Colorectal, and Ovarian (PLCO) trial.
Methods
We used three independently developed models of prostate cancer natural history to conduct a virtual PLCO trial. Simulated participants underwent pre-trial screening based on population patterns. The intervention arm followed observed compliance during the trial then resumed population screening. A contaminated control arm followed observed contamination during the trial then resumed population screening, while an uncontaminated control arm discontinued screening upon entry. We assumed a clinically significant screening benefit, applied population treatments and survival patterns, and calculated mortality rate ratios relative to the contaminated and uncontaminated control arms.
Results
The virtual trial reproduced observed incidence, including stage and grade distributions, and control arm mortality after 10 years of complete follow-up. Under the assumed screening benefit, the three models found that contamination increased the mortality rate ratio from 0.68–0.77 to 0.86–0.91, increased the chance of excess mortality in the intervention arm from 0–4% to 15–28%, and decreased the power of the trial to detect a mortality difference from 40–70% to 9–25%.
Conclusions
Our computer simulation models indicate that contamination substantially limited the ability of the PLCO to identify a clinically significant screening benefit. While the trial shows annual screening doesn’t reduce mortality relative to population screening, contamination prevents concluding whether screening reduces mortality relative to no screening.
Keywords: Computer simulation, early detection of cancer, mortality, prostate-specific antigen, prostatic neoplasms, randomized controlled trial
INTRODUCTION
The survival benefit due to prostate-specific antigen (PSA) screening for prostate cancer remains uncertain and controversial. Long-awaited results from the European Randomized study of Screening for Prostate Cancer (ERSPC) and the US-based Prostate, Lung, Colorectal, and Ovarian (PLCO) cancer screening trial have not resolved this critical issue. A significant reduction in prostate cancer mortality was observed in the ERSPC, which reported a prostate cancer mortality rate ratio for the intervention arm versus the control arm of 0.80 after a median of 9 years of follow-up [1]. This result was not replicated in the PLCO study, which reported corresponding mortality rate ratios 1.15 after 10 years (complete for 92% of participants) and 1.09 after 13 years (complete for 57% of participants) [2].
Reconciling these apparently conflicting results is challenging because they reflect the performance of different screening protocols in different populations under different circumstances. A key difference is that the ERSPC was conducted in a population that was relatively screening-naïve whereas the PLCO trial was conducted in a population in which screening was already becoming established. Not only did at least 45% of PLCO trial participants enter the trial with a history of screening [2], but those randomized to the control arm continued to be screened during the course of the trial at least as often as in the general population, averaging 2.7 routine PSA tests over the trial’s 6-year intervention period [3]. Thus the control arm was heavily contaminated by screening, and rather than comparing screening versus no screening, the PLCO trial effectively evaluated organized annual screening versus population screening [2,4]. A recent evidence review for the US Preventive Services Task Force noted the potential role of contamination in explaining the PLCO’s non-significant prostate cancer mortality rate ratio and the trend towards excess mortality in the intervention arm [5]. However, existing statistical methods to quantify the magnitude of its effect [6], as have been applied to the ERSPC [7], require stratifying outcomes within contaminated and uncontaminated subgroups, stratifications that may be sensitive to the definition of contamination and may not be possible using the PLCO surveys upon which published contamination estimates were based [3].
In this article we use three independently developed mathematical and computer simulation models to represent a virtual PLCO trial with both contaminated and uncontaminated control arms. The models were developed to study prostate cancer progression, screening, detection, and survival in the US population [8–10] as part of the Cancer Intervention and Surveillance Modeling Network (CISNET1); here we adapt them to study PLCO trial results. We assume a clinically significant benefit of screening and quantify the extent to which contamination masks the benefit in terms of its effect on the mortality rate ratio, on the chance of observing excess mortality in the intervention arm, and on the power of the trial to detect the assumed benefit.
METHODS
Overview of CISNET prostate models
In this article, we combine previously developed CISNET models of prostate cancer natural history with an updated model of population screening patterns and published data on the PLCO trial design. Each model is based on a specification of natural history that captures disease onset, progression, detection in the absence of screening, and survival. The natural history concepts differ across models, but all models were calibrated using common datasets on (a) population demographics: men aged 50–84 in the core 9 registries of the Surveillance, Epidemiology, and End Results (SEER) program [11] and (b) PSA screening patterns: a reconstruction [12] using Medicare claims and responses from the National Health Interview Survey (NHIS) in 2000 to estimate the probability of a first PSA test by birth cohort and calendar year, which we extended using responses from the NHIS in 2005. The calibrated models reproduce age-adjusted SEER incidence trends before and during the PSA era by SEER stages (local-regional or distant) and Gleason grade categories (2–7 or 8–10). Detailed model descriptions are available on the CISNET website2; here we briefly review the key model features and primary data sources for calibration.
The FHCRC model is PSA-based; we estimate PSA growth for cases and non-cases using serial screening data from the control arm of the Prostate Cancer Prevention Trial [13], and we represent the risk of disease onset as proportional to age and the risk of progression to metastasis and to disease detection in the absence of screening as proportional to PSA. Because the FHCRC model explicitly generates PSA trajectories, the PSA value at any testing event is known, and the consequences of a positive test, namely referral to biopsy, receipt of biopsy, and biopsy result given disease status, are generated as events in the individual’s disease history. The likelihood of compliance with biopsy referral is based on studies conducted within the PLCO trial population [14,15], and the sensitivity of biopsy to detect occult disease is assumed to increase over time in accordance with the diffusion of extended biopsy protocols during the PSA era [16]. Progression risks given PSA are then estimated via maximum likelihood so that the model matches incidence trends in the SEER population [10].
The MISCAN model is state-based; disease progresses through a sequence of states defined by stage and grade. The stage and grade transition rates are estimated using data from the Rotterdam section of the ERSPC [8]; the progression to disease detection in the absence of screening and the sensitivity of the PSA test to detect disease within each state are based on recalibration of these model parameters to reproduce disease incidence trends in the SEER population [17].
The UMICH model of natural history consists of three states: healthy, preclinical, and clinical (diagnosis in the absence of screening). This simple model is overlaid with a model of the time from onset to detection (delay time), which depends on the distribution of age and calendar year of diagnosis, and a model of stage and grade at diagnosis, which depends on the delay time [9]. Putting together these models of age/year incidence trends and stage/grade distributions with inputs on SEER incidence and US screening patterns produces a composite model for incidence in the SEER population [18].
Adapting the CISNET models to conduct a virtual PLCO trial
From 1993 to 2001, the PLCO trial enrolled 76,693 men aged 55–74 at 10 US study centers and randomized them to either an intervention or control arm [19]. Men in the intervention arm were offered annual PSA testing for 6 years and digital rectal exam testing for 4 years. This design provided 90% power to detect a 20% reduction in prostate cancer mortality [20]. Under the design assumptions about noncompliance and contamination, this corresponds to a 27% mortality reduction [20], which was deemed to be clinically significant. In order to achieve this level of power, trial investigators expected over 300 deaths in each arm after 10 years of complete follow-up. In practice, after 10 years of follow-up (complete for 92% of participants), the incidence of prostate cancer death was very low, with 98 and 85 deaths in the intervention and control arms and a mortality rate ratio of 1.15 (95% confidence interval 0.86 to 1.55).
We adapt the CISNET models to conduct a virtual PLCO trial by simulating a cohort of men with observed age distributions [19] in each arm at randomization. The models generate disease natural histories in the absence of screening, assign birth-cohort-specific ages at PSA screenings based on our extended model of the general US population [12], and determine all-cause mortality from US life tables; the generation algorithm ensures all men are alive and undiagnosed at entry into the trial. Lacking information on observed recruitment and for simplicity, we assume all enrollment into the virtual trial occurs on January 1, 1993.
Men randomized to the intervention arm switch to annual PSA screening with random 85% compliance at each scheduled screen [19] for the trial intervention period then resume population screening. Men randomized to the control arm switch to a 20% higher intensity of screening than the general population during the trial to match previous estimates of PLCO control arm contamination (including reproducing the average 2.7 routine PSA tests during the trial [3]) then resume population screening. Men in a third uncontaminated control arm discontinue PSA screening upon entry into the trial. Screening patterns in the three arms are illustrated in Figure 1. Digital rectal exam testing is not explicitly modeled since it is already reflected in the way the models project diagnosis in the absence of PSA screening.
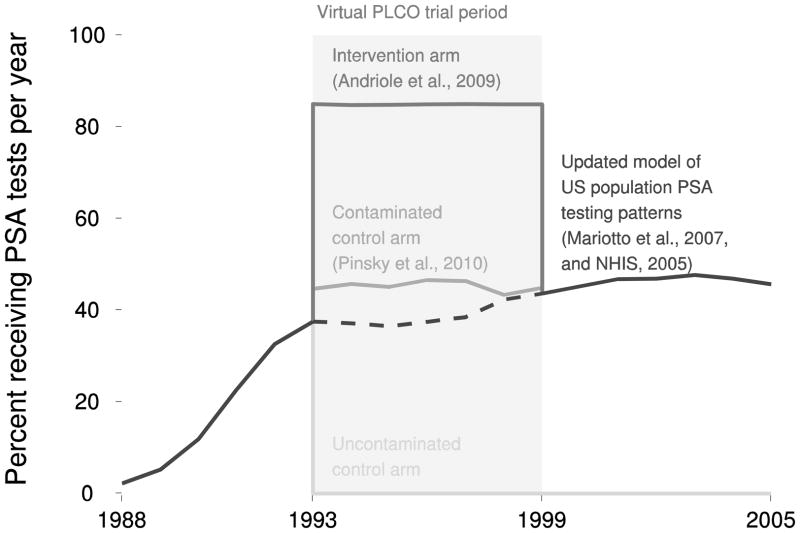
Fig 1. Percent of men in each arm of the virtual PLCO trial receiving PSA tests per year.
All simulated participants undergo pre-trial screening (solid black line before virtual trial period) based on our model of PSA testing patterns in the general US population applied to the virtual PLCO cohort. The intervention arm follows annual screening subject to observed compliance for the virtual trial period (dark gray line) then resumes population screening (solid black line after virtual trial period). The contaminated control arm follows a higher intensity of screening (solid medium gray line) than in the general population (dashed black line) for the virtual trial period then resumes population screening. The uncontaminated control arm discontinues screening upon entry into the trial (solid slight gray line).
All models assume 35% of control arm men who were tested and had PSA > 4 ng/mL, like their intervention arm counterparts [15], received a biopsy. All models assume that the trial’s sextant biopsy had 80% sensitivity to detect preclinical tumors [21,22]; for simplicity, all models assume this constant 80% sensitivity during and after the trial for both the intervention and control arms. All models randomly assign 84% of men diagnosed with local-regional stage disease to curative treatment based on proportions of SEER local-regional stage cases receiving radical prostatectomy (SEER codes 50, 58, 60, and 68 prior to 1997 and 50 and 60 beginning in 1998) or radiation therapy (SEER categories beam radiation, radioactive implants, radioisotopes, combination of beam with implants or isotopes, or radiation with method or source unspecified) for trial cohort ages and years. All models generate prostate cancer survival from clinical diagnosis in the absence of screening or treatment benefits using a common Poisson regression model fit to SEER data for cases diagnosed in 1983–1986, just prior to the advent of PSA screening. This baseline prostate survival is improved for non-metastatic cases who receive curative treatment using a hazard ratio of 0.62 based on the Scandinavian trial of radical prostatectomy versus watchful waiting [23].
To reflect the benefit of screening, all models project results under two different mechanisms that approximate a clinically significant 27% mortality reduction [20]. The stage-shift mechanism implies that cases shifted to an earlier stage and/or grade by screening earn the prostate cancer survival associated with the earlier tumor characteristics, with a corresponding increase in life expectancy. When a tumor is detected early, but with the same tumor characteristics as in the absence of screening, there can still be a modest survival advantage due to detection at an earlier age. The cure rate mechanism assumes a common constant cure rate among screen-detected non-metastatic cases who would have died of their disease in the absence of screening. Once screen detected, these cases are cured and go on to die of other causes in the presence of screening [24]. A preliminary study using the MISCAN model found that a constant cure rate of 35% allowed that model to reproduce the ERSPC’s non-attendance-adjusted 27% mortality reduction [1] based on data from the Rotterdam center, and all models use this value for the cure rate. Under either mechanism, overdiagnosed cases (i.e., cases detected by screening who would not otherwise have been diagnosed during their lifetimes) do not receive any benefit since they die of other causes both in the presence and absence of screening.
Each model simulates the virtual trial 100 times. To confirm that the model reasonably replicates the trial, we compare model-generated incidence, stage and grade distributions, and control arm mortality with published results. Following validation, we use the models to project mortality and calculate (a) mortality rate ratios of the intervention arm relative to the contaminated and uncontaminated control arms after 10 and 13 years of complete follow-up and corresponding 95% confidence intervals assuming a Poisson distribution for the number of deaths in each arm, (b) the percent of trials with excess mortality in the intervention arm, and (c) the percent of trials in which the 95% confidence interval for the mortality rate ratio excludes 1, i.e., the power of the trial. Calculations were performed using R [25] and figures were created using the package ggplot2 [26].
RESULTS
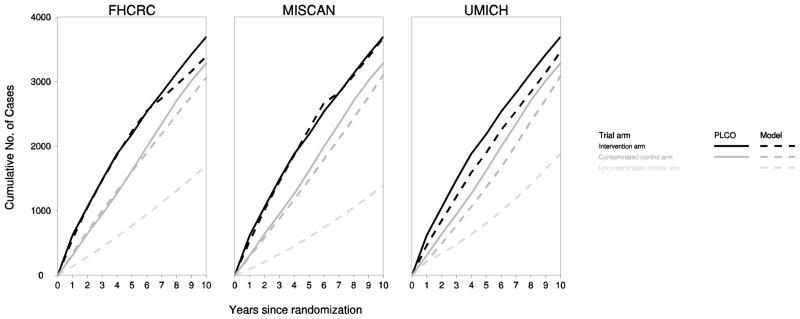
Figure 2 presents observed and model-projected cumulative incidence in the intervention and control arms for the three models. The models closely reproduced observed disease incidence, with projected incidence in the uncontaminated control arm considerably lower than in the contaminated control arm.
Fig 2. Observed and model-projected cumulative prostate cancer incidence in each arm of the virtual PLCO trial.
The figure illustrates cumulative number of prostate cancer diagnoses in the intervention arm (black), contaminated control arm (dark gray), and uncontaminated control arm (light gray) observed in the trial (solid lines) and projected by the models (dashed lines).
After 10 years of follow-up (complete for 92% of participants), PLCO investigators reported 4% of intervention arm and 5% of control arm cases were clinical stage III–IV; the models estimated 3–5% and 5–7% in these groups and 10–17% in the uncontaminated control arm were projected to be diagnosed in distant stage. Similarly, trial investigators reported 9% of intervention arm and 12% of control arm cases had Gleason score 8–10; corresponding model estimates were 10–20% and 14–20% in these groups and 19–32% in the uncontaminated control arm.
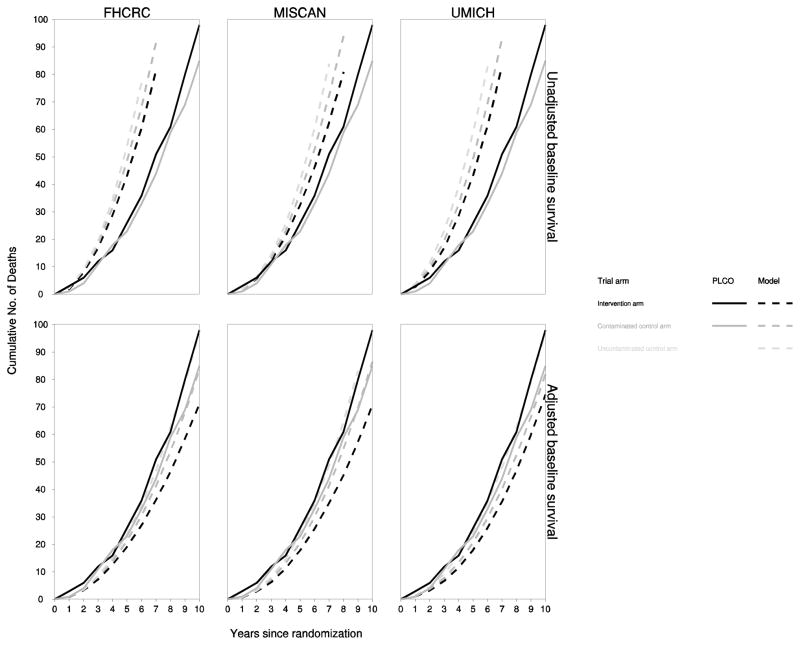
Despite closely reproducing incidence patterns and stage and grade distributions, the models substantially overprojected prostate cancer mortality. Figure 3 shows observed and model-projected cumulative mortality in the intervention and control arms for the three models. Prior studies of the PLCO population have indicated that not only was this population healthier than the general population [27], but it also had a higher level of education, higher socioeconomic standing, and a higher proportion of whites. These differences could have predisposed the PLCO population towards lower prostate cancer mortality than that in the general prostate cancer case population. In addition, the common Poisson model of baseline prostate cancer survival was fit using SEER cases diagnosed in 1983–1986 before the PSA test was introduced. By the start of the trial, PSA had become an established approach for disease surveillance after diagnosis leading to considerably earlier secondary treatment [28]. For this reason, and possibly also due to other improvements in disease management, it is possible that by the start of the trial prostate cancer survival had improved even before applying screening and primary treatment benefits.
Fig 3. Observed and model-projected cumulative prostate cancer mortality in each arm of the virtual PLCO trial.
The figure illustrates cumulative number of prostate cancer deaths in the intervention arm (black), contaminated control arm (dark gray), and uncontaminated control arm (light gray) observed in the trial (solid lines) and projected by the models (dashed lines). Model projections assume a stage-shift benefit for screening and a protective benefit of curative treatment. Results are presented separately for unadjusted (top panels) and adjusted (bottom panels) baseline prostate cancer survival to account for lower-than-expected observed mortality.
To account for lower-than-expected prostate cancer mortality, all models introduced a hazard ratio to improve baseline prostate cancer survival. Each model estimated a hazard ratio so that the model-generated mortality after applying screening and treatment benefits matched observed mortality in the control arm. The estimated hazard ratios were 0.39 (FHCRC), 0.50 (MISCAN), and 0.37 (UMICH). All prostate cancer mortality results presented below reflect model-generated outcomes using the modified prostate cancer survival models.
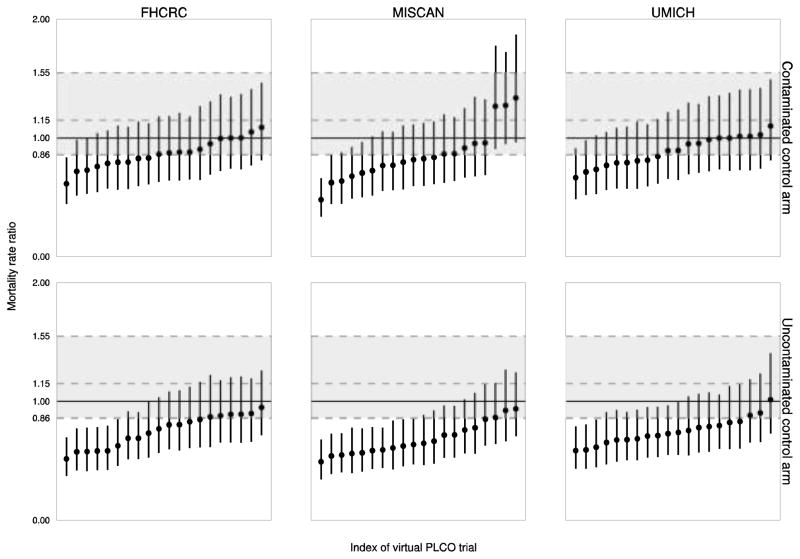
Figure 4 plots a sorted random sample of mortality rate ratios of the intervention arm relative to contaminated and uncontaminated control arms versus the observed mortality rate ratio after 10 years of complete follow-up. We note that both observed and model-projected 95% confidence intervals are relatively wide, indicating high variability in both actual and virtual trials. This is likely due to the rarity of the event of prostate cancer death despite the large sample size in each arm.
Fig 4. Observed and model-projected mortality rate ratios relative to contaminated and uncontaminated control arms.
The figure illustrates ratios of mortality rates of the intervention arm relative to the contaminated and uncontaminated control arms and corresponding 95% confidence intervals observed in the trial (dashed gray horizontal lines) and projected by the models (solid black vertical lines) after 10 years of complete follow-up. The model projections represent a sorted random sample of 20 mortality rate ratios and 95% confidence intervals are based on assumed Poisson distributions for the number of deaths.
Table 1 summarizes the average projected mortality rate ratio over 100 virtual trials, the percent of trials with excess mortality in the intervention arm, and the power of the trial. After 10 years of complete follow-up, the average mortality rate ratios relative to the uncontaminated control arm across the three models were 0.68–0.77 under the stage-shift and 0.71–0.80 under the cure rate. These values are consistent with a clinically significant 27% mortality reduction. Contamination increased the average mortality rate ratios to 0.86–0.91 under the stage-shift and to 0.81–0.95 under the cure rate. Contamination also increased the chance of excess mortality in the intervention arm from 0–4% to 15–28% under the stage-shift and from 0–10% to 10–30% under the cure rate. And contamination decreased the power of the trial to detect the assumed screening benefit from 40–70% to 9–25% under the stage shift and from 45–60% to 5–25% under the cure rate. Results are broadly consistent across models, across the two assumed mechanisms of screening benefit, and across 10 or 13 years of complete follow-up. In an additional sensitivity exercise (results not shown), we found that applying population screening to the contaminated control arm without an adjustment to reflect higher intensity of screening than the general population during the trial yielded very similar impacts of contamination.
Table 1.
Model-projected average mortality rate ratio of the intervention arm relative to the contaminated and uncontaminated control arms over 100 virtual trials, percent of trials with excess mortality in the intervention arm, and percent power of the trial. Results are reported separately under assumed stage-shift and cure rate mechanisms of screening benefit after 10 and 13 years of complete follow-up.
| Screening benefit | Years of follow-up | Control arm | Mortality rate ratio | Excess mortality in intervention arm | Power of the trial | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FHCRC | MISCAN | UMICH | FHCRC | MISCAN | UMICH | FHCRC | MISCAN | UMICH | |||
| Stage-shift | 10 | Uncontaminated | 0.75 | 0.68 | 0.77 | 0 | 0 | 4 | 40 | 70 | 41 |
| Contaminated | 0.87 | 0.86 | 0.91 | 15 | 15 | 28 | 15 | 25 | 9 | ||
| 13 | Uncontaminated | 0.75 | 0.66 | 0.79 | 0 | 0 | 2 | 60 | 90 | 51 | |
| Contaminated | 0.87 | 0.85 | 0.93 | 15 | 15 | 29 | 15 | 25 | 9 | ||
| Cure rate | 10 | Uncontaminated | 0.71 | 0.80 | 0.71 | 0 | 10 | 2 | 60 | 45 | 58 |
| Contaminated | 0.81 | 0.95 | 0.88 | 10 | 30 | 21 | 25 | 5 | 13 | ||
| 13 | Uncontaminated | 0.73 | 0.81 | 0.71 | 0 | 5 | 0 | 80 | 58 | 79 | |
| Contaminated | 0.85 | 0.97 | 0.89 | 5 | 42 | 18 | 20 | 11 | 15 | ||
DISCUSSION
The perceived negative finding from the PLCO trial that PSA screening does not save lives has generated a storm of questions, particularly in light of the positive finding from the ERSPC. Some studies comparing the two trials have argued that screening in the control arm of the PLCO trial could have been sufficient to mask a clinically significant benefit or to produce a false negative result [29–31]. The impact of contamination on the trial results has not previously been quantified but is critical to proper interpretation of the trial and synthesis of its results with those of the ERSPC and other studies.
In this article we use previously developed models of prostate cancer natural history and, assuming early detection confers a clinically significant survival benefit, quantified the impact of control arm contamination on relative mortality rates in a virtual PLCO trial. We find that control arm contamination substantially equalized mortality rates in the two arms, creating a nontrivial probability of excess mortality in the intervention arm and lowering the power of the trial to detect a mortality difference between the two arms. These impacts remain substantial after accounting for the lower-than-expected mortality in each arm.
Our results depend somewhat on the design assumptions when implementing the virtual trial. We assumed trial enrollment occurs on January 1, 1993, rather than being spread out between 1993 and 2001. A consequence is that we may underproject pre-trial screening; however, the three models estimated that 39–41% of virtual trial participants had at least 1 PSA test in the 3 years before entry, which is similar to the 45% estimated by trial investigators [2]. We ignored changes in trial protocol that increased the number of tests from 4 to 5 in 1994 and from 5 to 6 in 1995 and that excluded men with more than 1 PSA in the preceding 3 years starting in 1995. Conversely, our updated model of PSA testing in the US population, intensified to capture increased screening during the trial, implied that 68% of control arm participants received at least 1 routine PSA during the trial, which is only slightly lower than the 74% estimated by PLCO investigators [3]. Thus the virtual PLCO involved more screening in the intervention arm and less screening in the control arm than occurred in the actual trial, suggesting that our projected impact of contamination may be conservative. We assumed that intervention and control arm participants resumed population screening after the trial intervention period. We assumed SEER primary treatment patterns for detected cases. And we improved baseline prostate cancer survival to account for lower-than-expected prostate cancer mortality in the control arm. Because these assumptions apply equally to intervention and control arms, they likely have little effect on our projections of relative mortality rates.
Our results also depend on the assumed screening benefit. We chose a level of benefit deemed to be clinically significant by trial investigators [20] and consistent with that observed in the ERSPC. A smaller benefit would diminish while a greater benefit would increase the impact of contamination. Under this assumed benchmark level of benefit, the projected impact of contamination is robust to the assumed mechanism by which early detection confers benefit, to whether evaluation occurs after 10 or 13 years of complete follow-up, and to the three models of underlying disease natural history.
A more complete reconciliation of ERSPC and PLCO results is underway. In collaboration with investigators from both trials, we are using the CISNET models to quantify impacts of different background incidence, pre-trial screening, screening frequencies, PSA thresholds for test positivity, biopsy frequencies, and treatment distributions. While quantifying the contributions of these factors will provide deeper insights into reconciling the trial results, the role of PLCO contamination promises to remain a critical factor.
In summary, the PLCO trial results support the conclusion that organized annual screening does not reduce mortality relative to the level of screening in the control arm. However, because the level of screening in the control arm was substantial, the trial results do not support concluding that screening does not reduce mortality relative to no screening. Instead, a clinically significant benefit could have been masked by contamination, preventing simple synthesis with ERSPC results and limiting the value of the trial for informing recommendations about whether men should undergo PSA screening. Nonetheless, the PLCO trial remains an invaluable resource for learning about prostate cancer biology and epidemiology, PSA distributions and growth patterns, characteristics of the PSA test, and comparative effectiveness of screening strategies with varying testing frequencies.
Acknowledgments
We are grateful to Dr. Paul F. Pinsky for careful reading and helpful comments on an earlier draft. Any remaining errors are our own. This research was supported by U01CA157224-01 from the National Cancer Institute and U01CA157224 from the National Cancer Institute and the Centers for Disease Control. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute, the National Institutes of Health, or the Centers for Disease Control.
Footnotes
CONFLICT OF INTEREST
HJK received partial funding from Beckman Coulter to evaluate cost-effectiveness of the prostate health index. All other authors declare that they have no conflict of interest.
Contributor Information
Roman Gulati, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, USA.
Alex Tsodikov, Department of Biostatistics, University of Michigan, USA.
Elisabeth M Wever, Department of Public Health, Erasmus University Medical Center, The Netherlands.
Angela B Mariotto, Division of Cancer Control and Population Sciences, National Cancer Institute, USA.
Eveline AM Heijnsdijk, Department of Public Health, Erasmus University Medical Center, The Netherlands.
Jeffrey Katcher, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, USA.
Harry J de Koning, Department of Public Health, Erasmus University Medical Center, The Netherlands.
Ruth Etzioni, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, USA.
References
- 1.Schröder FH, Hugosson J, Roobol MJ, Tammela TL, Ciatto S, Nelen V, Kwiatkowski M, Lujan M, Lilja H, Zappa M, Denis LJ, Recker F, Berenguer A, Maattanen L, Bangma CH, Aus G, Villers A, Rebillard X, van der Kwast T, Blijenberg BG, Moss SM, de Koning HJ, Auvinen A. Screening and prostate-cancer mortality in a randomized European study. N Engl J Med. 2009;360 (13):1320–1328. doi: 10.1056/NEJMoa0810084. [DOI] [PubMed] [Google Scholar]
- 2.Andriole GL, Crawford ED, Grubb RL, 3rd, Buys SS, Chia D, Church TR, Fouad MN, Isaacs C, Kvale PA, Reding DJ, Weissfeld JL, Yokochi LA, O’Brien B, Ragard LR, Clapp JD, Rathmell JM, Riley TL, Hsing AW, Izmirlian G, Pinsky PF, Kramer BS, Miller AB, Gohagan JK, Prorok PC. Prostate Cancer Screening in the Randomized Prostate, Lung, Colorectal, and Ovarian Cancer Screening Trial: Mortality Results after 13 Years of Follow-up. J Natl Cancer Inst. 2012;104:1–8. doi: 10.1093/jnci/djr500. djr500 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pinsky PF, Black A, Kramer BS, Miller A, Prorok PC, Berg C. Assessing contamination and compliance in the prostate component of the Prostate, Lung, Colorectal, and Ovarian (PLCO) cancer screening trial. Clin Trials. 2010;7(4):303–311. doi: 10.1177/1740774510374091. 1740774510374091 [pii] [DOI] [PubMed] [Google Scholar]
- 4.Berg CD. The Prostate, Lung, Colorectal and Ovarian cancer screening trial: The prostate cancer screening results in context. Acta Oncol. 2011;50(Suppl 1):12–17. doi: 10.3109/0284186X.2010.531283. [DOI] [PubMed] [Google Scholar]
- 5.Chou R, Croswell JM, Dana T, Bougatsos C, Blazina I, Fu R, Gleitsmann K, Koenig HC, Lam C, Maltz A, Rugge JB, Lin K. Screening for Prostate Cancer: A Review of the Evidence for the U.S. Preventive Services Task Force. Ann Intern Med. 2011 doi: 10.1059/0003-4819-155-11-201112060-00375. 0003-4819-155-11-201112060-00375 [pii] [DOI] [PubMed] [Google Scholar]
- 6.Cuzick J, Edwards R, Segnan N. Adjusting for non-compliance and contamination in randomized clinical trials. Stat Med. 1997;16(9):1017–1029. doi: 10.1002/(SICI)1097-0258(19970515)16:9<1017::AID-SIM508>3.0.CO;2-V. [pii] [DOI] [PubMed] [Google Scholar]
- 7.Roobol MJ, Kerkhof M, Schroder FH, Cuzick J, Sasieni P, Hakama M, Stenman UH, Ciatto S, Nelen V, Kwiatkowski M, Lujan M, Lilja H, Zappa M, Denis L, Recker F, Berenguer A, Ruutu M, Kujala P, Bangma CH, Aus G, Tammela TL, Villers A, Rebillard X, Moss SM, de Koning HJ, Hugosson J, Auvinen A. Prostate cancer mortality reduction by prostate-specific antigen-based screening adjusted for nonattendance and contamination in the European Randomised Study of Screening for Prostate Cancer (ERSPC) Eur Urol. 2009;56(4):584–591. doi: 10.1016/j.eururo.2009.07.018. S0302-2838(09)00768-4 [pii] [DOI] [PubMed] [Google Scholar]
- 8.Draisma G, Boer R, Otto SJ, van der Cruijsen IW, Damhuis RA, Schröder FH, de Koning HJ. Lead times and overdetection due to prostate-specific antigen screening: Estimates from the European Randomized Study of Screening for Prostate Cancer. J Natl Cancer Inst. 2003;95 (12):868–878. doi: 10.1093/jnci/95.12.868. [DOI] [PubMed] [Google Scholar]
- 9.Tsodikov A, Szabo A, Wegelin J. A population model of prostate cancer incidence. Stat in Med. 2006;25 (16):2846–2866. doi: 10.1002/sim.2257. [DOI] [PubMed] [Google Scholar]
- 10.Gulati R, Inoue L, Katcher J, Hazelton W, Etzioni R. Calibrating disease progression models using population data: a critical precursor to policy development in cancer control. Biostatistics. 2010;11(4):707–719. doi: 10.1093/biostatistics/kxq036. kxq036 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Surveillance, Epidemiology, and End Results (SEER) Program. SEER*Stat Database: Mortality - All COD, Public-Use With State, Total US (1969–2005) National Cancer Institute, DCCPS, Surveillance Research Program, Cancer Statistics Branch; ( www.seer.cancer.gov) released April 2008. Underlying mortality data provided by NCHS ( www.cdc.gov/nchs) [Google Scholar]
- 12.Mariotto A, Etzioni R, Krapcho M, Feuer EJ. Reconstructing prostate-specific antigen (PSA) testing patterns among black and white men in the US from Medicare claims and the National Health Interview Survey. Cancer. 2007;109 (9):1877–1886. doi: 10.1002/cncr.22607. [DOI] [PubMed] [Google Scholar]
- 13.Goodman PJ, Thompson IM, Jr, Tangen CM, Crowley JJ, Ford LG, Coltman CA., Jr The prostate cancer prevention trial: design, biases and interpretation of study results. J Urol. 2006;175(6):2234–2242. doi: 10.1016/S0022-5347(06)00284-9. S0022-5347(06)00284-9 [pii] [DOI] [PubMed] [Google Scholar]
- 14.Pinsky PF, Crawford ED, Kramer BS, Andriole GL, Gelmann EP, Grubb R, Greenlee R, Gohagan JK. Repeat prostate biopsy in the prostate, lung, colorectal and ovarian cancer screening trial. BJU Int. 2007;99(4):775–779. doi: 10.1111/j.1464-410X.2007.06708.x. BJU6708 [pii] [DOI] [PubMed] [Google Scholar]
- 15.Grubb RL, 3rd, Pinsky PF, Greenlee RT, Izmirlian G, Miller AB, Hickey TP, Riley TL, Mabie JE, Levin DL, Chia D, Kramer BS, Reding DJ, Church TR, Yokochi LA, Kvale PA, Weissfeld JL, Urban DA, Buys SS, Gelmann EP, Ragard LR, Crawford ED, Prorok PC, Gohagan JK, Berg CD, Andriole GL. Prostate cancer screening in the Prostate, Lung, Colorectal and Ovarian cancer screening trial: update on findings from the initial four rounds of screening in a randomized trial. BJU Int. 2008;102(11):1524–1530. doi: 10.1111/j.1464-410X.2008.08214.x. BJU8214 [pii] [DOI] [PubMed] [Google Scholar]
- 16.Eichler K, Hempel S, Wilby J, Myers L, Bachmann LM, Kleijnen J. Diagnostic value of systematic biopsy methods in the investigation of prostate cancer: A systematic review. J Urol. 2006;175 (5):1605–1612. doi: 10.1016/S0022-5347(05)00957-2. [DOI] [PubMed] [Google Scholar]
- 17.Wever EM, Draisma G, Heijnsdijk EAM, Roobol MJ, Boer R, Otto SJ, De Koning HJ. Differences between PSA screening in the US and PSA screening in the European trial. JNCI 2009 [Google Scholar]
- 18.Chefo S, Tsodikov A. Stage-specific cancer incidence: An artificially mixed multinomial logit model. Stat Med. 2009;28 (15):2054–2076. doi: 10.1002/sim.3615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Andriole GL, Crawford ED, Grubb RL, 3rd, Buys SS, Chia D, Church TR, Fouad MN, Gelmann EP, Kvale PA, Reding DJ, Weissfeld JL, Yokochi LA, O’Brien B, Clapp JD, Rathmell JM, Riley TL, Hayes RB, Kramer BS, Izmirlian G, Miller AB, Pinsky PF, Prorok PC, Gohagan JK, Berg CD. Mortality results from a randomized prostate-cancer screening trial. N Engl J Med. 2009;360 (13):1310–1319. doi: 10.1056/NEJMoa0810696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Prorok PC, Andriole GL, Bresalier RS, Buys SS, Chia D, Crawford ED, Fogel R, Gelmann EP, Gilbert F, Hasson MA, Hayes RB, Johnson CC, Mandel JS, Oberman A, O’Brien B, Oken MM, Rafla S, Reding D, Rutt W, Weissfeld JL, Yokochi L, Gohagan JK. Design of the Prostate, Lung, Colorectal and Ovarian (PLCO) Cancer Screening Trial. Control Clin Trials. 2000;21 (6 Suppl):273S–309S. doi: 10.1016/s0197-2456(00)00098-2. [DOI] [PubMed] [Google Scholar]
- 21.Babaian RJ, Toi A, Kamoi K, Troncoso P, Sweet J, Evans R, Johnston DA, Chen M. A comparative analysis of sextant and an extended 11-core multisite directed biopsy strategy. J Urol. 2000;163 (1):152–157. [PubMed] [Google Scholar]
- 22.Presti JCJ, Chang JJ, Bhargava V, Shinohara K. The optimal systematic prostate biopsy scheme should include 8 rather than 6 biopsies: Results of a prospective clinical trial. J Urol. 2000;163(1):163–166. discussion 166–167. [PubMed] [Google Scholar]
- 23.Bill-Axelson A, Holmberg L, Ruutu M, Garmo H, Stark JR, Busch C, Nordling S, Haggman M, Andersson SO, Bratell S, Spangberg A, Palmgren J, Steineck G, Adami HO, Johansson JE. Radical prostatectomy versus watchful waiting in early prostate cancer. N Engl J Med. 2011;364(18):1708–1717. doi: 10.1056/NEJMoa1011967. [DOI] [PubMed] [Google Scholar]
- 24.Wever EM, Draisma G, Heijnsdijk EA, de Koning HJ. How does early detection by screening affect disease progression? Modeling estimated benefits in prostate cancer screening. Med Decis Making. 2011 doi: 10.1177/0272989X10396717. 0272989X10396717 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2011. [Google Scholar]
- 26.Wickham H. ggplot2: Elegant graphics for data analysis. Springer; New York: 2009. [Google Scholar]
- 27.Pinsky PF, Miller A, Kramer BS, Church T, Reding D, Prorok P, Gelmann E, Schoen RE, Buys S, Hayes RB, Berg CD. Evidence of a healthy volunteer effect in the prostate, lung, colorectal, and ovarian cancer screening trial. Am J Epidemiol. 2007;165(8):874–881. doi: 10.1093/aje/kwk075. kwk075 [pii] [DOI] [PubMed] [Google Scholar]
- 28.Cetin K, Beebe-Dimmer JL, Fryzek JP, Markus R, Carducci MA. Recent time trends in the epidemiology of stage IV prostate cancer in the United States: analysis of data from the Surveillance, Epidemiology, and End Results Program. Urology. 2010;75(6):1396–1404. doi: 10.1016/j.urology.2009.07.1360. S0090-4295(09)02709-5 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schröder FH, Roobol MJ. ERSPC and PLCO prostate cancer screening studies: what are the differences? Eur Urol. 2010;58(1):46–52. doi: 10.1016/j.eururo.2010.03.033. S0302-2838(10)00286-1 [pii] [DOI] [PubMed] [Google Scholar]
- 30.Studer UE, Collette L. What can be concluded from the ERSPC and PLCO trial data? Urol Oncol. 2010;28(6):668–669. doi: 10.1016/j.urolonc.2010.03.011. S1078-1439(10)00067-0 [pii] [DOI] [PubMed] [Google Scholar]
- 31.Croswell JM, Kramer BS, Crawford ED. Screening for prostate cancer with PSA testing: current status and future directions. Oncology (Williston Park) 2011;25(6):452–460. 463. [PubMed] [Google Scholar]