Analysis of ¹⁵N-¹H NMR Relaxation in Proteins by a Combined Experimental and Molecular Dynamics Simulation Approach: Picosecond-Nanosecond Dynamics of the Rho GTPase Binding Domain of Plexin-B1 in the Dimeric State Indicates Allosteric Pathways

Abstract

We investigate ps-ns dynamics of the Rho-GTPase Binding Domain (RBD) of plexin-B1, which plays a key role in plexin-mediated cell signaling. Backbone ¹⁵N relaxation data of the dimeric RBD are analyzed with the model-free (MF) method, and with the slowly relaxing local structure/molecular dynamics (SRLS-MD) approach. Independent analysis of the MD trajectories, based on the MF paradigm, is also carried out. MF is a widely popular and simple method, SRLS is a general approach, and SRLS-MD is an integrated approach we developed recently. Corresponding parameters from the RBD dimer, a previously studied RBD monomer mutant, and the previously studied complex of the latter with the GTPase Rac1, are compared. The L₂, L₃ and L₄ loops of the plexin-B1 RBD are involved in interactions with other plexin domains, GTPase binding, and RBD dimerization, respectively. Peptide groups in the loops of both the monomeric and dimeric RBD are found to experience weak and moderately asymmetric local ordering centered approximately at the ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$ axes, and ns backbone motion. Peptide groups in the α-helices and the β-strands of the dimer (the β-strands of the monomer) experience strong and highly asymmetric local ordering centered approximately at the ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$ axes (N–H bonds). N–H fluctuations occur on the ps time-scale. An allosteric pathway for GTPase binding, providing new insights into plexin function, is delineated.

1. Introduction

Over the last two decades, NMR spin relaxation has effectively revealed the dynamic nature of proteins.^1–7 However, the analysis of the experimental spin-relaxation data per se offers in many cases only partial insight into the details of protein dynamics, as physically realistic dynamic models often contain parameters that cannot be determined from the typically limited experimental data sets. This was realized early on, and a Model-Free (MF) method^8,9 was developed. MF features a small number of generalized parameters that broadly relate to the amplitude (S²) and timescale (τ_e) of ps-ns internal motions, whilst the global motion of the protein is treated separately. The MF approach has become more complex,¹⁰ but the issue of mode separability (as opposed to mode-coupling), as well as the asymmetric nature of the local motions which are not accounted for in MF, stimulated a number of researchers to look for alternative methods.^11–15

The attention of several groups has turned to computer simulations, which can reproduce MF-type generalized order parameters, and even experimental data.^16–19 Combining predictive calculations, such as molecular dynamics (MD) simulations, with experimental relaxation parameters has also become a strategy for interpreting the experimental data (e.g. see refs 20 and 21). However, so far these approaches have not analyzed the relaxation data from a tensorial perspective (required to account for features of asymmetry), and have not accounted for dynamical mode-coupling (the separability concept in ref 20 is based on geometric considerations).

The two-body coupled-rotator approach called slowly relaxation local structure (SRLS) has been developed for comprehensive analysis of molecular motion.^22–24 SRLS can be regarded as the generalization of MF, yielding the latter in simple limits. As applied to NMR relaxation in proteins,^25–28 it allows for general asymmetric properties of the global diffusion of the protein, the local diffusion of the probe, and the local ordering at the site of the motion of the probe. Thus, the restricted local motion is characterized by a local ordering tensor, S, and a local diffusion tensor, D₂. In addition, SRLS accounts rigorously for mode-coupling.

In the last decade, the SRLS approach has been applied extensively to ¹⁵N relaxation data from proteins.^25–28 It emerged as a method that describes protein motions at a physically realistic level, often not achievable with simpler methods such as MF. However, the SRLS calculations are often tedious, the number of parameters to be determined is in some cases large, and the uncertainty in the best-fit parameters determined with data-fitting might be considerable.

To address properly these important matters we developed recently a combined computational-experimental approach that integrates SRLS and MD; we called this method SRLS-MD.²⁹ Similar to SRLS, SRLS-MD describes the restricted local motion in terms of a local ordering tensor, S, and a local diffusion tensor, D₂. The principal values ( $S_0^2$ and $S_2^2$) of S are determined with MD simulations²⁹ extending over tens of ns. The coefficients of the coupling potential derived from these parameters, and known geometric features, are then fixed. This leaves the local diffusion rates, D_2,⊥ and D_2,||, and the orientation of the main ordering axis in the dipolar frame as the only variables in the data-fitting process. Varying only three parameters reduces significantly parameter uncertainty. As shown below, the physically well-defined (fixed and varied) parameters distinguish among loops, α-helices and β-strands. Importantly, they reveal features associated with biological function.

In this report, the briefly delineated SRLS-MD methodology (see ref 29 for details) is applied to ¹⁵N relaxation data from the plexin-B1 Rho-GTPase binding domain (RBD) dimer,^30,31 a protein that exhibits complex dynamics.^32,33 In parallel, these data are also subjected to MF analysis. Finally, MD trajectories of the dimer structure are analyzed in terms of the MF paradigm.

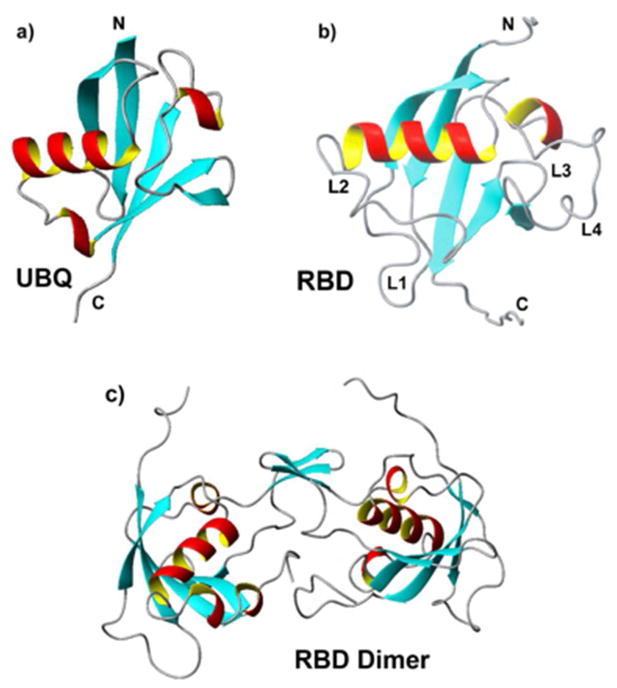
The RBD, which is part of the intracellular region of the plexin-B1 trans-membrane receptor,³⁴ has a fold that is similar to ubiquitin.³⁵ Like ubiquitin (Figure 1a), the RBD comprises a long helix that lies across a five-stranded β-sheet, and a shorter helix located close to the C-terminus (Figure 1b). Unlike ubiquitin, which contains short loops and tight turns that connect secondary structural elements, the RBD contains several long loops, L₁–L₄.^30,35 The L₂ loop (residues K50 – T62) is thought to be important for interactions with neighboring domains.³⁶ The L₃ loop (residues S69 – G73) is involved in Rho-GTPase binding. The L₄ loop (residues L77 – L89) is associated with dimer formation (Figure 1c).

Figure 1.

Ribbon diagram of a) human ubiquitin (PDB ID UBQ), b) the Rho-GTPase binding domain of human plexin-B1 (RBD) (PDB ID 2JPH) with principal loops, L₁–L₄, labeled, and c) the RBD dimer (modeled using the NMR structure of the monomer and X-ray crystallography structure of the dimerization interface, accession code 2R2O).

The plexin-B1 RBD has been associated with the inhibition of receptor function by stabilizing an inactive dimeric state.^31,36 The loop regions, the Rho GTPase binding interface and the dimerization region partly overlap in the dimer structure. It has been shown that GTPase binding and RBD dimerization oppose one another.^31,37 This suggested a model for receptor activation that involves destabilization of the dimeric RBD form by GTPase binding, in synergy with extracellular ligand binding.^31,34,37 Thus, the Rac1-bound form of the monomer may be considered a mimic of the activated receptor. The dynamic properties of the various RBD forms, including the monomer, the dimer and GTPase-bound form are thus of great interest, in particular given the suggestion that an allosteric network is associated with the signal transduction mechanism.^32,38,39

A monomeric form of the RBD, stabilized by the W90F mutation in the L₄ loop,⁴⁰ was studied previously with MF, MD and SRLS-MD.^29,32,33 Several RBD loops of this construct have been shown to be outstandingly mobile. The complex of the monomer mutant with the Rac1 GTPase was also studied previously with MF and MD.^32,33 On the other hand, the wild type dimeric RBD has not been investigated so far. Here, we carried out MD simulations of this RBD form, and analyzed the MD trajectories according to the MF paradigm. Furthermore, we acquired ¹⁵N T₁, T₂ and ¹⁵N–{¹H} NOE at magnetic fields of 14.1 and 18.8 T, and 298 K, and analyzed these data with MF and SRLS-MD.

Our long-term objective is to establish the relation between RBD structural dynamics and plexin function. To this end, we compare herein the MF, MD and SRLS-MD results obtained for the various RBD forms, with particular emphasis on loop dynamics. As shown below, the emerging picture constitutes a significant advancement toward achieving the goal set.

2. Materials and Methods

Sample preparation, NMR experiments and relaxation data analysis

The Rho-GTPase Binding Domain (RBD) of human plexin-B1 comprises residues 1742–1862, and two N-terminal lysine residues (here numbered as residues 1 – 122). This protein was expressed from a pet11a plasmid, and purified as described previously.³⁰ The NMR sample contained 750 μM protein, 4 mM DTT, 4 mM MgCL₂ and 10% (v/v) D₂O in a pH 6.8 buffer that mimics physiological conditions.^{32 15}N longitudinal relaxation rates R₁ = 1/T₁, ¹⁵N transverse relaxation rates R₂ = 1/T₂, and steady-state heteronuclear ¹⁵N–{¹H} NOEs were acquired at 298K on Bruker DRX instruments equipped with cryoprobes, operating at magnetic fields of 14.1 and 18.8 T. Previously developed pulse sequences^41,42 were used.

Eleven R₁ experiments were carried out with delays ranging from 2 to 2000 ms. Eight R₂ experiments were carried out with delays ranging from 12.8 to 153.6 ms. The heteronuclear ¹⁵N–{¹H} NOE was acquired in an interleaved manner, with a 4.5 s long proton saturation period. Recycle delays of 5 s were used in all of the experiments. The spectra were processed using nmrPipe.⁴³ Peak intensities were determined using Sparky.⁴⁴ The resonance assignments obtained previously for the RBD monomer³⁵ were used to assign the RBD dimer. Except for several exchange-broadened resonances in the dimerization interface, the chemical shifts of the monomer are virtually preserved. ¹⁵N R₁ and R₂, and the respective uncertainties based on triplicate experiments for three of the timepoints, were determined with the computer program Curvefit.⁴⁵ Uncertainties in the experimental ¹⁵N–{¹H} NOEs were determined from the baseline noise of the respective NMR spectra.

3. Theoretical Background

3.1. Model-Free

Based on the assumption that the global motion of the protein and the local motion of the probe are independent (i.e., decoupled), the total time correlation function is expressed as:⁸

$$C^t(t)=C^g(t)C^i(t),$$ (1)

where C^t(t) is the total time correlation function, C^g(t) = exp(−t/τ_m) is the time correlation function for global motion, and $C^i(t)=S^2+(1-S^2)exp(-t/{\tau }_e^{\prime })$ is the time correlation function for local/internal motion. τ_m is the correlation time for (isotropic) rotational reorientation of the protein. S² is the squared generalized order parameter defined as the value of Cⁱ(t) at long times. ${\tau }_e^{\prime }=({\tau }_e{\tau }_m)/({\tau }_e+{\tau }_m)$ where τ_e is the effective correlation time for local motion, defined as the area below Cⁱ(t) (required to be exact) divided by (1 − S²). Fourier transformation of eq 1 yields the measurable MF spectral density:⁸

$$J(\omega )=S^2\frac{{\tau }_m}{1+{\tau }_m^2{\omega }^2}+(1-S^2)\frac{{\tau }_e^{\prime }}{1+{\tau }_e^{\prime 2}{\omega }^2}.$$ (2)

If τ_e is much smaller than τ_m, one has ${\tau }_e^{\prime }\approx {\tau }_e$.

The extended MF spectral density (EMF) is given by:¹⁰

$$J(\omega )=S_f^2\left[S_s^2\frac{{\tau }_m}{1+{\tau }_m^2{\omega }^2}+(1-S_s^2)\frac{{\tau }_s^{\prime }}{1+{\tau }_s^{\prime 2}{\omega }^2}\right]+(1-S_f^2)\frac{{\tau }_f^{\prime }}{1+{\tau }_f^{\prime 2}{\omega }^2}.$$ (3)

The parameter ${\tau }_f({\tau }_f^{\prime })$ is the (effective) correlation time for fast local motion. The parameter ${\tau }_s({\tau }_s^{\prime })$ is the (effective) correlation time for slow local motion. $S_f^2$ and $S_s^2$ are squared generalized order parameters associated with these motions. The third term of eq 3 is often omitted under the assumption that ${\tau }_f^{\prime }$ is very small, obtaining thereby the reduced EMF formula.

3.2. Molecular Dynamics

Similar to our study of the RBD monomer,²⁹ we carried out molecular dynamics simulations with the NAMD molecular dynamics package using the all-atom empirical potential energy function CHARMM22 with the CMAP correction.⁴⁶ A 12 Å cut-off for non-bonded forces was used. Long-range electrostatic forces were accounted for with the standard particle-mesh Ewald method. This set-up, depicted in Table S1 of the Supporting Information, is similar to that used in ref 29, with the following new features. First, the RBD dimer was assembled by fusing the NMR structure of the W90F RBD monomer mutant (PDB accession code 2JPH) to the dimerization mini-β-sheet of the dimer X-ray crystallographic structure (PDB accession code 2R2O). The NMR structure was chosen for consistency with previous work,²⁹ because several regions (including the long L₁ loop) are not seen in the electron density map of the dimer crystal structure, and because the extensive loop regions might be affected by crystal contacts. Second, a larger simulation box, with explicit water treated with the TIP3P model, was used. Simulations of 55 ns in length were carried out in quadruplicate, using different seeds to increase sampling efficiency.

To eliminate the global tumbling from the analysis, the snapshots were superimposed on a reference frame, taken as the starting structure. Because the relative orientation of the monomers in the dimer changes slightly in the course of the simulations, the snapshots of each monomer were superimposed on their respective starting structure. S² and τ_e were derived from 5 – 55 ns long segments of the MD trajectories. S² was set equal to the value of Cⁱ(t) for t = 5 ns, as most Cⁱ(t) functions reached a plateau value at that time.

This assessment is based on the following considerations. For residues located in secondary-structure elements, virtually the same results were obtained in the time-regime extending from 5 to 10 ns. For residues located in loops and end-chain segments, convergence at later times is absorbed in most cases by larger errors in S² (see below). The errors in S² were estimated in terms of the differences among MD trajectories differing in their starting values (e.g., see Figure S2 of the Supporting Information). Agreement of the MD-based S² profile with the dimer structure (see below) supports this scheme.

3.3. SRLS-MD

SRLS treats two rotators, protein and probe (given in this case by the N–H bond in the context of the peptide-bond plane), associated with the diffusion tensors D₁ and D₂, respectively.^22–24 The rotators are coupled by a local potential of mean torque, U, which represents the spatial restrictions exerted by the immediate protein surroundings at the site of the motion of the NMR probe.^25–28 The local order parameters (i.e., the principal values of the local ordering tensor, S) are defined in terms of the potential U (see eqs 4 and 5 below). In the limit where the rotators are time scale separated (decoupled), the tensors D₁ and D₂ are isotropic, and the spatial restrictions are either very strong or very weak, axially symmetric, and centered at the Z-axis of all the magnetic tensors taken axial and collinear, one has D₂ = 1/(6τ_e) and ${(S_0^2)}^2=S^2$ (where $S_0^2$ is the axial order parameter). Thus, as already mentioned, in certain limiting cases the SRLS parameters yield the MF parameters.

In the general case, D₁, D₂ and S are rank 2 tensors allowed to have an arbitrary orientation and rhombic symmetry. Dynamical coupling between the rotators is accounted for rigorously.²² Figure 2 illustrates the main features of the SRLS frame scheme (the complete frame scheme appears in Figure 2 of ref 29). Z_D1 is the principal axis of the global diffusion tensor (Figure 2a). The Principal Axes System (PAS) of the local ordering tensor, S, called OF, is distributed with respect to the local director, given in this case by the equilibrium orientation of the N–H bond, NH_eq. The Euler angles Ω_NHeq–OF are the coordinates associated with this distribution; the angle β_NHeq–OF is shown in Figure 2b. The orientation of the OF frame with respect to the dipolar frame, DF, which points along the N-H bond, is given by the Euler angles (α_D, β_D, 0), where γ_D is set equal to 0 because the DF frame is axially symmetric. The orientation of the local diffusion frame with respect to the OF frame is given by the Euler angles (α_O, β_O, 0), where γ_O is set equal to 0 because the D₂ tensor has been taken axially symmetric. Typical values of the angles β_D and β_O are illustrated in Figure 2c. SRLS allows for mutually tilted magnetic ¹⁵N–¹H dipolar and (axial) ¹⁵N chemical shift anisotropy (CSA) tensors.

Figure 2.

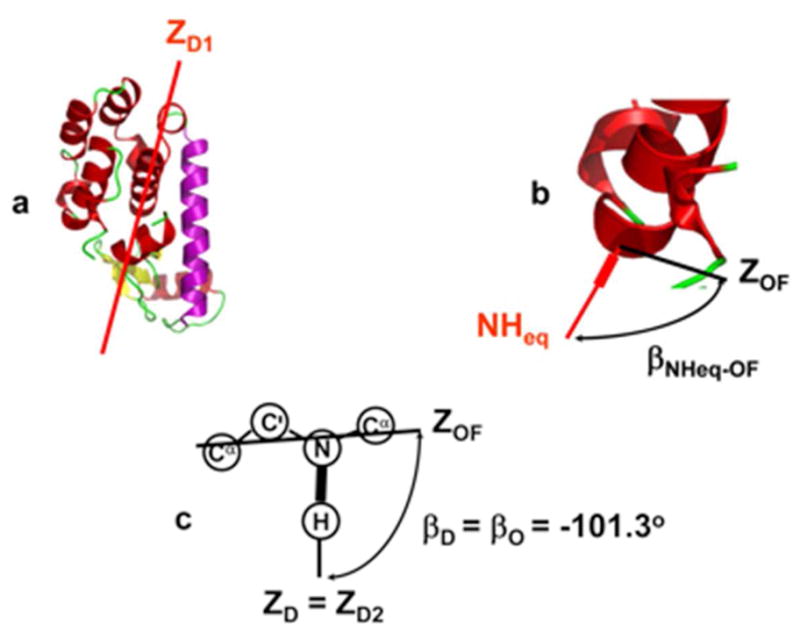
The main features of the SRLS frame scheme depicted on a typical protein structure. Given that SRLS (and its MF limit) relate to the motion of two bodies – the global motion of the protein and the restricted motion of the spin-bearing moiety (the probe) – the coordinate frames of the various tensors are fixed either in the protein, or in the probe. (a) Principal axis of the global diffusion tensor, Z_D1, fixed in the protein. (b) Local director, NH_eq, fixed in the protein. Main local ordering axis, Z_OF, fixed in the probe. The Euler angles Ω _NHeq–OF describe the distribution of the OF frame with respect NH_eq (the angle β _NHeq–OF is shown). (c) Main local ordering axis, Z_OF, principal axis of the local diffusion tensor, Z_D2, and principal axis of the dipolar tensor, Z_D (which points along the N–H bond). All three axes are fixed in the probe. The angles β_D and β_O are shown, with their typical value of −101.3°.

The potential, U(Ω_NHeq–OF), is expanded in the complete basis set of the Wigner rotation matrix elements. When only the lowest (L = 2) terms are preserved, one has:²³

$$\begin{array}{l}u({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})=\frac{U({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})}{k_{\text{B}}T}\\ \approx -c_0^2{D}_{0,0}^2\left({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}\right)-c_2^2\left[D_{0,2}^2\left({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}\right)+D_{0,-2}^2\left({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}\right)\right],\end{array}$$ (4)

where $c_0^2$ evaluates the strength of the local potential, and $c_2^2$ its non-axiality.

The order parameters are defined as:²³

$$\langle D_{0,m}^2({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})\rangle =\frac{\int d{\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}{D}_{0,m}^2({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}){\text{e}}^{-u({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})}}{\int d{\mathrm{\Omega }}_{\text{NHeq}-\text{OF}}{\text{e}}^{-u({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})}}.$$ (5)

For a local director with at least three-fold symmetry and a local ordering frame with at least two-fold symmetry, only the order parameters $S_0^2\equiv \langle D_{0,0}^2({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})\rangle$ and $S_2^2\equiv \langle D_{0,2}^2({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})+D_{0,-2}^2({\mathrm{\Omega }}_{\text{NHeq}-\text{OF}})\rangle$ survive.

In this study, the principal values of the local ordering tensor, $S_0^2$ and $S_2^2$, are derived from MD trajectories. The physical parameters $S_0^2$ and $S_2^2$ can be related to the MF parameter S² (see Supporting Information). The coefficients of the potential, $c_0^2$ and $c_2^2$, are calculated from $S_0^2$ and $S_2^2$ using eq 5, as outlined in ref 29 for the RBD monomer mutant. It was shown that the local potential in terms of which $S_0^2$ and $S_2^2$ are defined constitutes a good approximation to the local potential calculated from the MD trajectory.²⁹ The estimated error in $S_0^2$ and $S_2^2$ is approximately 7%. “Data-fitting” consists of minimizing the sum of the squared differences between corresponding experimental and calculated relaxation parameters divided by the respective experimental error.²⁵ To calculate the magnetic tensor components, the values of r_NH = 1.02 Å and ¹⁵N CSA σ_CSA = −170 ppm, have been used.³² The calculated relaxation parameters are obtained by solving the Smoluchowski equation for the appropriate set of parameters. A typical parameter set includes $c_0^2,c_2^2$, α_D, α_O and β_O fixed, and D_2,⊥, D_2,|| and β_D allowed to vary.

Note that over-fitting is avoided by typically starting the analysis with parameter values corresponding to the MF limit, and adding variables only when the results are not tenable physically. In addition, we ascertain that the variables used are statistically independent.

4. Results and discussion

4.1. Experimental NMR relaxation parameters

¹⁵N R₁, R₂ and {¹H}–¹⁵N NOE data are shown in Figure S1 and are listed in Table S2. Only a single set of resonances is seen in the HSQC NMR spectrum. The fact that the chemical environments in the RBD units are identical indicates that on average the dimer structure is symmetrical. A large part of the dimerization loop, L₄, and part of the α₂ helix are not detected in the HSQC spectrum, most likely because the respective NMR resonances are exchange-broadened beyond detection.

Excluding the terminal chain segments, where ¹⁵N R₁ decreases monotonically, the average ¹⁵N R₁ values are 1.55 and 1.3 s⁻¹ at field strengths of 14.1 and 18.8 T, respectively. The average ¹⁵N R₂ values for the secondary structure elements are 18.0 and 22.5 s⁻¹ at 14.1 and 18.8 T, respectively. The loops, in particular L₁ and L₃, and the terminal chain segments, have significantly smaller ¹⁵N R₂ values. Such clear ¹⁵N R₂-based discrimination between secondary structure elements and loops is associated with complex internal (most likely loop-related) dynamics. Most globular proteins do not contain long loops. Plexin-B1 RBD is quite unusual in this respect. The average ¹⁵N–{¹H} NOE values for the secondary structure elements are 0.85 and 0.95 at 14.1 and 18.8 T, respectively. The loops L₁ and L₃ are associated with substantially smaller NOEs. In the L₂ loop, the NOEs are similar to the average NOE of the secondary structure elements.

4.2. MF analysis

Global motion

The computer program RotDif,⁴⁷ which employs experimental ¹⁵N R₂/R₁ ratios of “rigid” N–H bonds (i.e., N–H bonds that experience negligible local motion) and a 3D structure, was applied. The NMR structure of the RBD monomer was used to assemble the dimer structure (see above). This initial analysis yielded a global correlation time, τ_m, of 9.8 – 10.8 ns and a ratio A = D_1,||/D_1,⊥ of 1.14 – 1.21 for the extent of axiality of the global diffusion tensor. These parameters are similar to the corresponding parameters for the monomer, where τ_m = 8.6 ± 0.4 ns and A =1.26 ± 0.12.³² This result is difficult to rationalize, given the differences in size between the two forms of the RBD. Furthermore, the complete ¹⁵N relaxation data set of the dimer form could not be fit with the MF-based computer program “Dynamics”^48,49 with these values of τ_m and A. It could be fit with τ_m = 16.5 ± 0.83 ns and A ~ 1. This value of τ_m is consistent with the size of the dimer. A ~ 1 is consistent with relatively fast monomer fluctuations in the dimer, implied by mobility at the monomer-monomer interface. On average, this yields a spherical solution structure that differs from the non-spherical crystal structure. A similar scenario was encountered for the RBD monomer, as discussed in detail in ref 29, and for the proteins E. coli adenylate kinase and the ribonuclease binase.^27,28 Since approximately 90% of the protein is in its dimeric state, we ignore effects associated with the monomer-dimer equilibrium (analysis of the data in terms a monomer-dimer equilibrium, as described by Fushman,⁴⁸ did not yield substantially improved results). Based on the evidence and considerations outlined above, we used isotropic global diffusion with τ_m = 16.5 ± 0.83 ns in all of the calculations described below.

Local motion

The squared generalized order parameter, S², derived by the MF approach, is interpreted as amplitude of local N–H motion with values ranging from 0 (unconstrained motion of the N–H bond) to 1 (N–H bond fixed in the protein).^8,9 The program Dynamics^48,49 was used to analyze the data shown in Figure S1. This data-fitting scheme features four models based on the MF formula (eq 2), and four models based on the EMF formula (eq 3). Out of 99 N–H bonds accessible with ¹⁵N relaxation measurements, 51% were fit with model 1 (only S² allowed to vary in the data-fitting process), 19% with model 2 (S² and τ_e allowed to vary), and 25% with model 5 ( $S_s^2,S_f^2$, and τ_s allowed to vary). The best-fit values obtained are given in Table S3. A conformational exchange contribution (to R₂), R_ex, of 7.0 s⁻¹ was required for residue T83. For the monomer, N–H bonds located near to, or within, the dimerization L₄ loop, required R_ex contributions.

SRLS accounts for conformational exchange contributions in the same manner as MF – by adding a R_ex term to the expression for 1/T₂. When R_ex is large, hence the credibility of conformational exchange is high, we exclude the respective N–H bond from the analysis. There is a one such case for the dimer – T38. MF found smaller R_ex contributions for several residues of the monomer. SRLS ascribed to these residues (as it did for most residues) anisotropic spatial restrictions (Figure 5) and realistic local geometry (Figure 7), rationalizing thereby the augmented experimental 1/T₂ values.

Figure 5.

Best-fit values of the order parameters $S_0^2$ (a) and $S_2^2$ (b) obtained for the RBD monomer mutant (black circles) and the RBD dimer (red squares) with MD simulations, as described in the text. The black bars on the right denote the average error of 7% in $S_0^2$ and $S_2^2$.

Figure 7.

Best-fit values of the Euler angle α_D (a), β_D (b), α_O (c) and β_O (d) obtained for the RBD monomer mutant (black circles) and the RBD dimer (red squares) with SRLS-based data-fitting, as described in the text. The average error of 10% does not exceed the symbol height.

S² is shown in Figure 3a for both the monomer and the dimer. For the secondary structure elements, the monomer values exceed the dimer values by 0.05 – 0.08. The largest differences are observed for the β₁ and β₅ strands, the α₂ helix and the tight β₂/α₁ turn. For the loops, S² for the dimer is similar to S² for the monomer. The dimer shows quite a few sporadic spikes, which are not seen in the corresponding MD-derived S² profiles (Figure 4a). While these features may result from a number of sources, including fixed N–H bond lengths and ¹⁵N CSA,⁵⁰ we ascribe them primarily to the utilization of oversimplified MF spectral densities incommensurate with the dynamic complexity of the plexin-B₁ RBD.

Figure 3.

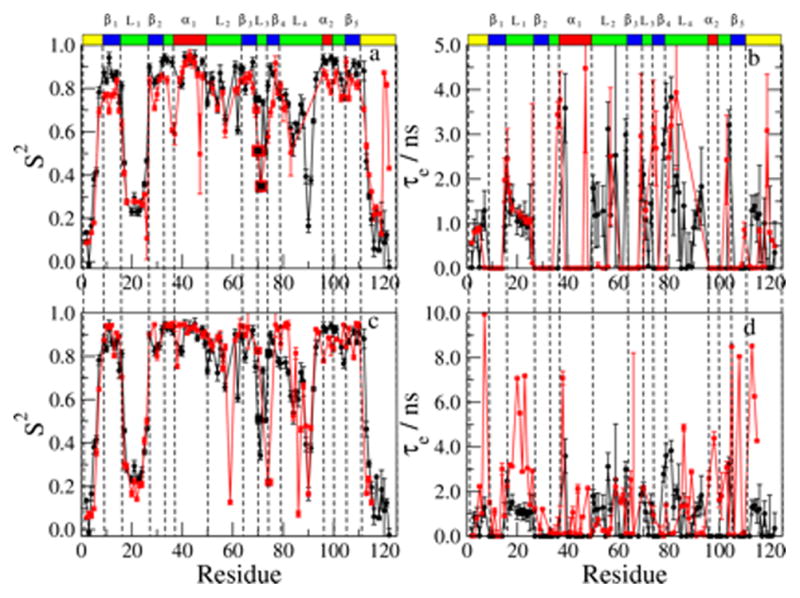
Best-fit values of S² and τ_e obtained with MF analysis. (Note that both τ_e and τ_s are denoted τ_e) S² (a) and τ_e (b) for the RBD monomer mutant (black circles) and dimer (red squares). S² (c) and τ_e (d) for the RBD monomer mutant (black circles) and its complex with the Rac1 GTPase (red squares). The data for the monomer mutant and its complex with the Rac1 GTPase were taken from ref 32.

Figure 4.

Average S² (a) and τ_e (b) values obtained with MD simulations for the RBD dimer as outlined in the text (shown as red squares). Average S² and τ_e values obtained with MD simulations for the RBD monomer mutant are shown as black circles for comparison. The data of the monomer mutant were taken from ref 32.

The effective correlation time for local motion is shown in Figure 3b for both RBD forms. As mentioned above, the experimental data were fit predominantly with models 1, 2 and 5. Model 1 pre-sets τ_e = 0, model 2 is expected to yield τ_e ≪ τ_m (i.e., ps τ_e values), and model 5 is expected to yield ns τ_e values (in this case, “τ_e” denotes “τ_s”; the same symbol is used to facilitate comparison with the similarly derived MD local motional correlation times). In practice, except for the terminal chain segments, model 2 yielded (similar to model 5) effective local motional correlation times on the order of several ns. Altogether, 50% of the N–H sites, including virtually all of the secondary structure elements and quite a few N–H bonds located in the L₂ and L₃ loops and the terminal chain segments, were fit with model 1. The remainder of the polypeptide chain, including L₁, parts of L₂ and L₃, and part of the terminal chain segments, has τ_e in the 0.5 – 4.5 ns range.

In general, the correlation times for local motion are somewhat larger for the dimer as compared to the monomer. In particular, the N-, and C-terminal chain segments and the L₁ and L₃ loops have similar, or slightly larger, τ_e values for the dimer. The L₂ loop, comprising residues K50 – T55, wraps around one side of the protein. While the S² values for the dimer and the monomer are similar in this loop, ns local motions are only experienced by the monomer.

Figure 3c shows the S² values for the monomer, superimposed on the S² values for its complex with the Rac1 GTPase (re-plotted from ref 32). In general, the differences between monomer and complex (Figure 3c) are small; they are smaller than the differences between monomer and dimer (Figure 3a). The L₃ loop, associated with GTPase binding, is an exception. For example, the S² values of G70 and A72 are substantially larger for the complex than for the monomer (Figure 3c); the corresponding differences between dimer and monomer are within experimental error. This is consistent with the fact that residues G70 and A72 are not part of the dimerization interface.

The τ_e values for the monomer and the RBD-Rac1 complex are shown in Figure 3d. Similar to the τ_e data for the dimer, the τ_e data for the complex show a large number of spikes. For quite a few residues of the L₁ loop, τ_e for the complex exceeds significantly τ_e for the monomer. This indicates that the L₁ loop is affected considerably by Rac1 binding. By contrast, the τ_e values for the dimer are virtually the same as the corresponding values for the monomer (Figure 3b).

The N-terminal part of the L₂ loop (residues K50 – T55) experiences significantly larger changes in τ_e upon dimerization than upon Rac1 binding. A similar pattern was observed for changes in S². This is interesting, since the chain segment K50 – T55, as well as the L₁ loop, are at considerable distance from both the dimerization interface and the GTPase binding site.

4.3. MD analysis

The squared generalized order parameter, S², and the effective correlation time for local motion, τ_e, were derived from time correlation functions as described in section 2. They are shown superimposed on the corresponding monomer data in Figure 4. In the secondary structure elements, corresponding S² values are virtually the same. In the L₄ loop and the first part of the L₂ loop, S² for the dimer is larger than S² for the monomer. In much of the L₁ loop and the terminal chain segments, S² for the dimer is smaller than S² for the monomer. Unlike the MF-based S² profile, the MD-based S² profile does not show sporadic spikes along the sequence.

The MD-derived τ_e values range from 0.2 to 1.8 ns (Figure 4b). Within the first part of the L₂ loop, τ_e for the dimer is on average smaller than τ_e for the monomer. This is consistent with the changes in S², indicating reduced (faster smaller-amplitude) fluctuations. In the C-terminal segment of the polypeptide chain, τ_e for the dimer is larger than τ_e for the monomer. In the L4 loop, τ_e for the dimer is substantially smaller than τ_e for the monomer.

The precision of the MD-derived parameters is low (see Figure S2). However, both S² and τ_e are consistent with the secondary structure of the RBD and the location of its loops. Upon dimerization the L₄ loop, which forms the interface between the monomer units in the dimer, becomes more rigid (larger S²) and less mobile (smaller τ_e). On the other hand, in the C-terminal segment of the L₁ loop S² is smaller for the dimer. One might conjecture that dimerization is accompanied by an allosteric mechanism involving loop regions of compensating rigidity and mobility.

The MD analysis features several important benefits versus the MF analysis. Thus, the MD analysis treats all of the N–H bonds in the same manner employing a single correlation function form. In comparison, the MF analysis, applied to the experimental data, uses several different models (predominantly 1, 2 and 5), i.e., employs several different spectral density functions. The MD analysis eliminates the global motion consistently based on a specific procedure. In comparison, the MF analysis models the global motion using filtered experimental data; this procedure is based on empirical filtering criteria. Finally, the MF analysis is prone to force-fitting (good statistics but inaccurate best-fit parameters, which have absorbed unaccounted for factors). As pointed out above, force-fitting accounts at least for some, if not the majority, of the sporadic spikes visible in Figure 3. Nevertheless, MF is useful in comparing (qualitatively) results from different systems (see below).

4.4. Comparison between MF and MD analyses

It is useful to compare corresponding MF (Figure 3) and MD (Figure 4) parameters. Superimposed S² and τ_e τ_e profiles for the monomer and the dimer are shown in Figure S3, after having eliminated sporadic spikes from the MF data. For the monomer, the S² profiles from MF and MD analyses are generally similar. Relatively small differences are observed in the C-terminal regions of the L₁ and L₄ loops, and the C-terminal chain segment. They can be ascribed to limited sampling of the MD trajectories (shown in Figure S2) and/or force-fitting in the MF analysis. For the dimer, the S² profiles from MF and MD are virtually the same, except for small differences in the C-terminal chain segment. The τ_e profiles from MF (also shown in Figure 3b) differ from their counterparts from MD (also shown in Figure 4b). MD yields τ_e of 1 – 3 ns for the loops (except for L₂) and terminal chain segments, and τ_e of 0.2 – 0.8 ns for the secondary structure elements. For the latter MF yields mostly τ_e = 0; these values are clearly artefactual. Quite remarkably, for the L₁ loop τ_e from MF is similar to τ_e from MD. For the L₂ loop MF yields irregular τ_e patterns for the monomer and τ_e = 0 for the dimer.

The features delineated above indicate that more elaborate methods of analysis are required to extract fully and properly the information inherent in the experimental data. We show below that significant progress is made along these lines by using SRLS-MD as method of analysis.

SRLS-MD analysis

The global diffusion was taken isotropic with τ_m = 16.5 ns (see above).

Local ordering

In the first step of the analysis, $S_0^2$ and $S_2^2$ are derived from the MD trajectories, as described briefly in section 2, and in detail in ref 29. $S_0^2$ is a physical measure of local ordering strength and $S_2^2$ is a physical measure of local ordering rhombicity (asymmetry). To calculate $S_0^2$ and $S_2^2$ using eq 5 one has to define the Euler angles Ω_NHeq–OF = (α_NHeq–OF, β_NHeq–OF, 0). NH_eq is given by the N–H orientation in the 3D (reference) structure. The orientation of the OF frame with respect to the known dipolar tensor frame, DF, is given by the Euler angles Ω_OF–DF = (α_D, β_D, 0). In previous SRLS studies of ¹⁵N spin relaxation in proteins,^26–28 we found with data-fitting that β_D = −101.3°. This corresponds to the main axis of the local ordering tensor, Z_OF, pointing along ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$. Main local ordering axes parallel to ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$ are encoded in other methods of ¹⁵N relaxation analysis, such as the 3D Gaussian Axial Fluctuations model.¹⁴ Crankshaft backbone motions revealed by MD studies⁵¹ are consistent with ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$ acting as main ordering axis. Based on these considerations, we set β_D = −101.3° and α_D = −90° (consistent with the stereo-chemistry of the peptide-bond plane) in the calculation of $S_0^2$ and $S_2^2$

In the next step of the analysis, $c_0^2$ and $c_2^2$ are calculated as described in ref 29 from $S_0^2$ and $S_2^2$ based on eqs 4 and 5. Thus, the MD component of the SRLS-MD analysis provides for every experimentally accessible N–H bond the parameters $c_0^2$ and $c_2^2$, which are used as fixed input to the SRLS-based data-fitting calculation. Additional parameters that are pre-set in this calculation include α_O = β_O = −90° (α_O and β_O define the orientation of the D₂ tensor with respect to the S tensor). In the SRLS frame scheme, this corresponds to the principal axis of D₂ pointing along the N–H bond, which is a physically tenable geometric scenario.

Thus, only the local diffusion rates, D_2,⊥ and D_2,||, and the tilt angle, β_D, between the principal axes of the local ordering and dipolar tensors, are left as variables in the data-fitting calculation. With β_D = −101.3° as starting value, this scheme yielded good statistics for approximately 75% of the data. For the remaining 25% of the data, to obtain good statistics we also allowed α_D, α_O and β_O to vary from starting values of −90°. Two cycles of optimization, allowing the set D_2,⊥, D_2,|| and β_D and the set α_D, α_O and β_O to vary sequentially, were carried out. The best-fit values obtained are given in Tables S4 and S5.

The order parameters $S_0^2$ and $S_2^2$ are shown in Figure 5. The axial order parameter, $S_0^2$ (Figure 5a), is negative. $S_0^2$ values approaching −0.5 correspond to strong perpendicular ordering. This agrees with the angle β_D being in most cases close to −101.3° (see Table S5), representing a main ordering axis approximately perpendicular to the local director (NH_eq). Except for the C-terminal chain segment, where the monomer exhibits stronger ordering that the dimer, the two RBD forms exhibit similar ordering strength. In general, the local ordering is strong in the secondary structure elements and substantially weaker in the loops and the terminal chain segments. In particular, very strong and uniform local ordering prevails in the α₁ and α₂ helices, and the β₁, β₃ and β₅ strands.

Weaker and quite diversified local ordering prevails in the β₂ and β₄ strands, which are adjacent to the C-termini of the L₁ and L₃ loops, respectively. Thus, the ordering properties of the L₁ and L₃ loops extend to their C-terminal secondary structure neighbors. This finding agrees with the fact that the β₂ and β₄ strands are located at the exterior of the protein, with every other N–H group facing the solvent. This spatial disposition is likely to impart to the β₂ and β₄ strands ordering properties akin to flexible loops. The L₁ loop, and for the monomer the L₄ loop, exhibit similar $S_0^2$ patterns, with the weakest ordering occurring in their middle. A different $S_0^2$ pattern is observed for the L₂ and L₃ loops, where the weakest ordering occurs near the N-, and C-termini, respectively. The local ordering at the N–H sites of the L₂ loop and the C-terminal chain segment is weaker in the dimer as compared to the monomer. Thus, insightful information on the strength of the local ordering is provided by the SRLS-MD analysis.

The rhombic order parameter, $S_2^2$, is shown in Figure 5b. The largest theoretical value of $\mid S_2^2\mid$ is $\sqrt{1.5}$. Negative $S_2^2$ means (in the SRLS frame scheme) that ordering perpendicular to the peptide-bond plane is preferential to ordering along the N–H bond. $\mid S_2^2\mid$ is large and quite uniform in the α-helices and most β-strands, and relatively small in the L₁ and L₃ loops, and for the monomer also in the L₄ loop. For both RBD forms, the central part of the L₂ loop exhibits relatively large rhombicity, comparable to that of the secondary structure elements.

The following comment is in order. The MF-versus-MD comparison based on the squared generalized order parameter is illustrated in Figure S3. An analogous SRLS-versus-MD comparison is not feasible because SRLS provides the axial, $S_0^2$, and rhombic, $S_2^2$, components of the local ordering tensor, S, whereas MD provides the squared generalized order parameter, S². However, it is appropriate to compare distribution functions, P_eq. We carried out a detailed comparison in this spirit for the monomer mutant.²⁹ Figure 8 of that article shows that the potential of eq 4, which describes the spatial restrictions at the site of the motion of the N–H bond, is a good approximation to the corresponding part of the CHARMM potential energy function used in the MD simulations. This result also applies to the plexin-B1 dimer, as it relates to the local spatial restrictions at the N–H sites of the plexin-B1 RBD.

Figure 8.

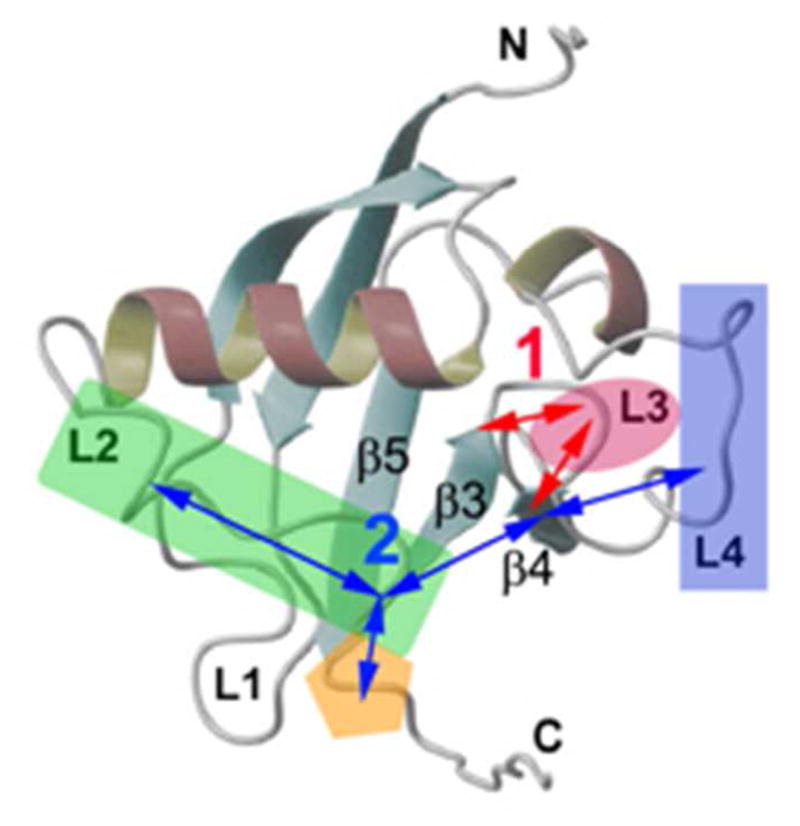
Illustration of allosteric pathways that are suggested by this study of RBD mainchain dynamics. The RBD is shown as ribbon diagram, as in Figure 1. Possible pathways 1 and 2 are shown. Dimerization engages pathway 1 (L₄ to β₄, L₂ and C-terminus), whereas GTPase binding (associated with the L3 loop) engages both pathway 1 and 2 (entropy compensation occurs between L3 and surrounding regions, e.g., the termini of β₃ and β₄).

The axial, $c_0^2$, and rhombic, $c_2^2$, coefficients of the SRLS potential of eq 4 are derived from $S_0^2$ and $S_2^2$ (eq 10 of ref 29). For strong local ordering the components of the local ordering tensor can be determined with higher accuracy than the coefficients of the local potential.^26,27 The errors in $S_0^2$ and $S_2^2$ were estimated at 7% (see above, and caption of Figure 5). Based on previous work,^26,27 we estimate the errors in $c_0^2$ and $c_2^2$ at 10%. Further discussion of error estimation in SRLS-based data-fitting, in general, appears in refs 26 and 27.

Local diffusion

Figure 6a shows the logarithm of the best-fit values of D_2,⊥. This represents slow backbone motion, comparable to the global tumbling. On the right we show corresponding values of τ_2,⊥ = 1/(6 D_2,⊥)^*. Several log(D_2,⊥) values within the β-strands are smaller than log(D₁); further studies are required to clarify this matter. Within the L₁, L₂ and L₃ loops and the C-terminal chain segment, log(D_2,⊥) is approximately 7.5. This corresponds to a correlation time, τ_2,⊥, of 5 ns, which is approximately 3 times faster than the correlation time for global tumbling of 16.5 ns. log(D_2,⊥) is increased relative to D₁ in the L₂ loop and for several N–H bonds located near the C-terminus of the polypeptide chain. This indicates that relatively fast ns backbone motions occur at these sites.

Figure 6.

Best-fit values of the local motional rates, D_2,⊥ (a) and D_2,|| (b), obtained for the RBD monomer mutant (black circles) and the RBD dimer (red squares) with SRLS-based data-fitting, as described in the text. On the right we show the correlation times, τ_2,⊥ = 1/(6 D_2,⊥) and τ_2,|| = 1/(D_2,||), that correspond to typical diffusion rate values, D_2,⊥ and D_2,||. The error in the motional rates D_1, D_2,⊥ and D_2,|| is estimated at 10%.

The logarithm of D_2,||, which represents N–H fluctuations, is shown in Figure 6b. The dynamic range of this parameter is large. The N–H fluctuations are particularly fast in the α₁ helix and the β₁, β₃ and β₅ strands, where <τ_2,||> = <1/(6 D_2,||)> ~ 10 ps. The strands β₁, β₃ and β₅ represent the core of the protein; fast N–H fluctuations are consistent with a relatively rigid core. The correlation time τ_2,|| is on average 50 ps for the L₁ loop and particularly large for the β₂ strand and most of the L₂ loop, where <τ_2,||> = 1 ns.

Clearly, SRLS provides insightful information on local motional modes in the plexin-B1 RBD.

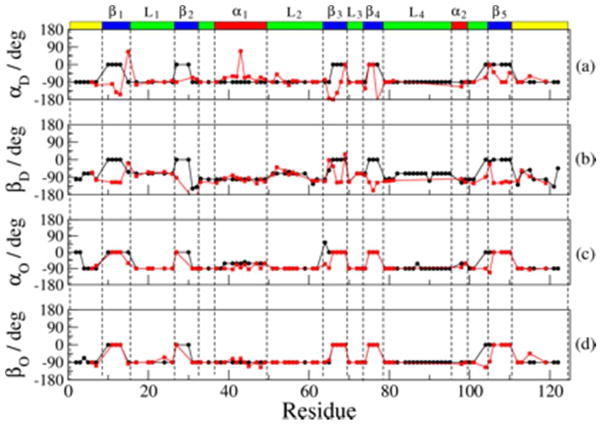
Local geometry

The angles α_D and β_D (S tensor orientation) and α_O and β_O (D₂ tensor orientation) constitute what we call “the local geometry”. These parameters are shown in Table S5, and are depicted pictorially in Figure 7. For the dimer, α_D is close to −90° (Figure 7a) and β_D is close to −101.3° (Figure 7b), indicating that ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$ is, within a good approximation, the main local ordering axis. For the monomer, β_D is zero for many β-strands, indicating that the main local ordering axis points along the N–H bond. For both the monomer and the dimer, α_O = β_O = −90° for the α-helices and the loops, and α_O = β_O = 0 for the β-strands (Table S5 and Figures 7c,d). That SRLS-MD reveals differences in the local geometry between monomer and dimer is of particular interest. The diversity of tensor orientations in the β-strands is more extensive for the monomer than for the dimer, in particular near their N- and/or C-termini. This suggests the establishment of geometric regularity by long-range allosteric effects associated with dimerization. Note that in MF and MF-based MD analyses, α_D = β_D = α_O = β_O = 0 is implicit. Hence, these methods cannot provide information on features of local geometry.

4.6. Allosteric pathways for GTPase binding and dimerization revealed by N–H bond dynamics

A pictorial representation appears in Figure 8. As pointed out above, the RBD dimer is associated with the stabilization of inactive receptor states^31,34 whereas the Rac1-bound form of the monomer may be considered a mimic of the activated receptor. Two regions of the protein structure are of particular interest in this context. They include the GTPase binding region (the L₃ loop, colored magenta in Figure 8) and the dimerization region (mainly the L₄ loop, colored blue in Figure 8). Although the C-terminal part of L₄ is not detected with ¹⁵N relaxation experiments, both X-ray crystallography and MD describe it as relatively rigid. By contrast, the L₃ loop, associated with GTPase binding, is substantially more flexible in the dimer (and monomer) as compared to the RBD-GTPase complex. This is evident by examining the S² profiles obtained with MF and MD (Figures 3c and 4a). The regions flanking the L₃ loop are more rigid in the dimer. Proceeding toward the N-, and C-termini of the polypeptide chain, one encounters chain segments that are more flexible in the dimer (e.g., the β₁ and β₅ strands and the a₂ helix).

In this context, “flexibility” is substantiated as follows by the SRLS-MD analysis. On average, the L₃ loop of the dimer exhibits the strongest local ordering (largest $\mid c_0^2\mid$), the smallest potential rhombicity (smallest $\mid c_2^2\mid$) (Table S4), the slowest backbone motion (smallest D_2,⊥), and the slowest N–H fluctuations (smallest D_2,||) (Figure 6) among all of the RBD loops. Thus, despite the relatively strong and nearly axial local restrictions experienced, the N–H bonds of loop L3 move relatively slowly both at the collective-backbone level, and at the individual-local level. This might be associated with the nature of their surroundings (cf. Figure 8).

The β₄ strand, which flanks the L₃ loop at its C-terminus, represents the “intersection” between the allosteric pathways 1 and 2 depicted in Figure 8. The local ordering is strong and rhombic in this β-strand. It decays to weak and nearly axial ordering in the C-terminal chain segment. The local ordering is also strong and rhombic in the β₃ strand, which flanks L₃ at its N-terminus. This β-strand is part of the allosteric pathway 1. The decay to weak and nearly axial ordering in the N-terminal chain segment occurs through oscillations between weak and moderately rhombic ordering in L₁, L₂ (colored green in Figure 8) and L₃, and strong and substantially rhombic ordering in α₁, β₁ and β₂. The N–H fluctuations (D_2,||), which are limited in L₃, are substantial in β₅ (toward the C-terminus) and β₃, α₁, L₁ and β₁. Dips in D_2,|| can also be seen in L₂ and β₂. The L₃ loop and the β₃ strand are associated with the allosteric pathway 1. SRLS-MD provides an insightful (mesoscopic) description of the structural dynamics of the dimeric RBD form.

Based on this analysis, we conjecture that the GTPase binds to the RBD dimer at an entropically favored site – the flexible L₃ loop – through a mechanism that involves an allosteric pathway that appears to materialize through variations in rigidity. Thus, the entropy lost at the L₃ loop is regained in other regions of the protein, in the manner specified above. This mechanism requires further support. However, other authors have described similar scenarios in the context of protein-protein interactions (cf. refs 32, 52–54).

Let us examine the implications of the MF analysis in the context of allostery. We have shown previously that Rac1 binding affects the dynamic state of the L₂ loop, despite this region being a great distance away from the GTPase binding site.³² The L₂ loop (Figure 8) is also affected by RBD dimerization, with ns motion experienced by the monomer being quenched by this process. MD simulations reveal substantial changes in S² and τ_e upon dimer formation (cf. L₄ loop in Figures 4 and 8). Another region that shows (complex) differences between monomer and dimer is the chain segment comprising residues 112 – 116, flanking the β₅ strand at its C-terminus (colored orange in Figure 8). Here, the polypeptide chain is fluctuating with increasing speed as it emerges from the tightly packed region of the RBD structure. Local motions on the ns time scale are no longer encountered, as shown by the τ_e values, and further elaborated by the SRSL local motional component D_2,⊥.

The local ordering in the L₂ loop and at the C-terminus of the polypeptide chain are relatively weak in both RBD forms (Figures 5 and 8). The tensor orientations are largely similar (Figures 7 and 8), and the motions captured by D_2,⊥ are quite a bit faster for the dimer (Figures 6 and 8). These results point to an allosteric change that is largely dynamic in nature, without substantial alteration of the local geometry/structure.^55–58 This finding is consistent with the lack of chemical shift perturbations in this region, revealed by comparing NMR spectra of the monomer and the dimer.⁴⁰

We may speculate about allosteric features/biological function emerging from this study as follows. Changes per se in L₃ are implied exclusively by GTPases binding. However, they correlate with long-range dynamic chances in other regions of the protein, extending up to the L₂ loop (pathway 2 in Figure 8). In addition, entropy compensation occurs between L₃ and the termini of the β₃ and β₄ strands (pathway 1 in Figure 8). Dimerization has no effect on L₃, possibly because this region still has to be available for binding the GTPase. The latter process is likely to be the first step of a mechanism that destabilizes the dimer (indeed, a dimeric GTPase-bound form has been crystallized³⁶). Both dimerization and more so GTPase binding have an allosteric effect on L₂, rigidifying this loop (pathway 2 in Figure 8, involving both L₄ and L₃). As mentioned above, this region of the RBD domain is of particular importance, as it makes contacts with the adjacent catalytic domains of plexin-B1. Further studies, including molecular dynamics simulations of the GTPase-bound state, are required to ascertain the validity of the allosteric mechanism described above.

5. Conclusions

Picosecond-nanosecond structural dynamics of the RBD of plexin-B1 in monomeric, dimeric and GTPase-bound forms has been investigated with ¹⁵N relaxation analyzed with the MF and SRLS-MD methods. Traditional MD simulations have also been carried out. The MF and MD analyses provide a semi-quantitative picture singling out the loops as being more flexible than the secondary structure elements. The MD analysis shows that upon dimerization a monomer-monomer interface with increased rigidity and reduced ns mobility is generated. SRLS-MD describes structural dynamics at every N–H site in terms of a rhombic local ordering tensor, S, and an axial local diffusion tensor, D₂. The former connotes “structure” and the latter connotes “motion”.

The local ordering is described by the physical order parameters, $S_0^2$ and $S_2^2$, in the context of realistic geometry of main ordering axis pointing along ${\text{C}}_{\text{i}-1}^{\alpha }-{\text{C}}_{\text{i}}^{\alpha }$. $S_0^2$ represents ordering strength and $S_2^2$ represents ordering rhombicity. The local diffusion is described by the components D_2,⊥ and D_2,|| of the local diffusion tensor, D₂, the principal axis of which is in most cases parallel to the N–H bond. D_2,|| represents fast, but not necessarily very fast, N–H fluctuations. D_2,⊥ represents ns backbone motion coupled automatically to the global tumbling. The $S_0^2,S_2^2$, D_2,⊥ and D_2,|| profiles are highly discriminating. An allosteric pathway that communicates GTPase binding and dimerization to other regions of the protein is revealed by these physical descriptors.