Quantum erasure with causally disconnected choice

Abstract

The counterintuitive features of quantum physics challenge many common-sense assumptions. In an interferometric quantum eraser experiment, one can actively choose whether or not to erase which-path information (a particle feature) of one quantum system and thus observe its wave feature via interference or not by performing a suitable measurement on a distant quantum system entangled with it. In all experiments performed to date, this choice took place either in the past or, in some delayed-choice arrangements, in the future of the interference. Thus, in principle, physical communications between choice and interference were not excluded. Here, we report a quantum eraser experiment in which, by enforcing Einstein locality, no such communication is possible. This is achieved by independent active choices, which are space-like separated from the interference. Our setup employs hybrid path-polarization entangled photon pairs, which are distributed over an optical fiber link of 55 m in one experiment, or over a free-space link of 144 km in another. No naive realistic picture is compatible with our results because whether a quantum could be seen as showing particle- or wave-like behavior would depend on a causally disconnected choice. It is therefore suggestive to abandon such pictures altogether.

Wave–particle duality is a well-known manifestation of the more general complementarity principle in quantum physics (1). Several single-photon experiments (2–6) confirmed both the wave and the particle nature of light. Another manifestation of complementarity is that the position and linear momentum of individual particles cannot be well-defined together as highlighted in Heisenberg’s uncertainty relation (7). Based on the concept of the Heisenberg microscope (7), von Weizsäcker (8, 9) discussed the gedanken experiment in which a photon interacts with an electron. In today’s language, after the interaction the photon and the electron are in an entangled state (10, 11) in which their positions and momenta are strongly correlated. Therefore, different complementary measurements on the photon allow choosing whether the electron acquires a well-defined position or a well-defined momentum. According to Bohr, “it obviously can make no difference as regards observable effects […] whether our plans of constructing or handling the instruments are fixed beforehand or whether we prefer to postpone the completion of our planning until a later moment […]” (p 230, ref. 1).

Wheeler later proposed an experiment on wave–particle duality in which the paths of a single photon, coming from a distant star, form a very large interferometer (12, 13). Inserting or not inserting a beam splitter at the end of the interferometer’s paths will allow one to either observe interference (wave behavior) or acquire path information (particle behavior), respectively. Wheeler proposed to delay the choice of whether or not to insert the beam splitter until the very last moment of the photon’s travel inside the interferometer. This rules out the possibility that the photon knew the configuration beforehand and adapted its behavior accordingly (*, 14). He then pointed out the seemingly paradoxical situation that it depends on the experimenter’s delayed choice whether the photon behaved as a particle or a wave. In Wheeler’s words: “We, now, by moving the mirror in or out have an unavoidable effect on what we have a right to say about the already past history of that photon” (13). Since then, Wheeler’s proposal has led to several experimental studies with single-photon interference (†, ‡, 15–19), which provided increasingly sophisticated demonstrations of the wave–particle duality of single quanta, even in a delayed-choice configuration.

Scully and Drühl proposed the so-called quantum eraser (20), in which maximally entangled atom–photon states were studied. In ref. 21, the atoms, which can be interpreted as the “system,” are sent through a double slit. Each atom spontaneously emits a photon, which can be regarded as the “environment,” carrying welcher-weg (which-path) information on which of the two slits the atom takes. No interference pattern of atoms will be obtainable after the double slit, if one ignores the presence of the photons, because every photon carries the welcher-weg information about the corresponding atom. The presence of path information anywhere in the universe is sufficient to prohibit any possibility of interference. It is irrelevant whether a future observer might decide to acquire it. The mere possibility is enough. In other words, the atoms’ path states alone are not in a coherent superposition due to the atom–photon entanglement.

If the observer measures the photons, his choice of the type of measurement decides whether the atoms can be described by a wave or a particle picture. First, when the photons are measured in a way that reveals welcher-weg information of the atoms, the atoms do not show interference, not even conditionally on the photons’ specific measurement results. Second, if the photons are measured such that this irrevocably erases any welcher-weg information about the atoms, then the atoms will show perfect but distinct interference patterns, which are each other’s complement and are conditioned on the specific outcomes of the photons’ measurements. These two scenarios illustrate a further manifestation of the complementarity principle, in addition to the wave–particle duality. There is a tradeoff between acquiring the atoms’ path information or their interference pattern via complementary measurements on the photons and not on the atoms themselves. A continuous transition between these two extreme situations exists, where partial welcher-weg information and interference patterns with reduced visibility can be obtained (22, 23).

The authors of refs. 20 and 21 proposed to combine the delayed-choice paradigm with the quantum eraser concept. Because the welcher-weg information of the atoms is carried by the photons, the choice of measurement of the photons—either revealing or erasing the atoms’ welcher-weg information—can be delayed until “long after the atoms have passed” the photon detectors at the double slit (p 114, 21). The later measurement of the photons “decides” whether the atoms can show interference or not, even after the atoms have been detected. This seemingly counterintuitive situation comes from the fact that in a bipartite quantum state the observed correlations are independent of the space–time arrangement of the measurements on the individual systems. Thereby, their proposed scheme significantly extended the concept of the single-photon delayed-choice gedanken experiment as introduced by Wheeler and stimulated a great deal of theoretical and experimental research (24–29). Also, the proposal (30) and the experimental realizations of delayed-choice entanglement swapping (31–34) were reported. Recently, a quantum delayed-choice experiment was proposed (35) and realized (36, 37). During the course of writing the present manuscript, we reported space-like separation between the outcomes of all measurements for the experiment in ref. 38. In addition, we used ultrafast switching as well as precisely timed random setting choices to conclusively ensure the space-like separation of all relevant events (setting choices, setting implementations, measurements). This also made possible many different space–time scenarios.

Here, we propose and experimentally demonstrate a quantum eraser under enforced Einstein locality. The locality condition imposes that if “two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system.” (p 779, ref. 10). Operationally, to experimentally realize a quantum eraser under Einstein locality conditions, the erasure event of welcher-weg information has to be relativistically space-like separated from the whole passage of the interfering system through the interferometer including its final registration. This means that in any and all reference frames no subluminal or luminal physical signal can travel from one event to the other and causally influence it. Implementing Einstein locality thus implies a significant step in the history of quantum eraser experiments.

The concept of our quantum eraser is illustrated in Fig. 1. We produce hybrid entangled photon pairs (39), with entanglement between two different degrees of freedom, namely the path of one photon denoted as the system photon, and the polarization of the other photon denoted as the environment photon. The system photon is sent to an interferometer, and the environment photon is sent to a polarization analyzer, which performs a measurement according to a causally disconnected choice (with respect to the interferometer-related events). Analogous to the original proposal of the quantum eraser (20, 21), the environment photon’s polarization carries welcher-weg information of the system photon due to the entanglement between the two photons. Depending upon the polarization basis in which the environment photon is measured, we are able to either acquire welcher-weg information of the system photon and observe no interference, or erase welcher-weg information and observe interference. In the latter case, it depends on the specific outcome of the environment photon which one out of two different interference patterns the system photon is showing. Results of our work have been reported^¶,§,||, and more information can be found in ref. 40.

Fig. 1.

Concept of our quantum eraser under Einstein locality conditions. Hybrid entangled photon-pair source, labeled as S, emits path-polarization entangled photon pairs. System photons are propagating through an interferometer (Right) and the environment photons are subject to polarization measurements (Left). Choices to acquire welcher-weg information or to obtain interference of the system photons are made under Einstein locality so that there are no causal influences between the system photons and the environment photons.

To test the quantum eraser concept under various spatiotemporal situations, we performed several experiments demonstrating the quantum eraser under Einstein locality on two different length scales. In the first experiment performed in Vienna in 2007, the environment photon is sent away from the system photon via a 55-m-long optical fiber. In the second experiment performed on the Canary Islands in 2008, they are separated by 144 km and connected via a free-space link. The scheme of our Vienna experiment is shown in Fig. 2A. First, we prepare a polarization-entangled state (41): , where and denote quantum states of horizontal and vertical linear polarization, and s and e index the system and environment photon, respectively. The orthogonal polarization states of the system photon are coherently converted into two different interferometer path states and via a polarizing beam splitter and two fiber polarization controllers. This approximately generates the hybrid entangled state (39). Details on imperfections and reduced state purity are in SI Text.

Fig. 2.

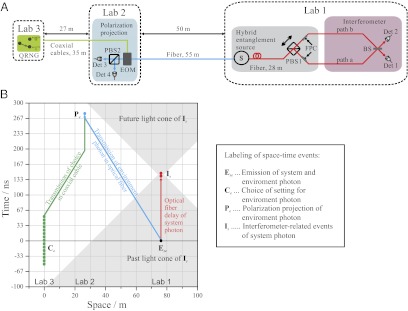
(A) Scheme of the Vienna experiment: In Lab 1, the source (S) emits polarization entangled photon pairs, each consisting of a system and an environment photon, via type-II spontaneous parametric down-conversion. Good spectral and spatial mode overlap is achieved by using interference filters with 1-nm bandwidth and by collecting the photons into single-mode fibers. The polarization entangled state is subsequently converted into a hybrid entangled state with a polarizing beam splitter (PBS1) and two fiber polarization controllers (FPC). Interferometric measurement of the system photon is performed with a single-mode fiber beam splitter (BS) with a path length of 2 m, where the relative phase between path a and path b is adjusted by moving PBS1’s position with a piezo-nanopositioner. The polarization projection setup of the environment photon consists of an electro-optic modulator (EOM) and another PBS (PBS2). Both photons are detected by silicon avalanche photodiodes (DET 1–4). The choice is made with a QRNG (44). (B) Space–time diagram. The choice-related events C_e and the polarization projection of the environment photon P_e are space-like separated from all events of the interferometric measurement of the system photon I_s. Additionally, the events C_e are also space-like separated from the emission of the entangled photon pair from the source E_se. Shaded areas are the past and the future light cones of events I_s. This ensures that Einstein locality is fulfilled. Details are provided in the main text and SI Text. BS, beam splitter; FPCs, fiber polarization controllers; PBS, polarized beam splitter.

The environment photon thus carries welcher-weg information about the system photon. Therefore, we are able to perform two complementary polarization projection measurements on the environment photon and acquire or erase welcher-weg information of the system photon, respectively. (i) We project the environment photon into the H/V basis, which reveals welcher-weg information of the system photon and no interference can be observed; (ii) We project the environment photon into the R/L basis (with and ) of left and right circular polarization states, which erases welcher-weg information. Contrary to the first case, the detection of the environment photon in polarization R (or L) results in a coherent superposition with equal probabilities for the states and , as Eq. 1 can be rewritten as

In case (ii), the polarization of the environment photon (either R or L) carries information about the relative phase between paths a and b of the system photon. This gives rise to complementary interference patterns (fringes or antifringes). Cases (i) and (ii) show that the which-path information and the fringe–antifringe information are equally fundamental. Note that similar setups have been proposed in refs. 25, 42, 43.

The following events are important and should be identified before the discussion of the space–time diagram: E_se is the emission of both the system photon and the environment photon from the source, C_e is the choice of the polarization measurement basis of the environment photon, P_e is the polarization projection of the environment photon, and I_s are all events related to the system photon inside the interferometer including its entry into, its propagation through, and its exit from the interferometer.

To guarantee Einstein locality for a conclusive test, any causal influence between choice C_e and projection P_e of the environment photon on one hand and interferometer-related events I_s of the system photon on the other has to be ruled out. Operationally, we require space-like separation of C_e, P_e with respect to I_s (Fig. 2B). All this is achieved by setting up the respective experimental apparatus in three distant laboratories. The choice is performed by a quantum random number generator (QRNG). (Details are given in SI Text). Its working principle is based on the intrinsically random detection events of photons behind a balanced beam splitter (44).

Note that our setup also excludes any dependence between the choice and the photon pair emission [“freedom of choice” (45, 46)], because we locate the source and QRNG in two separate laboratories such that space-like separation between the events C_e and E_se is ensured. In ref. 28, the choice is made passively by the environment photon itself and therefore is situated in the future light cone of both the emission of the photon pair and the measurement event of the system photon. Therefore, it is in principle conceivable that the emission event and system photon measurement event can influence the choice, which then only appears to be free or random.

In Fig. 3, we present the experimental results for measurements of the system photon conditioned on the detection of the environment photon with DET 4. In Fig. 3A, the probabilities that the system photon takes path a or b are shown when measurement (i), i.e., projection of the environment photon into the H/V basis and thus acquiring welcher-weg information, is performed. When the environment photon is subjected to measurement (i) and detected to have polarization V, the probability that the system photon propagates through path a is P(a|V) = 0.023(5), which is determined by blocking path b and summing up the coincidence counts over 120 s between both interferometer detectors and V detectors. Likewise, we find that the probability for propagation through path b is P(b|V) = 0.978(5). To quantify the amount of welcher-weg information acquired, we use the so-called welcher-weg information parameter (22, 24, 47, 48), . The value 0.955(7) of the parameter reveals almost full welcher-weg information of the system photon. As a consequence, when the relative phase between paths a and b is scanned, no interference pattern is observed, as shown in Fig. 3B. We integrate 20 s for each data point.

Fig. 3.

Experimental results. (A and B) When measurement (i) is performed (EOM is off), the detection of the environment photon in the state reveals the welcher-weg information of the system photon, being confirmed by measuring the counts of DET 1 and DET 2 conditional on the detection of the environment photon in DET 4. (A) We obtain that the system photon propagates through path a and path b with probabilities 0.023(5) (cyan) and 0.978(5) (yellow), respectively. The integration time is about 120 s. As a consequence of revealing welcher-weg information, phase-insensitive counts are obtained. Mean value of the counts is indicated with a black line, as shown in B. (C and D) When measurement (ii) is performed (EOM on), detection of the environment photon in erases the welcher-weg information of the system photon. (C) Probabilities of the system photon propagating through path a and path b are 0.521(16) (cyan) and 0.478(16) (yellow), respectively. The integration time is about 120 s. Because welcher-weg information is irrevocably erased, two oppositely modulated sinusoidal interference fringes with average visibility 0.951(18) show up as a function of the position change of PBS1, as shown in D. Error bars: ±1 SD, given by Poissonian statistics.

On the other hand, when the environment photon is subjected to measurement (ii), i.e., projection of the environment photon into L/R basis, the welcher-weg information is irrevocably erased. When it is detected to have polarization R, we obtain the probabilities of the system photon propagating through path a, P(a|R) = 0.521,^† and through path b, P(b|R) = 0.478^† (Fig. 3C). In this case , defined as , has the small value 0.077 (19). Accordingly, interference shows up with the visibility of as shown in Fig. 3D, where we integrate 20 s for each data point. This visibility is defined as , where C_max and C_min are the maximum and minimum counts of the system photon conditioned on the detection of the environment photon with DET 4. If the environment photon is detected to have polarization L, a π-phase–shifted interference pattern of the system photons shows up. These results, together with the space–time arrangement of our experiment, conclusively confirm the acausal nature of the quantum eraser concept.

Quantum mechanics predicts the correlations of the measurement results to be invariant upon change of the specific space–time arrangement. We therefore realized another five qualitatively different space–time scenarios, which are summarized in SI Text. All results obtained indeed agree with the expectation within statistical errors.

To quantitatively demonstrate the quantum eraser and the complementarity principle under Einstein locality, we use a bipartite complementarity inequality (22, 47, 48), namely,

which is an extension of the single-particle complementarity inequality (experimentally verified in ref. 19). Here, and are the parameters for two particles, as defined above. In an ideal experimental arrangement, inequality 3 is saturated. Under Einstein locality, we measure and in sequential experimental runs as a function of the applied voltage of the electrooptical modulator (EOM), which changes the polarization projection basis of the environment photon. Hence, we obtain a continuous transition between measurements (i) and (ii) and thus between particle and wave features. For each measurement, according to the QRNG output, the voltage of the EOM is randomly and rapidly switched between 0 and a definite value. The results are shown in Fig. 4. The dashed line is the ideal curve, where . The solid line is computed using actual nonideal experimental parameters, which are measured independently. The agreement between the calculation and the experimental data is excellent.

Fig. 4.

Experimental test of the complementarity inequality under Einstein locality, manifested by a tradeoff of the welcher-weg information parameter and the interference visibility. We vary the polarization projection basis of the environment photon via adjusting the applied voltage of the EOM. Note that the leftmost and the rightmost data points correspond to Fig. 3 A and B and 3 C and D, respectively. The dotted line is the ideal curve from the saturation of inequality in Eq. 3. The solid line is the estimation from the actual experimental imperfections, which are measured independently. Error bars: ±1 SD, given by Poissonian statistics.

A similar setup, but with significantly larger spatial and temporal separations, uses a 144-km free-space link between the interferometer and the polarization projection setup (shown in Fig. 5). The two laboratories are located on two of the Canary Islands, La Palma and Tenerife (46, 49, 50). Two different space–time arrangements are realized, one of which achieves space-like separation of all relevant events. Within this scenario, different times for the choice events are chosen. One arrangement is such that the speed of a hypothetical superluminal signal from the choice event C_e to the events related to the interferometer I_s would have to be about 96 times the speed of light, ruling out an explantation by prorogation influence (51). The other arrangement is such that the choice event C_e happens ∼450 μs after the events I_s in the reference frame of the source, which is more than 5 orders of magnitude higher for the amount of delay compared with the previously reported quantum eraser experiment (28). Even though the signal-to-noise ratio is reduced due to the attenuation of the free-space link (33 dB), results similar to the Vienna experiment are obtained after subtraction of the background. Details are in SI Text.

Fig. 5.

Satellite image of the Canary Islands of Tenerife and La Palma and overview of the experimental setup (Google Earth). The two laboratories are spatially separated by about 144 km. In La Palma, the source (S) emits polarization entangled photon pairs, which subsequently are converted to a hybrid entangled state with a PBS (PBS1) and a half-wave plate oriented at 45°. The interferometric measurement of the system photon is done with a free-space BS, where the relative phase between path a and path b is adjusted by moving PBS1’s position with a piezo-nanopositioner. The total path length of this interferometer is about 0.5 m. The projection setup consists of a quarter-wave plate (QWP), an EOM, and a PBS (PBS2), which together project the environment photon into either the H/V or ^+/− basis (with and ). Both the system photon and the environment photon are detected by silicon avalanche photodiodes (DET 1–4). A QRNG defines the choice for the experimental configuration fast and randomly. A delay card is used to adjust the relative time between the choice event and the other events. Independent data registration is performed by individual time-tagging units on both the system and environment photon sides. The time bases on both sides are established by global positioning system (GPS) receivers.

Furthermore, for all of the data obtained in the Vienna and Canary experiments, to achieve complete independence between the data registration of the system photon and the environment photon we use two time-tagging units and individually record the time stamps of their detection events. These data are compared and sorted to reconstruct the coincidence counts, long after the experiment is finished (52).

Our work demonstrates and confirms that whether the correlations between two entangled photons reveal welcher-weg information or an interference pattern of one (system) photon depends on the choice of measurement on the other (environment) photon, even when all of the events on the two sides that can be space-like separated are space-like separated. The fact that it is possible to decide whether a wave or particle feature manifests itself long after—and even space-like separated from—the measurement teaches us that we should not have any naive realistic picture for interpreting quantum phenomena. Any explanation of what goes on in a specific individual observation of one photon has to take into account the whole experimental apparatus of the complete quantum state consisting of both photons, and it can only make sense after all information concerning complementary variables has been recorded. Our results demonstrate that the viewpoint that the system photon behaves either definitely as a wave or definitely as a particle would require faster-than-light communication. Because this would be in strong tension with the special theory of relativity, we believe that such a viewpoint should be given up entirely.