Beatings in electronic 2D spectroscopy suggest another role of vibrations in photosynthetic light harvesting

Light harvesting by photosynthetic organisms is nature’s way to use solar energy for biomass growth. The process starts with light absorption in so-called antenna pigments, and is followed by transfer of the excited-state energy to reaction center proteins, where the energy is converted to an electrochemical gradient across the photosynthetic membrane (1). This potential is used to drive all energy-consuming processes in the photosynthetic organisms. Energy transfer in light harvesting occurs via various transport regimes. The limiting cases are the Förster-type incoherent excitation hopping from pigment to pigment and the exciton relaxation between energy levels, which are coherently delocalized over several antenna molecules. In both transfer regimes, vibrations play an important role in fulfilling the resonance condition of the rate equations. However, this is not the only way vibrations are used in light harvesting. The article in PNAS by Tiwari et al. (2) discusses the role of anticorrelated nuclear motions in driving energy transfer via nonadiabatic coupling (Fig. 1). The authors argue that the beatings observed in electronic 2D spectroscopy experiments of various antenna complexes are mainly of vibrational origin and provide evidence for this transport mechanism.

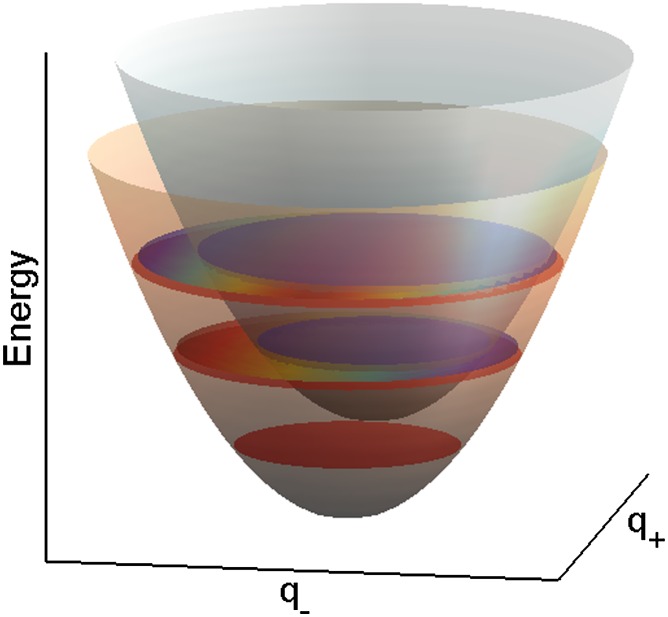
Fig. 1.

Nested adiabatic potential energy surfaces of electronically excited states of two pigments as a function of correlated and anticorrelated vibrational coordinates q+ and q−, respectively. The surfaces are shifted from each other in energy approximately by a vibrational energy quantum. As a result of a small Huang–Rhys factor, the surfaces are slightly displaced along the anticorrelated vibrational coordinate. Vibrational levels on different potential energy surfaces are in resonance, which facilitates strong nonadiabatic coupling, leading to rapidly varying electronic character of the exact nonadiabatic levels (illustrated by gradually changing colors). Nonadiabatic mixing of the levels on different pigments leads to efficient energy transfer.

Time-resolved laser spectroscopy has been a powerful tool for characterization of the light harvesting processes in detail. Early work in the 1970s was plagued by use of too high pulse intensities for studies of photosynthetic energy transfer. Wavelength-tunable, high repetition rate, and low pulse energy lasers drastically changed this situation in the beginning of the 1980s (3, 4). Soon, high-resolution structures of several photosynthetic pigment proteins became available, which greatly facilitated the interpretation of the energy and electron transfer processes (5).

The availability of ultrashort laser pulses not only allowed resolution of the fastest light-harvesting processes, but also made possible the preparation of coherent superposition of excited electronic and vibrational states of the molecules. Oscillatory features were observed in reaction centers (6) and antenna systems (7) and interpreted in terms of coherent vibrational motions. Remarkably, in the Fenna–Matthews–Olson (FMO) light-harvesting complexes, the pump-probe anisotropy showed clear oscillatory signals, which were interpreted as quantum beating between exciton levels (8).

In the late 1990s, Hybl et al. introduced electronic 2D spectroscopy (9), which matured in the next few years and became an effective technique for studying photosynthetic systems. The strongest asset of the method is its ability to acquire data with time and frequency resolution that is not limited by the broadband laser pulses. This resolution in the extra frequency dimension allowed detailed studies of excitation dynamics. First, the beating signals were confirmed in the FMO (10) and interpreted as signatures of a wavelike electronic energy transfer. Oscillations were also observed in other light harvesting complexes (11) as well as in the bacterial reaction center (12). All these beating signals were claimed to have excitonic character.

Interpretation of the observed long-lived oscillations in 2D spectroscopy measurements as electronic coherences has led to a revival of theoretical efforts in the quantum transport description of excitation dynamics in natural light harvesting. An important result of the work was the realization that the energy transport is most efficient in the intermediate regime between fully coherent and incoherent mode, where the electronic coupling and the electron–phonon interaction are of approximately the same magnitude (13). It was found that high efficiency can be obtained with a broad set of coupling parameters, possibly explaining the huge diversity of the antenna complexes that nature has built to implement efficient light collection in a variety of ways.

Compared with the simulation of quantum transport, much fewer reports have made a rigorous effort to calculate the true observable 2D signals using the quantum transport theory (14–16). Even methods, formally exact in treating bath memory effects, were not able to reproduce the long dephasing times of the oscillations unless unrealistically low spectral densities were used for the very low frequency region (17) or correlated static and dynamic disorder was assumed (16). Neither correlated nuclear motions nor spectral inhomogeneity is supported by any independent evidence from other studies. To the contrary, molecular dynamics simulations do not show any support for such correlations (18). The difficulties of rigorous distinction between electronic and nuclear origin of the observed oscillations have been recently discussed (19).

Initially, possible vibrational origin of the oscillatory features in the 2D signal in FMO was discarded because the nuclear modes in the frequency region of observed oscillations ∼150 cm⁻¹ are very weakly coupled to electronic transitions, leading to negligible Huang–Rhys factor S. In the 180 cm⁻¹ region, there are a few modes with the total S of ∼0.05; even this vibronic coupling is too weak to produce significant oscillatory features in 2D signals. From various spectroscopic techniques, the site energies of the pigments in FMO have been established. It turns out that the 0–1 vibronic transition of the lowest energy BChla molecule 180 cm⁻¹ mode has approximately the same energy as the purely electronic transition of one of the neighbors. Deeper consequences of such resonance for natural light harvesting have not been explicitly analyzed before. Using a vibronic exciton model, Christenson et al. (20) showed that, as a result of the resonance, the weak transition of mainly vibronic origin of the lowest energy BChla obtains a significant oscillator strength because of the mixing with the strong purely electronic transition at the neighboring molecule. In addition, the long-lived oscillations observed in the 2D experiments were explained by the fact that energy fluctuations of the vibrational levels of a molecule are correlated and, consequently, the corresponding coherences live long. The intensity borrowing is quite robust, and moving out from the resonance as a result of the inhomogeneous broadening does not influence the results appreciably.

Tiwari et al. (2) use an analogous resonance between the 0–0 and 0–1 vibronic transitions as a starting point in a dimer model. The authors calculate excitonic adiabatic potential energy surfaces of the dimer resulting from the anticorrelated part of the vibrational mode and the corresponding energy levels. They argue that, because of the near-resonance between the levels, the adiabatic approximation breaks down and nonadiabatic coupling has to be taken into account. Excitation dynamics caused by the nonadiabatic coupling in the context of light-harvesting complexes has been analyzed before in

The work of Tiwari et al. points at new, unexplored areas in the studies of photosynthetic light harvesting.

terms of curve-crossing and surface hopping (21, 22). Tiwari et al. (2) investigate the situation in which the potentials are nested and the crossing points are very far from the equilibrium, resembling the situation in internal conversion (Fig. 1). Still, nonadiabatic coupling will strongly mix the energy levels, which are nearly in resonance, resulting in transition dipole moments with very different strengths and orientations from the original ones. By using 2D signal calculations, the authors argue that all oscillating features of 2D spectroscopy of light-harvesting systems published so far could be explained in terms of ground-state coherent nuclear motions excited via enhanced transitions with strong vibronic character. The authors list four possible ways how the protein can regulate the energy transfer in the nonadiabatic framework: control of electronic coupling, adjustment of excitonic energy gap, control of the vibrational displacement, and possible control of how vibrations, which are coupled to the electronic transitions of the pigments, dissipate energy. The first three control mechanisms could be used to establish nested potential energy surfaces and optimize the nonadiabatic coupling. In such situations, the fourth somewhat unintuitive optimization mechanism becomes important for energy transfer.

The work of Tiwari et al. (2) points at new, unexplored areas in the studies of photosynthetic light harvesting. Naturally, many questions remain unanswered. For example, the question whether the beatings observed in electronic 2D spectroscopy experiments in photosynthetic systems can all be related to nuclear motions. Also, can these nuclear motions occur in electronic excited states? How general are the nested potentials with resonant vibrational levels in photosynthesis? These and many other questions provide numerous opportunities for future research on photosynthesis.