Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework

Abstract

The delocalized, anticorrelated component of pigment vibrations can drive nonadiabatic electronic energy transfer in photosynthetic light-harvesting antennas. In femtosecond experiments, this energy transfer mechanism leads to excitation of delocalized, anticorrelated vibrational wavepackets on the ground electronic state that exhibit not only 2D spectroscopic signatures attributed to electronic coherence and oscillatory quantum energy transport but also a cross-peak asymmetry not previously explained by theory. A number of antennas have electronic energy gaps matching a pigment vibrational frequency with a small vibrational coordinate change on electronic excitation. Such photosynthetic energy transfer steps resemble molecular internal conversion through a nested intermolecular funnel.

Photosynthesis, which powers life on our planet, is initiated when sunlight is captured by antenna proteins containing light-absorbing pigments. The antenna protein positions the pigments to couple them and alters their electronic energies to direct electronic energy transfer to a reaction center, which stores this energy chemically. Photosynthetic energy transfer is remarkably fast and efficient, often with quantum yields equal to one within experimental error (1, 2). Even with atomic resolution structures of several antennas and advances in quantum chemistry that provide the electronic structure and couplings between pigments (3), full understanding of the energy transfer mechanism and design principles has remained elusive.

Femtosecond 2D electronic spectroscopy (4) has revealed not only energy transfer pathways (2, 5) but also oscillations indicative of quantum mechanical coherence (2, 6) (with a single system having two or more distinct properties at the same time, like Schrödinger’s cat) that can persist throughout the energy transfer process (2D signatures of photosynthetic energy transfer). This coherence spans more than one pigment in the antenna (6, 7). Curiously, it has many signatures in common with coherence between electronic states, but the longest lifetimes at cryogenic temperatures are typical of coherence between vibrational states, inspiring studies to elucidate its origin and role in photosynthetic light harvesting (8–12).

Following Förster (13), electronic energy transfer is conventionally considered in an adiabatic framework [the Born–Oppenheimer approximation (14)], where the motions of fast electrons are separable from slow vibrations. In this framework, each electronic state has a potential energy surface on which molecules vibrate, and nonadiabatic changes in electronic state occur only when the molecules vibrate to a place on the potential surface where the adiabatic approximation breaks down. Within the adiabatic framework, an energy transfer step can be either adiabatic (Förster’s strong coupling) or nonadiabatic (Förster’s very weak coupling). Although Förster recognized that the adiabatic framework would be appropriate for electronic energy transfer in the very weak and strong coupling limits but not necessarily in between the limits (13), he also argued that the very weak and strong coupling limits overlapped for systems with continuous spectra (such as antennas).

Conical funnels (15), where electronic potential energy surfaces approach so closely that the adiabatic approximation breaks down, play an important role in photochemistry (15, 16) and often funnel molecules to lower-energy electronic states (internal conversion). A conical funnel may be either a conical intersection between adiabatic potential surfaces or a near miss, but it must allow a change in electronic state before vibrational equilibration (15). Recent experiments on molecules (17) have found that femtosecond pulse-driven passage through a conical funnel generates vibrational wavepackets on the ground electronic state that exhibit signatures of coherence between the excited electronic states connected by the funnel. In these experiments, quantum vibrational wavepacket width promotes nonadiabatic motion through the funnel, and signatures of electronic and vibrational coherence on the excited state can be rapidly suppressed by weak nonadiabatic coupling (17). This observation naturally raises the question of whether similar nonadiabatic dynamics drive photosynthetic energy transfer.

In antennas, several reported 2D signatures of photosynthetic energy transfer match calculations for coherence between excited electronic states [electronic coherence (EC)] and oscillating electronic-state populations [quantum transport (QT)] (10, 18). Antenna 2D spectra have overlapping excitonic resonances with oscillatory phase-twisted 2D peakshapes extending beyond resonance; methods for locating peaks and determining phase relationships are contested (19, 20). Some 2D signatures are incompatible with the usual adiabatic [Franck–Condon (FC)] (14) excitation of vibrational wavepackets. Although QT was proposed to explain oscillatory diagonal peaks (18), others argued that picosecond beat decay indicates a vibrational origin with amplitudes enhanced by vibrational–electronic coupling (21). Here, we show that one should expect small-amplitude vibrational wavepackets in which two pigments vibrate out of phase, that they give rise to nonadiabatic vibrational electronic mixing between the excited states, and that this mixing leads to delocalized anticorrelated vibrational wavepackets on the ground electronic state that exhibit the reported signatures. The anticorrelated vibrational wavepackets also generate signatures that have not been explained by previous models incorporating EC, QT, or vibrations. The model reproduces these signatures when the frequency of a FC active vibration is nearly resonant with the donor–acceptor electronic energy gap; this vibrational-electronic resonance drives energy transfer through nonadiabatic dynamics entirely outside the adiabatic framework.

Model

The dimer model used for this study starts with two pigments (A and B), each with an identical intramolecular harmonic vibration. Using energy in frequency units, the Hamiltonian for pigment A is

where is the identity operator, 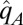and are the dimensionless position and momentum operators of the vibration with frequency , is the excited electronic state with vertical excitation energy , and is the FC displacement of the vibration (14). The Hamiltonian for pigment B has the same form but with a vertical excitation energy difference, Δ = (E_B − E_A). If either pigment is excited, the two pigments interact through a Coulombic coupling (3), which at long range can be calculated by the transition dipole approximation; therefore, , where the coupling J is assumed to be independent of the intramolecular vibrational coordinates. The two pigment system has a single electronic ground state (no pigments excited), two singly excited electronic states (one for each pigment), and a doubly excited electronic state (both pigments excited). The electronic states of coupled pigment systems are referred to as (Frenkel) excitons. The singly excited (single-exciton) electronic states are delocalized to some extent by the coupling, and the energy of the doubly excited state differs from E_B + E_A by the biexciton binding energy.

The above Hamiltonian is standard in energy transfer (2). An exact nonadiabatic treatment of the resulting states, their consequences in the 2D spectrum (including signals from the ground electronic state), and role in photosynthetic energy transfer are presented here. For a nonadiabatic treatment, it is useful to project the localized intramolecular vibrational coordinates into correlated and anticorrelated vibrational coordinates, and 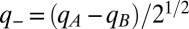, that are delocalized over both pigments. Förster (13) recognized that the delocalized, anticorrelated vibration, because it tunes the electronic energy gap between pigments, is the relevant vibrational coordinate for driving energy transfer at all coupling strengths, regardless of the extent of electronic delocalization. In the language of conical intersections (16), is the tuning coordinate g. In a delocalized, correlated intramolecular vibration, every bond length and angle vibrates with exactly the same phase on both molecules; in the delocalized, anticorrelated intramolecular vibration, every bond in one molecule contracts while it expands in the other (and every bond angle bends in the opposite sense). Proteins can alter pigment vibrations (22); in this case, correlated and anticorrelated vibrations need not be normal modes or vibrate with equal magnitude on two coupled pigments. This change of vibrational coordinates does not assume that vibrations are delocalized but reveals that only the projection of a vibration onto the delocalized, anticorrelated coordinate drives and can be driven by nonadiabatic mixing. The nonadiabatic interactions are thus more clearly seen by writing the single-exciton Hamiltonian as , with

and

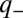uses a basis where the vibrational coordinate is delocalized and the electronic states are localized. Because depends only on and depends only on , the adiabatic correlated dynamics are exactly separable from the nonadiabatic anticorrelated dynamics. Thus, a correlated vibration, although it disrupts the quantum-phase relationship between the ground electronic state and both single-exciton states, does not alter the potential energy difference between single-exciton states, does not disrupt their quantum-phase relationship, and plays no role in nonadiabatic dynamics. [That is why correlated vibrations oscillate coherently on the excited state throughout the energy transfer process (23, 24).] In contrast, an anticorrelated vibration affects the excited states of pigments A and B oppositely in , tunes their potential energy difference, disrupts their quantum-phase relationship, and drives nonadiabatic dynamics. Both coordinates affect the absorption lineshape and 2D peakshapes. Because the anticorrelated vibration is delocalized over both coupled pigments, it cannot drive or be driven by nonadiabatic dynamics for a single-pigment system, explaining the results in refs. 6 and 7. In contrast to the adiabatic approximation, which first solves for electronic states of the dimer at fixed vibrational coordinates, the nonadiabatic treatment simultaneously solves for mixed vibrational–electronic states (SI Text).

Model parameters are very roughly based on one pair of excitons in the Fenna–Matthews–Olson (FMO) complex from green sulfur bacteria (1). Its pigment, bacteriochlorophyll a (BChl a) (22, 25), has FC active vibrations with frequency 200 cm⁻¹ and a stabilization energy of 5 cm⁻¹. In the dimer model, the transition dipoles of the two pigments are perpendicular. The coupling is J = 66 cm⁻¹ [typical in FMO (2)]. The difference in electronic energy between the two pigments, , has a static distribution with average = 150 cm⁻¹ (also typical) and variance . and are chosen so that the average energy gap between excitons () matches the vibrational energy . Based on the excitonic peaks in FMO absorption (26), such a resonance occurs between the first exciton and an exciton ∼200 cm⁻¹ higher; additional resonances seem likely (Table S1). The exciton splitting inhomogeneity, = 26 cm⁻¹, is slightly smaller than the value determined at 19 K from the anisotropy for a pair of excitons separated by ∼150 cm⁻¹ in FMO (27). Because correlated vibrations do not affect the nonadiabatic dynamics, the damping of correlated vibrations can be incorporated through nonlinear response functions (17). A critically damped Brownian oscillator with a frequency of 70 cm⁻¹ and a stabilization energy of 30 cm⁻¹ represents the correlated component of the low-energy phonon sideband (this stabilization energy reproduces the Stokes’ shift at 80 K) (2).

Fig. 1 shows that the vibrational and electronic states of in the adiabatic approximation gradually change electronic character with the anticorrelated vibrational coordinate. The derivatives of these adiabatic wavefunctions lead to nonadiabatic couplings that must be included to calculate the exact states (16, 17). The exact nonadiabatic states (which are both vibrationally and electronically mixed) exhibit a rapid variation in their electronic character over the entire range of coordinates, although the adiabatic energy levels are reasonably accurate. This breakdown of the adiabatic framework affects both the 2D spectra and the photosynthetic energy transfer process.

Fig. 1.

Isolated pigment (dashed potential curves and levels), coupled adiabatic (solid potential curves and levels), and exact nonadiabatic (levels not attached to any curve) excited-state vibrational–electronic levels for of the dimer model with . v_- is the quantum number of the anticorrelated vibration. Color shows the electronic-state character, which is a linear combination of the two pigment states, at each coordinate (SI Text). The electronic character does not change for isolated pigments and varies slowly for adiabatic states. Rapid changes in electronic character for the nonadiabatic levels over the entire coordinate range indicate a complete breakdown of the adiabatic framework.

With a constant Coulombic coupling between pigments, the adiabatic potentials for excitons in Fig. 1 do not intersect, and there is no conical intersection (pigments must translate or rotate relative to each other by more than the protein allows to send the coupling to zero). However, the nonadiabatic changes in electronic character with anticorrelated vibrational coordinate indicate a funnel. Because Eq. 2 indicates that the potentials are identical in correlated vibrational coordinates, extending the curves in Fig. 1 into 2D surfaces reveals a nonconical kind of funnel, in which adiabatic potential surfaces arising from two different molecules are nested inside each other in all intramolecular coordinates; the adiabatic framework breaks down everywhere inside this nested intermolecular funnel. Nesting requires that the vibrational displacement be small compared with the zero-point amplitude, whereas nonadiabatic coupling requires vibrational displacement or vibrational-dependent coupling.

2D spectra are generated by crossing three noncollinear femtosecond pulses (wave vectors k_a, k_b, and k_c) inside the sample, measuring the four-wave mixing field radiated with wavevector k_s = k_c + k_b − k_a as a function of τ (the delay between pulses a and b) and t (the time after pulse c) at a fixed T (the interval between the second and third pulses), and Fourier-transforming with respect to τ and t. For scans over all τ, the real part of the 2D spectrum (absorptive 2D spectrum) reveals net changes in sample absorption as a function of both the excitation (ω_τ) and detection (ω_t) frequencies. Some of the coherence signatures in 2D spectroscopy depend on whether τ is positive (pulse a is before pulse b for rephasing 2D spectra) or negative (pulse b is before pulse a for nonrephasing 2D spectra) and the physically meaningful relative signs of the frequencies. Fig. 2 shows an all-parallel pulse polarization 2D spectrum for the dimer model at T = 0 (it is simpler than the 2D spectrum of FMO, which involves 7 single-exciton states and 21 biexciton states). Oscillations in the marked 2D peaks as a function of T indicate quantum coherence. 2D spectra generally contain contributions from reduced ground-state absorption, excited-state stimulated emission, and excited-state absorption (total 2D spectra).

Fig. 2.

Real part of the ground electronic-state contribution to the rephasing 2D electronic spectrum for the dimer model with (E_A + E_B)/2 = 11,574 cm⁻¹ at a temperature of 80 K. Here, the vertical axis is the excitation frequency −ω_τ, and the horizontal axis is the detection frequency ω_t. The amplitude of the 2D spectrum for each frequency pair is indicated by color and contours at the 0%, 2%, 4%, 6%, 8%, and 10–90% levels. Positive and negative contours are solid and dashed, respectively. The waiting time is T = 0 fs. The 2D spectra are dominated by four resolved peaks, which oscillate in amplitude and shape with T. Diagonal peak maxima are marked by ○ (lower left, DP1; upper right, DP2); cross-peak maxima are marked by x (upper left, CP12; lower right, CP21).

In a 2D experiment, the first pulse pair can create vibrational coherence on the ground state (by stimulated Raman scattering) along with both vibrational and electronic coherence on the excited state (4). An adiabatic picture predicts that vibrational coherence will only cause weak modulations of the 2D spectra because of small FC vibrational displacements in antenna pigments. Furthermore, the adiabatic approximation predicts that vibrational coherence will have the same polarization signatures as electronic-state populations. The nonadiabatic wavefunctions illustrated in Fig. 1 generate dramatically different behavior. Stimulated Raman excitation of ground-state vibrational wavepackets can involve sets of transition dipoles identical to those sets involved in the excitation of EC. This electronically enhanced contribution to 2D spectra can be appreciated from Fig. 3, which uses wave-mixing diagrams (SI Text) to show the states and fields for four terms in the nonlinear optical response from the nonadiabatically coupled states of 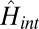. The first (leftmost) frequency is ω_τ (excitation), and the last (rightmost) frequency is ω_t (detection). Pathways corresponding to the diagonal peaks (DPs; DP1 and DP2) and the cross-peaks (CPs; CP12 and CP21) are arranged according to their position in the 2D spectrum shown in Fig. 2. For the pathway contributing to CP12, extensive mixing between v_- = 0 on B and v₋ = 1 on A (illustrated in Fig. 1) along the anticorrelated coordinate allows vibrational coherence on the ground state to be excited exclusively through strong electronic transitions with Δv₋ = 0 basis state character; the frequencies (arrow lengths) and transition dipole directions (orange vs. blue arrows using the color scheme in Fig. 1) are all the same as those frequencies and directions for excited-state EC (Fig. S1). The other paths are similar but not fully electronically enhanced at each step (black arrows); for example, in DP1 and CP21, interaction with pulse b depends on nonresonant mixing of on A and its vibrational overlap with on G. As a result, ground-state vibrational wavepackets closely mimic signatures of excited-state electronic wavepackets. In particular, the transition dipole sequences in Fig. 3 show that nonadiabatic excitation of anticorrelated ground-state wavepackets will generate oscillations that survive the polarized pulse sequence used on Light Harvesting Complex II (LHCII) from green plants (28).

Fig. 3.

Wave-mixing pathways (SI Text) for the oscillatory ground-state 2D signal (D₃ in ref. 4) showing resonant enhancement by nonadiabatic coupling of vibrational and electronic levels. For each diagram, the vertical axis is energy and time runs from left to right (neither drawn to scale). The pathways are arranged to correspond with peaks in the rephasing 2D spectrum (Fig. 2). Delocalized, anticorrelated vibrational levels on each electronic state are indicated by solid lines for v_- = 0, dashed lines for v_- = 1, and dotted lines for v_- = 2; their orange and blue colors indicate localized electronic basis states on pigments A and B, respectively. As in Fig. 1, resonant pairs of levels couple to form the nonadiabatic states (the first pair is roughly ). The orange (blue) vertical lines in the figure represent field–matter interactions using the A (B) electronic character of a mixed level, with no change in v_-, yielding a vibrational overlap integral approaching one. Thus, CP12 is fully electronically enhanced at every step, with all frequencies and transition dipole directions matching those frequencies and directions for purely electronic coherence (Fig. S1). Vertical lines in black represent weaker field–matter interactions—these interactions have small vibrational overlap or lack vibrational–electronic resonance. As a result, oscillations of DP1, DP2, and CP21 are not fully electronically enhanced.

Results

Three predicted signatures of EC between excited states in 2D spectra have been reported for antennas. Signature 1, diagonal peak amplitude beating, was first reported in the absorptive 2D spectra of FMO (29); Fig. 4 shows that signature 1 also arises from ground-state vibrations for both diagonal peaks in the 2D spectra. Signature 2, a negative cross-peak CP12 beating frequency (for positive ω_t) in the rephasing 2D spectrum, has been reported for PC645 (the phycocyanin PC645 antenna from the marine cryptophyte Chroomonas CCMP270) (30); Fig. 3 shows that signature 2 is also reproduced for nonadiabatic excitation of ground-state vibrations (SI Text and Fig. S1). Signature 3, cross-peak amplitude modulations that occur only in rephasing and not in nonrephasing 2D spectra, can arise from EC (30) without QT. Ref. 30 reports CP12 beats with a signal to noise ratio of 2.4:1 in rephasing 2D spectra but reports no CP12 beats (signal to noise ratio = 1.2:1) in the nonrephasing 2D spectra of PC645. Fig. 4, Upper vs. Lower compares the beating amplitudes in the rephasing and nonrephasing 2D spectra—CP12 beats are approximately five times weaker in the nonrephasing 2D spectrum, which is also consistent with experiment. For nonadiabatic excitation of ground-state vibrations, CP12 beats should be detectable with higher signal to noise nonrephasing 2D spectra. The ground-state vibrational origin for these three signatures naturally explains their robust behavior at physiological temperature, which was recently reported for FMO (31) and PC645 (30).

Fig. 4.

Absolute amplitudes and relative-phase relationships between the diagonal (DP1 and DP2) and cross-peaks (CP12 and CP21) as a function of waiting time T in the rephasing (Upper) and nonrephasing (Lower) ground electronic-state contributions to the 2D spectra for the dimer model. The transients are offset (additive constants in boxes) to show phase relationships but not multiplicatively scaled. The peaks oscillate at a vibrational frequency of 200 cm⁻¹, which is in resonance with the excitonic energy gap. In the rephasing 2D spectra, the cross-peak beats are 160° out of phase with each other, CP12 beats are 120° ahead of the diagonal peaks, and CP12 beats are ∼14 times stronger than CP21.

A ∼180° phase difference between opposite cross-peak beats has been reported in rephasing 2D spectra of PE545 (the phycoerythrin PE545 antenna from the marine cryptophyte Rhodomonas CS24) and attributed to EC (32). Contradicting this interpretation, for isolated peaks probed on center, Butkus et al. (20) show that opposite 2D cross-peaks oscillate in phase for both EC and adiabatic excitation of vibrations. A 160° phase difference arises from nonadiabatic excitation of anticorrelated ground-state vibrations (Fig. 4, Upper).

The calculations predict another significant experimental difference. According to models of EC (2) and QT (10), opposite cross-peaks (related by reflection across the 2D diagonal, such as CP12 and CP21) are expected to oscillate with equal amplitudes in a rephasing 2D spectrum (figure 5, top in ref. 10). In contrast, Fig. 4, Upper shows that anticorrelated ground-state vibrations create much stronger oscillations on CP12 (with excitation frequency |ω_τ| > detection frequency |ω_t|) than CP21. Diagrams (Fig. 3) show that CP12 involves resonant vibrational–electronic coupling between excited states at each step, whereas the weaker peak does not. Only beats for CP12, the cross-peak that the nonadiabatic anticorrelated vibration model predicts to be stronger, have been reported for FMO (18, 19) and PC645 (30). Figure 3b in ref. 32 shows both cross-peaks for PE545—they have asymmetric beat amplitudes with the stronger beats as calculated here.

A fourth 2D signature, oscillations of diagonal peaks with phase ∼90° behind CP12 oscillations in the rephasing 2D spectrum (10, 18), has been interpreted as evidence of QT, because EC alone cannot explain oscillations of the diagonal peaks in a rephasing 2D spectrum. It is not clear what determines the experimental-phase relationship in QT models (ref. 18 discusses a different phase relationship than shown in figure 5 in ref. 10). Fig. 4, Upper shows a 120° phase relationship between CP12 and DP2 near vibrational–electronic resonance. Ground-state vibrational wavepacket oscillations do not require a close resonance between intramolecular vibrational and electronic energy difference frequencies, but they are enhanced within a broad maximum (∼130-cm⁻¹ width) around resonance (Fig. S2). However, away from resonance, where nonadiabatic vibrational–electronic mixing is reduced and energy transfer between the pigments is presumably less efficient, the calculations show a 180° phase relationship between CP12 and the diagonal beats (Fig. S2). Therefore, a 90° phase relationship would suggest that electronic energy transfer involves nonadiabatic vibrational–excitonic resonance in FMO.

Discussion

Although peak overlap in the experimental 2D spectra of antennas can distort the amplitude and phase relationships found here for resolved peaks, the above observations suggest that efficient energy transfer proceeds through nonadiabatic interaction between two excitons that is resonantly enhanced by an FC active vibration of the monomeric pigment. The delocalized, anticorrelated vibration of the pigments may be the key component of the bath that exchanges energy with the electronic system in QT models. When the resonant mechanism is operative, the average energy gap between excitons should match a pigment vibrational frequency in the fluorescence or resonance Raman spectrum. Seven of nine off-diagonal beating frequencies reported for FMO match FC active vibrational frequencies of BChl a (Table S1). The two frequencies that do not match have only been reported in ref. 19. Furthermore, the vibrational frequencies that match off-diagonal beat frequencies in FMO are remarkably stable with respect to structural and isotopic perturbations (Table S1). Turner et al. (30) remark that pigment vibrational frequencies are close to frequencies in rephasing 2D spectra of PC645.

The calculations above all show the contribution to the 2D spectrum from ground-state vibrations. The ground-state signal is driven only by initial dynamics on the excited states while still coherent with the ground state, and therefore, it can be accurately calculated without including slower relaxation between excited states. Decay of coherence between the ground and excited states is included through damped correlated vibrations and gives rise to the antidiagonal width of the diagonal peaks (for the real absorptive 2D spectrum of the dimer model, this ∼80-cm⁻¹ width at waiting time T = 0 seems roughly comparable with the width for the resolved lowest exciton peak in the 2D spectrum of FMO) (29). EC plays no role in the timescales over which oscillations on the ground electronic state persist; they decay through vibrational dephasing on the ground electronic state.

Given that the key vibrational–electronic resonance between two excitons is established by the electronic absorption spectrum of FMO (26) and the fluorescence spectrum of BChl a (25), the above signatures of delocalized anticorrelated vibrations should be present in the 2D spectra of FMO (18, 31). They also seem to arise in antennas from cryptophyte marine algae (30, 32), which harvest different wavelengths. The breakdown of the adiabatic framework drastically alters the modeling and interpretation of antenna 2D spectra. Fig. 5 shows coherence signatures from the total 2D spectrum, which includes excited-state contributions (but without any relaxation of population or coherence between excited states). The experimentally reported phase relationships and asymmetrical cross-peak oscillation signatures in Fig. 4 are obscured by excited-state coherences. DP2 has a dominant oscillation with ∼1-ps period arising from the splitting between its nearly degenerate nonadiabatic levels (second and third levels in Fig. 1). DP1 has its deepest oscillations at the excitonic splitting Δ_ex in the nonrephasing 2D spectrum; these oscillations arise from EC and decay within ∼300 fs in Fig. 5. Comparison with Fig. 4 shows that amplitudes for ground- and excited-state beats at the vibrational–excitonic frequency are comparable after ∼300 fs.

Fig. 5.

Absolute amplitudes and relative-phase relationships between the diagonal and cross-peaks as a function of waiting time T in the total rephasing (Upper) and nonrephasing (Lower) 2D spectra for the dimer model, including ground-state bleaching, excited-state emission, and excited-state absorption for zero biexciton binding energy. Vertical scales can be compared directly with Fig. 4. As long as the irregular excited-state oscillations persist, the phase relationships in Fig. 4 will be obscured, and CP21 beats will have roughly the same amplitude as CP12 beats.

Broadly, three types of coherence at a common frequency Δ_ex ∼ ω arise with resonant nonadiabatic coupling, and therefore, there are roughly three coherence decay timescales. First, 2D signatures of excited-state coherence at Δ_ex (for resonance, Δ_ex ∼ ω) disappear on a timescale dictated by anticorrelated inhomogeneity and coupling; these signatures are gone by ∼300 fs for the dimer model ( = 26 cm⁻¹) and disappear by ∼200 fs for 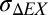= 34 cm⁻¹ [the anisotropy beat decay for this exciton splitting inhomogeneity is ∼180 fs in FMO (27)], although the model does not include any coherence decay for an individual dimer. Second, relaxation of excited-state coherence at the vibrational frequency ω (for resonance, ω ∼ Δ_ex) may have aspects of both vibrational and electronic coherence decay (perhaps this relaxation generates EC signatures identical to those signatures already present on the ground state—if not, this coherence probably decays before ground-state signatures are seen). Third, coherent vibrations on the ground state (and possibly correlated vibrations on the excited state) at ω should decay with typical vibrational timescales (approximately picoseconds). As a result, ground-state vibrational coherence is likely to survive longest, with frequencies that are nonadiabatically enhanced by vibrational–excitonic resonance generating the most persistent observed signatures. For antennas, the timescale on which the excited-state coherence signatures in Fig. 5 decay and give way to the ground-state coherence signatures in Fig. 4 is not yet clear, but it could be as short as ∼200 fs for FMO at 80 K.

Signatures found here may not be unique to nonadiabatic vibrational–excitonic resonance; for example, asymmetries across the 2D diagonal can occur for FC excitation of vibrations on electronic excitation (33). Models for antennas are needed to quantitatively test how much of the beating can be accounted for by resonant electronic enhancement of ground-state vibrations. Polarization sequences (28) may provide additional signatures (17). By analogy to the two-color pump-probe experiments that Vos et al. (23) used to distinguish between ground- and excited-state vibrations, two-color 2D spectra with pulses a/b of one color and pulse c of another color could separately probe for ground- and excited-state beating.

For energy transfer outside the adiabatic framework, the protein has at least four ways to control energy transfer: first, it can control the electronic coupling; second, it can control the excitonic energy gap; third, it can control the vibrational displacement (22); and fourth, it might control how the coupled vibration dissipates energy. Comparing two related phycocyanins, Womick and Moran (34) have calculated that a vibrational–excitonic resonance in one speeds up energy transfer. Resonance with an FC active vibration (or group of vibrations) may provide a way for the protein to select the energy acceptor for each donor. The first three control mechanisms dictate the strongest nonadiabatic interactions and establish a nested intermolecular funnel; the fourth mechanism may dictate how population relaxes down to the lowest, electronically decoupled v_- = 0 level, which completes the electronic energy transfer process (as long as ) (35). Vibrational relaxation on the ground electronic state of the isolated pigments is relevant to this completion; in a fully localized basis, energy transfer from the v = 0 level of excited pigment B can leave pigment A electronically excited with v = 0 and pigment B in its ground electronic state with v = 1 (a possibility excluded by approximations in refs. 21, 34, and 35).

Conclusions

Reported signatures of photosynthetic energy transfer in the 2D electronic spectra of antennas (Fig. S3 and Table S2) point to nonadiabatic vibrational–electronic mixing resonantly enhancing the amplitude of delocalized, anticorrelated vibrational wavepacket motion on the ground electronic state, which is likely to outlive electronic and vibrational–electronic coherence. Furthermore, the present mechanism predicts an asymmetry between opposite cross-peak oscillations (found for an antenna from cryptophyte marine algae, PE545) but not explained by EC or QT. The mechanism also predicts a reduced amplitude cross-peak beating in nonrephasing 2D spectra that is consistent with experiment but has not yet been reported. Although quantitative models with nonadiabatic vibrational–electronic resonance, electronic decoherence, and relaxation under physiological conditions are needed to develop a deeper picture of and perspective on this energy transfer mechanism, it is remarkable how closely beat frequencies in the 2D spectra of the FMO complex match the frequencies of FC active skeletal vibrations in its BChl a pigment. Thus, although additional studies are needed, it seems to us likely that resonant nonadiabatic coupling plays a role in photosynthetic energy transfer and that vibrational–electronic resonances in nested intermolecular funnels are an important design principle.

Methods

Nonadiabatic dynamics are fully incorporated using quantum states of the dimer Hamiltonian in sum-over-states formulas for the nonlinear optical response (4). 2D spectra also reflect interactions with the bath, which should be decomposed into correlated and anticorrelated parts. To approximate the anticorrelated component of both the phonon sideband and static inhomogeneities in the protein, the nonadiabatic problem is solved for members of an ensemble with a static Gaussian distribution of electronic site energy differences ( = 34 cm⁻¹), and the nonlinear responses are added. The temperature was fixed at 80 K to match experiments on FMO. The sum-over-states response was multiplied by the correlated Brownian oscillator response, and 2D Fourier transform (FT) spectra were calculated (SI Text) using a 3D FT algorithm. Calculation of a waiting time series of 2D spectra took ∼3 h on two hex-core 2.8-GHz Intel Westmere processors.