Surface Based Analysis of Diffusion Orientation for Identifying Architectonic Domains in the In Vivo Human Cortex

Abstract

Diffusion tensor MRI is sensitive to the coherent structure of brain tissue and is commonly used to study large-scale white matter structure. Diffusion in grey matter is more isotropic, however, several groups have observed coherent patterns of diffusion anisotropy within the cerebral cortical grey matter. We extend the study of cortical diffusion anisotropy by relating it to the local coordinate system of the folded cerebral cortex. We use 1mm and sub-millimeter isotropic resolution diffusion imaging to perform a laminar analysis of the principal diffusion orientation, fractional anisotropy, mean diffusivity and partial volume effects. Data from 6 in vivo human subjects, a fixed human brain specimen and an anesthetized macaque were examined. Large regions of cortex show a radial diffusion orientation. In vivo human and macaque data displayed a sharp transition from radial to tangential diffusion orientation at the border between primary motor and somatosensory cortex, and some evidence of tangential diffusion in secondary somatosensory cortex and primary auditory cortex. Ex vivo diffusion imaging in a human tissue sample showed some tangential diffusion orientation in S1 but mostly radial diffusion orientations in both M1 and S1.

Introduction

Diffusion-weighted MRI (DW-MRI) is sensitive to tissue micro-structure including: membranes, myelin, macro-molecules and packing geometry. This micro-structural sensitivity has most commonly been exploited for determining the geometry and structural integrity of white matter (WM) tracts through measurements of diffusion anisotropy. At conventional DW-MRI resolutions (8-27 mm³ voxels) grey matter (GM) does not generally exhibit a coherent pattern of diffusion anisotropy in adults and therefore methods such as diffusion tensor imaging (DTI) [Basser et al., 1994], diffusion spectrum imaging (DSI) [Wedeen et al., 2005], q-ball [Tuch, 2004], spherical deconvolution [Tournier et al., 2004] etc. are traditionally thought of as a white matter imaging techniques.

There is growing evidence, however, that measurements of diffusion anisotropy may be useful for probing GM micro-structure. One of the first observations of cortical diffusion anisotropy was from an in vivo pig imaging experiment in 1997 [Thornton et al., 1997]. There is also a rich literature of cortical diffusion anisotropy in the developing brain including data from in vivo human [McKinstry et al., 2002, Maas et al., 2004, Deipolyi et al., 2005,Mukherjee and McKinstry, 2006], fresh ex vivo human [Gupta et al., 2005,Trivedi et al., 2009] and perfusion fixed animal [Kroenke et al., 2007, Bock et al., 2010, Takahashi et al., 2010]. In fact it was thought by some that cortical diffusion anisotropy was a feature that is unique to the developing brain since, using their imaging methods, it disappeared at term (40 gestational weeks) [Mukherjee and McKinstry, 2006]. More recently, however, there have been reports of diffusion anisotropy in the adult cerebral cortex using high-resolution (sub-millimeter isotropic) DW-MRI of perfusion fixed animal [Dyrby et al., 2011] and fixed human [McNab et al., 2009, Miller et al., 2011,Leuze et al., 2012] brain specimens. Using recent in vivo acquisition strategies employing higher spatial resolutions, cortical diffusion anisotropy has now been observed in the adult human brain in vivo [Heidemann et al., 2010,Anwander et al., 2010,McNab et al., 2011], proving that it is not simply a feature of the tissue fixation process. While fractional anisotropy (FA) values reported in the cortex are much lower than the FA of white matter (e.g. ~0.2 in the cortex vs. 0.8 in WM) the orientation of maximal diffusion appears to follow the cortical folds. Initial reports identified the principal diffusion orientation within the cortex to be primarily radial (i.e. normal to the surface of the cortex). Therefore, cortical diffusion anisotropy appears to correlate with the local frame of the cortical surface, not to the global frame of the head. Anwander et. al. 2010 presented the first evidence that cortical regions might have differing micro-structure distinguishable with diffusion MRI. They found a primarily radial orientation in M1 and a tangential to the local cortical surface orientation in S1. More recently, members of the same group have found evidence of radial orientation in both M1 and S1 using 240μm isotropic resolution in a human fixed tissue specimen [Leuze et al., 2012].

It remains unclear which micro-structural properties of the cortex are the source of the observed anisotropic diffusion. Fibers present in the cortex display a range of myelination. In general the total cortical myelin content decreases with increasing distance from primary areas [Hellwig, 2002]. In white matter, myelination modulates the degree of diffusion anisotropy by about 20% [Gulani et al., 2001] but myelin is not the only source of WM diffusion anisotropy [Beaulieu and Allen, 1994]. Therefore, DW-MRI is also potentially sensitive to unmyelinated fibers in the cortex as well as other microstructures.

The dominant orientations of cortical fibers are radial and tangential to the surface normal [Vogt and Vogt, 1919]. Columnar functional units [Mountcastle, 1957] are defined by their radial connections between soma located in different lamina. Axons and dendrites within the cortex also spread tangentially within lamina which are parallel to the cortical surface. The inner and outer stripes of Baillarger [Baillarger, 1840] in layers IV and Vb respectively and the partially myelinated dendritic tufts in cortical layer I are prominent examples of tangential architecture. The intensity of the stripes of Baillarger on stained sections is a key landmark for cortical parcellations. Agranular cortex such as the primary somatosensory (S1) and primary auditory (A1) cortices exhibit both stripes of Baillarger while primary visual cortex (V1) only displays a single band (Stria of Gennari). In cortical regions classified as granular cortex, such as the primary motor cortex (M1), the stripes of Baillarger are much less salient despite having high myelin content [Lewis and Van Essen, 2000, Hellwig, 2002]. In addition, other cortical grey matter micro-anatomy such as the laminar arrangements of cell bodies is also structured relative to the local frame of the cortical surface.

In addition to characterizing cortical regions, the presence of tangential cortical fibers distinguishes stages of neuro-development and aging. Neurons which migrate from the ventricular germinal zone to the cortical plate are initially oriented radially [Sidman and Rakic, 1973]. Cortical maturation is associated with an increase in tangentially oriented fibers due to several different developmental events including dendritic elaboration [Marín-Padilla, 1992], formation of local circuits [Callaway and Katz, 1990], addition of thalamo-cortical fibers [Ghosh and Shatz, 1993] and disappearance of radial glia [Rivkin et al., 1995,Hardy and Friedrich, 1996]. Cortical changes associated with aging are sometimes viewed as a reversal of the events that take place during neuro-development [Scheibel et al., 1975]. For example, a progressive loss of tangentially oriented dendrite systems has been observed on Golgi stains [Scheibel et al., 1975]. The importance of these changes suggest that cortical diffusion anisotropy measures might be useful in studying disorders of development and aging.

The primary motor and somatosensory cortices represent two extremely different types of cortex (agranular and granular respectively). They are located directly adjacent to one another and are highly constrained relative to the cortical folds across multiple subjects. This makes M1 and S1 an excellent test-bed for detecting differences in cortical cyto- and myelo-architecture using diffusion anisotropy. Here we provide a more comprehensive study of the result by Anwander et. al. [Anwander et al., 2010] which showed predominantly radial diffusion in the primary motor cortex (M1) and mainly tangential diffusion in the adjacent primary somatosensory cortex (S1). We extend their analysis by bringing several recently developed techniques to bear for investigating diffusion anisotropy in the cortex. We apply cortical surface reconstructions [Fischl et al., 1999, Dale et al., 1999] to visualize diffusion measures relative to the cortical-coordinate system (e.g. radial or tangential), and a laminar analysis method [Polimeni et al., 2010] to characterize the depth-dependence of diffusion measures in the cortex, and assess partial volume effects. Additionally we show that primary auditory cortex (A1) and secondary somatosensory cortex (S2) display signatures of tangential architecture similar to, but not as replicable as S1. In addition to highly replicable M1/S1 results across 6 in vivo subjects we provide further supporting evidence at higher spatial resolution from an ex vivo specimen (0.5mm isotropic voxels), as well as from anesthetized rhesus macaque (0.7 mm isotropic voxels).

Methods

In Vivo Human 1 mm isotropic diffusion data (N=6)

Data were acquired on 6 healthy adult subjects scanned after institutional review and informed consent on a 3T Siemens Tim Trio using the Siemens 32-channel brain array. Each acquisition started with a 1 mm isotropic Multi-Echo Magnetization Prepared Rapid Gradient Echo (MEMPRAGE) (TI / TR / TE1 / TE2 / TE3 / TE4 / α = 1200 / 2510 / 1.6 / 3.5 / 5.4 / 7.2ms / 13°, 2×GRAPPA, Tacq = 6min). Then 65 minutes of diffusion data was acquired using a 2D single-shot 1 mm isotropic resolution twice-refocused DW-SE- EPI (TR/TE= 6360/100ms, matrix size = 218 ×218, R=3, partial Fourier = 6/8, 34 slices, BW = 1146 Hz/pixel, 2 averages of 256 directions at b=1000 s/mm², and 50 b=0 images interspersed every 9 volumes). Slices were prescribed coronally to maximize coverage of M1 and S1 in as few slices as possible. The four diffusion gradient lobes applied within the twice-refocused spin echo scheme were prescribed with Gmax=36 mT/m. The first and last diffusion gradient lobes had a duration of 5 ms. The middle two diffusion gradient lobes had a duration of 20 ms. The total time from the start of the first diffusion gradient lobe to the end of the last diffusion gradient lobe was 75 ms.

In order to obtain an estimate of our temporal Signal-to-Noise Ratio (SNR) we acquired an additional dataset in a healthy volunteer using the same parameters as above except repeating the same diffusion-encoding orientation 100 times. An SNR estimate within the cortex was obtained by taking the mean of the time-series from an ROI within the cortex and dividing it by the time-series standard deviation for an ROI in the background noise. We then corrected this SNR measure for the magnitude bias associated with 32-channel data combined using root-sum-of-squares (rss) [Constantinides et al., 1997].

Laminar depth analysis

Surface reconstructions of the white matter (WM) surface and the pial surface were generated by FreeSurfer [Dale et al., 1999] from the MEMPRAGE data. The white matter surface represents the boundary between the white matter and the cortical grey matter. Between the WM and pial surfaces, 9 intermediate surfaces, evenly spaced throughout the cortical depth, were computed as described by Polimeni et. al. [Polimeni et al., 2010]. Therefore, for each subject and for each cerebral hemisphere we reconstructed 11 surfaces in total including : the WM surface, the pial surface and 9 intermediate surfaces. The first intermediate surface was located at 10% of the cortical thickness away from the WM surface, the second intermediate surface at 20% and so on. The algorithm for generating the intermediate surfaces is described in Polimeni et. al. 2010 [Polimeni et al., 2010]. Herein, the white matter surface will be referred to as the 0th surface, the next closest surface to the white matter as the 1st surface etc. etc. up to the pial surface which will be the 10th surface.

Cortical thickness maps were derived from the bounding WM and pial surfaces [Fischl and Dale, 2000]. In order to correct for subject motion and the effects of B₀ field drift, the b=0 images were registered using FMRIB Software Library (www.fmrib.ox.ac.uk/fsl) Linear Image Registration Tool (FLIRT) [Jenkinson and Smith, 2001] to the first b=0 image in the series. The registered b=0 images were averaged together. The diffusion weighted images (DWI) were then registered to the mean b=0 image using FLIRT with a mutual information cost function. The diffusion tensor model [Basser et al., 1994] was fit to the DWIs using the FMRIB Software Library Diffusion Toolbox (FDT) (www.fmrib.ox.ac.uk/fsl). To assess the morphology of the diffusion tensors, the skewness [Basser, 2006]. Positive skewness values identified prolate diffusion tensors (cigar-shaped). Negative skewness values identified oblate diffusion tensors (pancake-shaped). In order to assess the orientation of the oblate tensors we looked at the dot product of the principal eigenvector and the surface normal (i.e. the radiality index) as well as the dot product of the secondary eigenvector and the surface normal. When both dot products were each less than 0.5, the the oblate tensor was determined to be oriented such that the long axes (i.e. the principal and secondary eigenvectors) were within the tangential plane.

The averaged b=0 image was aligned to the surfaces with a boundary-based registration method [Greve and Fischl, 2009]. Voxel-wise diffusion tensor statistics—FA, Mean Diffusivity (MD) and the principal eigenvector—were projected onto the collection of surface reconstructions using the transformation produced from the boundary-based registration and nearest-neighbor interpolation. If any part of a voxel in the DTI volume intersected with a given surface then it was included in that surface. Since the depth sub-divisions were narrower than the voxel dimensions, a given voxel may be included in more than one surface.

It may seem counterintuitive to divide the cortex into 11 surfaces when, at 1 mm resolution, we have at most half as many voxels across the cortex at any given location. It is true that at a single cortical location there is no way to supersede the voxel resolution. However, when we pool across multiple cortical locations/regions of cortex, it is advantageous to use intermediate surfaces at a finer spacing than our voxel size because the uniform voxel grid creates a staggered sampling of the folded cortical surface. Therefore, although we may have only a few voxels across the cortex at any particular cortical location, those few voxels are sampling different cortical depths at different cortical locations. Since the voxel grid produces provides sufficiently staggered sampling of the different surfaces/laminae, every lamina is sampled nearly uniformly.

To characterize the orientation of the cortical surface, a surface normal vector, v̂_N is retrieved for each surface tessellation mesh. The primary eigenvector of the diffusion tensor ê₁ is measured relative to the surface normal and quantified as a radiality index; r:

$$r=\mid {\widehat{v}}_N\cdot {\widehat{e}}_1\mid$$ (1)

As such, a radiality index of r = 1 represents cortical diffusion that is predominantly radial and a radiality index of r = 0 represents tangential cortical diffusion. Voxels with an FA value below 0.05 were excluded from our analysis. Masks of the crowns, fundi and banks were created by smoothing and thresholding the mean curvature (H) map (from FreeSurfer). Specifically, banks, crowns and fundi were defined respectively as: | H | ≤ 0.15mm^–1, H < -0.15mm^–1 and H > 0.15mm^–1. A GM/WM/Cerbro-Spinal Fluid (CSF) partial volume map was generated as described previously [Polimeni et al., 2010] and used to assess contamination from WM or CSF.

Tractography

Streamline tractography was used in an attempt to visualize the trajectories of pathways between the cortex and the underlying white matter. Streamlines were reconstructed based on the diffusion tensor model using the Diffusion Toolkit and TrackVis (Ruopeng Wang, Van J. Wedeen, TrackVis.org, Martinos Center for Biomedical Imaging, Massachusetts General Hospital) which employs the standard Fibre Assignment by Continuous Tracking (FACT) algorithm [Mori et al., 1999]. For this tracking the angle threshold was set to 90°.

Ex Vivo Human Specimen 0.5 mm isotropic data (N=1)

A left hemisphere from a 79 year old male with no clinical history of central nervous system disease, dementia, major psychiatric illness, or head trauma was obtained from the Neuropathology Department at Masschusetts General Hospital and had been fixed for 6 years in 10% formalin before imaging. The post-mortem interval was 24 hours. For surface reconstruction, Fast Low Angle SHot (FLASH) (TR=20ms, TE=1.8ms-15.92ms, flip angle = 5:5:30, 1mm isotropic resolution) [Fischl et al., 2004] data were acquired on the whole hemisphere using a 1.5T Siemens. In order to utilize the FreeSurfer surface reconstruction pipeline [Dale et al., 1999, Fischl and Dale, 2000] which assumes in vivo T₁-weighted contrast (i.e. WM > GM > CSF), we used the multiple echoes as well as parameter maps generated from the multi-echo, multi-flip FLASH data [Fischl et al., 2004] to synthesize a linear combination of volumes that is optimal with respect to image contrast. Specifically, we acquired multi-echo FLASH (TR=20ms, TE=1.8ms-15.92ms, flip angles = 5°,10°,15°,20°,25°,30°and 1 mm isotropic voxels).

The cortical surfaces were computed from an optimal weighted combination of the multi-echo, multi-flip angle FLASH scans. This required manually delineating ROIs containing small regions of grey matter, white matter, fluid and air (note that these ROIs did not completely outline each of these tissue classes, but rather were used as representative of the signal properties of each class). Using these signal values, we constructed an energy function that measured the contrast between the various tissue classes in a weighted sum of the 51 underlying volumes (8 echoes for 6 different flip angles plus 3 parameter maps). Two optimal weighting vectors were estimated - one that maximized the normalized signed contrast between white matter and grey matter to synthesize a volume that is T₁-weighted in appearance, and one that maximized the normalized signed contrast between grey matter and embedding fluid. This latter volume was used to mask out non-brain regions in the grey/white contrast image. The resulting volume was used as input to the standard FreeSurfer surface deformation described in [Fischl et al., 1999, Fischl and Dale, 2000].

For diffusion imaging, the hemisphere was cut yielding an M1/S1 sample which fit in an 10 cm diameter cylinder. This sample was placed in a proton-free fluid, Fomblin LC/8 (Solvay Solexis Inc.). Diffusion images were acquired using 0.5 mm isotropic resolution on a 4.7T Bruker Biospec Avance system equipped with 400 mT/m gradients. The acquisition used a 3D Stejskal-Tanner spin-echo sequence (TR/TE =350/25 ms , matrix size = 128 × 112 × 88, 20 directions at b = 4500 s/mm² (δ=6ms, Δ=11ms), and 2 b=0 images. Total acquisition time was 20 hours. The b=0 diffusion weighted images were aligned to the cortical surfaces from the hemisphere using the boundary-based registration method [Greve and Fischl, 2009].

In Vivo Anesthetized Rhesus Macaque 0.7 isotropic data (N=1)

All procedures were approved by the Massachusetts General Hospital Subcommittee on Research Animal Care and are in accordance with National Institutes of Health guidelines for the care and use of laboratory animals. Data were acquired on 1 male rhesus monkey (Macaca mulatta; 4 years old) on a 3T Siemens Tim Trio using an insert head gradient (AC88, Gmax= 80mT/m, slew rate = 400T/m/s) and a custom-built, surgically implanted 8-channel head receive coil [Janssens et al., 2012]. The monkey was anesthetized with isoflurane and positioned in a sphinx position, and his head was fixed with a head post. The acquisition consisted of an 0.6 mm isotropic MEMPRAGE using (TI/TR/TE_avg/α=900/2100/3.65ms/9°, Tacq = 9min.). Diffusion weighted single shot 2D twice refocused SE-EPI with 0.7 mm isotropic resolution were acquired using (TR/TE= 6960/77ms, matrix size = 148 ×148, iPAT=3, partial Fourier = 6/8, 61 axial slices, BW = 1408 Hz/pixel). Total diffusion acquisition was 3 hours long including 5 averages of 256 directions at b=1000 s/mm², and 50 b=0 images interspersed every 9 volumes.

Surface reconstructions, DTI, radiality indices and partial volume analyses were performed as described above for the 1 mm isotropic human data. Cortical surface reconstructions for the macaque data required significant modifications and manual intervention compared to the conventional FreeSurfer [Dale et al., 1999] pipeline. In the conventional pipeline, human data is first transformed to Tailarach space such that atlases may provide key baseline information to assist with bias field correction, skull stripping and tissue segmentation. Since a corresponding macaque atlas was unavailable, the automated bias field correction required a higher number of iterations and a careful selection of the stopping threshold. The brain center and radius were manually defined to assist with the automated skull stripping. Automated tissue segmentation required manual definition of the pons and corpus callosum as well as many control points throughout the white matter.

Results

In Vivo Human 1 mm isotropic data (N=6)

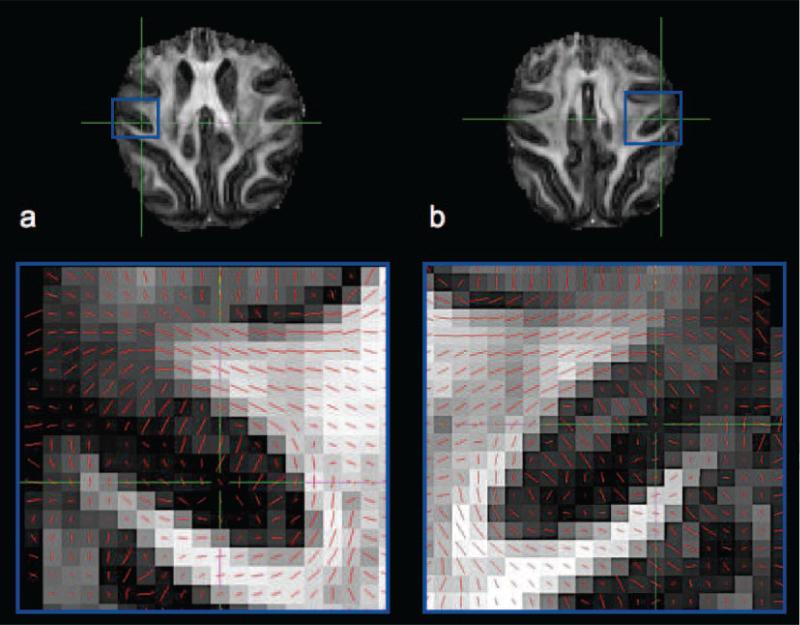
Figure 1 shows a subset of the in vivo human 1 mm isotropic DTI data for one subject. The FA and directionally encoded color (DEC) maps (Fig. 1a and b) exhibit high SNR and low levels of distortions. Figure 1c shows an axial slice of the FA map in region surrounding the central sulcus with the principal eigenvector of the diffusion tensor superimposed using line representations. The principal eigenvector in cortical voxels anterior to the central sulcus (i.e. M1) appears radial while those in S1, located posterior to the central sulcus, appear tangential. Still, it is difficult to fully appreciate the cortical diffusion anisotropy relative to the highly convoluted geometry of the cortex using the traditional slice representation.

FIG. 1.

DTI from one subject including a) a fractional anisotropy map (coronal), b) a directionally-encoded colour map (coronal) and c) principal diffusion orientations (red lines) superimposed on FA map in the region of S1 and M1 (axial).

The coherent anisotropy seen within the CSF in Figure 1bc seems to indicate an orientation bias within our data. There exist many potential sources of an orientation bias in a diffusion-weighted imaging experiment (e.g. gradient imperfections, imaging gradients unaccounted for in the b-matrix calculation, eddy currents, mis-registration, brain pulsation) and as of yet we have not narrowed down the source of the apparent coherent anisotropy in the CSF. Artifactual FA values within CSF are an order of magnitude lower compared to the cortex ( 0.02 compared to 0.2 respectively) so it is a small effect.

The temporal SNR estimate in the cortex was 12.9. Performing the same calculation for an ROI at the center of the brain (within white matter and subcortical grey matter) gave an SNR estimate of : 4.5. We see then that the well known spatial sensitivity profile of an array coil, which imposes a higher sensitivity at the edge of the brain compared to the center, works to our favour since we are only interested in the data from the cortex. SNR in the center of the head is also lowered by our GRAPPA reconstruction (R=3), which is of course also related to the coil sensitivities.

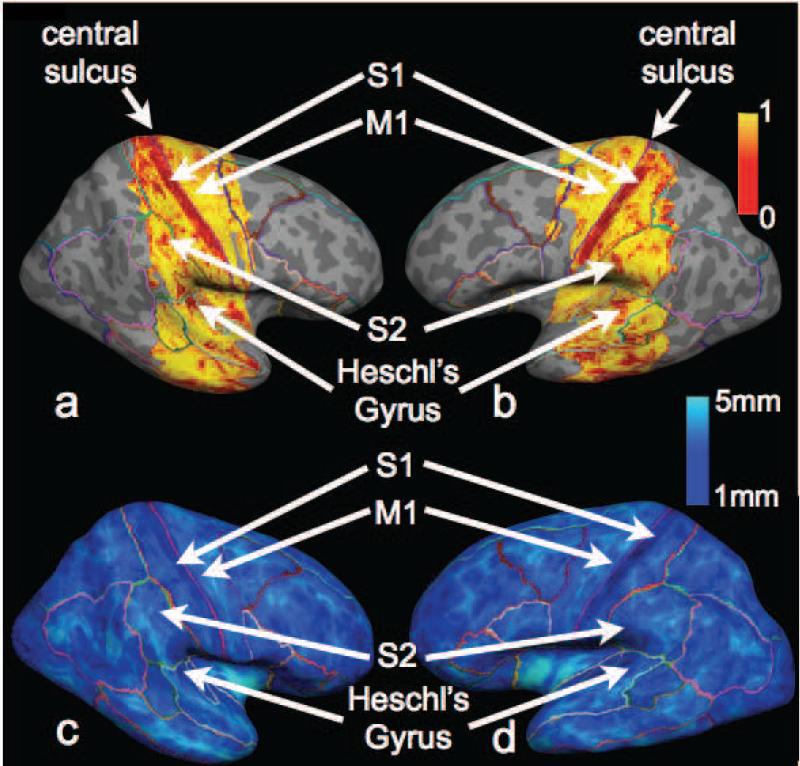
Figure 2 depicts the radiality index (red=tangential, yellow=radial) plotted on the folded and inflated surfaces for the middle cortical depth for all six human subjects. The most dominant feature is the red stripe that is visible on all subjects and represents a volume where the cortical diffusion is primarily tangential to the cortical surface. Figure 3a and b shows radiality plotted on the inflated surface representation for one of the 6 subjects (subject 2 in Fig. 2). The boundaries of FreeSurfer's automatic parcellation (colored lines) are also superimposed on the surface and show that the tangential red stripe corresponds closely to the region of the primary somatosensory cortex (S1). Directly adjacent to S1, the motor cortex (M1) appears largely radial, as do most other areas that were encompassed by our imaging region. Heschl's gyrus containing primary auditory cortex (A1) and secondary somatosensory cortex (S2) also show predominantly tangential diffusion. Cortical thickness plots for the same subject (Fig. 3cd) show that the primary somatosensory cortex is about half as thick as the adjacent motor cortex ( 1.5+/- 0.1 mm vs. 2.7 +/- 0.2 mm) and therefore more prone to partial volume effects. Figure 4 shows the tissue composition on average for both hemispheres and all 6 subjects in hand-drawn ROIs of a) S1 and b) M1 across 10 cortical depths. Whereas cortical depths 2-6 have very little partial voluming of white matter or cerebrospinal fluid for M1 (Fig. 4b), S1 has significant partial voluming at all depths except for depth 6 (Fig. 4a). For depths 4,5, and 6 the mean percentage of WM partial volume was 15%, 8%, and 4% respectively in S1 and 1.7%, 0.6%, 0.2% in M1. As expected, the 0.5 mm resolution ex vivo acquisition showed considerably lower partial volume contamination (6.3%, 1.8%, and 0.1% for depths 4,5,6 in S1).

FIG. 2.

Radiality at the middle cortical depth plotted on the folded (top) and inflated surfaces (bottom) for six subjects. The dominant feature is a red stripe (representing primarily tangential diffusion) that corresponds closely with the primary somatosensory cortex.

FIG. 3.

Top: Radiality plotted for the middle cortical depth for the left (a) and right (b) hemispheres of one subject. S1, S2 and Heschl's gyrus (A1) exhibit tangential diffusion. M1 and most other cortical areas encompassed by our imaging region exhibit radial diffusion. Bottom: Cortical thickness maps obtained via FreeSurfer in the same subject show that the S1 is about half the thickness of M1 (~1.5 mm compared to 2.7 mm respectively).

FIG. 4.

Partial volume analysis of different tissue types across 11 cortical depths for in vivo (a:S1,b:M1) and ex vivo (c:S1,d:M1) data. The left axis represents the mean voxel tissue composition across hand-drawn regions of interest on both hemispheres.

Figure 5 displays the group average after surface-based alignment of a) mean diffusivity, b) fractional anisotropy and c) radiality on the inflated surface and across 6 cortical depths corresponding to surfaces 0, 2, 4, 6, 8 and 10 spanning from the white matter surface (0th surface) to the pial surface (10th surface) and for both cerebral hemispheres. The slice positioning was not identical between subjects. Therefore, for the group average, vertices for which we had data from at least four of the 6 subjects were included in Figure 5. As expected, mean diffusivity is less at the white matter surface reflecting the hindered diffusion of the WM component. Mean diffusivity gradually increases towards the pial surface where presumably CSF contamination contributes. Fractional anisotropy is highest at the white matter surface and decreases towards the pial surface. Radiality (Fig. 5c) is generally low at the white matter, increases in the middle cortex depths and decreases again near the pial surface. However, the red, tangential stripe in S1 is consistent across all depths. Also there are two conspicuous yellow stripes of radial diffusion at the white matter surface (Fig. 5c i and iv). Plotting the mean radiality at the white matter surface (i.e. Fig. 5c i and iv) on the curved surface representation (Fig. 6a), it becomes clear that these stripes of radial diffusivity correspond to the crowns of the pre- and post-central gyri. The observation that only the crowns of gyri exhibit radial diffusion at the interface between the white matter and the grey matter is potentially indicative of fibers turning sharply at the WM/GM border along the banks of a gyrus and following a straight path at the crown of the gyrus. Tractograpy in Figure 6c demonstrates these patterns.

FIG. 5.

Depth-dependent features of a) mean diffusivity (MD) b) fractional anisotropy (FA) and c) radiality. Values are overlaid on the inflated surface and represent the group average for regions where data from at least 4 out of 6 subjects overlapped. i-vi represent surfaces 0, 2, 4, 6, 8 and 10 for the right hemisphere and vii-xii represent surfaces 0, 2, 4, 6, 8 and 10 for the left hemisphere. The 0th surface represents the interface between the white matter and the cortical grey matter. The 10th surface represents the pial surface. In general MD increases and FA decreases when progressing from the white matter to the pial surface. Radiality is low at the white matter surface, higher at the middle cortical depths and lower at the pial surface with the exception of S1 (indicated by white arrows) which displays low radiality at all cortical depths.

FIG. 6.

Mean radiality at the interface between the white matter and the cortex for the right (a) and left (b) hemispheres. Only those cortical regions where data from at least 4 of the 6 subjects overlapped were included. The white matter interface exhibits mostly tangential diffusion with the exception of the crowns of the gyri which appear radial. c) Tractography of connections between WM and cortical GM are consistent with the radiality patterns in a) and b). At the crown of the gyrus the pathways appear to follow a straight line between the WM and cortical GM. Along the banks the pathways exhibit a sharp turn at the WM/GM boundary.

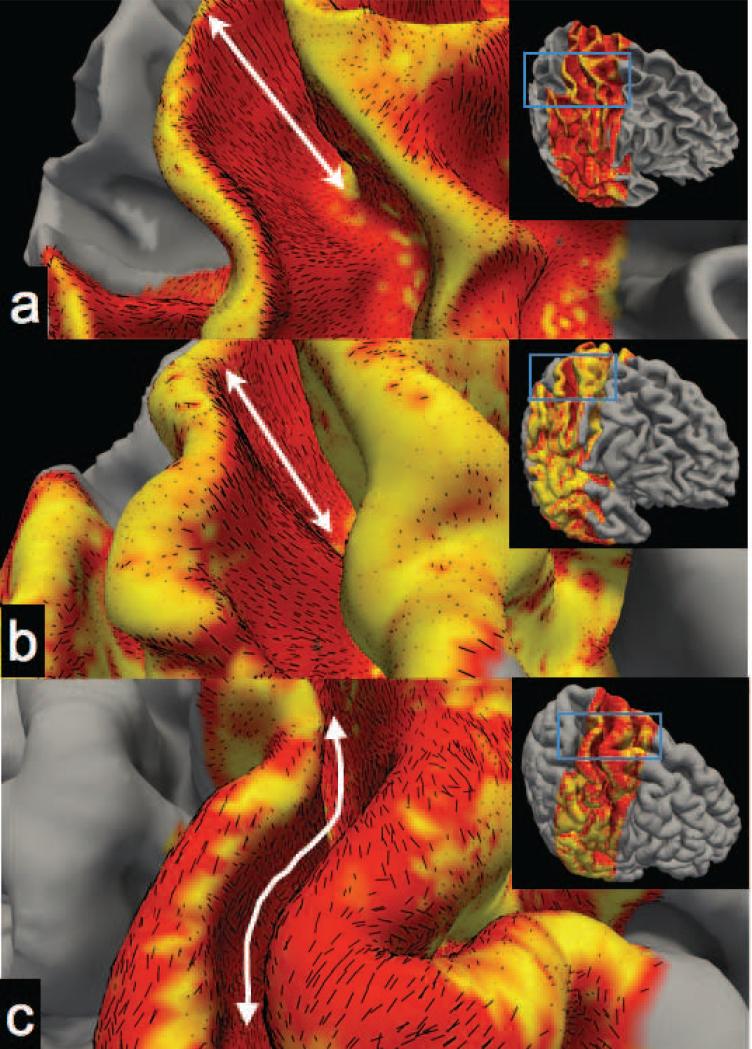
The radiality index provides a convenient visualization of the diffusion anisotropy within the cortical reference frame. For regions with radial diffusion, the orientation is uniquely described. In areas of tangential diffusion the radiality index does not distinguish the specific orientation the tangential plane. We therefore plot the tangential component of the principal eigenvector as a short line-segment on the folded cortical surface reconstruction (Fig. 7). This serves to both visualize the diffusion orientation with respect to the cortical folding pattern and the degree of spatial coherence of tangential diffusion. At the white matter surface and central depths (Fig. 7a,b) the tangential diffusion on the bank of the S1 sulcus is coherently directed along the path between the fundus and the crown. Note, at the middle cortical depth the diffusion is only tangential (red) in the S1 region of Figure 7. At the pial surface (Fig. 7c) the diffusion is tangential in extended areas but oriented differently than the deeper cortical depths. At the pial surface the tangential diffusion appears to follow the “elevation” contours of the cortical topology (i.e. along the length of the fundus and crown).

FIG. 7.

The tangential component of the primary eigenvector of the diffusion tensor (represented as yellow lines) superimposed on the radiality plots on the curved cortical surfaces for a) the interface of the white matter and the cortex, b) the middle cortical depth and c) the pial surface. Double-sided arrows highlight the dominant orientation of the vector field, i.e. between the crown and the fundus for a) and b) and along the length of the fundus and crown for c).

In Figure 8, we plot radiality versus FA is plotted for the middle cortical depth of the post-central, pre-central, supra-marginal and transverse-temporal regions (as defined by aparc.a2009s.annot available in FreeSurfer) for left and right hemispheres of all 6 subjects (N = 262419). A weak but significant correlation was found between radiality and FA (p < 0.05 for 0.1878 < r < 0.1951). Confidence bounds were based on an asymptotic normal distribution of 0.5 log((1 + r)/(1 – r), with an approximate variance equal to 1/(N – 3). The possibility of a quadratic relationship between radiality and FA was also explored. Fitting a second order polynomial yielded : y = 0.075x² + 0.0110x + 0.0787 where y=FA and x=radiality and the norm of the residuals was 25.4319.

FIG. 8.

Radiality versus fractional anisotropy at the middle cortical depth including the post-central, pre-central, supra-marginal and transverse-temporal regions (as defined by aparc.a2009s.annot available in FreeSurfer) for left and right hemispheres of all 6 subjects.

Figure 9 displays the distribution of the radiality index for crowns, fundi, and banks used for Figure 8. as classified by local curvature. Table 1 summarizes the percentage of vertices studied in Figure 9 that displayed radial and tangential diffusion (radial:= radiality > 0.6, tangential:= radiality < 0.4) for locations classified by curvature within each of three categories: crowns, banks and fundi. This suggests that local curvature is not associated with a particular diffusion orientation and the tangential diffusion observed in S1 is not simply due to its location on a sulcal bank.

FIG. 9.

Histograms showing the distribution of radiality measurements for a) crowns, b) banks c) fundi including vertices within the post-central, pre-central, supra-marginal and transverse-temporal regions (as defined by aparc.a2009s.annot available in FreeSurfer) for left and right hemispheres of all 6 subjects.

Table 1.

Curvature	% Radial Diffusion Vertices	% Tangential Diffusion Vertices
Crowns	71.88%	17.59%
Banks	71.01%	18.73%
Fundi	77.89%	12.63%

Skewness calculations within hand-drawn surface labels at the middle cortical depth and across the 6 in vivo human datasets found the percentage of vertices representing oblate diffusion tensors to be 33.4% and 31.5% within S1 and M1 respectively. Therefore, the majority of diffusion tensors in both cortical regions were prolate with a well-defined principal diffusion orientation. Also, the fraction of oblate versus prolate diffusion tensors in each cortical region was nearly equal.

For those diffusion tensors classified as oblate within S1, 36.1% were oriented such that the principal and secondary eigenvectors were in the tangential plane. For the oblate diffusion tensors in M1, 8.8% were oriented such that the principal and secondary eigenvectors were in the tangential plane. Therefore, the majority of the oblate tensors were not oriented with their long axes in the tangential plane and, as such, do contribute some uncertainty to the radiality estimates. However, these oblate diffusion tensors represent a relatively small fraction of the vertices in each cortical region.

Ex Vivo Human Specimen 0.5 mm isotropic data (N=1)

Figure 10 shows ultra-high-resolution DTI (0.5 mm isotropic) of a fixed human brain specimen containing M1 and S1. The higher spatial resolution affords 2-3 voxels across S1 cortex and 4-5 voxels across M1. M1 exhibits predominantly radial diffusion while the anisotropy in S1 appears less coherent showing some tangential diffusion and some radial diffusion. Figure 11 shows radiality surface plots of the ex vivo data. The somewhat noisy data in the cortex and less robust surface reconstruction associated with ex vivo data render somewhat noiser radiality surface plots, however, evidence of tangential diffusion in S1 and radial diffusion in M1 is still observable in the middle cortical depths.

FIG. 10.

DTI at 0.5 mm isotropic resolution of a fixed human brain specimen containing the brain regions surrounding the central sulcus including S1 and M1. a) and b) coronal images of directionally encoded colour (DEC) and fractional anisotropy (FA) respectively. c) and d) axial images of DEC and FA. e) Axial image of the region defined by the red box in c). The high radiality in M1 corresponds closely with observations in in vivo human and macaque data. S1 appears tangential is certain regions but radial in other regions.

FIG. 11.

Radiality surface plots for the fixed human brain specimen containing the brain regions surrounding the central sulcus including S1 and M1. Six cortical depths are shown, representing surfaces 0, 2, 4, 6, 8 and 10 where the 0th surface is the white matter surface and the 10th surface is the pial surface. White arrows point to M1. Posterior to M1, the S1 cortex shows evidence of the tangential diffusion observed in vivo at lower spatial resolution.

In Vivo Anesthetized Rhesus Macaque 0.7 isotropic data (N=1)

The long scan time, head-post stabilization, head-insert gradients and an implanted 8 channel RF array-coil combined to yield a high SNR, high-resolution in vivo macaque DTI data. In the region of the central sulcus, cortical diffusion anisotropy patterns in M1 and S1 are similar to those observed in humans (i.e. M1=radial diffusion, S1=tangential diffusion) (Fig. 12). Looking at the radiality plotted on the curved and inflated surfaces across multiple cortical depths (Fig. 13) the laminar patterns are also similar that observed in humans (i.e. more tangential at the white matter and pial surfaces and more radial at the middle cortical depths).

FIG. 12.

Axial DTI in in vivo macaque (0.7 mm isotropic) showing the principal eigenvectors of the diffusion tensor superimposed on the FA map in the region of central sulcus. The observed cortical diffusion anisotropy is consistent with the human data, i.e. radial diffusion in M1 (anterior to the central sulcus) and tangential diffusion in S1 (posterior to the central sulcus).

FIG. 13.

Radiality index for in vivo macaque plotted on right (a-b) and left (c-d) hemispheres and on curved (a and c) and inflated (b and d) surfaces for six equally spaced cortical depths corresponding to surfaces 0, 2, 4, 6, 8 and 10 which range from the white matter surface (0th surface) on the left to the pial surface (10th surface) on the right.

Discussion

Laminar Analysis

In this study we project diffusion measures onto intermediate laminar surfaces. We have divided the cortex into 10 equally spaced depth regions defined by 11 surfaces. For the thickest cortex ( 3 mm), this subdivides the cortex into depth regions approximately 3× smaller than our 1 mm voxels. Thus the analysis includes a form of population analysis that can determine if a diffusion measure is biased toward a specific cortical depth. One limitation of the laminar-style analysis is that the cortical depths represent percentages of local cortical thickness and do not directly correspond with the histologically defined cortical layers I-VI. At the crowns of the gyri, the lower cortical layers are expanded radially and the upper layers compressed, while at the fundi the reverse occurs [Van Essen and Maunsell, 1980, Hilgetag and Barbas, 2006]. Thus in our scheme, the correspondence to the layers will depend on the local curvature. It is also important to appreciate that any given voxel may be associated with more than one intermediate surface and therefore a comparison of two different regions of cortex with different cortical thicknesses (such as S1 and M1) will show the thinner cortex having less variation across cortical depths since the computed intermediate surfaces are closer together and share more voxels between them.

The defining feature of the cortex is its laminar organization of neurons and vasculature that changes across difference functionally distinct regions. Although, the laminar analysis does not correspond directly to the histologically defined cortical layers which vary their spacing according to curvature, it gets us closer to this type of characterization. The laminar analysis framework also provides the ability to smooth the data tangentially, which can increase sensitivity to laminar features.

Partial Volume Effects

Partial volume dilution of grey matter voxels with highly organized and anisotropic white matter is a major barrier to concluding that S1 displays an intrinsic signature of tangential diffusion. This is particularly problematic for S1 since it is among the thinnest cortical areas in the brain (~2 mm). Within the S1, the orientation of tangential diffusion at the middle cortical depth (Fig. 7b) shows the same orientation as the underlying white matter (Fig. 7a), i.e. it is aligned along the line between the crown and the fundus of the gyrus. However, the partial volume analysis (Fig. 4a) supports the conclusion that isolation of the middle layer provides nearly pure (91%) cortical grey matter. The partial volume effects at the pial surface support this interpretation. Voxels known to be heavily partial-volumed with the pial surface and CSF (depth 0 and 1) also show predominantly tangential orientation. But analysis of the direction shows that in S1 the pial/CSF contaminated voxels have approximately orthogonal orientation compared to the central and deep layers. While we do not know the source of the observed anisotropy of these surface voxels, the transition in direction gives us confidence that we have enough spatial resolution to resolve and exclude these edge effects.

The partial volume estimates presented in this study are based on the nominal voxel size and do not take into account point spread function effects such as T₂* blurring across the EPI acquisition window. For a conservative T₂* estimate of 30 ms and our readout duration of 46 ms, the T₂* point spread will increase in the voxel dimension along the phase-encode direction (S-I) by 8.16%.

A significant result that argues against white matter partial-voluming as being the source of the observed cortical tangential diffusion is that we do not find a strong correlation between radiality and fractional anisotropy (Fig. 8). If in fact, all observations of cortical tangential diffusion were merely a white matter partial voluming effect, then we would expect to see higher cortical FA correlated with lower radiality and we do not. This is very clear in Figure 5bc.

Orientation Bias

Coherent anisotropy is observed within the CSF in our in vivo data. There exist many potential sources of an orientation bias in a diffusion-weighted imaging experiment (e.g. gradient imperfections, imaging gradients not considered in the b-matrix calculation, eddy currents, mis-registration and brain pulsation) and as of yet we have not narrowed down the source of the apparent coherent anisotropy in the CSF. Since the FA values within the CSF are only ~0.02, the potential effect seems small, especially since voxels with FA < 0.05 were excluded from our anlayses. If our data had significant orientational bias (from any source) it seems unlikely that we would be able to measure such consistent and widespread radial diffusion patterns that follow so closely to the folding patterns of the cortex in all different orientations. Also, our SNR estimate of 12.9 within the cortex indicates that we are well above the threshold of SNR < 5 for which magnitude noise bias starts affect diffusion measurements [Jones and Basser, 2004]. So we do not expect this to be the source of the potential bias.

Tangential Diffusion

Evidence of tangential diffusion in S1, S2 and auditory areas is supported by the higher resolution in vivo macaque data and to a lesser extend by the ex vivo human data. The presence of tangentially oriented fibers in S1 is also supported by prior literature showing myelin stains S1 of Macaque fascicularis [Lewis and Van Essen, 2000]. Further, functionally distinct regions of S1 in adult and infant macaque monkeys have been shown to be organized as stripes along the crown-to-fundus axis of the gyral wall with apparent connections within each somatotopic stripe but not between somatotopic groups [Qi and Kaas, 2004]. In fact, septum (regions devoid of myelin) have been observed between the stripes forming different somatotopic regions [Qi and Kaas, 2004]. This basic organization is consistent with the diffusion directions observed in S1 in Figure 7b if the diffusion direction is due to diffusion along the intra-cortical fibers within these regions.

Leuze et. al.s recent findings in fixed tissue [Leuze et al., 2012] show radial diffusion in both M1 and S1 but also lower radiality in S1 and tangential diffusion at both the white matter/grey matter interface and at the pial surface. When the entire thickness of the S1 cortex is averaged into only one or two voxels (as is nearly the case with our in vivo data) the resulting dominant orientation of diffusion might be tangential. We do not discount the issue of partial voluming with white matter but it seems possible, based on Leuze et. al.s observations that intra-cortical partial voluming across the thinner S1 cortex could lend itself to our tangential diffusion observations as well.

One hypothesis for the observation of tangential diffusion in S1 and A1 is simply the absence or at least rarity of the very large and radially oriented pyramidal cells. Prior studies [Hackett et al., 2001], show that large pyramidal cells are rare within auditory core. Even though S1 has significant radial organization, if its radial fibers are of a smaller radius and/or are packed with a different density, then we may not be as sensitive to these smaller compartments when using the long diffusion and echo times typical of a clinical scanner. Our in vivo acquisition, using a twice-refocused bipolar diffusion encoding and Gmax = 40mT/m had an effective diffusion time of 75 ms, whereas our ex vivo acquisition, which employed the conventional Stejskal-Tanner diffusion-weighted spin echo on a small bore scanner equipped with Gmax = 400 mT/m achieved a diffusion time of 11 ms. Shorter diffusion times are required in order to probe smaller tissue compartments [Callaghan, 1991]. T₂ effects also affect our sensitivity to tissue compartments of different sizes. Highly restricted water tends to have shorter T₂ values and therefore the ex vivo acquisition with an echo time of 25 ms, may offer sensitivity to signals from small compartments that we cannot detect with the 100 ms echo time of our in vivo acquisition.

Surface-Based Alignment

Surface-based alignment enables multi-subject averaging of surface overlays based on the primary folding pattern of the cortex [Fischl et al., 1999]. Cortical features that correspond closely to the primary folding pattern can be enhanced by averaging data from multiple subjects as was done in Figure 2. However, some cortical regions, such as the primary auditory cortex, are less consistently located by the folding pattern. Therefore the surface-based alignment and subject averaging procedure may diminish features in these areas. This would be consistent with our observation that the tangential diffusion observed in the region of A1 was not augmented by subject averaging (Fig. 5c).

Crossing Fibers

Crossing fibers are pervasive throughout cortex. Potential sources of cortical diffusion anisotropy include individual axons (myelinated and/or un-myelinated), axonal bundles, dendrites, interdigitated fibres, intra- and/or extra-axonal diffusion, packing geometry and density. Recently Jespersen et. al. [Jespersen et al., 2012] developed a quantitative relationship between water diffusion anisotropy and neuronal morphology within the immature ferret cortex, as determined by the rapid Golgi technique and confocal microscopy. Based on co-registered MRI and Golgi data, Jespersen found excellent agreement between diffusion anisotropy and the volume fraction of neuropil (axons and dendrites). In a separate study, crossing fibers were detected in the deeper cortical layers of ex vivo porcine cortex [Dyrby et al., 2011].

Still, compared to the nearly two decades of literature describing white matter diffusion anisotropy relatively little is known about diffusion anisotropy in the cortex. For this reason, we chose to keep the analysis of the cortical diffusion patterns as simple as possible in the first instance. Our goal was to map the dominant diffusion orientation at each cortical location and depth. The diffusion tensor becomes oblate or completely isotropic in the presence of intra-voxel crossing fibers of equal diffusivity. However, for crossing fibers of unequal diffusivity it is still possible to detect the orientation of maximal diffusivity and it is our hypothesis that in many cases there is a dominant diffusion orientation within voxels in cortex. This hypothesis is supported by our skewness calculations which show that on average two thirds of the diffusion tensors at the middle cortical depth are prolate. Still, modeling diffusion patterns in the cerebral cortex is a nascent field and little is known about the robustness of the diffusion tensor model within cortex. Sensitivity to the dominant diffusion orientation could possibly be increased with a model that is a closer representation of the underlying cortical architecture. Future work aims to explore more complicated models of diffusion such as the one recently proposed by Jespersen et. al. in developing cortex [Jespersen et al., 2012] and to assess the dependence of these methods on spatial resolution, angular resolution, spin-displacement resolution and SNR.

Since our primary concern was systematic errors in determining the GM structure due to partial volume effects with WM, the acquisition was optimized for small isotropic voxels. While it is often advantageous in a clinical setting to prescribe very high in-plane resolution and thick slices (e.g. 0.8 mm × 0.8 mm × 5 mm [Holdsworth et al., 2009]), the highly folded cortex necessitates isotropic voxels in order to avoid directional biases. The use of parallel imaging to minimize distortions was also critical. Targeting a specific brain region and minimizing the number of slices enabled a shorter TR and more averages provided adequate SNR to support the small isotropic voxels.

Surface Reconstruction

The definition of the white matter/grey matter border using either automatic surface reconstruction or manual delineation will always be subjective since there is a gradation of diminishing myelin content at the grey/white matter border. FreeSurfer depends on T₁-weighted contrast to define the grey/white border. Since T₁ is sensitive to myelin content, cortical regions with high myelin content might have a more ambiguous delineation. Nonetheless, we found, as has been shown previously [Fischl and Dale, 2000], that FreeSurfer's cortical thickness estimates are in close agreement with those reported by Von Economo and Koskinas [Von Economo and Koskinas, 1925]. FreeSurfer's use of image intensity gradients for surface placement provides it with sub-voxel accuracy, as evidenced by Han et. al. 2006 [Han et al., 2006] which demonstrated 120 μm reproducibility of the FreeSurfer method when reconstructing surfaces from 1 mm data, from the same individual based on data acquired on different days. To achieve a precision that is ~1/10 of voxel's length argues to the robustness of FreeSurfer's sub-voxel placement. Still, the observed tangential diffusion in S1 could reflect a systematic misplacement of the WM/GM border such that there are increased partial volumes of highly ordered WM in this area.

Macaque Imaging

While the white matter features of the macaque brain are much smaller than the corresponding white matter tracts in humans, the monkey cortex is nearly as thick as the human brain and therefore higher spatial resolution actually achieves more voxels across the cortex. The detailed atlases that exist for the monkey brain based on electrophysiology experiments also make the monkey cortex an attractive target to study the potential sources of the observed cortical diffusion anisotropy.

Ex Vivo Imaging

The ex vivo diffusion imaging results are not in direct correspondence with the in vivo data. Figure 10 displays relatively small portions of S1 with a tangential orientation and larger portions with a radial orientation. Therefore, this ex vivo data is perhaps in closer agreement with Leuze et. al.'s ex vivo data [Leuze et al., 2012]. A couple of effects that could cause a discrepancy between in vivo and ex vivo diffusion imaging results are: 1) tissue may be degraded by an unknown amount due to autolysis during the post-mortem interval [D'Arceuil et al., 2007] and 2) tissue fixation is known to induce changes in the size and/or exchange of restrictive tissue compartments as a result of protein cross-linking [Shepherd et al., 2009]. Either of these two effects could change the diffusion sensitivity to a particular feature of cortical architecture. Additionally, there is the question of whether vascular compartments affect our diffusion signal. We would expect a vascular contribution to propagate in very different way in vivo compared to ex vivo. Vascular contributions to diffusion imaging is an area worthy of further investigation since cortical vasculature also has a coherent radial orientation.

Even if tissue degradation and fixation effects are not significant, the differences in ADC values, q-values and diffusion times between the ex vivo and in vivo acquisitions may sensitize the diffusion-weighted signal to different microstructural features. At this point many studies have validated that white matter diffusion anisotropy properties are, for the most part, preserved in fixed tissue, however, there has been much less focus on comparing in vivo and ex vivo grey matter diffusion anisotropy.

A final consideration is that the surface-based analysis of ex vivo data (Figure 11) is also more prone to error because it is more challenging to reconstruct an accurate cortical surface representation from fixed tissue due to tissue deformations and reduced relaxation times that change the tissue contrast in the images from which the surfaces are derived. As an example of tissue deformations problems, one can imagine the scenario in which grey matter on one sulcus is pressed up against grey matter from the opposing sulcus, making it very challenging to achieve an accurate segmentation of the cortical ribbon. Calculating the radiality index accurately requires both high SNR diffusion data and accurate surface reconstructions.

Summary of Study Findings

In this study, we have used a surface-based analysis to characterize cortical diffusion anisotropy, for the first time, in the cortical reference frame (radial versus tangential as well as the orientation within the tangential plane). We also present the first laminar analysis of cortical diffusion data and provide estimates of partial voluming.

Large regions of cortex and especially primary motor cortex display predominantly radially oriented diffusion. In vivo human and macaque data display tangential diffusion in S1 and less reproducibly in A1 and S2. Ex vivo human data show portions of S1 with a tangential orientation and larger portions with a radial orientation. The in-plane orientation of tangential diffusion in S1 at the middle cortical depth is the same as the underlying white matter (between the crown and fundus).

Our partial volume analysis based on the nominal 1 mm isotropic voxel size shows that isolation of the middle laminar layer provides nearly pure (91%) cortical grey matter. T₂* point spread was estimate to cause an increase the voxel size by 8.16%.

Significance

MRI studies commonly measure gross cortical properties such as thickness [Fischl and Dale, 2000]. Cortical thinning has been well-characterized relative to normal aging [Salat et al., 2004]. Localized cortical thinning has been shown to be a predictive marker of Alzheimer's disease [Holland et al., 2009], early onset schizophrenia [Douaud et al., 2007] and treatment outcomes of epilepsy patients [Bernhardt et al., 2010]. Detection of localized cortical thickening has provided new evidence of brain plasticity relating to stroke recovery [Schaechter et al., 2006] and specialized training [Draganski et al., 2004]. Yet, little is known about what these cortical thickness changes represent such as which layer(s) are affected and the precise underlying structures (e.g. cell density or size, fiber myelination, or dendrite arborization) undergoing these changes. Non-invasive MRI signatures of these cortical organizations could transform our understanding of brain function development, aging, plasticity, neuronal disease etiology and progression as well as providing a useful clinical tool. Diffusion MRI is an ideal modality to probe cortical architecture since it is sensitive to sub-voxel tissue geometry. In this study we show that diffusion MRI is capable of isolating unique cortical substructure and that the observed orientations provide coherent signatures of cortical areas. It is hoped that further advances in diffusion imaging will provide even more detailed signatures of cortical architecture and that these methods will improve clinical evaluation of disorders of the cortex.

Highlights.

• A diffusion MRI technique for examining the microstructure of the cerebral cortex.

• Diffusion anisotropy can be reliably detected in the in vivo human cerebral cortex.

• Framework for relating cortical diffusion orientation to local cortical orientation.

• Framework for studying cortical depth-dependent features of diffusion.

• Assessment of partial volume effects.

• Cerebral cortical diffusion is predominantly orthogonal to the surface of the cortex.

• In vivo data shows tangential diffusion in S1 and to a lesser extent S2 and A1.

• Ex vivo data shows mostly radial diffusion and some tangential diffusion in S1.