Abstract
We demonstrate that conformational exchange processes in proteins on microsecond-to-millisecond time scales can be detected and quantified by solid-state NMR spectroscopy. We show two independent approaches that measure the effect of conformational exchange on transverse relaxation parameters, namely Carr–Purcell–Meiboom–Gill relaxation-dispersion experiments and measurement of differential multiple-quantum coherence decay. Long coherence lifetimes, as required for these experiments, are achieved by the use of highly deuterated samples and fast magic-angle spinning. The usefulness of the approaches is demonstrated by application to microcrystalline ubiquitin. We detect a conformational exchange process in a region of the protein for which dynamics have also been observed in solution. Interestingly, quantitative analysis of the data reveals that the exchange process is more than 1 order of magnitude slower than in solution, and this points to the impact of the crystalline environment on free energy barriers.
Introduction
Functional processes in proteins, such as enzymatic catalysis, ligand binding, or allosteric signal transmission, rely on the ability of proteins to sample multiple conformational states, differing in structure and free energy. There is increasing evidence that the actual functional states of proteins are in many cases higher-energy conformers in dynamic equilibrium with the major, lowest-energy conformer, rather than the lowest-energy state itself.1−4 In many cases, the exchange processes between these different functional states occur on a microsecond-to-millisecond (μs–ms) time scale, which also coincides with typical time scales of enzyme catalysis and protein folding. Therefore, the accurate characterization of dynamic processes on this time scale, and the identification and structural characterization of higher-energy conformations in equilibrium as well as the relative populations and exchange kinetics, are of primary importance for understanding protein function. Due to their low population and short lifetimes, detecting and characterizing such higher-energy conformers is a major experimental challenge.
NMR spectroscopy in the solution state plays a prominent role in studies of conformational exchange processes and is able to provide information at atomic resolution.5 In NMR, the presence of low-populated conformational states, exchanging with the major conformation on μs–ms time scales, is manifest as enhanced decay of single- or multiple-quantum coherences. Thus, a first indication about conformational exchange processes may be obtained from inspection of transverse relaxation rates (e.g., R2 rate constants of 15N). Higher-than-average values of R2 may indicate the presence of exchange processes. In solution NMR, a variety of more quantitative and direct techniques have been developed to probe conformational exchange processes with great detail and accuracy.5,6 The most prominent ones of those are Carr–Purcell–Meiboom–Gill (CPMG) relaxation-dispersion (RD)6,7 and R1ρ relaxation-dispersion8 techniques and the analysis of differential relaxation of multiple-quantum coherences9−11 These methods allow the determination of thermodynamic and kinetic parameters in terms of relative populations and exchange-rate constants, as well as site-specific chemical-shift differences between the major, observable state and the higher-energy conformation. Structural information about these minor, not directly observable states can thus be obtained.
Studies of protein dynamics in the solid state have recently attracted great interest,12−18 motivated by numerous important biophysical questions related to insoluble proteins, such as the dynamics and gating of membrane proteins in native membranes or the conformational flexibility in fibrils. Magic-angle spinning (MAS) solid-state NMR methods that probe either fast (sub-microsecond) motions or slow (ms-to-seconds) dynamics in an atom-resolved manner are available,19−21 but so far a quantitative investigation of processes occurring on the μs–ms time scale has remained a major challenge.
In this article, we present approaches for the detection and quantitative measurement of μs–ms conformational exchange processes by MAS solid-state NMR that exploit the effect that conformational exchange processes have on single- and multiple-quantum line widths. We demonstrate two independent approaches, namely the measurement of differential line broadening of zero- and double-quantum coherences and CPMG RD. Both approaches rely on differences between line widths (or, equivalently, lifetimes) to extract information about conformational exchange, rather than on the line widths themselves. This is crucial, as solid-state NMR line widths typically contain contributions from coherent mechanisms (e.g., dipolar dephasing).22 We find that under suitably chosen experimental conditions, these differences in line widths are only weakly dependent on coherent dephasing mechanisms, allowing thus—to a good approximation—the quantitative analysis of the experimental data in terms of conformational exchange (vide infra).
In order for our approaches to be successful, it must be ensured that the lifetimes of the involved single- and multiple-quantum coherences are sufficiently long that the differences can be measured with the necessary precision. For example, CPMG RD experiments, such as used in solution state, typically use delays of tens of milliseconds, during which the coherence decay is monitored in the presence of a train of refocusing pulses. In a typical solid protein sample undergoing MAS at moderate frequency, coherence lifetimes are generally only a few milliseconds at most, without high-power proton decoupling, and CPMG approaches are, therefore, not readily applicable. High-power 1H decoupling can extend these lifetimes to 10–20 ms, although at the cost of sample heating, which impedes quantitative dynamical analysis. We circumvent these limitations by using highly deuterated protein samples and high MAS frequencies. As reported earlier by several groups, 15N single-quantum lifetimes in such conditions become very long, often exceeding 100–200 ms.23−25 As we find here, even heteronuclear multiple-quantum 1H–15N coherences have lifetimes of tens of milliseconds under such conditions. These long lifetimes open the way to use transverse relaxation parameters for quantitative measurement of conformational exchange. We make use of this potential, and obtain insight into conformational exchange processes in microcrystalline ubiquitin. We find evidence for a conformational exchange process involving residues that also undergo exchange in solution, but at a rate that is more than 1 order of magnitude slower than in solution.
Results and Discussion
Differential Zero- and Double-Quantum 1H–15N Line Broadening Reveals Conformational Exchange
As a first approach for the study of conformational exchange in solid protein samples, we investigate the differential rate of dephasing of 1H–15N multiple-quantum coherences (MQC). Differential line broadening of zero- and double-quantum coherences (ZQC/DQC) is expected whenever the isotropic and/or anisotropic components of the chemical shifts of the two involved nuclei undergo simultaneous fluctuations.9,26 This effect has been exploited in solution state to probe conformational exchange,10,27,28 and is often referred to as differential zero- and double-quantum relaxation. (Although when considering μs–ms processes, it is not a relaxation phenomenon in the sense of Redfield theory.29 In this paper, we will preferentially use the terms “differential line width” or “differential decay” instead of “differential relaxation”.) Here, we explore the feasibility of exploiting these effects in the solid state, by studying correlated chemical-shift modulation in amide 1H–15N spin pairs.
We first analyze the properties of differential ZQC and DQC decay in the solid state by numerical spin simulations. To this end we consider the simplest possible model, a two-spin 1H–15N system undergoing stochastic jumps between two distinct conformations differing in the orientation of the bond vector and CSA tensor orientations and/or in the isotropic chemical shifts of the two nuclei. Figure 1 shows representative results of such simulations for a system undergoing exchange between a major (90%) and a minor (10%) conformation. Shown is the differential ZQC/DQC decay rate, ΔRMQ = RDQ – RZQ, for various exchange-rate constants. In order to identify the origin of the differential decay, separate simulations were performed for (i) a scenario where minor and major state have different isotropic chemical shifts but identical chemical-shift anisotropy (CSA) tensors (blue), and (ii) a situation where the two states have identical isotropic shifts, but the two CSA tensors undergo orientational fluctuations (green). Modulation of the isotropic shifts only (scenario i), leads to differential MQC decay rates if exchange occurs on a time scale of microseconds to a few milliseconds, slightly depending on the exchange parameters and chemical-shift differences. This is identical to solution-state NMR,9,26,30 and the simulations can be fully described by a formalism derived previously (see Supporting Information, Figure S1).30 Fluctuations of the magnitude and/or the orientations of the two CSA tensors (scenario ii) also induce differential decay, which can be understood as an interference between MAS and these CSA fluctuations. The origin of such fluctuations may be an exchange process between a major and a minor conformation, as shown in Figure 1, or bond librations within a continuum of conformers, such as restricted orientational diffusion (Figure S2). Irrespective of the precise motional model, such CSA/CSA modulations will lead to strong differential MQ decay whenever they occur on a time scale of tens of nanoseconds to about one millisecond. Finally, we note that via either of the two mechanisms (CSM/CSM or CSA/CSA), the ΔRMQ can be positive or negative, depending on the sign of the isotropic chemical-shift changes of the two nuclei, and the CSA parameters (see Figures S3 and S4). Taken together, these simulations indicate that the differential multiple-quantum line broadening in the solid state is a sensitive reporter of conformational-exchange processes on time scales in the range of tens of nanoseconds to milliseconds.
Figure 1.
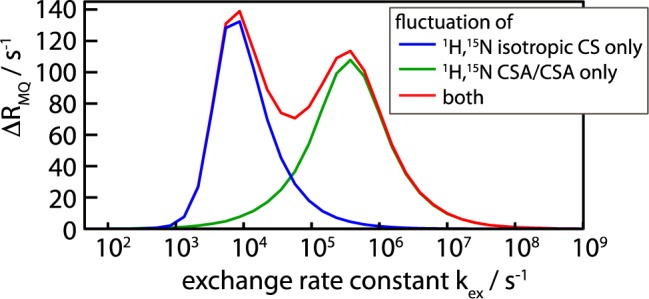
Numerical simulations of the differential decay rates of zero- and double-quantum coherences (differential multiple-quantum decay rate), ΔRMQ = RDQ – RZQ, in a 1H–15N spin pair undergoing exchange. A two-site exchange system involving a major state (populated at 90%) and a minor state (10%) was assumed, with an exchange rate kex = kAB + kBA, where kAB denotes the forward rate constant. ΔRMQ is shown as a function of the exchange-rate constant. The different simulations assume either only isotropic chemical-shift modulation (ΔνN = 160 Hz, ΔνH = 800 Hz), only CSA/CSA modulations (jumps by 30°), or both, as indicated in the insert. Details about the simulation parameters and additional simulations are provided in the Supporting Information.
To test the practical usefulness of differential MQC decay for dynamics studies in the solid state, we have applied the experiment shown in Figure 2a to u-[2H,15N]-labeled microcrystalline ubiquitin, reprotonated stochastically at 20% of the exchangeable sites, undergoing MAS at a frequency of 50 kHz, at a sample temperature of 300 K. In the pulse sequence of Figure 2a, an initial state 2HxNx (a combination of ZQ and DQ coherences) is prepared utilizing scalar coupling. Such a J-coupling transfer is enabled by the long coherence lifetimes of 1H and 15N.25 During the subsequent MQC evolution delay, the operator 2HyNy builds up from the initial 2HxNx whenever ZQC and DQC decay differently. From two separate experiments, probing the 2HxNx and 2HyNy operators, respectively, one can quantify the differential decay rate ΔRMQ = RDQ – RZQ. For this experiment to be successful, it is necessary that the MQC are sufficiently long-lived, such that the buildup can be followed. Under the conditions employed in this study, we were able to follow the 1H,15N MQC decay over tens of milliseconds.
Figure 2.
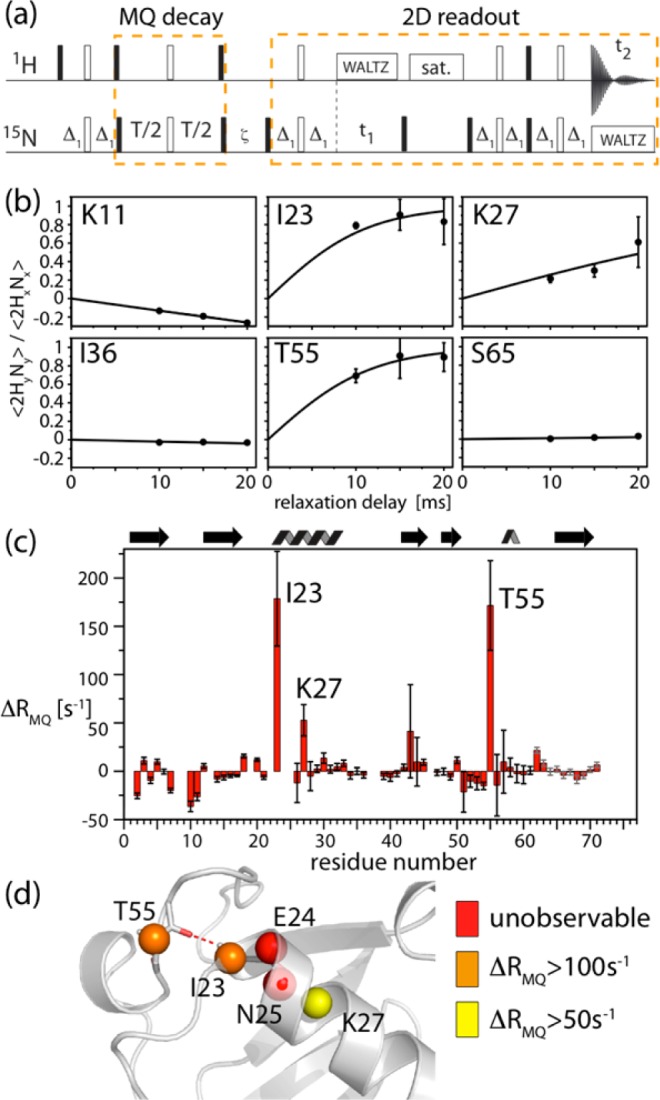
Measurement of differential multiple-quantum decay rates. (a) Pulse sequence used in this study. Differential zero- and double-quantum line broadening is obtained from separate experiments that probe the coherences, 2HxNx and 2HyNy, respectively, which are selected by setting the phases of the pulses at the end of the MQC evolution delay.9 Details about delays and phase settings are shown in Figure S6 in the Supporting Information. (b,c) Experimental data obtained on a microcrystalline sample of ubiquitin at 300 K: (b) Representative examples of the buildup of 2HyNy from 2HxNx, along with best-fit curves, ΔRMQ = (2 atanh(⟨2HyNy⟩/⟨2HxNx⟩))/T. Error bars were obtained from 2 times the standard deviation of the spectral noise. (c) Fitted residue-wise differential multiple-quantum decay-rate constants ΔRMQ, using three different relaxation delays. Error margins were determined from Monte Carlo simulation based on error bars determined from twice the spectral noise. Residues with particularly large ΔRMQ are indicated. Note that, in principle, a single relaxation delay would suffice to determine ΔRMQ. (d) Residues for which large ΔRMQ are observed (I23, K27, T55) as well as unobservable resonances (E24, N25) in 1H-detected HSQC-type spectra31 are plotted onto the structure. The H-bonding of I23(HN)-R54(CO) is indicated.
Figure 2b shows experimental buildup curves of the state 2HyNy from 2HxNx for a set of representative residues. Fits of the differential decay-rate constant ΔRMQ to these curves are indicated as solid lines, and residue-wise values of ΔRMQ are shown in Figure 2c. Most strikingly, large ΔRMQ values are observed for residues I23, K27, and T55, with respective values of ΔRMQ = 179 ± 47, 53 ± 16, and 172 ± 44 s–1, greatly exceeding average values for the other residues (average value of −1.4 s–1, standard deviation 12.3 s–1). Figure 2d shows the location of these residues in the structure of ubiquitin.
The large values of ΔRMQ reveal fluctuations of the isotropic and/or anisotropic components of the chemical shifts of the 1H/15N nuclei of residues I23, K27, and T55. As shown above, the two mechanisms (CSA/CSA, CSM/CSM) are sensitive to different time scales of motion. From the present data alone it is not possible to determine whether the underlying process involves CSA/CSA fluctuations, (tens of nanoseconds to tens of microseconds time scale), or if it arises from fluctuations of the isotropic chemical shifts (tens of microseconds to a few milliseconds). However, several arguments indicate that isotropic chemical-shift modulations on a μs–ms time scale are at the origin of the differential decay. The most important experimental evidence comes from our recently reported 15N–1H dipole/15N CSA cross-correlated relaxation measurements.31 This cross-correlated relaxation rate is sensitive to motion occurring on the same time scale for which CSA/CSA fluctuations induces differential MQC decay.32 Notably, residues I23, K27, and T55 did not show elevated 15N–1H dipole/15N CSA cross-correlated relaxation-rate constants, showing that these residues do not undergo large-scale nanosecond-to-microsecond motion.31 This finding rules out the possibility that CSA/CSA fluctuations are the main reason for the observed the differential MQC decay. As a further indication for isotropic chemical-shift modulations, the neighboring residues E24 and N25 are invisible in proton-detected scalar-coupling-based NMR spectra,31 presumably as a consequence of short coherence decay times. Thus, the pronounced differential MQC decay found here for the three residues strongly suggest the presence of a conformational exchange process involving fluctuations of isotropic chemical shifts occurring on a time scale of tens of microseconds to a few milliseconds. CPMG RD data below confirm this analysis. In principle, it would be possible to discriminate between isotropic and anisotropic chemical-shift fluctuations as the cause the of the large differential decay-rate constants by performing the experiment at a different MAS frequency, which alters the position of the maximum of the CSA/CSA contribution (see Figure S5), or through rf irradiation during the MQC evolution.33,34
Figure 2c shows that some variation in ΔRMQ values is also found for other residues in ubiquitin. We ascribe these residue-wise differences to local variations of motional amplitudes, causing enhanced ΔRMQ via the CSA/CSA mechanism; for example, larger than average |ΔRMQ| are observed in the loop comprising Gly10 and Lys11, for which we have previously reported extended mobility on a time scale of hundreds of nanoseconds.31 The relatively large ΔRMQ for L43 is not statistically significant; indeed, CPMG experiments do not show any conformational exchange for this residue (see below).
15N CPMG Relaxation-Dispersion Experiments
In order to obtain more quantitative insight into the exchange process revealed by the above MQC decay data, we explored single quantum 15N CPMG RD as a second experimental strategy to probe conformational dynamics in the solid state. CPMG RD experiments measure the 15N coherence decay as a function of the repetition rates of CPMG refocusing pulses, νCPMG. In order to be quantitatively accurate, it must be ensured that all coherence decay mechanisms that are not due to isotropic chemical-shift fluctuations do not depend on the CPMG frequency (any CPMG frequency-independent contribution to decay rates, however, would not hinder quantitative accuracy). These mechanisms are (i) Redfield relaxation (in solution and in the solid state), and (ii) coherent mechanisms leading to a decay, in particular dipolar dephasing in the solid state. In order to ensure that the former (Redfield relaxation) is independent of the CPMG frequency, two approaches have been proposed in solution state: a relaxation-compensated scheme on the one hand,35 that ensures that in-phase coherence (Nx) and anti-phase coherence (2HzNy) evolve for the same amount of time irrespective of νCPMG, as well as an approach that only measures the decay of in-phase coherence, by suppressing the buildup of anti-phase coherence through 1H decoupling.36 For reasons of decoupling efficiency, in the latter approach the 1H decoupling field is slightly varied between different CPMG frequencies.36 In the solid state, this latter approach is complicated by the fact that varying the 1H decoupling field strength induces artifacts related to partial interference between MAS and 1H irradiation, which can lead to a partial reintroduction of dipolar couplings (see Figure S8). Therefore we opted here for the former approach, a constant-time37 relaxation-compensated35 scheme. This experiment measures the effective rate of 15N coherence decay, R2eff, as a function of the CPMG pulsing rate (see Figure 3a), by using a single constant time delay without 1H decoupling. Long 15N SQ coherence lifetimes even without 1H decoupling25 under fast MAS conditions enable this experiment.
Figure 3.
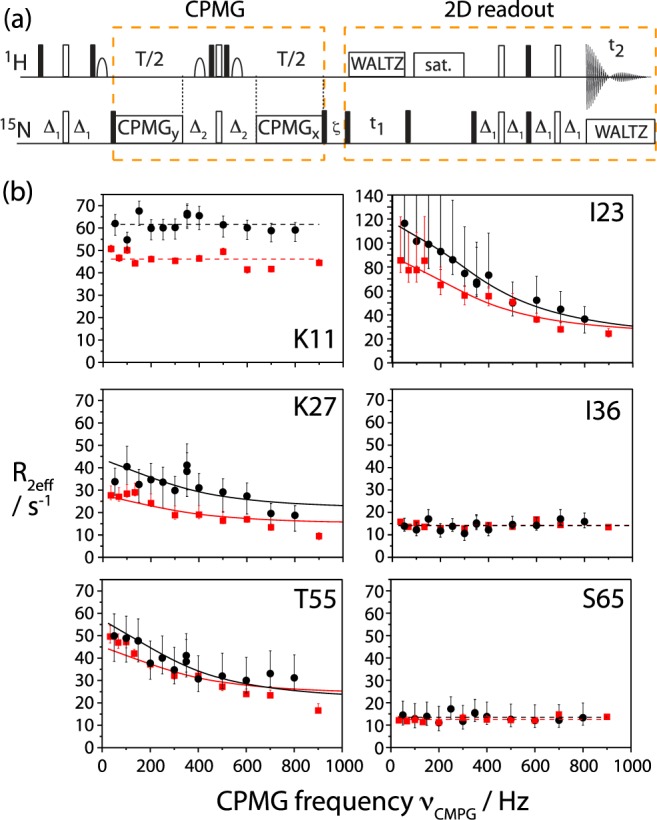
(a) Pulse sequence used in this study to measure 15N CPMG relaxation-dispersion data on deuterated proteins in the solid state. Details are shown in the Supporting Information. (b) 15N CPMG RD solid-state NMR data obtained on microcrystalline ubiquitin at 300 K sample temperature, collected at a 1H Larmor frequency of 600 MHz (red) and 800 MHz (black). Note the different scale in the data of Ile23. Upper and lower error bars of R2eff were determined from Monte Carlo simulations, based on twice the spectral noise (see Figure S17). For residues I23, K27, and T55, solid lines represent the Bloch–McConnell fit, in other cases lines represent the mean values of the individual data points. Data for all other residues are shown in the Supporting Information.
In addition to ensuring that the Redfield relaxation part is independent of νCPMG, it must also be ensured that the decay induced via coherent mechanisms (dipolar dephasing) is independent of the CPMG frequency. We have investigated this issue experimentally and through numerical simulations, as follows. Representative experimental CPMG dispersions, i.e., the effective transverse decay rate, R2eff, as a function of the pulse repetition rate νCPMG, are shown in Figure 3b, measured at two different B0 field strengths (14.1 and 18.8 T). Measurements at several B0 field strengths are valuable as the isotropic chemical shift changes upon exchange (in Hertz) depend on the magnetic field, and thus dispersion profiles change with B0.38 Large dispersions, i.e. a pronounced dependence of R2eff on νCPMG, are observed for residues I23, K27, and T55—the same residues for which large ΔRMQ values also pointed to conformational exchange of these residues. However, the overwhelming majority of residues display flat CPMG dispersion curves, as exemplified in Figure 3b (K11, I36, S65). The observation of such flat CPMG curves indicates that the νCPMG-dependent variations of decay due to coherent mechanisms are small, a consequence of the strong reduction of the dipolar coupling network in our sample. In order to obtain a more detailed understanding of the properties of CPMG experiments in a rotating solid sample undergoing exchange, as required for any quantitative interpretation, we then turned to numerical spin simulations. These simulations, shown in the Supporting Information (Figures S9–S15), reveal that in the general case, CPMG dispersion profiles in a rotating solid are more complex than in solution. Interference effects between time-dependent fluctuations of anisotropic interactions (dipolar couplings, CSA), MAS rotation, and the CPMG pulses may arise. These interferences generally lead to increased decay rates R2eff. These increased decay rates are only slightly dependent on the CPMG frequency (a νCPMG-independent shift of dispersion profiles would be irrelevant for data analysis). Variations of R2eff with νCPMG that are not due to isotropic chemical-shift fluctuation are estimated to be below about 5 s–1. This is within the error bar of our experiments. We therefore conclude from experimentally observed flat CPMG curves and from simulations, that the possible systematic errors in the CPMG curves—which might prohibit quantitative interpretation of such curves in terms of dynamics—are below our experimentally observed error bars. The large dispersions observed for I23, K27, and T55 (Figure 3) are clearly dominated by isotropic chemical shift fluctuations.
We therefore applied the Bloch-McConnell formalism, which is strictly valid in solution-state, but which neglects any effects specific to solid-state NMR, to interpret the dispersion profiles found for residues I23, K27, and T55. A common exchange event for the three residues was modeled, with a population of the minor state, pB, and exchange rate constant kex = kAB + kBA (where kAB and kBA denote forward and backward rate constants), along with individual residue-specific chemical-shift differences between major- and minor-state, ΔωAB. Solid lines in Figure 3b show the best-fit curves for such a fit. The data can be explained by a higher-energy conformation populated to pB = 10.0% (±3.2%), and an exchange rate kex = 2100 s–1 (±700 s–1). The chemical-shift differences, |ΔωAB|, for Ile23, Lys27, and Thr55 were obtained as 3.8 ppm (±1.2 ppm), 1.5 ppm (±0.6 ppm), and 2.0 ppm (±0.7 ppm), respectively. We note that fitting the residues individually results in identical populations and rate constants (within error margins) as a joint fit, although at lower precision.
We also verified that the use of the simplistic Bloch–McConnell treatment, i.e., the neglect of the effect of coherent mechanisms, does not introduce large systematic errors. To this end, we simulated a larger (4-spin) system undergoing exchange with the above parameters, as well as MAS and fluctuations of anisotropic interactions. The exchange parameters resulting from a Bloch–McConnell fit to these simulations shows that the systematic errors in the fitted values of pB, kex and |ΔωAB| are below their respective random error levels given above (see Table S1).
The extracted exchange parameters for I23, K27, and T55 can be used to estimate the differential decay experimental data: the proton chemical shift difference required to reproduce the experimental ΔRMQ, based on these exchange parameters, are of the order of 0.5 ppm (see Figure S19).
Finally, we note that the plateau levels of R2eff vary substantially among the non-exchanging residues. For example, while for Ile36 and Ser65 we find values of R2eff in the range of 10–20 s–1, Lys11, which also displays a flat dispersion curve, has much faster transverse decay (about 50–70 s–1; Figure 3b). The absolute values of these plateaus cannot rigorously be interpreted in terms of motion, as these plateau levels contain contributions from coherent dephasing mechanisms. However, the variability in these values between different residues points to previously identified large amplitude motions on nanosecond time scales in this region of the protein (loop spanning residues 8–11), which increases the transverse relaxation-rate constants.31
Comparison to Conformational Exchange in Solution
The above data reveal a conformational exchange process in microcrystalline ubiquitin in which the N-terminal part of the α-helix and the adjacent loop (Figure 2d) are in exchange with a minor conformation populated to 10%. At 300 K this process occurs at a rate of about 1400–2800 s–1. It is interesting to compare our findings to data obtained in solution. Comparative studies of dynamics in solution and in crystals have been reported recently for the case of sub-microsecond motion,12,39−41 and we can perform such a comparison here for the first time for μs–ms motion.
Conformational exchange processes in ubiquitin have been addressed in a number of solution-state NMR studies.10,28,42−46 Two regions have been found to undergo exchange, (i) the region comprising residues I23-N25 and T55, i.e., the N-terminal part of the α-helix and the adjacent loop, and (ii) residue V70; these processes are thought to be independent.46,47 The exchange process involving V70 is fast in solution, and could initially only be detected with T1ρ measurements at low temperatures, including supercooled water,45,46 and later with experiments that selectively probe μs motion.43 Even at low temperatures (260–278 K), the exchange process involving V70 occurs at a time scale of about 100 μs.45,46 Such fast motions would not induce CPMG dispersions of significant amplitude, and may thus escape from detection in our CPMG experiment, particularly as our experiments were performed at higher temperature (300 K), where the process is expected to be even faster. An exchange process on a time scale of tens of microseconds should, however, induce differential MQC decay via the CSA/CSA mechanism, which we do not observe. This suggests possible differences in the motion of V70 between solution and microcrystals.
Interestingly, the other region for which conformational exchange is present in solution, i.e. the N-terminal part of the helix and adjacent loop, corresponds exactly to the region for which our experiments reveal conformational exchange. However, the rate constant of this process is clearly different. In solution, the conformational exchange process occurs at a rate of about 12500–25000 s–1,10,44,46 at temperatures of 277–280 K, i.e., ∼20 K lower than the temperature used here (300 K). At 298 K, the process is essentially undetectable by T1ρ measurements in solution, presumably because it is too fast (several tens of thousands per second). The population of the higher-energy conformation could not be obtained from solution-state measurements, as populations and chemical-shift differences cannot be disentangled in the fast exchange regime from T1ρ measurements. Our data show that in the crystalline state the motional rate constant is more than 1 order of magnitude slower than in solution. We also investigated whether differences in the solvent conditions, such as pH or viscosity may explain such a large slowdown of the motion. However, solution-state CPMG and differential MQC decay data in solvent conditions very similar to the crystallization conditions, including up to 45% (v/v) precipitant, do not show any detectable exchange (Figures S20 and S21). Thus, we conclude that it is indeed the crystalline environment that causes the slowdown of the exchange process.
It is interesting to speculate about the origin of the different exchange rates in solution and microcrystals. In solution state, a mechanistic picture of the observed conformational exchange process has been proposed recently, primarily from mutation studies47 and analyses of chemical shifts,44 as well as from inspection of conformational heterogeneity in various solution and X-ray structures. The conformational heterogeneity is illustrated in Figure 4, showing ubiquitin’s structure in the microcrystals used in this study (a,b) and in solution (c,d). Most importantly, these structures differ in the conformation of the loop D52 to T55. In microcrystals (panels a, b) this loop adopts a type II β-turn conformation, with a H-bond between E24 (side chain) and G53 (NH). The available solution structure, as well as other crystal structures (e.g., PDB 1ubi), show a type I β-turn conformation and a H-bond between D52 (NH) and E24 (CO); i.e., the two structures differ by a flip of the peptide plane D52-G53. The exchange process as detected by solution NMR is thought to correspond to an exchange between the type I and the type II β-turn, as well as to the breaking of the H-bond of I23(NH)-R54(CO) and side-chain reorganization.10,44,47
Figure 4.
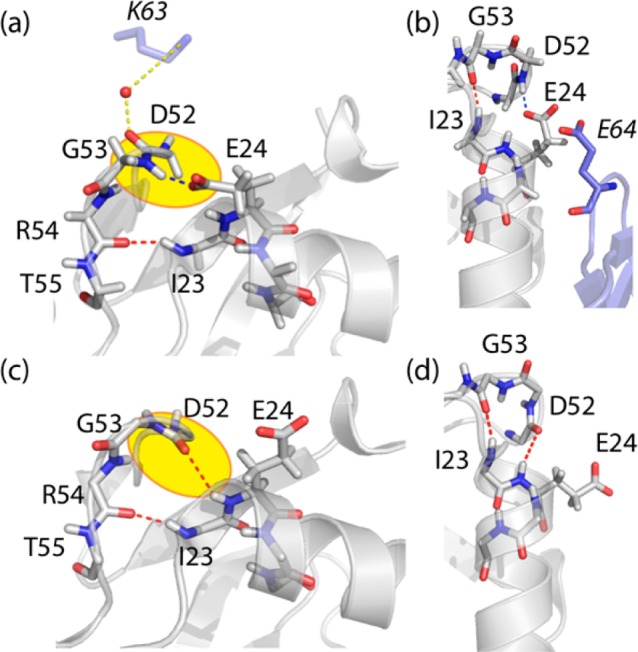
Structural comparison of the microcrystals used in this study, PDB 3ons(48) (a,b), and a solution structure of ubiquitin, PDB 1d3z(49) (c,d). Intramolecular H-bonding among backbone atoms and H-bonds involving side chains are indicated in red and blue. Water-mediated intermolecular H-bonds are shown in yellow. Neighboring molecules in the crystal lattice are shown in light blue in (a) and (b), highlighting residues K63 and E64 of the neighboring molecules. Note the different conformation of the loop E51-R54 in the two structures (a,b) and (c,d), resulting in a flip of the orientation of NH(G53) and CO(D52).
The structural differences between the major conformational states in solution (type I β-turn) and in microcrystals (type II β-turn) provide one explanation for the different exchange rate constants: it appears that the relative energies of the lowest-energy state and higher-energy states are reversed in solution and microcrystals. In addition, a number of intermolecular contacts could also contribute to a slowdown of the motion in microcrystals. Particularly, in microcrystals the backbone carbonyl of D52 is H-bonded via a water molecule to a lysine of a neighbor molecule (Figure 4a), and the conformation of E24’s side chain is stabilized by an intermolecular contact to E64 of another molecule (Figure 4b), thus stabilizing the type II β-turn conformation. An exchange process involving a flip of the backbone of D52/G53, would require that all these interactions be broken. The free-energy barrier that needs to be overcome for breaking these interactions in microcrystals would certainly slow down the exchange process.
Conclusions
In summary, we have provided the first direct quantitative analysis of the μs–ms dynamics of a protein in the solid state, using two independent approaches based on transverse coherence decay. To the best of our knowledge, transverse decay parameters have not been used in a quantitative manner as measures of μs–ms conformational exchange in solid-state NMR. The advent of deuteration and fast MAS is changing this situation, thus providing new possibilities for studying dynamics quantitatively.
The measurement of the differential MQC decay explored here allows identifying the regions undergoing slow motional processes. In contrast to solution-state experiments, both isotropic and anisotropic chemical-shift fluctuations contribute to the differential MQC decay and report on events on long time scales (hundreds of nanoseconds to milliseconds). We foresee that similar approaches will be useful for spin pairs other than 1H,15N, e.g., 13C,15N or 13C,13C pairs. From a suite of such experiments using different nuclei, a comprehensive picture of the exchange process may be obtained. Moreover, in the solid state MQC may be established even for spins remote in sequence, and the differential decay of these coherences may provide insight into correlated motions over longer distances. Recent reports of proton–proton double-quantum transfer over up to 10 Å may indicate one possible route in this direction.50,51 At this point, we did not attempt a quantitative analysis of differential MQC decay in terms of exchange parameters. Such an analysis is complicated by the fact that a single experimental observable, i.e., the differential line broadening, is sensitive to a number of parameters, including chemical-shift parameters for two nuclei and exchange rates. As shown here, CPMG RD experiments can provide such quantitative information about conformational exchange processes. When combined with advanced deuteration and back-protonation schemes, similar approaches as used here for 15N may become applicable also to other backbone and side-chain moieties. For example, using sparse random protonation52 or methyl-selective labeling,39,41 very long 13C coherence lifetimes are achieved, which enable CPMG experiments, opening possibilities toward a detailed characterization of higher-energy conformations in proteins in the solid state. Deuteration and fast MAS will also enable the measurement of other probes of conformational exchange, such as T1ρ RDs, and may also be interpretable in terms of quantitative exchange parameters. Progress in this direction has been reported recently.22,53
This study has focused on a microcrystalline protein. We find the conformational exchange process to be altered by the crystalline environment, relative to free solution. This direct demonstration of the impact of the environment on dynamics is of physicochemical interest, and it also indicates that one must be careful in interpreting data from crystalline preparation in terms of biological relevance in solution state. Importantly, the proposed experiments open new avenues for the study of more complex molecules, for which the solid state is the biologically relevant preparation, such as membrane proteins and amyloid fibrils. It has been shown recently that proton-detected experiments, akin to the approaches used here, can also be applied to highly deuterated samples of membrane proteins or amyloid fibrils.54,55 Long heteronuclear coherence lifetimes in such samples are expected to enable similar experiments as shown here. Further improvements in experimental design in terms of more efficient coherence transfers (CP instead of INEPT), proton decoupling, and optimized levels of protonation may be envisaged to improve sensitivity, which will be particularly useful for such challenging samples. We foresee that studies of μs–ms motion will be instrumental for understanding complex biomolecular processes, such as allosteric binding and gating of membrane proteins.
Materials and Methods
Protein Preparation
u-[2H,15N]-ubiquitin was produced by bacterial overexpression in D2O based media, and purified using standard procedures. Prior to crystallization, the protein was dissolved in a D2O/H2O mixture (ratio 8/2) at pH 9 for several days to ensure uniform back-protonation of exchangeable hydrogen sites at the desired H/D ratio. Microcrystals were obtained by addition of methylpentanediol (MPD) at pH 4.3, as described,56 using a mixture of D2O/H2O and MPD-d12.31 The resulting ratio of H/D on exchangeable sites was approximately 8/2. Protein microcrystals were filled into a 1.3 mm Bruker rotor or a 1.8 mm rotor, using an ultracentrifuge device.57
NMR Experiments
Differential MQC decay experiments and RD experiments at 800 MHz 1H Larmor frequency were carried out on a Bruker Avance III 800 MHz spectrometer, equipped with a 1.3 mm HCN triple-resonance probe. The MAS frequency was set to νr = 50kHz and stable to within 10 Hz. CPMG RD experiments at 600 MHz 1H Larmor frequency were carried out on a Bruker Avance II spectrometer. A custom-made 1.8 mm triple-resonance probe (Ago Samoson, Tallinn, Estonia) was used for these measurements, and the sample was spun at 45 kHz. Additional measurements, shown in the Supporting Information (Figures S8 and S15), were recorded on a Varian DirectDrive 600 MHz spectrometer, equipped with 1.6 mm fast-MAS triple-resonance HXY probe. The effective sample temperature was adjusted to 300 K in all cases, using the bulk water line as a chemical-shift thermometer. All spectra were referenced to internal DSS (3-(trimethylsilyl)-1-propanesulfonic acid, sodium salt). Pulse-sequence details and delay settings are specified in the Supporting Information. Solution-state NMR spectra (Supporting Information) were collected on a 600 MHz Varian DirectDrive spectrometer equipped with a triple-resonance probe operating at room temperature. In CPMG experiments at 800 MHz, 12 different CPMG frequencies (νCPMG = 50, 100, 150, 200, 250, 300, 350, 400, 500, 600, 700, 800 Hz) and an additional duplicate data point at νCPMG = 350 Hz were collected, while at 600 MHz, 11 values of νCPMG were measured (33.3, 66.7, 100, 133.3, 200, 300, 400, 500, 600, 700, 900 Hz). In all instances the CPMG frequency is defined as νCPMG = 1/(2δ), where δ is the spacing between the centers of successive π pulses, thus following the most widely used definition in solution-state studies.
Data Analysis
All spectra were processed with nmrPipe58 and visualized with NMRView (OneMoon Scientific. Inc.). All peak intensities were obtained from NMRView, and further processed using MATLAB/Octave scripts. Differential MQC decay rates were obtained as ΔRMQ = (2 tanh–1(⟨2HyNy⟩/⟨2HxNx⟩))/T, where T is the evolution delay. Errors were estimated from 1000 Monte Carlo runs, taking 2 times the standard deviation of the spectral noise as uncertainties of the individual peak intensities. Relaxation-dispersion data were analyzed by numerical integration of the Bloch-McConnell equations in MATLAB. Data for the three residues were jointly fit to a two-state exchange model. Error bars of the individual R2eff data points were obtained by taking 2 times the standard deviation of the spectral noise as estimates of the uncertainties of the peak intensities. Error bars of R2eff were allowed to be asymmetric, i.e., different toward higher/lower values (see Figure S17). Error bars of the extracted exchange parameters were obtained from 10 000 Monte Carlo runs, based on these asymmetric error estimates of R2eff. Additionally, we estimated the error bars of the exchange parameters from inspection of the reduced χ2 surface of the fit procedure, and error estimates are similar (see Figure S16). Numerical simulations of the spin evolution in an exchanging system during the two pulse sequences, as shown in the Supporting Information, were performed using the GAMMA simulation software.59
Acknowledgments
This work was supported by the French National Research Agency ANR (Project ANR-10-PDOC-011-01 ProtDynByNMR), the Austrian Science Foundation FWF (project P22735), the Swiss National Science Foundation (Grant 200020_134681), and the European Commission under the Seventh Framework Program (FP7), contract Bio-NMR261863. We thank the TGIR-RMN THC FR3050 for access to the 800 MHz spectrometer at the Center for High-Field NMR in Lyon. We thank Prof. Robert Konrat (Max F. Perutz Laboratories, Vienna) for discussions and Dr. Matthias Huber (ETH Zürich) and Isabel Ayala (IBS Grenoble) for protein preparation. We thank Agilent for providing access to equipment.
Supporting Information Available
Numerical simulations of the differential MQC decay experiment and the CPMG dispersion experiment in a rotating solid undergoing exchange; details on the pulse sequences; experimental CPMG RD data and MQC decay data for all residues; solution-state experiments of conformational exchange. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Supplementary Material
References
- Brüschweiler S.; Schanda P.; Kloiber K.; Brutscher B.; Kontaxis G.; Konrat R.; Tollinger M. J. Am. Chem. Soc. 2009, 131, 3063–3068. [DOI] [PubMed] [Google Scholar]
- Henzler-Wildman K.; Thai V.; Lei M.; Ott M.; Wolf-Watz M.; Fenn T.; Pozharski E.; Wilson M.; Petsko G.; Karplus M.; Hubner C.; Kern D. Nature 2007, 450, 838–U13. [DOI] [PubMed] [Google Scholar]
- Tzeng S.; Kalodimos C. Nature 2009, 462, 368–U139. [DOI] [PubMed] [Google Scholar]
- Boehr D.; McElheny D.; Dyson H.; Wright P. Science 2006, 313, 1638–1642. [DOI] [PubMed] [Google Scholar]
- Palmer A. Chem. Rev. 2004, 104, 3623–3640. [DOI] [PubMed] [Google Scholar]
- Mittermaier A. K.; Kay L. E. Trends Biochem. Sci. 2009, 34, 601–611. [DOI] [PubMed] [Google Scholar]
- Neudecker P.; Lundstrom P.; Kay L. E. Biophys. J. 2009, 96, 2045–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer A.; Massi F. Chem. Rev. 2006, 106, 1700–1719. [DOI] [PubMed] [Google Scholar]
- Kloiber K.; Konrat R. J. Biomol. NMR 2000, 18, 33–42. [DOI] [PubMed] [Google Scholar]
- Salvi N.; Ulzega S.; Ferrage F.; Bodenhausen G. J. Am. Chem. Soc. 2012, 134, 2481–2484. [DOI] [PubMed] [Google Scholar]
- Früh D.; Tolman J. R.; Bodenhausen G.; Zwahlen C. J. Am. Chem. Soc. 2001, 123, 4810–4816. [DOI] [PubMed] [Google Scholar]
- Chevelkov V.; Xue Y.; Linser R.; Skrynnikov N. R.; Reif B. J. Am. Chem. Soc. 2010, 132, 5015–5017. [DOI] [PubMed] [Google Scholar]
- Helmus J.; Surewicz K.; Surewicz W.; Jaroniec C. J. Am. Chem. Soc. 2010, 132, 2393–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andronesi O. C.; Becker S.; Seidel K.; Heise H.; Young H. S.; Baldus M. J. Am. Chem. Soc. 2005, 127, 12965–12974. [DOI] [PubMed] [Google Scholar]
- Byeon I.-J. L.; Hou G.; Han Y.; Suiter C. L.; Ahn J.; Jung J.; Byeon C.-H.; Gronenborn A. M.; Polenova T. J. Am. Chem. Soc. 2012, 134, 6455–6466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorieau J. L.; Day L. A.; McDermott A. E. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 10366–10371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange A.; Gattin Z.; Van Melckebeke H.; Wasmer C.; Soragni A.; van Gunsteren W. F.; Meier B. H. ChemBioChem 2009, 10, 1657–1665. [DOI] [PubMed] [Google Scholar]
- Giraud N.; Blackledge M.; Goldman M.; Bockmann A.; Lesage A.; Penin F.; Emsley L. J. Am. Chem. Soc. 2005, 127, 18190–18201. [DOI] [PubMed] [Google Scholar]
- Torchia D. A. J. Magn. Reson. 2011, 212, 1–10. [DOI] [PubMed] [Google Scholar]
- Palmer A. G.; Williams J.; McDermott A. J. Phys. Chem. 1996, 100, 13293–13310. [Google Scholar]
- Krushelnitsky A.; deAzevedo E.; Linser R.; Reif B.; Saalwaechter K.; Reichert D. J. Am. Chem. Soc. 2009, 131, 12097–12099. [DOI] [PubMed] [Google Scholar]
- Lewandowski J. R.; Sass H. J.; Grzesiek S.; Blackledge M.; Emsley L. J. Am. Chem. Soc. 2011, 133, 16762–16765. [DOI] [PubMed] [Google Scholar]
- Chevelkov V.; Rehbein K.; Diehl A.; Reif B. Angew. Chem., Int. Ed. 2006, 45, 3878–3881. [DOI] [PubMed] [Google Scholar]
- Lewandowski J. R.; Dumez J. N.; Akbey U.; Lange S.; Emsley L.; Oschkinat H. J. Phys. Chem. Lett. 2011, 2, 2205–2211. [Google Scholar]
- Schanda P.; Huber M.; Verel R.; Ernst M.; Meier B. H. Angew. Chem., Int. Ed. 2009, 48, 9322–9325. [DOI] [PubMed] [Google Scholar]
- Frueh D. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 41, 305–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wist J.; Frueh D.; Tolman J. R.; Bodenhausen G. J. Biomol. NMR 2004, 28, 263–272. [DOI] [PubMed] [Google Scholar]
- Dittmer J.; Bodenhausen G. J. Am. Chem. Soc. 2004, 126, 1314–1315. [DOI] [PubMed] [Google Scholar]
- Redfield A. G. IBM J. Res. Devel. 1957, 1, 19–31. [Google Scholar]
- Wang C.; Palmer A. G. J. Biomol. NMR 2002, 24, 263–268. [DOI] [PubMed] [Google Scholar]
- Schanda P.; Meier B. H.; Ernst M. J. Am. Chem. Soc. 2010, 132, 15957–15967. [DOI] [PubMed] [Google Scholar]
- Skrynnikov N. Magn. Reson. Chem. 2007, 45, S161–S173. [DOI] [PubMed] [Google Scholar]
- Verde M.; Ulzega S.; Ferrage F.; Bodenhausen G. J. Chem. Phys. 2009, 130, 074506. [DOI] [PubMed] [Google Scholar]
- Korzhnev D. M.; Kloiber K.; Kay L. E. J. Am. Chem. Soc. 2004, 126, 7320–7329. [DOI] [PubMed] [Google Scholar]
- Loria J.; Rance M.; Palmer A. G. J. Am. Chem. Soc. 1999, 121, 2331–2332. [Google Scholar]
- Hansen D. F.; Vallurupalli P.; Kay L. E. J. Phys. Chem. B 2008, 112, 5898–5904. [DOI] [PubMed] [Google Scholar]
- Tollinger M.; Skrynnikov N.; Mulder F.; Forman-Kay J.; Kay L. E. J. Am. Chem. Soc. 2001, 123, 11341–11352. [DOI] [PubMed] [Google Scholar]
- Millet O.; Loria J.; Kroenke C.; Pons M.; Palmer A. J. Am. Chem. Soc. 2000, 122, 2867–2877. [Google Scholar]
- Schanda P.; Huber M.; Boisbouvier J.; Meier B. H.; Ernst M. Angew. Chem., Int. Ed. 2011, 50, 11005–11009. [DOI] [PubMed] [Google Scholar]
- Lorieau J.; McDermott A. J. Am. Chem. Soc. 2006, 128, 11505–11512. [DOI] [PubMed] [Google Scholar]
- Agarwal V.; Xue Y.; Reif B.; Skrynnikov N. J. Am. Chem. Soc. 2008, 130, 16611–16621. [DOI] [PubMed] [Google Scholar]
- Majumdar A.; Ghose R. J. Biomol. NMR 2004, 28, 213–227. [DOI] [PubMed] [Google Scholar]
- Hansen D. F.; Feng H.; Zhou Z.; Bai Y.; Kay L. E. J. Am. Chem. Soc. 2009, 131, 16257–16265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massi F.; Grey M.; Palmer A. G. Protein Sci. 2005, 14, 735–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills J. L.; Szyperski T. J. Biomol. NMR 2002, 23, 63–67. [DOI] [PubMed] [Google Scholar]
- Ban D.; Funk M.; Gulich R.; Egger D.; Sabo T. M.; Walter K. F. A.; Fenwick R. B.; Giller K.; Pichierri F.; de Groot B. L.; Lange O. F.; Grubmüller H.; Salvatella X.; Wolf M.; Loidl A.; Kree R.; Becker S.; Lakomek N.-A.; Lee D.; Lunkenheimer P.; Griesinger C. Angew. Chem., Int. Ed. 2011, 50, 11437–11440. [DOI] [PubMed] [Google Scholar]
- Sidhu A.; Surolia A.; Robertson A. D.; Sundd M. J. Mol. Biol. 2011, 411, 1037–1048. [DOI] [PubMed] [Google Scholar]
- Huang K.-Y.; Amodeo G. A.; Tong L.; McDermott A. Protein Sci. 2011, 20, 630–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornilescu G.; Marquardt J. L.; Ottiger M.; Bax A. J. Am. Chem. Soc. 1998, 120, 6836–6837. [Google Scholar]
- Linser R.; Bardiaux B.; Higman V.; Fink U.; Reif B. J. Am. Chem. Soc. 2011, 133, 5905–5912. [DOI] [PubMed] [Google Scholar]
- Huber M.; Hiller S.; Schanda P.; Ernst M.; Böckmann A.; Verel R.; Meier B. H. ChemPhysChem 2011, 12, 915–918. [DOI] [PubMed] [Google Scholar]
- Asami S.; Schmieder P.; Reif B. J. Am. Chem. Soc. 2010, 132, 15133–15135. [DOI] [PubMed] [Google Scholar]
- Krushelnitsky A.; Zinkevich T.; Reichert D.; Chevelkov V.; Reif B. J. Am. Chem. Soc. 2010, 132, 11850–11853. [DOI] [PubMed] [Google Scholar]
- Linser R.; Dasari M.; Hiller M.; Higman V.; Fink U.; Lopez del Amo J.-M.; Markovic S.; Handel L.; Kessler B.; Schmieder P.; Oesterhelt D.; Oschkinat H.; Reif B. Angew. Chem., Int. Ed. 2011, 50, 4508–4512. [DOI] [PubMed] [Google Scholar]
- Ward M. E.; Shi L.; Lake E.; Krishnamurthy S.; Hutchins H.; Brown L. S.; Ladizhansky V. J. Am. Chem. Soc. 2011, 133, 17434–17443. [DOI] [PubMed] [Google Scholar]
- Igumenova T.; McDermott A.; Zilm K.; Martin R.; Paulson E.; Wand A. J. Am. Chem. Soc. 2004, 126, 6720–6727. [DOI] [PubMed] [Google Scholar]
- Bockmann A.; Gardiennet C.; Verel R.; Hunkeler A.; Loquet A.; Pintacuda G.; Emsley L.; Meier B.; Lesage A. J. Biomol. NMR 2009, 45, 319–327. [DOI] [PubMed] [Google Scholar]
- Delaglio F.; Grzesiek S.; Vuister G.; Zhu G.; Pfeifer J.; Bax A. J. Biomol. NMR 1995, 6, 277–293. [DOI] [PubMed] [Google Scholar]
- Smith S.; Levante T.; Meier B.; Ernst R. J. Magn. Reson. 1994, 106, 75–105. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


