Theoretical Investigations and Density Functional Theory Based Quantitative Structure–Activity Relationships Model for Novel Cytotoxic Platinum(IV) Complexes

Abstract

Octahedral platinum(IV) complexes are promising candidates in the fight against cancer. In order to rationalize the further development of this class of compounds, detailed studies on their mechanisms of action, toxicity, and resistance must be provided and structure–activity relationships must be drawn. Herein, we report on theoretical and QSAR investigations of a series of 53 novel bis-, tris-, and tetrakis(carboxylato)platinum(IV) complexes, synthesized and tested for cytotoxicity in our laboratories. The hybrid DFT functional wb97x was used for optimization of the structure geometry and calculation of the descriptors. Reliable and robust QSAR models with good explanatory and predictive properties were obtained for both the cisplatin sensitive cell line CH1 and the intrinsically cisplatin resistant cell line SW480, with a set of four descriptors.

Introduction

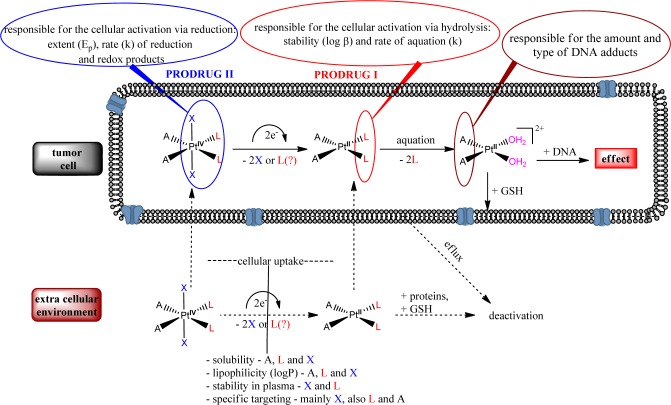
Platinum complexes are among leading drugs in anticancer chemotherapy. Since the discovery of the cytotoxic effect of cisplatin and its Food and Drug Administration (FDA) approval in 1978, seven other Pt(II) compounds were introduced in clinics worldwide (carboplatin and oxaliplatin) or in selected countries (nedaplatin, lobaplatin, heptaplatin, miriplatin, and dicycloplatin).¹⁻³ Approximately 30 more Pt(II) and Pt(IV) complexes have been or are in clinical trials at different stages.¹ Despite the great medical success of platinum-based cytostatics, there are some major drawbacks that restrict their usage, mainly severe dose-limiting side effects, intrinsic or/and acquired resistance, and the uncomfortable and cost intensive way of administration (iv infusion). Thousands of metal compounds have been synthesized and investigated during the past decades with the aim of breaking these limitations. Nevertheless, in order to design a metal-based drug with improved pharmacological profile, details of the mechanism of action, toxicity, and resistance have to be studied⁴ and structure–activity relationships have to be drawn. It is generally accepted that square planar platinum(II) complexes are acting like prodrugs, containing two carrier ligands and two leaving groups. The two leaving groups are exchanged in the cell, forming reactive aqua species capable of forming DNA adducts responsible for the cytotoxic effects of the compounds (Figure 1). Octahedral Pt(IV) complexes also possess antimalignant properties and can act as prodrugs for Pt(II) agents (reduction in vivo to the corresponding Pt(II) counterparts).

Figure 1.

Scheme of the mechanism of action of platinum-based cytostatics.

The first comprehensive SAR study of cytotoxic metal complexes was reported by Cleare and Hoeschele in 1973, where a wide variety of Pt(II) compounds was investigated for its antitumor activity in a sarcoma 180 mouse model.⁵ Results from variation of carrier ligands, leaving groups, geometry, and charge and some physicochemical parameters like solubility and kinetics of hydrolysis affecting the antimalignant properties of cisplatin analogues were studied. The authors found that the cis geometry and neutral charge of the complexes, chloride or dicarboxylates as leaving groups, and primary amines as carrier ligands are crucial for the biological activity within the series studied. Today, different compound classes are known, violating the classical SAR set up by Cleare and Hoeschele, as for example complexes with trans geometry featuring high cytotoxicity.⁶ Theoretical study attempts and a quantitative structure–activity relationship (QSAR) model for the anticancer activity of 26 Pt(II) complexes in vivo in mice models was reported in 1982.⁷ Nevertheless, QSAR analysis results based on in vitro cytotoxicity of Pt(II) compounds in different cell lines were first published 23 years later.⁸ Reliable models with good predictive strength, based on four molecular descriptors (chosen from 197), were obtained for a series of 16 Pt(II) complexes, including the clinically established drugs cisplatin, carboplatin, and oxaliplatin. The results confirmed the structure–activity relationships (SAR) reported by Cleare and Hoechele. Later, Sarmah and Deka reported QSAR and quantitative structure–properties relationship (QSPR) models for several platinum complexes, using density functional theory (DFT) and MM derived descriptors.⁹ The authors showed that DFT and molecular mechanics (MM+) methods could be used successfully in the prediction of lipophilicity and cytotoxicity of platinum compounds. Furthermore, the usage of solvent models for calculation of the descriptors gave better results than those obtained in the gas phase.

As mentioned above, Pt(IV) complexes act as prodrugs of their Pt(II) counterparts and represent an important part of recent metal-based anticancer research. Their geometries and physicochemical features (octahedral coordination sphere with a maximum of six ligands, kinetic inertness in ligand-exchange reactions, reduction under hypoxic conditions, etc.) present advantages in fine-tuning of the pharmacological profile, providing the possibility for oral administration, targeted therapy, reduced side effects, etc.¹⁰ As summarized in Figure 1, there are more parameters (in comparison with platinum(II) complexes), which should be taken into account when designing a Pt(IV) based drug. Some SARs based on a small set of Pt(IV) complexes have been established during the past decade.¹¹ It was shown that cytotoxicity of the compounds is dependent on their redox potential and lipophilicity and that these parameters have optimal values when the axial ligands are carboxylates.¹² However, it was found recently that redox potential does not always correlate with the rate of reduction and that the equatorial ligands can also play a crucial role.^13,14 Moreover, reduction of Pt(IV) complexes is not always accompanied by release of the axial ligands; in some rare cases a more complicated picture can be observed.^15,16

cis-Diam(m)inebis(carboxylato)dichloridoplatinum(IV) and cis-diam(m)inetetrakis(carboxylato)platinum(IV) complexes with cytotoxicity ranging from low nanomolar to high micromolar IC₅₀ values have recently been reported from our group (see Figure 2).^14,17−20 It was found that cytotoxicity in general increases with increasing lipophilicity of the axial ligands, but this effect is much more pronounced in the diam(m)inedichloridobis(carboxylato) complex series; moreover, compounds featuring amide moieties in the axial ligands are less effective than expected from their log P values.^20,21 The tetracarboxylato complexes have shown in principle a lower cytotoxic potency and a different redox kinetic behavior.¹⁴ In order to find quantitative explanations of the phenomena and to rationalize the further development of antimalignant Pt(IV) complexes, we enlarged the series by including three diamminetris(carboxylato)platinum(IV) complexes, prodrugs of nedaplatin, and performed a QSAR study based on DFT calculated and constitutional molecular descriptors. Moreover, with the help of the calculations, we tried to better understand the redox behavior of the complexes in the series to explain the experimental data and to group them in subseries.

Figure 2.

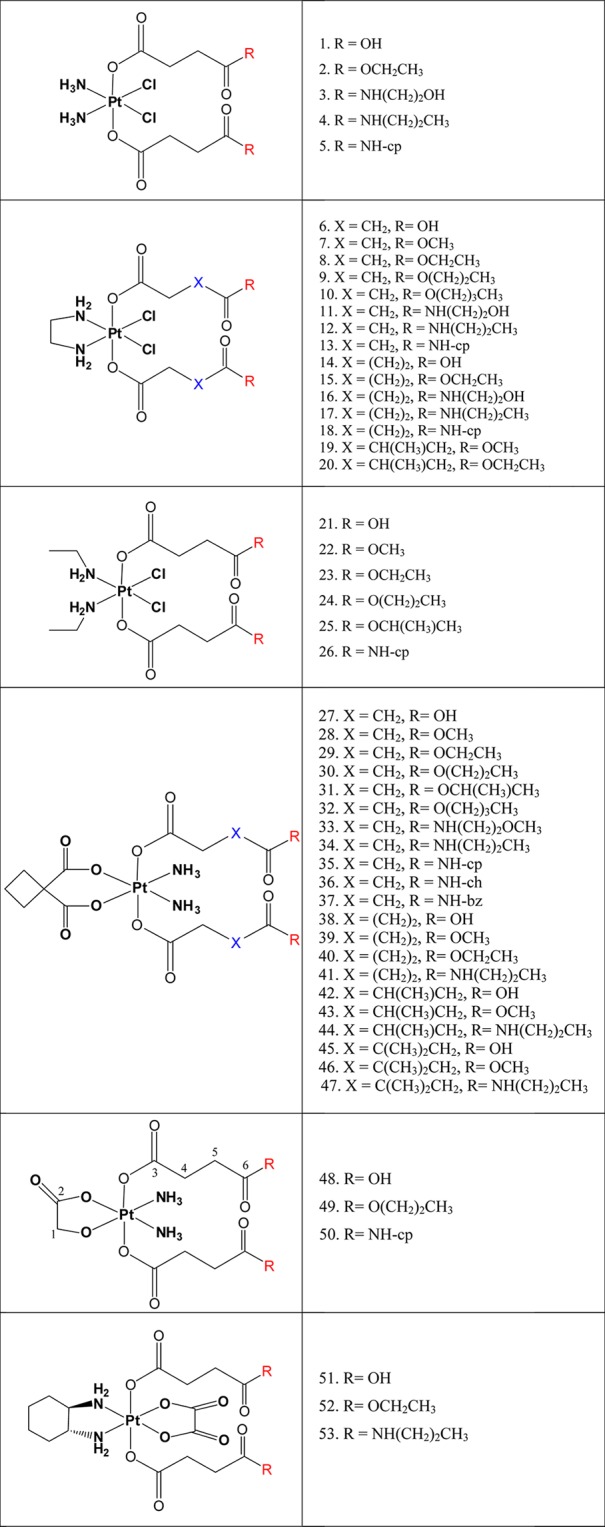
Schematic formulas of the investigated complexes.

Up to now, there is only one report of a QSAR study for Pt(IV) complexes;²² models based on the cytotoxicity of 23 compounds in two tumor cell lines were developed, using experimentally determined (log P_o/w and E_p) and theoretical descriptors. Later, the authors suggested QSPR models able to predict the lipophilicity and the redox potential of Pt(IV) complexes, using (a slightly broadened) series from the QSAR study. The semiempirical method PM6 was used for optimization of the structures and calculation of the descriptors.²³ Total and polar surface area, orbital energies, atomic charges, and dipole moments were found to be significant descriptors.

To the best of our knowledge, there is still no QSAR study on Pt(IV) complexes based on DFT derived descriptors in the literature. Herein, we report theoretical and QSAR investigations on 53 novel Pt(IV) complexes (listed in Figure 2), synthesized and tested in our laboratories, using the hybrid DFT functional wb97x for optimization of the structure geometry and calculation of the descriptors. MLR, PCA, and simulated annealing were employed for the development of the statistical models.

Results and Discussion

Synthesis and Characterization

The entire set of 53 Pt(IV) complexes, which are an object of this study, is presented in Figure 2. On the basis of the equatorial ligands, the compounds can be divided into six subseries, namely, derivatives of cisplatin (1–5), its ethylenediamine analogue (6–20), its bis(ethylamine) analogue (21–26), carboplatin (27–47), nedaplatin (48–50), and oxaliplatin (51–53). The axial ligands are represented by dicarboxylato chains, containing different spacers between the two carbonyl groups and diverse terminal moieties such as esters, amides, or free carboxylic acids. Synthesis and detailed characterization of compounds 1–20 and 51–53 are given in refs (17), (18), and (19), and those for 21–47 are given in refs (14) and (20). Nedaplatin derivatives (48–50) were synthesized using analogous procedures. Their detailed characterization is based on ¹H, ¹³C, ¹⁵N, and ¹⁹⁵Pt 1D and 2D NMR measurements. Interestingly, two different-shaped signals for the NH₃ groups can be observed in the ¹H spectra of compounds 48–50: a broad signal at around 6.1 ppm and a multiplet around 6.6 ppm in which the ¹⁴N–¹H and ¹⁹⁵Pt–¹H couplings can be seen. The existence of two signals in the ¹H and ¹⁵N spectra can be explained by the unsymmetrical surroundings of the NH₃ groups, one is in trans position to carboxylate and the other one to alcoholate.

Cytotoxicity

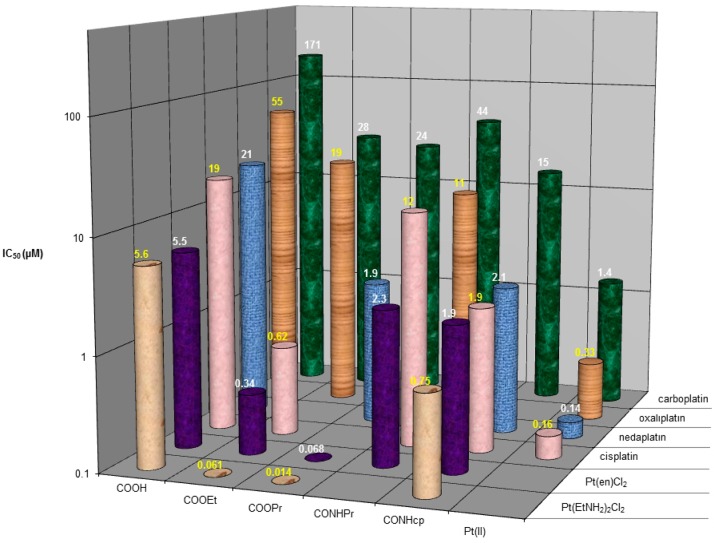
All complexes (1–53) were tested for in vitro cytotoxicity in comparison with cisplatin, carboplatin, oxaliplatin, and nedaplatin in two human tumor cell lines (CH1 ovarian carcinoma and SW480 colon carcinoma), using the MTT colorimetric assay. The resulting IC₅₀ values are listed in Table 1. The cell line CH1 is sensitive to the clinically applied platinum drugs, while the second one (SW480) is resistant to them with the exception of oxaliplatin. The set of compounds covers a large range of cytotoxicity with nanomolar IC₅₀ values up to 174 μM in the cell line CH1 and from 0.1 μM to negligible activity (>500 μM) in the cell line SW480. In general, the diam(m)inebis(carboxylato)dichlorido complexes (1–26, subset 1) show higher activity in comparison with the tri- and tetrakis(carboxylato)diam(m)ine compounds (27–53, subset 2). With increasing the lipophilicity, complexes with higher cytotoxicity than the clinically applied platinum(II) drugs could be obtained in subset 1, while this observation is not valid for the compounds in subset 2. In general for all complexes in the set, cytotoxicity is dependent on lipophilicity, but this is much more pronounced for the diam(m)inedicarboxylatodichlorido complexes. When the axial ligands are compared, terminal ester groups are most favorable for antiproliferative activity, followed by amide derivatives; compounds featuring terminal carboxylic or hydroxy groups in the axial chain showed the lowest cytotoxic potency (see Figure 3). In subset 2, cytotoxicity of amide and ester derivatives is comparable. Lack of activity of all compounds from the subset (except for oxaliplatin analogues 51–53 and partially for nedaplatin analogues 49–50) in the cisplatin-resistant cell line SW480 can be observed (Table 1).

Table 1. Cytotoxicity of the Investigated Platinum(IV) Complexes in Comparison with the Clinically Applied Platinum(II) Drugs in the CH1 and SW480 Human Cancer Cell Lines.

	IC50 (μM)a			IC50 (μM)a
compd	CH1	SW480	compd	CH1	SW480
1	19 ± 1	136 ± 16	30	24 ± 5	>500
2	0.62 ± 0.32	3.8 ± 1.0	31	8.6 ± 1.7	350 ± 39
3	28 ± 2	183 ± 28	32	11 ± 6	181 ± 44
4	12 ± 4	48 ± 4	33	62 ± 26	>500
5	1.9 ± 0.2	24 ± 4	34	44 ± 8	>500
6	5.5 ± 2.2	95 ± 5	35	15 ± 5	>500
7	0.68 ± 0.20	16 ± 1	36	28 ± 2	>500
8	0.34 ± 0.11	4.1 ± 0.5	37	31 ± 13	>500
9	0.068 ± 0.024	0.63 ± 0.20	38	114 ± 23	>500
10	0.018 ± 0.007	0.22 ± 0.08	39	33 ± 13	>500
11	24 ± 3	142 ± 23	40	7.7 ± 1.4	>250
12	2.3 ± 1.1	31 ± 15	41	89 ± 7	>500
13	1.9 ± 0.2	19 ± 9	42	128 ± 48	>500
14	32 ± 19	160 ± 10	43	23 ± 9	>500
15	1.1 ± 0.2	3.5 ± 0.1	44	49 ± 13	>500
16	21 ± 8	90 ± 21	45	125 ± 35	>500
17	22 ± 12	43 ± 22	46	22 ± 8	>500
18	7.8 ± 1.0	21 ± 5	47	33 ± 4	>500
19	0.17 ± 0.05	2.9 ± 1.0	48	21 ± 6	>500
20	0.055 ± 0.006	0.96 ± 0.4	49	1.9 ± 0.3	100 ± 6
21	5.6 ± 1.6	40 ± 12	50	2.1 ± 0.3	161 ± 33
22	0.16 ± 0.05	1.0 ± 0.3	51	55 ± 28	44 ± 9
23	0.061 ± 0.015	0.30 ± 0.05	52	19 ± 5	14 ± 3
24	0.014 ± 0.002	0.11 ± 0.01	53	11 ± 2	12 ± 5
25	0.0094 ± 0.0012	0.39 ± 0.07	cisplatin	0.16 ± 0.03	3.50 ± 0.29
26	0.75 ± 0.10	6.1 ± 0.6	carboplatin	1.36 ± 0.40	85 ± 28
27	171 ± 1	>500	oxaliplatinb	0.33 ± 0.09	0.30 ± 0.08
28	32 ± 10	>500	nedaplatin	0.14 ± 0.05	6.3 ± 1.3
29	28 ± 4	>500

^aThe reported 50% inhibitory concentrations are the means ± standard deviations obtained from three independent experiments.

^bData taken from ref (24).

Figure 3.

Comparative diagram of the cytotoxicity (IC₅₀ values, logarithmic scale) of some Pt(IV) complexes from the series in the CH1 cell line, depending on their equatorial ligands (y axis) and the terminal moieties of the axial ligands (x axis), and the clinically approved Pt(II) drugs: cisplatin, carboplatin, oxaliplatin, and nedaplatin.

Crystal Structure

The result of the X-ray diffraction analysis of 7 is shown in Figure S1 in Supporting Information. The compound crystallized in the triclinic centrosymmetric space group P1̅. The Pt(IV) atom has an octahedral coordination geometry with one ethylenediamine and two chlorido ligands in the equatorial plane and two 4-methoxysuccinates coordinated in axial positions. The bond lengths and angles are well comparable with the crystal structure of analogous complex 6 previously published.¹⁷ Interestingly, the orientations of the axial ligands in complex 7 are different from those observed in 6. This is probably due to dissimilar crystal packing and H-bonding pattern. An analogous difference in the conformational behavior was observed in the structures of complexes 1 and 22, whereas the 4-methoxysuccinate ligands in 22 have a straight orientation²⁰ while in 1 one succinate is twisted and the other is straight.¹⁸

Geometry Optimization

Comparison of geometry parameters, obtained after the optimization procedure in vacuum, in a water model and from the available X-ray data for compounds 1, 6, 7, 22, and 38 is shown in Table S1 (Supporting Information). A good agreement between experiment and calculation could be observed.

Analysis of the Calculated Physicochemical Parameters

The dipole moments (μ) vary from 3 to 15 D, implying that all the complexes are quite polar compounds (Table S2). Nevertheless, no trend in the alteration of this parameter within the investigated compounds could be found.

The energies of solvation (E_s and E_s′) differ from 70 to 160 kJ mol^–1 for all compounds. In general the complexes exerting carboxylic or amide groups in the axial ligands have higher solvation energies compared with their ester analogues. The distribution of the electron density, based on electrostatic potential (ESP) for compounds of the two subtypes, shows that the most electropositive regions in the molecule could be found around the nitrogen donor atoms and the most negative around the oxygen and chlorine atoms (Figure 4).

Figure 4.

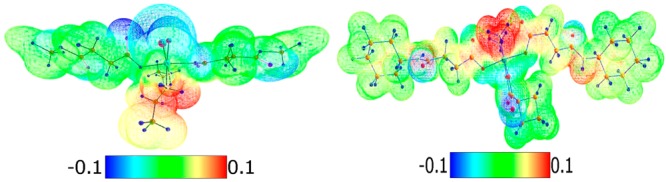
ESP color mapped electron density for complexes 22 (left) and 36 (right).

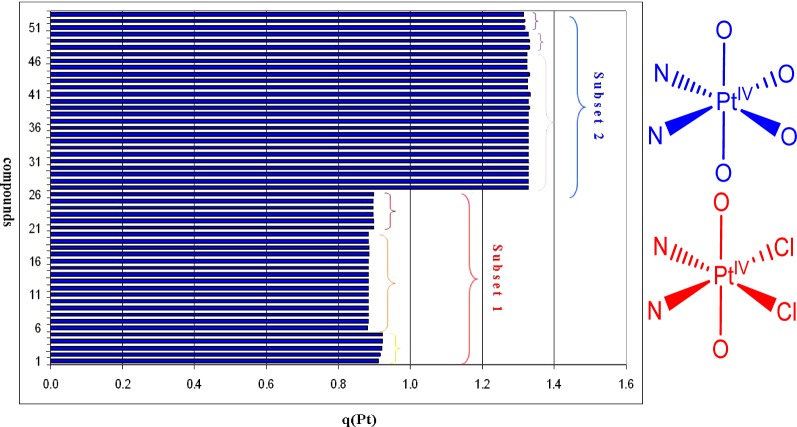
The natural population analysis (NPA) charge at Pt (q(Pt)) differentiates well the two major subtypes (in structure deviation and in cytotoxic activity): bis(carboxylato)dichlorido complexes (subset 1) versus tris- and tetrakis(carboxylato) complexes (subset 2). It also shows some minor discrimination in the two subtypes, dependent mainly on differences in the equatorial ligands. Expectedly, the deviations of the terminal fragments of the axial ligands do not affect the charge at the Pt atom. A plot of the NPA charge at Pt for the 53 investigated complexes (average values from the calculated conformers of compounds of 2 and 50 are used) is shown in Figure 5.

Figure 5.

NPA charge at the Pt atom (in au), calculated for complexes 1–53. A scheme of the coordination sphere of subsets 1 and 2 is presented on the right.

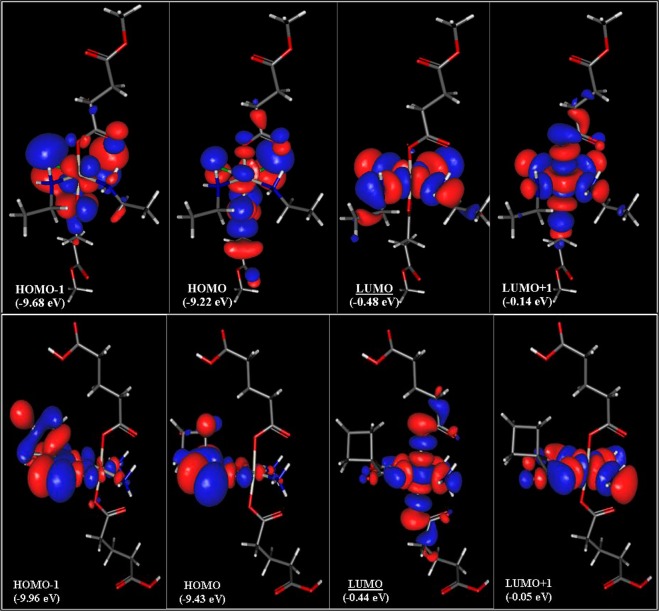
The described circumstances make q(Pt) a good descriptor for a further QSAR model. In Figure 6, a qualitative MO analysis of the frontier orbitals, together with their energies for complexes 22 and 38, is shown. The low (negative) values of E_HOMO (<−9 eV) and the good correlating high ionization potentials (between 8 and 10 eV in vacuum and between 7 and 8.5 eV in water) are a logical consequence of the inability of Pt(IV) complexes to act as reductants. However, a clear tendency of the change of these parameters in the series cannot be observed.

Figure 6.

Frontier orbitals (with their energies) of complexes 22 (top) and 38 (bottom).

The negative values of E_LUMO (Table S3, Figure 6) show that the compounds can act as oxidants and can be reduced relatively easily. The nedaplatin derivatives (complexes 48–50) have higher (close to zero, even slightly positive for complexes 49 and 50b) values of E_LUMO, which probably is connected with their eventual lower oxidative capability. In general, a clear relationship between the variations of E_LUMO with the structures in the series could not be found. Interestingly, the values of the electron affinity in gas phase (between 0.6 and 1.8 eV) and their corresponding vertical (between 2 and 3 eV) and adiabatic (around 4 eV) redox potentials in water do not correlate with each other as would be expected. In principle, the small differences observed between the values of the adiabatic redox potential in water imply that the investigated compounds can be reduced with relatively equal effort. The different tendencies for the vertical and adiabatic electron affinity in water also show that the acceptance of an electron in aqueous media is associated with significant changes in the geometry and the energy of the system. It is interesting to follow how the geometry of the complexes has been changed with the acceptance of one electron. From the NPA charges it can be concluded that the extra electron mainly resides on the Pt atom (and the coordinated chloride, in the case of complexes of subset 1), a Pt(III) radical is formed, and expectedly the largest and important geometry alterations will be in the Pt coordination sphere. In Table 2, a comparison of the bond lengths changes between the neutral and the anion radical (both optimized in water) for complexes 24 and 28 is shown.

Table 2. Bond Length Changes in Complexes 24 and 28 after the Acceptance of an Electron in Aqueous Medium.

	complex
Δ bond length (Å)	24	28
Pt–O1ax	0.04	0.35
Pt–O2ax	0.03	0.37
Pt–N1	0.34	0.01
Pt–N2	0.01	0.01
Pt–Cl1/Pt–O3eq	0.04	0.04
Pt–Cl2/Pt–O4eq	0.34	0.04

Table 2 shows that addition of an electron to a complex from subset 2 results in an elongation of Pt–O_ax bonds while Pt–N and Pt–O_eq in the equatorial sphere remain almost unchanged. These observations are in accordance with the expected reduction and loss of the axial ligands. Contrary to bis(carboxylato)dichlorido complexes from subset 1 (with the exception of some of the cisplatin analogues, namely, complexes 1, 2c, and 3), the axial Pt–O bonds have shifted insignificantly but the equatorial Pt–Cl and trans standing Pt–N have been elongated by more than 0.3 Å. In principle, the last findings correlate well with the shape of the LUMO orbitals which, for complexes from subset 2, are mainly situated around the axial ligands while for those from subset 1 they could be found in the square-planar sphere around platinum (Figure 6). Consequently, a different mechanism of reduction between the complexes of the two main subtypes is expected.

Reduction Model Studies

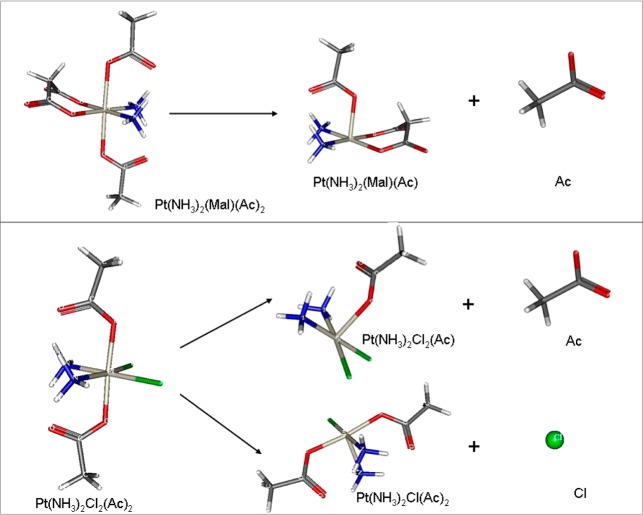
In order to gain a deeper insight into the mechanism of reduction of Pt(IV) prodrugs, further investigations based on two simple model systems, namely, (OC-6-33)-bis(acetato)diamminedichloridoplatinum(IV) (M1), representing complexes of subset 1, and (OC-6-33)-bis(acetato)diamminemalonatoplatinum(IV) (M2), representing complexes of subset 2 (Figure S2, Supporting Information), were performed. Applying again the most prominent hypothesis for the reduction pathway of Pt(IV) complexes featuring axial carboxylato ligands, which is an outer sphere reduction going via a Pt(III) intermediate,¹⁵ the structures of M1, M2, and their analogous monoanionic Pt(III) radicals were optimized in a water model. The same was done for the respective intermediates of reduction, the pentacoordinate complex after cleavage (ionic or radical) of one ligand (acetate or chloride). The energy of the cleaved acetate and chloride in water was also calculated. The possible ligand dissociation reactions after one-electron reduction are presented schematically in Figure 7. The dissociation energies, calculated for possible ionic or radical cleavage of a ligand (chloride or acetate) from the neutral Pt(IV) complexes or from their anion radicals, are listed in Table 3.

Figure 7.

Scheme of possible reduction reactions to pentacoordinated Pt complex for M1 (bottom) and M2 (top).

Table 3. Energies (in kJ/mol) Required for Dissociation of a Ligand from Complexes M1 and M2.

reaction of reduction	M2-ac	M1-ac	M1-Cl
PtIVL6 → (PtIVL5)+ + L–	305.6	303.7	246.7
PtIVL6 → (PtIIIL5)• + L•	251.3	251.6	256.9
(PtIVL6)•– = (PtIIIL6)•– → (PtIIIL5)• + L–	124.8	113.5	88.0

As presented in Table 3, reasonable dissociation energies are observed only when a ligand is cleaved from a Pt(IV) complex, which has already accepted an electron (and has been transformed into a Pt(III) radical). From the obtained values, it can be concluded that cleavage of equatorially bound chloride from the ionized complex M1 requires less energy than dissociation of axial acetate. Furthermore, the dissociation of an axial carboxylato ligand appears to happen more easily in the case of bis(carboxylato)dichlorido complexes (like M1) in comparison to tetracarboxylato species (like M2). The last findings correlate with the experimental data from electrochemical experiments, where it was found that bis(carboxylato)dichlorido(ethane-1,2-diammine)platinum(IV) complexes (6–20) have similar but slightly higher redox potentials (approximately −0.6 V vs NHE) than the corresponding carboplatin analogues (27–47) (approximately −0.7 V vs NHE).^14,21 Nevertheless, the electron affinity (the energy released after the attachment of an electron to a neutral complex) is much higher than the obtained dissociation energies: 380.2 kJ/mol for M1 and 392.0 kJ/mol for M2. For this reason, reduction of both complexes with dissociation of acetate or chloride is possible, which is in agreement with Gibson’s observation for more than one product of reduction of diacetatodiam(m)inedichloridoplatinum(IV) complexes²⁵ as well as with the nonaxial ligand loss reduction recently reported by Hambley/Gibson¹³ and Cullinane.²⁶

The thermodynamically comparable redox properties (in theory and experimentally) for both types of compounds were different with respect to their kinetic behavior. Compounds of subset 1 were reduced by ascorbic acid much more quickly than those from subset 2.¹⁴ In order to learn more about the kinetics of reduction, modeling of the energy change as a function of elongation of the Pt–acetate bond (in both models) or Pt–Cl (in M1) was performed. Unfortunately, the attempts to find an energy barrier and the corresponding transition state are unsuccessful so far. It looks like that the rate-limiting factor of reduction is the transfer of an electron to the Pt(IV) atom, not breaking of the Pt–ligand bond as a result of the one-electron transfer. In this context the kinetics of reduction of platinum(IV) complexes are dependent not only on the compound itself but also on the bioreducing agent (ascorbate, glutathione, cysteine, methionine, etc.) and the surrounding pH.²⁷⁻²⁹ How these factors influence the behavior of Pt(IV) complexes will be a matter of further investigation.

QSAR Analysis. Initial Screening of the Descriptors

From the initial screening of the correlation between properties and biological response, it was found that the most significant descriptors for the biological activity (as single parameters) in both cell lines are the number of H-bond acceptors (H_acc), charge at the Pt atom (q(Pt)), vertical and adiabatic electron affinities (E_eas and E_eas′), followed by the number of H-bond donors (H_don) (see Table 4).

Table 4. Significance of the Descriptors (as Single Parameters), Based on the Properties–Biological Response Correlation^a.

correlation with the response	CH1 cells	SW480 cells
strong (R > |0.5|)	Hacc, q(Pt), Eeas′, Hdon, Eeas	Hacc, q(Pt), Eeas
middle (R < |0.5|)	COOH, Es′, Es, Eea	Hdon, Eeas′
weak (R < |0.3|)	EHOMO, MW, Ei, H/Lgap, Eis	Es′, Es, COOH, MW, EHOMO, Eea, ELUMO, Eis, Vm, Ei
very weak (R < |0.15|)	Vm, α, μ, SASA, ELUMO	α, μ, SASA, H/Lgap

^afor the abbreviations see the experimental section.

A strong correlation between MW, V_m, and α can be found. The charge at Pt, the vertical redox potential (E_eas), and the number of H-bond acceptors also have a strong correlation with each other. Expectedly, there is an excellent correlation between E_HOMO and the ionization energy (E_i) as well as among the vertical and adiabatic solvation energies. A good agreement between E_LUMO and E_ea, as well as among the HOMO/LUMO gap and first ionization energy in vacuum could be also observed during the descriptor analyses. From a group of descriptors having strong correlations with each other, only a single one is expected to contribute to a good QSAR model. With the aim of using the final QSAR model for screening purposes, it is advantageous to select the descriptor in each group as one that requires the least computational effort, e.g., the molecular weight is much easier to calculate than the molecular polarizability; vertical solvation energy can be calculated more quickly than adiabatic.

The most promising models based on a single descriptor or a combination of two, three, four, or five descriptors were chosen with the help of simulated annealing. It was demonstrated that the best merit for both cell line models could be derived by combination of four descriptors; utilizing more than five descriptors decreased the merit. How R² and Q² of the models change with increasing the number of the descriptors is shown in Figure S3 (Supporting Information).

QSAR Models for the Cell Line CH1

Statistical data for the best regression models for cytotoxicity in the cell line CH1 are summarized in Table 5. Additional statistical information for these and other models based on one, two, three, four, or five descriptors is presented in Table S4 (Supporting Information).

Table 5. Statistical Data for the Best Regression Models for Cytotoxicity in the Cell Line CH1 of the 53 Investigated Pt(IV) Complexes.

no. of variables	descriptors	R2	Q2(LTOP)	rms
1	Hacc	0.51	0.48	0.78
2	Hdon, Hacc	0.70	0.67	0.62
3	q(Pt), Eeas′, Hdon	0.79	0.75	0.53
4	α, q(Pt), Eeas′, Hdon	0.86	0.82	0.45
4	MW, q(Pt), Eeas′, Hdon	0.85	0.81	0.47
4	MW, Eeas′, Hdon, Hacc	0.85	0.82	0.46
4	α, Eeas′, Hdon, Hacc	0.85	0.82	0.46
5	MW, α, q(Pt), Eeas’, Hdon	0.87	0.84	0.43
6	MW, α, q(Pt), Eeas′, Es, Hdon	0.88	0.84	0.43

Models derived by using only one descriptor (the good autocorrelating q(Pt) or H_acc), expectedly have low explanatory and predictive properties (R² and Q² under 50%). Essential improvement could be achieved by adding H_don; R² increased to nearly 70%, and the predictability was over 65%, respectively. Further enhancement could be obtained by adding a third descriptor to the best two-variable models (H_don and H_acc or q(Pt) and H_don). R² over 75% is achieved by including the adiabatic redox potential in water (E_eas′). The developed models also showed high predictive strength (Q² > 75%) and robustness, which was proved in the external validation under severe conditions (Table S5, Supporting Information). Interestingly, by inclusion of the presence/absence of COOH in the combination of the H_don and H_acc model, only constitutional (easy to calculate) molecular descriptors with R² = 75% and Q² = 72% could be obtained (Table S4). The latter also showed good Pred.R² on the external validation and can be a good alternative for screening when quantum mechanical calculations are not possible or too expensive. Combining α or the autocorrelated MW with q(Pt) and H_don gave models with moderate explanatory (∼72%) and predictive (∼69%) properties, which totally failed in the external validation, partition e where all nedaplatin derivatives (48–50) are in the predictive set (Tables S5 and S6).

Reliable (R² ≥ 80%) and predictive (Q² ≥ 70%) models could be constructed only by adding a fourth descriptor. The best results are obtained via combining polarizability with the best two three-descriptor models, where R² of 86%, Q² of 82%, and AAR < 0.4 could be achieved. Using MW (easy to calculate and having strong correlation with α) instead does not decrease the quality of the models. The external validation proved the robustness and the predictive properties and showed that the most reliable model is built by using MW, E_eas′, H_don, and H_acc as variables. Developing a model by adding a fifth descriptor can slightly increase the R² and Q² values only when autocorrelating descriptors (e.g., α and MW, E_eas and E_eas′) are included, which results in overfitting and fake higher predictability.

The complete regression equation for the final predictive model we have chosen is as follows:

The plot of experimental and predicted pIC₅₀ values of the model is shown in Figure 8.

Figure 8.

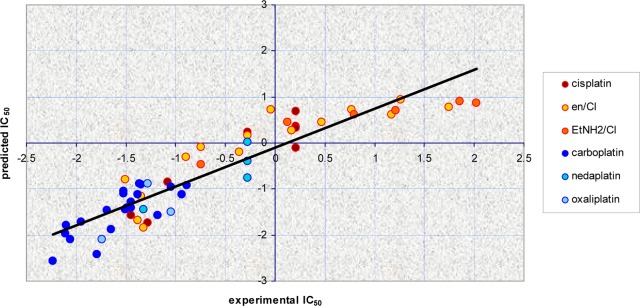
Predicted (with the selected four-variable model) vs experimental cytotoxicity in the cell line CH1. The coloring is based on the subtypes containing the same equatorial ligands.

In the PCA method all variables are combined into new descriptors that are ranked according their ability to describe the variation in the descriptor data. For the present case, 85% of the variance could be explained by five components, but a QSAR model using five components performs no better than the four-component MLR model (R² = 0.83). Since the PCA approach requires the calculation of all descriptors, the MLR approach is better suited for screening purposes. When PCA was applied on the four descriptors (MW, E_eas′, H_don, and H_acc) used for developing our MLR model, three components, together explaining 88% of the variance, were obtained (their loading plots are shown in Figure S4, Supporting Information). The score plot, obtained by combination of the first two of them (PC1 and PC2, explaining 73% of the variability), grouped well the complexes in five clusters (Figure 9). The compounds from subsets 1 and 2 were split, depending on the terminal moieties of the axial ligands, separating the more active esters in one cluster from the less active amides and free carboxylic acids in another. Compounds 3, 11, and 16, featuring terminal CH₂OH and equipped with the lowest cytotoxicity in subset 1, formed another cluster. Interestingly, nedaplatin derivatives (48–50) from subset 2 grouped together with the amides and free carboxylic acids from subset 1, and esters 17 and 18 (having three CH₂ groups spacer between the carbonyls in the axial chains) from subset 1 grouped together with amides and carboxylic acids from subset 2.

Figure 9.

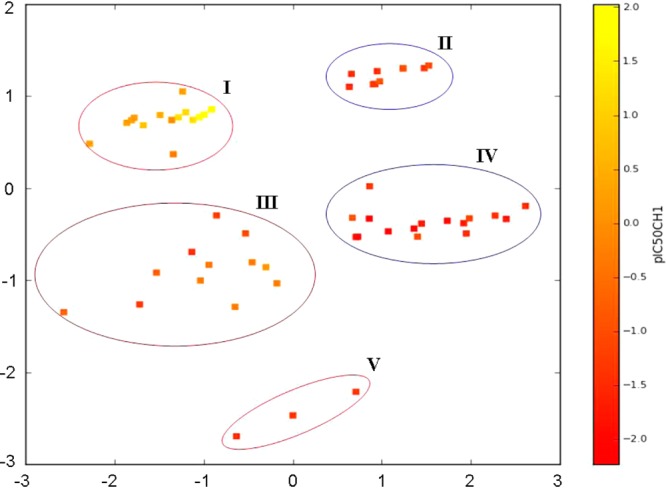
Scoring plot derived from PCA on the four descriptors (MW, E_eas′, H_don, and H_acc) used in the proposed model for cytotoxicity in the CH1 cells: cluster I, esters from subset 1; cluster II, esters from subset 2; cluster III, amides and free carboxylic acids from subset I and nedaplatin derivatives (48–50); cluster IV, amides and free carboxylic acids from subset 2 and complexes 17 and 18 from subset 1; cluster V, compounds with terminal CH₂OH groups in the axial ligands.

QSAR Models for the Cell Line SW480

Statistical data for the best regression models for cytotoxicity in the SW480 cell line are summarized in Table 6. Additional statistical information for these and other one- to five-variable regressions is presented in Table S6 (Supporting Information).

Table 6. Statistical Data for the Best Regression Models for Cytotoxicity in the SW480 Cell Line of the 53 Investigated Pt(IV) Complexes.

no. of variables	descriptors	R2	Q2(LTOP)	rms
1	Hacc	0.63	0.60	0.75
2	q(Pt), Hdon	0.73	0.70	0.65
3	Es, Hdon, Hacc	0.77	0.73	0.61
4	Es, Hdon, Hacc, COOH	0.80	0.75	0.59
4	Ei, Eeas, Eeas′, Hdon	0.80	0.76	0.58
4	Ei, Eea, Eeas, Hdon	0.82	0.79	0.54
5	EHOMO, Ei, Eea, Eeas, Hdon	0.84	0.80	0.52
5	q(Pt), H/Lgap, Ei, Eeas, Hdon	0.82	0.78	0.56
6	EHOMO, Ei, Eea, Es, Eeas, Hdon	0.85	0.81	0.51
7	EHOMO, Ei, Eea, Es, Es′, Eeas, Hdon	0.86	0.80	0.52

Using only one descriptor cannot give a model with good explanatory and predictive properties (R² and Q² under 65%). Including a second (q(Pt) and H_don) increases R² up to 73% and Q² to 70%. However, in order to reach values over 75%, models with a combination of three or four descriptors should be used. Increasing the number of variables to more than four gives models with marginally higher R², but this is mainly due to overfitting, since they contain autocorrelated descriptors (E_HOMO or H/Lgap and E_i). The actual predictability of the best models, featuring three, four, or five descriptors, using external validation, is summarized in Table S7 (Supporting Information). The lowest predictive capability of the models could be observed on training sets c and e where most of the ethylenediamine derivatives or the oxaliplatin, nedaplatin, and part of the carboplatin analogues are moved to the predictive set.

The complete regression equations for the final predictive models we have chosen are the following:

1

2

3

The plot of the predicted vs experimental pIC₅₀ values for the models is shown in Figure 10. Model 3 gives the best linear fit (R² = 0.82 vs R² =0.80 for models 1 and 2) and can predict better the activity of the oxaliplatin analogues (51–53), the only compounds from subset 2, showing some activity in the cell line SW480 (due to the DACH carrier ligand). On the other hand, model 1 showed higher predictive R² (near 60%) in the severe cross-validation partitioning e and in addition is built from easy to calculate molecular descriptors. It is therefore favorable for screening of new compounds.

Figure 10.

Predicted (with the selected four-variables model) vs experimental cytotoxicity in the SW480 cell line: top, model 1; middle, model 2; bottom, model 3. The coloring is based on the subtypes containing the same equatorial ligands.

As most of the compounds from subset 2 did not show cytotoxic activity in the SW480 cell line and IC₅₀ could not be detected up to 500 μM, in the current study IC₅₀ of 600, 1000, and 2000 μM were used as input for their cytotoxic activity. By an increase of these values from 600 to 2000, slightly better models with increased R² and Q² could be observed (Table S8); however, the AAR values increased too and the results from the external validation deteriorate slightly. The data, presented in Table 6, are based on the optimal input IC₅₀ of 1000 μM. The tables in Supporting Information are based on the study using IC₅₀ = 600 μM for complexes inactive in SW480 cells.

Model 2 showed the smallest difference between the predicted pIC₅₀ values for the inactive carboplatin analogues (−2.8 ± 0.4) for input value pIC₅₀ = −3.0 (IC₅₀ = 1000 μM).

Applying PCA, using the descriptors from the chosen four-variable models, showed that 88–89% of the variance in the set can be explained by three components. By plotting of the scores of PC1 and PC3 (covering 60% of the variance) produced from model 3 descriptors combination, a nice clustering of the series could be observed (Figure 11). Similar to the clustering obtained with the CH1 cells model PCA, the compounds split into subsets 1 and 2 esters and subsets 1 and 2 amide and free carboxylic acids. Compounds 3, 11, and 16 are again in a separate cluster, and complexes 17 and 18 from subset 1 are in the subset 2 amides and acids cluster. In addition the EtNH₂ ester derivatives (22–25) built a subcluster.

Figure 11.

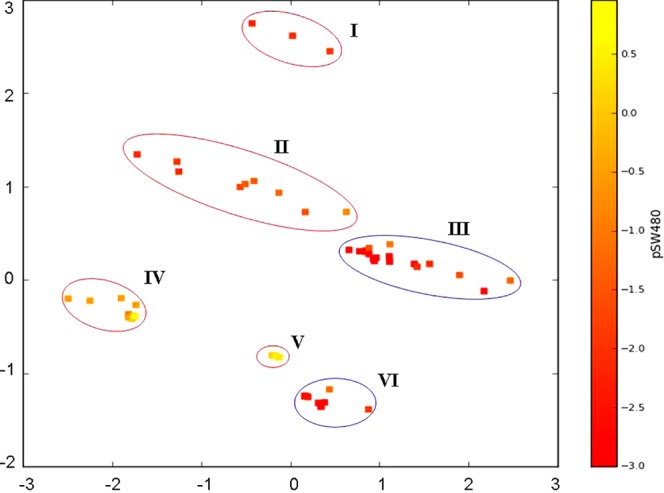
Score plot derived from PCA using four descriptors (E_i, E_ea, E_eas, and H_don), applied for modeling the cytotoxicity in SW480 cells (model 3): cluster I, compounds with a terminal free CH₂OH group in the axial ligands; cluster II, amides and free carboxylic acids from subset 1; cluster III, amides and free carboxylic acids from subset 2 and 17 and 18 from subset 1; cluster IV, esters from subset 1 (without the EtNH₂ derivatives); cluster V, esters from subset 1/the EtNH₂ derivatives; cluster VI, esters from subset 2.

Conformational Differences

Four different conformers for compound 2 and two different conformers for compound 50 were generated (Figure S5, Supporting Information), and their molecular properties were calculated. The descriptors with the smallest differences were q(Pt), α, E_HOMO, H/Lgap, E_i, E_is, E_eas, and E_eas′, with RSD < 2%. A moderate effect of the conformation was observed on V_m and SASA (RSD < 8%). The dipole moment (μ) and solvation energies (E_s and E_s′) are more dependent on the conformation, where RSD rises to 17% in the case of μ. The autocorrelating E_LUMO and E_ea showed great dependency on the conformation, which excludes them from the list of descriptors able to produce reliable models. The influence of the conformations of complex 2 on the predicted cytotoxicity from the best chosen four-descriptor models is summarized in Table 7.

Table 7. Average IC₅₀ Values for Conformers of Complex 2, Derived from the Best Four-Variable QSAR Models, for CH1 and SW480 Cells in Comparison to Experimental Data^a.

cell line	CH1	RSD, %	SW480 model 1	RSD, %	SW480 model 2	RSD, %	SW480 model 3	RSD, %
exptl	0.62 ± 0.32	52	3.8 ± 1.0	26	3.8 ± 1.0	26	3.8 ± 1.0	26
linear fit	0.59 ± 0.46	80	10.9 ± 4.9	45	8.3 ± 8.6	104	4.6 ± 4.8	104
cross-validat predictions (LOOP)	0.60 ± 0.50	83	12.6 ± 6.4	52	8.6 ± 9.3	108	5.0 ± 5.5	110
ext validationb	0.91 ± 0.77	85	35.2 ± 19.5	55	42.3 ± 10.6	25	3.7 ± 3.6	97

^aResults are presented as the mean ± sd.

^bValues from partitioning, where all the conformers are in the training set.

In comparison to model 1, models 2 and 3 gave better results with respect to cytotoxicity in SW480 cells. However, the dependency on conformers was higher (high RSD values). This circumstance is expected, since the conformation has a significant impact on descriptor E_ea. The vertical and adiabatic redox potentials in water have small conformational dependence but also close values in the series, which pronounce the effect of the conformation to the predicted cytotoxicity.

Free–Wilson QSAR Model

In order to judge the contribution of different substituents to the biological activity of the compounds, Free–Wilson QSAR models for cytotoxicity of the complexes in the CH1 and SW480 cell lines were developed. The models are based on the concept that each substituent makes an additive and constant contribution to the biological activity regardless of substituent variation in the rest of the molecule.³⁰ Each compound was presented as a binary string with a length of 24 substituents (the different equatorial ligands, spacers between the two carbonyls, and terminal functional groups in the axial ligands). A term is equal to 1 when a substituent is present at a particular position and 0 when it is absent. The contribution of each substituent was calculated using MLR, and the following models were obtained:

for which R² = 0.90, Q² = 0.76, and AAR = 0.28.

for which R² = 0.91, Q² = 0.80, AAR = 0.26.

In the above equations, A is the carrier ligand, L the leaving groups, X the spacer between the two carbonyl groups in the axial ligands, and R the terminal functional group of the axial chains. Explanation of results and predictability of the models with the given set of substituents is good. The highest positive effect on the cytotoxicity in both cell lines have A = EtNH₂, L = Cl, R= COOEt, COOPr and COOBut. The lowest cytotoxic effect is due to A = NH₃, L = CBDA, R = COOH, and CONH(CH₂)₂OH. The spacers between the carbonyl groups in the axial chains have a lower impact on the cytotoxicity in the series. In the model for SW480 cells, A = DACH and L = ox have a slightly positive effect on the cytotoxicity, contrary to the model for CH1 cells. In contrast, R = COOiPr has a much higher positive effect on the pIC₅₀ values in the cell line CH1 than in SW480 cells.

Conclusions

Reliable, robust, and predictive four-variable models for the in vitro cytotoxicity of bis-, tris-, and tetrakis(carboxylato)platinum(IV) complexes in cisplatin sensitive CH1 cells and intrinsically cisplatin resistant SW480 cells were developed. The QSAR model of choice (R² = 85%, Q² = 82%) for CH1 cells was built using the combination of MW, H_don, H_acc and E_eas′. For the SW480 cell line, models consisting of E_s, H_don, H_acc, and COOH (R² = 80%, Q² = 75%) and E_i, E_eas, E_eas′, and H_don (R² = 80%, Q² = 76%) were proposed. The autocorrelating descriptors q(Pt), H_acc, and E_eas distinguished well the two main subtypes of compounds, namely, bis(carboxylato)dichlorido (subset 1) from tris- and tetrakis(carboxylato) (subset 2) complexes and showed some minor discrimination within the subsets, depending on different equatorial ligands. H_acc predicted a slightly higher activity for nedaplatin analogues compared to the other compounds in subset 2 (the case of CH1 cells), while q(Pt) and E_eas discriminated oxaliplatin analogues as more active (the case of SW480 cells). The constitutional descriptor H_don discriminated the main functionalities on the axial ligands: amides and free carboxylic acids from esters. Therefore, the latter is crucial for building a good model. MW as a descriptor indicates the increase of lipophilicity (respectively, cytotoxicity) in the series with increasing the size of the axial chains or the size of equatorial amines. E_eas′ and E_s, redox behavior and solubility correspond to important physicochemical parameters of Pt(IV) complexes and expectedly show significance for the prediction of the biological response. The results of the study represent a step toward a better understanding of the biological behavior of Pt(IV) carboxylato complexes and their further rational development.

Experimental Section

All reagents and solvents were obtained from commercial suppliers and were used without further purification. Water was purified through reverse osmosis, followed by double distillation. For column chromatography, silica gel 60 (Fluka) was used. ¹H, ¹³C, ¹⁵N, ¹⁹⁵Pt, and two-dimensional ¹H–¹H COSY, ¹H–¹³C and ¹H–¹⁵N HSQC, and ¹H–¹³C HMBC NMR spectra were recorded with a Bruker Avance III 500 MHz NMR spectrometer at 500.32 MHz (¹H), 125.81 MHz (¹³C), 107.55 MHz (¹⁹⁵Pt), and 50.70 MHz (¹⁵N) in DMF-d₇ or D₂O (in the case of nedaplatin and its dihydroxido Pt(IV) analogue) at ambient temperature. The splitting of proton resonances in the ¹H NMR spectra are defined as follows: s = singlet, bs = broad singlet, d = doublet, t = triplet, and m = multiplet. ¹⁵N chemical shifts were referenced relative to external NH₄Cl, whereas ¹⁹⁵Pt chemical shifts were referenced relative to external K₂[PtCl₄] (see Figure 2, compounds 48–50, including NMR numbering scheme). IR spectra were recorded with a Bruker Vertex 70 FT-IR spectrometer (4000–400 cm^–1) by using an ATR unit. Intensities of reported IR bands are defined as follows: br = broad, s = strong, m = medium, and w = weak. Electrospray ionization mass spectrometry was carried out with a Bruker Esquire 3000 instrument using MeOH/H₂O as solvent. Elemental analyses were performed using a Perkin-Elmer 2400 CHN elemental analyzer at the Microanalytical Laboratory of the University of Vienna, Austria, and are within ±0.4% of the calculated values, confirming their ≥95% purity (see Table S9, Supporting Information).

Synthesis and characterization of complexes 1–47 and 51–53 are described in refs (14), (17), and (20). The synthetic procedure for compounds 48–50, their precursor nedaplatin, and its dihydroxidoplatinum(IV) analogue is reported herein. Synthesis and characterization of compound 48 was reported recently.²²

(SP-4-3)-Diammineglycolatoplatinum(II) (Nedaplatin)

Nedaplatin was prepared starting from K₂PtCl₄ via cis-Pt(NH₃)₂I₂. An amount of 1.206 g (2.4972 mmol) of the latter was suspended in 36 mL of triply distilled water, and 870 mg (4.7564 mmol) of silver glycolate were added. The suspension was left stirring overnight in the dark, and then the obtained silver iodide was filtered through a sintered glass funnel with a filter paper disk (MN GF-3). The clear solution was stirred at room temperature in the dark for 4 h, and then Amberlite·HCl (conditioned with NaOH to its OH form) was added slowly in small portions to the solution of the complex while stirring until pH (9–10) was achieved. The mixture was left stirring overnight in the dark. Then Amberlite and traces of reduced Pt(0) were filtered off through a sintered glass funnel with a filter paper disk (MN GF-3). The volume of the filtrate was reduced and cooled in the fridge. The obtained precipitate was filtered off, washed with acetone, and dried in a vacuum desiccator over P₂O₅ to yield 498 mg of a white to pale yellow solid. Yield: 498 mg (69%). ¹H NMR: δ = 4.02 (s (with Pt satellites) H-1) ppm. ¹³C NMR: δ = 194.8 (C-2), 68.1 (C-1) ppm. ¹⁹⁵Pt NMR: δ = −47 ppm. IR (ATR): ν = 3201 br, 2995 br (ν_N–H); 2889 br; 1613 s, 1578 s (ν_C=O); 1443 w; 1337 s, 1319 m, 1060 w cm^–1. Anal. (C₂H₈N₂O₃Pt) C, H, N.

(OC-6-44)-Diammineglycolatodihydroxidoplatinum(IV)

Nedaplatin (1.0995 g, 3.6267 mmol) was suspended in 22 mL of triply distilled water, and then an amount of 11 mL of 30% H₂O₂ was added. The mixture was stirred for 3 h at 30 °C (in the dark). The volume of the clear yellow solution obtained was reduced on a rotavapor, cooled in the fridge, and then precipitated with a sufficient amount of cold acetone. The precipitation was finalized with the help of ultrasonic waves and then the final product was filtered off, washed with acetone, and dried in vacuo to obtain a white to pale yellow solid. Yield: 1.3150 g (94%). ¹H NMR: δ = 4.30 (s + d, ³J_Pt,H = 20.8 Hz, H-1) ppm. ¹⁹⁵Pt NMR: δ = 3222 ppm. IR (ATR): ν = 3462 br (ν_PtO-H); 3229 br, 3045 br (ν_N–H); 2791 w; 1653 s, 1588 m (ν_C=O); 1346 s, 1308 s; 1060 w cm^–1.

(OC-6-42)-Diamminebis(3-carboxypropanoato)glycolatoplatinum(IV) (48)

Succinic anhydride (950 mg, 9.4934 mmol) and 800 mg (2.0607 mmol) of (OC-6-44)-diammineglycolatodihydroxidoplatinum(IV) were suspended in dry DMF (26 mL), and the reaction mixture was stirred at 60 °C for 8 h. During this time, the solid material dissolved to form a pale yellow solution. DMF was then removed under reduced pressure. The residue was suspended in acetone with the help of ultrasonic waves, filtered off, and washed with acetone. The pale yellow solid obtained was then dried in vacuo. Yield: 1.0865 g (98%). ¹H NMR: δ = 12.36 (bs, 2H, COOH), 6.47 (m, 3H, NH₃), 6.05 (bs, 3H, NH₃), 4.08 (bs, 2H, H-1), 2.56 (t, ³J_H,H = 6.5 Hz, 4H, H-4 or H-5), 2.49 (t, ³J_H,H = 6.5 Hz, 4H, H-4 or H-5) ppm. ¹³C NMR: δ = 187.0 (C-2), 180.1 (C-3 or C-6), 174.0 (C-3 or C-6), 70.8 (C-1), 30.6 (C-4 or C-5), 29.8 (C-4 or C-5) ppm. ¹⁵N NMR: δ = −58.6, −50.7 ppm. ¹⁹⁵Pt NMR: δ = 3460 ppm. IR (ATR): ν = 3201 br, 3109 br (ν_N–H); 2934 br; 1715 m, 1654 s, 1620 s, 1574 s (ν_C=O); 1405 w; 1340 s, 1307 s, 1242 m, 1198 m, 1162 m, 1049 w cm^–1. Anal. (C₁₀H₁₈N₂O₁₁Pt) C, H, N.

(OC-6-42)-Diammineglycolatobis((4-propyloxy)-4-oxobutanoato)platinum(IV) (49)

CDI (253 mg, 1.5566 mmol) in dry DMF (9 mL) was added to a solution of 48 (408 mg, 0.7593 mmol) in dry DMF (10 mL), and the mixture was heated to 60 °C. After 10 min of being stirred, the solution was cooled to room temperature and CO₂ was removed by flushing with argon. Sodium propanolate in n-propanol (9 mL) (a piece of Na (15 mg), dissolved in 10 mL of n-propanol) was added to the solution and stirred for 30 h at room temperature. Then propanol and DMF were removed under reduced pressure to form a yellow oil. The crude product was purified by column chromatography (EtOAc/MeOH, 4:1), then isolated from an EtOAc suspension, and dried in vacuo to yield a white to pale yellow powder. Yield: 95 mg (20%). ¹H NMR: δ = 6.57 (m, 3H, NH₃), 6.12 (bs, 3H, NH₃), 4.06 (bs, 2H, H-1), 4.01 (t, ³J_H,H = 6.5 Hz, 4H, H-7), 2.57 (m, 4H, H-4), 2.53 (m, 4H, H-5), 1.62 (m, 4H, H-8), 0.91 (t, ³J_H,H = 7.2 Hz, 6H, H-9) ppm. ¹³C NMR: δ = 186.9 (C-2), 179.8 (C-3), 172.6 (C-6), 70.8 (C-1), 65.6 (C-7), 30.5 (³J_Pt,C = 41.0 Hz, C-4), 29.9 (C-5), 21.9 (C-8), 9.9 (C-9) ppm. ¹⁵N NMR: δ = −58.3, −49.7 ppm. ¹⁹⁵Pt NMR: δ = 3464 ppm. IR (ATR): ν = 3301 br, 3212 br, 3048 br (ν_N–H); 2971 br; 1729 m, 1707 s, 1621 s, 1585 m (ν_C=O); 1483 w; 1435 m, 1345 m, 1316 s, 1249 w, 1180 s, 1166 m, 1105 m, 984 w cm^–1. ESI MS (positive): m/z 643.9 [M + Na⁺]⁺. ESI MS (negative): m/z 620.8 [M – H⁺]⁻, 656.7 [M + Cl^–]⁻. Anal. (C₁₆H₃₀N₂O₁₁Pt·0.5H₂O) C, H, N.

(OC-6-42)-Diamminebis((4-cyclopentylamino)-4-oxobutanoato)glycolatoplatinum(IV) (50)

CDI (176 mg, 1.0835 mmol) in dry DMF (7 mL) was added to a solution of 48 (284 mg, 0.5285 mmol) in dry DMF (9 mL), and the mixture was heated to 60 °C. After 10 min of being stirred, the solution was cooled to room temperature and CO₂ was removed by flushing with argon. Cyclopentylamine (115 μL, 1.1628 mmol) in 4 mL of dry DMF was added to the solution and stirred for 24 h at room temperature (the solution changed to a yellow suspension). DMF was removed under reduced pressure to form a pale brown solid. The crude product was purified by column chromatography, using EtOAc/MeOH = 2:1, and subsequently isolated from an EtOAc suspension, washed with EtOAc and Et₂O, and dried in vacuo to yield an almost white solid. Yield: 116 mg (33%). ¹H NMR: δ = 7.78 (d, ³J_H,H = 6.6 Hz, 2H, CONH), 6.49 (m, 3H, NH₃), 6.06 (bs, 3H, NH₃), 4.09 (m, 2H, H-7), 4.06 (s, 2H, H-1), 2.50 (t, ³J_H,H = 7.4 Hz, 4H, H-4 or H-5), 2.36 (t, ³J_H,H = 7.3 Hz, 4H, H-4 or H-5), 1.83 (m, 4H, H-8), 1.66 (m, 4H, H-9), 1.52 (m, 4H, H-9), 1.44 (m, 4H, H-8) ppm. ¹³C NMR: δ = 187.0 (C-2), 180.7 (C-3), 171.2 (C-6), 70.9 (C-1), 50.8 (C-7), 32.5 (C-8), 31.8 (C-4 or C-5), 31.5 (C-4 or C-5), 23.6 (C-9) ppm. ¹⁵N NMR: δ = −58.7, −50.2, 106.7 ppm. ¹⁹⁵Pt NMR: δ = 3459 ppm. IR (ATR): ν = 3269 br, 3058 br (ν_N–H); 2958 br; 1697 m, 1632 m, 1571 s (ν_C=O); 1483 m; 1441 s, 1339 w, 1319 m, 1255 m, 1195 m, 1106 s, 997 w cm^–1. ESI MS (positive): m/z 694.0 [M + Na⁺]⁺, 671.0 [M + H⁺]⁺. ESI MS (negative): m/z 669.9 [M – H⁺]⁻, 705.8 [M + Cl^–]⁻. Anal. (C₂₀H₃₆N₄O₉Pt·0.5H₂O) C, H, N.

Crystallographic Structure Determination

Yellow crystals of 7, suitable for X-ray data collection, were obtained after slow evaporation of a MeOH/EtOAc solution. X-ray diffraction measurement was performed on a Bruker X8 APEXII CCD diffractometer. A single crystal was positioned at 40 mm from the detector, and 1638 frames were measured, each for 15 s over 1° scan width. The data were processed using SAINT software.³¹ Crystal data, data collection parameters, and structure refinement details are given in Table S10 (Supporting Information). The structure was solved by direct methods and refined by full-matrix least-squares techniques. Non-H atoms were refined with anisotropic displacement parameters. H atoms were inserted in calculated positions and refined with a riding model. The isotropic thermal parameters were estimated to be 1.2 times the values of the equivalent isotropic thermal parameters of the atoms to which hydrogens were bonded. Structure solution was achieved with SHELXS-97 and refinement with SHELXL-97,³² and graphics were produced with ORTEP-3.³³

Cytotoxicity Assays

CH1 (ovarian carcinoma, human) cells were a gift from Lloyd R. Kelland (CRC Centre for Cancer Therapeutics, Institute of Cancer Research, Sutton, U.K.). SW480 (colon carcinoma, human) cells were kindly provided by Brigitte Marian (Institute of Cancer Research, Department of Medicine I, Medical University of Vienna, Austria). Cells were grown in 75 cm² culture flasks (Iwaki/Asahi Technoglass) as adherent monolayer cultures in complete medium, i.e., minimal essential medium (MEM) supplemented with 10% heat-inactivated fetal bovine serum, 1 mM sodium pyruvate, 4 mM l-glutamine, and 1% v/v nonessential amino acids (from 100× ready-to-use stock) (all purchased from Sigma-Aldrich) without antibiotics. Cultures were maintained at 37 °C in a humidified atmosphere containing 5% CO₂ and 95% air. Cytotoxicity in the cell lines mentioned above was determined by the colorimetric MTT assay (MTT = 3-(4,5-dimethyl-2-thiazolyl)-2,5-diphenyl-2H-tetrazolium bromide, purchased from Fluka). Cells were harvested from culture flasks by trypsinization and seeded in 100 μL aliquots in complete medium into 96-well microculture plates (Iwaki/Asahi Technoglass) in the following densities to ensure exponential growth of untreated controls throughout the experiment: 1.5 × 10³ (CH1) and 2.5 × 10³ (SW480) viable cells per well. Cells were allowed to settle and resume exponential growth in drug-free complete culture medium for 24 h, followed by the addition of dilutions of the test compounds in 100 μL/well of the same medium. After continuous exposure for 96 h, the medium was replaced by a 100 μL/well RPMI 1640 medium (supplemented with 10% heat-inactivated fetal bovine serum and 4 mM l-glutamine) plus 20 μL/well solution of MTT in phosphate-buffered saline (5 mg/mL) (all purchased from Sigma-Aldrich). After incubation for 4 h, medium/MTT mixtures were removed, and the formazan product formed by viable cells was dissolved in DMSO (150 μL/well). Optical densities at 550 nm were measured with a microplate reader (Tecan Spectra Classic), using a reference wavelength of 690 nm to correct for unspecific absorption. The quantity of viable cells was expressed as the percentage of untreated controls, and 50% inhibitory concentrations (IC₅₀) were calculated from concentration–effect curves by interpolation. Evaluation is based on the mean from three independent experiments, each comprising triplicates per concentration level.

Theoretical Calculations

All calculations were performed with the Gaussian 09 software package.³⁴ The starting structures for optimizations (complexes 1, 6, 7, 22, 38) were taken from the available X-ray data;^14,17,18,20 the crystal structure of complex 7 is reported herein. The other compounds were modeled by modification of the latter. A complete conformational search is not feasible for systems with as many degrees of freedom as the present. Furthermore, there are very few force fields capable of handling Pt complexes. In order to see the influence of different conformations to the calculated parameters and to the QSAR models, four different conformers of compound 2 and two of compound 50 were modeled and their geometry was optimized (Figure S5, Supporting Information). In principle, the possible conformational uncertainties are in the chains of the axial ligands because the surroundings around the platinum atoms were taken from the crystallographic data. For compounds 19, 20, 42, 43, and 44, which have two chiral centers in the axial carbon chains, the meso RS forms were taken for the calculations. These compounds were tested for cytotoxicity as a mixture of RR/SS/RS = 1:1:2 stereoisomers. In the particular case, stereochemistry will not affect essentially the activity because the chiral centers are in the middle of the carbon chains of the axial ligands, which are supposed to be lost after the activation of the complexes via reduction in vivo. In contrast, in the case of oxaliplatin, featuring DACH (1,2-diaminocyclohexane), the R,R configuration of the ligand should be respected (compounds 51–53).

The DFT long-range corrected hybrid wb97x functional was used for all calculations³⁵ in connection with the Def2-SVP basis set³⁶ with effective core potential³⁷ for optimizing the geometries and calculation of the molecular descriptors. For the calculations of polarizability and dipole moment the basis set were augmented by a set of diffuse functions.

Geometry optimizations were performed in the gas phase and in a water solvent model by using the IEFPCM³⁸ method. Solvent accessible surface area (SASA) was extracted after single point energy calculation of the gas optimized structures in water environment with the ipcm³⁹ method, where the cavity is defined by a self-consistent isodensity contour in a water solvent model. Atomic charges were calculated using the NPA approach.⁴⁰

The molar volume and the HOMO and LUMO energies were taken from the gas phase optimized geometries. The energies of solvation were calculated by extracting the energies in water environment (using the iefpcm method) with (adiabatic E_s′) or without (vertical E_s) optimization from the total energies in gas phase. For estimation of the ionization potential and electron affinity, the energies of the corresponding anion and cation radicals were calculated in the gas phase and in solvent, with (only for the anion radicals) and without geometry optimization.

QSAR Analysis. QSAR Data Set

The pIC₅₀ = log(1/IC₅₀) values, used to develop the QSAR models, were taken from the MTT assays, described in refs (14) and (18−20) for complexes 1–47 and 51–53 and in the present paper for complexes 48–50. The cytototoxicity data in CH1 and SW480 cells for all investigated compounds in comparison with the clinically approved platinum-based drugs cisplatin, carboplatin, oxaliplatin, and nedaplatin are summarized in Table 1.

By use of QM calculations, the following descriptors were extracted: molar volume (V_m), dipole moment (μ), polarizability (α), charge on the Pt atom (q(Pt)), energy of the HOMO and LUMO (and the corresponding HOMO–LUMO gap), SASA, vertical and adiabatic solvation energies (E_s and E_s′), vertical gas-phase ionization energies (E_i) and electron affinities (E_ea), and vertical and adiabatic oxidation (E_is) and reduction (E_eas and E_eas′) potentials in the water solvent model. In addition molecular weight (MW), number of H-bonds donors (H_don), numbers of H-bonds acceptors (H_acc), and presence/absence of carboxylic groups (COOH) in the axial ligands as constitutional molecular descriptors were used. The values of the used descriptors in the present study are summarized in Tables S3 and S4 (Supporting Information).

Chemometric Methods and Statistics

QSAR analysis was performed with the QSAR program⁴¹ developed by the Ponder group and Schrödinger Strike 2.0 for Maestro application.⁴² Standard multiple linear regression (MLR) and principal component analysis (PCA) methods were used to analyze the data, and simulated annealing was employed to identify the best combinations of descriptors. All descriptors were centered and autoscaled prior to analysis.

The robustness of the models and their predictivity were evaluated through R², Q² (R² of cross-validated predictions, using the leave-one-out procedure (LOOP) or leave-two-out procedure (LTOP)), AAR (average absolute error), and rms (root mean squared error). The actual predictive capability of every model was checked with external validation by splitting the data set into training and predictive sets. Five different ways of partitioning the data into training and predictive data sets were used in order to test the robustness of the QSAR model. In each case the training set encompassed 75% of the data while the remaining 25% was selected as (a) random, including 14 compounds representing every subtype, (b) including cisplatin and its bis(ethylamine) analogue derivatives (complexes 1–5, counting all conformers for 2 and 21–26), (c) including most of the ethylenediamine analogues (complexes 6–19), (d) including most of the carboplatin analogues (27–40), and (e) including oxaliplatin, nedaplatin, and the other part of the carboplatin analogues (complexes 41–53, counting both conformers of 50). By use of the models derived from the training sets, the pIC₅₀ values in the predictive sets were calculated and R² predictive, AAS, and RMS were measured.

Glossary

Abbreviations Used

FDA

Food and Drug Administration

ESP

electrostatic potential

SAR

structure–activity relationship

QSAR

quantitative structure–activity relationship

QSPR

quantitative structure–property relationship

DFT

density functional theory

MLR

multiple linear regression

MM

molecular mechanics

log P_o/w

logarithm of partition coefficient between n-octanol and water

E_p

redox potential

NPA

natural population analysis

PC

principal component

PCA

principal component analysis

RSD

relative standard deviation

CDI

1,1′-carbonyldiimidazole

Supporting Information Available

Figures with ORTEP view of 7, chemical structures of the model systems used in the reduction studies, dependency of the QSAR model properties from the descriptors number, loading plots derived from the PCA of the CH1 cells four variable model, and superposition of the optimized conformers of complexes 2 and 50; tables with comparison of calculated and experimental geometrical parameters, calculated descriptors, and additional statistical data for chosen QSAR models and their external validation, dependency of the QSAR model properties from the input IC₅₀ values used for the inactive compounds, elemental analysis data, structure refinement details for 7; X-ray crystallographic data in CIF format. This material is available free of charge via the Internet at http://pubs.acs.org. Crystallographic data have been deposited with the Cambridge Crystallographic Data Center with number CCDC 909001. Copies of data can be obtained, free of charge, on application to CCDC, 12 Union Road, Cambridge CB2 1EZ, U.K. (deposit@ccdc.com.ac.uk).

The authors declare no competing financial interest.