Toward the Mechanism of Ionic Dissociation in Water

Abstract

We investigate the solvent effects leading to dissociation of sodium chloride in water. Thermodynamic analysis reveals dissociation to be driven energetically and opposed entropically, with the loss in entropy due to an increasing number of solvent molecules entering the highly coordinated ionic solvation shell. We show through committor analysis that the ion–ion distance is an insufficient reaction coordinate, in agreement with previous findings. By application of committor analysis on various constrained solvent ensembles, we find that the dissociation event is generally sensitive to solvent fluctuations at long ranges, with both sterics and electrostatics of importance. The dynamics of the reaction reveal that solvent rearrangements leading to dissociation occur on time scales from 0.5 to 5 ps or longer, and that, near the transition state, inertial effects enhance the reaction probability of a given trajectory.

Introduction

Characterizing the dynamics of rare events is vital to the understanding of large-scale structural changes that occur in many complex systems in nature and technology. Rare events typically involve many cooperative parts that act together in a complicated way along a transition from one long-lived state to another, and the determination of the collective variables responsible for the reaction dynamics can provide much insight into the physical mechanism underlying a transition. In the best circumstance, a reaction coordinate is found, a function of these collective variables that alone is sufficient to track the progress of a reaction. Unfortunately, finding an adequate description of the reaction in terms of a reaction coordinate or even only identifying the collective variables is a challenging task: not only is sampling computationally demanding due to the rare nature of the transition, but the reaction also proceeds through a high-dimensional phase space and so it is often difficult to discern which variables promote the transition. Despite many novel techniques for reaction analysis,^1,2 finding a good reaction coordinate remains a challenge for many processes occurring in complex systems.

In this paper, we investigate the kinetic pathways leading to ionic dissociation, in particular the dissociation of Na⁺Cl^– in water. Microscopically, this system contains metastable associated and dissociated states, separated by a free energy barrier preventing frequent transitions. Along a reaction in which the ion pair transitions between associated and dissociated states, a number of system rearrangements must take place which crucially involve the surrounding solvent molecules. The first simulations of this system were performed by McCammon et al.^3,4 and Rey et al.⁵ who used umbrella sampling and constrained solute simulations, respectively, to investigate solvent structure and thermodynamic properties as the interionic distance r_ion = |r_Na⁺ – r_Cl^–| is varied. More recent work by Geissler et al.⁶ employed transition path sampling to study the reaction, showing under careful statistical analysis that r_ion alone is a poor reaction coordinate in describing dissociation, and that the surrounding solvent must be taken into account in a good reaction coordinate. Despite this work and others, a complete description of the solvent motion leading to dissociation is missing. While the ultimate goal is to find a reaction coordinate for the event, even a complete set of solvent variables that jointly account for the dissociation process is still unknown, and hence further investigation is needed.

In the current study, we shed some more light on water’s unique role by investigating the thermodynamic and dynamical properties of the dissociation reaction. Our main results are organized as follows. After describing our model, we present a thermodynamic description of the reaction in terms of competing thermodynamic driving forces, showing that dissociation is an energetically favorable but entropically unfavorable process. We argue that the decrease in solvent entropy upon dissociation is due to an increasingly larger number of highly coordinated solvent molecules in the first hydration shell as the ions move apart. We then investigate the relative importance of various system variables in promoting dissociation. As with previous studies,⁶ we employ statistical analysis of dissociation (committor) probabilities on data from various constrained ensembles: For data with constrained r_ion, we verify that r_ion is indeed important in the reaction but does not capture the entire mechanism, in confirmation with earlier studies.⁶ Various solvent degrees of freedom are then constrained to pinpoint the range over which the solvent influences the dissociation event. We then investigate various dynamical aspects of dissociation, highlighting time scales under which solvent rearrangements occur which drive dissociation, and the importance of inertial effects near the transition state. Finally, our results are summarized and discussed.

Model

The system we studied consists of one Na⁺ ion and one Cl^– ion immersed in a bath of N_w = 216 water molecules. The ion pair and ion–water interactions were modeled using the OPLS force field,⁷ which includes short-ranged Lennard-Jones and long-ranged Coulomb terms. More specifically, the ion–ion interaction is given by

1

where e is the elementary charge, ε₀ is the permittivity of free space, and Lennard-Jones parameters for the ion pair are σ_ion = 3.8355 Å and ε = 0.075 603 420 1 kJ/mol. The water molecules interact via the rigid TIP4P model.⁸ Calculations of the long-ranged electrostatic forces from periodic boundary conditions were handled with particle mesh Ewald summation. The simulations were performed at a constant temperature of T = 300 K and constant volume of V = (18.64 Å)³, which was chosen from an equilibrated constant-pressure simulation under ambient conditions. To sample the NVT ensemble, the system evolved under Langevin dynamics with a friction coefficient corresponding to a time scale of 0.1 ps. Our simulations were performed with the program Gromacs,⁹ with a time step of δt = 2 fs and integration performed via a stochastic leapfrog algorithm.¹⁰

To begin our analysis, we generated 10 trajectories sampling the canonical ensemble, totaling 80 ns, that involved 227 transitions between associated and dissociated states. Initial conditions for each of the 10 trajectories were taken from a previous simulation run using the same Langevin dynamics. Each of the 10 points were separated by 400 ps from their neighbors, such that they can be considered statistically independent. We calculate the free energy along the interionic distance r_ion as

2

by histogramming r_ion from the concatenated trajectories. Here k_B is the Boltzmann constant. From Figure 1, we see that F(r_ion) contains a metastable associated state with a corresponding free energy minimum at r_ion = 2.7 Å. This minimum is separated from the solvent-separated state, centered around 5 Å, by a barrier of 5 k_BT. For future reference, we identify the associated state as all configurations for which r_ion < 3.2 Å, the dissociated state as r_ion > 4.4 Å, and the transition region to be 3.2 Å ≤ r_ion ≤ 4.4 Å.

Figure 1.

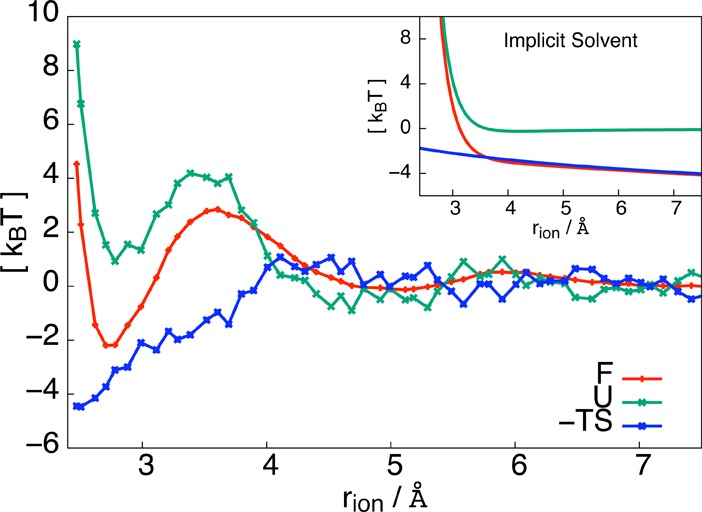
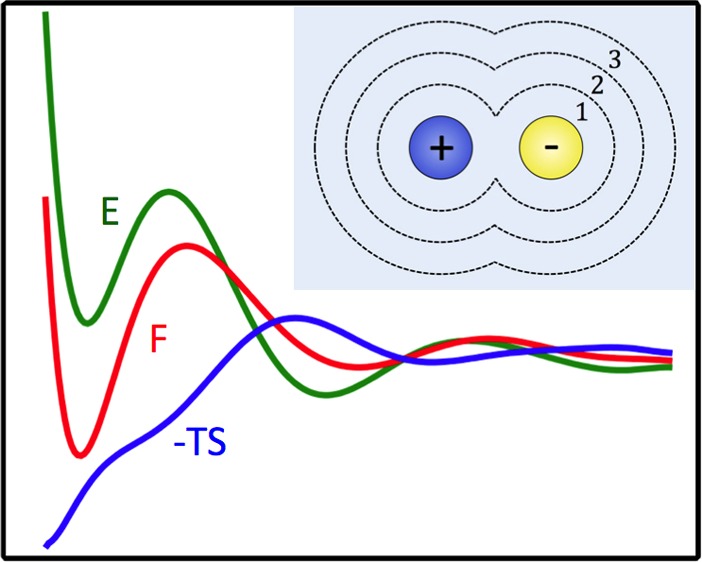
Thermodynamics of ionic dissociation. The free energy (red) as a function of r_ion displays a stable associated state at r_ion = 2.7 Å, separated from the dissociated state by a free energy barrier of 5 k_BT. Also plotted are the average energy (green) and negative entropy (blue) as a function of r_ion. Dissociation is driven energetically and opposed by entropy. The inset shows the free energy, the energy, and the entropic contribution for an implicit solvent model, in which the electrostatic interaction between the two ions is reduced by a factor of ε = 80.

Thermodynamics of Ionic Dissociation

To gain an understanding of ionic dissociation, we first investigate the thermodynamics of the process along the order parameter r_ion. In the NVT ensemble, the Helmholtz free energy F contains energetic and entropic contributions, which we calculate as a function of the ion pair separation (see Figure 1). The energy profile is computed from a number of simulations, in each of which r_ion is constrained to a value between 2.47 and 7.51 Å. For each simulation, the potential energy E was averaged over a 100-ns-long trajectory. Plotted in green is U(r_ion) = ⟨E⟩_rion – ⟨E⟩_∞, the average energy, after subtracting the asymptotic value. The entropy S, plotted in blue, is identified from

3

Note that the errors on U and S are due to the large energy fluctuations of the many solvent–solvent interactions in the bulk. We see, in Figure 1, that the associated state is stabilized energetically, with a 3 k_BT barrier to overcome before energetically favorable dissociation occurs. The entropy S leads to an attractive contribution to the free energy opposing dissociation in the range r_ion < 4.0 Å, a behavior familiar from entropy-driven hydrophobic association.¹¹ Thus, the energy and entropy shown in Figure 1 show markedly different behavior than in the implicit solvent case, where the solvent is modeled simply by a dielectric constant ε = 80 which screens the electrostatic interaction of the ion pair by rescaling the Coulomb term in eq 1 by a factor of 1/ε. In this case, the energy has only one minimum at the associated state, and the driving force to dissociation is entirely entropic, due to an available configuration space that grows as r_ion². This confirms that the solvent plays a nontrivial role in the dissociation process. We note that this thermodynamic picture is contrary to the behavior of a model protein–ligand complex in water, as found in recent simulation studies by McCammon.^12,13 For oppositely charged protein and ligands, the dissociation is an enthalpically unfavorable and entropically favorable process.

To further investigate the influence of the solvent on the system entropy, we plot in Figure 2 the average numbers n_Na and n_Cl of water molecules within the first solvation shell of Na⁺ and Cl^–, respectively. [The solvation shell radii for each ion correspond to the respective minimum in the ion-oxygen radial distribution function, 3.34 Å for Na⁺ and 3.74 Å for Cl^– (data not shown).] During the dissociation process, the solvation numbers of the Na⁺ and Cl^– ions increase by about 2 and 1, respectively. In Figure 2, we also plot in blue the average number of water molecules simultaneously in the solvation shells of both ions. While for the associated state there is one shared molecule, the number of such molecules starts to increase at about r_ion = 3.3 Å and reach 2 at r_ion = 4 Å, where the solvation number of the ions saturate. The number of shared water molecules then falls to 1 as the solvent-separated state is reached around r_ion = 5 Å and finally to 0 around r_ion = 6 Å. Since the number of shared water molecules is constant for r_ion ≲ 3.3 Å, the increase in the average solvation numbers n_Na and n_Cl is due to additional water molecules entering the respective solvation shells from the bulk. In the range 3.3 Å ≲ r_ion ≲ 4.0 Å, however, the total number of water molecules in the combined solvation shells of Na⁺ and Cl^– grows only slowly, while the solvation numbers in the individual shells increase by a total of about 1 water molecule due to a solvent reorganization that creates an additional shared water molecule. This is consistent with early work of McCammon and others¹⁴ on ionic dissociation, who found that dissociation is preceded by solvent reorganization in the first solvation shell, leading to the addition of a shared water molecule as the transition state is approached. As the interionic distance grows further, the solvation numbers of the individual ions stay roughly constant, while the number of shared water molecules decreases to 0 for sufficiently separated ions. During this final stage of the dissociation, 2 water molecules enter the solvation shell of the ions from the bulk to compensate for the loss of shared water molecules. During the entire dissociation process, the total number of water molecules in the combined solvation shells of Na⁺ and Cl^– increases by about 4 on average.

Figure 2.

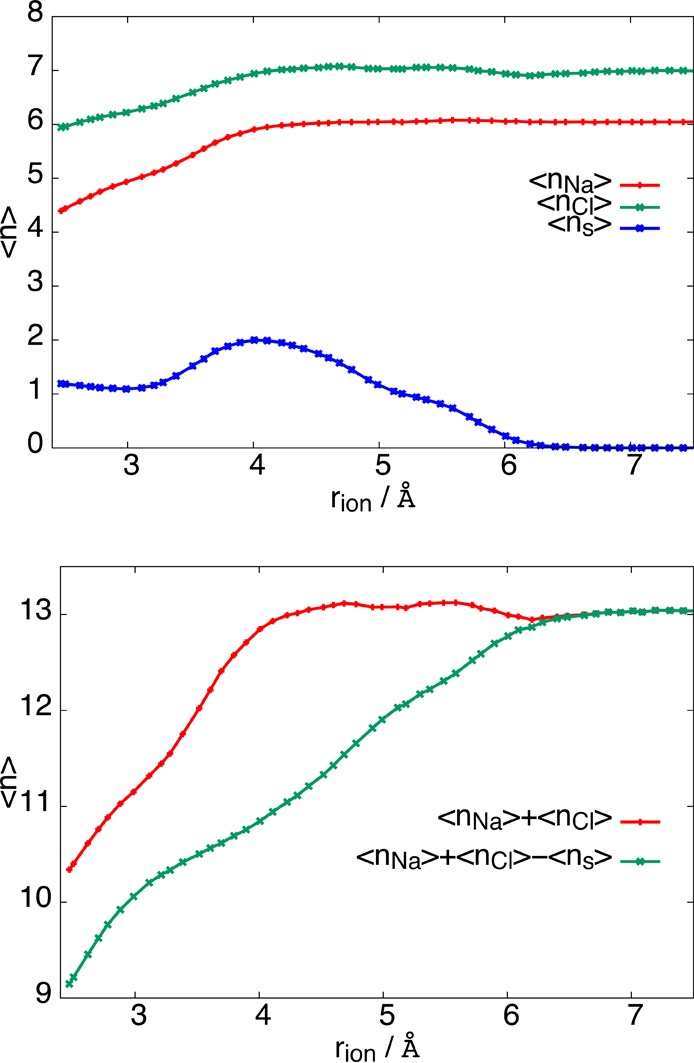
Top: Average number ⟨n_Na⟩ and ⟨n_Cl⟩ of water molecules in the first solvation shell of Na⁺ and Cl^–. Shown in blue is the number ⟨n_s⟩ of waters common to the solvation shells of both ions. Bottom: Sum ⟨n⟩ = ⟨n_Na⟩ + ⟨n_Cl⟩ of the number of water molecules in the first solvation shells of Na⁺ and Cl^– and total number of water molecules ⟨m⟩ = ⟨n_Na⟩ + ⟨n_Cl⟩ – ⟨n_s⟩ in the combined first solvation shell.

As shown in Figure 2, the solvation numbers n_Na and n_Cl show the same roughly linear increase with interionic distance as the entropy (see Figure 1), suggesting that the entropy change during dissociation is due to the reduced freedom of motion of water molecules tightly bound to the ions. Indeed, water molecules in the first solvation shell of ions have been observed in simulations to be orientationally highly restricted,¹⁵ reducing the configurational space available to the molecules compared to the bulk. The orientational restraints acting on first solvation shell molecules are particularly pronounced for water molecules shared by both ions. As the ions dissociate, the number of such “low entropy” solvent molecules increases, leading to a net entropy decrease in the system. For interionic distances of r_ion ≈ 4 Å and larger, the entropy is approximately constant even though the number of total water molecules in the combined first solvation shells of the two ions continues to increase (see green line in the bottom panel of Figure 2). In this regime, the sum n_Na and n_Cl, which double counts shared water molecules and equals the number of close constacts of water molecules with one of the ions, remains constant. This indicates that the entropy is related to the number of such close contacts rather than the total number of solvating water molecules. This conclusion is confirmed by the linear behavior of the entropy in the 3.3 Å ≲ r_ion ≲ 4.0 Å, where the total number of solvating water molecules grows only slowly but the number of close contacts increases due to the increase of shared water molecules. For r_ion ≲ 3.3 Å, on the other hand, the number of close contacts increases due to water molecules entering the first solvation shells of the ions from the bulk. Thus, as shown in Figure 3, overall there is a roughly linear relationship between the number of close contacts and the entropy, where each close contact contributes an entropy decrease of Δs ≈ 1.9k_B.

Figure 3.

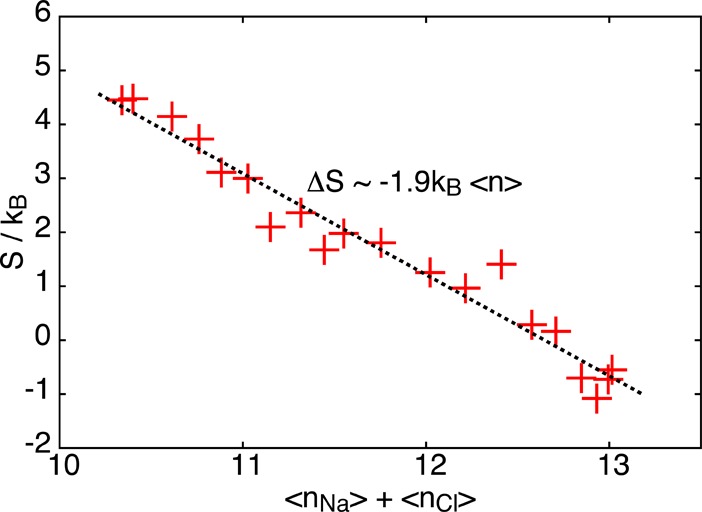
Entropy S as a function the number ⟨n⟩ = ⟨n_Na⟩ + ⟨n_Cl⟩ of close contacts between the ions and water molecules in the first solvation shell. The dotted line denotes a linear fit to the data.

The above analysis, however, provides only a partial picture of ionic dissociation: As shown previously,⁶ the interionic distance r_ion can be used as an order parameter to distinguish between the associated and dissociated states but fails in describing the progress of the dissociation. In other words, r_ion is a poor reaction coordinate implying that solvent degrees of freedom must be explicitly taken into account. In the next section, we corroborate this finding and carry out a new type of statistical analysis to identify the range within which solvent degrees of freedom affect the dissociation process.

Transition Path Analysis

One of the major goals of characterizing a reaction pathway is the determination of the system variables that are important for the reaction to proceed. This set of variables, if known, provides a basis for understanding the physical mechanism underlying a complex transition. A good reaction coordinate r will in general be a function of a number of such collective variables, which together completely specify the progress of a reaction. In this section, we employ committor analysis first to test the quality of r_ion as a reaction coordinate, confirming results of previous studies,⁶ and then to examine the influence of various solvent degrees of freedom on the dissociation process.

In searching for the important collective variables, or optimally a reaction coordinate, we ultimately seek a projection of phase space that preserves the dynamical information pertaining to the reaction. This dynamical information is captured by the committor probability, p_B(x), a key tool in determining these collective variables. For a system containing two long-lived stable states, labeled A and B, p_B(x) is defined as the probability that a trajectory initiated from configuration x will relax to state B before reaching state A. As such, p_B is a statistical measure of the progress of a reaction. In particular, configurations with p_B = 1/2 can be considered to be transition states, as they have equal probability to relax into A or B.

While the perfect reaction coordinate is the committor itself,^16,17r^†(x) = p_B(x), a good reaction coordinate r(x) will to a good accuracy specify p_B(x), in the sense that the committor can be written as p_B(x) ≈ p_B[r(x)] and the reaction information is contained in the variables in r(x). Thus, for a good reaction coordinate, the distribution of p_B values for configurations restricted to a particular value of r should be sharply peaked around some characteristic value.

The quality of a trial reaction coordinate can then be investigated by probing this distribution of committor values. For a trial reaction coordinate r̂, one calculates p_B values for configurations in the constrained equilibrium ensemble with r̂(x) = const. A distribution P_r̂(p_B) is estimated by histogramming the p_B values of the constrained ensemble, and the quality of r̂ is assessed from the shape of P_r̂(p_B): if P_r̂(p_B) is a sharply peaked function of p_B, then the degrees of freedom specified by r̂(x) determine to a good approximation the fate of the reaction. If however P_r̂(p_B) is not sharply peaked, then other degrees of freedom not included in r̂(x) play a role in specifying how the reaction will proceed, and thus r̂(x) is an insufficient reaction coordinate.

In the following sections, we assess the relative importance of various system variables in Na⁺Cl^– dissociation by applying committor analysis to various constrained ensembles. In our solvated Na⁺Cl^– system, we define B as the dissociated state, for which r_ion > 4.4 Å, and A as the associated state, r_ion < 3.2 Å. For our committor calculations, p_B(x) is estimated by shooting off N_s independent trajectories starting from x, with initial velocities drawn from the corresponding Maxwell–Boltzmann distribution. The estimate for p_B(x) is given by the fraction of these trajectories that reach the dissociated state before associating, with an error

4

For our calculations, N_s = 100 shots were performed for each p_B estimate such that σ ≤ 0.05. Note that this statistical error of the estimated committor leads to a broadening of the committor distribution that can be statistically quantified and needs to be taken into account in the interpretation of committor distributions.^18,19

In investigating the thermodynamics of dissociation above, the sampling of the canonical NVT ensemble and constrained ensembles was performed with Langevin dynamics. For the following dynamical studies, however, we will be interested in deterministic Hamiltonian dynamics. Hence, the shooting trajectories for calculation of p_B values will be performed by integrating Hamilton’s equations of motion.

Constrained Interionic Distance r_ion

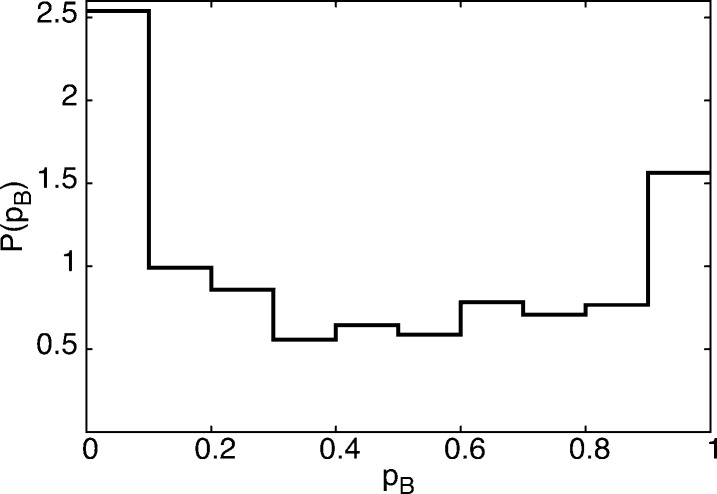
In characterizing the kinetic pathways to ionic dissociation, we first test the performance of the interionic distance r_ion as a reaction coordinate. Such a calculation for r_ion has been done previously,⁶ but we repeat it here, because we use a slightly different force field for the ion–ion interaction and the ion–water interaction here. To test whether r_ion alone is a good reaction coordinate, we apply committor analysis on configurations with constrained r_ion. Committor values were estimated for 665 configurations having 3.45 Å ≤ r_ion ≤ 3.75 Å (narrowing the width of r_ion^* did not qualitatively change the behavior of our results) taken from the equilibrium run used to generate Figure 1, which involved many transitions between associated and dissociated states. The constraint range of r_ion was chosen around the position of the top of the free energy barrier (see Figure 1). We plot in Figure 4 the distribution of p_B values on this constrained surface. Because this range of r_ion corresponds to the top of the free energy barrier, one would expect for a good reaction coordinate a sharp unimodal distribution centered at p_B = 0.5. What one sees, however, is a bimodal distribution peaked at p_B ≈ 0 and 1 and relatively low population at 0.5. Hence, there are structures with the same interionic distance r_ion but very different relaxation behavior, indicating that the solvent degrees of freedom are important in the system committing to associate or dissociate. As this behavior was observed previously by Geissler et al.⁶ for a different force field, these findings highlight that the solvent’s role in dissociation is robust and of general importance in describing the reaction.

Figure 4.

Distribution of p_B values for equilibrium configurations x restricted to r_ion(x) = r_ion^*, corresponding to the top of the free energy barrier shown in Figure 1. The bimodal behavior indicates that r_ion alone is not a sufficient reaction coordinate.

Constrained Solvent

Since the interionic distance r_ion alone is an insufficient reaction coordinate, the surrounding solvent must play a crucial role in the system committing to associate or dissociate. To study the role of the solvent more closely, we seek to identify which water molecules are important in the reaction, with the specific goal of finding a length scale over which the water molecules influence the reaction. Specifically, we perform committor analysis, on a constrained system as above, where in addition to a fixed interionic distance r_ion, we also constrain or “freeze” water molecules within a particular probe range of the ion pair. Committor analysis applied to this system in which a part of the water molecules is held at fixed positions will guide us in finding the length scale that determines the range of solvent influence on dissociation: If the distribution of p_B values on these constrained configurations is sharply peaked, then the dissociation event is only sensitive to the frozen molecules within the given probe range; if, however, the remaining unfrozen molecules in the periphery of the simulation box strongly influence the reaction, then the p_B distribution will not show a single pronounced peak. A similar strategy has been used to deduce the role of the solvent in protein folding.²⁰

We wish to find the probe range over which the peripheral variable solvent molecules cease to influence p_B. In the limit of a very small probe range, only the ions are restrained, and we expect to see a distribution of p_B values like Figure 4, where the other unfrozen molecules are clearly influencing the fate of the ion pair. In the opposite limit of a very large probe range, the entire simulation box is frozen and we expect a p_B distribution that is very sharply peaked about some characteristic value. We seek the smallest probe range over which the variability of p_B becomes small enough that we are confident the molecules within the probe range specify the fate of the reaction. To this end, three separate probe ranges were considered, set by the hydration structure of the ion pair: either all molecules up through the first, second, or third hydration shells were frozen (see Figure 5).

Figure 5.

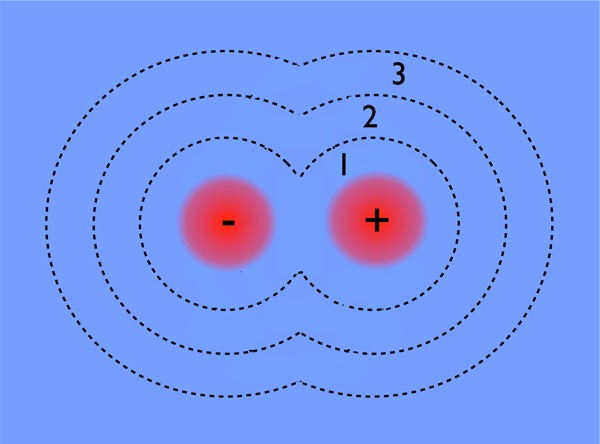
Depiction of the first three solvation shells of the ion pair, which were selectively constrained to investigate solvent influence on ionic dissociation. The solvation shell radii of the three shells were defined by the respective minima in the ion–oxygen radial distribution function, calculated as 3.34, 5.47, and 7.80 Å for Na⁺ and 3.74, 6.20, and 8.18 Å for Cl^–.

To begin the analysis, one of the three probe ranges is chosen, centered around the ion pair, within which all waters are constrained. A representative initial configuration is selected, from which 125 new configurations are generated by evolving the system dynamically, each with identical solvent positions within the probe range but variable positions outside. We enforced these constraints on the dynamics by simply not allowing the positions of the relevant waters to be updated during the integration of the Langevin equation of motion. This dynamical scheme samples a constrained equilibrium state that is equivalent to a reduced system (the solvent outside the probe region), in the presence of a static external field (imposed by the frozen solvent molecules and ion pair within the probe region). Committor analysis is then performed on this constrained state by calculating p_B values for each of the 125 configurations and histogramming the obtained committor values. Note that in the trajectories generated for the committor calculation all constraints used to prepare the initial conditions were released.

The results of the committor analysis are shown in Figure 6, where each subfigure corresponds to a given probe range. Plotted within a given probe range are three distributions, colored red, green, and blue, which correspond to three distinct sets of 125 configurations with frozen solvent having p_B values near 0, 0.5, and 1, respectively. For the smallest probe range, where the solvent is constrained only in the first hydration shell (part a), there is a very wide distribution of p_B values for each of the three configuration sets. In part b, where the first two solvation shells are constrained, the distributions are not as broad as in part a but still show rather large p_B variability, implying that molecules farther out are of importance. Finally, when all three solvation shells are constrained, in part c, we see a much tighter distribution of p_B values, which suggests that the commitment to associate or dissociate is, to a fair degree, determined by the solvent molecules within the first three solvation shells. These results are consistent with studies of Geissler et al.,⁶ who found that the dissociation couples to solvent motion between the second and third solvation shells. Interestingly, the p_B = 0.5 configuration set (green) shows the broadest distribution for all three probe ranges, implying that p_B is particularly sensitive to long-ranged solvent motion near the transition state. This is consistent with previous studies,⁶ who came to the same conclusion from studies of the mean solvent force on the ion pair at the transition state.

Figure 6.

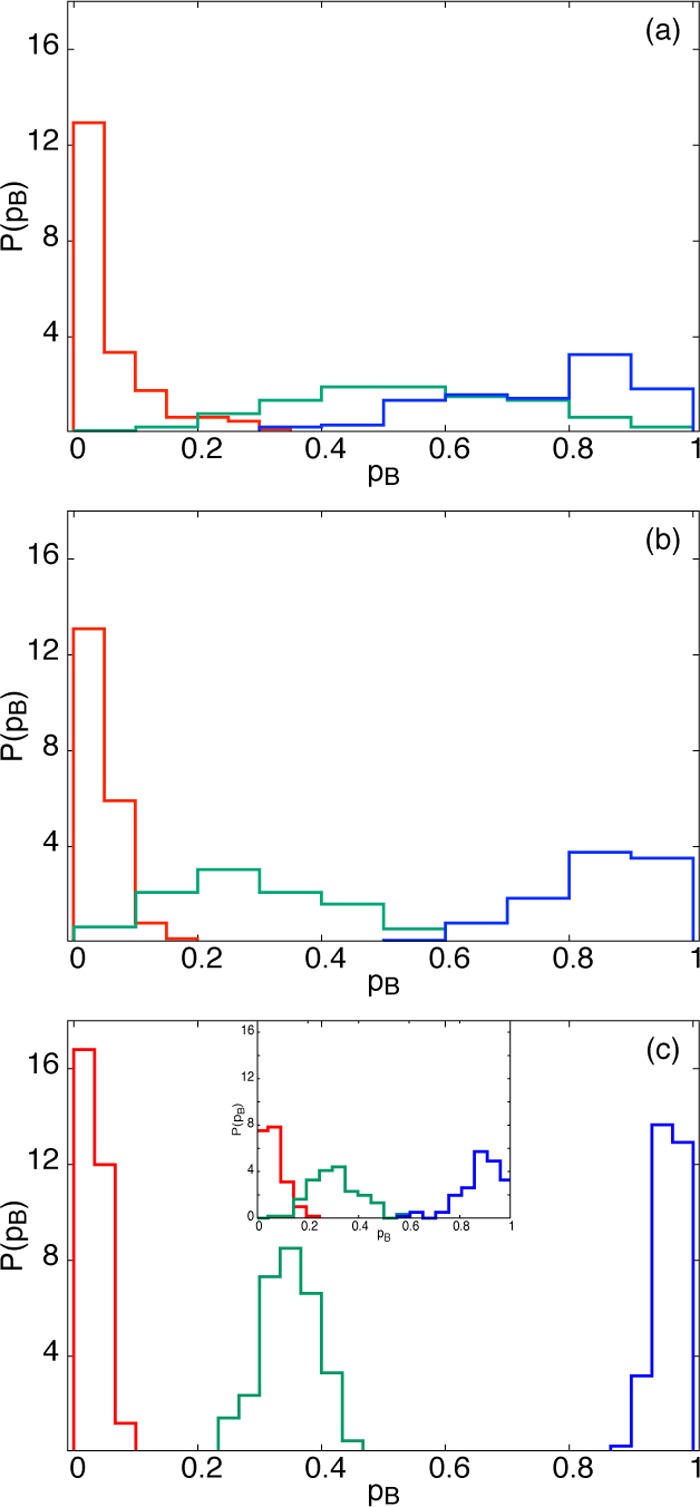
Committor analysis applied to configurations containing “frozen” (identical) solvent coordinates in (a) the first, (b) the first two, and (c) the first three solvation shells, and properly equilibrated outer shells. In each figure, the colors distinguish between different sets of frozen solvents, chosen near the associated state (red), transition region (green), and dissociated state (blue). When freezing the first three solvation shells on a larger system of N = 905 water molecules, the committor distributions are not as tight (inset of panel), further demonstrating that solvent effects on dissociation are long-ranged.

The committor results of Figure 6c, with three frozen solvation shells, correspond to freezing roughly one-half of the N_w = 216 water molecules. To check the effect of system size on our results, we performed the same committor analysis on a system of 905 waters, with identical frozen positions as the smaller system but with a much larger number of peripheral water molecules. For this larger system, we observe a weaker tightening of the committor distribution as compared to the small system (see the inset of Figure 6c), further indication that solvent effects for this system are indeed long-ranged.

As pointed out recently,²¹ a reduction of the number of degrees of freedom arising from additional constraints leads to a narrowing of the committor distribution P(p_B), even if the constraints are not related to the reaction coordinate. To verify that the tightening of the committor distribution observed for frozen solvation shells is not caused by the dimensionality loss of the constrained system, we carried out additional simulations in which the frozen water molecules were chosen at random rather than based on their distance to the ion pair. Specifically, we performed committor calculations analogous to those described in the previous paragraphs but on a constrained ensemble, in which in addition to the ion pair roughly 100 randomly chosen water molecules were kept at fixed positions. The total number of water molecules was N_w = 216 and the number of fixed water molecules was chosen to correspond with the number of molecules in the first three solvation shells, which also contain roughly 100 molecules. The results of these calculations, shown in Figure 7, yielded committor distributions that are much broader than those obtained with the frozen solvation shells. Thus, the narrowing of the committor distributions observed in the latter case is due to the importance of water molecules close to the ion pair rather than to the reduced dimensionality caused by constraining the position and orientation of water molecules.

Figure 7.

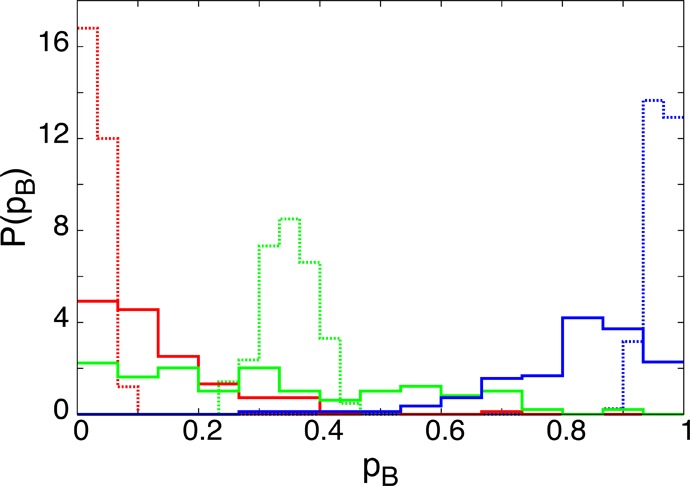
Committor distributions for configurations containing roughly 100 “frozen” water molecules chosen at random (solid lines) together with committor distributions for three frozen solvation shells (dashed lines). Results are shown for configurations close to the associated state (red), the transition region (green), and the dissociated state (blue).

Whether one considers the smaller or larger system, the waters within the first three hydration shells seem to capture the reaction to a good degree. Can this picture be refined further? Specifically, what is the relative importance of steric forces to electrostatics? Because of the long-ranged influence of solvent on p_B, we would expect electrostatics to play an important role. To test this conjecture, we generated a set of 125 configurations having identical oxygen positions within the first three solvation shells but variable hydrogen and dummy atom positions for our 4-point TIP4P model. Because the Lennard-Jones forces are specified by the oxygen position alone, the only variable forces within the three solvation shells are due to electrostatic interactions. The resulting committor distributions, shown in Figure 8, are still somewhat broad both for the smaller system (main figure) and the larger system (inset). This indicates that the charge distribution of the waters is of general importance, and that the p_B is determined by a combination of steric and electrostatic effects.

Figure 8.

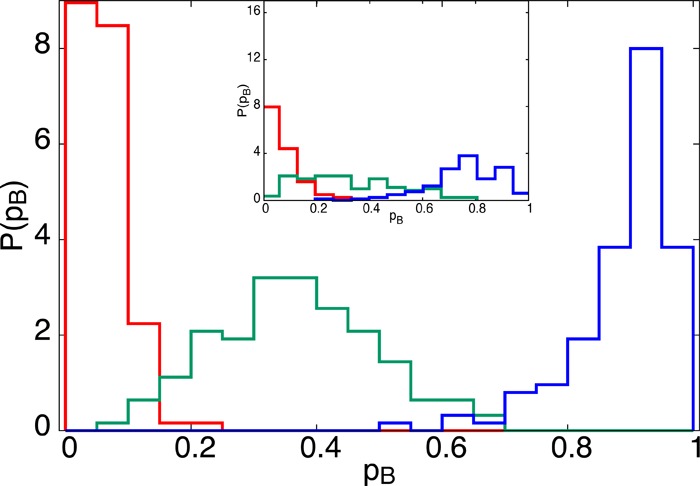
The effect of water orientations on p_B. All configurations within each color contain identical oxygen coordinates but have varying orientations of the water molecules in the first three solvation shells. We analyzed three sets of oxygen positions, chosen near the associated (red), transition (green), and dissociated (blue) states. The inset displays results of the analogous calculation performed for N = 905 water molecules.

Time Scales of p_B Fluctuations

In this section, we investigate the time fluctuations of p_B, with the goal of finding the relevant time scales under which the solvent rearranges itself to promote dissociation. We capture the dynamics of the entire solvent by calculating p_B along a trajectory with constraint r_ion = 3.73 Å, near the peak of the free energy barrier, which we plot in Figure 9a. This is contrasted with Figure 9b, where our trajectory contains a constrained first solvation shell as well as constrained r_ion = 3.73 Å. We see qualitatively that the p_B fluctuations are somewhat suppressed when the first solvation shell is fixed in addition to r_ion, consistent with committor analysis of previous sections (compare Figures 4 and 6a). In Figure 9a where all solvent is free, we observe two time scales: on a large time scale of roughly 5 ps, we observe large p_B fluctuations between 0 and 1, and on a shorter time scale of roughly 0.5 ps, we see oscillatory-like fluctuations of a much smaller magnitude. Because this smaller time scale persists in Figure 9b, when we freeze the first solvation shell, it is tempting to conclude that the smaller fluctuations are due to solvent rearrangements outside the first solvation shell, and the larger p_B fluctuations are due to the water rearrangements in the first solvation shell, which occur on time scales 10 times as large.

Figure 9.

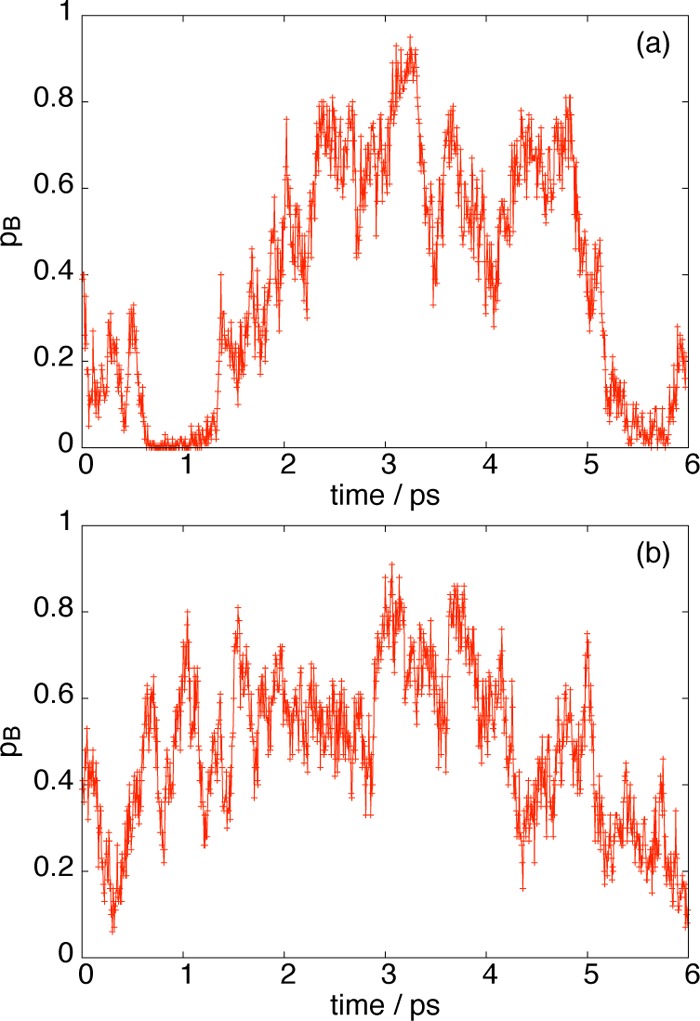
Time dependence of p_B[x(t)] for trajectories generated from Langevin dynamics with (a) constrained r_ion and (b) constrained r_ion and first solvation shell.

Inertial Effects

The reaction pathways characterizing rare events will ultimately depend upon the system dynamics. Observables such as kinetic rate constants, committor values, and transition probabilities are generally properties of the underlying dynamics governing the time evolution of the system. By analyzing transition pathways for various types of dynamics, one can then learn something about the relative importance of certain dynamical features in facilitating a rare transition. In this section, we will compare our calculations for Hamiltonian dynamics to analytic results for diffusive dynamics, highlighting the importance of inertial effects in enhancing reaction probability.

To track the differences that arise in these two dynamical regimes, we compare the committor probability p_B to the transition path probability p_TP. While p_B(x) is the probability that a trajectory passing through x relaxes into B, p_TP(x) quantifies the probability that a trajectory passing through x is a transition pathway. For a given configuration x, p_TP(x) is estimated by generating N_TP = 100 trajectories from x by integrating Hamilton’s equations forward and backward in time with initial velocities sampled from the Maxwell–Boltzmann distribution. In the diffusive regime, Hummer¹⁶ showed that p_TP is determined solely by p_B:

5

We compare this analytic result to correlations we observe between p_TP and p_B when using Hamiltonian dynamics (i.e., deterministic frictionless dynamics described by Hamilton’s equations of motion).

In Figure 10, we display a scatter plot of p_TP vs p_B for equilibrium configurations constrained to r_ion = r_ion^* (data from Figure 4), plotted against the analytic result, eq 5, for diffusive dynamics. While for configurations close to p_B = 0 and 1 we see similar behavior between the two regimes, near the transition state, p_TP is enhanced relative to diffusive behavior. Hence, for Hamiltonian dynamics, inertial effects enhance the reaction probability near the transition state by up to 40–50%. This is intuitive: Under Hamiltonian dynamics, when the system evolves from A and up to the transition state, the probability to complete the transition by moving down to the reactant region B will be influenced by the instantaneous value of the momenta at the top of the free energy barrier. However, under diffusive dynamics, this enhancement is not present simply because the momenta are equilibrated instantaneously, providing no means to help push the system to the other side.

Figure 10.

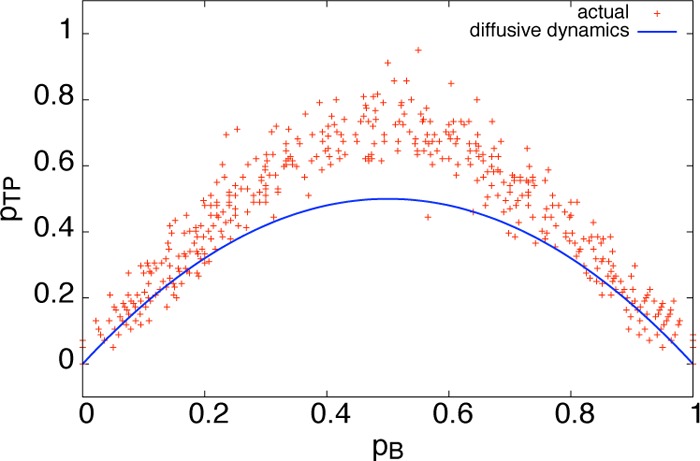
Inertial effects near the transition state. The calculated transition path probability p_TP is plotted against the committor probability p_B for configurations constrained to r_ion = r_ion^*. Our results under Hamiltonian dynamics, shown in red, show a deviation of the observed p_TP from the analytic result under diffusive dynamics.¹⁶ These inertial effects enhance p_TP near the transition state.

Discussion and Conclusions

In this study, we investigated the dissociation pathways of Na⁺Cl^– in water. We showed that the thermodynamics of dissociation is driven energetically, and opposed entropically, with the loss of entropy explained by an increasing number of highly coordinated solvent molecules in the first solvation shell as the ions separate. By performing committor analysis on the system with various constraints, we showed that (a) the interionic distance is an insufficient reaction coordinate, in accordance with previous findings, (b) the influence of the solvent on ionic dissociation is long-ranged, extending out into the third solvation shell, and (c) both steric effects and electrostatics contribute to the system’s commitment to dissociation. We also highlighted the time scales under which solvent fluctuations influence dissociation, as well as the importance of inertial effects near the transition state.

In characterizing the kinetic pathway to dissociation, the ultimate goal is to find a good reaction coordinate for the system. Despite the seeming simplicity of the solute, two atoms, finding an accurate description of the solvent is a difficult task. Previous attempts have shown correlations between Na⁺Cl^– dissociation and solvation numbers⁶ and other orientational indicators of local solvent density.^6,22,23 Geissler et al.⁶ have suggested a mechanism whereby dissociation is accompanied by insertion of a water molecule from the bulk into the first solvation shell, preceded by a buildup of water density in the second solvation shell and a depletion between the second and third shells at the transition state. This picture is consistent with our findings that dissociation is sensitive to solvent rearrangements at these ranges.

We have applied, with little success, a maximum likelihood approach¹ to find an optimal reaction coordinate that depends on these and other solvent variables sensitive to solvent density rearrangements. We have also found weak correlations between p_B and (a) the net solvent dipole along the interionic axis as well as (b) the net solvent force along the interionic axis. The microscopic mechanism leading to ionic dissociation, however, is still not completely known, and more study is needed.

The authors declare no competing financial interest.