Cascade of Reduced Speed and Accuracy After Errors in Enzyme-Free Copying of Nucleic Acid Sequences

Abstract

Non-enzymatic, template-directed synthesis of nucleic acids is a paradigm for self-replicating systems. The evolutionary dynamics of such systems depend on several factors, including the mutation rates, relative replication rates, and sequence characteristics of mutant sequences. We measured the kinetics of correct and incorrect monomer insertion downstream of a primer-template mismatch (mutation), using a range of backbone structures (RNA, DNA, and LNA templates and RNA and DNA primers) and two types of 5′-activated nucleotides (oxyazabenzotriazolides and imidazolides, i.e., nucleoside 5’-phosphorimidazolides). Our study indicated that for all systems studied, an initial mismatch was likely to be followed by another error (54-75% of the time) and extension after a single mismatch was generally 10-100 times slower than extension without errors. If the mismatch was followed by a matched base pair, the extension rate recovered to nearly normal levels. Based on these data, we simulated nucleic acid replication in silico, which indicated that a primer suffering an initial error would lag behind properly extended counterparts due to a cascade of subsequent errors and kinetic stalling, with the typical mutational event consisting of several consecutive errors. Our study also included different sequence contexts, which suggest the presence of cooperativity among monomers affecting both absolute rate (by up to two orders of magnitude) and fidelity. The results suggest that molecular evolution in enzyme-free replication systems would be characterized by large ‘leaps’ through sequence space rather than isolated point mutations, perhaps enabling rapid exploration of diverse sequences. The findings may also be useful for designing self-replicating systems combining high fidelity with evolvability.

Introduction

Copying genetic information is fundamental to life. In biological systems, this process is carried out by high-fidelity polymerase enzymes acting on energy-rich but kinetically stable substrates (nucleoside triphosphates). However, template-directed synthesis of a complementary nucleic acid strand can occur without enzymes, mediated by the association of activated nucleotides with the template sequence and subsequent formation of internucleotide linkages.^1-3 Such systems illustrate that the chemistry of relatively simple molecules could potentially give rise to self-replication even without the relative sophistication of evolved enzymes.^4-9 In this paper, we study template-directed, non-enzymatic extension of RNA and DNA using two different activation chemistries, in order to better understand the chemical properties of these self-replicating systems that influence their ability to transmit genetic information and evolve.

The origin of life is believed to have progressed through an ‘RNA world’, in which RNA served as the carrier of genetic information and as the functional molecule (e.g., ribozymes) for primitive life forms.^10-13 The sequence information of RNA can be copied non-enzymatically in model systems,^14-17 suggesting that non-enzymatic, templated polymerization may have been an early mode of replication for the first functional RNAs, bridging prebiotic chemistry and the RNA world.

Mis-incorporation rates during non-enzymatic extension are quite high (error rate of 7-26% per base, averaged over all bases, depending on the system),^18-20 with an RNA system showing higher mutation rates than a comparable DNA system.²⁰ This suggests that the amount of information that could be passed from one generation to the next would be severely limited by errors during replication.^21,22 However, the extension process is slower for erroneous copies compared to correct copies, and this kinetic difference essentially favors faithful copies and permits a greater amount of information to be accurately propagated. In a particular DNA model system for non-enzymatic extension (primer terminated by a 3′-amino-2′,3′-dideoxynucleoside and the incoming monomer being a nucleoside 5′-phosphorimidazolide), mis-incorporation events slowed copying of the next nucleotide by up to two orders of magnitude.²³

Understanding the fate of error-containing sequences during non-enzymatic polymerization is critical for understanding nucleic acids as intrinsically self-replicating systems. Errors during replication can be problematic, since they degrade information and slow polymerization, but they are also the raw material for evolutionary change. Knowledge of the frequency and consequences of errors will help us understand informational limits and evolution in non-enzymatic contexts, such as the RNA world. In addition, non-enzymatic polymerization may reflect the intrinsic chemistry underlying nucleic acid replication. For example, non-enzymatic mutation rates correlate well with the thermodynamic stabilities of the corresponding duplexes.²⁰

In the present work, we investigate the downstream ‘fate’ of nascent sequences to be extended non-enzymatically after a terminal mismatch, simulating copying after an initial mis-incorporation event. In particular, we measured the mutation rate after the initial error, as well as the extension rate one or multiple bases downstream from the initial error(s). The overall picture that emerged is that an initial error would trigger a cascade of stalling and mutation that would create large clusters of mutations and substantially slow production of a mutant sequence. To understand the generality of this phenomenon, we varied the 5′-activation chemistry of the electrophile (nucleotide oxyazabenzotriazolide vs. nucleotide imidazolide, also referred to as a nucleoside 5’-phosphorimidazolide), the backbone structure of the template (DNA, RNA, or locked nucleic acid (LNA)), the backbone structure of the primer (DNA or RNA), and the sequence context (two unrelated contexts and systematic variation of the downstream template base for both contexts). We also used the complementary techniques of gel electrophoresis and mass spectrometry to analyze the extension reactions. Interestingly, imidazolides as nucleotide monomers and RNA as template gave faster reaction rates than oxyazabenzotriazolides reacting on DNA templates, a system previously described as particularly fast-reacting.²⁴ While each nucleic acid system has its own features, the phenomenon that an initial error triggers a cascade of extension problems appears to be general. The co-occurrence of multiple mutations suggests that these systems may be able to rapidly explore diverse areas of sequence space.

Methods

Materials and methods for assays monitored by mass spectrometry (MS)

TMP and EDC·HCl were from Fluka (Deisenhofen, Germany), dAMP, dCMP, dGMP, imidazole, triphenylphosphine, 2,2′-dithiodipyridine, 2-[4-(2-hydroxyethyl)-1-piperazine]ethanesulfonic acid (HEPES) and Dowex 50 WX8-200 cation exchange resin were from Acros (Geel, Belgium). 7-Aza-1-hydroxybenzotriazole (HOAt) was from TCI (Zwijndrecht, Belgium). NMR spectra were recorded on a Bruker Avance 500 spectrometer equipped with a 5 mm BBO probe head. Deuterated water (99.9% D) was purchased from Euriso-Top (Saclay Gif/Yvette, France). The ESI mass spectra were acquired on Finnigan LC-Q Duo spectrometer, using Excalibur Qual Browser 2.0 Software. Activated deoxynucleotides were measured in negative mode. Labeled peaks are pseudomolecular ions ([M-H]^-). The MALDI TOF mass spectra were acquired on a Bruker REFLEX IV spectrometer, using software packages XACQ 4.0.4 and XTof 5.1. Oligonucleotides were all measured in linear negative mode. A mixture of 2,4,6-trihydroxyacetophenone (0.3 M in EtOH) and diammoniumcitrate (0.1 M in H₂O) in ratio (v:v = 2:1) was used as MALDI matrix. The determination of the concentrations of the solutions was performed by UV-Vis analysis (on Nanodrop spectrometer, Peqlab, Germany).

Oligonucleotides for assays monitored by mass spectrometry

Unmodified DNA and RNA oligomers were purchased from Biomers (Ulm, Germany) in salt-free form and were used without further purification. 3′-Aminoterminal primers 2a, 2c, 2g, and 2t were synthesized and purified as described previously¹⁹ and characterized by mass spectrometry (Supporting Information).

Oligonucleotides for assays monitored by polyacrylamide gel electrophoresis (PAGE)

The fluorescent 5′ Cy3-labeled, 3′-aminoterminal RNA and DNA primers 7g, 7t, and 10 were made by reverse synthesis in the W. M. Keck Biotechnology Resource Laboratory at Yale University (New Haven, CT, USA) as previously described.²⁰ The primers were polyacrylamide gel electrophoresis (PAGE)-purified, and masses were verified by matrix-assisted laser desorption/ionization time of flight (MALDI-TOF) mass spectrometry. DNA and RNA oligonucleotide templates were synthesized and desalted by Bioneer Corporation (Alameda, CA, USA). RNA and DNA excess primer were also from Bioneer Corporation. LNA sequences were synthesized by Exiqon, Inc (Woburn, MA, USA).

Preparation of activated monomers

For assays analyzed by mass spectrometry, oxyazabenzotriazolides of deoxynucleotides (OAt esters) were synthesized via activation of dNMPs with EDC/HOAt, as previously described.²⁴ Mixing of equimolar quantities of the four OAt esters as previously described ¹⁹ gave solutions that were directly used for assays. Imidazolides of dNMPs were prepared via redox condensation using imidazole, 2,2′-dithiodipyridine and triphenylphosphine, as described for ribonucleotides by Lohrmann and Orgel.²⁵ Briefly, a mixture of the dNMP (0.1 mmol, previously dried at 0.1 mbar), imidazole (68 mg, 1 mmol), and 2,2′-dithiodipyridine (66 mg, 0.3 mmol) was dissolved in a mixture of DMF/DMSO (1.5 mL, 1:1, v:v) under argon. Triethylamin (50 μL, 0.3 mmol) and triphenylphosphin (53 mg, 0.2 mmol) were added to the reaction mixture. After stirring for 2.5 h at room temperature, the clear yellow solution was added dropwise to a cold solution of sodium perchlorate (50 mg, 40 mmol) in a mixture of diethylether/aceton (20 mL, 1:1, v:v) and triethylamin (1.5 mL, 10 mmol). After stirring for 30 min and subsequent centrifugation, the supernatant was aspirated, and the pellet was washed with diethylether/acetone (20 mL, 1:1, v:v). After centrifugation, the resulting colorless pellet was dried at 0.1 mbar and stored at -20°C. Yield: 60-90 %. The imidazolides were analyzed by ³¹P NMR spectroscopy and were found to be >98% activated. Again, equimolar mixtures containing all four imidazolides of dNMPs were prepared from four freshly prepared solutions of activated monomers in water. Concentrations in stock solutions were determined based on UV absorbance, using the following extinction coefficients: dAMP: ε₂₅₉ = 15,400 M^-1 cm^-1, dCMP: ε₂₇₁ = 9,100 M^-1cm^-1, dGMP: ε₂₅₃ = 13,700 M^-1cm^-1, TMP: ε₂₆₀ = 7,400 M^-1cm^-1.

For assays with gel electrophoresis as readout, syntheses of guanosine 5′ phosphorimidazolides (ImpG) and all 2′-deoxynucleoside 5′-phosphorimidazolides (ImpdN) were done according to a previously published protocol.²³ The adenosine, cytosine, and uridine 5′-phosphorimidazolides (ImpA, ImpC, and ImpU, respectively) were synthesized by GL Synthesis Inc. (Worcester, MA, USA). Activated nucleotides were characterized by mass spectrometry and high-performance liquid chromatography (HPLC) as previously described ²³ and were found to be >93% pure.

Characterization data of the imidazolide-activated monomers are given in Supporting Figures S30-S37. Characterization data for the OAt esters were published previously²⁴ and ESI-MS are given in Supporting Figures S38-S39.

Non-enzymatic, templated extension reactions analyzed by PAGE

Copying reactions were performed using monomers pre-activated at the 5′-phosphate. Primers featured a 3′-amino moiety, which replaces the 3′-hydroxyl found in natural DNA. In each reaction, exactly one template, primer, and monomer were used in combination. A primer (0.325 μM) and a template (1.3 μM) were mixed in water, incubated at 95° C for 5 min., and annealed by cooling to room temperature on a benchtop for 5 min. Next, 1 μL of 1 M Tris (pH 7) and 0.5 μL of 4 M NaCl were added, and the activated monomer was added to a final concentration of 10 mM for A, C, or G and final concentration of 40 mM for U, for reactions in the RNA system. For reactions using the DNA/LNA template, reactions tended to be fast, so to improve measurements the monomer concentration was 1 or 5 mM for A, C, and G, and monomer concentration for T was 4 times the corresponding A, C, and G concentration (details given with rate constants in Supporting Table S5). The total reaction volume was 10 μL. Samples for reaction time points were taken as appropriate for the assay. A negative control sample was taken by adding water in place of the monomer. A volume of 1 μL of the reaction mixture was taken at each time point and added to 9 μL of a loading buffer. The latter consisted of an aqueous solution containing 8M urea, 100 mM ethylenediaminetetraacetic acid (EDTA), and 18-65 μM of a competitor RNA sequence. For reactions using the DNA/LNA template, the solution contained 4 μM of a competitor DNA sequence. The competitor sequence, or excess primer, had the same sequence as the primer except the excess primer was not fluorescent and had no backbone modification. Samples were heated to 95° C before running the samples on a 20% PAGE gel. The rate of extension was estimated as the initial rate of disappearance of the unextended primer by linear regression of the initial phase of the reaction. Every reaction was done at least in duplicate; standard deviations were calculated from 2 or more replicates.

Assays monitored by mass spectrometry (MS)

Mass spectrometrically monitored non-enzymatic primer extensions were carried out in 10 μL buffer (200 mM HEPES, including 400 mM NaCl and 80 mM MgCl₂). For experiments with OAt-activated monomers the pH was adjusted to 8.9. Assays with imidazolides were carried out at pH 7.0. The oligonucleotides (3′-aminoprimer, 36 μM, and template, 54 μM) were annealed in reaction buffer by cooling from 90°C to 20 °C, and the monomers (activated dAMP, dCMP, dGMP and TMP) were added at 20° C, using aqueous stock solutions. Samples (0.8 μL) were taken at stated intervals, diluted to 15 μL, and kept on Dowex cation exchange beads (NH ⁺₄ form) for 3 min. A sample of the supernatant was used for MALDI-TOF MS analysis, as previously described.²⁴ The estimated detection limit for minor extension products is ≤1 %.

Based on a pseudo-first order kinetic model for primer conversion,¹⁸ where the primer/template complex is one reactant, and the activated nucleotide the other, monoexponential fits to kinetic data were performed using Origin Pro 10.0 software, with f(t) = Y₀ (1 - exp(-k t)). Here, Y₀ is the pre-exponential factor, used to determine maximum primer conversion, and k is the global rate constant for primer conversion. The corresponding global second order rate constant k′ for primer conversion was obtained by dividing k by the monomer concentration. To determine individual rate constants for each of the four monomers (A/C/G/T), a second fit was then performed, using f(t) = a₁ (1 - exp(-k t)) as fit function, where a₁ is a pre-exponential factor, used to determine the fraction of the product formed with a given monomer, and k is the global rate constant for primer conversion. Calculated rate constants for individual extension products i are k_i = [a_1i / (a_1A + a_1C + a_1G + a_1T)] k, as required for competing reactions involving one common starting material. Second order rate constants k′ were again obtained by dividing k_i by the concentration of the monomer. All fits gave r² values > 0.98, as determined using the fit algorithm of the Origin software.

Non-templated reaction with aminonucleoside

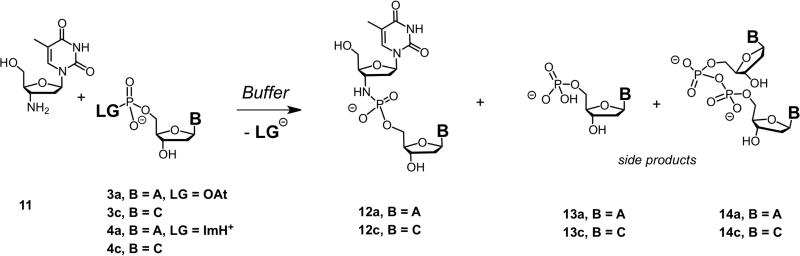
Kinetic data for the non-templated extension of a single aminonucleoside were acquired via ³¹P NMR spectroscopy. Reaction conditions were as follows: 3′-amino-2′-3′-dideoxythymidine 11 (100 mM), activated 2′-deoxynucleotide 3a, 3c, 4a, or 4c (100 mM), and 10% deuterated aqueous buffer (200 mM HEPES, 400 mM NaCl, 80 mM MgCl₂), at pH 8.9 for OAt activation, or pH 7.0 for imidazole activation, uncorrected for deuterium effect, and 20° C. Formation of the dinucleoside 3′-N-5′-O-phosphoramidate (TA 12a or TC 12c) dimer, hydrolyzed monomer (13a or 13c) pyrophosphate (14a or 14c), were measured over time based on the following chemical shifts: δ (ppm) = 6.8 (12c); 6.9 (12a); 3.4 (13c); 3.6 (13a); -0.1 (3c); -0.2 (3a) -9.1 (4c), -9.2 (4a); -11.3 (14a/14c).

Calculation of stalling factor and fidelity

The stalling factor (S) is calculated by dividing the rate of extension after a perfectly matched primer-template terminus (k_match) divided by the rate of extension for a mismatched terminus having the same template sequence (k_mismatch), simulating an error in the growing primer (S = k_match/k_mismatch). S_G considers only correct incorporation (e.g., monomer G across template C; S_G = k_{G, match}/k_{G, mismatch}). Alternatively, the analogous factor S_p considers rates of primer extension by all monomers (S_p = k_{total, match}/k_{total, mismatch}). Mutation frequencies (also called mutation rates or error rates) are calculated as the rate of an incorrect incorporation divided by the total rate of incorporation for any monomer (e.g., for mis-incorporation of A across C, f_A = k_A/(k_A+k_C+k_G+k_{T(or U)}). To calculate mutation rates using DNA/LNA-templated reactions that were carried out at lower monomer concentration (to better estimate fast rates), the reaction rates were corrected for the absolute monomer concentration, assuming that the reaction was first-order. The fidelity is the rate of a correct Watson-Crick incorporation divided by the total rate of incorporation of any monomer (for the previous example, fidelity = f_G = k_G/(k_A+k_C+k_G+k_{T(or U)})).

Thermodynamic calculation of base-pairing probability

Using the co-folding routine from the Vienna package for RNA secondary structure folding,^26,27 we estimated the probability that a given primer-template complex would form a base pair at the terminus. We suppressed spurious alternative structures by requiring base pairs at Watson-Crick matches between primer and template.

Computer simulation of polymerization

In order to understand how the various kinetic effects observed experimentally would affect the overall process of non-enzymatic polymerization, we simulated the monomer-by-monomer copying of random template sequences (50-mer) using a Gillespie algorithm.²⁸ Given a random template sequence of length L=50 nt, monomers are incorporated in a stepwise fashion, where rate and accuracy of the incorporation reactions depend on the sequence context in the template and on the number of immediately preceding errors (or the distance to the last error). We did not consider boundary effects (e.g., initiation, priming, termination, strand-separation reactions). We generated 1000 random sequences. For each sequence, the stochastic simulation was repeated 1000 times. We recorded five observables: (1) the time T until completion, (2) the time T₀ until completion assuming no stalling (approximating the polymerization time for a perfect copy), (3) the relative polymerization time of the sequence (T_r = T/T₀), (4) the number n of observed errors, and (5) the number n_c of clusters of consecutive errors. Each simulated sequence was copied in silico to completion (producing its 50-mer reverse complement).

The simulation is based on experimentally observed rate constants (see Supporting Information for full description). In brief, the simulation included the following: incorporation rates (DNA/DNA system, Table 1 and 2 from ¹⁹), mutation frequencies (Table 5 from ¹⁹), stalling after a single or multiple mismatch (Tables 1 and 2, Supporting Figure S1 from the present study), and mutation frequencies after a mismatch (Tables 1 and 2 from the present study). Polymerization rate after a mismatch closure (i.e., mismatched region followed by matched base(s)) was calculated using theoretical estimates of the probability that the terminal base pair was formed, thereby extending the observations described below.

Table 1. Extension rates, mutation frequencies, and stalling factors after matches and different mis-matches in a DNA system^a.

Apparent first-order rate constants (k) are given. Subscript ‘G’ refers to formation of correctly extended product. Subscript ‘total’ refers to total primer conversion to both correctly or incorrectly extended products. Relative incorporation frequency (f) is given for the base indicated by the subscript, Fidelities (equivalently, f_G for these reactions) are also shown by horizontal bars (0 = no bar, 1 = full bar). Stalling factors are calculated for extension by the correct monomer (S_G); note that slight differences between S_G calculated from raw data and the corresponding k_G ratio from the table may occur due to rounding (non-significant digits are not presented in the table).

Reactants	kG (h-1)	ktotal (h-1)	fC/fT/fA	Fidelity (fG)	SG
1tg, 2a, 3a-t	0.06	0.18	0.15/0.09/0.35	0.41	14
1tg, 2c, 3a-t	0.86	1.3	0.03/0.03/0.07	0.87	-
1tg, 2g, 3a-t	0.09	0.46	0.04/0.02/0.81	0.13	9.3
1tg, 2t, 3a-t	0.1	0.2	0.07/0.06/0.23	0.63	8.4
1tc, 2a, 3a-t	0.06	0.19	0.12/0.09/0.45	0.34	20
1tc, 2c, 3a-t	0.01	0.04	0.14/0.12/0.48	0.26	110
1tc, 2g, 3a-t	1.2	1.8	0.01/0.01/0.1	0.88	-
1tc, 2t, 3a-t	0.02	0.06	0.1/0.12/0.47	0.31	74
1ta, 2a, 3a-t	0.04	0.13	0.11/0.11/0.5	0.28	13
1ta, 2c, 3a-t	0.02	0.08	0.1/0.14/0.54	0.22	27
1ta, 2g, 3a-t	0.05	0.19	0.09/0.09/0.59	0.24	9.4
1ta, 2t, 3a-t	0.48	0.64	0.01/0.01/0.07	0.91	-

^aUnderlined reactants indicate a matched base pair. Reactions were analyzed by MS. See Supporting Table S6 and Figures S7-9 for more details.

Table 2.

Extension rates, mutation frequencies, and stalling factors after a single mis-match for RNA vs. DNA templates.^b

Reactants	kG (h-1)	ktotal (h-1)	k’G (h-1M-1)	fC/fT/fA	Fidelity (fG)	SG
5uu, 2a, 4a-t	5.2	5.4	1400	0/0/0.01	0.99	-
5uu, 2c, 4a-t	0.22	0.66	61	0.1/0.1/0.59	0.21	24
5uu, 2g, 4a-t	1.3	1.9	370	0.01/0.01/0.19	0.79	4
5uu, 2t, 4a-t	0.09	0.26	25	0.08/0.12/0.41	0.39	58
1tt, 2a, 4a-t	1.9	1.9	510	0/0/0.01	0.99	-
1tt, 2c, 4a-t	0.04	0.14	9	0.1/0.12/0.53	0.25	52
1tt, 2g, 4a-t	0.12	0.32	34	0.01/0.02/0.66	0.3	15
1tt, 2t, 4a-t	0.06	0.16	17	0.02/0.02/0.62	0.34	30
5uu, 2a, 3a-t	0.65	0.95	180	0.01/0.03/0.11	0.85	-
5uu, 2c, 3a-t	0.02	0.08	5	0.08/0.06/0.66	0.2	34
5uu, 2g, 3a-t	0.2	0.64	57	0.04/0.09/0.55	0.32	3.2
5uu, 2t, 3a-t	0.03	0.14	9	0.07/0.16/0.55	0.22	19
1tt, 2a, 3a-t	2.5	2.5	680	0/0/0.01	0.99	-
1tt, 2c, 3a-t	0.03	0.09	9	0.06/0.06/0.57	0.32	79
1tt, 2g, 3a-t	0.15	0.8	43	0.01/0.01/0.9	0.08	16
1tt, 2t, 3a-t	0.15	0.4	43	0.03/0.07/0.43	0.47	16

^bSecond-order rate constants are labeled k’. Rates measured by MS assay; see Supporting Table S7 and Figures S3-6 for more details.

Table 5.

Rate of template-free extension.^d

Monomer	Conversion after 96 h	Product distribution (%) dimer (12) : free phosphate (13) : pyrophosphate (14)	k′ (h-1M-1)
dAMP-OAt (3a)	99 %	97 : 1 : 2	3.0
dCMP-OAt (3c)	99 %	94 : 5 : 1	3.2
dAMP-ImH+ (4a)	84 %	84 : 14 : 2	0.5
dCMP-ImH+ (4c)	75 %	82 : 16 : 2	0.4

^dSecond-order rate constant for conversion (k′) is given, together with the extent to which hydrolysis product (dNMP-OH) and symmetrical pyrophosphate were formed at the end of the assay. See Scheme 4 for structures.

The sensitivity of the simulation results to changes in parameter values was checked in the following ways. To determine if the results depend on sequence context, we selected a rate constant at random from the table of rates. This negates correlations along the sequence (i.e., the rate of incorporation for each base does not depend on the surrounding sequence) and suppresses correlations between incorporation rates (speed) and mutation profile (accuracy). To determine if the results are sensitive to our assumptions regarding the rate of extension after a mismatched region of 2 or more bases, we simulated three different scenarios (see Supporting Information). To determine the effect of decreased stalling factors or relatively large background (untemplated) reaction rates, we carried out simulations in which the stalled rate of polymerization was always >10% of the non-stalled rates of polymerization. To determine the effect of increasing mutation rates, we increased all mutation rates by 2-fold.

Results

Stalling of non-enzymatic extension following a single mis-incorporation

Previous work in a DNA system with nucleoside 5′-phosphorimidazolides indicated that extension stalls after a single mis-incorporation, presumably due to the mismatched primer-template geometry at the reactive terminus.²³ We extended these observations by: 1) measuring stalling in another DNA system with an unrelated sequence context and OAt activation chemistry, 2) comparing extension of the same DNA primer annealed to DNA vs. RNA templates, 3) comparing imidazolides and OAt esters as activated monomers, and 4) measuring extension after mismatches in an RNA primer, RNA template system. In this section, we focus on extension from the mismatch by the correct monomer; fidelity after a mismatch is addressed in a following section.

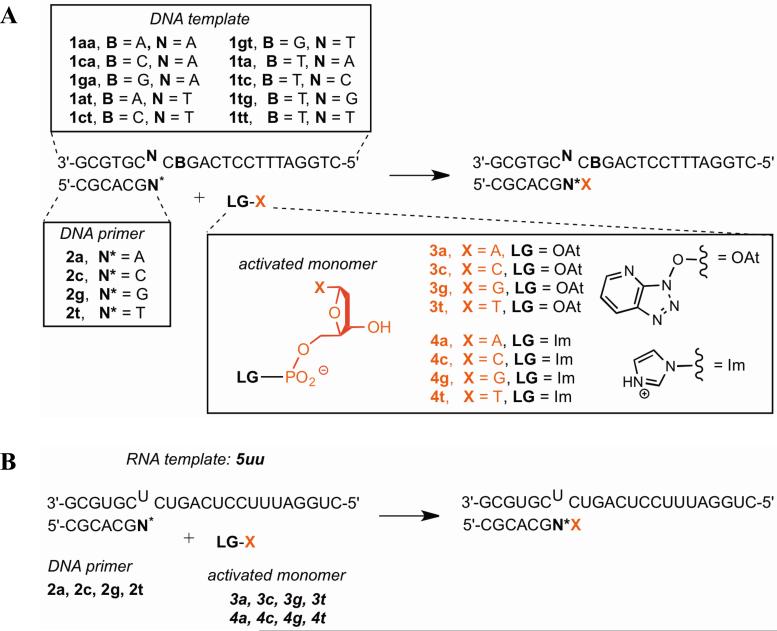
Extension of DNA primer on DNA template using OAt esters as activated monomers (Scheme 1A)

Scheme 1. Experimental systems for non-enzymatic extension.

(A) DNA template and primer; (B) RNA template, DNA primer. All primer sequences contain a 3′-amino-2′,3′- dideoxynucleotide as the 3′ terminal nucleotide.

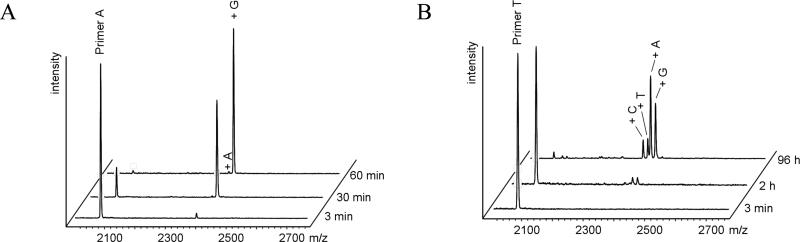
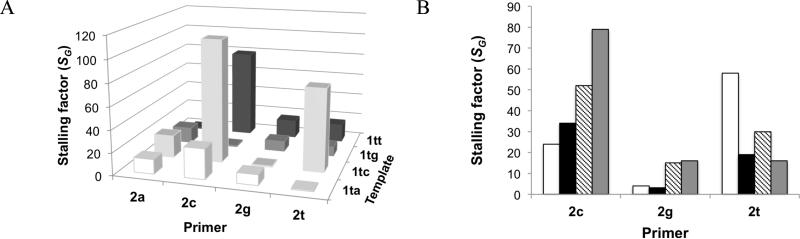
Extension rates for all 4 possible matched base pairs and 12 possible mismatched base pairs were measured using an assay analyzed by mass spectrometry under conditions that allow for quantitative read-out (Figure 1A,B).²⁹ The calculated stalling factors S_G ranged from 8-110, meaning that most mismatches slowed down extension by the correct monomer by one or two orders of magnitude (Table 1,2; Figure 2A). The highest stalling factors were associated with pyrimidine-pyrimidine mismatches. Stalling factors previously observed in a completely different DNA sequence context with nucleoside 5′-phosphorimidazolides were slightly higher, in the range of 20-300,²³ indicating that the surrounding sequence context (or leaving group; see below) can affect stalling by 2-3-fold. If one considers extension by any monomer (S_p) rather than only by the correct monomer, stalling factors are decreased by 2-3-fold (Supporting Figure S1A), because mis-incorporation happens readily after a mismatch but not after a Watson-Crick base pair (see section on ‘Low fidelity after a mismatch’).

Figure 1. Representative primer extension assay by MALDI-TOF mass spectra.

Shown are a fast extension (A: 2a with template 1tt and 3a-t) and a slow and inaccurate extension (B: 2t with template 1tc and 3a-t).

Figure 2. Stalling factors for different systems.

Shown here are the (A) DNA primer, DNA template system with OAt esters and (B) different template backbone and leaving groups. The stalling factor is the ratio of polymerization rate from matched terminus to rate of extension from mis-matched terminus. Stalling factors are calculated for extension by the correct monomer (S_G); by definition, S_G = 1 for extension after a matched base pair. In (B), white is template 5uu with 4a-t; black is 5uu with 3a-t; hatched is 1tt with 4a-t; gray is 1tt with 3a-t (also shown in (A)).

Extension of DNA primer on DNA vs. RNA template with OAt esters (Scheme 1A,B)

To see if the extension rates and amount of stalling differ between an RNA and DNA template, we compared the reactions of the DNA primers 2a, 2c, 2g, and 2t with RNA template 5uu against the analogous reactions of the same primers with DNA template 1tt. In terms of absolute reaction rates, the DNA template gave somewhat faster extension by the correct monomer after a correctly matched terminus compared to the RNA template (~4-fold; Table 2). Considering stalling after a mismatch, overall the DNA template gave slightly greater (~2-fold) stalling than the RNA template, although stalling was similar after the T/T (1tt with 2t) and T/U (5uu with 2t) mismatches (Figure 2B; Supporting Figure S1B).

Extension of DNA primer on DNA and RNA templates with nucleoside 5′-phosphorimidazolide activated monomers (Scheme 1A,B)

To see if the identity of the leaving group influenced the rates and amount of stalling, we compared reactions using imidazolides 4a-t with reactions using OAt esters 3a-t. On the DNA template, the identity of the 5′ activated leaving group did not greatly affect absolute rates (within 5-fold; Table 2) and indeed affected the rates to a smaller degree than could have been expected based on assays comparing oxyazabenzotriazolides with 2-methylimidazolides.²⁴ For the RNA template, the imidazolides gave faster reactions than the OAt esters (by at most one order of magnitude). Stalling factors did not appear to be affected systematically by the identity of leaving group (Figure 2B; Supporting Figure S1B).

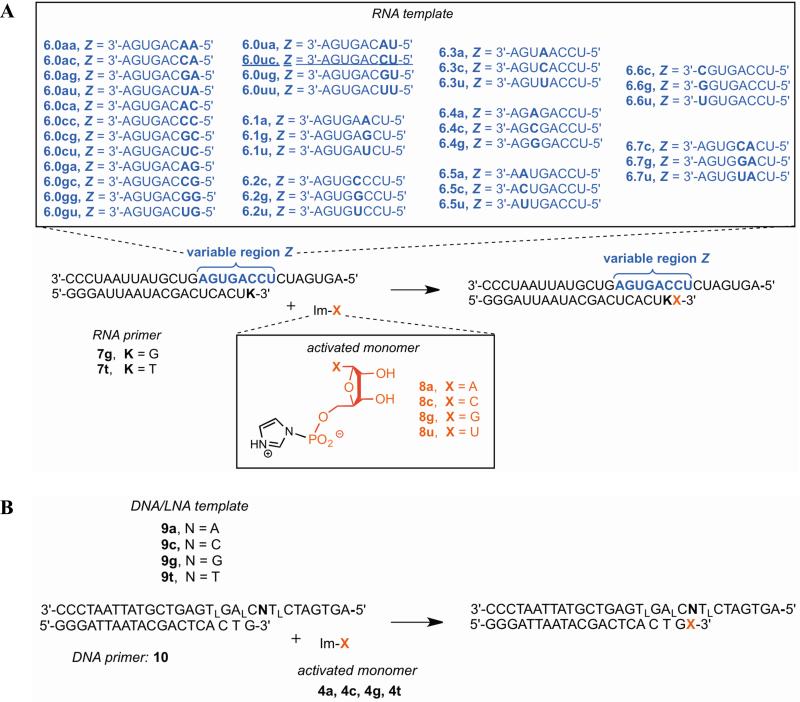
Extension of RNA primer with RNA template and nucleoside 5′-phosphorimidazolide activated monomers (Scheme 2A)

Scheme 2. Experimental systems for non-enzymatic extension (continued).

(A) RNA template, RNA primer; (B) mixed DNA/LNA template, DNA primer. All primer sequences contain a 3′-amino-2′,3′-dideoxynucleotide as the 3′ terminal nucleotide.

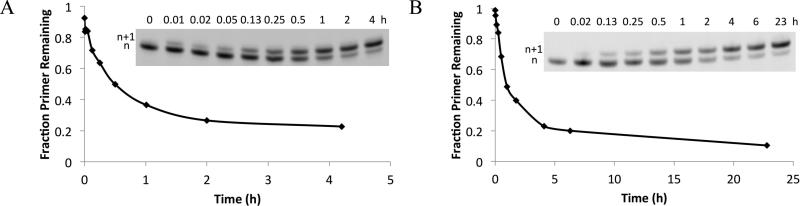
We also measured extension rates from one matched and three mismatched termini in an RNA template - RNA primer system, using primer 7g and template 6.0uc vs. 6.1a, 6.1g, or 6.1u (Table 3). An assay with PAGE read-out was used to measure extension over time (Figure 3A,B). The reaction rate for correct extension in the RNA system was similar to that for the analogous RNA template - DNA primer (5uu, 2a, 4a-t) and DNA template – DNA primer (1tt, 2a, 4a-t) reactions having the same base pair terminus in a different sequence context (Table 2). Extension from the mismatches (6.1a-u) was between 1-2 orders of magnitude slower than using 6.0uc. Although we did not examine extension from all possible matches and mismatches in the RNA system to calculate stalling factors, this illustrates that non-enzymatic extension of RNA is relatively slow after a mismatch, to a roughly similar extent as DNA.

Table 3. Extension rate after single mismatch with an RNA template and RNA primer.

Rates measured by PAGE assay; see Supporting Figures S12-13 for more details. Standard deviations are given among replicates.

Reactants	Template:primer terminus	kG (h-1)
6.0uc, 7g, 8g	C:G	4 ± 1
6.1a, 7g, 8g	A:G	0.1 ± 0.01
6.1g, 7g, 8g	G:G	0.12 ± 0.02
6.1u, 7g, 8g	U:G	0.33 ± 0.16

Figure 3. Representative primer extension assay by PAGE.

Shown are a fast extension (A: 7g on template 6.0ca with 8u) and a slow extension from a mismatch (B: 7t on template 6.0uc with 8g); lines are drawn to connect successive data points.

Recovery of extension rate downstream of a single mismatch

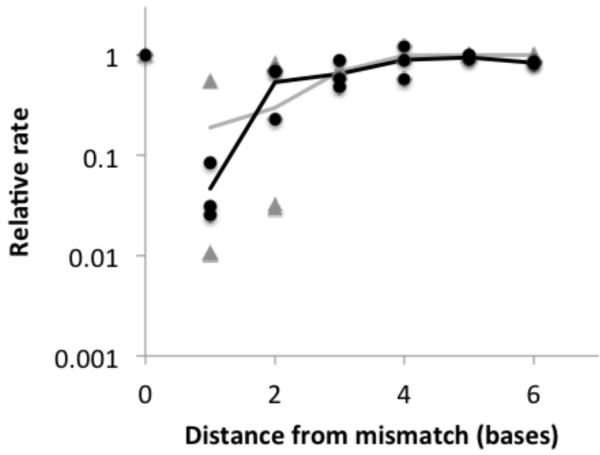
If correct extension were to follow a mismatch, one might suppose that the extension rate would return to normal at some point after the mismatch when the distortion no longer influences the reactive structure. We measured the extension rate of RNA primer-template complexes in which the reactive terminus containing correct Watson-Crick base pairs occurred progressively downstream of a single mismatch (Scheme 2A, Table 3, Figure 4, Supporting Table S1). This series of reactions contained primer 7g, monomer 8g, and one of templates 6.1-6.6, and was monitored by the PAGE assay. The extension rate was essentially normal shortly after the mismatch. The greatest stalling occurred immediately after the mismatch, as described earlier. If the correct base occurred after the mismatch, then extension proceeded at the next base with a slightly reduced, but nearly normal rate (within a factor of 2). Extension at distance 3 and greater proceeded at approximately the normal rate.

Figure 4. Recovery of extension rate following a single mismatch.

Distance (x-axis) is the number of bases from the mismatch to the end of the primer before reaction, including the mismatch itself (‘0’ is no mismatch; ‘1’ is incorporation immediately after the mismatch, etc). Black circles are experimental values, averaged over replicates, for several primer-template complexes, where the relative rate is k/k₀ (k is the observed rate and k₀ is the rate with no mismatch). Black line is the average among complexes for experimental values at the same distance. Gray triangles are theoretical values for different primer-template complexes, where the relative rate is equal to (P_ck_t + P_ok_n)/k_t, where P_c and P_o are the probabilities that the base pair is closed or open, respectively, and k_t and k_n are the rates of templated and non-templated extension, respectively. Gray line is the average among different complexes for theoretical values at the same distance. See Supporting Table S1 for experimental rates and errors.

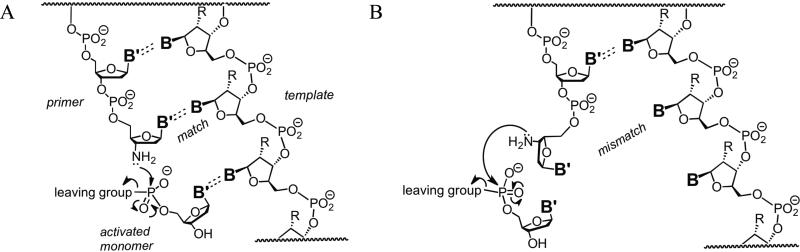
To understand the physical basis for the recovery of extension rate, we hypothesized that the reaction can proceed by two routes. If the primer-template complex forms the proper geometry at a matched terminus, the reaction proceeds quickly. If the primer-template complex does not form a matched terminus, the reaction proceeds at a slower, essentially non-templated rate (Scheme 3). If this hypothesis were correct, the rate of extension from a terminus would be largely determined by the probability that the terminus forms a closed base pair. Using RNA folding calculations based on well-established free energy rules for RNA secondary structure formation,^26,27 we estimated the probability that each of our primer-template complexes would form a closed base pair at the terminus. The qualitative behavior of the recovery of extension rate inferred from this probability was in reasonable agreement with the relative extension rates measured in our experiments (Figure 4).

Scheme 3.

Templated (A) and non-templated (B) primer extension with activated 2′-deoxynucleoside 5′-monophosphates, with nucleophilic attack of the primer terminus and release of the leaving group. The degree of stalling of extension after a mismatch is limited by the background rate of non-templated extension. R = H or OH; B and B′ are nucleobases.

Low fidelity after a mismatch

Given the improper primer-template structure of a mismatch, we wondered whether an initial mis-incorporation would engender additional errors. We measured the mis-incorporation frequencies (f) after a mismatch in the DNA system, the RNA template – DNA primer system, and the RNA system. We also compared reactions with OAt esters with imidazolides in the DNA system. Mis-incorporation rates were generally quite high after a mismatch.

Mis-incorporation after a mismatch in the DNA system (Scheme 1A)

We measured the fidelity with OAt esters 3a-t after all 4 matches and 12 possible mismatches (Tables 1 and 2), after which the templating base was C. The observed post-mismatch fidelities ranged from 8-63%, with an overall average fidelity of 31% (averaging over all four possible template bases for a given primer). Some fidelities were below the expectation for random incorporation (25%). The lowest observed fidelities in the DNA system occurred after a G/T mismatch (1tt with 2g; 8%) and after a G/G mismatch (1tg with 2g; 13%).

Mis-incorporation after a mismatch between RNA template and DNA primer (Scheme 1B)

We compared post-mismatch fidelities for template 1tt with fidelities using the analogous RNA template 5uu with the same primers (2a, 2c, 2g, 2t) and monomers (3a-t) (Table 2). On average, the overall fidelity was similar for 1tt (29%) and 5uu (25%), although 1tt was more variable (8-47% for different mismatches) than 5uu (20-32%).

Mis-incorporation after a mismatch for OAt esters vs. imidazolides (Scheme 1A,B)

To understand whether the identity of the leaving group affects post-mismatch fidelity, we compared reactions (templates 1tt and 5uu on primers 2a-2t) using the OAt esters 3a-t with otherwise identical reactions using imidazolides 4a-t (Table 2). The fidelities were similar on DNA template 1tt (29% for 3a-t, 30% for 4a-t). A greater difference was seen on the RNA template 5uu (25% for 3a-t, 46% for 4a-t), largely due to the relatively high fidelity (79%) with primer 2g (a G/U mismatch) using 4a-t, which contrasts with the low fidelity after the same mismatch using 3a-t.

Mis-incorporation after a mismatch in the RNA system (Scheme 2A)

For the RNA system, we measured mis-incorporation after a C/T mismatch (templates 6.0ua, 6.0uc, 6.0ug, 6.0 uu, with RNA primer 7t), with all 4 possible templating bases (Table 4). Overall fidelity after a mismatch was just 38%. The fidelities for copying templating bases G (5%) and U (22%) in this context were similar to or even less than that expected from random incorporation (25%). For comparison, the fidelity of extension after a proper Watson-Crick base pair in this system is 83%.²⁰ Reaction rates of incorporation were quite low after a mismatch, with only G incorporation across C in the template being efficient (k = 0.49 hr^-1, with a relatively high post-mismatch fidelity of 88%); all other reaction rates were at least 10-fold slower.

Table 4.

Incorporation and mis-incorporation frequencies after a mismatch in an RNA system.^c

Reactants	Templating base/monomer	k (h-1)	f
6.0ua, 7t, 8u	A/U	0.037 ± 0.007	0.4 ± 0.008
6.0ua, 7t, 8a	A/A	0.021 ± 0.01	0.22 ± 0.07
6.0ua, 7t, 8c	A/C	0.002 ± 0.0006	0.02 ± 0.01
6.0ua, 7t, 8g	A/G	0.034 ± 0.002	0.36 ± 0.06
6.0uc, 7t, 8g	C/G	0.49 ± 0.12	0.88 ± 0.02
6.0uc, 7t, 8a	C/A	0.04 ± 0.03	0.07 ± 0.04
6.0uc, 7t, 8c	C/C	0.003 ± 0.002	0.004 ± 0.002
6.0uc, 7t, 8u	C/U	0.028 ± 0.001	0.05 ± 0.02
6.0ug, 7t, 8c	G/C	0.005 ± 0.002	0.05 ± 0.009
6.0ug, 7t, 8a	G/A	0.018 ± 0.01	0.18 ± 0.07
6.0ug, 7t, 8g	G/G	0.04 ± 0.003	0.42 ± 0.06
6.0ug, 7t, 8u	G/U	0.03 ± 0.007	0.35 ± 0.01
6.0uu, 7t, 8a	U/A	0.02 ± 0.003	0.22 ± 0.07
6.0uu, 7t, 8c	U/C	0.003 ± 0.002	0.02 ± 0.01
6.0uu, 7t, 8g	U/G	0.05 ± 0.01	0.44 ± 0.06
6.0uu, 7t, 8u	U/U	0.03 ± 0.005	0.31 ± 0.005

^cRelative frequency (f) of each incorporation is given for individual monomers, inferred from rates measured in reactions containing a single monomer (measured by PAGE assay). Underline indicates correct incorporation. See Supporting Figures S10-12 and Figure 5A.

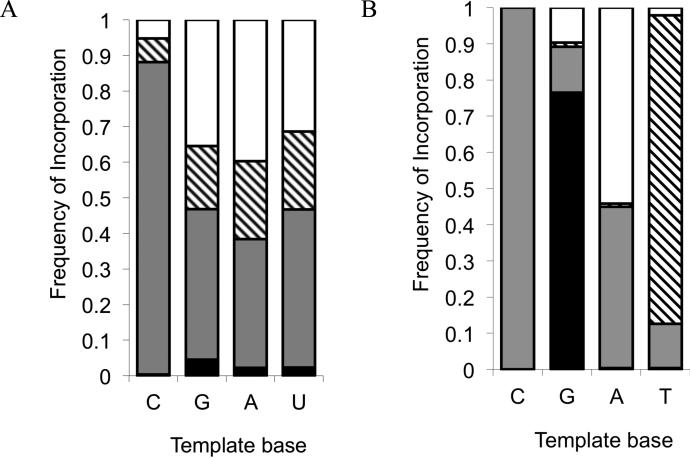
The relative proportion of incorporation of each of the four possible nucleotides tended to be quite similar regardless of the identity of the templating base (Figure 5A). This suggests that the ability of the incoming nucleotide to base pair in a Watson-Crick fashion with the template base is not very important if the primer terminus is mis-matched. To determine if the extension after a mismatch is essentially non-templated, we estimated the rate of extension in the absence of template, using a model reaction of the activated monomers (Scheme 4). The reaction proceeds at a slow but measurable rate (Table 5). For the OAt ester monomers, the non-templated model reaction is >60-fold slower than the templated reaction. For the imidazolides, the non-templated reaction is >1100-fold slower than the templated reactions. Although the identity of the base is relatively unimportant, the incorporation cannot be considered completely non-templated, as the absolute rate of incorporation can be 1-2 orders of magnitude higher with a template than without (compare k′ in Table 2 vs. Table 5).

Figure 5. Mutation frequencies.

Data are shown for (A) the RNA system after single mismatches, and (B) the LNA/DNA system (Supporting Table S5). Patterns correspond to the activated monomers as follows: black = C, gray = G, hatched = A, white = U.

Scheme 4.

Model reaction performed for determining the rates of template-free reaction between an activated deoxynucleoside-5′-monophosphate and an aminoterminal nucleic acid (LG = leaving group, B = nucleobase).

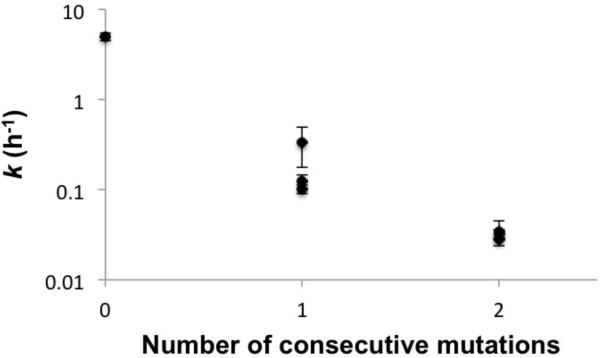
Additional stalling after two consecutive errors

Given our observation that the fidelity of incorporation immediately following a mismatch is very low, a single error would usually be followed by another error. We suspected that this phenomenon would increase the distortion of the primer-template complex, leading to additional stalling. We measured the extension rate downstream of two consecutive errors in the RNA system (6.7c-u with 7g and 8g). The presence of two consecutive mutations decreased the extension rate by an additional factor of ~6 compared to a single mutation (Supporting Table S2, Figure 6).

Figure 6. Extension rate vs. number of mutations.

Average values for different mismatches are shown as different points, with standard deviation indicated by error bars. See Table 3 and Supporting Table S2 for details.

Fidelity after two consecutive errors

To determine if the mutation rate was similarly high after two consecutive errors, we measured the incorporation frequencies for a single sequence context in which the template base was C (Supporting Table S2), using the RNA system (6.7c with 7g). Without errors, copying C in this context is a very high fidelity reaction (99.2%).²⁰ After a single mismatch, copying C had an apparent fidelity of 88% (Figure 5A; Table 3). After two consecutive mismatches, the apparent fidelity stayed at a similar level of 89%.

Sequence context can have large effects on extension rate and fidelity

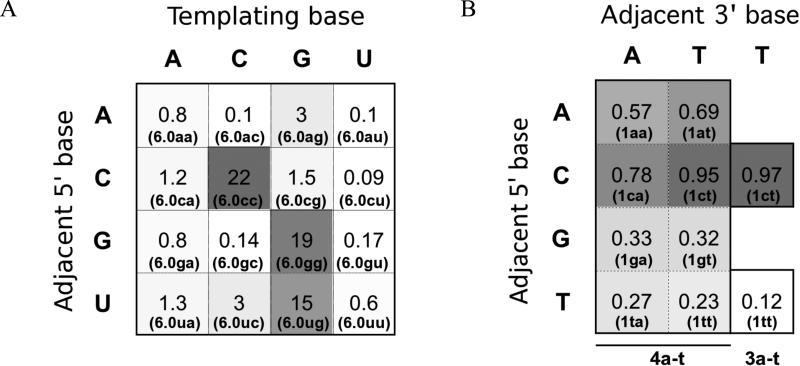
Previous work had shown that the identity of the templating base could affect extension rates and error rates in non-enzymatic, template-directed RNA extension (reaction rate for correct incorporation varied by a factor of >30 depending on the templating base; the total error rate varied by >50-fold depending on the templating base).²⁰ We wondered whether farther sites on the template could cause similarly large variation in reaction rates. We systematically varied the templating base and the base immediately 5′ of the templating base (16 possibilities) and measured the reaction rate in the RNA system (template series 6.0 with primer 7g and the correct monomer (8a, 8c, 8g, or 8u)). In many cases, the neighboring base did not affect the reaction rate for a given templating base, but in some cases the rate was substantially affected (Figure 7A, Supporting Table S3), by a factor of up to 200 (template base C). The largest extension rates occurred when the template consisted of two identical nucleotides (CC, GG). 6.0cc was particularly fast compared to reactions with the same templating base but different adjacent bases (6.0ac, 6.0gc, 6.0uc).

Figure 7. The effect of sequence context on rate (A) and fidelity (B).

Template sequences are from series 6.0 (A) and series 1 (B). The templating base is positioned across from the incoming nucleotide; the adjacent 5′ and 3′ bases are positioned immediately 5′ and 3′of the templating base, respectively. Heat maps are shown with each square shaded according to the relative values given in each square (higher value = darker square), for first-order rate constants (h^-1) in (A) or fidelities f_G in (B). Template is given in parentheses. Activated monomers are indicated at the bottom of panel B. See Supporting Tables S3-4 for more details.

The presence of cooperativity was also studied by measuring the fidelity of incorporation after a mismatch in the DNA system (templates 1 with 2g and 4a-t). In particular, the role of the base immediately 5′ of the templating base was studied. Two different mismatches (A and T) were examined across terminal base G in the primer, with template base C being copied while the adjacent 5′ base was varied (4 possibilities for each mismatch). As seen for absolute rates, the reactions with the highest fidelities contained template ‘CC’ (1ca, 1ct), again suggesting cooperativity among monomers enhancing the reaction efficiency, at least for G monomers (Figure 7B, Supporting Table S4). The identity of the leaving group was also altered for two reactions using 3a-t instead of 4a-t, but this did not appear to have a systematic effect on the fidelities.

Fidelity and reaction rates are influenced by backbone conformation

Prior work had found that the non-enzymatic copying of RNA differed from that of DNA in at least two respects: 1) reaction rates of RNA were higher, and 2) prominent G:U wobble pairing led to higher mutation rates in RNA.^3,20,30 To understand the chemical basis for these differences, we replaced multiple nucleotides in the DNA template sequence by a locked nucleic acid (LNA), as shown in templates 9a-t in Scheme 2B. The effect of these replacements is to ‘lock’ the conformation of the helix into the A-form rather than the usually preferred B-form for DNA.^31,32 We measured the mutation frequencies for all 4 template bases with primer 10 and monomers 4a-t in separate reactions monitored by the PAGE assay. We found that the LNA-templated reactions were faster and lower fidelity than their DNA-templated counterparts (Figure 5B, Supporting Table S5). Quantitative estimates of pairwise similarities of the mutation profile using templates 9a-t with analogous reactions using DNA and RNA templates and primers²⁰ (a total of 5 different backbone combinations in the same sequence context) was obtained in two ways, by calculating the Pearson correlation coefficients and the scalar (dot) products. The DNA/LNA templates produced a mutation profile that was most similar to the system with an RNA template and DNA primer (Supporting Figure S23).

Integrated simulation of non-enzymatic replication

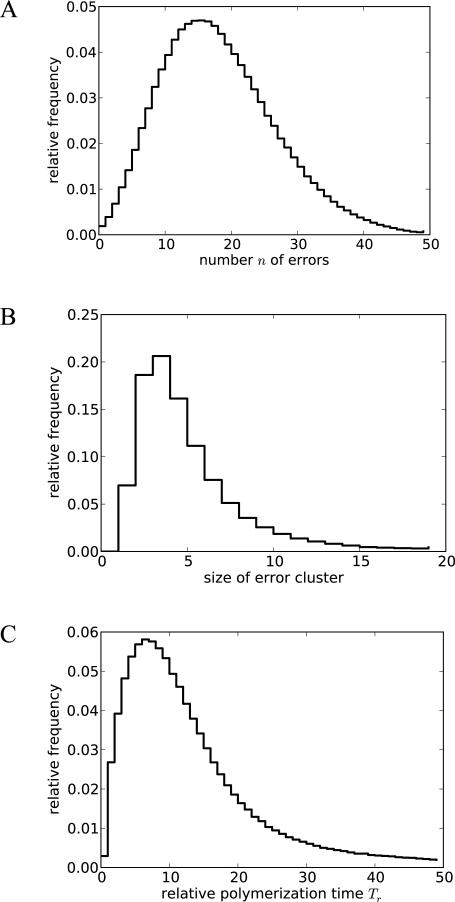
To understand how the various effects measured in our experiments would combine to affect polymerization times and mutation rates during non-enzymatic replication, we used the data gathered here and from previous work¹⁹ as parameters for a stochastic simulation of the complete copying of random 50-mer sequences (Scheme 5). The simulations were based on the DNA template - DNA primer system, for which the most extensive data were collected, as well as general lessons learned from all systems (e.g., recovery of extension rates after an error and relative rates following multiple mismatches; see Methods for details). We found that the proportion of errors per base, averaged over the entire pool of simulated sequences, was very high (35%) compared to the measured mis-incorporation rate after a perfectly matched primer-template terminus (~12%), due to the fact that an initial error tended to cause multiple subsequent errors (Figure 8A). Error clusters consisted of 5 consecutive errors, on average (Figure 8B). Polymerization times were substantially increased (Figure 8C). A small fraction (0.2%) of sequences did not contain errors and therefore had a normal polymerization time (T_r = 1), but on average the sequences took much longer to polymerize due to stalling after mismatches (average T_r = 17).

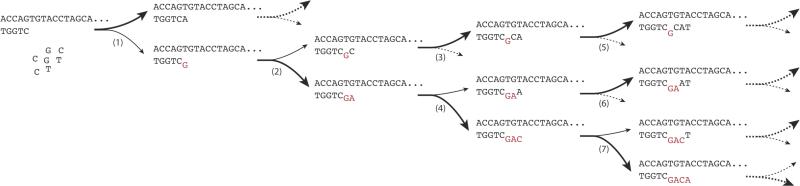
Scheme 5. Reaction scheme for the simulation.

Polymerization proceeds along an arbitrary template sequence. Reaction (1) is a possible initiation point for a cascade of errors. If an incorrect nucleotide is incorporated, the fidelity and the speed of the following reactions are reduced. If reaction (2) is followed by a correct incorporation, extension occurs at a reduced reaction rate in reactions (3) and (5) until the normal rate is recovered. More likely, (2) is followed by another error, which leads to an even stronger reduction in the rate of reaction (4) and a slower recovery in reaction (6) and subsequent steps. Yet another error in (4) leads to a slow reaction (7) and so forth.

Figure 8. Computed effect of the cascade of mutations on copying of 50-mers.

Histograms are shown for (A) number of errors per sequence, (B) average size of error clusters per sequence, and (C) relative polymerization time compared to a perfect copy (T_r).

To understand how these simulation results change in response to changes in rate constants, we carried out several analogous analyses under different scenarios, as might occur if the activation chemistry, backbone, or other conditions were slightly altered (Supporting Information). Artificially increasing the misincorporation rate 2-fold for all mutations increased the proportion of errors per base to 54%; this is less than a 2-fold increase because most mutations actually occur post-mismatch, and their conditional probabilities of occurring do not change if the initial mutation rate is increased. Decreasing the importance of stalling by setting the non-templated reaction rate to be at least 10% of the incorporation rates decreased the mean polymerization time by roughly 2-fold (average T_r = 9). Because we averaged our results over an ensemble of sequences, they were not sensitive to the presence or absence of sequence correlations (i.e., successive incorporations are not independent due to contextual effects, but this non-independence is not a major effect). Finally, we used different assumptions for the rate of extension following regions of multiple mismatches. All of these modifications did not change the qualitative finding that non-enzymatic template-directed polymerization leads to a segregation of mutations onto full-length sequence copies, such that a small fraction of copies contains a large fraction of the copying errors.

Discussion

To understand how polymerization would be affected by mutations, this paper integrates data from two experimental laboratories using different assay techniques. While an exhaustive study of sequence contexts and several different activation chemistries and backbones would be ideal, for experimental necessity we explored a limited range of these parameters. Nevertheless, the general lessons extracted from different experimental systems were similar, lending greater confidence to the interpretation of the results. We found that the presence of an error causes further extension to stall by 1-2 orders of magnitude for a DNA primer (on both a DNA or RNA template) and for an RNA system, supporting prior work.²³ Whether the template and primer were RNA or DNA and whether the leaving group was ImH or OAt^- did not have a major effect on stalling after a mismatch. Nucleoside 5′-phosphorimidazolides have been used by several different laboratories as a model system for non-enzymatic extension.^{14,16,20,33-35} The substituents of the imidazole ring have been found to influence the rate and regiospecificity of the polymerization reaction of RNA monomers, with 2-methylimidazole giving the greatest yield,³⁶ although 2-methylimidazole was shown to be a poorer catalyst for the extension of 2'-aminoterminal DNA primers than other imidazoles.^37,38 Imidazoles and 4-aminopyridines were also found to be favorable leaving groups for montmorillonite-promoted RNA polymerization compared to other possibilities.³⁹ However, the influence of the leaving group on mutation rates and stalling was previously unknown. Since the leaving group had little effect, differences in magnitude of stalling factors (2-3-fold) observed for the DNA system here compared to prior work²³ is likely due to the difference in sequence context. Stalling after mismatches can be important for increasing information capacity by essentially reducing production of erroneous full-length copies, if polymerization can occur only during a limited time window.⁴⁰

The presence of an isolated single mismatch did not affect extension rates farther downstream, if the mismatch were followed by a correct Watson-Crick base pair. Indeed, the downstream extension rates correlated well with the predicted base-pairing probability for the terminal base pair.

Incorporation after a mismatch was extremely error-prone in all systems tested, with fidelity (i.e., frequency of correct incorporation) close to that of random incorporation (25%). The fidelities of some reactions were even less than the expectation for random incorporation, but some fidelities were relatively high. High post-mismatch fidelity tended to occur across templating base C, perhaps because the templated incorporation of G across C is particularly robust, and incorporation of the G monomer (across from any base) is also particularly efficient.^2,3 This pattern suggests that the templating base does not direct the post-mismatch reaction, although the presence of a template did give higher reaction rates than a model non-templated reaction. Since an initial mismatch was likely to be followed by another error, we tested stalling and fidelity after two consecutive mismatches. This situation caused greater stalling than a single mismatch (by 6-fold), and incorporation was again very error-prone with a similar pattern of mis-incorporation as observed after a single mismatch. Our simulations predict that the cycle of misincorporation and stalling would usually repeat several times, until the correct base is incorporated by chance, essentially allowing the duplex to close so templated polymerization may proceed.

The background rate of non-enzymatic extension limits both the frequency of correct incorporation and the amount of stalling after a mismatch. One might wonder whether very high post-mismatch stalling factors could essentially stop the production of mutant sequences, or whether template-based discrimination among monomers (based on Watson-Crick pairing) might approach the very low thermodynamically determined limit on error rate.⁴¹ However, the nontemplated background rate establishes a basal rate of incorrect incorporation and limits the system from approaching very high fidelity through either mechanism. This limit is apparently reached earlier than the thermodynamic limit on fidelity (based on the difference in free energy between correct and incorrect duplexes), which is much lower than the observed per-base fidelities.²⁰ In the model background reaction, imidazolides reacted more slowly than OAt esters, suggesting that greater accuracy could be eventually obtained in a system using imidazolides. Differences in the rate of hydrolysis may be partially responsible for the large difference between the factors. One might speculate that the kinetically stable triphosphate activation chemistry used in extant life is important for high replication fidelity, since the background rate is negligible.

The local structure around the incorporation site can have large effects on extension rate. Reaction rates varied over two orders of magnitude for different sequence contexts in the template. As suggested by others,⁴² there appears to be a cooperative effect, perhaps from stacking of adjacent monomers (particularly G), that enhances the rate of extension. Additional evidence for higher-order effects with G-monomers was also found by Deck et al.³⁵ The contextual effects found here suggest that homopolymeric tracts would be favored, possibly decreasing sequence diversity. However, in a prebiotic context, this effect may be countered by a different replication mechanism, template-directed ligation, which tends to increase compositional diversity.⁴³ Another effect of local structure is that RNA polymerization reactions have a different mutation profile than the corresponding reactions with DNA, with G-U wobble pairing causing high mutation rates for RNA.^20,30 We found that the mutation profile of an LNA-templated reaction resembled that of an RNA-templated reaction, implicating the A-form helix as the source of this difference.

This study, and similar studies that require observation of slow reaction rates, are enabled by the amine nucleophile, which is more reactive than the hydroxyl of native DNA or RNA. The amine is isosteric and isoelectronic to the hydroxyl group, such that one might not expect the substitution to have a large effect on relative rates.¹⁹ Primer extensions with amino-terminal primers give higher yields than those using hydroxy-terminated primers because the desired extension reaction competes more favorably with hydrolysis. The pK_a of the protonated form of 3'-amino-2',3'-dideoxythymidine has been determined to be 7.7, i.e. close to neutrality, meaning that a significant fraction of the amine is unprotonated.¹⁹ The use of an amine may have subtle effects on the conformation of the ribose ring, which might influence the ratio between the rates of templated vs. non-templated extension. The difference in nucleophiles may influence the quantitative results, but we do not necessarily expect it to influence the qualitative and comparative effects reported in our study.

Our essential finding is that a single mutation would trigger a cascade of subsequent mutations and kinetic slowing. To understand the cumulative effect of this cascade, we simulated the copying of 50-mer sequences based on the experimentally observed rate constants. Our simulations show that initial errors would tend to create relatively large stretches of consecutive mutations, suggesting that relatively large changes would occur at a single evolutionary step. For example, if the size of a ribozyme were 30 bases, the simultaneous mutation of 5 consecutive bases would cause an evolutionary ‘leap’ through a relatively large region of sequence space with correspondingly large structural or phenotypic changes. While point mutations could occasionally lead to large structural changes,⁴⁴ the relative rarity of functional RNA sequences has led to the speculation that other mechanisms, such as ligation and recombination, may have been needed to effectively explore sequence space during early evolution.^45,46 For example, several in vitro evolution attempts to improve the activity of an RNA polymerase ribozyme⁴⁷ (capable of ~14 polymerization reactions) resulted in relatively modest gains.⁴⁸ This led some to speculate that the ribozyme occupied a fitness maximum in sequence space and therefore could not be further improved.^45,49 However, recent work produced an improved version (capable of copying a 95-mer) that contained 4 mutations and an additional 11-mer segment.⁵⁰ This illustrates that substantial improvements in activity might require rather large jumps through sequence space. The cascade of subsequent mutations following upon an initial error could enable such jumps, possibly increasing the likelihood of large, saltatory changes. Indeed, this mechanism may be a way to address the ‘yin-yang’ of low error rates: that is, low mutation rates permit greater complexity because more information can be retained, but low rates also imply low adaptive evolvability in case a sequence is far from its fitness optimum (or if environmental conditions change).⁵¹ In the case studied here, the proportion of erroneous bases would be quite high (35% according to our simulations), due to cascading errors, but the additional mutations are kinetically segregated to the copies that already contain errors. This cascade does not reduce the number of perfect copies, but decreases the similarity between mutant sequences and the original template. This situation could combine the ability to store substantial genetic information with high evolvability. A potential downside is that fine-tuning by single-base changes would be slow, so the features of this system would be most useful for early, rough exploration rather than local optimization in sequence space.

Conclusion

The informational and kinetic characteristics of polymerization of mutant sequences are important features determining how evolution occurs in the space of all possible sequences. Our results also suggest possible avenues for systematic studies to achieve higher fidelity in similar systems. Faster templated reactions coupled with a slow background reaction should lead to self-copying systems with greater fidelity.