Abstract
Background and Objectives
Cognitive-behavioral therapies are currently the gold standard for panic disorder treatment, with well-documented treatment response. However, following interventions, some individuals continue to improve, while others experience a return of symptoms. The field lacks reliable ways to predict follow-up symptomology. In the current study, a cluster analysis with a repeated measures design was conducted to examine change patterns over 12 weeks of cognitive behavioral group therapy for panic disorder. The central aim of the study was to evaluate if change patterns predict level of panic symptom severity at a six month follow-up in this sample.
Methods
Individuals with panic disorder (N = 36) completed a measure of panic symptoms (Panic Disorder Severity Scale) at the outset of every therapy session and at a six month follow-up.
Results
Results revealed three patterns of change in this specific trial, which significantly predicted level of panic symptoms six months post-treatment, beyond initial or final level of panic symptoms, and beyond total symptom change.
Limitations
Given the relatively small, lab-based sample, replications in other settings and samples will be important.
Conclusions
Overall, results provide initial evidence that change patterns are meaningful predictors of panic symptom severity well after the final session of treatment.
Keywords: change patterns, panic disorder, follow-up, cluster analysis
Cognitive-behavioral therapy (CBT) is well-documented as the gold standard treatment for panic disorder, with approximately 74% of individuals diagnosed panic-free at the end of treatment (see Gould, Otto, & Pollack, 1995). However, in the months following CBT, some individuals continue to improve, while others experience a return of previously remitted panic symptoms or “slippage” (Gould et al.; Lambert & Ogles, 2004). In fact, effect sizes for symptom change from post-treatment to six month follow-up range from −.26, indicating slippage (Telch et al., 1993), to .56, indicating further gains (Öst, 1988). Currently, the field is lacking consensus on how to predict symptom levels following treatment termination.
Change patterns during therapy may be a useful way to predict panic levels in the months following CBT. Although the literature for examining change patterns and treatment trajectories in psychopathology is growing (e.g., Cuijpers, van Lier, van Straten, & Donker, 2005; Stulz & Lutz, 2007), there is minimal literature documenting the relationship between patterns of change over the course of treatment for panic disorder and panic symptoms in the months following treatment. In the current study, we use a repeated measures design to evaluate if variation in change patterns predicts level of panic symptom severity at a six month follow-up beyond total symptom change, panic level at baseline, and panic level post-treatment in a given sample.
Change patterns over the course of treatment
The majority of the literature on CBT for panic examines static values on a variable, or evaluates pre- to post-treatment change. While these methods provide valuable information about treatment efficacy, they conceal potentially significant differences in the treatment trajectory for different subpopulations of individuals (see Krause, Howard, & Lutz, 1998; Lutz, Stulz, & Köck, 2009; Stulz & Lutz, 2007). For example, two individuals may have identical beginning and ending symptom levels, but different change patterns during treatment and different follow-up levels of panic. A goal of the present work is to evaluate to what extent such a difference in the change pattern during a specific treatment trial can account for differences at follow-up.
The current study uses a k-means cluster analytic approach (see Forgy, 1965) to examine change patterns over the course of treatment for individuals with panic disorder in a lab-based treatment study. Only a small number of studies have used cluster analytic approaches to identify patterns of change over the course of clinical interventions, such as family-based aggression prevention (Hanish & Tolan, 2001), antipsychotic treatment for schizophrenia (Lambert et al., 2009), and medication for bipolar mania (Lipkovich, Houston, & Ahl, 2008). Importantly, in Lambert et al., cluster membership predicted recovery and subjective well-being in individuals with schizophrenia at a three year follow-up, suggesting that patterns of change may have predictive value.
A few studies have examined change patterns in panic disorder, although none have used change patterns to predict follow-up levels of panic symptoms. Aaronson et al. (2008) used a repeated measures design to examine panic symptom severity levels over 11 weeks of CBT. The change patterns of treatment responders and non-responders were compared. Results indicated that 76% of treatment responders experienced a 40% reduction in panic symptom severity by the sixth week of CBT, compared to only 36% of the non-responders, suggesting that many individuals with panic who will respond to CBT will have done so by the midpoint of treatment. Stanley et al. (1996) evaluated patterns of change on levels of self-reported state fear, agoraphobia, and social fear over the course of ten weeks of treatment for panic. Change patterns were compared for individuals receiving cognitive therapy and those receiving relaxation training. Differences between the curves were evaluated, but subpopulations within treatment conditions were not explored. Finally, Clerkin, Teachman, and Smith-Janik (2008)1 investigated rapid symptom reduction (“sudden gains”) in cognitive-behavioral group therapy (CBGT) for panic, and found that sudden gains in treatment after the second treatment session predicted greater symptom reduction and change in anxiety sensitivity, relative to patients who did not experience a sudden gain. However, other change patterns over the course of treatment were not explored.
We extend this line of research by using cluster analysis to determine change patterns in a given sample, rather than comparing responders to non-responders, or comparing two different treatment conditions, or only looking at isolated changes, such as sudden gains. Additionally, we evaluate how change patterns predict level of panic at a six month follow-up. Of note, the present study does not aim to characterize all possible patterns of change that could occur in panic disorder (this would necessitate an extremely large sample and multiple treatment conditions), but rather to determine whether patterns of change can predict follow-up symptomatology beyond more standard predictors of outcome (i.e., initial and post-treatment levels of panic symptom severity) in this trial.
The field is still in the early stages of determining reliable ways to predict panic symptom level following treatment termination. Across studies, the majority of predictor variables (e.g., demographics, personality traits) have not consistently predicted follow-up symptom levels (see review by Steketee & Shapiro, 1995). As Ramnero and Öst (2004) state, “the results from this line of research have generally proven unrewarding” (p. 176). Given the predictive value of change patterns seen for psychological problems (Lambert et al., 2009), a logical next step is to evaluate if change patterns in treatment for panic disorder can predict panic symptom level at follow-up.
In the current study, we use a cluster analytic, repeated measures approach to characterize change patterns that occur over 12 weeks of CBGT for panic disorder, and then evaluate how the patterns of change predict panic level at six month follow-up (controlling separately for total symptom change, panic level at baseline, and panic level post-treatment) in this trial. Given past research emphasizing the predictive validity of change patterns, we expect that the change patterns found through the cluster analysis will significantly predict panic symptom severity six months after treatment termination. Moreover, we expect these patterns to predict follow-up beyond more commonly examined predictors of treatment outcome, including initial level, final level, and total change in symptom severity over the course of treatment.
Method
Participants
Participants (N = 43) were adults who took part in a 12-week CBGT intervention for panic disorder. To justify the term “change pattern,” only participants who attended at least three of the twelve therapy sessions were included in the current study. This resulted in a final sample of 36 individuals (66.70% with agoraphobia, 69.40% female, mean age = 39.42, SD = 15.63, Range = 18–71). Thirty-two participants reported their ethnicity as Caucasian, two as African-American, one as biracial, and one as “other”. The average total duration of panic at intake was 15.22 years (SD = 15.86, Range = 2 months-61 years).
Although panic disorder was the primary diagnosis for all participants (based on the Structured Clinical Interview for DSM-IV diagnoses, SCID-IV; First, Spitzer, Gibbon, & Williams, 1995), the sample had high levels of comorbidity. At intake, 58.30% of the sample had current comorbid Axis I diagnoses, including other anxiety disorders (36.1%), mood disorders (22.2%), and eating disorders (5.6%). Additionally, at intake 52.8% of participants reported current psychotropic medication use, and 8.3% reported ongoing psychosocial treatment (for issues other than CBT for panic).
Detailed descriptions of recruitment procedures can be found in Teachman, Smith-Janik, and Saporito (2007) and Teachman, Marker, and Smith-Janik (2008). Additionally, see Teachman et al. (2008) for a Consolidated Standards of Reporting Trials (CONSORT) figure, which reports data relevant to attrition and exclusion during the study’s initial stages.
Materials2
Structured Intake Interview
The SCID was administered to potential participants to ascertain that all participants had a primary diagnosis of panic disorder (based on symptom severity and degree of interference in functioning) and to assess Axis I comorbidity. Inter-rater reliability for the SCID diagnoses was high (kappa = .96) following re-rating of approximately 15% of the interviews by an independent doctoral level assessor.
Baseline Mood and Anxiety Measures
The Anxiety Sensitivity Index (ASI; Reiss, Peterson, Gursky, & McNally, 1986) is a 16-item questionnaire that assesses a person’s concern about anxiety-related symptoms (e.g., “It scares me when I become short of breath”). The ASI has adequate psychometric properties (Telch, Shermis, & Lucas, 1989). In the current sample, Cronbach’s alpha pre-treatment was 0.88. The Fear Questionnaire – Agoraphobia subscale (FQ-Agoraphobia; Marks & Mathews, 1979) is a 5-item subscale that assesses level of avoidance toward common agoraphobic situations, such as walking alone in busy streets. The subscale has good psychometric properties (Cox, Swinson, & Shaw, 1991). Cronbach’s alpha pre-treatment was 0.76. The Beck Depression Inventory-II (BDI-II; Beck, Steer, & Brown, 1996) is a widely used 21-item self-report inventory of depression symptoms. In this sample, Cronbach’s alpha was 0.90 pre-treatment.
Measure of Panic Disorder Severity
The Panic Disorder Severity Scale (PDSS; Shear et al., 1997) is a 7-item measure that provides a composite severity score of frequency, distress, and impairment associated with panic attacks (scores range from 0–28). Although the PDSS was designed to be administered by a clinician, several prior studies have successfully used the PDSS as a self-report measure (e.g., Otto, Pollack, Penava, & Zucker, 1999; Penava, Otto, Maki, & Pollack, 1998; Teachman, 2005). In the present study, the PDSS was modified slightly to provide a description of panic attacks so that participants could easily complete the PDSS in a self-report format. The PDSS was administered weekly throughout therapy to examine change in panic severity. In the current sample, Cronbach’s alpha was .78 pre-treatment, and .95 at the final treatment session.
Treatment
Participants completed twelve 90-minute weekly sessions of CBT following the widely-used Panic Control Treatment protocol (Barlow & Craske, 1994), which was modified slightly to fit a group format. Treatment sessions covered psychoeducation, relaxation training, cognitive restructuring, and exposures. Exposures involved interoceptive exercises designed to help participants learn to tolerate feared bodily sensations, and homework assignments designed to reduce agoraphobic avoidance. There were nine treatment groups that were co-led by a pair of advanced-level doctoral students that were extensively trained in CBT techniques and the panic treatment protocol. Therapists received weekly supervision by a licensed clinical psychologist (the third author). All sessions were either observed (via one-way mirror) or reviewed through audio tape recordings.
Procedure
Following informed consent, participants completed the SCID intake interview. Baseline mood and anxiety measures (ASI, FQ-Agoraphobia, and BDI-II) were completed prior to treatment session 1. At intake, the start of every treatment session, and six months after treatment, participants completed the PDSS.
Overview of Data Analysis
The statistical package R was used for all data analyses (R Development Core Team, 2011). Prior to a k-means cluster analysis, it is necessary to account for missing data (Everitt, Landau, & Leese, 2009). Most participants (66%) had zero, one, or two missing occasions. Linear interpolation, a “connect the dots” imputation technique in longitudinal data, was used to fill in missing values (Meijering, 2002). Linear interpolation can artificially induce a linear pattern of change only if two conditions are met: (1) the total amount of missingness is high, and (2) the number of consecutive missing occasions is large, so linear interpolation spans large gaps. Neither of these conditions was met with the current dataset. Overall, 83 occasions out of a possible 432 are missing, and the vast majority (83%) of the gaps where missing values were linearly interpolated were small, spanning only one or two missing occasions. Therefore, it is unlikely that linear interpolation biased the data toward a linear pattern of change.
Linear interpolation resulted in a dataset in which each of the 36 participants had a set of twelve occasions. The k-means cluster analysis was performed on these data (Forgy, 1965). The cluster analysis partitioned the data into a number of clusters, k, by selecting k different mean profiles, called cluster centers, which minimize the sums of squared differences of cluster members from the cluster centers. Thus, k-means cluster analysis seeks to find maximally homogenous groups of participants. Cluster membership is determined by finding the mean profile that has the smallest sums of squared differences from a participant’s data: that is, the cluster center that is closest to the observed data for that participant. Given that the data used in the k-means cluster analysis were repeated measurements, mean profiles can be interpreted as trajectory profiles. Cluster membership was then used to predict the level of panic symptom severity at six month follow-up. Additionally, the predictive validity of cluster membership to explain follow-up panic level was examined after controlling separately for initial level of panic, level of panic post-treatment, and total change in panic symptom severity over the course of treatment.
A Note on Sample Size
Cluster analysis was selected for this analysis specifically because it does not require a large sample size. For example, Dolnicar (2002) states, "There are no rules-of-thumb about the sample size necessary for cluster analysis," (p. 2) and documents instances where cluster analysis is performed on as few as 10 cases. Mooi and Sarstedt (2011) reiterate Dolnicar's sentiments: "there is no generally accepted rule of thumb regarding minimum sample sizes for the relationship between the objects and the number of clustering variables used" (p. 243), and further suggest that considerations must be made on a case by case basis. In our study, we believe that clustering is defensible with our sample size because of the distinct patterns of change observed via clustering and their predictive power in determining six-month follow-up.
Results
Table 1 displays means and standard deviations for the symptom measures (PDSS, ASI, FQ-Agoraphobia, and BDI-II) pre-treatment.
Table 1.
Descriptive statistics (Means and SDs) for baseline measures
| Measure | M | SD |
|---|---|---|
| Panic Disorder Severity Scale | 12.14 | 4.17 |
| Anxiety Sensitivity Index | 30.48 | 11.21 |
| Fear Questionnaire-Agoraphobia | 28.00 | 8.53 |
| Beck Depression Inventory-II | 12.40 | 8.91 |
Results of Cluster Analysis
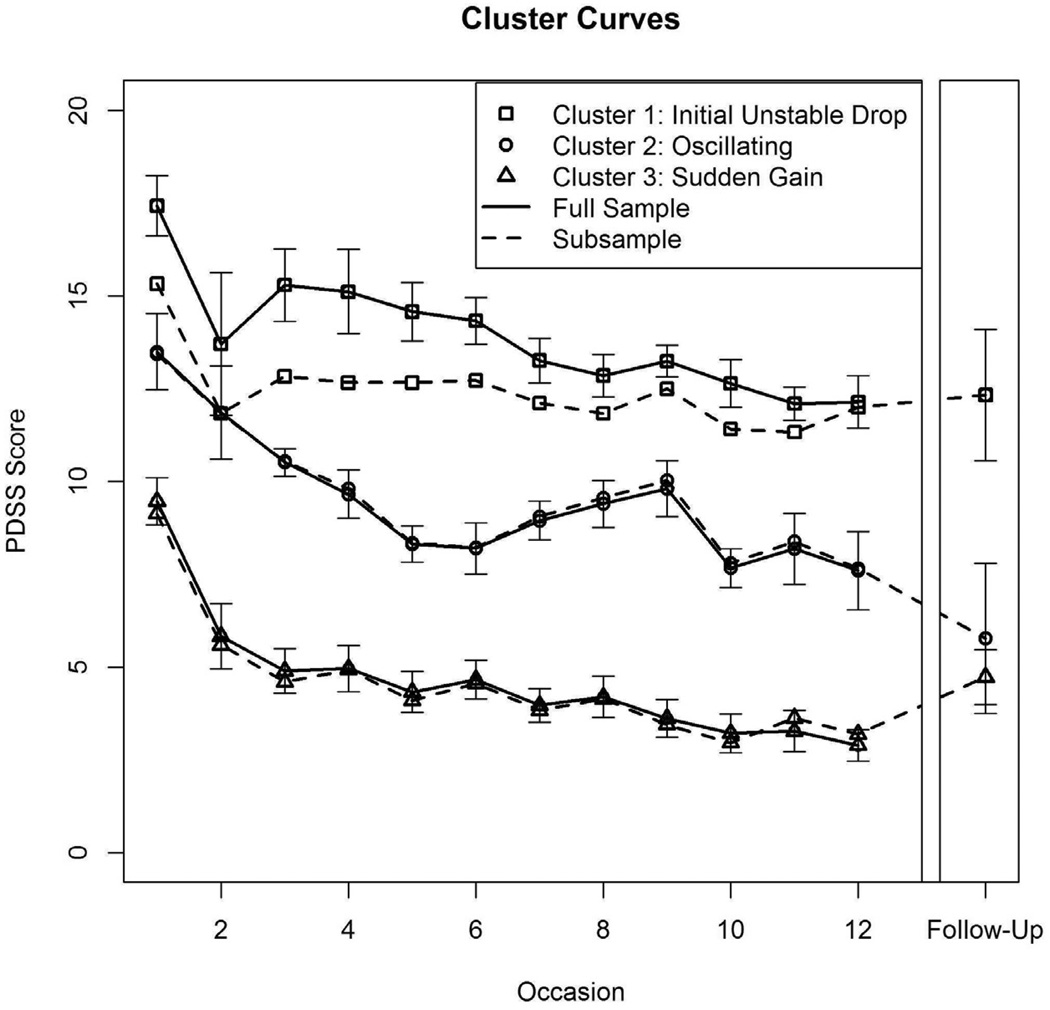
To characterize the patterns of change in this sample, a k-means cluster analysis was performed on the linearly interpolated data. We selected the number of clusters by applying Cattell’s (1966) line, or elbow, criterion to a quasi-scree plot which suggested two to four clusters. The quasi-scree plot was constructed using a model comparison approach. A cluster analysis was performed using one cluster, then two clusters, and similarly up to 15 clusters. This yielded 15 nested models to compare: one model with each number of clusters from one to 15. The fit3 of each model was plotted against the number of clusters in a similar fashion to a scree test in exploratory factor analysis, and the scree test rules for picking the number of factors were applied (i.e., looking for the elbow on the scree plot). Concerns about cluster size (that is, how many people fall on each cluster) moderated the results of the quasi-scree test to ensure that no cluster size was too small. Considerations of the size of each cluster aided in the decision between a two, three, or four cluster solution, in that models with clusters with only one member were disallowed. The consideration of cluster size is important because cluster size is not necessarily uniform, so one cluster might have only one person, whereas another might have twenty people, making results difficult to interpret. Based on these considerations (and because three is the midpoint in the acceptable range of clusters), three clusters were selected (Cluster 1 n = 7, Cluster 2 n = 10, Cluster 3 n = 19). The results of the k-means cluster analysis are shown in Figure 1 by solid lines. Keep in mind that patterns reflect three different group means, rather than individuals’ patterns of change. Cluster analysis tries to find groups that are as homogeneous as possible, but individuals within a group still vary.
Figure 1.
Patterns of change in panic symptom severity over the course of treatment
Note: The solid lines indicate the full sample (Cluster 1 n = 7, Cluster 2 n = 10, Cluster 3 n = 19). The dashed lines indicate the subsample with follow-up data (Cluster 1: n = 3, Cluster 2: n = 9, Cluster 3: n = 15). Error bars at each point are standard errors, and represent a 68% confidence interval. Occasion refers to treatment session. PDSS refers to Panic Disorder Severity Scale.
Given that the cluster analysis was performed on the linearly interpolated data, there is naturally some concern that the interpolation method somehow led to observed differences across the clusters. Some of these concerns were addressed previously by noting that the overall amount of missingness was not very high (83 missing observations out of a possible 432), and gaps between measured values tended to be only one or two sessions. However, the interpolation could still have potentially biased the assignment of a person to a cluster. To test for this possibility, chi-square tests were performed, which revealed that the number of missing occasions per person did not differ across clusters (χ2 (df=2) =.77, p=.68). Importantly, these results do not change when looking at only the part of the sample that has follow-up data (χ2 (df=2) = 0.37, p = 0.83). Next, it was important to show that the three identified clusters actually account for the variability in patterns of change. Cluster membership accounted for fully 41% of the variability in trajectories4, suggesting a large effect (Cohen, 1992). Thus, the data seems well-characterized by three clusters.
What Patterns of Change Occurred in our Sample?
Next, we include a description of the three change patterns that occurred in our sample. Cluster 1’s mean had a PDSS score of 17.43 (SD = 2.15) at session 1, with a 24.15% drop in PDSS scores between session 1 and session 2, followed by symptom fluctuations following the drop (i.e., some return of symptoms, followed by a negative slope as symptom level returned to the level reached at session 2). The cluster’s PDSS score was 12.14 (SD = 1.86) at session 12. This cluster thus reflects an initial drop in symptoms, followed by some instability in maintenance of gains, and is thus labeled “Initial Unstable Drop cluster.” Cluster 2’s mean had a PDSS score of 13.50 (SD = 3.24) at session 1. It had a negative slope in PDSS scores between sessions 1 to 6, a positive slope occurring between sessions 6 to 9, followed by another negative slope occurring between sessions 9 to 12. The PDSS was 7.60 (SD = 3.31) at session 12. This cluster thus showed an oscillating pattern, and is labeled “Oscillating cluster.” Cluster 3’s mean had a baseline PDSS score of 9.47 (SD = 2.76), a 38.89% drop in symptoms between sessions 1 and 2, followed by a small drop (negative slope) between sessions 2 to 12. For Cluster 3, the PDSS was 2.89 (SD = 1.86) at session 12. This cluster thus reflects a sudden gain5 (corresponding to sudden gains criteria outlined by Tang & deRubeis, 1999), followed by a small degree of ongoing symptom decline, and is therefore labeled “Sudden Gain cluster.”
The drop in PDSS score between sessions 1 and 2 in the Sudden Gain cluster is considered a sudden gain because the magnitude of the drop meets the three criteria described in Tang and DeRubeis (1999): it is large in absolute terms (drop is 13.16% of maximum PDSS score), it is large relative to panic symptom severity before the gain (drop is over 25% of the pre-gain session’s PDSS score), and it is large relative to symptom fluctuations following the gain (PDSS score at session 1 is significantly different from the average PDSS scores of sessions three to five; paired samples t(18) = 5.79, p < .001, d = 2.10). Although similarly large in absolute terms, the drop between sessions 1 and 2 in the Initial Unstable Drop cluster is not considered a sudden gain because it is not large relative to panic symptom severity before the gain (i.e., the drop is less than 25% of the pre-gain session’s PDSS score).
Differences between Clusters
To examine differences between the clusters on traditional markers of symptom levels, ANOVAs were conducted comparing the three clusters’ PDSS scores at session 1, session 12, and at follow-up. Not surprisingly, the ANOVAs revealed a significant inter-cluster difference in initial level of panic (F(2, 33) = 22.26, p < 0.001, ŋ2 = .57, adjusted ŋ2 = .55) and final level of panic (F(2, 29) = 32.77, p < .001, ŋ2 = .69, adjusted ŋ2 = .67). In both cases, follow-up tests indicated the Sudden Gain cluster was lower than the Oscillating cluster, which was in turn lower than the Initial Unstable Drop cluster (all p < .05; see Figure 1). Additionally, the between-cluster difference in follow-up PDSS scores was significant, F(3, 24) = 20.30, p < .001, ŋ2 = .72, adjusted ŋ2 = 0.68. Cluster means at follow-up were as follows: PDSS score of 12.33 (SD = 3.05) for the Initial Unstable Drop cluster, 5.78 (SD = 6.08) for the Oscillating cluster, and 4.73 (SD = 2.88) for the Sudden Gain cluster. Follow-up tests indicated that the Initial Unstable Drop cluster was different from both the Oscillating cluster (t(25) = −2.32, p = 0.069, d = −0.93, marginally significant), and the Sudden Gain cluster (t(25) = −2.84, p = 0.023, d = −1.13), and the Sudden Gain cluster and Oscillating cluster were not statistically distinct (t(25) = −0.59, p=0.826, d = -0.23)6. Notably, an ANOVA comparing the three clusters’ total amount of change in PDSS scores across treatment indicated no significant cluster difference, F(2, 29) = 0.66, p = 0.523, ŋ2 = .04, adjusted ŋ2 = −0.02 (Mean total change for Initial Unstable Drop cluster = −4.40, SD = 3.29; Mean total change for Oscillating cluster = −5.78, SD = 3.30; Mean total change for Sudden Gain cluster = −6.50, SD = 3.89). This null total change finding is noteworthy because it indicates that it is the pattern of change that differentiates the clusters, not simply how much change occurs.
To further differentiate the Initial Unstable Drop and Sudden Gain clusters (beyond the differences in their starting level and nature of the drop in symptoms from session 1 to 2), we examined differences in the change process from session 2 to 12 by testing how well the change processes followed a linear path. While fitting a straight line (i.e., a first order polynomial) to each cluster from session 2 to session 12 yielded statistically significant predictions for both the Initial Unstable Drop and Sudden Gain clusters (Initial Unstable Drop: F(1, 9) = 25.29, p < 0.001, R2 = 0.74, R2 adjusted = 0.71; Sudden Gain: F(1, 9) = 112.08, p < 0.001, R2 = 0.93, R2 adjusted = 0.92), the effect sizes (R2s) are markedly different. This indicates that from session 2 to session 12, the Sudden Gain cluster fits a straight line very well, but the Initial Unstable Drop cluster follows a comparatively less linear pattern of change. In fact, to achieve a similar degree of fit for the Initial Unstable Drop cluster (as found for the Sudden Gain cluster with the linear estimate), a cubic (third order polynomial) or even quartic (fourth order polynomial) function is required (Cubic: F(3, 7) = 17.94, p < 0.01, R2 = 0.88, R2 adjusted = 0.84; Quartic: F(4, 6) = 27.97, p < 0.001, R2 = 0.95, R2 adjusted = 0.92). This implies that the Initial Unstable Drop cluster is characterized by a higher degree of "ups and downs" (i.e., a less linear pattern of change) after the initial gain than is the Sudden Gain cluster.
Reliable Change in Each Cluster
The reliable change index was calculated (following Jacobson & Truax, 1991) for each participant at the end of treatment and also at follow-up. Given that absolute change was similar across clusters, the clusters had similar percentages of participants showing reliable change at the end of treatment. Specifically, the Initial Unstable Drop cluster had 71.4%, the Oscillating cluster had 60.0%, and the Sudden Gain cluster had 63.3% of participants with a reliable change index over 1.96 (χ2 (df = 2) = 0.09; p = 0.96). Note that this χ2 is parallel to the ANOVA reported in the Differences Between Clusters subsection, in which the total change was found not to differ across clusters.
At follow-up, the clusters differed in terms of the percentage of participants with reliable change. The Initial Unstable Drop cluster and Sudden Gain cluster had 33.3% and 26.7% of participants showing reliable change, respectively. By contrast, the Oscillating cluster had 66.7% of participants showing reliable change.
Given the observed proportions of reliable change at follow-up (0.33, 0.67, and 0.26), a focused a χ2 test was performed to examine the statistical significance of the inter-cluster difference in reliable change, focusing on whether the Oscillating cluster differs from the Sudden Gain and Initial Unstable Drop cluster in terms of the proportion of people who experience reliable change. Grouping the Sudden Gain and Initial Unstable Drop clusters together and comparing their proportion of reliable change to that of the Oscillating cluster showed that the Oscillating cluster was indeed different from the other two clusters (χ2 (df = 1) = 4.94, p = 0.026). Note that conducting a less focused test of inter-cluster differences (which tested for differences across all clusters, rather than testing a specific contrast) in proportion of people showing reliable change from the beginning of treatment to follow-up was not statistically significant; χ2 (df = 2) = 2.25, p = 0.32.
As seen in Figure 1, the level of panic symptom severity in the Sudden Gain cluster increased from the end of treatment to the six-month follow-up (plausibly due to a floor effect at post-treatment), whereas the Oscillating cluster continued to decrease (albeit non-significantly) in panic symptom severity. Hence, there was on average more absolute change from the beginning of treatment to follow-up in the Oscillating cluster compared to the other two clusters.
How well do Patterns of Change Predict Follow-up?
To determine how well cluster membership predicts panic symptom severity on the PDSS at six month follow-up, simultaneous linear regression was conducted. Because cluster membership is a discrete variable, each cluster was dummy coded (participants were coded as on the cluster or not) prior to the regression analysis. Cluster membership was a good predictor of follow-up, accounting for 25% of the variability in six month follow-up scores, R2 = 0.257.
Within clusters, PDSS scores did not significantly change between session 12 and follow-up for either the Initial Unstable Drop or Oscillating clusters (both p > .10 using a paired samples t-test). However, PDSS scores significantly increased (i.e., worsened) between session 12 and follow-up for the Sudden Gain cluster, t(14) = 2.38, p < .05, d = −1.27 using a paired samples t-test. Of note, individuals following this change pattern did very well (i.e., low in symptom severity) in absolute terms at session 12, and continued to do well at follow-up, even though there was a significant increase in PDSS scores.
Can Patterns of Change Incrementally Predict Follow-up Symptom Severity?
To evaluate the incremental validity of cluster membership as a predictor of PDSS scores at six month follow-up, and to show that cluster membership predicted follow-up levels of panic symptom severity above and beyond level of symptom severity, we conducted a series of regressions. First, we ran three bivariate regressions to determine whether the typical cluster level characteristics (initial level of symptom severity at session 1, final level of symptom severity at session 12, and total change of symptom severity over the course of treatment) were significant predictors of panic symptom severity at follow-up. As expected, when entered independently, each of these characteristics explained a significant amount of variance in follow-up PDSS scores (initial level: F(1, 25) = 4.25, p < .05, R2 = 0.15, adjusted R2 = 0.11; final level: F(1, 25) = 30.02, p < .001, R2 = 0.55, adjusted R2 = 0.53; total change: F(1, 25) = 4.82, p < .05, R2 = 0.16, adjusted R2 = 0.13), replicating prior literature (e.g., Woodman, Noyes, Black, Schlosser, & Yagla, 1999).
Next, we conducted two hierarchical regressions with the typical predictors of panic symptom severity entered, followed by cluster membership (reflecting patterns of change; see Tables 2a and 2b). As expected, when cluster membership was entered into the regression after initial and final level of panic symptom severity, cluster membership remained a significant predictor of PDSS scores at follow-up (F(2, 22) = 4.13, p < .05, ΔR2= 0.12, partial R2 = 0.27)8. Similarly, cluster membership explained a significant amount of variance in PDSS scores at follow-up beyond the total amount of change in panic symptoms (entered in a separate regression analysis because of dependence on initial and final level of panic; F(2, 23) = 3.47, p < .05, ΔR2 = 0.18, partial R2 = 0.21). These results suggest that cluster membership is predictive of panic level at follow-up, even when controlling for the effects of initial level, final level, and total change in panic symptoms.
Table 2.
| a. Model Comparison: Cluster membership explains unique variance in follow-up symptoms beyond initial and final level of panic. | |||||
|---|---|---|---|---|---|
| Predictors | Adjusted R2 | R2 | ΔR2 | partial R2 | p-value |
| Initial Level | 0.11 | 0.15 | - | - | - |
| Initial Level and Final Level | 0.51 | 0.55 | 0.4 | 0.47 | <.001 |
| Initial Level, Final Level, and Cluster Membership | 0.61 | 0.67 | 0.12 | 0.27 | <.05 |
| b. Model Comparison: Cluster membership explains unique variance in follow-up symptoms beyond total change in level of panic. | |||||
|---|---|---|---|---|---|
| Predictors | Adjusted R2 | R2 | ΔR2 | partial R2 | p-value |
| Total Change | 0.13 | 0.16 | - | - | - |
| Total Change and Cluster Membership | 0.26 | 0.34 | 0.18 | 0.21 | <.05 |
Note: Outcome variable is Panic Disorder Severity Scale (PDSS) score at six month follow-up.
Total change is calculated as the Session 12 PDSS score minus the Session 1 PDSS score.
Discussion
In the current study, we conducted a cluster analysis with a repeated measures design to identify change patterns over 12 weeks of cognitive behavioral group therapy for panic disorder. Results revealed three change patterns: a Sudden Gain cluster, an Oscillating cluster, and an Initial Unstable Drop cluster. These change patterns significantly predicted follow-up beyond initial level of panic, final level of panic, and total symptom change in this trial. Although the sample size was small, significant effects indicate that patterns of change were able to predict follow-up levels of panic symptom severity in this sample. Together, these results suggest that individuals follow different change trajectory profiles over the course of treatment (even when they change the same overall amount), and these trajectory profiles have implications for symptom severity months after treatment terminates.
The three change patterns identified in our sample were distinct in terms of initial and final levels of panic symptom severity, a finding typical of prior change pattern literature (Hanish & Tolan, 2001; Lambert et al., 2009; Lipkovich et al., 2008). However, the total change in panic symptom severity was similar for the three change patterns. This finding adds support to previous claims that evaluating only pre- to post-treatment change conceals important differences in change patterns (e.g., Krause et al., 1998; Lutz et al., 2009; Stulz & Lutz, 2007).
In line with our hypotheses, cluster membership accounted for a large proportion of variability in panic symptom severity at six month follow-up in this trial. This finding is consistent with previous research demonstrating the predictive value of change patterns (e.g., Lambert et al., 2009; Lutz et al., 2009). Our finding that cluster membership predicted follow-up levels of panic symptom severity beyond initial, final, and total change in panic symptoms suggest that patterns of change provide unique information about who is likely to maintain gains following treatment, and who is likely to experience slippage. Given the lack of reliable predictors of panic symptoms at follow-up across past studies (see Steketee & Shapiro, 1995), the considerable variance explained by change patterns in the current study is notable. Determining which aspects of each change pattern are most important for predicting follow-up (e.g., the difference in slopes between sessions 1 and 2, the difference in slopes between sessions 2 and 12) is an empirical question that should be considered in future research with larger samples.
The Sudden Gain cluster predicted low levels of panic symptom severity at follow-up. These results are consistent with past research emphasizing the benefits of sudden gains (e.g., Clerkin et al., 2008; Tang & deRubeis, 1999). Additionally, these findings provide support for the clinical meaningfulness of sudden gains (see unresolved questions in Hoffman, Schulz, Meuret, Moscovitch, & Suvak, 2006). Although the present study did not evaluate why the Sudden Gain cluster predicts favorable outcomes at follow-up, it seems plausible that the early sudden gain could have increased both self-efficacy and treatment credibility, leading to further gains.
The Oscillating cluster predicted follow-up levels of panic that were similar to the Sudden Gain cluster, and outperformed the other two clusters in regards to proportions of participants showing reliable change at follow-up. Given previous literature highlighting the stability of sudden gains (e.g., Tang & DeRubeis, 1999), it is somewhat surprising that the Oscillating cluster outperformed the Sudden Gain cluster in regards to reliable change at follow-up. However, sudden gains are more likely to be followed by a return of symptoms if they occur following session 1 (as opposed to following later sessions; see Clerkin et al., 2008), so the lower level of reliable change in the Sudden Gain cluster in the current study may be due to the fact that the sudden gain in our sample occurred following session 1. Alternatively, the lower proportion of participants showing reliable change at follow-up in the Sudden Gain cluster may be due to a floor-effect at post-treatment. Although the PDSS has lower possible values, it seems unlikely that participants recovering from panic disorder would score much lower than did participants in the Sudden Gain cluster, given that a 7 on the PDSS corresponds to only “mild” or “slight” levels of symptomatology for each item on the scale. Another possible explanation for the finding that the Oscillating cluster outperformed the Sudden Gain cluster in regards to reliable change at follow-up concerns the Oscillating cluster’s recovery from the small reversal in the second half of treatment, which may have taught these individuals how to cope with obstacles. As a result, following treatment cessation, the Oscillating participants may have been better prepared to deal with panic-related set-backs.
Finally, the Initial Unstable Drop cluster predicted the highest level of panic symptom severity at follow-up. While speculative, perhaps these individuals may have felt discouraged or experienced a decrease in self-efficacy following the sessions where no continued improvement occurred, which may have left them vulnerable when treatment ended. Future studies should consider measuring self-efficacy and treatment credibility/motivation throughout treatment to evaluate if it determines who plateaus or experiences symptom fluctuations, and who continues to improve (see Casey, Oei, & Newcombe, 2005).
A few caveats should be considered. First, in light of our small sample size, and the fact that our sample comes from a lab-based study that was completed in a controlled setting with selection criteria, replications using other settings and samples with panic disorder (e.g., community mental health centers) will be important to enhance generalizability of the findings. Nevertheless, the finding that patterns of change have predictive value in this specific sample is in line with previous research (e.g., Lambert et al., 2009; Lutz et al., 2009). Second, although it is unlikely that linear interpolation biased our change patterns, it is possible that change patterns may have looked different if the participants had no missing data, or if another data imputation method was employed. Third, although patterns of change predicted follow-up beyond initial and final panic symptom severity, it is likely that panic levels at both time-points influenced the formation of the clusters. Notably, the decision to allow initial and final levels of panic to influence cluster formation was made because we feel this approach is more externally valid; we thus chose to later control for these influences statistically in the prediction of follow-up, rather than eliminating their influence on cluster formation and the definition of a pattern of change. Finally, we only examined change patterns in one measure (the PDSS); albeit one that is a widely used index of multiple aspects of panic severity.
Despite these limitations, this study provides evidence that in the current sample, clusters are predictors of panic symptom severity well after treatment has terminated. Future studies with larger sample sizes can help clarify which patterns of change are typical over the course of different treatments. Further, determining why people follow different change trajectory profiles is an interesting future empirical question, which could help clinicians to better tailor treatment to their particular clients. Overall, results highlight the importance of monitoring progress throughout treatment and applying new statistical approaches to best characterize complex change patterns.
Research Highlights.
We examined change patterns over cognitive behavioral group therapy for panic.
Individuals completed a measure of panic at every session and six months later.
Change patterns predicted level of panic symptoms six months post-treatment.
Acknowledgments
The authors would like to thank Professor John Nesselroade and the members of the Teachman Program for Anxiety Cognition and Treatment (PACT) Lab for their insightful comments and suggestions. The authors would also like to thank the research assistants, clinical evaluators, and therapists that assisted with this study. This research was supported by NIMH R03PA03039 and NIA R01AG033033 grants to Bethany Teachman.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Note, Clerkin et al. used the same dataset reported here.
The materials reported here are part of a larger study assessing a range of cognitive biases in panic disorder. For a complete listing of measures, please contact the third author.
The fit of each cluster is defined by the sum of squared differences of the observations from the cluster centers (i.e., the cluster means), where better fit is indicated by a number closer to zero. Subsequently, the fit of each model is defined as the sum of the fits for each cluster within the model. Any model with more clusters necessarily fits better than a model with fewer clusters, but there are diminishing returns of model fit as the number of clusters increases.
This R2 was obtained as the proportion of reduction in the total sums of squares relative to the total sums of squares. The total sums of squares for the data was calculated as the sum of the total sums of squares for each time point; i.e., the sum of the sum of squared differences from the mean at each time point. The sums of squares for the model was calculated as the sum of the within-cluster sums of squares; i.e., the sum of squared differences of each observation from its corresponding cluster center. The R2 was the difference between the total sums of squares and the model sums of squares as a proportion of the total sums of squares: (SStotal-SSmodel) / SStotal. This is in exact correspondence with the definition of R2 as the proportional reduction in error (e.g., Maxwell & Delaney, 2003, p. 104).
Other authors have used the term “early improvement” (Lambert et al., 2009; Lutz, Stulz, & Köck, 2009) to refer to gains made early in treatment.
Note that these p-values are adjusted for multiple comparisons, and are slightly larger than the p-values that correspond to the t-values reported with their degrees of freedom.
Note, nine people were excluded from this analysis due to missing follow-up data, reducing cluster sizes to n = 3 for Cluster 1 (Initial Unstable Drop cluster), n = 9 for Cluster 2 (Oscillating cluster), and n = 15 for Cluster 3 (Sudden Gain cluster). Note that this suggests that participants with higher panic symptom severity scores were less likely to provide data at follow-up. The three clusters for the 27 participants with follow-up data are shown in Figure 1 by dashed lines. Note that the trajectory profile of the Initial Unstable Drop cluster changes somewhat when those participants without follow-up data are excluded. However, the change is a shift in mean symptom level, rather than a change in pattern, so it is not discussed in detail because it does not alter our conclusions about patterns of change in this specific sample, the primary focus of this paper.
Note that this F-test and the following one are tests of the null hypothesis that data follow the simpler of two proposed nested regression models. Rejection of the null hypothesis indicates that the data do not follow the simpler model. This is directly analogous to the likelihood ratio test for structural equation models and is an ideal way to compare two or more nested models (Chambers & Hastie, 1992).
References
- Aaronson CJ, Shear MK, Goetz RR, Allen LB, Barlow DH, White KS, Gorman JM. Predictors and time course of response among panic disorder patients treated with cognitive-behavioral treatment. Journal of Clinical Psychiatry. 2008;69:418–424. doi: 10.4088/jcp.v69n0312. [DOI] [PubMed] [Google Scholar]
- Barlow DH, Craske MG. Mastery of our Anxiety and Panic-II. Albany, NY: Graywind; 1994. [Google Scholar]
- Beck AT, Steer RA, Brown GK. Beck Depression Inventory-II Manual. San Antonio, TX: The Psychological Corporation; 1996. [Google Scholar]
- Casey LM, Newcombe PA, Oei TPS. Cognitive mediation of panic severity: The role of catastrophic misinterpretation of bodily sensations and panic self-efficacy. Cognitive Therapy and Research. 2005;29:187–200. [Google Scholar]
- Cattell RB. The scree test for the number of factors. Multivariable Behavior Research. 1966;1:245–276. doi: 10.1207/s15327906mbr0102_10. [DOI] [PubMed] [Google Scholar]
- Chambers JM, Hastie TJ. Statistical Models in S. Boca Raton, FL: Chapman & Hall/CRC; 1992. [Google Scholar]
- Clerkin EM, Teachman BA, Smith-Janik SB. Sudden gains in group cognitive-behavioral therapy for panic disorder. Behaviour Research and Therapy. 2008;46:1244–1250. doi: 10.1016/j.brat.2008.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. A power primer. Psychological Bulletin. 1992;112:155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Cox BJ, Swinson RP, Shaw BF. Value of the Fear Questionnaire in differentiating agoraphobia and social phobia. British Journal of Psychiatry. 1991;159:842–845. doi: 10.1192/bjp.159.6.842. [DOI] [PubMed] [Google Scholar]
- Cuijpers P, van Lier PAC, van Straten A, Donker M. Examining differential effects of psychological treatment of depressive disorder: An application of trajectory analyses. Journal of Affective Disorders. 2005;89:127–146. doi: 10.1016/j.jad.2005.09.001. [DOI] [PubMed] [Google Scholar]
- Dolnicar S. A Review of unquestioned standards in using cluster analysis for data-driven market segmentation. CD Conference Proceedings of the Australian and New Zealand Marketing Academy Conference 2002, (ANZMAC 2002); Melbourne: Deakin University; 2002. Dec 2–4, [Google Scholar]
- Everitt BS, Landau S, Leese M. Cluster Analysis. Fourth ed. Hoboken, NJ: Wiley; 2009. [Google Scholar]
- First MB, Spitzer RL, Gibbon M, Williams JBW. Structured clinical interview for DSM-IV Axis I disorders. Washington, DC: American Psychiatric Association; 1995. [Google Scholar]
- Forgy EW. Cluster analysis of multivariate data: Efficiency versus interpretability of classifications. Biometrics. 1965;21:768–769. [Google Scholar]
- Gould RA, Otto MW, Pollack MH. A meta-analysis of treatment outcome for panic disorder. Clinical Psychology Review. 1995;15:819–844. [Google Scholar]
- Hanish LD, Tolan PH. Patterns of change in family-based aggression prevention. Journal of Marital and Family Therapy. 2001;27(2):213–226. doi: 10.1111/j.1752-0606.2001.tb01158.x. [DOI] [PubMed] [Google Scholar]
- Hofmann SG, Schulz SM, Meuret AE, Moscovitch DA, Suvak M. Sudden gains during therapy of social phobia. Journal of Consulting and Clinical Psychology. 2006;74:687–697. doi: 10.1037/0022-006X.74.4.687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson NS, Truax P. Clinical significance: A statistical approach to defining meaningful change in psychotherapy research. Journal of Consulting and Clinical Psychology. 1991;59:12–19. doi: 10.1037//0022-006x.59.1.12. [DOI] [PubMed] [Google Scholar]
- Krause MS, Howard KI, Lutz W. Exploring individual change. Journal of Consulting and Clinical Psychology. 1998;66:838–845. doi: 10.1037//0022-006x.66.5.838. [DOI] [PubMed] [Google Scholar]
- Lambert MJ, Ogles BM. The efficacy and effectiveness of psychotherapy. In: Lambert MJ, editor. Bergin and Garfield’s handbook of psychotherapy and behavior change. 5th ed. New York: Wiley; 2004. pp. 139–193. [Google Scholar]
- Lambert M, Schimmelmann BG, Schacht A, Karow A, Wagner T, Wehmeier PM, Naber D. Long-term patterns of subjective wellbeing in schizophrenia: Cluster, predictors of cluster affiliation, and their relation to recovery criteria in 2842 patients followed over 3 years. Schizophrenia Research. 2009;107:165–172. doi: 10.1016/j.schres.2008.08.035. [DOI] [PubMed] [Google Scholar]
- Lipkovich IA, Houston JP, Ahl J. Identifying patterns in treatment response profiles in acute bipolar mania: A cluster analysis approach. Article 65. BMC Psychiatry. 2008;8 doi: 10.1186/1471-244X-8-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutz W, Stulz N, KÖck K. Patterns of early change and their relationship to outcome and follow-up among patients with major depressive disorders. Journal of Affective Disorders. 2009;118:60–68. doi: 10.1016/j.jad.2009.01.019. [DOI] [PubMed] [Google Scholar]
- Marks IM, Mathews AM. Brief standard self-rating for phobic patients. Behaviour Research and Therapy. 1979;17:263–267. doi: 10.1016/0005-7967(79)90041-x. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Delaney HD. Designing experiements and analyzing data: A model comparison perspective. Mahwah, NJ: Lawrence Erlbaum; 2003. [Google Scholar]
- Meijering E. A chronology of interpolation: From ancient astronomy to modern signal and image processing. Proceedings of the IEEE. 2002;90:319–342. [Google Scholar]
- Mooi E, Sarstedt M. A Concise Guide to Market Research. Berlin, Germany: Springer-Verlag; 2011. [Google Scholar]
- Öst LG. Applied relacation vs. progressive relaxation in the treatment of panic disorder. Behaviour Research and Therapy. 1988;26:13–22. doi: 10.1016/0005-7967(88)90029-0. [DOI] [PubMed] [Google Scholar]
- Otto MW, Pollack MH, Penava SJ, Zucker BG. Group cognitive-behavior therapy for patients failing to respond to pharmacology for panic disorder: a clinical case series. Behaviour Research and Therapy. 1999;37:763–770. doi: 10.1016/s0005-7967(98)00176-4. [DOI] [PubMed] [Google Scholar]
- Penava SJ, Otto MW, Maki KM, Pollack MH. Rate of improvement during cognitive-behavioral group treatment for panic disorder. Behaviour Research and Therapy. 1998;36:665–673. doi: 10.1016/s0005-7967(98)00035-7. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R Foundation for Statistical Computing. Vienna, Austria: 2011. R: A language and environment for statistical computing. ISBN 3-900051-07-0, URL http://www.R-project.org/. [Google Scholar]
- Ramnero J, Öst L. Prediction of outcome in the behavioural treatment of panic disorder with agoraphobia. Cognitive Behaviour Therapy. 2004;33:176–180. doi: 10.1080/16506070410031691. [DOI] [PubMed] [Google Scholar]
- Reiss S, Peterson RA, Gursky DM, McNally RJ. Anxiety sensitivity, anxiety frequency and the prediction of fearfulness. Behaviour Research and Therapy. 1986;24:1–8. doi: 10.1016/0005-7967(86)90143-9. [DOI] [PubMed] [Google Scholar]
- Shear MK, Brown TA, Barlow DH, Money R, Sholomskas DE, Woods SW, Papp LA. Multicenter collaborative Panic Disorder Severity Scale. American Journal of Psychiatry. 1997;154:1571–1575. doi: 10.1176/ajp.154.11.1571. [DOI] [PubMed] [Google Scholar]
- Stanley MA, Beck JG, Averill PM, Baldwin LE, Deagle EA, Stadler JG. Patterns of change during cognitive behavioral treatment for panic disorder. The Journal of Nervous and Mental Disease. 1996;184:567–572. doi: 10.1097/00005053-199609000-00009. [DOI] [PubMed] [Google Scholar]
- Steketee G, Shapiro LJ. Predicting behavioral treatment outcome for agoraphobia and obsessive compulsive disorder. Clinical Psychology Review. 1995;15:317–346. [Google Scholar]
- Stulz N, Lutz W. Multidimensional patterns of change in outpatient psychotherapy: The phase model revisited. Journal of Clinical Psychology. 2007;63:817–833. doi: 10.1002/jclp.20397. [DOI] [PubMed] [Google Scholar]
- Tang TZ, deRubeis RJ. Sudden gains and critical sessions in cognitive-behavioral therapy for depression. Journal of Consulting and Clinical Psychology. 1999;67:894–904. doi: 10.1037//0022-006x.67.6.894. [DOI] [PubMed] [Google Scholar]
- Teachman BA. Information processing and anxiety sensitivity: Cognitive vulnerability to panic reflected in interpretation and memory biases. Cognitive Therapy and Research. 2005;29:479–499. [Google Scholar]
- Teachman BA, Marker CD, Smith-Janik SB. Automatic associations and panic disorder: Trajectories of change over the course of treatment. Journal of Consulting and Clinical Psychology. 2008;76:988–1002. doi: 10.1037/a0013113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teachman BA, Smith-Janik SB, Saporito J. Information processing biases and panic disorder: relationships among cognitive and symptom measures. Behaviour Research and Therapy. 2007;45:1791–1811. doi: 10.1016/j.brat.2007.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telch MJ, Lucas JA, Schmidt NB, Hanna HH, Jaimez TL, Lucas RA. Group cognitive-behavioral treatment of panic disorder. Behavior Research and Therapy. 1993;31:279–287. doi: 10.1016/0005-7967(93)90026-q. [DOI] [PubMed] [Google Scholar]
- Telch MJ, Shermis MD, Lucas JA. Anxiety sensitivity: Unitary personality trait or domain-specific appraisals? Journal of Anxiety Disorders. 1989;3:25–32. [Google Scholar]
- Woodman CL, Noyes R, Black DW, Schlosser S, Yagla SJ. A 5-year follow-up study of generalized anxiety disorder and panic disorder. Journal of Nervous and Mental Disease. 1999;187:3–9. doi: 10.1097/00005053-199901000-00002. [DOI] [PubMed] [Google Scholar]