Abstract
Many cell phenomena that involve shape changes are affected by the intrinsic deformability of the plasma membrane. Far from being a passive participant, the plasma membrane is now known to physically, as well as biochemically, influence cell processes ranging from vesicle trafficking to actin assembly. Here we review current understanding of how changes in plasma membrane tension regulate cell shape and movement as well as how cells sense plasma membrane tension.
Keywords: membrane tension, motility, cell shape
One way that cells interact with the world around them is biochemically, for example by triggering intracellular signaling cascades upon binding of soluble extracellular ligands. More recently, it has become clear that physical interactions are also an important currency of information transfer in cells and tissues ([1,2]; and reviewed in [3]). In particular, tension in the plasma membrane has been shown to regulate many cell behaviors, including vesicle trafficking [4] and cell motility [5,6]. The plasma membrane (PM) is often described by the fluid mosaic model [7], which characterizes it as a two-dimensional continuous fluid bilayer of lipids with freely diffusing embedded proteins. In this paradigm, the bilayer is considered a uniform semipermeable barrier that serves as a passive matrix for membrane proteins. However, this model is incomplete; lipids are now known to have a much more active role in regulating membrane structure and biological function ([8,9,10] and reviewed in [11]), and the mechanical properties of the PM need to be included for a complete picture.
Mechanically, membranes have a low shear modulus (a result of the fluid nature of the lipid bilayer; 4-10 10-3 N/m [12,13,14]), a high elastic modulus (due to the small stretch in bilayers; 103 N/m2 [15,16]), a variable viscosity (which depends on membrane composition; 0.36-2.1 10-3 Pa s for an erythrocyte [16]), and a bending stiffness strongly influenced by membrane proteins and cytoskeletal elements (10-19 Nm [17,18,19]). Membrane tension is related to the force needed to deform a membrane. Historically, the term membrane tension has been applied to define different concepts, and this has lead to confusion in the literature. Initially membrane tension was measured in lipid vesicles (Box 1) in which the force needed to stretch the membrane is the in-plane membrane tension (Tm, N/m). In cells, the force needed to deform the PM is greater than that for a pure lipid vesicle due to contributions from membrane proteins and membrane-to-cortex attachments (MCA)(γ, N/m), which link the membrane to the underlying cortex and also resist membrane deformation. Thus, PM tension (T), also known as apparent membrane tension or effective membrane tension, is the sum of Tm and γ (Box 2).
Research in recent decades has established the importance of PM tension as a physical regulator of cell motility and morphology [6,20,21,22,23], but the mechanism(s) of tension sensation and how membrane tension is integrated in the cell's mechanical properties is unknown. We will focus on how PM tension affects and is affected by other cellular processes and will outline possible mechanisms for membrane tension sensation.
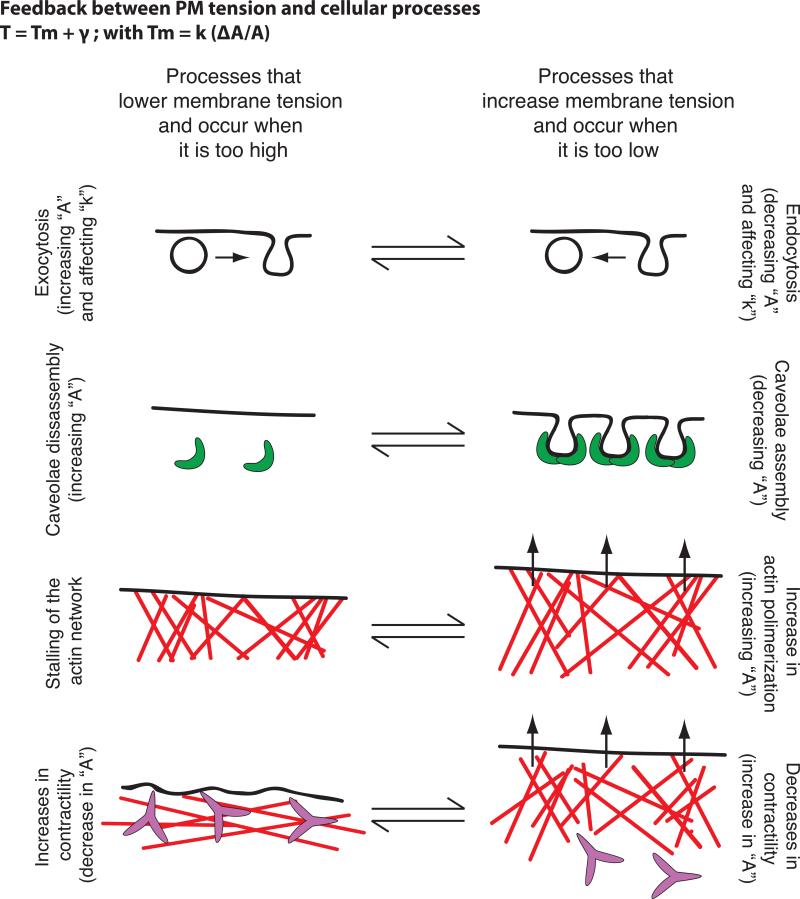
Feedback between plasma membrane tension and cellular processes
Some studies point to PM tension being a constant parameter within a given cell type [24]. However, it is unclear if cells have a preferred “set point” for PM tension, and if so how cells measure their PM tension. Moreover, in cells, biological membranes are active in the sense that they are constantly maintained out of equilibrium by cellular processes that contribute to changes in PM area, composition or MCA protein activity. This adds complexity but also gives the cell multiple routes of adjustment. Several cellular processes affect and are affected by PM tension (Fig. 1):
Figure 1. Feedback between plasma membrane tension and cellular processes.
Examples of cellular processes that occur when PM tension is too high and that lead to its reduction (left) or that occur when PM tension is too low and lead to its increase (right) — vesicle trafficking, caveolae formation, actin polymerization and changes in myosin based. In brackets we comment on the parameters of Eq. 1 and 2 in Box 2 that are predicted to change in each of these processes.
Exocytosis and clathrin mediated endocytosis
PM tension regulates the balance between exocytosis and endocytosis in a number of systems; exocytosis (which is stimulated by high membrane tension) acts to decrease PM tension, whereas endocytosis (which is stimulated by low membrane tension) increases it ([25] and reviewed in [4,24,26]). These opposing effects of vesicle trafficking could enable cells to keep tension close to a set point [27]. When the PM reservoir is reduced following cell spreading, there is a two-fold increase in PM tension followed by activation of exocytosis and myosin-based contraction [20]. The rate of spreading and the time point at which exocytosis and myosin contraction occur are highly dependent on PM tension. These data implicate tension in coordinating membrane trafficking, acto-myosin contraction, and PM area change. More recently, MCA has been shown to determine the actin dependence of clathrin-coat assembly [21]. Clathrin-mediated endocytosis is independent of actin dynamics in many circumstances but requires actin polymerization in others. On the apical surface of polarized cells where MCA is higher [21,28] or following cell swelling, actin engagement is necessary to convert a coated pit into a vesicle [21].
Caveolae
Caveolae, invaginations of the PM that are formed by caveolins, are physiological membrane reservoirs that have recently been shown to enable cells to accommodate sudden changes in PM tension [29,30]. Increases in tension through cell stretching or hypo-osmotic shock induce disassembly of caveola, while recovering iso-osmolarity leads to complete caveolae reassembly [29]. How caveolae buffer PM tension is not yet fully understood, as the amount of released area upon membrane tension surge is very small (approximately 0.3%) [29].
Actin network assembly
To generate lamellipodia-like protrusions during cell crawling, growing actin filaments must generate sufficient local force to displace the PM [5,20,23]. Indeed, actin-based protrusion can lead to an increase in in-plane membrane tension as the force of polymerization unfolds wrinkles in the membrane during cell spreading [20]. Moreover, an increase in PM tension constrains the spread of the existing leading edge and prevents the formation of secondary fronts in chemotactic cells such as neutrophils [6]. In these cells, increasing cell tension by micropipette aspiration is sufficient to act as a long-range inhibitor of the signals that promote actin assembly at the leading edge. Conversely, the reduction of PM tension through hyper-osmotic shock produces global activation of leading edge signals [6]. Because the front is the likely source of tension, any fluctuation in front size is immediately balanced by compensatory changes in tension levels, providing a possible mechanism of homeostasis [5,6].
Models of the plasma membrane as a global mechanical regulator
Several models suggest a role of PM tension as a global mechanical regulator that coordinates cell protrusion and retraction. PM tension has been suggested to optimize motility by streamlining filament polymerization in the direction of movement [22]. A model of actin network polymerization in an inextensible membrane bag can quantitatively predict both cell shape and speed and recapitulate the natural phenotypic variability in a large population of motile epithelial fish keratocytes [23]. If PM tension is assumed to be spatially homogenous at all points along the cell boundary, the force per filament is inversely proportional to the local filament density. Therefore at the center of the leading edge, the membrane resistance per filament is small, allowing filaments to grow rapidly and generate protrusion. As filament density gradually decreases towards the cell sides and the cell rear, the forces per filament caused by PM tension increase until polymerization is stalled and the actin network disassembles [23]. More recently, [31] hypothesize a simple disassembly clock mechanism in which the rear position of a lamellipodium is determined by where the actin network has disassembled enough for membrane tension to crush the actin network and haul it forward. Finally, PM tension could also limit bleb expansion [32], but direct experimental evidence is still missing.
Role of cytoskeletal- vs. plasma membrane- tension
Both cytoskeletal tension (also referred to as contractility) and membrane tension are capable of transmitting forces over long range to spatially and temporally regulates cell polarity and cell migration [23,28,33]. Membrane tension antagonizes actin based-protrusion by being the barrier growing actin filaments fight in order to protrude the membrane [23] and contractility opposes protrusion by pulling actin filaments away from the membrane [34]. The relative contribution of cytoskeletal versus membrane tension is likely to vary in different cell types:
In Dictyostelium, contractility plays an important role in restricting signals to the leading edge. Upon deletion of myosin 2, cytoskeletal tension is reduced dramatically [35] and there is an increase in lateral pseudopod number [36] and in Ras activation [37]. These data support a predominant role of contractility in Dictyostelium polarity, but whether PM tension also plays a significant role remains unknown.
In fibroblasts, a combination of cytoskeletal and membrane tension limit cell protrusion. Increasing membrane tension by hypo-osmotic shock halts spreading, whereas decreasing it by adding lipids increases the rate of cell spreading, enhances lamellipodial extension, and transiently causes uniform spreading [5]. On the other hand, decreasing contractility through myosin inhibition causes faster spreading and a larger final spread area [34] and increasing it with biaxial cellular stretching downregulates Rac activity [38].
In fish keratocytes, decreasing contractility through myosin inhibition does not destroy keratocyte polarity and only slightly reduces migration speed, suggesting a predominant role for PM tension in this system [23,39].
In neutrophils, membrane tension also appears to be the dominant inhibitory mechanism for cell polarization. Membrane tension increases during neutrophil protrusion and decreasing membrane tension through hypo-osmotic shock results in the expansion of leading-edge signals and a loss of polarity [6]. On the other hand, decreasing cytoskeletal tension with myosin inhibition has no effect on leading-edge signals [6].
To what extent myosin inhibition, osmotic shock, or other tension perturbations affect both membrane tension and contractility remains unknown. Moreover, it is likely that cytoskeletal and membrane tension are interdependent, myosin 2 activity is required to reduce PM tension at the end of spreading [20] and its inhibition increases PM tension in resting neutrophils [6].
Finally, it is important to note that these conclusions (along with most other investigations of cytoskeletal tension) rely on myosin inhibition, but it is also possible that filament disassembly-based changes in cytoskeletal tension could contribute to cell polarity and movement in the absence of myosin activity.
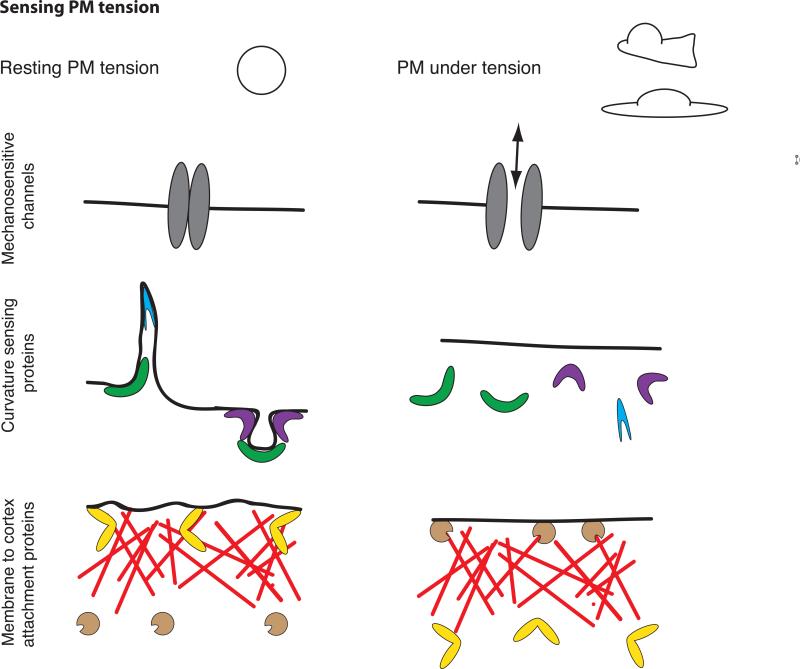
Sensing plasma membrane tension
The molecular mechanisms by which cells sense and respond to mechanical signals are not fully understood. There are several mechanisms by which a cell could read PM tension (Fig. 2):
Figure 2. Sensing membrane tension.
PM in a resting cell (left) or following an increase in PM tension, as observed during cell protrusion or cell spreading (right). PM tension could be sensed by the opening of stretch activated ion channels (top), the dissociation of curvature-sensitive membrane-binding proteins (middle), or changes in the activity of membrane-to-cortex attachment proteins (bottom).
Mechanosensitive channels
Stretch activated ion channels are the best understood sensors of PM tension. For these channels, changes in PM tension affect the probability of channel opening. Some examples are found in prokaryotes (the ion channel MscL) [40], primary osteoblasts [41], and specialized sensory cells [42]. Mechanosensitive channels can sense membrane tension over a wide dynamic range. The magnitude of tension sensing varies from signals barely above the thermal noise in hair cells [42] to a set point for activation near the lytic tension of the bilayer for MscL [40].
Perturbation of the ion gradients across the PM and the influx/efflux of water can also dramatically increase/decrease PM tension. Osmotic changes have been used to manipulate PM tension [6,20,21,29], but whether cells use this mechanism to change membrane tension remains to be seen.
Curvature sensing proteins
A number of proteins have domains (like BAR- or ALPS- domains) that associate with curved membranes, either because they are sensitive to curvature or because they induce curvature (or both) (reviewed in [43]). High PM tension could reduce the binding of I-BAR proteins by limiting the membrane bending that is necessary for their binding to the membrane [44]. In this manner, the many GEFs and GAPs with curvature sensing domains could regulate GTPases in a tension-dependent manner [45]. Indeed, ArfGAP1, which contains an ALPS domain, has a preference for positively curved membranes (like those generated during vesicle formation) or areas with disrupted packing of lipids. ArfGAP1 preferentially induces hydrolysis of GTP of Arf in these regions [46,47]. High curvature could be both sensed and generated at the leading edge through the action of individual proteins such as amphiphysin I (BAR-domain containing effector in clathrin-mediated endocytosis), whose density on the membrane determines whether it senses or induces curvature [48]. Additionally, the activation of N-WASP-mediated actin polymerization by proteins containing an F-BAR domain depends on membrane curvature [49]. This suggests the possibility of feedback between curvature and actin dynamics [50]: curvature-sensing/inducing proteins could stimulate actin polymerization in a curvature-dependent manner, and actin polymerization could decrease curvature to maintain homeostasis.
Membrane to cortex attachment proteins
MCA proteins, which provide links between the PM and the actin cytoskeleton, could also sense PM tension. External forces have been found to modulate the activity of some MCA proteins. Candidates include filamin [51] and the myosin 1 family of single-headed and membrane-associated myosins, both of which can simultaneously interact with the cytoskeleton and the PM. Filamin A is a central mechanotransduction element of the cytoskeleton that interacts with FilGAP, a GTPase activating protein specific for Rac; the loss of this interaction due to high stresses increases Rac activation and actin polymerization [52]. Myosin 1c is an MCA protein that dynamically provides tension to sensitize mechanosensitive ion channels responsible for hearing [53]. Myosin 1b dramatically alters its motile properties in response to external force; the rate of myosin 1b detachment from actin decreases 75-fold under forces of 2 piconewtons or less [54]). This suggests a potential mechanism that remains to be tested: if sensation of PM tension decreases MCA protein activity, it could also generate a homeostatic feedback loop.
Global vs. local membrane tension
Asymmetries in contractility are sufficient to polarize both protrusion and adhesion. [55]. Are there also inhomogeneities in membrane tension, and if so are they functionally relevant? Membrane lipids flow like a liquid and can almost instantaneously equilibrate in-plane tension across the cell [39]. The lack of large-scale flows has been interpreted as indicating uniform PM tension in several cell lines, including keratocytes [23]. However, a lack of flow could also be achieved by the presence of local barriers that limit lipid movement, which are known to exist, at least over short timescales [56]. Interestingly, PM tension is inhomogeneous in epithelia and neurons ([21,24,29,30] and reviewed in [4]). For these cells it was observed that in-plane tension is homogenous across a cell and only the MCA component is different in different membrane compartments. Is this always the case? A septin ring has been observed in T lymphocyte migration [57]; if the ring provides a lipid diffusion barrier, it could enable transient differences in PM tension in immune cells during motility. MCA and in-plane tension can be distinguished by different means (Box 1) and future studies should assess the sources and prevalence of PM tension inhomogeneity. It is important to note that even uniform membrane tension could orchestrate the initiation and maintenance of cell polarity if it opposes cytoskeletal protrusions that are locally regulated (in which protrusions grow until they generate enough tension that enables some protrusions to survive and all others to be extinguished).
Future directions
There are many open questions regarding membrane tension. Do cells have a set point for PM tension? If so, how is it maintained? Does membrane tension regulation differ for isolated cells versus cells in a tissue? How do motile cells interpret changes in PM tension? How do cytoskeletal tension and PM tension interrelate? Further research will be necessary to determine which signaling currencies are altered by changes in PM tension and to clarify how membrane tension contributes and is affected by endocytosis and exocytosis, actin dynamics, and myosin activity.
Box 1: Techniques to measure and manipulate membrane tension.
Measuring membrane tension
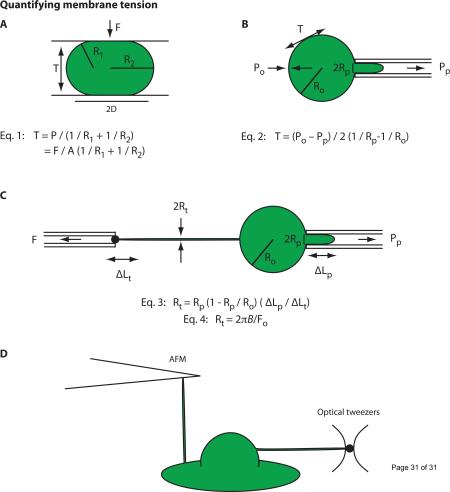
Experiments to determine mechanical properties of biological membranes began in the 1930s using sea urchin eggs and red blood cells [58,59]. Since then new higher resolution techniques have been developed. Here we list the most commonly used approaches for measuring membrane tension:
→ Compression of the cell with two plates (Fig. IA) and micropipette aspiration (Fig. IB) have been extensively used for studying the mechanical properties of membranes in lipid vesicles, urchin eggs, and red blood cells [15,18,58,59,60,61]. However, these techniques are only applicable to lipid vesicles or suspension cells with simple morphologies and cannot be used for cells with complex morphologies such as neurons or neutrophils. Moreover, in cells, isolating the contribution of PM tension to these measurements is complicated by the fact that a significant portion of the measured forces can be due to deformations of the cytoskeleton, in particular the actin cortex that lies immediately under the PM.
→ Tethers (which lack a continuous cytoskeleton) have been studied to measure PM tension. Initially these experiments were performed using a micropipette to hold cells or lipid vesicles and using a second pipet to extract a membrane tether (Fig. IC) [62]. More recently AFM cantilevers, optical tweezers and magnetic tweezers have enabled higher resolution measurements of PM tension (Fig. ID) [63,64,65]. Read box 2 for an in depth description of how tethers can be used to measure membrane tension.
→ A FRET based biosensor was recently developed for assaying tension in the cytoskeleton and at sites of adhesion [66]. Although the field currently lacks comparable imaging-based sensors for membrane tension, such a tool would enable less invasive analysis of the spatial and temporal dynamics of PM tension in living cells. Moreover, intracellular organelles are not accessible for tether experiments and such technology would allow us to answer if the plasma membrane the sole organelle that can act as a mechanical sensor.
Manipulating membrane tension
→ Vesicle fusion, lipid addition, and changes in osmolarity have been used to manipulate in-plane tension [6,67], but none of these techniques are quantitative unless they are combined with simultaneous measurements of tension such as tether pulling. Moreover, how much those techniques affect cytoskeletal components is unknown. Alternatively, pulling multiple tethers with an AFM [68] can be used to simultaneously measure and manipulate membrane tension.
Box 2: Quantifying membrane tension and MCA from tethers.
The mathematical relation between tether force (Fo) and tension is known for lipid vesicles [15,61,69]. In cells, the tether force is generated by a combination of (i) in-plane tension of the lipid-bilayer (Tm), (ii) membrane-bending stiffness (B), and (iii) membrane-to-cortex attachments (MCA) (γ) [17,70]. The in-plane tension and cytoskeleton adhesion terms are difficult to separate and are therefore combined into a single term (T) which is known by multiple names: PM tension, apparent membrane tension, or effective membrane tension [17]:
| (1) |
(i) In-plane membrane tension (Tm) is the result of the membrane being an inelastic fluid that equilibrates stresses within milliseconds [39]:
| (2) |
k = elastic area stretch modulus, which depends on lipid composition, and A = cell surface area.
Tm and k completely characterize the differential equation of state for planar surfaces. However, when the surface is not a plane (e.g., when it is rippled due to thermally-driven fluctuations), measurements of these parameters include the entropic elasticity of the membrane.
Tm appears to be uniform throughout the whole cell, even across the junctions of epithelial cells [27], and on cell blebs in which the membrane separates from acto-myosin cortex [28,72]. (ii) The membrane bending stiffness (B) relates to the force needed to bend the membrane for a given radius of curvature. It has been experimentally measured for tethers in lipid vesicles. It is approximately 10-19 Nm for a typical lipid bilayer, red cell and neutrophil membrane [17,18,19]. It can also be calculated from measurements of tether radius as a function of the static force:
| (3) |
(iii) The membrane-to-cortex attachment force can be expressed as adhesion energy per unit area (γ). It results from a variety of MCA proteins that connect the actin cytoskeleton and the plasma membrane [73] and non-specific binding of the membrane-to-cortex components. It was long believed that MCA was the result of only specific protein-protein interactions, but some experimental findings suggest otherwise. For instance, the fact that tether forces are rapidly reversible with no hysteresis has been used to favor a continuum model with non-specific binding of the membrane-to-cortex components [17,24].
To separate MCA and in-plane tension, we can measure Fb, the tether force in the absence of MCA contribution. This can be experimentally achieved by performing tether measurements on nascent blebs, which are locally devoid of cytoskeletal support, or in cells in which the cytoskeleton has been depolymerized. Under these conditions, the adhesion term (γ) equals 0 [28], and the in-plane tension is given by:
| (4) |
The adhesion energy can then be calculated using eqs. 1 and 4 if we assume that the in-plane tension is constant over smooth regions of the cell surface:
| (5) |
A recent model has related pulling force–velocity profiles to the density of cross-linkers and the lipid bilayer viscosity [74], providing a possible means of discriminating the two PM tension components in a wider range of cellular contexts.
Experimentally, the tether force in cytoskeletal-unsupported region is typically less than half of that on regions supported by the cytoskeleton (Fb <0.5 Fo). Applying this inequality to equation 5, we see that over 75% of the PM tension term is the result of MCA. In-plane tension can increase markedly with hypotonic swelling [29,75]. However, under normal conditions, large changes in PM tension are thought to primarily reflect changes in MCA [76].
Figure I: Quantifying membrane tension. (A) The spherical cell or lipid vesicle is compressed with known force (F) between two parallel plates. R1 and R2 are the radii of the principal curvatures of the surface. The internal pressure P (P = F/A) is the applied force F divided by the contacted area (A = πD2) between the plate and the cell or vesicle. This pressure is in equilibrium with the surface tension T (Eq. 1). (B) The membrane of a spherical cell or lipid vesicle is deformed by a micropipette. Pp is the pressure in the pipet, and Po is the pressure in the reservoir. Ro and Rp are the radii of the cell or vesicle and the pipet. The resulting isotropic stress in the membrane is the surface tension T, and is determined by Eq. 2. (C) Initially tethers were formed using a micropipette to hold samples with a suction pressure. A bead in a second pipet was used to extract a membrane tether with force F. Rp and Ro and is the radii of the pipet and cell or vesicle. The tether radius Rt can be calculated from the change in the length of membrane projection in the pipet (ΔLp) caused by the tether length change (ΔLt) as seen in Eq. 3 or can be derived from the membrane bending stiffness / static tether force relationship as seen in Eq. 4 [17] for cells with simple morphologies, such as red blood cells or lipid vesicles. (D) Atomic force microscopy cantilevers and optical tweezers provide higher-resolution measurements of PM tension [63,64,77,78]. Read box 2 for an in depth description of how tethers can be used to measure membrane tension
Acknowledgments
We apologize for not being able to cite all contributions because of space restrictions, and acknowledge the many scientists who contributed to the field of PM tension. We thank Ewa Paluch, Christer S. Ejsing, Martin Bergert and Patricia Bassereau for a critical reading of the manuscript. This work was supported by NIH GM084040 and NIH GM074751.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Weber GF, Bjerke MA, DeSimone DW. A mechanoresponsive cadherin-keratin complex directs polarized protrusive behavior and collective cell migration. Developmental Cell. 2012;22:104–115. doi: 10.1016/j.devcel.2011.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yonemura S, Wada Y, Watanabe T, Nagafuchi A, Shibata M. alpha-Catenin as a tension transducer that induces adherens junction development. Nature Cell Biology. 2010;12:533–542. doi: 10.1038/ncb2055. [DOI] [PubMed] [Google Scholar]
- 3.Yu H, Mouw JK, Weaver VM. Forcing form and function: biomechanical regulation of tumor evolution. Trends Cell Biology. 2011;21:47–56. doi: 10.1016/j.tcb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Apodaca G. Modulation of membrane traffic by mechanical stimuli. Am J Physiol Renal Physiol. 2002;282:F179–190. doi: 10.1152/ajprenal.2002.282.2.F179. [DOI] [PubMed] [Google Scholar]
- 5.Raucher D, Sheetz MP. Cell spreading and lamellipodial extension rate is regulated by membrane tension. The Journal of Cell Biology. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Houk AR, Jilkine A, Mejean CO, Boltyanskiy R, Dufresne ER, et al. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Singer S, Nicolson G. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
- 8.Hamill OP, Martinac B. Molecular basis of mechanotransduction in living cells. Physiol Rev. 2001;81:685–740. doi: 10.1152/physrev.2001.81.2.685. [DOI] [PubMed] [Google Scholar]
- 9.Helms J, Zurzolo C. Lipids as targeting signals: lipid rafts and intracellular trafficking. Traffic. 2004;5:247–254. doi: 10.1111/j.1600-0854.2004.0181.x. [DOI] [PubMed] [Google Scholar]
- 10.van Meer G, Sprong H. Membrane lipids and vesicular traffic. Current opinion in cell biology. 2004;16:373–378. doi: 10.1016/j.ceb.2004.06.004. [DOI] [PubMed] [Google Scholar]
- 11.Cao X, Surma MA, Simons K. Polarized sorting and trafficking in epithelial cells. Cell research. 2012;22:793–805. doi: 10.1038/cr.2012.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Evans E. New membrane concept applied to the analysis of fluid shear- and micropipette-deformed red blood cells. Biophysical Journal. 1973;13:941–954. doi: 10.1016/S0006-3495(73)86036-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Engelhardt H, Sackmann E. On the measurement of shear elastic moduli and viscosities of erythrocyte plasma membranes by transient deformation in high frequency electric fields. Biophysical Journal. 1988;54:495–508. doi: 10.1016/S0006-3495(88)82982-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hénon S, Lenormand G, Richert A, Gallet F. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophysical Journal. 1999;76:1145–1151. doi: 10.1016/S0006-3495(99)77279-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hochmuth R, Mohandas N, Blachshear P. Measurement of the elastic modulus for red cell membrane using a fluid mechanical technique. Biophysical Journal. 1973;13:747–762. doi: 10.1016/S0006-3495(73)86021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hochmuth R, Waugh R. Erythrocyte membrane elasticity and viscosity. Ann Rev Physiol. 1987;49:209–219. doi: 10.1146/annurev.ph.49.030187.001233. [DOI] [PubMed] [Google Scholar]
- 17.Hochmuth FM, Shao JY, Dai J, Sheetz MP. Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophysical Journal. 1996;70:358–369. doi: 10.1016/S0006-3495(96)79577-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bo L, Waugh RE. Determination of bilayer membrane bending stiffness by tether formation from giant, thin-walled vesicles. Biophysical Journal. 1989;55:509–517. doi: 10.1016/S0006-3495(89)82844-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shao J-Y, Xu J. A modified micropipette aspiration technique and its application to tether formation from human neutrophils. J Biomech Eng. 2002;124:388–396. doi: 10.1115/1.1486469. [DOI] [PubMed] [Google Scholar]
- 20.Gauthier NC, Fardin MA, Roca-Cusachs P, Sheetz MP. Temporary increase in plasma membrane tension coordinates the activation of exocytosis and contraction during cell spreading. Proceedings of the National Academy of Sciences. 2011;108:11467–11472. doi: 10.1073/pnas.1105845108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Boulant S, Kural C, Zeeh J-C, Ubelmann F, Kirchhausen T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nature Cell Biology. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Batchelder EL, Hollopeter G, Campillo C, Mezanges X, Jorgensen EM, et al. Membrane tension regulates motility by controlling lamellipodium organization. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:114429–114434. doi: 10.1073/pnas.1010481108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Keren K, Pincus Z, Allen G, Barnhart E, Marriott G, et al. Mechanism of shape determination in motile cells. Nature. 2008;453:475–480. doi: 10.1038/nature06952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dai J, Sheetz MP. Regulation of endocytosis, exocytosis, and shape by membrane tension. Cold Spring Harb Symp Quant Biol. 1995;60:567–571. doi: 10.1101/sqb.1995.060.01.060. [DOI] [PubMed] [Google Scholar]
- 25.Gauthier NC, Rossier OM, Mathur A, Hone JC, Sheetz MP. Plasma membrane area increases with spread area by exocytosis of a GPI-anchored protein compartment. Molecular Biology of the Cell. 2009;20:3261–3272. doi: 10.1091/mbc.E09-01-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sheetz MP. Glycoprotein motility and dynamic domains in fluid plasma membranes. Annu Rev Biophys Biomol Struct. 1993;22:417–431. doi: 10.1146/annurev.bb.22.060193.002221. [DOI] [PubMed] [Google Scholar]
- 27.Sheetz M. Cell control by membrane-cytoskeleton adhesion. Nature Reviews Molecular Cell Biology. 2001;2:392–396. doi: 10.1038/35073095. [DOI] [PubMed] [Google Scholar]
- 28.Dai J, Sheetz MP. Membrane tether formation from blebbing cells. Biophysical Journal. 1999;77:3363–3370. doi: 10.1016/S0006-3495(99)77168-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sinha B, Köster D, Ruez R, Gonnord P, Bastiani M, et al. Cells respond to mechanical stress by rapid disassembly of caveolae. Cell. 2011;144:402–413. doi: 10.1016/j.cell.2010.12.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gervásio OL, Phillips WD, Cole L, Allen DG. Caveolae respond to cell stretch and contribute to stretch-induced signaling. Journal of Cell Science. 2011;124:3581–3590. doi: 10.1242/jcs.084376. [DOI] [PubMed] [Google Scholar]
- 31.Ofer N, Mogilner A, Keren K. Actin disassembly clock determines shape and speed of lamellipodial fragments. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:20394–20399. doi: 10.1073/pnas.1105333108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tinevez J-Y, Schulze U, Salbreux G, Roensch J, Joanny J-F, et al. Role of cortical tension in bleb growth. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mayer M, Depken M, Bois JS, Jülicher F, Grill SW. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467:617–621. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- 34.Cai Y, Rossier O, Gauthier NC, Biais N, Fardin M-A, et al. Cytoskeletal coherence requires myosin-IIA contractility. Journal of Cell Science. 2010;123:413–423. doi: 10.1242/jcs.058297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pasternak C, Spudich J, Elson E. Capping of surface receptors and concomitant cortical tension are generated by conventional myosin. Nature. 1989;341:549–551. doi: 10.1038/341549a0. [DOI] [PubMed] [Google Scholar]
- 36.Wessels D, Soll D, Knecht D, Loomis W, Lozanne AD, et al. Cell motility and chemotaxis in Dictyostelium amebae lacking myosin heavy chain. Developmental Biology. 1988;128:164–177. doi: 10.1016/0012-1606(88)90279-5. [DOI] [PubMed] [Google Scholar]
- 37.Lee S, Shen Z, Robinson DN, Briggs S, Firtel RA. Involvement of the cytoskeleton in controlling leading-edge function during chemotaxis. Molecular Biology of the Cell. 2010;21:1810–1824. doi: 10.1091/mbc.E10-01-0009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Katsumi A, Milanini J, Kiosses WB, del Pozo MA, Kaunas R, et al. Effects of cell tension on the small GTPase Rac. The Journal of Cell Biology. 2002;158:153–164. doi: 10.1083/jcb.200201105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kozlov MM, Mogilner A. Model of polarization and bistability of cell fragments. Biophysical Journal. 2007;93:3811–3819. doi: 10.1529/biophysj.107.110411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sukharev S. Mechanosensitive channels in bacteria as membrane tension reporters. FASEB J. 1999;13:55–61. doi: 10.1096/fasebj.13.9001.s55. [DOI] [PubMed] [Google Scholar]
- 41.Charras GT, Williams BA, Sims SM, Horton MA. Estimating the sensitivity of mechanosensitive ion channels to membrane strain and tension. Biophysical Journal. 2004;87:2870–2884. doi: 10.1529/biophysj.104.040436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Denk W, Webb WW. Forward and reverse transduction at the limit of sensitivity studied by correlating electrical and mechanical fluctuations in frog saccular hair cells. Hearing Research. 1992;60:89–102. doi: 10.1016/0378-5955(92)90062-r. [DOI] [PubMed] [Google Scholar]
- 43.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nature Reviews Molecular Cell Biology. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 44.Zhao H, Pykäläinen A, Lappalainen P. I-BAR domain proteins: linking actin and plasma membrane dynamics. Current Opinion Cell Biology. 2011;23:14–21. doi: 10.1016/j.ceb.2010.10.005. [DOI] [PubMed] [Google Scholar]
- 45.Kreuk Bd, Nethe M, Fernandez-Borja M, Anthony E, Hensenbergen P, et al. The F-BAR domain protein PACSIN2 associates with Rac1 and regulates cell spreading and migration. Journal of Cell Science. 2011;124:2375–2388. doi: 10.1242/jcs.080630. [DOI] [PubMed] [Google Scholar]
- 46.Bigay J, Gounon P, Robineau S, Antonny B. Lipid packing sensed by ArfGAP1 couples COPI coat disassembly to membrane bilayer curvature. Nature. 2003;426:563–566. doi: 10.1038/nature02108. [DOI] [PubMed] [Google Scholar]
- 47.Ambroggio E, Sorre B, Bassereau P, Goud B, Manneville JB, et al. ArfGAP1 generates an Arf1 gradient on continuous lipid membranes displaying flat and curved regions. The EMBO journal. 2010;29:292–303. doi: 10.1038/emboj.2009.341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sorre B, Callan-Jones A, Manzi J, Goud B, Prost J, et al. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:173–178. doi: 10.1073/pnas.1103594108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Takano K, Takano K, Toyooka K, Suetsugu S. EFC/F-BAR proteins and the N-WASP-WIP complex induce membrane curvature-dependent actin polymerization. The EMBO Journal. 2008;27:2817–2828. doi: 10.1038/emboj.2008.216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Peleg B, Disanza A, Scita G, Gov N. Propagating cell-membrane waves driven by curved activators of actin polymerization. PLoS ONE. 2011;6:e18635. doi: 10.1371/journal.pone.0018635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tempel M, Goldmann WH, Dietrich C, Niggli V, Weber T, et al. Insertion of filamin into lipid membranes examined by calorimetry, the film balance technique, and lipid photolabeling. Biochemistry. 1994;33:12565–12572. doi: 10.1021/bi00208a006. [DOI] [PubMed] [Google Scholar]
- 52.Ehrlicher AJ, Nakamura F, Hartwig JH, Weitz DA, Stossel TP. Mechanical strain in actin networks regulates FilGAP and integrin binding to filamin A. Nature. 2011;478:260–263. doi: 10.1038/nature10430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Holt J, Gillespie S, Provance D, Shah K, Shokat K, et al. A chemical-genetic strategy implicates myosin-1c in adaptation by hair cells. Cell. 2002;108:371–381. doi: 10.1016/s0092-8674(02)00629-3. [DOI] [PubMed] [Google Scholar]
- 54.Laakso JM, Lewis JH, Shuman H, Ostap EM. Myosin I can act as a molecular force sensor. Science. 2008;321:133–136. doi: 10.1126/science.1159419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wittmann T, Waterman-Storer CM. Cell motility: can Rho GTPases and microtubules point the way? Journal of Cell Science. 2001;114:3795–3803. doi: 10.1242/jcs.114.21.3795. [DOI] [PubMed] [Google Scholar]
- 56.Kusumi A, Nakada C, Ritchie K, Murase K, Suzuki K, et al. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu Rev Biophys Biomol Struct. 2005;34:351–378. doi: 10.1146/annurev.biophys.34.040204.144637. [DOI] [PubMed] [Google Scholar]
- 57.Tooley AJ, Gilden J, Jacobelli J, Beemiller P, Trimble WS, et al. Amoeboid T lymphocytes require the septin cytoskeleton for cortical integrity and persistent motility. Nature Cell Biology. 2009;11:17–26. doi: 10.1038/ncb1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cole KS. Surface Forces of the Arbacia egg. Journal of Cellular and Comparative Physiology. 1932;1:1–9. [Google Scholar]
- 59.Norris CH. The tension at the surface, and other physical properties of the nucleated erythrocyte. Journal of Cellular and Comparative Physiology. 1939;4:117–128. [Google Scholar]
- 60.Evans E. Minimum energy analysis of membrane deformation applied to pipet aspiration and surface adhesion of red blood cells. Biophysical Journal. 1980;30:265–284. doi: 10.1016/S0006-3495(80)85093-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Evans E, Yeung A. Hidden dynamics in rapid changes of bilayer shape. Chemistry and Physics of Lipids. 1994;73:39–56. [Google Scholar]
- 62.Hochmuth RM, Wiles HC, Evans EA, McCown JT. Extensional flow of erythrocyte membrane from cell body to elastic tether. II. Experiment. Biophysical Journal. 1982;39:83–89. doi: 10.1016/S0006-3495(82)84493-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dai J, Sheetz MP. Cell membrane mechanics. Methods Cell Biology. 1998;55:157–171. [PubMed] [Google Scholar]
- 64.Diz-Muñoz A, Krieg M, Bergert M, Ibarlucea-Benitez I, Muller DJ, et al. Control of Directed Cell Migration In Vivo by Membrane-to-Cortex Attachment. PLoS Biology. 2010;8:e1000544. doi: 10.1371/journal.pbio.1000544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Heinrich V, Waugh RE. A piconewton force transducer and its application to measurement of the bending stiffness of phospholipid membranes. Ann Biomed Eng. 1996;24:595–605. doi: 10.1007/BF02684228. [DOI] [PubMed] [Google Scholar]
- 66.Grashoff C, Hoffman BD, Brenner MD, Zhou R, Parsons M, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Stewart MP, Helenius J, Toyoda Y, Ramanathan SP, Muller DJ, et al. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 68.Sun M, Graham JS, Hegedus B, Marga F, Zhang Y, et al. Multiple membrane tethers probed by atomic force microscopy. Biophysical journal. 2005;89:4320–4329. doi: 10.1529/biophysj.104.058180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Waugh R, Song J, Svetina S, zeks B. Local and nonlocal curvature elasticity in bilayer membranes by tether formation from lecithin vesicles. Biophysical Journal. 1992;61:974–982. doi: 10.1016/S0006-3495(92)81904-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sheetz MP, Dai J. Modulation of membrane dynamics and cell motility by membrane tension. Trends Cell Biology. 1996;6:85–89. doi: 10.1016/0962-8924(96)80993-7. [DOI] [PubMed] [Google Scholar]
- 71.Needham D, Evans E. Structure and mechanical properties of giant lipid (DMPC) vesicle bilayers from 20 degrees C below to 10 degrees C above the liquid crystal-crystalline phase transition at 24 degrees C. Biochemistry. 1988;27:8261–8269. doi: 10.1021/bi00421a041. [DOI] [PubMed] [Google Scholar]
- 72.Charras G, Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nature Reviews Molecular Cell Biology. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 73.Sheetz M, Sable J, Dobereiner H. Continuous membrane-cytoskeleton adhesion requires continuous accommodation to lipid and cytoskeleton dynamics. Annu Rev Biophys Biomol Struct. 2006;35:417–434. doi: 10.1146/annurev.biophys.35.040405.102017. [DOI] [PubMed] [Google Scholar]
- 74.Brochard-Wyart F, Borghi N, Cuvelier D, Nassoy P. Hydrodynamic narrowing of tubes extruded from cells. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:7660–7663. doi: 10.1073/pnas.0602012103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Dai J, Sheetz M, Wan X, Morris C. Membrane tension in swelling and shrinking molluscan neurons. J Neurosc. 1998;18:6681–6692. doi: 10.1523/JNEUROSCI.18-17-06681.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Raucher D, Stauffer T, Chen W, Shen K, Guo S, et al. Phosphatidylinositol 4,5-bisphosphate functions as a second messenger that regulates cytoskeleton-plasma membrane adhesion. Cell. 2000;100:221–228. doi: 10.1016/s0092-8674(00)81560-3. [DOI] [PubMed] [Google Scholar]
- 77.Dai J, Sheetz MP. Mechanical properties of neuronal growth cone membranes studied by tether formation with laser optical tweezers. Biophysical Journal. 1995;68:988–996. doi: 10.1016/S0006-3495(95)80274-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Krieg M, Helenius J, Heisenberg C-P, Muller DJ. A bond for a lifetime: employing membrane nanotubes from living cells to determine receptor-ligand kinetics. Angew Chem Int Ed Engl. 2008;47:9775–9777. doi: 10.1002/anie.200803552. [DOI] [PubMed] [Google Scholar]