A subject-specific anisotropic visco-hyperelastic finite element model of the female pelvic floor stress and strain during the second stage of labor

Abstract

Objectives

To develop an improved model representation of the biomechanics of the levator muscles during the second stage of labor and to use a sensitivity analysis to explore the pathomechanics of levator muscle injury.

Methods

A subject-specific finite element model of human pelvic floor and fetal head was developed based on in vivo MRI data of a fetal head and maternal pelvis. An anisotropic visco-hyperelastic constitutive model employed material parameters estimated from biaxial tests on pelvic floor tissues. Boundary conditions reflected both anatomic constraints and the curve of Carus. A short second stage of labor, scaled to 10 minutes, was then simulated using a single expulsive push made in the absence of levator co-contraction.

Results

Large levator stresses occured near the levator hiatus reaching 9 MPa at the pubovisceral muscle enthesis. The dominant principal stresses were located at, and aligned with, the edge of the hiatus. Muscle stretch bordering the levator hiatus was inhomogeneous: The average levator was 3.55 with a high of 4.64 at the pubovisceral muscle enthesis. Decreasing perineal body stiffness by 40%, 50%, and 60% led to reductions in the maximum principal stretch ratio at the pubovisceral muscle enthesis of 8%, 13%, and 18%, respectively.

Conclusions

The pubovisceral muscle enthesis and the muscle near the perineal body are the regions of greatest strain thereby placing them at highest risk for stretch-related injury. Decreasing perineal body tissue stiffness significantly reduced tissue stress and strain, and therefore injury risk, in those regions.

1. Introduction

Female pelvic floor impairments, including urinary incontinence, fecal incontinence and pelvic organ prolapse, result in approximately 11% of U.S. women eventually requiring surgery (Olsen et al.,1997). Delivering vaginally greatly increases a woman’s risk for requiring surgery for pelvic organ prolapse (Mant et al., 1997). One reason may be that levator ani muscle damage can occur during vaginal birth (Hoyte et al., 2001; DeLancey et al., 2003; Dietz et al., 2005; Kearney et al., 2006) and this can lead to difficulty in maintaining closure of the levator hiatus (for review, see Ashton-Miller & DeLancey 2009).

Several computer models of vaginal birth have been developed. For example, Lien et al. (2004) used a 3-D geometric model to calculate the average stretch of the levator ani muscles at the end of the second stage of labor. Subsequently, a series of finite element models have appeared (d'Aulignac et al., 2005; Martins et al., 2007; Noakes et al., 2008; Hoyte et al., 2008; Parente et al., 2008, 2009a, 2009b, 2010). While these models have provided insight, they are limited by a paucity of pelvic floor muscle constitutive data derived from biaxial tests; rather, constitutive models derived from uniaxial tests have been the norm. In addition, some models were based on cadaver levator muscle geometry with the lack of muscle tone representing a potential source of inaccuracy in modeling in vivo muscle deformation (see Discussion). Finally, some of these models used simplified boundary conditions and did not always consider the mechanical interaction between the fetal head and maternal pelvic floor.

The aim of this study, therefore, is to present a pelvic floor model that: (1) employs material constitutive relations derived from biaxial tests of human pelvic floor muscle; (2) uses subject-specific geometry of the matched maternal levator ani and fetal head based on magnetic resonance imaging of a living subject; (3) employs a widely recognized fetal head kinematic trajectory known as the curve of Carus; and (4) represents levator ani muscle boundaries using known anatomic and physiologic constraints. In addition the perineal body, recently hypothesized as a possible ‘fusible link’ (Ashton-Miller & DeLancey 2009), is incorporated for the first time. In that hypothesis, the more flexible the perineal body during late pregnancy, the less the ventral pelvic floor muscle will have to stretch to accommodate the passage of fetal head in late second stage, thereby protecting the muscle from injury. A sensitivity analysis was therefore conducted to test this hypothesis.

2. Methods

2.1. 3D geometric model and finite element mesh

The geometries of the levator ani muscle and fetal head used in this study were based upon sequential 1.5 T, proton density, magnetic resonance scans (Sigma Horizon LX, General Electric, Inc.) of a healthy nulliparous 34-year-old woman and fetus at 40-week gestation. A 20×20 cm field of view was used for the sagittal scans and 16×16 cm for the axial and coronal scans. All slices were 4-mm thick with a 1-mm gap between slices. The outlines of each pelvic floor structure and the fetal head were traced on each MR scan, vetted by the senior clinical author, then lofted to form a 3D volume-rendered geometric model using 3D slicer, an open-source software for visualization and image computing (www.slicer.org). The resulting volume-rendered model was then imported into I-DEAS (v. 9.0, EDS, Inc., Plano, TX) and converted to a surface-rendered model, which was again vetted by the senior clinical author. The resulting 3D surface of the levator ani muscle includes the pubovisceral muscle (also known as the pubococcygeal muscle), along with its component parts (puboperineal and puboanal), as well as the iliococcygeal muscle (Fig. 1). The fetal head geometry was modified to incorporate the effect of molding during vaginal delivery, based on Carlan et al. (1991) ad modam Lien et al. (2004). HyperMesh 9.0 (Altair, Irvin, CA) was used to generate the finite element mesh from the 3D surfaces, and the ABAQUS explicit solver V6.8 (SIMULIA, Providence, RI) was used to solve the equations.

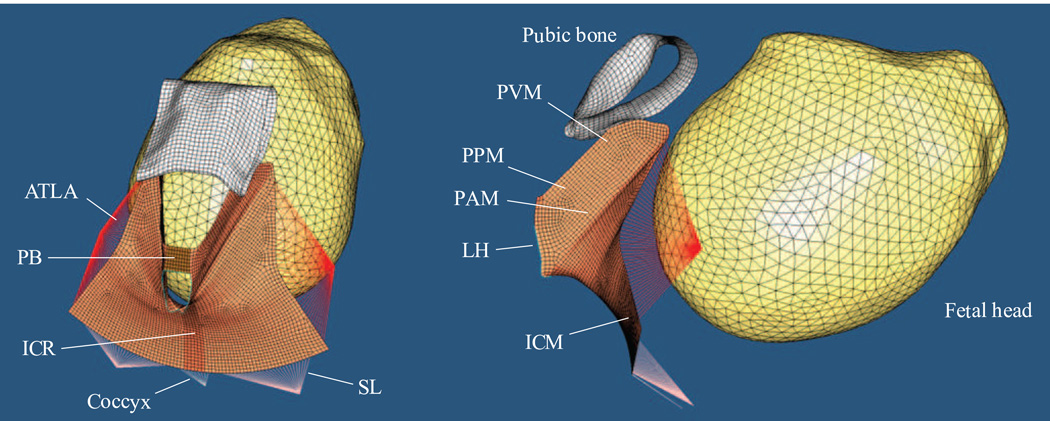
Figure 1.

The 3D finite element model, including perineal body (PB), levator ani muscle (subdivided into pubovisceral muscle (PVM), puboperineal muscle (PPM), puboanal muscle (PAM), iliococcygeal muscle (ICM), iliococcygeal raphe (ICR)), fetal head, the surface of the pubic bone, coccyx, and connective tissues that include the arcus tedineus levator ani (ATLA) and sacrospinous ligaments (SL). LH denotes levator hiatus.

2.2. Boundary conditions

The pubic bone did not participate in the computation but only served as a reference for defining the Curve of Carus and muscle attachments, so all of its six degrees-of-freedom were set to zero. Based on obstetrics textbooks and the clinical experience of one of the authors (JOLD), a sequence of fetal head positions and orientations, relative to the pubic bone, were determined so that the trajectory and rotation of the fetal head were generated using spline interpolation to simulate the curve of Carus (Fig. 2).

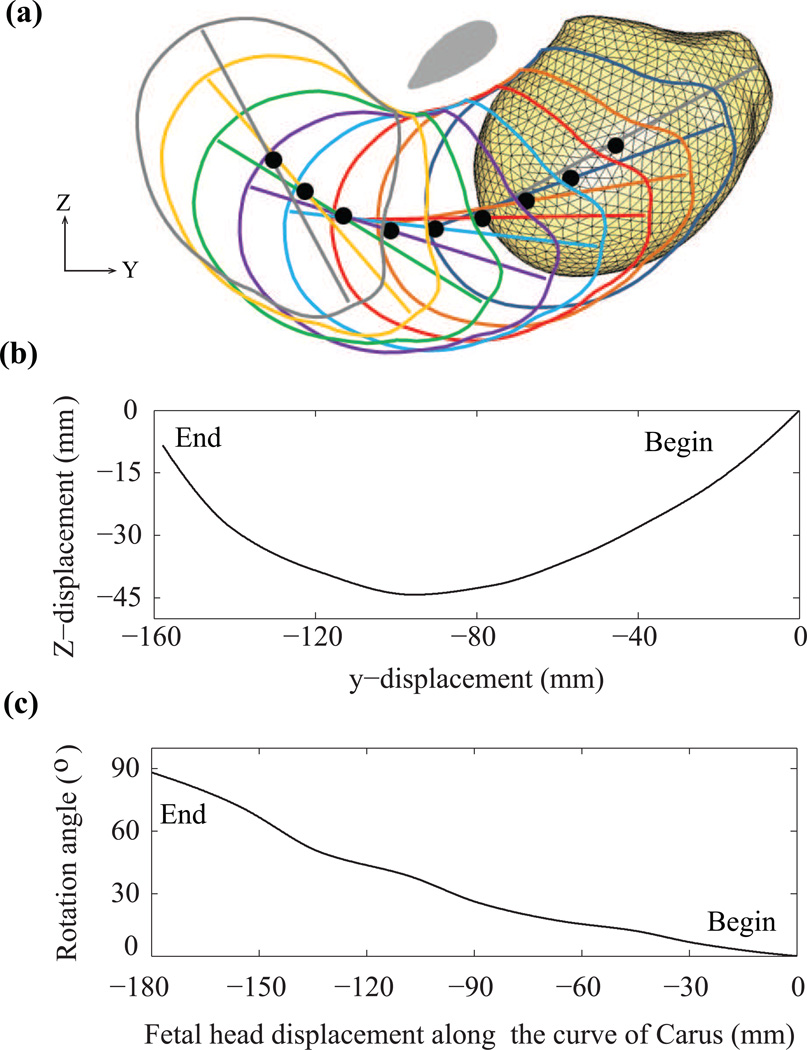
Figure 2.

(a) Curve of Carus (black dots) for prescribing the displacement and rotation of the fetal head during the second stage, starting from a position in which the tip of the head is at the level of the line connecting the ischial spines bilaterally. The elliptical gray region is the cross-section of the pubic bone in the mid-sagittal plane. (b) The interpolated fetal head displacement. (c) The interpolated fetal head rotation. The numbers (mm) represent the distance the tip of the head has travelled along the curve of Carus.

In ABAQUS, the connector element CONN3D2 has the capability of simulating general constitutive behaviors; therefore it was used to model the anatomic constraints of the levator muscle insertions and the connective tissues. The pubovisceral muscle originates from the dorsal aspect of the pubic bone, as well as the insertion of the arcus tensineus levator ani (ATLA, “levator arch”) near the ischial spine; these boundary conditions were set to be translationally fixed but rotationally free. The coccyx, represented by CONN3D2 elements, was considered to rotate in the midsagittal plane as a rigid body about a transversely-oriented hinge joint at the sacrococcygeal junction. The sacrospinous ligaments constraining the posterior margin of the iliococcygeal muscle, and the levator arch constraining the lateral margin of iliococcygeal muscle, were modeled by CONN3D2 elements embedded with 3 orthogonal springs. The stiffnesses of these springs were tuned to preclude unrealistic motions of the edges of the iliococcygeal muscle.

2.3. Constitutive model for the pelvic floor muscles

In this study, both the levator ani and the perineal body were assumed to be anisotropic, viscous, and hyperelastic. A specific form of strain energy function proposed by Holzapfel et al. (2000) was used to describe the anisotropic nonlinear elastic response

$$W=C·(I_1-1)+\{\begin{array}{cc}\frac{k_1}{2k_2}[e^{k_2{({\lambda }^2-1)}^2}]\hfill & \lambda \ge 1\hfill \\ \hfill 0\hfill & \lambda <1\end{array}$$ (1)

where the first term represents the contribution from the isotropic ground substance matrix. A simple neo-Hookean model was used because it is relatively easy to implement nonlinear optimization when extracting material parameters from experimental data, and also this model has been implemented in some commercial FEM codes. A higher order hyperelastic model, such as Mooney-Rivlin, may better reproduce nonlinear material behavior, but the increased number of material parameters comes at the cost of reduced mathematical stability when extracting material parameters from tests. The second term represents the contribution due to fiber reinforcement, and λ is the stretch ratio of the fiber. Here, it is assumed that all fibers are perfectly aligned at each material point.

Quasi-linear viscoelasticity (QLV) theory (Fung, 1972) was used to model the time dependent behavior of the pelvic floor muscles. In this theory, the 2nd Piola-Kirchhoff stress at time t, S(t), is given by the convolution integral of Green-Lagrangian strain history, E(t), and the reduced relaxation function, G(t), in indicial notation

$$S_{ij}(t)=S_{kl}^e(0)G_{ijkl}(t)+{\int }_0^t{G}_{ijkl}(t-\tau )\frac{\partial S_{kl}^e[E_{ij}(\tau )]}{\partial \tau }d\tau$$ (2)

Our biaxial tests on the levator ani muscle showed that the reduced relaxation function is relatively independent of fiber direction (Jing, 2010), we therefore adopted G_tfkl(t) − G(t) in this study, using the following specific form of Prony series for G(t)

$$G(t)=G_{\infty }+\frac{1-G_{\infty }}{i_{\mathit{\text{max}}}-i_{\mathit{\text{min}}}+1}\sum _{i=i_{\mathit{\text{min}}}}^{i_{\mathit{\text{max}}}}\mathit{\text{exp}}(-\frac{t}{{10}^i})$$ (3)

where G_∞ is the long-term normalized stress level. The advantage of using this form is that it can approximate the linear relaxation transition commonly observed in the plot G(t)~log(t) on tensile test data of soft tissues (Tschoegl, 1989).

Based on our biaxial tests on seven fresh human levator ani and five fresh perineal body specimens (Jing (2010), data regression using nonlinear optimization gave a converged solution for the six material parameters in this anisotropic visco-hyperelastic model. The values used in this study are listed in Table 1 where the effect of pregnancy has been taken into consideration by scaling values based on our results of testing control and pregnant vaginal specimens collected from rat and squirrel monkey (Jing, 2010). When specifying material anisotropy, the fiber directions of levator ani muscle and perineal body were based on the findings of Shobeiri et al., 2008.

Table 1.

	C (MPa)	k1(MPa)	k2	G∞	imin	imax
Levator ani	0.181	0.083	0.32	0.22	−1	3
Perineal body	0.293	0.037	0.65	0.17	−1	3

The finite element model consisted of a total of 7,608 nodes and 9,153 elements. The levator ani and perineal body were simulated with deformable membrane elements, while the fetal head was simulated as a rigid body. A constant translational velocity and a changing angular velocity (Fig. 2c) were prescribed to drive the fetal head to move along the curve of Carus. The simulation started from where the fetal head is 23 mm away from the levator ani muscle, and ended when the fetal head completed an extension of 90 degree. To save computational cost, the simulation period was scaled to 10 minutes, and the corresponding sacrifice in model accuracy is addressed in the Discussion. It took about 3.5 hours to complete a single simulation in a computational environment involving a Pentium dual core 3.0 GHz CPU with 3G RAM and running Windows XP.

3. Results

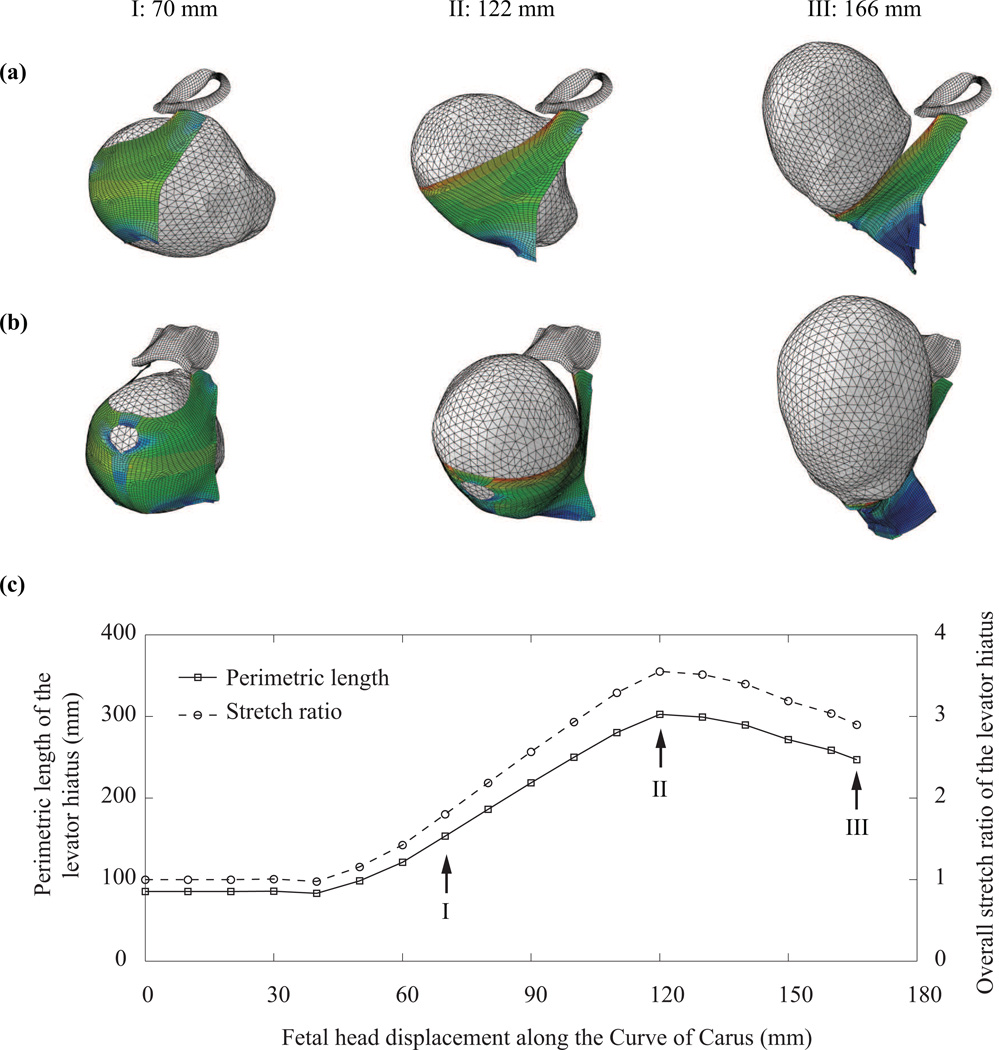
The simulated descent of the fetal head at three displacements along the curve of Carus, 70 mm, 122 mm, and 166 mm, is shown in Fig. 3 (a–b). These three stations correspond, respectively, to early contact between fetal head and pelvic floor muscles, peak stretching of levator hiatus, and full delivery of the fetal head. The predicted overall stretch of the levator hiatus during the fetal head descent is plotted in Fig.3(c). The levator hiatus, initially 85 mm in perimeter, was stretched to the highest perimeter value of 302 mm when the tip of the head had reached 122 mm along the curve of Carus: fetal crowning was considered to then have occurred as the bi-occipital diameter passed the levator hiatus, which corresponds with the suboccipito-bregmatic diameter of the fetal skull (from the lowest posterior point of the occipital bone to the center of the anterior fontanel). The peak overall levator stretch ratio at fetal head crowning was predicted to be 3.55.

Figure 3.

(a) Left lateral view and (b) three quarter view of the simulated descent of the fetal head at three fetal head displacements along the curve of Carus showing the central pubic bones and levator ani: (I) 70 mm, (2) 122mm, and (3) 166mm. (c) The changes in perimetric length and overall stretch ratio of the levator hiatus during the second stage of labor.

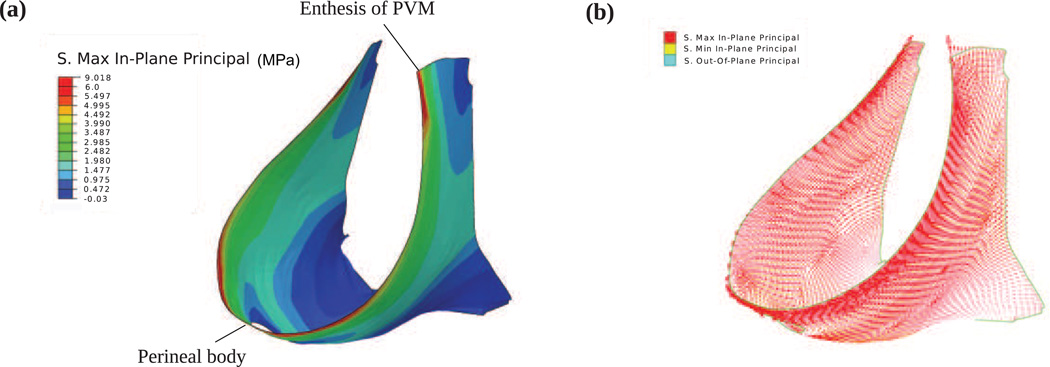
The predicted stress distribution in the pelvic floor muscles at fetal crowning is shown in Fig. 4a. Large stresses were concentrated along the levator hiatus, with the peak stress (~9.0 MPa) occurring at the enthesis of the pubovisceral muscle, and the second highest peak stress (~7.2 MPa) occurring near the perineal body. The plot of the three principal stresses is shown in Fig.4b which shows that, compared with the maximum principal stress (red), the minimum (yellow) and out-of-plane (blue) principal stresses are negligible, indicating that the pelvic floor muscles are under mainly tensile stretch; shearing deformation was negligible. It can also be seen that the dominant component was in-plane and aligned with the edge of levator hiatus. This stress pattern implies a higher risk of muscle stretch injury near the levator hiatus than elsewhere, and the tearing direction would be perpendicular to the hiatus’ edge.

Figure 4.

Stress distribution in the pelvic floor muscles at fetal crowning. (a) maximum in-plane stress; (b) the three principal stresses.

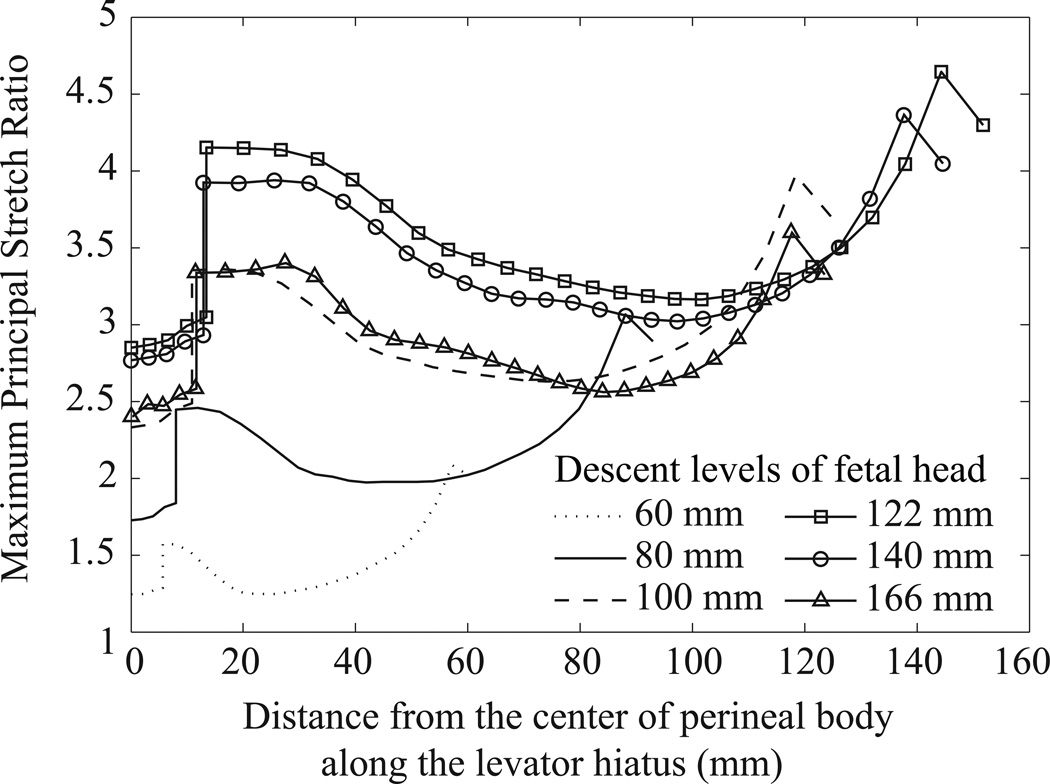
To identify regions most vulnerable to a stretch-related tearing injury, the calculated maximum principal stretch ratio was plotted along the levator hiatus as a function of the distance to the center of perineal body (Fig. 5). Note that the discontinuity in the curves is an artifact reflecting the discontinuity between the measured values of tissue stiffness for the perineal body and levator ani muscle tissue. The model predicted that the distribution of local stretch ratio along the levator hiatus was inhomogeneous. For example, at fetal crowning, the highest peak stretch ratio (4.64) occurred at the enthesis of the pubovisceral muscle, and the second highest value (4.15) was located near the perineal body region. These two areas of large stretch coincide with the clinically observed locations known to be at high risk for tissue injury (Kearney et al., 2006).

Figure 5.

The distribution of the maximum principal stretch ratio along the levator hiatus, at different fetal descent levels. The abscissa is the distance to the center of perineal body along the hiatus, so the left and right ends of each curve correspond to the perineal body region and the enthesis of the pubic bone.

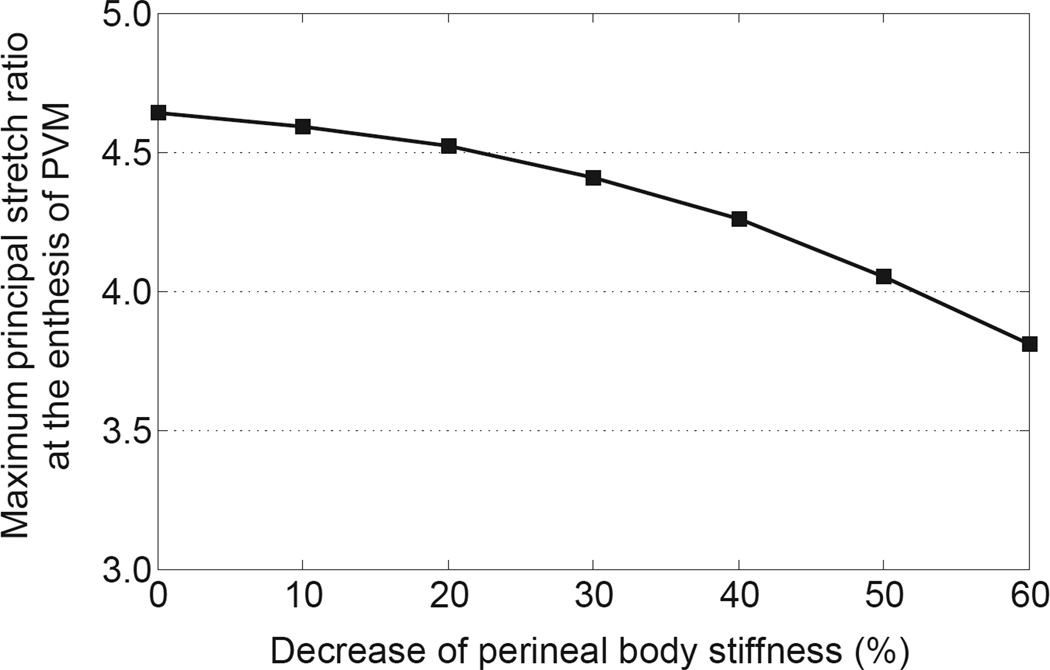
The perineal body is the last tissue part of the pelvic floor to be reached by the fetal head associated with crowning, hence it is reasonable to believe that its stretchability, as determined by its stiffness, plays an important role in accommodating the passage of the fetal head. Perineal body ripening (‘softening’) was found to help reduce the peak stretch ratio at the enthesis of the pubovisceral muscle (Fig. 6). For example, when the perineal body stiffness decreased by 40%, 50%, and 60%, the maximum principal stretch ratio at the enthesis of the pubovisceral muscle was decreased by 8.2%, 12.8%, and 17.8%, respectively. However, if the change in perineal stiffness was small, less than 20%, the effect on reducing pubovisceral muscle injury was negligible.

Figure 6.

Prediction of the effect of perineal stiffness on the maximum principal stretch ratio at the enthesis of the pubovisceral muscle.

4. Discussion

Novel findings include the peak levator stress being found to occur when the fetal head had traveled approximately three-quarters of the total distance it had to travel along the curve of Carus; this occured when the suboccipito-bregmatic plane of the fetal skull and the bi-occipital diameter pass the levator hiatus. Secondly, throughout labor the pubovisceral muscle enthesis underwent the largest stretch and stress values. Model validation comes from this being the very location at highest risk for a muscle defect on MR scans taken after difficult vaginal births (for example, Kearney et al., 2006). This portion of the levator muscle hiatus originates from a fixed boney origin (Kim et al. 2011) and therefore is vulnerable to a large enthesial stress. The adjacent iliococcygeal levator region, however, originates from the soft tissue levator arch which can deflect caudally, thereby relieving stress on the iliococcygeal muscle. The large stress at the pubovisceral enthesis also results from a combined distraction due to both the profile of the fetal head and the perineal descent, whereby the perineal body is displaced ventrocaudally during labor (for example, Lien et al. 2004). A third novel finding is that the highest levator stresses occur along the margin of the levator hiatus, where tissue tears are observed to occur during difficult vaginal births (DeLancey 2003, Dietz 2005). A fourth novel finding relates to a first description of levator muscle mechanical stress distribution during vaginal birth. The final novel finding is the quantitative demonstration of how much decreasing perineal body stiffness reduces levator muscle tissue stress and strain, thereby reducing the risk for stretch-related injury and supporting the ‘fusible link’ hypothesis (Ashton-Miller and DeLancey 2009, see below).

In our model, the displacement and rotation of fetal head were prescribed to ensure that the trajectory of fetal head descent was close to the curve of Carus for this particular subject. The quantitative results would likely be sensitive to a different displacement trajectory or rotation history, but the qualitative results should hold. Our model prediction of an average levator hiatus stretch ratio of 3.55 is consistent with the value of 3.26 suggested by a geometric model (Lien et al., 2004), and within the range of 1.62 ~ 3.76 suggested by a statistical study on 227 women (Svabik et al., 2009), but it is higher than the maximum stretch ratios predicted by other pelvic floor models, such as 1.63 (Parente et al., 2008) and 2.85 (Hoyte et al., 2008). In the former case, the reason is likely due to an unintended artifact introduced through the use of pelvic floor muscle geometry being obtained from a cadaver: due to loss of muscle tone the cadaver levator hiatus will already have been distended by the sustained pressure of the embalming fluid, hence the lower stretch ratio that was predicted. We found that the stretch along the levator hiatus was inhomogeneous, and the two areas of greatest stretch, the pubovisceral muscle enthesis and the perineal body, coincide with the clinically observed locations of high risk of tissue injury. It was also predicted that the dominant principal stresses at the region of levator hiatus were aligned with the hiatal margin, as has been observed during delivery (Dietz et al. 2007), implying that should tearing of tissue occur, it would occur in an opening rather than a shearing mode.

To our knowledge, this is the first computer model to investigate the sensitivity of the stretch of pubovisceral muscle to the stiffness of the perineal body in a test of the `fusible link' hypothesis (Ashton-Miller and DeLancey, 2009). The perineal body is a relative difficult structure to image, thus we used the technique described by Larson et al. (2010) to obtain its shape for this subject-specific model; other subjects might have different shapes and those could affect model predictions. The effect of perineal stiffness may be clinically meaningful. Clinical trials have demonstrated the reduced occurrence of visible perineal trauma by stretching the perineal tissues before and during labor (Beckmann et al., 2006). During late pregnancy the perineal tissues do undergo increased pliability as is evident when a hand must be inserted into the vagina to rotate the fetal head; something that could not be done in the non-pregnant state. Strategies might be developed in the future to induce “ripening” of the perineal tissues in much the same way that is used for when the cervix has not ripened prior to induction. In fact, during the second stage of labor, hyaluronidase (HAase) has been injected into the perineal region to prevent maternal trauma (Oleary et al., 1965; Scarabotto et al., 2008). It has been reported that after 3 ~ 4 minutes following injection of HAase in the perineal region, the perineal tissues exhibited softening, flexibility, and relaxation, facilitating the passage of the fetus through the vaginal canal (Oleary et al., 1965). Our results provides support for decreasing the stiffness of perineal body in order to mitigate the stretch at the pubovisceral muscle enthesis, thereby helping to reduce the risk of levator ani injury. Conversely, inadequate ripening on the perineal body will increase the risk for enthesial tears and a prolonged labor.

The second stage of labor poses specific challenges for computer modeling. One has been the lack of a sound constitutive model for pelvic floor muscle. In this study, we adopted an anisotropic visco-hyperelastic constitutive model which has been successfully applied to model many soft tissues (Hozapfel et al., 2000), and the material parameters of this model were estimated from our biaxial tests on human pelvic floor tissues. A second challenge is the lack of any data on how pregnancy alters levator properties during pregnancy. We addressed this challenge by taking into account the measured difference between pregnant and non-pregnant specimens collected from rats and squirrel monkeys.

A limitation of the present model is that the fetal head was driven at a given velocity along the kinematic trajectory described by the curve of Carus. During the second stage of labor, the fetus is indeed driven by myometrial contraction and increases in intrauterine pressure, but the pressure undergoes cyclic variations over about 90 minutes. In the present study the simulation period was only 10 minutes. While such a short second stage can indeed occur, it is not long enough to allow long-term tissue relaxation to come into play. As a result, the calculated stress levels are likely overestimated compared with a more average duration second stage, but they do provide an approximation for a short second stage, and they might help explain the increased risk of anal sphincter laceration (Kearney et al. 2006). The stretch values and sensitivity analysis results should still therefore be valid.

A second limitation is that, despite making allowance for fetal head molding in our simulation, it was only done statically. Hence the present model predicts levator stress and strain states for the case of a more rigid fetal head; lower values would be expected with a more compliant head.

A third limitation was that we modeled the pubovisceral muscle with its subcomponents and the iliococcygeal muscles as a single continuous structure rather than as a series of sub-structures. This simplified matters computationally, but a future model might maintain separate sub-structures to increase model accuracy.

A fourth limitation is that we neglected active levator muscle contraction. Although active contraction of the pelvic floor muscle tends to hinder fetal head descent (Parente et al., 2010), the present model most accurately simulates a short second stage of labor during which the mother successfully inhibits contraction of her levator muscles.