Poly ɛ-caprolactone nanoparticles loaded with Uncaria tomentosa extract: preparation, characterization, and optimization using the Box–Behnken design

Abstract

Purpose

The aim of this research was to develop and optimize a process for obtaining poly ɛ-caprolactone (PCL) nanoparticles loaded with Uncaria tomentosa (UT) extract.

Methods

Nanoparticles were produced by the oil-in-water emulsion solvent evaporation method. Preliminary experiments determined the initial conditions of the organic phase (OP) and of the aqueous phase (AP) that would be utilized for this study. Ultimately, a three-factor three-level Box–Behnken design (BBD) was employed during the optimization process. PCL and polyvinyl alcohol (PVA) concentrations (X₁ and X₂, respectively) and the AP/OP volume ratio (X₃) were the independent variables studied, while entrapment efficiency (Y₁), particle mean diameter (Y₂), polydispersity (Y₃), and zeta potential (Y₄) served as the evaluated responses.

Results

Preliminary experiments revealed that the optimal initial conditions for the preparation of nanoparticles were as follows: OP composed of 5 mL ethyl acetate/acetone (3/2) mixture containing UT extract and PCL, and an AP of buffered PVA (pH 7.5) solution. Statistical analysis of the BBD results indicated that all of the studied factors had significant effects on the responses Y₁, Y₂, and Y_4, and these effects are closely described or fitted by regression equations. Based on the obtained models and the selected desirability function, the nanoparticles were optimized to maximize Y₁ and minimize Y₂. These optimal conditions were achieved using 3% (w/v) PCL, 1% (w/v) PVA, and an AP/OP ratio of 1.7, with predicted values of 89.1% for Y₁ and 280 nm for Y₂. Another batch was produced under the same optimal conditions. The entrapment efficiency of this new batch was measured at 81.6% (Y₁) and the particles had a mean size of 247 nm (Y₂) and a polydispersity index of 0.062 (Y₃).

Conclusion

This investigation obtained UT-loaded nanoparticle formulations with desired characteristics. The BBD approach was a useful tool for nanoparticle development and optimization, and thus should be useful especially in the realm of phytotherapeutics, in which varied compositions may be assessed in quantitative and qualitative terms.

Introduction

Uncaria tomentosa (UT), commonly known as “cat’s claw,” is a Peruvian Amazon forest plant species currently being used in the treatment of many health problems, including fever, inflammation, viral infections, and cancer.¹ One of the most promising therapeutic activities of this plant is its anti-tumorigenic action. The effects of UT extracts on various tumor cell lines have been investigated and decreases in cell growth have been reported as a result of distinct mechanisms, including cytotoxicity and apoptotic cell death.^2,3

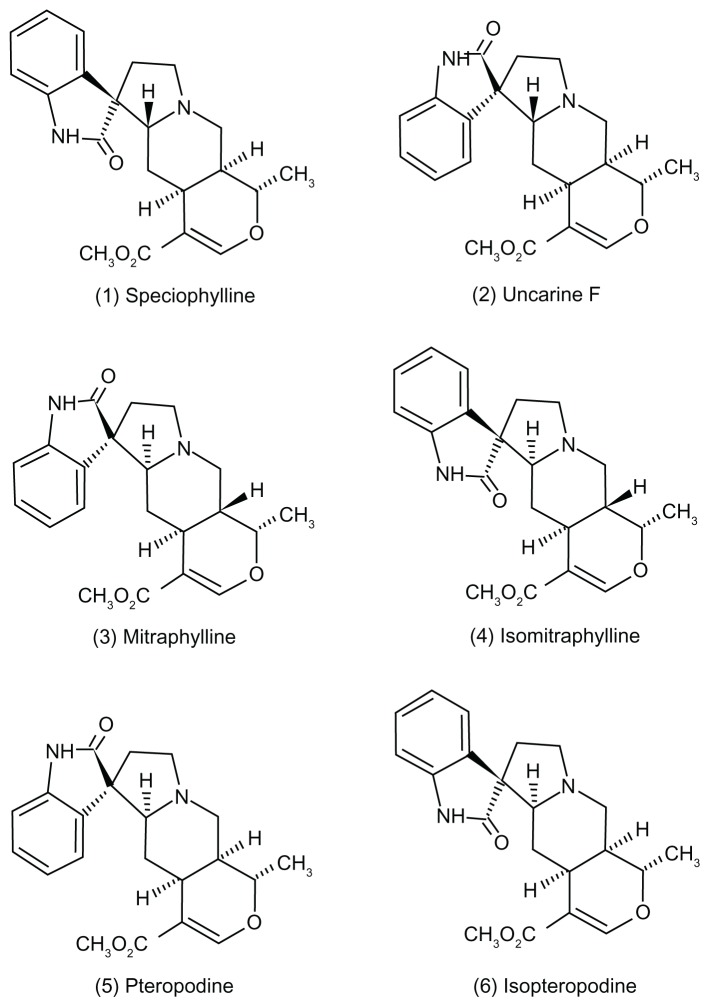
The anticancer properties of UT have been mainly attributed to the pentacyclic oxindole alkaloids, including speciophylline, uncarine F, mitraphylline, isomitraphylline, pteropodine, and isopteropodine, present in hydroalcoholic extracts (Figure 1). Pilarski et al⁴ evaluated the composition and antitumor activity of different UT extracts and observed that alkaloids of lower polarity (isomitraphylline, pteropodine, and isopteropodine) appeared to contribute more significantly to its anti-tumorigenic effects. However, other researchers have proven the anti-tumorigenic effect of the alkaloid mitraphylline against various tumor cell lines.^5,6 Therefore, it is likely that the anticancer activity of UT is due to the combined activity of its different components, including alkaloids, rather than the properties of any one isolated compound.

Figure 1.

Structures of the major oxindole alkaloids present in the Uncaria tomentosa extract.

Anti-tumorigenic-type activities can be improved significantly with nanotechnology, as tumor tissues have a neovasculature composed of an endothelium with large fenestrations (from 200 to 780 nm) that allow nanoparticle (NP) permeation and accumulation in these tissues. This characteristic allows site-specific targeting of active principles and, in doing so, helps to avoid side effects.^7–9 Polymeric NPs have been widely used as drug carriers and, in most cases, are comprised of biodegradable polymers such as poly ɛ-caprolactone (PCL), polylactic acid, and poly(lactic-co-glycolic acid).^10,11 PCL is a synthetic, biodegradable, biocompatible polymer often used in the formulation of NPs, because it is a low cost material, is approved by the US Food and Drug Administration, and undergoes slow degradation in the body.¹²

The use of NPs as carriers for natural compounds has been studied over the past few years.^13–17 Some studies have even reported PCL as the polymeric matrix of choice.^18–20 In these studies, the use of isolated active principles in preparing NP formulations was investigated. However, the use of plant extracts is much less reported.²¹ Developing NPs that are both loaded with natural compounds and have high entrapment efficiencies can be a real challenge, particularly if hydrophilic active principles are involved. Many of these formulation studies have reported entrapment efficiency (EE) values of around 50%.^19,22–24 Special attention is being given to the process of loading natural anti-tumorigenic substances into NP systems; “nanochemoprevention” is thus becoming an increasingly explored concept worldwide.²⁵

For NP development, it is important that drug delivery systems have predictable release behavior and size distribution and reproducible drug loading. These factors can potentially be controlled by certain formulation and process variables, which still need to be determined and quantified. Design of experiments (DOE) is a useful tool for this task, since it can reduce the number of experiments needed for improving formulations and assist researchers in understanding relationships between studied factors and responses of interest.^26–28 Several design methods are available for DOE and the choice of method depends on the objective of the study. When the objective is to screen for significant factors that affect responses, full factorial or fractional factorial designs are preferred. Some studies have indeed established such designs as ideal for NP development.^24,29,30 Three-level factorial designs, such as the central composite design and Box–Behnken designs (BBDs) are more sophisticated design methods that are being used for optimizing formulation conditions. This is because these design methods provide suitable mathematical models – for example, the quadratic model – with which to predict the responses being studied. BBDs are suitable for exploring quadratic response surfaces and constructs according to a second-order polynomial model, thus assisting in the optimization of a process that uses a small number of experimental runs.^31–33 Due to these advantages, BBDs have been recently applied towards the optimization of different types of formulations, including nanostructured systems. Through application of a three-factor, three-level BBD,^26,27,32 Hao et al²⁶ successfully optimized solid lipid NP formulations that were loaded with chloramphenicol during 17 experimental runs. The effects of the lipid and surfactant concentrations, as well as the effects of the drug/lipid ratio on loading efficiency and turbidity were investigated. This investigation allowed an optimized formulation with EE above 80% to be obtained.²⁶ Two other studies have also outlined the use of a BBD in optimizing, over 15 experimental runs, chitosan NPs that were obtained from the complexing of polyelectrolytes. Optimized formulations loaded with insulin²⁷ and gatifloxacin³² that presented high entrapment efficiencies were obtained in these studies.

The aim of the present research was to develop PCL NPs loaded with UT extract that possess suitable physicochemical characteristics. A BBD was utilized to determine the influence of some factors on NP size, EE, and formulation optimization.

Materials and methods

Materials

The UT dried extract (4.5% of total alkaloids) was kindly donated by Herbarium Laboratório Botânico (Colombo, Brazil). PCL (M_w 70,000–90,0000 g/mol) and polyvinyl alcohol (PVA; M_w 31,000–50,000 g/mol, 87%–89% hydrolyzed) were purchased from Sigma-Aldrich (St Louis, MO, USA). Methylene chloride (MC), ethyl acetate (EA), and acetone (AC) were purchased from Tedia Brazil (Rio de Janeiro, Brazil).

Preparation of the organic solvent containing UT extract

Approximately 1 g of the UT dried extract was dispersed into 50 mL of the selected organic solvent (MC, EA, or AC) and sonicated for 20 minutes. The mixture was filtered twice through filter paper then the solution obtained was filtered through a 0.45 mm membrane. The content of alkaloids in the organic solution was analyzed by high-performance liquid chromatography (HPLC) using a Merck Hitachi LaChrom Elite® HPLC system with a diode array detector L-2455 (Hitachi High Technologies America, Pleasanton, CA, USA), using a PerkinElmer C18 column (150 × 4.6 mm, 3 μm) (Waltham, MA, USA), flow rate of 0.8 mL/min, 245 nm for alkaloid detection, and a previously validated gradient method.³⁴ Six signs, with retention times (t_R) of 10, 13, 15, 20, 22, and 31 minutes, were found in the chromatogram obtained from the UT-extract analyses. The extract was standardized using mitraphylline (t_R = 15 minutes) and isopteropodine (t_R = 31 minutes) as markers, with concentrations of 14.1 and 7.1 mg/g, respectively. The concentration of mitraphylline and isopteropodine present in the organic solvent was determined and the total amount of alkaloids present in the chromatogram (total alkaloids) was also measured.

NP formulation

PCL NPs were prepared using the oil-in-water emulsion solvent evaporation method. In the early steps of development, an appropriate amount of PCL was dissolved in 3 mL of an organic solvent containing dissolved UT extract. This organic phase was added dropwise to 6 mL of an aqueous PVA solution (0.5% w/v) while being sonicated at an energy output of 100 W (UP100H ultrasonic processor, Hielscher, Teltow, Germany) in an ice bath during a ~6-minute period, resulting in an oil-in-water emulsion. Then the organic solvent was evaporated under reduced pressure, at 25°C, to allow the formation of a NP suspension.

Preliminary experiments

Before choosing which factors were to be employed in the BBD, several experiments were carried out to obtain an acceptable NP. Thus, the standard conditions described above were modified during preliminary experimentation. As can be seen in the batch compositions presented in Table 1, changes were made to the organic solvent, the amount of PCL, the aqueous phase pH (with or without buffer), the PVA concentration, and the volume of the aqueous phase. All of the formulations in this preliminary stage were prepared in triplicate and NP size and entrapment efficiencies were evaluated.

Table 1.

Composition of the nanoparticle suspension batches produced during preliminary experimentation

Batch	Organic phase		Aqueous phase
	Amount of PCL (mg)	Type and volume (mL) of organic solvent	PVA concentration (% w/v)	Volume (mL)	pH
NP1	50	MC (3)	0.5	6	5
NP2	50	EA (3)	0.5	6	5
NP3	100	EA (3)	0.5	6	5
NP4	100	EA (3)	0.5	6	7.5*
NP5	100	EA (3)	0.5	6	9.0*
NP6	100	EA (3)	0.5	6	10.0*
NP7	100	EA (3)	0.5	6	10.0**
NP8	100	EA:AC (3:2)	0.5	6	7.5*
NP9	100	EA:AC (3:2)	1.0	6	7.5*
NP10	100	EA:AC (3:2)	1.0	10	7.5*
NP11	100	EA:AC (3:2)	1.0	15	7.5*

Notes:

^*Adjusted with phosphate buffer;

^**adjusted with NaOH.

Abbreviations: AC, acetone; EA, ethyl acetate; MC, methylene chloride; PCL, poly ɛ-caprolactone; PVA, polyvinyl alcohol.

BBD

After evaluating the results from the preliminary experiments, it was decided that a three-factor, three-level BBD with five replicates at the center point (middle level) would be used to optimize NP formulation. The permanent conditions were chosen as follows: pH of the aqueous phase (7.5), organic solvent volume (5 mL), and the ratio of solvents used in the organic phase (EA:AC) was 3:2. The independent variables for investigation were PCL concentration (X₁), PVA concentration (X₂), and the aqueous phase/organic phase (AP/OP) volume ratio (X₃), all using the low, medium, and high values (levels) described in Table 2. These values were chosen based on results obtained during preliminary experimentation and from values reported routinely in the literature.^18,23

Table 2.

Variables employed in the Box–Behnken design

Factors (independent variables)	Levels
	−1	0	1
X1: PCL concentration in the OP (% w/v)	1	2	3
X2: PVA concentration in the AP (% w/v)	1	2	3
X3: AP/OP volume ratio	1	2	3
Responses (dependent variables)	Constraints
	Low	High	Goal
Y1: Entrapment efficiency (%)	60	100	100
Y2: Nanoparticle mean diameter (nm)	280	400	280
Y3: Polydispersity index	Not applied	Not applied	Not applied
Y1: Zeta potential (mV)	Not applied	Not applied	Not applied

Abbreviations: AP, aqueous phase; OP, organic phase; PCL, poly ɛ-caprolactone; PVA, polyvinyl alcohol.

The responses (dependent variables) utilized in this investigation were EE (Y₁), particle mean diameter (Y₂), polydispersity index (Y₃), and zeta potential (Y₄). The optimization was performed using a desirability function and certain constraints, displayed in Table 2, to obtain X₁, X₂, and X₃ levels, to maximize EE while minimizing the mean diameter. The BBD matrix, with batches produced and corresponding observations for the dependent variables, is presented in Table 3.

Table 3.

Box–Behnken design matrix and corresponding results for the dependent variables

Batch	Independent variables			Dependent variables
	X1 (% w/v)	X2 (% w/v)	X3	Y1 (%)	Y2 (nm)	Y3	Y4 (mV)
1	1	1	2	67.37	215.7	0.223	−5.69
2	3	1	2	84.18	227.3	0.171	−0.835
3	1	3	2	38.81	131.9	0.093	−1.63
4	3	3	2	67.15	187.6	0.176	−0.031
5	1	2	1	71.82	260.7	0.127	−3.38
6	3	2	1	87.05	338.6	0.183	−0.506
7	1	2	3	38.41	110.7	0.112	−5.92
8	3	2	3	61.16	205.3	0.220	−0.902
9	2	1	1	81.86	375.2	0.171	−0.187
10	2	3	1	79.90	264.3	0.080	−3.52
11	2	1	3	65.44	227.4	0.221	−7.29
12	2	3	3	30.61	188.8	0.232	−1.53
13c	2	2	2	72.01	199.4	0.216	−3.82
14c	2	2	2	70.79	195.1	0.220	−4.1
15c	2	2	2	69.76	198.4	0.179	−4.64
16c	2	2	2	75.05	195.2	0.174	−4.65
17c	2	2	2	61.96	223.4	0.218	−3.40

Note: “c” indicates the replicates at the center point of the design.

Particle mean size and zeta potential

The NP suspensions were diluted in distilled water before size and polydispersity measurements were taken with a Zetasizer Nano ZS90 (Malvern Instruments, Malvern, UK), at 25°C. The zeta potential of the NP suspension was measured using the same instrument either directly or after dilution in the buffer solution.

UT extract EE and loaded alkaloid mass (LA)

The percentage of UT alkaloids entrapped in the NPs was calculated using an indirect method. Using this method, the NP suspension was ultra-centrifuged for 40 minutes at 4°C and at 82,000 g in a Optima LE 80K Ultracentrifuge (Beckman Coulter, Brea, CA, USA). The supernatant was then filtered through a 0.45 μm membrane and directly injected into the HPLC system coupled with a diode array detector L-2455. The separation process was performed using the previously mentioned PerkinElmer C18 column at a flow rate of 0.8 mL/min, 245 nm, for the detection of alkaloids, using a previously validated gradient method.³⁴ The sediment obtained from centrifugation of the NP suspension was resuspended in water and re-centrifuged to determine the amount of alkaloid adsorbed onto the NP surface.

The initial mass of the added alkaloid was calculated using the alkaloid concentration in the organic solvent. The LA was calculated by taking the difference between the initial mass of alkaloid added to the organic phase (W_initial) and the alkaloid mass in the supernatant (W_supernatant) (Equation 1). The EE was calculated using the ratio of LA to the initial mass of added alkaloid, according to Equation 2.

$$\text{LA}={\text{W}}_{\text{initial}}-{\text{W}}_{\text{supernatant}}(\text{mg})$$ (1)

$$\text{EE}=[({\text{W}}_{\text{initial}}-{\text{W}}_{\text{supernatant}})/{\text{W}}_{\text{initial}}]\times 100\%$$ (2)

Data analysis

Statistical analysis of the preliminary results was performed using the Student’s t-test, for the comparison of two means, and by analysis of variance, for the comparison of more than two means, using GraphPad Prism® (v 5.0; GraphPad Software, La Jolla, CA, USA). Optimization was performed based on the method developed by Derringer and Suich,³⁵ which uses the solver function of Microsoft Excel^® 2007 (Microsoft, Redmond, WA, USA).

Results and discussion

Preliminary experiments

Organic phase investigations

The choice of organic solvent and the amount of polymer (PCL) used in the study were assessed during a preliminary study of the properties of the NPs. MC and EA were considered for use in the organic phase, since these solvents are commonly utilized in the solvent evaporation method. The results presented in Table 4 indicate that the alkaloid mass load increased without changing the EE (NP1 × NP2) when EA was used as the organic solvent. This result can be explained by taking into account the different solubilities of the alkaloids present in the two solvents (about 0.150 mg/mL for EA and 0.107 mg/mL for MC) – when EA is used as the solvent, this results in a higher initial alkaloid content in the organic phase. However, when MC was used in the organic phase, the mean diameter and polydispersity of the NPs increased dramatically. This result is likely to be due to the fact that MC is less polar than EA and this property hampered the distribution of the solvent droplets throughout the aqueous phase.³⁶ In addition, MC has much quicker evaporation rates compared with EA, which can lead to an increase in the mean diameter and the polydispersity index. Therefore, EA was chosen as the solvent for the organic phase because, along with its lower toxicity profile,³⁷ it demonstrated better results with regards to particle size and alkaloid mass loading.

Table 4.

Influence of organic solvent and amount of polymer on the nanoparticle properties

Batch	Composition		Nanoparticle properties**
	Solvent	PCL amount (mg)	Mean diameter (nm)	PI	Entrapment efficiency (%)	Loaded alkaloid mass (mg)
NP1	MC	50	386.0 ± 50.1a	0.256 ± 0.039a	38.2 ± 0.3*	0.121 ± 0.025a
NP2	EA	50	223.5 ± 1.7b	0.051 ± 0.018b	33.0 ± 2.1a	0.151 ± 0.010b
NP3	EA	100	260.0 ± 15.1*	0.135 ± 0.013b	44.6 ± 3.3b	0.217 ± 0.003c

Notes:

^**Mean ± standard deviation; analysis of variance Tukey’s test (α = 0.05): means with different letters indicate significant differences and the symbol * indicates that the mean is not significantly different from the other means in this analysis.

Abbreviations: EA, ethyl acetate; MC, methylene chloride; PCL, poly ɛ-caprolactone; PI, polydispersity index.

Table 4 shows that by increasing the PCL concentration, the EE and the LA correspondingly increased (NP2 × NP3), generating results similar to those reported by Byun et al.¹⁸ These results are linked to an increase in apparent viscosity – with an increase in polymer concentration, diffusion of the alkaloids into the aqueous phase is reduced and leads to higher levels of inclusion into the NPs.²³ Since it resulted in a higher EE and an adequate particle size in the organic phase, the amount of PCL was maintained at 100 mg for subsequent preliminary testing.

Aqueous phase and initial alkaloid content investigations

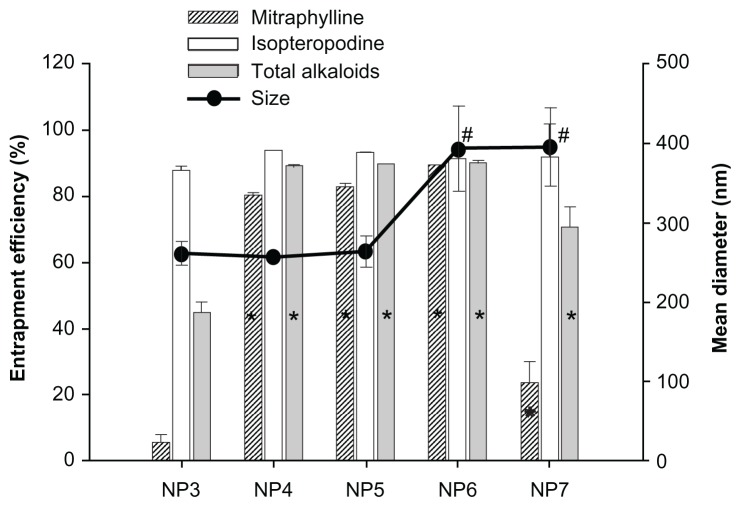
As pH influences the partition of alkaloids between organic phase and aqueous phase, there was the potential for pH to affect the EE of NPs containing alkaloid components. For this reason, the influence of the aqueous phase pH, as well as the specific effects of the buffer, was investigated. Modifications to the NP3 batch (aqueous phase pH near 5.0) were performed, resulting in four different batches of NPs. Three batches were prepared using a phosphate buffer: pH 7.5 (NP4), 9.0 (NP5) and 10.0 (NP6). In the fourth batch (NP7), the aqueous phase pH was adjusted to 10 using an NaOH solution. It was confirmed that the pH of the aqueous phase has a significant effect on the entrapment of total alkaloids. Since alkaloids are weak bases and their degree of ionization is reduced in alkaline mediums, their interaction with the hydrophobic PCL matrix is thus favored.^23,38Figure 2 shows that using an aqueous phase with a pH of 5.0 led to an EE in the NP3 that was statistically lower than when the aqueous phase ranged from pH 7.5 to 10.0 (NP4 to NP7). This increase in EE can be mainly attributed to the effect of pH on the inclusion of alkaloids having higher pKa values, such as mitraphylline, in which entrapment probably depends on the degree of ionization. In contrast, alkaloids with lower pKa values, such as isopteropodine, are most often present in their non-ionized form when pH values are above 6.5.³⁹ Therefore, variations seen in the aqueous phase pH that occurred within the evaluated range did not affect the EE of isopteropodine. The use of a buffer for pH adjustment resulted in a higher EE than when NaOH was used for that purpose. Actually, the use of buffer did increase the saline concentration of the aqueous phase, which probably contributed to a reduction of the alkaloid solubility. This reduced solubility led to a decrease in the diffusion of the alkaloid into the aqueous phase, thus resulting in a significant increase in EE.²³ In addition, the buffer avoided there being drastic pH variations in the aqueous phase, thus providing a higher concentration of alkaloid in a non-ionized form that was then able to interact with the PCL matrix.

Figure 2.

Influence of aqueous phase pH on the entrapment efficiency and mean diameter of nanoparticles. NP3: pH 5.0 (without pH adjustment); NP4: pH 7.5; NP5: pH 9.0; NP6: pH 10.0 (phosphate buffer); NP7: pH 10.0 (adjusted with NaOH).

Notes: For the analysis of variance Dunnett’s test (a = 0.05): results significantly different from NP3 are represented by * for entrapment efficiency and by # for mean diameter.

Although pH values of 7.5 and 9 did not significantly affect the mean diameter, when the aqueous phase pH was adjusted to 10, the NPs became enlarged with sizes above 300 nm. Since the buffered aqueous phase showed no significant differences in terms of particle size and EE when pH values ranged between 9 and 7.5, a pH of 7.5 was selected as the pH for the buffered aqueous phase for use in subsequent tests, as this pH lies within the physiological range.

Despite the optimized EE obtained with NP4, the initial alkaloid mass used in the preparation of NPs was low due to low solubility and of the alkaloids in EA (Table 5). To increase alkaloid solubility, thus the initial mass used, the organic phase was modified by adding AC to EA so that that an EA/AC volume ratio of 3:2 (NP8) was achieved. Considering that the solubility of alkaloids in AC (0.450 mg/mL) is about three times higher than in EA, the mass of total alkaloids added to the organic phase was increased from 0.4 to 1.2 mg. The capacity of a drug to solubilize in solvent is an important factor to consider, since it determines whether the encapsulation process will be successful. Several studies have reported the use of co-solvents to increase EE during NP preparation.^18,23,40 As presented in Table 5, the high initial content of alkaloids in the organic phase resulted in a significant increase in the loaded mass of alkaloids, maintaining a high EE (above 80%). However, the mean diameter and the polydispersity of the NPs also significantly increased.

Table 5.

Influence of initial alkaloid content in the organic phase on nanoparticle properties

Batch	Composition		Nanoparticle properties*
	Organic phase	Initial alkaloid mass (mg)	Entrapment efficiency (%)	Loaded alkaloid mass (mg)	Mean diameter (nm)	PI
NP4	EA	0.4	88.5 ± 0.4a	0.351 ± 0.001a	255.3 ± 3.4a	0.071 ± 0.023a
NP8	EA:AC	1.2	83.8 ± 3.8a	0.993 ± 0.044b	408.3 ± 13.9b	0.200 ± 0.017b

Notes:

^*Mean ± standard deviation; Student’s t-test (α = 0.05): means with different letters indicate significant differences.

Abbreviations: AC, acetone; EA, ethyl acetate; PI, polydispersity index.

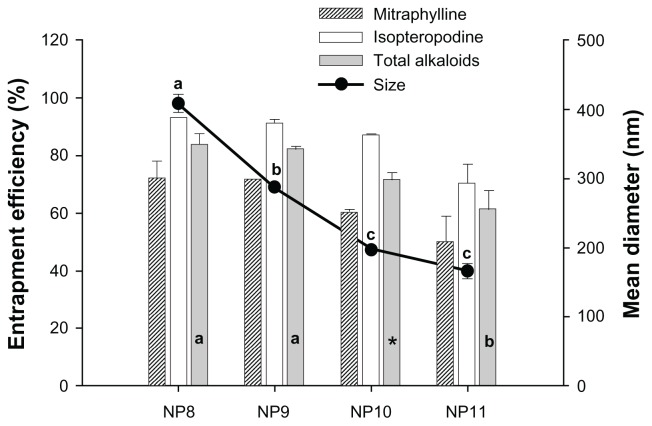
To reduce particle size, while maintaining a high amount of included alkaloid mass inside the NPs, the concentration of PVA, as well as the volume of the aqueous phase of NP8 (6 mL of PVA 0.5% v/v), was modified, resulting in three additional formulations: NP9, NP10, and NP11, in which the aqueous phase was composed of 6, 10, and 15 mL of PVA 1.0% v/v, respectively. Figure 3 shows that NP9 had smaller particle sizes than NP8 and this size reduction was statistically significant. This reduction in NP size relates to the increase in PVA concentration of the aqueous phase, since the volume remained unchanged. PVA is a polymer that acts as an emulsifying agent. It reduces the interfacial tension that exists between the organic and aqueous phases and contributes to the formation of smaller droplets during the emulsification process. Moreover, PVA can form a film that surrounds droplets, avoiding coalescence during the evaporation of the organic solvent, thus preventing aggregation of the formed NPs.^23,41

Figure 3.

Influence of polyvinyl alcohol (PVA) concentration and aqueous phase (pH 7.5) volume on the entrapment efficiency and mean diameter of nanoparticles.

Notes: NP8: 6 mL of 0.5% PVA; NP9, NP10, and NP11: 6, 10, and 15 mL of 1.0% PVA, respectively. Analysis of variance Tukey’s test (α = 0.05): different letters indicate significant differences and * indicates that the mean is not significantly different from the other means.

The batches designated NP10 and NP11 had smaller particle sizes than NP9 and this size reduction was statistically significant, as shown in Figure 3. The reduction of mean particle diameter was related to the increase in aqueous phase volume, since the concentration of PVA was unchanged. Furthermore, the increased aqueous phase volume and, consequently, higher amounts of PVA, significantly reduced the EE of the total amount of alkaloids (NP11). This reduction can be explained by considering the decreased mean size of NPs, as well as the solubilizing effect of PVA, which allows partitioning of alkaloids into the aqueous phase. Statistical analysis of the data in Figure 3 shows that there was a significant linear trend between the results, since the coefficient of determination (R²) was 0.9362 for the mean diameter and 0.8499 for the EE of the total alkaloids (analysis of variance [ANOVA] linear trend test, α = 0.05). The PVA concentration and the volume of the aqueous phase were further investigated using the BBD to establish the relationship between these factors and the responses of interest.

BBD

Fitting of response data into the regression models

The results obtained for EE (Y₁), mean particle diameter (Y₂), polydispersity index (Y₃), and zeta potential (Y₁) from the 17 experiments that employed the BBD are presented in Table 3. These results were analyzed using Statistica software (“pure error” was chosen as the error term for the ANOVA tests) to determine the significance of the independent variables (X₁, X₂, and X₃) and their interactions, as well as for generating the regression models. The regression coefficients and the corresponding P values obtained for each response are presented in Table 6. The nonsignificant coefficients were eliminated so that the regression equations could be recalculated only when using significant parameters. This resulted in reduced models; the regression coefficients obtained from these are presented in Table 7. All the responses (Y₁–Y₄) showed a non-linear relationship with regard to the factors investigated (X₁–X₃). This was the case because at least one coefficient with more than one factor was presented, which indicated the presence of interaction effects. NP mean diameter (Y₂) and zeta potential (Y₄) were presented in higher order terms, in addition to the interactions that indicated quadratic relationships. Among the four responses evaluated, the PCL and PVA concentrations (X₁ and X₂, respectively), as well as the AP/OP volume ratio (X₃), showed significant differences. Positive coefficients indicate that synergistic effects influenced the response, while negative coefficients indicate the presence of antagonistic effects.

Table 6.

Coefficients of the complete regression equation obtained for the responses evaluated in the Box–Behnken design

Regression coefficients	Equation for the responses
	Y1 (P value)	Y2 (P value)	Y3 (P value)	Y4 (P value)
b0	69.91* (<0.0001)	202.29* (<0.0001)	0.201* (<0.0001)	−4.122* (0.0001)
b1	10.39* (0.0038)	29.98* (0.0021)	0.024* (0.0389)	1.793* (0.0007)
b2	−10.30* (0.0039)	−34.13* (0.0013)	−0.026* (0.0327)	0.911* (0.0087)
b3	−15.63* (0.0008)	−63.33* (0.0001)	0.028* (0.0248)	−1.006* (0.0062)
b12	2.88 (0.3020)	11.03 (0.1395)	0.034* (0.0408)	−0.814* (0.0390)
b13	1.88 (0.4830)	4.19 (0.5231)	0.013 (0.3152)	0.536 (0.1174)
b23	−8.22* (0.0279)	18.08* (0.0393)	0.025 (0.0887)	2.273* (0.0011)
b11	−2.69 (0.3202)	−23.41* (0.0160)	−0.025 (0.0828)	1.265* (0.0085)
b22	−2.85 (0.2965)	11.70 (0.1156)	−0.010 (0.4148)	0.810* (0.0367)
b33	−2.61 (0.3325)	49.91* (0.0010)	−0.016 (0.2322)	0.180 (0.5308)

Notes:

^*significant values.

Table 7.

Coefficients of the reduced regression equations obtained for the evaluated responses

	Y1	Y2	Y3	Y4
Regression coefficients
b0	66.08 (P < 0.0001)	207.22 (P < 0.0001)	0.177 (P < 0.0001)	−4.046 (P < 0.0001)
b1	10.39 (P = 0.0038)	29.98 (P = 0.0021)	0.024 (P = 0.0389)	1.793 (P = 0.0007)
b2	−10.30 (P = 0.0039)	−34.13 (P = 0.0013)	−0.026 (P = 0.0327)	0.911 (P = 0.0087)
b3	−15.63 (P = 0.0008)	−63.33 (P = 0.0001)	0.028 (P = 0.0248)	−1.006 (P = 0.0062)
b12	–	–	0.034 (P = 0.0408)	−0.814 (P = 0.0390)
b13	–	–	–	–
b23	−8.22 (P = 0.0279)	18.08 (P = 0.0393)	–	2.273 (P = 0.0011)
b11	–	−22.80 (P = 0.0174)	–	1.275 (P = 0.0083)
b22	–	–	–	0.820 (P = 0.0352)
b33	–	50.53 (P = 0.0010)	–	–
Analysis of variance of the regression
R2	0.9363	0.9451	0.5601	0.9482
MSR/MSr (Fcritical)	44.09 (F4,12 = 3.26)	28.70 (F6,10 = 3.22)	3.80 (F4,12 = 3.26)	22.85 (F7,9 = 3.29)
MSlack of fit/MSpure error (Fcritical)	0.91 (F8,4 = 6.04)	3.54 (F6,4 = 6.16)	3.48 (F8,4 = 6.04)	1.98 (F5,4 = 6.26)

Notes: MS_R, mean square due to regression; MS_r, residual mean square; MS_{lack of fit}, mean square for lack of fit; MS_{pure error}, mean square for pure error; F_critical, scored F_ν1,ν2 value, at 95% confidence interval, where “ν1” and “ν2” are the degrees of freedom for the numerator and denominator, respectively.

Statistical analysis (ANOVA) of the reduced models (Table 7) was performed. The ratio between the mean square of regression and the residual mean square (MS_R/MS_r), the coefficient of determination (R²), and the statistical test for measuring fit (MS_{lack of fit}/MS_{pure error}) were used to evaluate the significance of the regression equations and the efficiency of the models in predicting responses. As can be seen from Table 7, the regression equations obtained for the responses Y₁ (EE), Y₂ (mean diameter), and Y₄ (zeta potential) were considered significant, with no evidence of lack of fit. These equations could be useful for prediction purposes. However, the regression equation obtained for the polydispersity index (Y₃) presented a very low R² value, so this model cannot be considered suitable for the prediction of polydispersity index values, in spite of the existence of significant regression values with adequate fit.

The zeta potential of NPs obtained from non-charged polymers, such as PCL, depends on several factors, including the concentration of charged drugs or surfactants in the aqueous phase. PCL NPs, for example, may have a zeta potential value of about −50 mV (with some charged drugs) or a less expressive value occurring around −5 mV.¹¹ As the charge of UT NPs depends on the degree of entrapped alkaloids, the zeta potential values obtained in the experiments were inexpressive, as expected. These measurements of the zeta potential value could not adequately represent the stability of the NP suspension. Subsequently, only the Y₁ and Y₂ responses were chosen for optimization and for further investigation of the relationships between factors and responses obtained from the surface response plots.

Response surface analysis

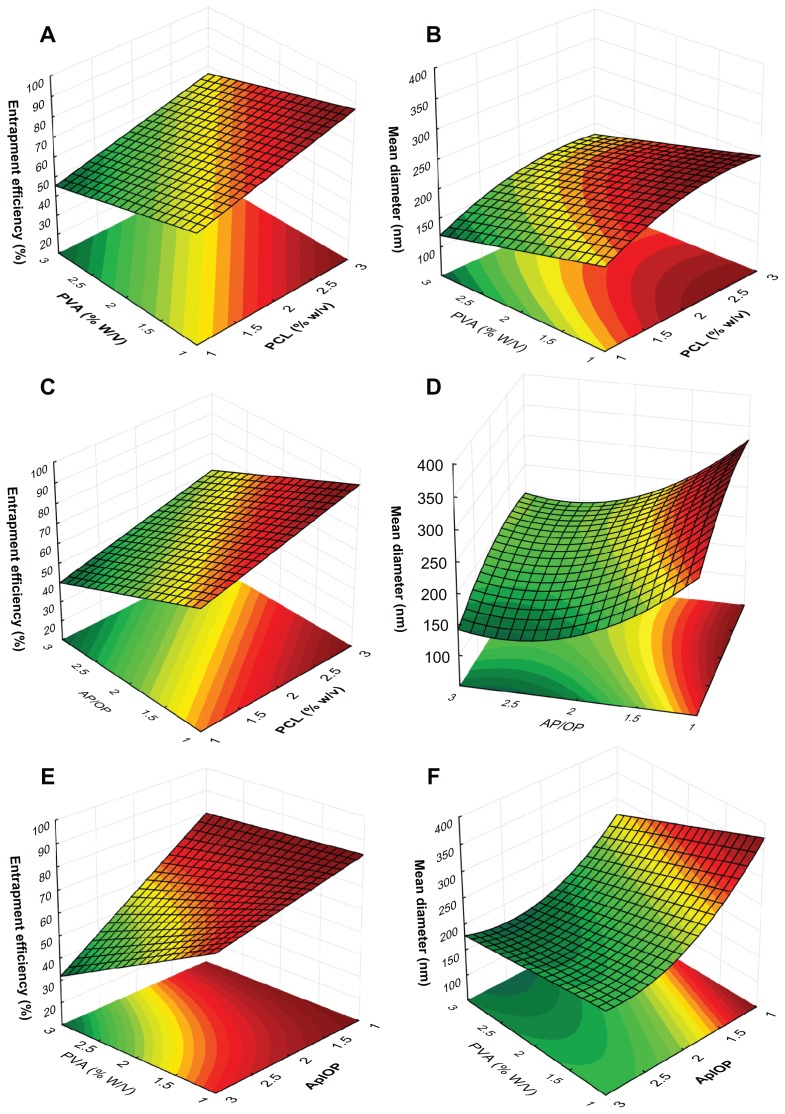
Response surface plots were constructed based on the polynomial functions obtained for Y₁ and Y₂ (Equations 3 and 4, respectively), which resulted in the three-dimensional graphs that are presented in Figure 4, panels A–F. These graphs were used to evaluate the effects of two independent variables on the responses, keeping the third independent variable at a constant level.²⁷

Figure 4.

Response surface plot showing the effects of poly ɛ-caprolactone (PCL) (X₁) and polyvinyl alcohol (PVA) (X₂) concentrations with an aqueous phase/organic phase (AP/OP) ratio of two on entrapment efficiency (Y₁) (A) and particle size (Y₂) (B); effect of PCL concentration (X₁) and AP/OP volume ratio (X₃) with a PVA concentration of 2% on entrapment efficiency (Y₁) (C) and particle size (Y₂) (D); effect of PVA concentration (X₂) and AP/OP volume ratio (X₃) with a PCL concentration of 2% on entrapment efficiency (Y₁) (E) and particle size (Y₂) (F).

$${\text{Y}}_1=66.08+10.39{\text{X}}_1-10.30{\text{X}}_2-15.73{\text{X}}_3-8.22{\text{X}}_2{\text{X}}_3$$ (3)

$${\text{Y}}_2=207.22+29.98{\text{X}}_1-34.13{\text{X}}_2-63.33{\text{X}}_3+18.08{\text{X}}_2{\text{X}}_3-22.80{\text{X}}_1^2+50.53{\text{X}}_3^2$$ (4)

Figure 4, panels A, C, and E show that the EE increases with increasing PCL concentration (X₁) and with decreasing both the PVA concentration (X₂) and the AP/OP ratio (X₃). This is in accordance with the regression equation obtained for Y₁ (Table 7), which presents coefficients with a positive sign for X₁ and negative signs for X₂ and X₃. The interaction between X₂ and X₃ was considered significant upon evaluation of the regression equation (Table 7) and its effect is clearly shown in Figure 4E. It has been observed in other studies that a reduction in the PVA concentration leads to an increase of about 40% in EE when the AP/OP ratio is at a high level. At lower levels of the AP/OP ratio, EE is extremely high and is practically not affected by the PVA concentration. Besides, the decrease in the AP/OP ratio causes an expressive rise in EE when the PVA concentration is at a high level, since high PVA concentrations increase the solubility of UT alkaloids. Therefore, modifications to the aqueous phase volume produce more rigorous changes in the partition of alkaloids between aqueous phase and OP, leading to more significant effects on the EE.

The effects of X₁, X₂, and X₃ and their interactions on the mean diameter of particles are described in Figure 4, panels B, D, and F. The increase to both the PVA concentration and the AP/OP ratio, and the decrease in PCL concentration, resulted in a decrease in NP size, as confirmed by the regression coefficient signs obtained for Y₂ (Table 7). Moreover, the regression equation shows that X₃ has a more significant effect on NP size than X₁ or X₂. This result is clearly affirmed by the surface response plots for mean diameter. It was observed, as shown in Figure 4B, that at the midpoint of the AP/OP ratio, the variations in PCL and PVA concentrations resulted in particle sizes below 250 nm. Figure 4, panels D and F, show an increase in the AP/OP ratio, which first decreased then increased the NP size. For lower values of X₃, the increase in aqueous phase volume increased the amount of PVA present in the system, contributing to a reduction in the NP mean diameter. However, when the X₃ value was above 2.5, the increase in aqueous phase volume reduced the net shear stress of the system, thereby overcoming the effect of PVA and resulting in a mean particle size increase.^23,41

The response surface plots and regression models demonstrate that the investigated factors have similar effects on EE and mean diameter. Therefore, the development of NPs with high EEs, along with reduced size, could prove to be a substantial challenge. Such a challenge highlights the importance of attempting optimization of the formulation conditions. An evaluation of the response surface graphs suggests that higher amounts of PCL combined with lower levels of PVA and a mid-level AP/OP ratio are the best conditions to use for formulations. Formulations produced under these conditions would result in NPs with a suitable EE above 80% and a suitable mean size of about 250 nm.

Optimization

The set criteria of maximum EE (Y₁) and minimal particle size (Y₂), following the Derringer and Suich³⁵ desirability function, and the constraints established in Table 2, provided the basis for determining the optimal NP formulation. The solver function of the Excel software, through its mathematical approach, was used to analyze various response variables as well as the established constraints. The results of this analysis indicated that an optimized formulation would be composed of PCL 3% w/v, PVA 1% w/v, and an AP/OP ratio of 1.7, with a predicted EE of 89.1% and mean particle diameter of 280 nm. To confirm the validity of the optimization procedure, a new batch of UT NPs was prepared using the optimized conditions developed via the procedure. In this new batch, the organic phase was composed of 5 mL of the AE:AC (3:2) mixture, which contained approximately 1.2 mg of UT alkaloids and 150 mg of PCL, and an aqueous phase composed of 8.5 mL buffered 1.0% w/v PVA solution (pH 7.5). This optimized NP formulation presented an EE of 81.6%, mean particle size of 247.3 nm, and a polydispersity index of 0.062.

The results obtained for the optimized NP formulation in this study are very promising, considering that the loaded material is a complex mixture of components present in the UT extract, rather than a specific substance. Most publications that have explored the development of NPs loaded with natural compounds have reported the use of isolated substances, with EEs obtained in these formulations remaining only near 50%,^19,22–24 particularly when the natural component loaded was not extremely lipophilic. In contrast, the use of BBD as the chosen DOE method was effective for obtaining optimal formulations for the development of NPs that possess good EEs. Significantly, the BBD allowed the use of a reduced number of experiments while still maintaining efficacy. Moreover, it has been shown that while PCL NPs are biodegradable, extended drug release is maintained.^20,22 Such features, along with novel drug-targeting approaches, will make the NPs studied here a promising therapeutic for cancer treatment, especially given that UT extract has already demonstrated proven anti-tumorigenic activities.^4–6

Conclusion

The preliminary experiments performed and the final experimental design in this study have provided important information towards the development of UT extract-loaded PCL NPs that possess suitable physicochemical parameters. The BBD used provided well-fitting polynomial equations for the evaluated responses and was successfully employed in the optimization of the NP formulations. The optimal conditions for NP production were determined, in which the organic phase was composed of 5 mL of AE:AC (3:2) mixture, ~1.2 mg of UT alkaloids, and 150 mg of PCL, while the aqueous phase contained 8.5 mL of a buffered 1.0% w/v PVA solution (pH 7.5). These conditions resulted in a formulation with an EE of 81.6%, a mean particle size of 247.3 nm, and a polydispersity index of 0.062. Therefore, the obtained formulation had the desired drug content and particle size characteristics for ensuring that the UT alkaloids would be able to target tumor tissues.

In vitro and in vivo studies are needed and should be performed to examine whether the NPs that were the subject of this study can indeed provide improved delivery of UT extract, allowing its anticancer properties to effectively target tumor tissues.