Abstract
We examined how feedback delay and stimulus offset timing affected declarative, rule-based and procedural, information-integration category-learning. We predicted that small feedback delays of several hundred milliseconds would lead to the best information-integration learning based on a highly regarded neurobiological model of learning in the striatum. In Experiment 1 information-integration learning was best with feedback delays of 500ms compared to delays of 0 and 1,000ms. This effect was only obtained if the stimulus offset following the response. Rule-based learning was unaffected by the length of feedback delay, but was better when the stimulus was present throughout feedback than when it offset following the response. In Experiment 2 we found that a large variance (SD=150ms) in feedback delay times around a mean delay of 500ms attenuated information-integration learning, but a small variance (SD=75ms) did not. In Experiment 3 we found that the delay between stimulus offset and feedback is more critical to information-integration learning than the delay between the response and feedback. These results demonstrate the importance of feedback timing in category-learning situations where a declarative, verbalizable rule cannot easily be used as a heuristic to classify members into their correct category.
Keywords: Category-learning; Information-integration; Feedback delay, Dopamine, Calcium
1. Introduction
Feedback is critical to learning, and its importance has been demonstrated across a variety of domains (Pashler, Cepeda, Wixted, & Rohrer, 2005; Butler, Karpicke, & Roediger III, 2007; Butler, & Roediger III, 2008; Metcalfe, Kornell, & Finn, 2009; Smith & Kimball, 2010; Butler & Winne, 1995; Hattie & Temperley, 2007; Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005). We receive feedback on educational tests, job performance, athletic endeavors, and social interactions. We also receive feedback for simple, mundane actions like unlocking a car door, clicking an icon on a computer, or issuing a command to a smart phone. Feedback can be presented in a variety of different ways, and there can be subtle differences in the properties of the feedback we are presented with as well as the properties of the environment in which feedback is given.
In this work we examine how feedback timing affects rule-based and procedural forms of perceptual category learning by deriving predictions from a prominent neurobiological theory of learning in the striatum. We first review work on the neurobiology of learning in the striatum that suggests that feedback timing is critical for procedural learning. We then present the perceptual category-learning paradigm we use to test our predictions derived from this theory, and results from three experiments that suggest that feedback and stimulus offset timing is critical for optimizing procedural forms of learning.
1.1 The neurobiology of procedural learning
Neurobiological models of procedural learning assume that medium spiny cells in the caudate nucleus link large groups of visual cortical cells associated with specific regions of perceptual space with abstract motor programs in supplementary motor areas associated with specific responses (e.g. Ashby et al., 1998; Ashby & Waldron, 1999, Maddox & Ashby, 2004; Ashby & Ell, 2001; Wilson, 1995; Alexander, DeLong, & Strick, 1986). These stimulus-response connections are strengthened by dopamine reward signals from the substantia nigra pars compacta and this leads to long term potentiation (LTP) of the medium-spiny cell synapses in the caudate (e.g. Wickens, 1993; Wickens & Kotter, 1995). In category-learning the feedback that follows the response induces the dopamine reward signal, but long term potentiation also depends on increases in intracellular calcium concentration. These increases are triggered by the response that releases glutamate from the corticostriatal synapses. Importantly, several models of LTP in the striatum propose that best strengthening of striatal synapses requires simultaneous glutamatergic and dopaminergic input to medium-spiny cells in the striatum. (e.g. Wickens & Kotter, 1995; Lindskog, Kim, Wikstrom, Blackwell, & Kotaleski, 2006; Fernandez, Schiappa, Girault, & Novierre, 2006).
These models suggest that the increase in intracellular calcium concentration levels occurs quickly and is very short lived, with calcium concentrations peaking several hundred milliseconds after a response has been made, and then rapidly declining (Fernandez et al., 2006). Because learning is best when dopamine and calcium levels peak simultaneously a short delay in feedback of approximately 500ms after the response may be best for learning. The short delay may be better than no delay because calcium concentrations have had time to peak by the time the dopamine reward signal arrives following the feedback presentation, and it may be better than a longer delay (1000ms or more) because calcium concentrations have not yet declined when the dopaminergic feedback signal arrives. Delays of 2500ms or more have been shown to negatively affect procedural category learning (Maddox et al., 2003; 2005), yet, to our knowledge no prior work has examined whether differences in feedback delays as small 500ms will affect learning. Our goal in the present work is to test an empirical question regarding the timing of the feedback delay that is motivated by neurocomputational theories of learning in the striatum that suggest that a feedback delay of approximately 500ms may lead to the best procedural learning. In the next section we present the perceptual category-learning paradigm we utilize to test our neurobiologically motivated predictions regarding feedback timing.
1.2 Perceptual Category-Learning
One laboratory domain that offers an excellent setting for studying the effects of feedback is perceptual category-learning. In these tasks participants are repeatedly presented with simple perceptual stimuli that have been separated by the experimenter into two or more categories. The participant must learn from corrective feedback which stimuli belong in each category. For example, lines may be presented that differ in length and orientation and participants must decide which properties of the stimuli can be used to correctly classify stimuli into each category (e.g. long lines are in Category 1 and short lines are in Category 2). Perceptual category-learning is an ideal setting for examining how various feedback properties enhance learning because simple stimuli are used that participants likely do not have any pre-experiment experience with. Additionally, the type of learning processes required to correctly classify the stimuli can be manipulated by the experimenter.
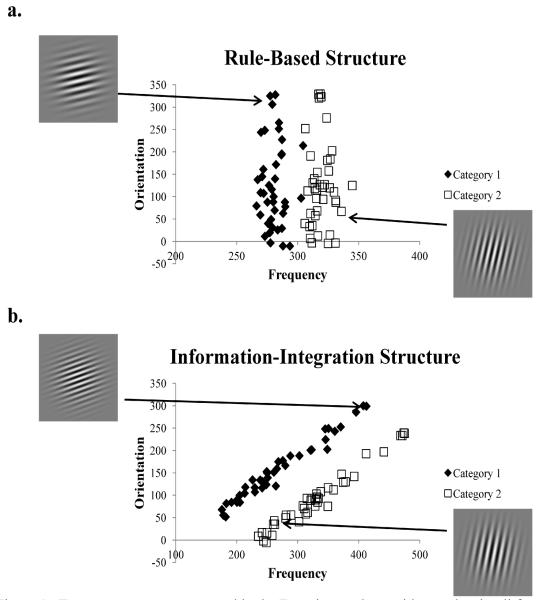
Much previous research has examined category learning when participants must learn two different types of category structures: rule-based and information-integration (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Maddox & Ashby, 2004; Smith et al., 2011). The goal of the present work is to examine how manipulating two basic properties of feedback, feedback delay and stimulus presence during feedback, affect learning in these two types of perceptual category learning tasks. The rule-based and information-integration structures we use in our experiments are presented in Figure 1. The stimuli are sine-wave gratings, called “Gabor” patches, that vary in spatial frequency (i.e. how close together the bars are) and spatial orientation (i.e. tilt of the stimulus relative to the bottom of the computer screen). The biggest distinction between the rule-based and information-integration structures is the ease with which a rule can be used to classify the Gabor patches into their correct category. In the rule-based structure shown in Figure 1a a rule along the spatial frequency dimension can be used to classify stimuli into each category with a high degree of accuracy (e.g. “If the bars are far apart then it’s in Category 1, but if they are close together then it’s in Category 2”). Thus, there is a simple rule, or heuristic that can be employed to achieve a high level of accuracy.
Figure 1.
Two category structures used in the Experiment along with sample stimuli from each category. (a) A unidimensional rule-based structure, and (b) a two-dimensional information integration structure. Actual stimulus size was 200 × 200 pixels presented on a screen with resolution set at 1024 × 768. Participants sat approximately two feet from the screen.
In the information-integration structure shown in Figure 1b the rule that distinguishes the members of each category is more difficult to verbalize because it is not aligned with the perceptual dimensions. A rule that distinguishes the members of each category in the information integration structure could be stated as “If the orientation of the stimulus is greater than its spatial frequency then it’s in Category 1, otherwise it’s in Category 2.” This rule is considered more difficult to verbalize than the simple rule along the frequency dimension (Stanton & Nosofsky, 2007). A conjunctive rule that is much easier to use like “If the orientation is flat and the bars are far apart then it is in Category 1, otherwise it’s in Category 2,” could be used to achieve a level of accuracy that is above chance, but using this rule would lead to incorrect classifications of many stimuli.
An advantage of using these tasks is that “decision-making” models can be fit to the data that assume that a specific type of rule or strategy was used to classify the stimuli (Maddox & Ashby, 1993; Maddox, 1999). A main goal of fitting these models is to determine whether participants were using verbalizable rules or a procedural learning strategy that is difficult to verbalize. In these models the decision bound represents the bound separating stimuli that are classified into each category.
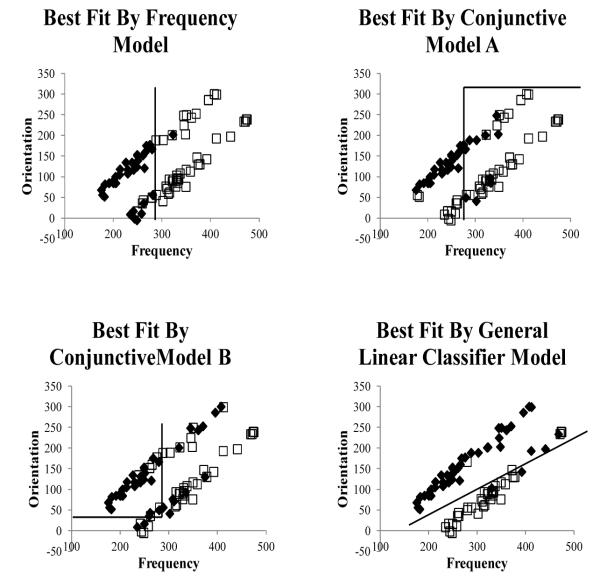
Stimuli further from the bound are more likely to be classified into the assumed category than stimuli closer to the bound. Figure 2 shows response patterns from four participants in our first experiment who performed the information-integration task who were best fit by models that assumed different rule-based or information-integration strategies. Figure 2a shows responses for a participant who used a frequency rule strategy and Figures 2b and 2c show responses from participants who used conjunctive rule strategies. Figure 2d shows responses from a participant who was best fit by a model that assumed a procedural learning strategy, where the decision-bound was oblique to the perceptual dimensions. Rule-use can lead to reasonably high levels of accuracy in the information-integration task. For example, the proportions of correct responses for participants whose responses are plotted in Figures 2a, 2b, and 2c are .76, .84, and .73, respectively - well above chance. However, the proportion of correct responses for the participant whose responses are plotted in Figure 2d was .93. Thus, rule-use in the information-integration task can lead to accuracy levels that are well above what would be expected by chance, but participants must use a procedural learning strategy to achieve the highest level of performance.
Figure 2.
Response patterns of participants who are best fit by models assuming rule-based or information-integration strategies in the information-integration task. Stimuli that were classified into Category 1are represented by black diamonds and stimuli that were classified into Category 2 are represented by white squares. (a) Responses for a participant whose data were best fit by a frequency rule model. (b) Responses for a participant whose data were best fit by a conjunctive rule model. (c) Responses for a participant whose data were fit by a different type of conjunctive rule model. (d) Responses for participants whose data were best fit by an information-integration model.
Much previous work suggests that classifying the stimuli with a procedural learning strategy like the one used by the participant whose responses are plotted in Figure 2d can be best achieved through a form the procedural learning in the striatum that we reviewed above where the visual properties of the stimuli are associated with response processes, and feedback is critical to strengthening these stimulus-response connections (Ashby et al., 1998; Willingham, Wells, Farrell, & Stemwedel, 2000; Ashby, Ell, & Waldron, 2003). As detailed above, there is much neurobiological evidence that feedback triggers a dopamine signal that mediates this type of stimulus-response learning (Wickens & Kotter, 1995; Wickens, Reynolds, & Hyland, 2003). This work suggests that providing feedback around 500ms after the response may lead to better procedural learning than providing feedback immediately, or after a longer delay (1000ms). We test this theory behaviorally, in human participants, by giving feedback either immediately or 500ms or 1,000ms after the response in Experiment 1. Participants perform either a rule-based or an information-integration category learning task where they receive feedback 0ms, 500ms, or 1000ms after a response. Because a simple rule can be used in the rule-based task we do not predict that differences in feedback delays will affect performance in this task because procedural learning is not necessary. However, feedback timing should affect performance in the information-integration task as it will affect whether participants use sub-optimal rules or a procedural form of learning that is optimal for the task.
1.3 Rule-Use and Stimulus Presence
The primary goal of our experiments is to test the effects of feedback timing that are motivated by the neurobiological theory of dopaminergic and glutamatergic activation in the striatum during learning. However, we also consider whether having the stimulus present throughout the presentation of feedback as opposed to having it disappear following the response will also have an effect on learning. As discussed above, unidimensional and conjunctive rules can be used to achieve accuracy levels that are well above chance in the information-integration task, but the use of such rules is not the optimal strategy for the task. Rule-use can be viewed as counterproductive for the information-integration task, and factors that enhance rule use will likely attenuate performance. In addition to manipulating feedback delay we also manipulated whether the stimulus was present or absent on the screen during feedback. To our knowledge the effect of stimulus presence during feedback has not been directly addressed. We reasoned that having the stimulus present would encourage rule-use more than having the stimulus offset upon the response. The presence of the stimulus during feedback may allow participants to evaluate why the rule they used to classify the stimulus did or did not lead to a correct classification on that trial. However, the absence of the stimulus during feedback may make it more difficult to evaluate the efficacy of the rule that was used, and may lead participants to rely on a procedural learning strategy.
Based on this reasoning we manipulated whether the stimulus was present or absent during feedback between subjects by having the stimulus offset at the end of the trial (stimulus present) or immediately following feedback (stimulus absent). We predicted that stimulus presence would enhance rule use and lead to better performance on the rule-based task, but worse performance on the information-integration task, compared to performance when the stimulus was absent during feedback. Alternatively, it is possible that stimulus presence during feedback would not affect rule-use during these tasks, and thus performance would not be affected in either task.
1.4 Overview of the Experiments
In Experiment 1 we test the effects of feedback delay and stimulus presence during feedback in rule-based and information-integration category learning tasks. To do this we used a 3 (feedback delay of 0ms, 500ms, or 1,000ms) × 2 (stimulus present or absence during feedback) × 2 (rule-based or information-integration task) between subjects design. To foreshadow, we find that rule-based performance is best when the stimulus is present throughout feedback, and there is no effect of feedback delay. Information-integration performance is best when the stimulus is absent and there is a 500ms delay, with each of the other conditions leading to lower levels of accuracy and poorer fits of models that assumed a procedural learning strategy.
Experiments 2 and 3 further examine the role of feedback timing in information integration category learning tasks. In Experiment 2 we examine whether varying feedback delay times around 500ms affects information-integration learning. Our results show that a large variance in feedback delay time harms performance, but a small variance does not. In Experiment 3 we examine how stimulus offset delays and feedback delays affect information-integration learning in an attempt to determine whether the delay between the response and feedback or the delay between the stimulus offset and feedback is most critical for information-integration learning. We find some support for the notion that the delay between stimulus offset and feedback presentation is most critical for learning, however these differences are much smaller than in the first two experiments.
2. Experiment 1
2.1 Methods
The experiment was a 2 (Stimulus Present vs. Absent) × 3 (Feedback Delay: 0ms, vs. 500ms, vs. 1000ms) × 2 (Rule-Based vs. Information Integration) between-subjects experiment designed to investigate the effects of two feedback manipulations, stimulus presence and feedback delay, on two types of category-learning tasks.
2.1.1 Participants
240 members of the University of Texas at Austin’s research pool participated in the experiment for course credit or monetary compensation. Participants were randomly assigned to one of the 12 between-subjects conditions outlined above. Data from one participant in the stimulus offset, 1000ms feedback delay, information-integration category structure condition, and one participant in the no stimulus offset, 1000ms feedback delay, rule-based category structure condition were lost due to a computer malfunction. One participant’s data in the stimulus offset, 1000ms feedback delay condition was immediately excluded because they made the same response over the last four blocks of the experiment.
2.1.2 Materials
The experiment was performed on PCs using Matlab software. The screen resolution for each computer was set at 1024 × 768 pixels on 15″ monitors. The category structures used in the Experiment are shown in Figure 1. The stimuli were sine wave gradients (gabor patches) that varied in their spatial frequency and spatial orientation. Examples of the stimuli used are also shown in Figure 1. Each stimulus was 200 × 200 pixels in size, and was placed at the center of the screen on each trial. Each stimulus covered about 4° of visual angle. There were eighty unique stimuli for each type of category structure, and the stimuli were evenly divided into two categories. The stimuli are identical to the stimuli used in previous work from our labs (Markman, Maddox, & Worthy, 2006; Worthy, Markman, & Maddox, 2009; Zeithamova & Maddox, 2006). Table 1 lists the category distribution parameters for the stimuli in each task. The units are arbitrary units that were converted to a stimulus by deriving the frequency [f = .25 + (xi/50)] and the orientation [o=yi(π/500)]. The d’ for the rule-based task was 4.5 and the d’ for the information integration task was 10.3. The purpose of having a larger d’ for the information-integration task is to better equate accuracy rates between the two tasks.
Table 1. Category Distribution Parameters for the Rule-Based and Information-Integration Category Structures Used in Experiment 1.
| Category Structure | μ x | μ y | σ x 2 | σ y 2 | covxy |
|---|---|---|---|---|---|
| Rule-Based | |||||
| Category A | 280 | 125 | 75 | 9000 | 0 |
| Category B | 320 | 125 | 75 | 9000 | 0 |
| Information-Integration | |||||
| Category A | 275 | 150 | 4538 | 4538 | 4351 |
| Category B | 324 | 101 | 4538 | 4538 | 4351 |
2.1.3 Procedure
Participants performed five 80-trial blocks of either a rule-based or information-integration category learning task shown in Figure 1. Each of the eighty stimuli was presented once during each of the five blocks. The order of stimulus presentation was randomized for each block.
At the beginning of the experiment participants were told that they would be determining whether a series of “wavy-objects” belonged to Category 1 or Category 2, and that there would be an equal number of stimuli in each category. On each trial a stimulus appeared and participants had as long as they wished to make a response. Following a response the stimulus would either stay on the screen, in the stimulus present condition or disappear in the stimulus absent condition. One small difference between the current experiment and previous experiments that have investigated the effects of feedback delay in the same perceptual category learning paradigm (Maddox et al., 2003; Maddox & Ing, 2005) is that there was no visual mask presented during the feedback delay in the current experiment because there would have been no way to present a mask in the immediate feedback condition.
The feedback delay interval began following the response. Participants waited either 0ms, 500ms, or 1000ms for corrective feedback, depending on what condition they had been assigned to. Following the feedback delay interval, feedback would be presented for 3500ms. This time was chosen to enhance the stimulus presence manipulation so that participants in the no-stimulus offset conditions would have a good deal of time longer to examine the stimulus throughout feedback. The word “Correct” appeared if the response was correct, and “No that was in (1 or 2)” appeared if they were incorrect. When the 3500ms feedback presentation period was over the next trial began immediately. There was no inter-trial interval.
At the end of each 80-trial block participants were allowed to take a break. No feedback was given regarding the cumulative performance for the previous block. Participants were instructed to press a key when they were ready to begin the next block of trials.
2.2 Results
We first present accuracy analyses for each task and we then present model-based analyses. For the model-based analyses we used decision-bound models like the ones depicted in Figure 2. The primary goal of this analysis is to determine the types of strategies participants used to solve the task. This is particularly informative for the information-integration task where accuracy levels that are well above chance can be achieved by using unidimensional or conjunctive rules.
2.2.1 Accuracy Analyses
To simplify the presentation of our results we present accuracy rates for participants in each condition during the final 80-trial block of trials. This analysis allows us to focus on performance when the task should have been reasonably well-learned.
2.2.1.1 Rule-based Accuracy Analyses
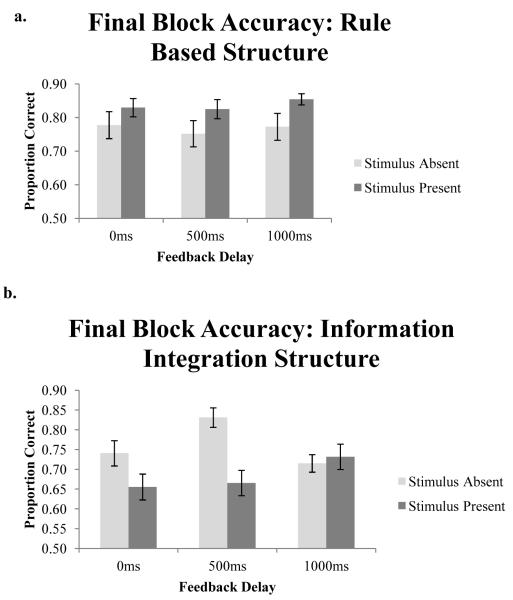
Figure 3a shows the proportion of correct responses for participants in each rule-based condition during the final block of the Experiment. A 2 (Stimulus Offset) × 3 (Feedback Delay) revealed a main effect of stimulus offset, F(1,112)=6.33, p<.05, η2=.05. Participants performed significantly better in the stimulus present condition (M=.84) than in the stimulus absence condition (M=.77). The effect of feedback delay and the stimulus offset × feedback delay interaction were non-significant (both F<1).
Figure 3.
Proportion of correct responses for participants in each condition in Experiment 1 during the final block of trials. (a) Accuracy for participants performing a rule-based task. (b) Accuracy for participants performing an information-integration task.
2.1.1.2 Information-integration Accuracy Analyses
Figure 3b shows the proportion of correct responses for participants in each information integration condition during the final block of the experiment. A 2 (Stimulus Offset) × 3 (Feedback Delay) revealed a main effect of stimulus offset, F(1,113)=10.37, p<.01, η2=.08. Participants were more accurate in the stimulus absent condition (M=.76) than in the stimulus present condition (M=.68). The effect of feedback delay did not reach significance, F(1,113)=1.46, p>.10, but there was a significant stimulus presence × feedback delay interaction, F(1,113)=4.73, p<.05, η2=.08. To identify the locus of the interaction we examined feedback delay within each stimulus presence condition. There was no effect of feedback delay within the stimulus present condition, but there was a significant effect of feedback delay within the stimulus absent condition, F(2,56)=5.27, p<.01, η2=.16. An LSD post-hoc comparison showed that performance was significantly better in the 500ms delay condition (M=.83) than in the 0ms (M=.74, p<.05) or 1,000ms conditions (M=.71, p<.01).
2.2.2 Model-Based Analyses
2.2.2.1 Modeling Method
We fit a series of decision bound models that assume that a decision-bound is used to classify stimuli into each category. As outlined above a series of models with different assumptions or restrictions on where the decision bound can be placed are fit to the data. Models with bounds that are perpendicular to the stimulus dimensions are considered rule-based models, and models with bounds that are oblique to the stimulus dimensions are considered procedural learning models. We fit a total of seven models to the data for each task. These models are summarized in Table 2. We fit two unidimensional rule-based models that placed a decision boundary along either the spatial frequency or spatial orientation dimension. The location of the boundary was a free parameter, and a second free parameter represented perceptual and criterial noise. Higher noise indicates a less deterministic adherence to the choice assumed by the model, and is associated with a poorer fit. We also fit two rule-based models that assumed a conjunctive strategy. These models are depicted in Figures 2b and 2c. These models had free parameters that represented the location of the bound along each perceptual dimension and a parameter that represented the perceptual and criterial noise. We also fit a procedural learning model like the one depicted in Figure 2d. This model, also known as the General Linear Classifier, has free parameters for the slope and y-intercept of the linear bound, and a free parameter for perceptual and criterial noise. We also fit optimal models for each task that assumed that the decision bound was set in the optimal location for each task. These models had only one free parameter for perceptual and criterial noise. Finally, we also fit a random responder model that had one free parameter that represented the probability of classifying an object into Category 1 on any given trial. This model allowed us to examine whether participants were simply behaving randomly. Following the presentation of our modeling results we present an accuracy analysis where participants who were best fit by the random responder model are excluded.
Table 2. Summary of Decision Bound Models.
| Parameters | Parameter Description | |
|---|---|---|
| Rule-Based | ||
| Spatial Frequency | 1 | Frequency, Criterial Noise |
| Spatial Orientation | 2 | Orientation, Criterial Noise |
| Conjunctive A | 3 | Frequency, Orientation, Criterial Noise |
| Conjunctive B | 3 | Frequency, Orientation, Criterial Noise |
| Optimal Model for Rule-Based Task | 1 | Criterial Noise |
| Information-Integration | ||
| General Linear Classifier | 1 | Criterial Noise |
| Optimal Model for Information- Integration Task |
3 | Criteral Noise, Slope, y-intercept |
| Random Responder | 1 | Probability of responding ‘1’ |
We fit the data from the final block of trials for each participant on an individual basis by minimizing negative log-likelihood. We used Akaike weights to compare the relative fit of each model (Wagenmakers & Farrell, 2004; Akaike, 1974). Akaike weights are derived from Akaike’s Information Criterion (AIC) which is used to compare models with different numbers of free parameters. AIC penalizes models with more free parameters. For each model, i, AIC is defined as:
| (1) |
where Li is the maximum likelihood for model i, and Vi is the number of free parameters in the model. Smaller AIC values indicate a better fit to the data. We first computed AIC values for each model and for each participant’s data. Akaike weights were then calculated to obtain a continuous measure of goodness-of-fit. A difference score is computed by subtracting the AIC of the best fitting model for each data set from the AIC of each model for the same data set:
| (2) |
From the differences in AIC we then computed the relative likelihood, L, of each model, i, with the transform:
| (3) |
Finally, the relative model likelihoods are normalized by dividing the likelihood for each model by the sum of the likelihoods for all models. This yields Akaike weights:
| (4) |
These weights can be interpreted as the probability that the model is the best model given the data set and the set of candidate models (Wagenmakers & Farrell, 2004).
2.2.2.2 Modeling Results
2.2.2.2.1 Rule-Based Modeling Results
We computed the Akaike weights for each model for each participant. Table 3 presents the average Akaike weights for each model for participants in each condition. For the rule-based task we summed the Akaike weights for the Frequency and Optimal model for participants in each condition. This provides information regarding the evidence for use of a rule along the spatial frequency dimension for participants in each condition. A 2 (Stimulus Offset) × 3 (Feedback Delay) revealed a main effect of stimulus presence, F(1,112)=5.97, p<.05, η2=.05. There was less evidence for the use of a rule along the spatial frequency dimension in the stimulus absent condition (M=.52) than in the stimulus present condition (M=.63). Next we summed the Akaike weights for the Orientation model and the two conjunctive models. This provides information regarding the evidence for the use of rules other than a unidimensional frequency rule. A 2 (Stimulus Offset) × 3 (Feedback Delay) showed no effect of stimulus presence or feedback delay, and no significant interaction (All F<1). A 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVA for the Akaike weights for the GLC also showed no effect of stimulus presence, F(2,112)=1.15, p>.10, no effect of feedback delay, and no significant interaction (both F<1). For the Akaike weights for the random responder model a 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVA revealed a main effect of stimulus presence, where evidence for the random responder model was higher for participants in the stimulus absent condition (M=.15) than for participants in the stimulus present condition (M=.04).
Table 3. Akaike Weights for Each Model.
| Freq. | Orient. | CJ A | CJ B | GLC | Opt. | Random | |
|---|---|---|---|---|---|---|---|
| Rule-Based Task | |||||||
| Stimulus Absent | |||||||
| 0ms Delay | .36 | .00 | .04 | .14 | .11 | .22 | .12 |
| 500ms Delay | .24 | .00 | .06 | .18 | .11 | .25 | .16 |
| 1000ms Delay | .30 | .00 | .01 | .17 | .16 | .19 | .17 |
| Stimulus Present | |||||||
| 0ms Delay | .33 | .00 | .03 | .19 | .09 | .29 | .07 |
| 500ms Delay | .40 | .00 | .06 | .16 | .12 | .20 | .05 |
| 1000ms Delay | .41 | .00 | .04 | .17 | .13 | .25 | .00 |
| Information-Integration Task | |||||||
| Stimulus Absent | |||||||
| 0ms Delay | .08 | .05 | .19 | .18 | .13 | .26 | .10 |
| 500ms Delay | .03 | .00 | .13 | .04 | .40 | .37 | .02 |
| 1000ms Delay | .18 | .04 | .08 | .26 | .24 | .18 | .01 |
| Stimulus Present | |||||||
| 0ms Delay | .09 | .00 | .11 | .20 | .28 | .05 | .25 |
| 500ms Delay | .07 | .06 | .13 | .14 | .22 | .14 | .25 |
| 1000ms Delay | .07 | .00 | .08 | .24 | .27 | .25 | .09 |
Note: Akaike weights for Frequency (Freq.), Orientation (Orient.), and Conjunctive Rule models (CJA and CJB), and for the Information-Integration models, or the General Linear Classifier model (II), the Optimal model for each task (Opt.) and the Random Responder model (Random).
2.2.2.2.1 Information-Integration Modeling Results
For participants who performed the information integration task we first summed the Akaike weights for the optimal and GLC models. This represents the evidence that participants were using a procedural learning strategy where the decision-bound was oblique to both perceptual dimensions. A 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVA showed no effect of feedback delay, F(2,111)=2.47, p>.10, and no effect of stimulus presence, F(2,113)=2.09, p>.10, but there was a significant interaction F(1,113)=3.86, p<.05, η2=.06.
We performed separate ANOVAs on the summed Akaike weights for the GLC and the optimal model in each stimulus presence condition. In the stimulus present condition there was a significant effect of feedback delay, F(2,57)=4.89, p<.05, η2=.15. An LSD post-hoc comparison showed that evidence for the procedrual models was higher for participants in the 500ms delay condition (M=.77) than in the 0ms delay condition (M=.39, p<.01), or the 1,000ms delay condition (M=.42, p<.05). Within the stimulus absent condition there was no effect of feedback delay, F(2,56)=1.13, p>.10.
Next we examined the summed Akaike weights for the four rule-based models. These represent the evidence for rule use in the final block of the experiment. A 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVA showed no effect of feedback delay, F(2,113)=1.95, p>.10, no effect of stimulus presence, F<1, and no significant interaction F(2,113)=1.99, p>.10. For the Akaike weights for the random responder model, a 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVA showed a significant effect of stimulus presence F(1,113)=8.75, p<.01, η2=.07. There was greater evidence for random responding in the stimulus present condition (M=.20) than in the stimulus absent condition (M=.04). The effect of feedback delay, F(2,113)=1.98, p>.10, and the interaction (F<1) did not reach significance.
2.2.3 Accuracy Analyses without Random Responders
For the rule-based task we found that participants in the stimulus absent condition showed more evidence of random responding than participants in the stimulus present condition, while we observed the opposite pattern in the information-integration conditions. The issue of random responding has been discussed in previous work, and participants who show evidence of behaving randomly have sometimes been removed from analyses (e.g. Newell, Dunn, & Kalish, 2010, Maddox & Ing, 2005). It is difficult or impossible to determine whether participants are responding randomly because they have not adequately learned the task or whether they are doing so intentionally. However, it is important to examine the degree to which random responding, for whatever reason, led to performance differences in the task.
To examine this issue we performed 2 (Stimulus Offset) × 3 (Feedback Delay) ANOVAs on the final block accuracy levels for both task types after removing participants who had Akaike weights of .50 or higher for the random responder model. For the rule-based task the effect of stimulus presence was no longer significant, F(1,98)=1.13, p>.10, and the effect of feedback delay and the interaction were also non-significant (both F<1).
For the information-integration task the effect of stimulus presence was marginally significant, F(1,100)=3.38, p<.10, η2=.04, and the feedback delay × stimulus presence interaction was also marginally significant, F(2,100)=3.01, p<.10, η2=.06. An ANOVA with feedback delay as the independent variable within the stimulus absent condition showed a significant effect of feedback delay, F(2,54)=5.42, p<.01, η2=.17, and an LSD post-hoc test showed that accuracy for participants in the 500ms delay condition was marginally higher than accuracy for participants in the 0ms delay condition (p<.10), and significantly higher than accuracy for participants in the 1,000ms delay condition (p<.01).
2.3 Discussion
The results support our predictions based on a prominent neurobiological theory of learning in the striatum (e.g. Wickens & Kotter, 1995; Lindskog et al., 2006; Fernandez, et al., 2006). Accuracy in the information-integration task was highest when there was a feedback delay of 500ms and the stimulus was absent throughout feedback. These effects were only slightly attenuated when we excluded random responders. Data from participants in the stimulus absent 500ms delay condition were better fit by procedural learning models that assumed a linear decision bound that was oblique to each perceptual dimension, than by models that assumed unidimensional or conjunctive rules or random responding.
For the rule-based task performance was best when the stimulus was present on the screen throughout feedback, and there was no effect of feedback delay. The computational modeling analyses suggests that data from participants in the stimulus present condition were better fit by the models that assumed a rule along the spatial frequency dimension compared to participants in the stimulus absent condition. However, the effect of stimulus presence disappeared when participants who showed high evidence of random responding were removed from the analysis. In the rule-based task 5% of participants in the stimulus present condition were classified as random responders compared to 18% of participants in the stimulus absent condition. This difference is significant by a binomial test (p<.05). While it is impossible to tell whether participants were best fit by the random responder model due to intentionally random behavior or because they were trying to perform well but could not adequately learn the task due to the stimulus presence manipulation, the significant difference in the number of random responders between the two conditions supports the notion that the stimulus presence manipulation was the source of the disparity.
3. Experiment 2
In Experiment 1 we found that a 500ms feedback delay led to the best information-integration category-learning as long as the stimulus was absent during feedback. In Experiment 2 we tested whether the degree of variance in feedback delay around a mean feedback delay of 500ms would affect performance. Participants were randomly placed into one of two feedback delay variance conditions. In the low variance condition the feedback delay intervals had a standard deviation of 75ms, and in the high variance condition the feedback delay intervals had a standard deviation of 150ms around the mean feedback delay interval of 500ms. We predicted that the participants in the low variance condition would outperform participants in the high variance condition because feedback would be given at times that led to better procedural learning on a larger portion of trials in the low variance condition compared to the high variance condition. Such a finding would conceptually replicate and extend the findings of Experiment 1 and support the neurocomputational theory of learning in the striatum that predicts that calcium and dopamine levels simultaneously peak, leading to the best procedural learning, if feedback is given several hundred milliseconds after a response has been made.
3.1 Method
Forty participants from the University of Texas community participated in the experiment for course credit or monetary compensation. The materials and procedure were the same as those in the stimulus absent information-integration condition from Experiment 1 with the exception that the corrective feedback delay intervals were normally distributed around a mean feedback delay interval of 500ms. Participants performed 5 80-trial blocks of the information integration task.
3.2 Results
3.2.1 Accuracy Analyses
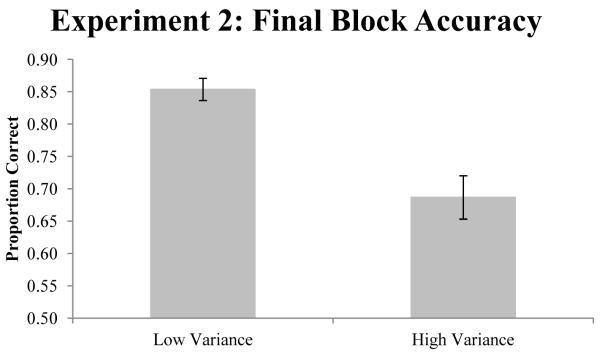
Figure 4 shows the overall proportion of correct responses during the final block of trials. An ANOVA comparing performance for participants performing the task with low and high variance in feedback delay intervals showed a significant difference between the two conditions, F(1,38)=19.70, p<.001, η2=.34. Participants who performed the task with low variance in the length of feedback delay intervals were more accurate than participants who performed the task with high variance.
Figure 4.
Proportion of correct responses during the final block of trials.
3.2.2 Model-based analyses
We fit the same set of decision bound models that were fit to the data for participants in the information-integration condition in Experiment 1. Table 4 shows the Akaike weights for each model for participants in each condition during the final block of trials. These weights can be interpreted as evidence that each model was the best model given the data and the set of models fit.
Table 4. Akaike Weights for Each Model.
| Freq. | Orient. | CJ A | CJ B | GLC | Opt. | Random | |
|---|---|---|---|---|---|---|---|
| Low Variance | .00 | .00 | .10 | .15 | .39 | .36 | .00 |
| High Variance | .08 | .04 | .02 | .15 | .30 | .19 | .22 |
Note: Akaike weights for Frequency (Freq.), Orientation (Orient.), and Conjunctive Rule models (CJA and CJB), and for the Information-Integration models, or the General Linear Classifier model (II), the Optimal model for each task (Opt.) and the Random Responder model (Random).
We performed the same analyses done for the information-integration task data from Experiment 1. We first examined the summed weights for the optimal and general linear classifier models which assumed a decision-bound that was oblique to each perceptual dimension. An ANOVA showed a marginally significant effect of feedback delay variance, F(1,38)=3.91, p<.10, η2=.09. Participants in the low variance condition (M=.75) had higher Akaike weights for the procedural learning models than participants in the high variance condition (M=.49). An ANOVA on the summed Akaike weights for the four rule-based models was not significant (F<1), but there was a significant difference in evidence for the random responder model, F(1,38)=6.05, p<.05, η2=.14.
3.2.3 Accuracy Analyses without Random Responders
To examine the extent to which the difference in accuracy between the two conditions was due to random responders we excluded data sets that had Akaike weights for the random responder model that were greater than .50. This excluded five participants from the high variance condition and zero participants from the low variance condition. An ANOVA on the proportion of correct responses during the final block of trials for the remaining participants was significant, F(1,33)=11.42, p<.01, η2=.25.
3.3 Discussion
Accuracy for participants in the low feedback delay variance condition was significantly higher than accuracy for participants in the high feedback delay variance condition. Decision-bound models showed a marginal difference in procedural strategy use, and a significant difference in random responding, but no difference in rule-based strategy use. The difference in accuracy remained significant after excluding participants who were fit best by the random responder model. These results demonstrate that information-integration learning is best when feedback is consistently given around 500ms after the response has been made.
4. Experiment 3
We conducted a third experiment designed to further examine the effects of feedback timing on information-integration learning in finer detail. In the 500ms delay stimulus absent condition in Experiment 1 (where the robust effect of corrective feedback delay interval was found) the stimulus offset immediately following the response. The immediate offset of the stimulus combined with the proprioceptive feedback associated with the button-press provided both visual and tactile cues that a response had been made and that feedback was forthcoming. In Experiment 3 we examine the effects of decoupling the visual and proprioceptive information that a response has been received by introducing small delays between when a response is made and when the stimulus offsets.
The neurobiological theory of learning in the striatum that we reviewed in the Introduction asserts that the visual properties of the stimuli are associated with response processes. In the stimulus offset conditions in Experiments 1 and 2 the stimulus offset when a response was made and feedback delays of 500ms led to the best learning. However, one remaining question is whether it is the delay between the response (made by a button press) and feedback presentation, or the delay between the stimulus offset and the feedback presentation that affects performance. We examine this issue in the present Experiment by manipulating when the stimulus offsets from the screen. Specifically we examine performance under three conditions:
The stimulus offsets immediately following a response and feedback is presented 500ms after the response (this is identical to the condition that led to the best information-integration learning in Experiment 1),
The stimulus offsets 250ms following the response and feedback arrives 250ms later (500ms delay between response and feedback), and
The stimulus offsets 250ms after the response and feedback arrives 500ms later (750ms delay between response and feedback).
The first condition is a replication of the condition from Experiment 1 that led to the best procedural learning. The latter two conditions examine whether the delay between response and feedback (Condition 2), or between the stimulus offset and feedback (Condition 3) are most critical to learning.
4.1 Methods
Seventy-five participants from the University of Texas community participated in the experiment for course credit or monetary compensation. The procedure was the same as that for participants in the information-integration stimulus absent conditions from Experiment 1 with the exception that the stimulus offset and corrective feedback delay intervals were manipulated between subjects. The stimulus offset delay and feedback delay intervals for participants in each of the three conditions are listed above. Each participant performed five 80-trial blocks of the information integration task.
4.2 Results
4.2.1 Accuracy analyses
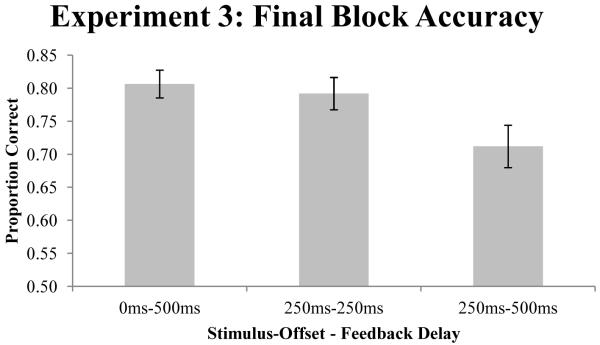
Figure 5 shows the proportion correct for each condition during the final block of trials. An ANOVA over the final block accuracy was significant, F(2,72)=3.76, p<.05, η2=.10, and an LSD post-hoc test showed that participants in the 250ms-250ms offset-delay condition performed significantly worse than participants in the 0ms-500ms offset-delay condition and participants in the 250ms-500ms offset delay condition (both p<.05). There was no difference in final block accuracy between participants in the 0ms-500ms and 250ms-500ms conditions (p>.10).
Figure 5.
Final block accuracy for participants in each condition in Experiment 3. The numbers for each condition listed along the x-axis indicate the stimulus offset delay followed by the corrective feedback delay.
4.2.2 Model-based analyses
We used the same decision-bound modeling approach used in our first two experiments. Table 5 lists the Akaike weights for participants in each condition. An ANOVA on the summed Akaike weights for the general and optimal linear classifier models was not significant, F(2,72)=1.14, p>.10. An ANOVAs for the summed Akaike weights for the four rule-based models was also non-significant (F<1), and an ANOVA on the Akike weights for the random responder model was also non-significant, F(2,72)=1.18, p>.10.
Table 5. Akaike Weights for Each Model.
| Freq. | Orient. | CJ A | CJ B | GLC | Opt. | Random | |
|---|---|---|---|---|---|---|---|
| 0ms -500ms | .08 | .00 | .14 | .17 | .21 | .39 | .00 |
| 250ms - 250ms | .07 | .00 | .25 | .13 | .23 | .29 | .05 |
| 250ms - 500ms | .16 | .03 | .04 | .25 | .14 | .26 | .11 |
Note: Akaike weights for Frequency (Freq.), Orientation (Orient.), and Conjunctive Rule models (CJA and CJB), and for the Information-Integration models, or the General Linear Classifier model (II), the Optimal model for each task (Opt.) and the Random Responder model (Random).
4.2.3 Accuracy Analyses without Random Responders
We also examined accuracy for each condition after excluding participants who had Akaike weights for the random responder model that were greater than .50 for the final block of trials. This excluded zero participants from the 0ms-500ms condition, three participants from the 250ms-250ms condition, and two participants from the 250ms-500ms condition. After removing these participants, an ANOVA was non-significant, F(2,72)=1.79, p>.17. An LSD post-hoc showed a marginally significant difference between participants in the 0ms-500ms and 250ms-250ms conditions (p<.10), but the difference between participants in the 250ms-250ms and 250ms-500ms conditions did not reach significance (p>.10).
4.3 Discussion
Accuracy was worse when the stimulus offset 250ms after the response was made and feedback was given 250ms later, compared to conditions where feedback was given 500ms after the stimulus offset. These results suggest that the delay between when the stimulus offsets and when feedback is given may be more important than the delay between when the response is made and when feedback is given. However, decision-bound modeling showed no qualitative differences in strategy use between participants in each condition, and the effects of stimulus offset and feedback delay timing were attenuated when random responders were excluded from the analysis. One interpretation of these results is that participants in the 250ms-250ms condition may have simply been more distracted by the delay in stimulus offset, and this led to particularly poor performance for participants in those conditions. However, this does not account for the performance for participants in the 250ms-500ms condition that was no different than performance for participants in the 0ms-500ms condition. The total delay between when the button press response was made and when feedback was given was between 500ms-750ms in all three conditions, and such small differences may not lead to different levels of performance or to qualitative differences in strategy use (e.g. increased rule-use).
5. General Discussion
Across three experiments we found that feedback delay timing had large effects on information-integration category learning. These effects were only found when the stimulus was absent following the response, and we found no evidence that rule-based category learning was affected by feedback delay timing. Long feedback delays hurt procedural learning. This coincides with previous work that showed a similar effect, but with much longer feedback delays (2500ms in Maddox et al., 2003 and Maddox & Ing, 2005, versus 1000ms in Experiment 1). We also found that no delay, or immediate feedback presentation, hurt procedural learning, as did a large variance in feedback delay times around a mean time of 500ms (Experiment 2).
These results support neurobiological theories of procedural learning that suggest that this form of learning is best when calcium (mediated by glutamate) and dopamine levels peak simultaneously, and that this is likely to occur when feedback is given 500ms after a response has been made. This type of stimulus-response learning may be most needed when simple verbalizable rules cannot be used to categorize stimuli into the correct category. While we did not ask participants whether they could verbalize a rule they were using to distinguish the members of each category much previous work has been grounded on the assumption that the optimal strategy is more difficult to verbalize in the information-integration task than in the rule-based task (Ashby et al., 1998; Ashby & Maddox, 2005; Minda & Miles, 2010; Stanton & Nosofsky, 2007).
In addition to the finding that information-integration learning was best when the stimulus was absent and feedback was given approximately 500ms after the response we also found that performance in the rule-based task was better when the stimulus was present throughout feedback than when it offset following the response. This supported our a priori prediction that having the stimulus present throughout feedback presentation may facilitate rule-use by allowing participants extra time to evaluate the efficacy of the rule they used to classify the stimulus on each trial. However, this difference was entirely due to a significantly higher proportion of random responders in the stimulus absent condition (18%) than in the stimulus present condition (5%). Interpreting random responding is difficult and many previous researchers have excluded random responders from their analyses (e.g. Newell et al., 2010, Maddox & Ing, 2005). Here we included analyses both with and without random responding so the results could be viewed both ways.
One characteristic of the unidimensional rule-based task used in Experiment 1 is that there is not a sub-optimal strategy that can be used to achieve a an above-chance level of performance like there is in the information-integration task. For example, unidimensional and conjunctive rules can lead to accuracy levels that are well above chance in the information-integration task as illustrated in Figure 2, but using a rule along the spatial frequency dimension is the only viable strategy in the rule-based task. The question of whether some participants were intentionally responding randomly or whether they failed to learn the rule along the spatial frequency dimension is difficult or impossible to answer.
One way that future work could avoid this problem is to use rule-based tasks where sub-optimal rules can lead to accuracy that is above chance. For example, other work from our labs has utilized a category structure where the use of a conjunctive rule can lead to perfect accuracy, but the use of unidimensional rules can lead to reasonably high, but imperfect accuracy rates (Worthy, Brez, Markman, & Maddox 2011; Maddox, Markman, & Baldwin, 2006; Grimm, Markman, Maddox, & Baldwin, 2009). Such a category structure may make the difference between sub-optimal and random behavior more discernible.
5.1 Rule-use versus procedural learning strategies
The distinction between rule-based and procedural learning strategies has been a major focus of category-learning research over the past twenty years (Ashby et al., 1998; Ashby & Ell, 2001; Nomura, et al., 2007; Daniel & Pollmann, 2010; Seger & Cincotta, 2002). Much of this research has focused on differences between rule-based and procedural learning systems, but this view has been challenged by others who propose a single category-learning system (e.g. Newell et al., 2010; Stanton & Nosofksy, 2007; Nosofky & Johansen, 2000; Zaki & Nosofksy, 2001). A shortcoming of these single-systems views is that they ignore evidence that different brain regions mediate different forms of learning (Poldrack & Packard, 2003). Brain regions like the striatum that mediate procedural forms of learning operate in different ways that brain regions like the hippocampus and prefrontal cortex that mediate declarative forms of learning
A recent study by Smith and colleagues found no difference in the rate at which pigeons learned rule-based and information-integration categories, yet humans learned rule-based categories three to ten times faster than equivalent information-integration categories (Smith et al., 2011; Maddox et al., 2003; Ashby, Ell, & Waldron, 2003). This suggests that the use of abstract rules to classify members of each category is an analytic process that is phylogenetically new (see also Smith, J.D., Beran, M.J., Crossley, M.J., Boomer, J., & Ashby, F.G., 2010). Humans may have developed a privileged ability to use rules as easy heuristics to learn to categorize stimuli much more quickly than they would if rule-use was difficult (Gigerenzer & Brighton, 2009). The use of rules or heuristics can be adaptive or advantageous in many situations, but rule-use can also be counterproductive in some situations, as in the information-integration learning tasks like the one we used in the present work. Our results demonstrate that it is important to consider the type of problem that must be learned and the neurobioloical processes that mediate that form of learning when considering how to best provide feedback, and the ease with which rules can be used to solve the problem is an important factor.
5. Conclusion
Here we demonstrated that feedback timing is critical in learning situations where abstract, analytical rule-based strategies lead to sub-optimal performance. This is one of the first behavioral studies to show that manipulations of feedback predicted by neurobiological studies have a significant effect on learning at the behavioral level in humans. Information-integration category learning was best when feedback was given approximately 500ms after a response was made across three separate experiments. Both shorter and longer delays, as well as high variance in feedback delay times led to poorer learning, as did having the stimulus present throughout feedback. In contrast, rule-based learning was unaffected by feedback delay timing and best when the stimuli were present throughout feedback. These results expand our knowledge of how feedback can be given to ensure the best learning in different situations.
Acknowledgements
This research was supported by NIMH grant MH077708 to ABM and WTM and a supplement to NIMH grant MH077708 to DAW. We thank Bo Zhu, Devon Greer and other members of the Maddox Lab for their help with data collection.
References
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19:716–723. [Google Scholar]
- Alexander GE, DeLong MR, Strick PL. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annual Review of Neuroscience. 1986;9:357–381. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Crossley MJ. Interactions between declarative and procedural-learning categorization systems. Neurobiology of Learning and Memory. 2010;94:1–12. doi: 10.1016/j.nlm.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby FG, Ell SW. The neurobiology of category learning. Trends in Cognitive Sciences. 2001;5:204–210. doi: 10.1016/s1364-6613(00)01624-7. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ell SW, Waldron EM. Procedural learning in perceptual categorization. Memory & Cognition. 2003;31:1114–1125. doi: 10.3758/bf03196132. [DOI] [PubMed] [Google Scholar]
- Butler AC, Karpicke JD, Roediger HL., III The effect of type and timing of feedback on learning from multiple-choice tests. Journal of Experimental Psychology: Applied. 2007;13:273–281. doi: 10.1037/1076-898X.13.4.273. [DOI] [PubMed] [Google Scholar]
- Butler AC, Roediger HL., III Feedback enhances the positive effects and reduces the negative effects of multiple-choice testing. Memory & Cognition. 2008;36:604–616. doi: 10.3758/mc.36.3.604. [DOI] [PubMed] [Google Scholar]
- Butler DL, Winne PH. Feedback and self-regulated learning: A theoretical synthesis. Review of Educational Research. 1995;65:245–281. [Google Scholar]
- Daniel R, Pollmann S. Comparing the neural basis of monetary reward and cognitive feedback during information-integration category learning. Journal of Neuroscience. 2010;30:47–55. doi: 10.1523/JNEUROSCI.2205-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ell SW, Ing AD, Maddox WT. Criterial noise effects on rule-based category learning: The impact of delayed feedback. Attention, Perception, & Psychophysics. 2009;71:1263–1275. doi: 10.3758/APP.71.6.1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gigerenzer G, Brighton H. Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science. 2009;1:107–143. doi: 10.1111/j.1756-8765.2008.01006.x. [DOI] [PubMed] [Google Scholar]
- Grimm LR, Markman AB, Maddox WT, Baldwin GC. Stereotype threat reinterpreted as a regulatory mismatch. Journal of Personality and Social Psychology. 2009;96:288–304. doi: 10.1037/a0013463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattie J, Timperley H. The power of feedback. Review of Educational Research. 2007;77:81–112. [Google Scholar]
- Lindskog M, Kim M, Wikstrom MA, Blackwell KT, Kotaleski JH. Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLoS Computational Biology. 2006;2(9):e119. doi: 10.1371/journal.pcbi.0020119. DOI: 10.1371/journal.pcbi.0020119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Bohil CJ. Delayed feedback effects on rule-based and information-integration category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:650–662. doi: 10.1037/0278-7393.29.4.650. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG. Dissociating explicit and procedural-learning based systems of perceptual category learning. Behavioural Processes. 2004;66:309–332. doi: 10.1016/j.beproc.2004.03.011. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Baldwin GC, Markman AB. Regulatory focus effects on cognitive flexibility in rule-based classification learning. Memory and Cognition. 2006;34:1377–1397. doi: 10.3758/bf03195904. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Bohil CJ, Ing AD. Evidence For a Procedural Learning-Based System in Category Learning. Psychonomic Bulletin & Review. 2004;11:945–952. doi: 10.3758/bf03196726. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Filoteo JV. Striatal contribution to category learning: Quantitative modeling of simple linear and complex non-linear rule learning in patients with Parkinson’s disease. Journal of the International Neuropsychological Society. 2001;7:710–727. doi: 10.1017/s1355617701766076. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ing AD. Delayed feedback disrupts the procedural learning system but not the hypothesis testing system in perceptual category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31:100–107. doi: 10.1037/0278-7393.31.1.100. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Lauritzen JS, Ing AD. Cognitive complexity effects in perceptual classification are dissociable. Memory & Cognition. 2007;35:885–894. doi: 10.3758/bf03193463. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Love BC, Glass BD, Filoteo JV. When more is less: Feedback effects in perceptual category learning. Cognition. 2008;108:578–589. doi: 10.1016/j.cognition.2008.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markman AB, Maddox WT, Worthy DA. Choking and excelling under pressure. Psychological Science. 2006;17:944–948. doi: 10.1111/j.1467-9280.2006.01809.x. [DOI] [PubMed] [Google Scholar]
- Metcalfe J, Kornell N, Finn B. Delayed versus immediate feedback in children’s and adults’ vocabulary learning. Memory & Cognition. 2009;37:1077–1087. doi: 10.3758/MC.37.8.1077. [DOI] [PubMed] [Google Scholar]
- Miles SJ, Minda JP. The effects of concurrent verbal and visual tasks on category learning. Journal of Experimental Psychology: Learning, Memory & Cognition. doi: 10.1037/a0022309. in press. [DOI] [PubMed] [Google Scholar]
- Nomura EM, Maddox WT, Filoteo JV, Ing AD, Gitelman DR, Parrish TB, Mesulam M-M, Reber PJ. Neural correlates of rule-based and information-integration visual category learning. Cerebral Cortex. 2007;17:37–43. doi: 10.1093/cercor/bhj122. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Gluck MA, Palmeri TJ, McKinley SC, Glauthier P. Comparing model of rule-based classification learning: A replication and extension of Shepard, Hovland, and Jenkins. 1994 doi: 10.3758/bf03200862. 1961. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Johansen MK. Exemplar-based accounts of multiple-system phenomena in perceptual categorization. Psychonomic Bulletin & Review. 2000;7:375–402. [PubMed] [Google Scholar]
- Pashler H, Cepeda NJ, Wixted JT, Rohrer D. When does feedback facilitate learning of words. Journal of Experimental Psychology: Learning, Memory & Cognition. 2005;31:3–8. doi: 10.1037/0278-7393.31.1.3. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Packard MG. Competition among multiple memory systems: converging evidence from animal and human brain studies. Neuropsychologia. 2003;41:245–251. doi: 10.1016/s0028-3932(02)00157-4. [DOI] [PubMed] [Google Scholar]
- Seger CA, Cincotta CM. Striatal activity in concept learning. Cognitive, Affective, & Behavioral Neuroscience. 2002;2:149–161. doi: 10.3758/cabn.2.2.149. [DOI] [PubMed] [Google Scholar]
- Shepard RN, Hovland CI, Jenkins HM. Learning and memorization of classifications. Psychological Monographs. 1961;75 13, Whole No. 517. [Google Scholar]
- Smith JD, Ashby FG, Berg ME, Murphy MS, Spiering B, Cook RG, Grace RC. Pigeons’ categorization may be exclusively nonanalytic. Psychonomic Bulletin & Review. 2011;2:414–421. doi: 10.3758/s13423-010-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JD, Beran MJ, Crossley MJ, Boomer J, Ashby FG. Implicit and explicit category learning by macaques (Macaca mulatta) and humans (Homo sapiens) Journal of Experimental Psychology: Animal Behavior Processes. 2010;36:54–65. doi: 10.1037/a0015892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith TA, Kimball DR. Learning from feedback: Spacing and the delay-retention effect. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:80–95. doi: 10.1037/a0017407. [DOI] [PubMed] [Google Scholar]
- Spiering BJ, Ashby FG. Response processes in information-integration category learning. Neurobiology of Learning and Memory. 2008;90:330–338. doi: 10.1016/j.nlm.2008.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenmakers EJ, Farrell S. AIC model selection using Akaike weights. Psychonomic Bulletin & Review. 2004;11:192–196. doi: 10.3758/bf03206482. [DOI] [PubMed] [Google Scholar]
- Wickens J. A Theory of the Striatum. Pergamon Press; New York: 1993. [Google Scholar]
- Wickens J, Kotter R. Cellular models of reinforcement. In: Houk JC, Davis JL, Beiser DG, editors. Models of Information Processing in the Basal Ganglia. MIT Press; Cambridge, MA: 1995. pp. 187–214. [Google Scholar]
- Wickens JR, Reynolds JNJ, Hyland BI. Neural mechanisms of reward-related motor learning. Current Opinion in Neurobiology. 2003;13:685–690. doi: 10.1016/j.conb.2003.10.013. [DOI] [PubMed] [Google Scholar]
- Willingham DB, Wells LA, Farrell JM, Stemwedel ME. Implicit motor sequence learning is represented in response locations. Memory & Cognition. 2000;28:366–375. doi: 10.3758/bf03198552. [DOI] [PubMed] [Google Scholar]
- Wilson CJ. The contribution of cortical neurons to the firing pattern of striatal spiny neurons. In: Houk JC, Davis JL, Beiser DG, editors. Models of Information Processing in the Basal Ganglia. MIT Press; Cambridge, MA: 1995. pp. 29–50. [Google Scholar]
- Worthy DA, Brez CC, Markman AB, Maddox WT. Motivational influences on cognitive performance in children: Focus over fit. Journal of Cognition and Development. 2011;12:103–119. doi: 10.1080/15248372.2010.535229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worthy DA, Markman AB, Maddox WT. What is pressure? Evidence for social pressure as a type of regulatory focus. Psychonomic Bulletin and Review. 2009;16:344–349. doi: 10.3758/PBR.16.2.344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaki SR, Nosofsky RM. A single-system interpretation of dissociations between recognition and categorization in a task involving object-like stimuli. Cognitive, Afective, & Behavioral Neuroscience. 2001;1:344–359. doi: 10.3758/cabn.1.4.344. [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT. Dual task interference in perceptual category learning. Memory & Cognition. 2006;34:387–398. doi: 10.3758/bf03193416. [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT. The role of visuospatial and verbal working memory in perceptual category learning. Memory & Cognition. 2007;35:1380–1398. doi: 10.3758/bf03193609. [DOI] [PubMed] [Google Scholar]