Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Jan 31;3:1178. doi: 10.1038/srep01178

Epidemic potential of an emerging vector borne disease in a marginal environment: Schmallenberg in Scotland

Paul R Bessell 1,a, Kate R Searle 2, Harriet K Auty 3, Ian G Handel 1, Bethan V Purse 2, B Mark deC Bronsvoort 1
PMCID: PMC3560360  PMID: 23378911

Abstract

During 2011 Schmallenberg virus (SBV) presented as a novel disease of cattle and sheep that had apparently spread through northern Europe over a relatively short period of time, but has yet to infect Scotland. This paper describes the development of a model of SBV spread applied to Scotland in the event of an incursion. This model shows that SBV spread is very sensitive to the temperature, with relatively little spread and few reproductive losses predicted in years with average temperatures but extensive spread (>1 million animals infected) and substantial reproductive losses in the hottest years. These results indicate that it is possible for SBV to spread in Scotland, however spread is limited by climatic conditions and the timing of introduction. Further results show that the transmission kernel shape and extrinsic incubation period parameter have a non-linear effect on disease transmission, so a greater understanding of the SBV transmission parameters is required.

Reports of short-term pyrexia, diarrhoea and reduced milk production in dairy herds in Western Germany in August 2011 prompted identification of a new emerging disease, that became known as Schmallenberg virus1,2 (SBV). An Orthobunyavirus of the Simbu serogroup, SBV is closely related to Akabane and Shamonda viruses. Similar to Akabane virus, SBV infection can cause clinical disease in cattle, sheep and goats, characterised by pyrexia, reduced milk production, abortions and congenital malformations among offspring whose mothers are infected during a particular period of pregnancy1,2. Aside from congenital infection, the main transmission route is via arthropod vectors (principally Culicoides spp)1,3,4,5,6. During late 2011 and early 2012 cases were identified in a number of northern European countries7 including 276 farms in England and the Channel Islands where SBV was identified in aborted or malformed calves or lambs (as of 26th July 2012)8.

As a newly identified pathogen, the epidemiology of SBV is not yet fully known. However, information available so far on the clinical picture and transmission routes suggest it is sufficiently similar to Akabane virus to use knowledge of Akabane to assist our understanding of SBV9. Furthermore, recent studies of the epidemiology of another Culicoides-borne arbovirus, Bluetongue virus (BTV), can be used to draw inference for the epidemiology of SBV within vector populations. Previous studies have suggested that the potential for spread of arboviruses in Europe may be driven by climate change10,11,12 and such changes, specifically temperature increases, may determine the potential for spread of SBV and other arboviruses in Scotland.

Previous studies13,14,15 have characterised the Culicoides populations in Scotland which include a number of species, principally C. pulicaris and C. obsoletus that feed on wildlife and livestock species, and one species C. impunctatus that also feeds on humans. These species have very different ecologies13,15 with C. impunctatus dominating in bog and heathland habitats whilst other C. pulicaris complex species and C. obsoletus complex species are primarily associated with pastural livestock farming.

Some information is available on vectoral capacity of these species for BTV that also has relevance for SBV transmission. Relative to C.obsoletus and C. pulicaris complex species, C. impunctatus is thought to be an inefficient vector species, due to its wide host preference including humans16, lower ability to replicate BTV in the laboratory than other Palaearctic species (0.4% versus 0.5–13% in C.obsoletus and C. pulicaris complex species17,18) and autogeny, where the female may lay its first batch of eggs without taking a bloodmeal19. However, its high population densities in Scotland and northern England (landing rates of 10–635 midges/min on an exposed human arm17) may compensate for these characteristics and allow C. impunctatus to transmit BTV and potentially SBV.

At the time of writing there have been no confirmed cases of animals being infected in Scotland. One seropositive animal has been found, that is believed to have been infected prior to import from southern England. However, due to the proximity to England and the large abundance of Culicoides vectors throughout Scotland13,15 there remains a risk of introduction of SBV into the Scottish vector and livestock population. Assessment of the likely extent of spread and ramifications in Scotland would aid control and deployment of resources following introduction. Therefore, the aims of this paper are as follows:

  1. To investigate the likely extent and impact of an SBV epidemic in Scotland.

  2. To explore the effect of temperature on the risk of SBV spread in Scotland and the potential effect of climatic warming on SBV transmission.

  3. To explore the importance of the parameters of SBV transmission, in particular the parameters relating to the vector.

Results

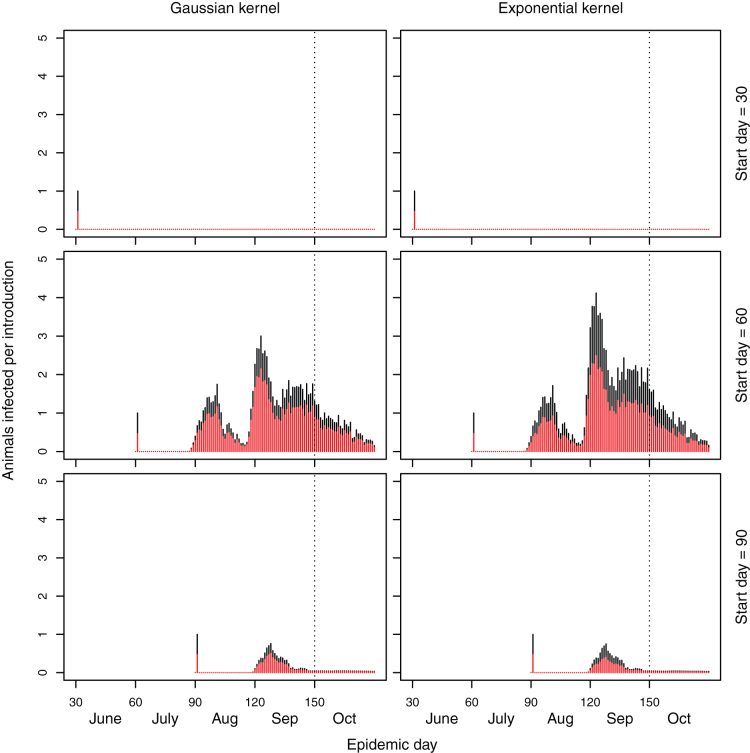
A stochastic simulation model was used to investigate the likely transmission of SBV in Scotland. The model incorporates the transmission of disease from host to vector and from vector to host following the introduction of disease (seeding) on between 1 and 10 farms. Transmission between and within individual farms is determined by a transmission kernel that describes the vector dispersal potential. The distribution of the number of sheep and cattle infected under the baseline model is shown in Figure 1.

Figure 1. Stacked barplots of the number of sheep (red bars) and cattle (black bars) infected on each day of the simulated epidemic under the baseline implementation in which the mean temperature is used.

Figure 1

Open in a new tab

The dashed line represents the start of the period in which in-lamb ewes may be at risk of reproductive losses.

Under the baseline scenario using the mean temperature the resulting number of animals infected is relatively low (Table 1, Figure 1). There is a small epidemic if disease is introduced on day 60, with around 14 ewes with potential reproductive losses (Table 1, Figure 1). There is little disease spread if there is introduction earlier or later than day 60.

Table 1. Summary of results from the different model implementations in this study.

Baseline model–mean temperature
Start day Kernel Proportion spread mean (sd) farms affected mean (sd) cattle infected mean (sd) sheep infected mean (sd) ewes at risk*
30 Gaus 0.009 5.51 (2.89) 2.93 (1.92) 2.59 (1.80) 0.00 (0.01)
Exp 0.01 5.52 (2.90) 2.94 (1.95) 2.59 (1.80) 0.00 (0.01)  
60 Gaus 0.983 368 (242) 172 (161) 379 (351) 13.0 (18.2)
Exp 0.981 300 (203) 275 (295) 401 (427) 12.8 (20.2)  
90 Gaus 0.982 52.0 (47.4) 21.2 (39.1) 38.3 (67.5) 0.73 (7.09)
Exp 0.980 46.3 (31.3) 26.9 (52.0) 31.9 (51.4) 0.57 (5.44)  
120 Gaus 0 5.49 (2.87) 2.93 (1.93) 2.56 (1.77) 0.00 (0)
Exp 0 5.49 (2.86) 2.94 (1.94) 2.55 (1.77) 0.00 (0)  
Open in a new tab

*Ewes at risk of reproductive losses.

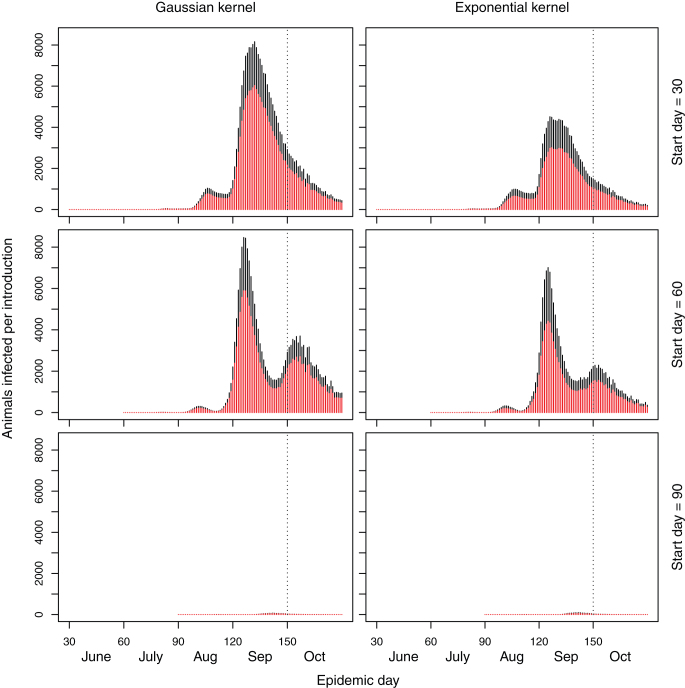
Under the extreme case scenario using the maximum observed temperature (mean difference between mean and maximum temperature is 1.96°C), there is substantial disease spread (Table 1, Figure 2). The key determinant of the size of epidemic is the date of introduction (Table 1, Figure 2). The greatest number of infected animals follows a disease introduction on day 60 (30th June) as this period corresponds with the highest temperatures and therefore the highest potential for spread. Infection on day 90 results in only a small number of infected animals (Figure 2). The epidemic spreads in distinct waves (Figure 1) that correspond with the Extrinsic Incubation Period (EIP). The number of sheep that are at risk of reproductive losses is considerably higher with an introduction on day 60 compared to introduction on day 30. The proportion of infected cattle that are at risk of reproductive losses is not shown because: 1) the window at which cattle are at risk is much wider (between days 62nd and 173rd day of pregnancy20) and 2) the window over which cattle are serviced (mated) is widely distributed through the year. Therefore many of the cattle infected may be at risk of reproductive losses, but these factors make the precise impact harder to predict than they are in sheep.

Figure 2. Stacked barplots of the number of sheep (red bars) and cattle (black bars) infected on each day of the simulated epidemic when the maximum temperature is used.

Figure 2

Open in a new tab

The broken line represents start of the period in which in-lamb ewes may be at risk of reproductive losses. Note the different scale compared to Figure 1.

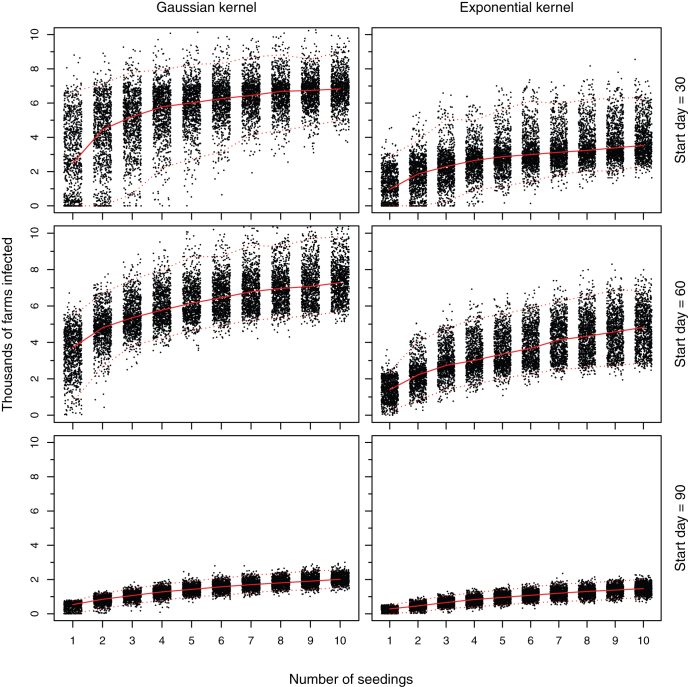
A further key determinant of the extent of the size of the epidemic under the maximum temperature scenario is the number of seedings. For an epidemic started on day 60, the number of infected farms increases by around 360 for each additional disease introduction (Figure 3; linear regression estimate 374.7 for the Gaussian kernel and 344.8 for the exponential kernel, both p < 0.001).

Figure 3. The number of farms infected against the number of disease introductions under the extreme case maximum temperature scenario.

Figure 3

Open in a new tab

The solid red line represents the median and the broken red lines the 2.5 and 97.5 percentiles. The points have been jittered to ease interpretation.

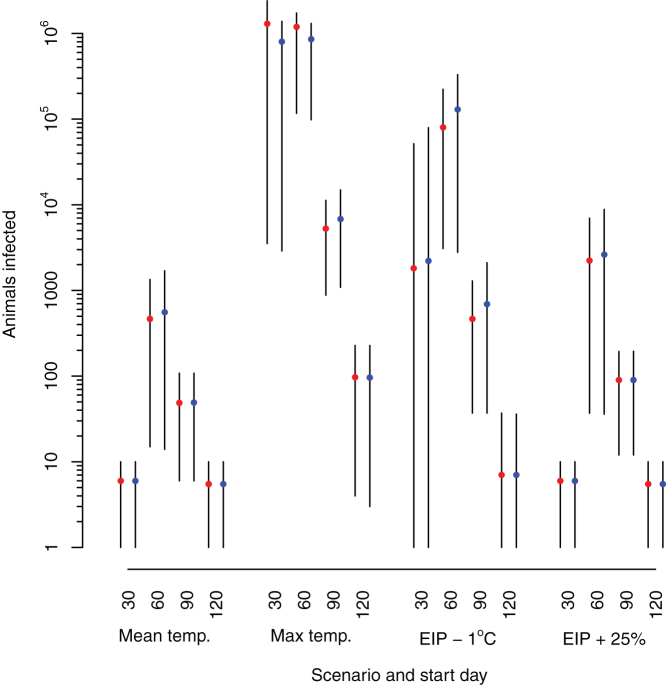
Under the baseline (mean temperature) scenario, the model is slightly sensitive to raising the incubation rate of the EIP by 25% with slightly larger epidemics with disease introduced on day 60 (Table 1, Figure 4). However, the effect of lowering the minimum temperature of the EIP by 1°C has a large effect on the size of the epidemic, with an increase of around 200 times on the number of animals infected compared to the baseline scenario (Table 1, Figure 4).

Figure 4. Comparison of the numbers of animals infected under the scenarios in Table 1.

Figure 4

Open in a new tab

Red points correspond to the exponential kernel, blue points to the Gaussian kernel. The black lines represent the range from the 10th to the 90th percentiles.

The distribution of parish level risk of transmission illustrated by the expected number of infectious vectors resulting from an infected animal on day 60 under the extreme case maximum temperature scenario is shown by Figure 5. There is a distinct concentration of higher risk in the south-west with some patches of higher risk in northerly areas.

Figure 5. The expected number of infectious bites (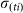Inline graphic) resulting from an infected host on the 30th June (day 60) under the extreme case maximum temperature scenario.

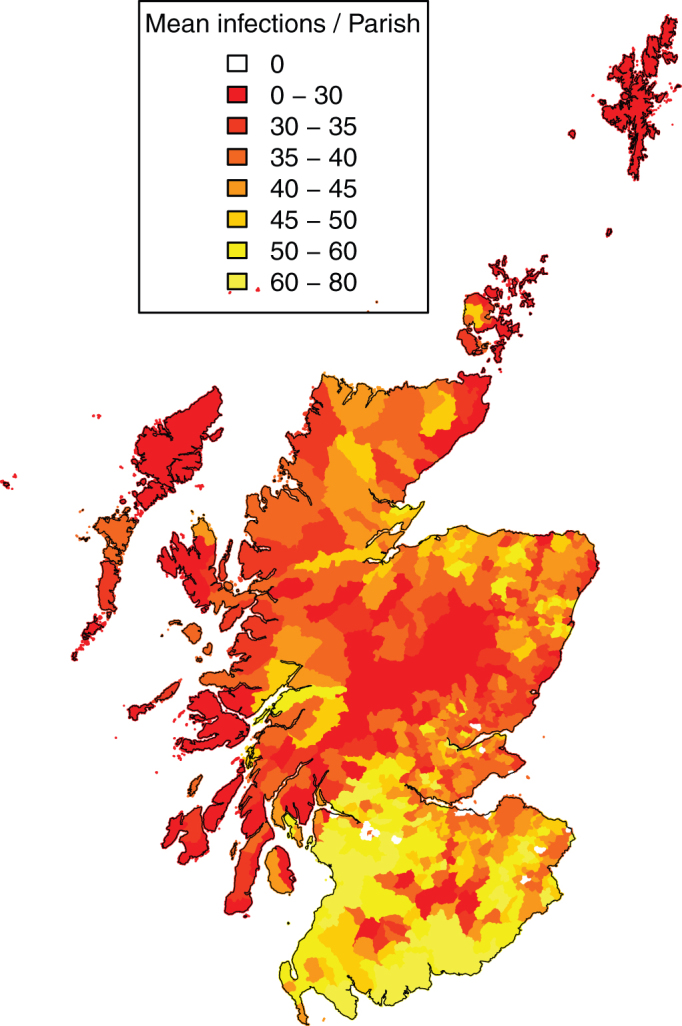
Figure 5

Open in a new tab

This is shown as the parish level mean.

Discussion

This paper has described the development and results of a model to combine both within farm and between farm spread of SBV using knowledge already acquired of SBV and Akabane virus epidemiology then applied to the Scottish context using studies of Culicoides ecology and understanding of BTV. The model simulates introduction of the virus through windborne spread from England or Ireland or introduction through the movement of infected animals into Scotland. The findings of this paper support the findings of similar studies of BTV that shows that it would be possible for Culicoides borne disease to spread in Scotland21,22.

Under the extreme case scenario, assuming of the maximum observed temperatures, the extent of disease spread depends heavily upon the time of introduction during the vector season. Introduction on day 30 or 60 result in similar sized epidemics, however, the epidemics are around 100 times smaller following an introduction on day 90 (Figure 2). Introduction on day 120 results in very small numbers of secondary cases (Table 1). Under the baseline, mean temperature scenario, large epidemics only occur with introduction on day 60. These differences associated with the timing of introduction are the result of a number of factors, principally the remaining period of vector activity, bi-modal distribution of Culicoides abundance, temperature at the time of introduction and the remaining duration of the season of vector activity. Assuming that the disease is introduced through England or Ireland, monitoring the disease spread in these countries could be used to predict the likely arrival time in Scotland and therefore the extent of spread after arrival. Multiple seedings are used here to initiate the epidemic because multiple farms may be at risk from such wind borne vector introductions23.

The model results suggest that given the maximum temperature conditions, the impacts of SBV in terms of reproductive losses among sheep will be large. This is in agreement with reports from England and elsewhere in Europe20,24, where widespread birth malformations among sheep have been reported. Losses in Scotland could be reduced by delaying tupping by 15 days, thus avoiding a substantial proportion of the at-risk window (Figure 2). These results are based on the assumption that one third of ewes will be tupped during October for lambing during February, which may be inaccurate. However, the earliest tupping flocks are likely to be in the lowland, southern areas that are also the highest risk areas for SBV (Figure 5). Furthermore, this model assumed that all pregnant animals infected during the at risk period are at risk of reproductive losses, but the true proportion of these animals would go on to suffer abortions or birth malformations is currently unknown, so the observed number of reproductive losses in an epidemic may be lower. In addition to losses among sheep, a large number of cattle will become infected and this could manifest clinically in drops in milk production or calf birth malformations and reproductive losses.

Under the baseline scenario, the size of the epidemic was exponentially smaller than the maximum temperature scenario, with around one thousandth of the numbers of animals infected (Table 1, Figure 4). However, these analyses show that even during an average year SBV does present a risk to livestock in Scotland. If average temperatures and frequency of warm periods in Scotland increase as a result of global warming then the risk of vector borne disease spread in Scotland and elsewhere in Europe will continue to increase.

At the time of writing there was no published literature on the EIP of SBV infection within Culicoides vectors. As a result, the EIP had to be taken from studies of BTV and this parameter may not be an accurate reflection of the infection process of SBV within Culicoides. As a result we explored alternative parameters for the EIP that would result in more efficient disease transmission. Reducing the interval between infection cycles by increasing the EIP incubation rate by 25% results in around 4 times more animals infected (Table 1, Figure 4). Alternatively reducing the baseline temperature for virus incubation results in a substantially larger epidemic, by both increasing the numbers of areas with appropriate conditions for spread and increasing the rate of spread by lowering the temperature is possible (Table 1, Figure 4). The EIP incubation rate 25% faster and the baseline temperature 1°C cooler are within the ranges of values and their 95% credible limits of parameters for the EIP of BTV and African Horse Sickness identified in a recent review by Carpenter et al25, so can be considered as credible values for SBV. The sensitivity of the model to these parameters highlights the need to better understand the parameters for SBV transmission if we are to accurately predict the spread of the disease.

Rather than separating within farm from between farm spread, this model incorporated both into a single transmission kernel to reflect the blood feeding behaviour of the vector. The kernel did not directly allow for wind-borne transmission that could be incorporated using an irregular shaped kernel. However, it has been demonstrated elsewhere that the role of wind in spreading vector borne disease over land is relatively minor26 and that the relatively unpredictable nature of the wind speed and direction over complex topography makes this difficult to use in a predictive model. Furthermore, under the maximum temperature scenario the Gaussian kernel resulted in more animals on more farms being infected. This is because the Gaussian kernel allows the virus to spread more rapidly to new areas, where as the exponential kernel limits transmission and ensures that locally the epidemic burns-out faster. However the reverse is true when the mean temperature is used. This is because under the lower temperatures there are fewer areas suitable for spread. The tighter exponential kernel is more effective in ensuring that infection remains within these areas, whereas the wider Gaussian kernel allows more opportunity for the virus to escape these risk areas to areas that are less favourable for spread and conditions are less likely to lead to further transmission.

In conclusion, the climatic conditions in Scotland are at the lower end of the scale that is suitable for SBV transmission, but are still adequate for the disease to spread. However, given warmer than average (but still feasible) temperatures SBV could spread very quickly within Scotland with significant impacts in both the sheep and cattle populations. This is upon the assumption that SBV will spread with similar parameters as BTV and is highly dependant upon the nature of vector movement with respect to a transmission kernel. Furthermore, how the disease spreads within Scotland is very dependant upon the precise nature of the EIP of SBV.

Methods

The model used in this analysis is a stochastic simulation model comprising two main compartments: a) the transmission from livestock host to vector; and b) the transmission from vector to host. Different introduction scenarios are simulated by seeding of infection on to farms to represent importation of infected animals or windborne virus spread.

A number of assumptions have been made in this model:

  1. Movements of exposed or infectious animals are not explicitly considered. A movement of an animal during its short latent or infectious period could spread disease to different areas of the country but was not considered here due to the fluidity of the movement network27,28,29,30. In these analyses we use one kernel that implicitly includes movements31 and one that does not26.

  2. The range of dispersal of the vector can be modelled using a kernel. Vector dispersal is influenced by many factors including weather26,32. However, localised wind patterns are difficult to model in the long term and it has been demonstrated elsewhere that during periods of intense midge activity BTV transmission behaves in a similar manner to direct transmission33 suggesting a kernel is a suitable approximation.

  3. The animal is equally infectious on each day of its infectious period.

  4. Once infected an animal will recover with full immunity and will not be susceptible to further infection.

  5. As with other studies20,31,34 Culicoides vectors are assumed to be equally likely to feed on a cow as a sheep. Studies on C. imicola, indicate that the vector has a preference for feeding on cattle rather than sheep. However, C. imicola is not a species native to Scotland. The only study of species found in Scotland show that insects have a preference for horses over cattle and sheep, but insufficient insects were trapped on cattle and sheep to make further inferences35.

  6. The attractiveness of a farm for vector feeding is based on the number of livestock on the farm and is determined by distance and the number of livestock.

  7. Ewes are at risk of reproductive losses when infected between days 28–56 of pregnancy20 and most sheep in Scotland are tupped (mated) between September and November for lambing between February and April. Therefore, in this model, any in-lamb ewe that is infected after day 150 (during October) is at risk of reproductive losses including birth malformations and abortions. These ewes are just those that were tupped during September: we assume that one third of breeding ewes are tupped during September and the other two thirds during October and November. The proportion of the sheep population that is maintained as breeding stock is 51% on the Scottish June agricultural census. The corresponding at-risk period for cattle may be as wide as 62–173 days into pregnancy20 and cattle births are distributed more evenly through the year relative to sheep births.

  8. Scotland can be regarded in isolation. During an epidemic involving southern Scotland there is likely to be some transmission with farms in northern England. However, as this is likely to be a two-way exchange we consider that this would have minimal effect on the epidemic.

  9. No disease control measures will be employed.

  10. The EIP for SBV will be the same as for BTV. This is explored in sensitivity analysis.

Model description (a) – animal to vector transmission

For an infectious farm i, at time t the number of vectors that will feed on an infectious animal and survive sufficient time to lay an infectious bite is defined by a daily rate 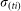Inline graphic. The actual number of infectious bites is taken from a Poisson distribution (Pois(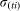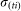Inline graphic)). Inline graphic is defined as:

graphic file with name srep01178-m1.jpg

where

graphic file with name srep01178-m2.jpg

describes the number of vectors feeding on an infected animal with nv as the expected number of vectors (set to a fixed value of 250036), vt adjusts for the expected number of vectors at time t, following a bimodal distribution based upon Searle et al14:

vt = 0.25 when t < 30 (31st May) or t > 140 (September 18th) and t is between 65 (5th July) and 100 (9th August) days

vt = 1 otherwise.

vi is a term that describes the likely vector abundance given the landcover in a 1km buffer around i, with the more competent species associated with pasture and less competent species associated with heathland:

graphic file with name srep01178-m3.jpg

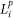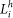where Inline graphic and Inline graphic are the proportion of land within the 1 km buffer classed as pasture and heathland respectively.

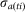Inline graphic is the number of infectious animals on i at time t.

σv is the probability of transmission from animal host to vector and is equal to 0.19, based upon experimental infections3.

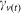Inline graphic describes the probability of a midge surviving sufficient time to lay one or more infectious bites and is dependent upon three parameters: the vector mortality rate37 (Vm), the EIP (Ve) and the interval between blood meals (vb).

graphic file with name srep01178-m4.jpg

where T is the temperature and the daily survival probability is 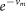Inline graphic.

The time to the vector being infectious is described by the EIP which has been parameterized for BTV, since no value is available for SBV (derived from Carpenter et al17):

graphic file with name srep01178-m5.jpg

Following the vector becoming infectious, the time until the first potentially infectious blood meal is taken as half the interval between blood meals38 where:

graphic file with name srep01178-m6.jpg

In order to account for a vector taking more than one potentially infectious meal, the infectious bite rate of a vector is given by:

graphic file with name srep01178-m7.jpg

This assumes that the midge will not survive to lay more than 10 infectious bites (although the probability of surviving more than two bites being very small and is almost negligible).

Model description (b) – vector to animal transmission

An infected vector from farm i will infect an animal on farm j (i can be the same as j) with probability defined by:

graphic file with name srep01178-m8.jpg

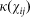where Inline graphic is a spatial transmission kernel based upon the Euclidean distance between farms i and j (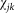Inline graphic) and describes the distances a vector will travel between infection and the laying of infectious bites. 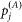Inline graphic describes the attractiveness of a farm to a vector, and is equal to the number of susceptible hosts (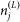Inline graphic) on holding j.

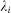Inline graphic is a scaling parameter that ensures that any potentially infectious bite is laid only once:

graphic file with name srep01178-m9.jpg

The probability of successful transmission from vector to host is given by σT = 0.7739 and following infection the animal is latently infected (non-infectious) for two days and infectious for four days1

The model parameters are summarised in Table 2.

Table 2. The parameters used in this model.

Parameter Description Derivation Values
σti Rate describing the number of infected flies from a single infected animal on a single day. Inserted into a random Poisson distribution.   ≥0
nv Expected number of vector bites per day After Gerry et al36 and consistent with studies from Scotland Searle et al14, Blackwell et al15. 2500
vi Spatial adjustment to nv based upon landscape suitability and Culicoides species competence. After Purse et al13. 0.5 ≤ vi ≤ 1
LP Proportion of 1 km buffer identified as pasture CORINE landcover 200040 ≤1
Lh Proportion of 1 km buffer identified as heathland CORINE landcover 200040 ≤1
vt Temporal adjustment to nv based upon temporal peaks in Culicoides abundance After Searle et al14. 0.25, 1
T Temperature. See supplementary material 9.3 −19°C
vm Temperature dependant vector mortality rate. After Gerry et al37 <1
ve Extrinsic (within vector) incubation period After Carpenter et al25 work on BTV  
vb Time interval between bites After Mullens et al38 work on BTV  
σv Probability of transmission between host and vector. After Veronesi et al3 0.19
nL Number of susceptible livestock. From the Scottish June agricultural census.  
σT Probability of transmission from vector to host Derived from Baylis et al39 0.77
latent period Period between infection and viraemia within the animal Approximation from experimental infections of 3 cattle1. 2 days
Infectious period Period of infectiousness of an animal Approximation from experimental infections of 3 cattle1. 4 days
Open in a new tab

Model implementation

The model assumes a potential vector activity season from May to October (inclusive) which is within the duration of vector activity observed in studies in Scotland14,15. The model introduces infection on different start dates from the 1st June (being the first month at which temperatures are suitable for within vector incubation) with 30 day intervals between start days (up to start day = 120 (29th August)).

The model is initiated by introducing disease on certain ‘seed’ farms. The seeds are assumed to be introductions from England, so a farm is more likely to be a seed if it is further south (described in the supplementary information) with seeds sampled at random (with replacement, so it is possible for a seed farm to become infected twice). The seed is infected by a single random animal becoming infected.

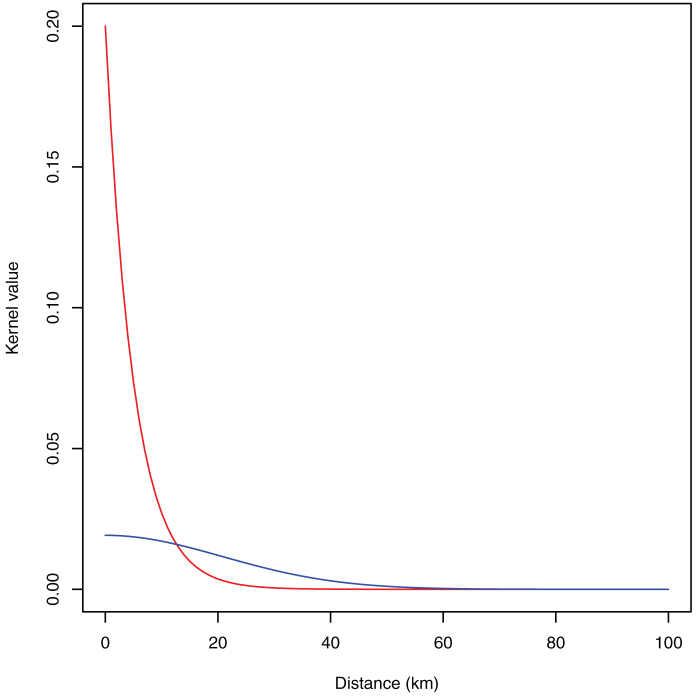
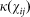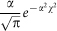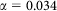Two shapes of transmission kernel Inline graphic are considered; a Gaussian kernel based upon Szmaragd et al31, described by Inline graphic where Inline graphic and an exponential kernel 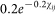Inline graphic based upon Sedda et al26 (Figure 6). For each combination of parameters (two kernel shapes, 4 start days, 1 to 10 seeds) 1000 iterations were run resulting in 80000 model runs.

Figure 6. The shape of the exponential kernel (red line) and Gaussian kernel (blue line).

Figure 6

Open in a new tab

Data

The unique parish-holding (PH) identifiers were taken from the Scottish June agricultural census for 2011. This comprised 52,543 holdings of which the 20,877 with at least one head of cattle or one sheep were selected. Coordinates for the holdings were identified from Animal Movement Licensing Scheme (AMLS) location data or British Cattle Movement Scheme (BCMS) Cattle Tracing System (CTS) Postcode Address Field (PAF) data. Landcover variables were derived from the CORINE 2000 Landcover map40.

Temperature data were extrapolated for each farm from the UK Met Office UK CIP archive of temperature data interpolated and gridded to 5 km2 cells between 1990 and 200641. These data were processed using the methodology described in Supplementary material to extract the mean monthly temperature for each cell during the period in question.

Sensitivity analysis

To explore the sensitivity of the model to certain parameters sensitivity analysis was conducted by altering the parameter and rerunning the model with the new values and comparing these results to those from the baseline (mean temperature) scenario. Analysis was conducted to explore the effects of using the maximum mean monthly temperature of each grid cell over the period of the data (1990–2006). The parameter for EIP is taken from studies of BTV and the parameter for SBV may have a different minimum incubation temperature or a different virus replication rate. Thus an equation with a minimum temperature 1°C cooler:

graphic file with name srep01178-m10.jpg

and a virus replication rate 25% faster:

graphic file with name srep01178-m28.jpg

were used in sensitivity analysis.

Author Contributions

P.R.B., B.M.deC.B. and I.G.H. conceived and designed the study, P.R.B. performed the analysis and drafted the manuscript, K.R.S. and B.V.P. contributed to aspects of arbovirus epidemiology and HKA contributed to veterinary aspects of SBV. All authors have read, made changes to and approved the manuscript.

Supplementary Material

Supplementary Information

Supplementary information for: Epidemic potential of an emerging vector borne disease in a marginal environment: Schmallenberg in Scotland

srep01178-s1.doc (167.5KB, doc)

Acknowledgments

This work was undertaken as part of the Scottish Government EPIC project. IGH was supported through Institute Strategic Grant funding from the BBSRC. KRS and BVP are partly supported by EU grant FP7-261504 EDENext and this paper is catalogued by the EDENext Steering Committee as EDENext084 (http://www.edenext.eu). The contents of this publication are the sole responsibility of the authors and don't necessarily reflect the views of the European Commission.

References

  1. Hoffmann B. et al. Novel orthobunyavirus in Cattle, Europe, 2011. Emerg Infect Dis 18, 469–72 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Lievaart-Peterson K., Luttikholt S. J. M., Van den Brom R. & Vellema P. Schmallenberg virus infection in small ruminants – First review of the situation and prospects in Northern Europe. Small ruminant research 106, 71–76 (2012). [Google Scholar]
  3. Veronesi E. et al. Implicating Culicoides biting midges as vectors of Schmallenberg virus using semi- quantitative RT-PCR. PLoS ONE (2013) (In press). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Elbers A. R. W., Meiswinkel R., Van Weezep E., Van Oldruitenborgh-Oosterbaan M. M. S. & Kooi E. Schmallenberg Virus in Culicoides spp. Biting Midges, the Netherlands, 2011. Emerg Infect Dis 19, 106–109 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. De Regge N. et al. Detection of Schmallenberg virus in different Culicoides spp. by real-time RT-PCR. Transbound Emerg Dis 59, 471–5 (2012). [DOI] [PubMed] [Google Scholar]
  6. Rasmussen L. D. et al. Culicoids as vectors of Schmallenberg virus. Emerg Infect Dis 18, 1204–6 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. EFSA “Schmallenberg” virus: analysis of the epidemiological data 1. 1–30 (Parma, 2012). [Google Scholar]
  8. Roberts H. Update No. 10 on Schmallenberg Virus in Northern Europe. 1–4 (London, 2012). [Google Scholar]
  9. Elbers A. R. W. et al. Seroprevalence of Schmallenberg Virus Antibodies among Dairy Cattle, the Netherlands, Winter 2011–2012. Emerg Infect Dis 18, 1065–1071 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gould E. A. & Higgs S. Impact of climate change and other factors on emerging arbovirus diseases. Trans R Soc Trop Med Hyg 103, 109–21 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gould E. A., Higgs S., Buckley A. & Gritsun T. S. Potential arbovirus emergence and implications for the United Kingdom. Emerg Infect Dis 12, 549–55 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Purse B. V. et al. Climate change and the recent emergence of bluetongue in Europe. Nat Rev Microbiol 3, 171–81 (2005). [DOI] [PubMed] [Google Scholar]
  13. Purse B. V. et al. Impacts of climate, host and landscape factors on Culicoides species in Scotland. Med Vet Entomol 26, 168–177 (2011). [DOI] [PubMed] [Google Scholar]
  14. Searle K. R. et al. Identifying environmental drivers of insect phenology across space and time: Culicoides in Scotland as a case study. Bull Entomol Res (2012). (In press). [DOI] [PubMed] [Google Scholar]
  15. Blackwell A. et al. An Assessment of Presence, Distribution and Abundance in Scotland of Culicoides Midge Species and their Potential as Vectors of Animal Disease. (Edinburgh, 2009). [Google Scholar]
  16. Blackwell A., Mordue A. J. & Mordue W. Identification of blood meals of the Scottish biting midge, Culicoides impunctatus, by indirect enzyme-linked immunosorbent assay (ELISA). Med Vet Entomol 8, 20–24 (1994). [DOI] [PubMed] [Google Scholar]
  17. Carpenter S., Lunt H. L., Arav D., Venter G. J. & Mellor P. S. Oral Susceptibility to Bluetongue virus of Culicoides (Diptera: Ceratopogonidae) from the United Kingdom. J Med Entomol 43, 73–78 (2006). [DOI] [PubMed] [Google Scholar]
  18. Jennings D. M. & Mellor P. S. The vector potential of British Culicoides species for bluetongue virus. Vet Microbiol 17, 1–10 (1988). [DOI] [PubMed] [Google Scholar]
  19. Boorman J. & Goddard P. Observations on biology of Culicoides impunctatus Goetgh (Diptera:Ceratopogonidae) in Southern England. Bull Entomol Res 60, 189 (1970). [DOI] [PubMed] [Google Scholar]
  20. EFSA “Schmallenberg” virus: Analysis of the Epidemiological Data and Assessment of Impact. EFSA Journal 10, 2768 (2012). [Google Scholar]
  21. Gubbins S. et al. Assessing the consequences of an incursion of a vector-borne disease I. Identifying feasible incursion scenarios for bluetongue in Scotland. Epidemics 2, 148–54 (2010). [DOI] [PubMed] [Google Scholar]
  22. Szmaragd C., Gunn G. J. & Gubbins S. Assessing the consequences of an incursion of a vector-borne disease. II. Spread of bluetongue in Scotland and impact of vaccination. Epidemics 2, 139–47 (2010). [DOI] [PubMed] [Google Scholar]
  23. Gloster J., Burgin L., Witham C., Athanassiadou M. & Mellor P. S. Bluetongue in the United Kingdom and northern Europe in 2007 and key issues for 2008. Vet Rec 162, 298–302 (2008). [DOI] [PubMed] [Google Scholar]
  24. Roberts H. Update No. 9 on Schmallenberg Virus in Northern Europe. 1–5 (London, 2012). [Google Scholar]
  25. Carpenter S. et al. Temperature dependence of the extrinsic incubation period of orbiviruses in Culicoides biting midges. PLoS ONE 6, e27987 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sedda L. et al. A new algorithm quantifies the roles of wind and midge flight activity in the bluetongue epizootic in northwest Europe. Proc R Soc B 279, 2354–2362 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Green D. M., Kiss I. Z., Mitchell A. P. & Kao R. R. Estimates for local and movement-based transmission of bovine tuberculosis in British cattle. Proc R Soc B 275, 1001–5 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Vernon M. C. & Keeling M. J. Representing the UK's cattle herd as static and dynamic networks. Proc R Soc B 276, 469–76 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Volkova V. V., Howey R., Savill N. J. & Woolhouse M. E. J. Potential for transmission of infections in networks of cattle farms. Epidemics 2, 116–22 (2010). [DOI] [PubMed] [Google Scholar]
  30. Volkova V. V., Howey R., Savill N. J. & Woolhouse M. E. J. Sheep movement networks and the transmission of infectious diseases. PLoS ONE 5, e11185 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Szmaragd C. et al. A modeling framework to describe the transmission of bluetongue virus within and between farms in Great Britain. PLoS One 4, e7741 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Scotter D. R., Lamb K. P. & Hassan E. An Insect Dispersal Parameter. Ecology 52, 174 (1971). [Google Scholar]
  33. Santman-Berends I. M. G. A., Stegeman J., Vellema P. & Van Schaik G. Comparing methods to estimate the reproduction ratio of Bluetongue. Proceedings of SVEPM 176–185 (2012). [Google Scholar]
  34. Hartemink N. A. et al. Mapping the basic reproduction number (R0) for vector-borne diseases: a case study on bluetongue virus. Epidemics 1, 153–61 (2009). [DOI] [PubMed] [Google Scholar]
  35. Viennet E. et al. Host preferences of Palaearctic Culicoides biting midges: implications for transmission of orbiviruses. Med Vet Entomol (2012) (In press). [DOI] [PubMed] [Google Scholar]
  36. Gerry A. C., Mullens B. A., Maclachlan N. J. & Mecham J. O. Seasonal transmission of bluetongue virus by Culicoides sonorensis (Diptera: Ceratopogonidae) at a southern California dairy and evaluation of vectorial capacity as a predictor of bluetongue virus transmission. J Med Entomol 38, 197–209 (2001). [DOI] [PubMed] [Google Scholar]
  37. Gerry A. C. & Mullens B. A. Seasonal abundance and survivorship of Culicoides sonorensis (Diptera: Ceratopogonidae) at a southern California dairy, with reference to potential bluetongue virus transmission and persistence. J Med Entomol 37, 675–88 (2000). [DOI] [PubMed] [Google Scholar]
  38. Mullens B. A., Gerry A. C., Lysyk T. J. & Schmidtmann E. T. Environmental effects on vector competence and virogenesis of bluetongue virus in Culicoides: interpreting laboratory data in a field context. Vet Ital 40, 160–6 (2004). [PubMed] [Google Scholar]
  39. Baylis M., O'Connell L. & Mellor P. S. Rates of bluetongue virus transmission between Culicoides sonorensis and sheep. Med Vet Entomol 22, 228–37 (2008). [DOI] [PubMed] [Google Scholar]
  40. Bossard M., Feranec J. & Otahel J. CORINE Land Cover technical guide - Addendum 2000. (Copenhagen, 2000). [Google Scholar]
  41. Perry M. & Hollis D. The generation of monthly gridded datasets for a range of climatic variables over the UK. Int J Climatol 25, 1041–1054 (2005). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information for: Epidemic potential of an emerging vector borne disease in a marginal environment: Schmallenberg in Scotland

srep01178-s1.doc (167.5KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES