Modeling the impact of common noise inputs on the network activity of retinal ganglion cells

Abstract

Synchronized spontaneous firing among retinal ganglion cells (RGCs), on timescales faster than visual responses, has been reported in many studies. Two candidate mechanisms of synchronized firing include direct coupling and shared noisy inputs. In neighboring parasol cells of primate retina, which exhibit rapid synchronized firing that has been studied extensively, recent experimental work indicates that direct electrical or synaptic coupling is weak, but shared synaptic input in the absence of modulated stimuli is strong. However, previous modeling efforts have not accounted for this aspect of firing in the parasol cell population. Here we develop a new model that incorporates the effects of common noise, and apply it to analyze the light responses and synchronized firing of a large, densely-sampled network of over 250 simultaneously recorded parasol cells. We use a generalized linear model in which the spike rate in each cell is determined by the linear combination of the spatio-temporally filtered visual input, the temporally filtered prior spikes of that cell, and unobserved sources representing common noise. The model accurately captures the statistical structure of the spike trains and the encoding of the visual stimulus, without the direct coupling assumption present in previous modeling work. Finally, we examined the problem of decoding the visual stimulus from the spike train given the estimated parameters. The common-noise model produces Bayesian decoding performance as accurate as that of a model with direct coupling, but with significantly more robustness to spike timing perturbations.

1 Introduction

Advances in large-scale multineuronal recordings have made it possible to study the simultaneous activity of complete ensembles of neurons. Experimentalists now routinely record from hundreds of neurons simultaneously in many preparations: retina (Warland et al. 1997; Frechette et al. 2005), motor cortex (Nicolelis et al. 2003; Wu et al. 2008), visual cortex (Ohki et al. 2006; Kelly et al. 2007), somatosensory cortex (Kerr et al. 2005; Dombeck et al. 2007), parietal cortex (Yu et al. 2006), hippocampus (Zhang et al. 1998; Harris et al. 2003; Okatan et al. 2005), spinal cord (Stein et al. 2004; Wilson et al. 2007), cortical slice (Cossart et al. 2003; MacLean et al. 2005), and culture (Van Pelt et al. 2005; Rigat et al. 2006). These techniques in principle provide the opportunity to discern the architecture of neuronal networks. However, current technologies can sample only small fractions of the underlying circuitry; therefore, unmeasured neurons can have a large collective impact on network dynamics and coding properties. For example, it is well-understood that common input plays an essential role in the interpretation of pairwise cross-correlograms (Brody 1999; Nykamp 2005). To infer the correct connectivity and computations in the circuit requires modeling tools that account for unrecorded neurons.

Here, we investigate the network of parasol retinal ganglion cells (RGCs) of the macaque retina. Several factors make this an ideal system for probing common input. Dense multi-electrode arrays provide access to the simultaneous spiking activity of many RGCs, but do not provide systematic access to the nonspiking inner retinal layers. RGCs exhibit significant synchrony in their activity, on timescales faster than that of visual responses (Mastronarde 1983; DeVries 1999; Shlens et al. 2009; Greschner et al. 2011), yet the significance for information encoding is still debated (Meister et al. 1995; Nirenberg et al. 2002; Schneidman et al. 2003; Latham and Nirenberg 2005). In addition, the underlying mechanisms of these correlations in the primate retina remain under-studied: do correlations reflect direct electrical or synaptic coupling (Dacey and Brace 1992) or shared input (Trong and Rieke 2008)? Consequently, the computational role of the correlations remains uncertain: how does synchronous activity affect the information encoded by RGCs about the visual world?

Recent work using paired intracellular recordings revealed that neighboring parasol RGCs receive strongly correlated synaptic input; ON parasol cells exhibited weak direct reciprocal coupling while OFF parasol cells exhibited none (Trong and Rieke 2008). In contrast with these empirical findings, previous work modeling the joint firing properties and stimulus encoding of parasol cells modeled their correlations with nearly instantaneous direct coupling effects, and did not account for the possibility of common input (Pillow et al. 2008). Here, we introduce a model for the joint firing of the parasol cell population that incorporates common noise effects. We apply this model to analyze the light responses and synchronized firing of a large, densely-sampled network of over 250 simultaneously recorded RGCs. Our main conclusion is that the common noise model captures the statistical structure of the spike trains and the encoding of visual stimuli accurately, without assuming direct coupling.

2 Methods

2.1 Recording and preproccesing

Recordings

The preparation and recording methods were described previously (Litke et al. 2004; Frechette et al. 2005; Shlens et al. 2006). Briefly, eyes were obtained from deeply and terminally anesthetized Macaca mulatta used by other experimenters in accordance with institutional guidelines for the care and use of animals. 3–5 mm diameter pieces of peripheral retina, isolated from the retinal pigment epithelium, were placed flat against a planar array of 512 extracellular microelectrodes, covering an area of 1800 × 900 µm. The present results were obtained from 30–60 min segments of recording. The voltage on each electrode was digitized at 20 kHz and stored for off-line analysis. Details of recording methods and spike sorting have been given previously (Litke 2004; see also Segev et al. 2004). Clusters with a large number of refractory period violations (>10% estimated contamination) or spike rates below 1 Hz were excluded from additional analysis. Inspection of the pairwise cross-correlation functions of the remaining cells revealed an occasional unexplained artifact, in the form of a sharp and pronounced ‘spike’ at zero lag, in a few cell pairs. These artifactual coincident spikes were rare enough to not have any significant effect on our results; cell pairs displaying this artifact are excluded from the analysis illustrated in Figs. 4–6 and 11.

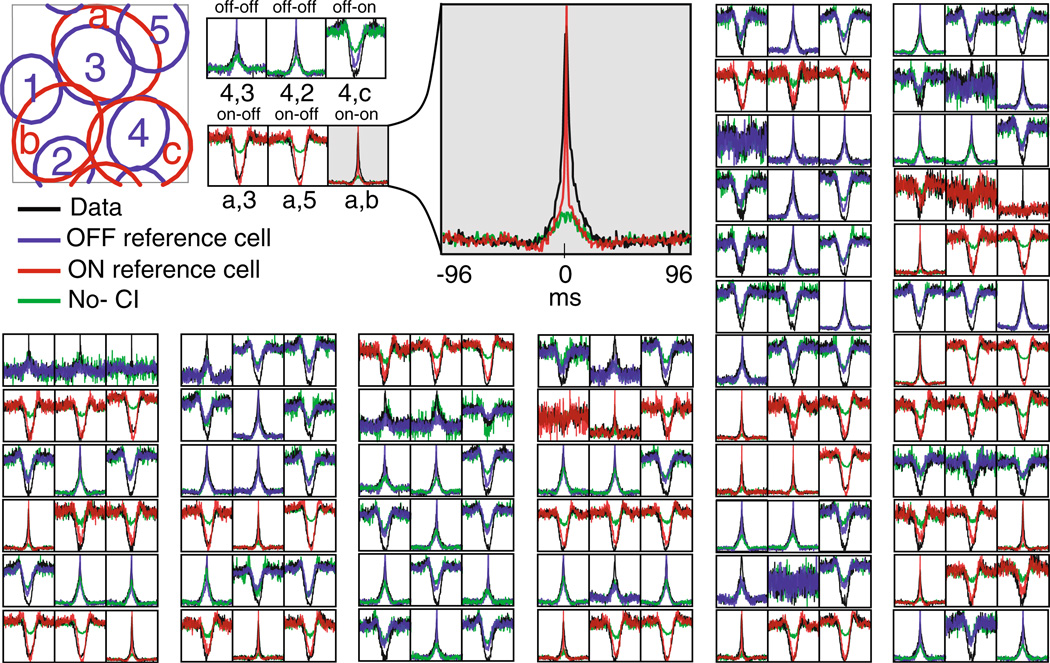
Fig. 4.

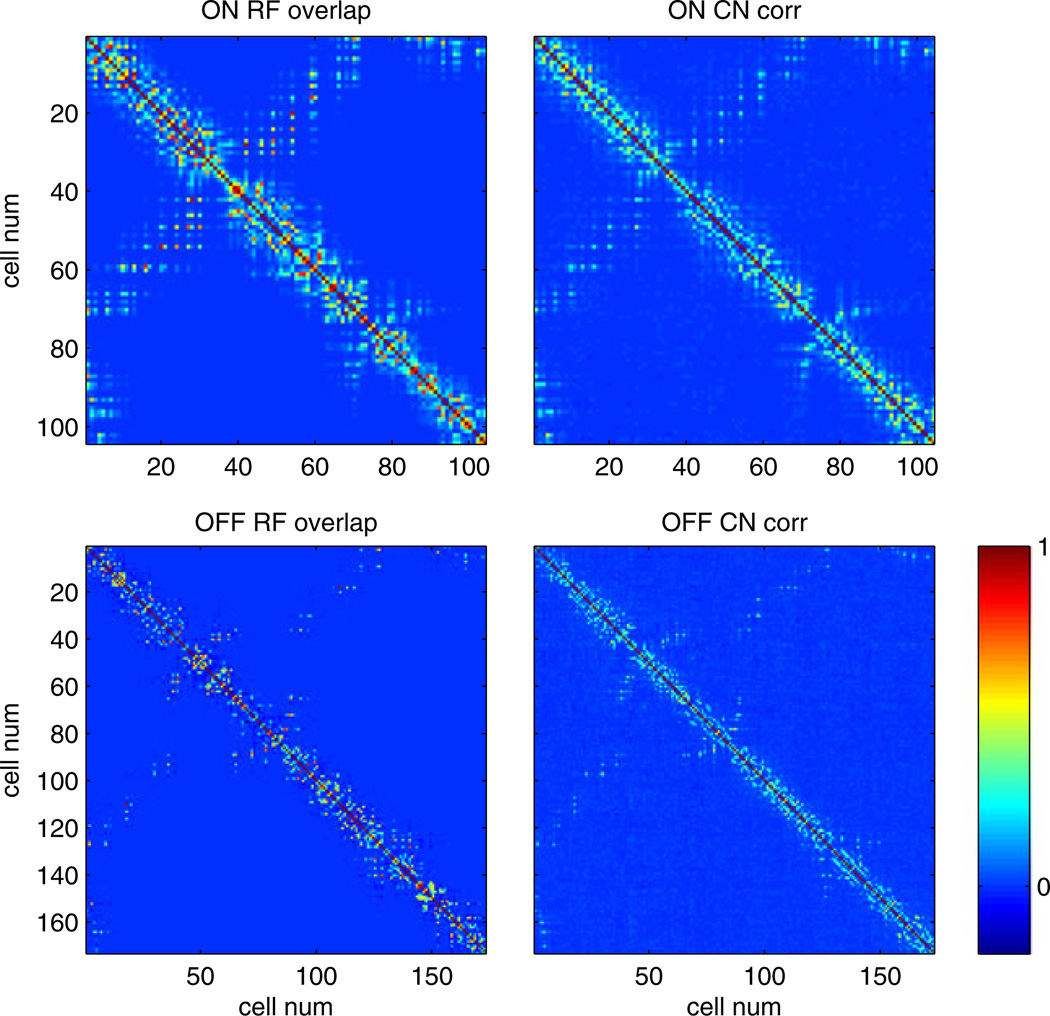
Comparing the inferred common noise strength (right) and the receptive field overlap (left) across all ON–ON and OFF–OFF pairs. Note that these two variables are strongly dependent; Spearman rank correlation coefficent = 0.75 (computed on all pairs with a positive overlap, excluding the diagonal elements of the displayed matrices). Thus the strength of the common noise between any two cells can be predicted accurately given the degree to which the cells have overlapping receptive fields. The receptive field overlap was computed as the correlation coefficient of the spatial receptive fields of the two cells; the common noise strength was computed as the correlation value derived from the estimated common noise spatial covariance matrix C_s (i.e., C_s(i, j)/ $\sqrt{{\mathbf{C}}_s(i,i){\mathbf{C}}_s(j,j)}$ ). Both of these quantities take values between −1 and 1; all matrices are plotted on the same color scale

Fig. 6.

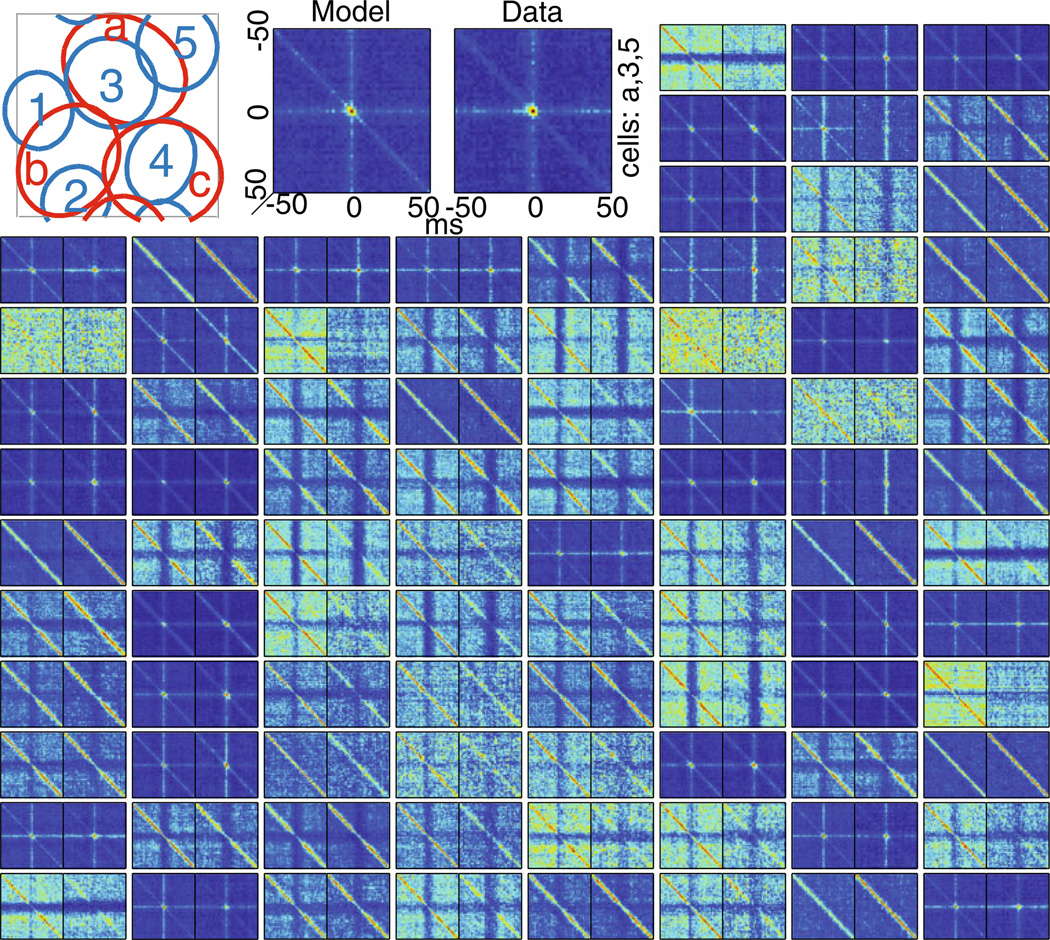
Comparing real and predicted triplet correlations. 89 example third-order (triplet) correlation functions between a reference cell (a in the schematic receptive field) and its two nearest-neighbors (cells 3 and 5 in the schematic receptive field). Triplet correlations were computed in 4-ms bins according to C(τ₁, τ₂) = [〈y₁(t)y₂(t + τ₁)y₃(t + τ₂)〉 − 〈y₁(t)〉〈y₂(t)〉 〈y₃(t)〉]/(〈y₂(t)〉〈y₃(t)〉dt). Color indicates the instantaneous spike rate (in 4 ms bins) as a function of the relative spike time in the two nearest neighbor cells for time delays between −50 to 50 ms. The left figure in each pair is the model (Fig. 1(C)) and the right is data. The color map for each of the two plots in each pair is the same. For different pairs, the color map is renormalized so that the maximum value of the pair is red. Note the model reproduces both the long time scale correlations and the peaks at the center corresponding to short time scale correlations

Fig. 11.

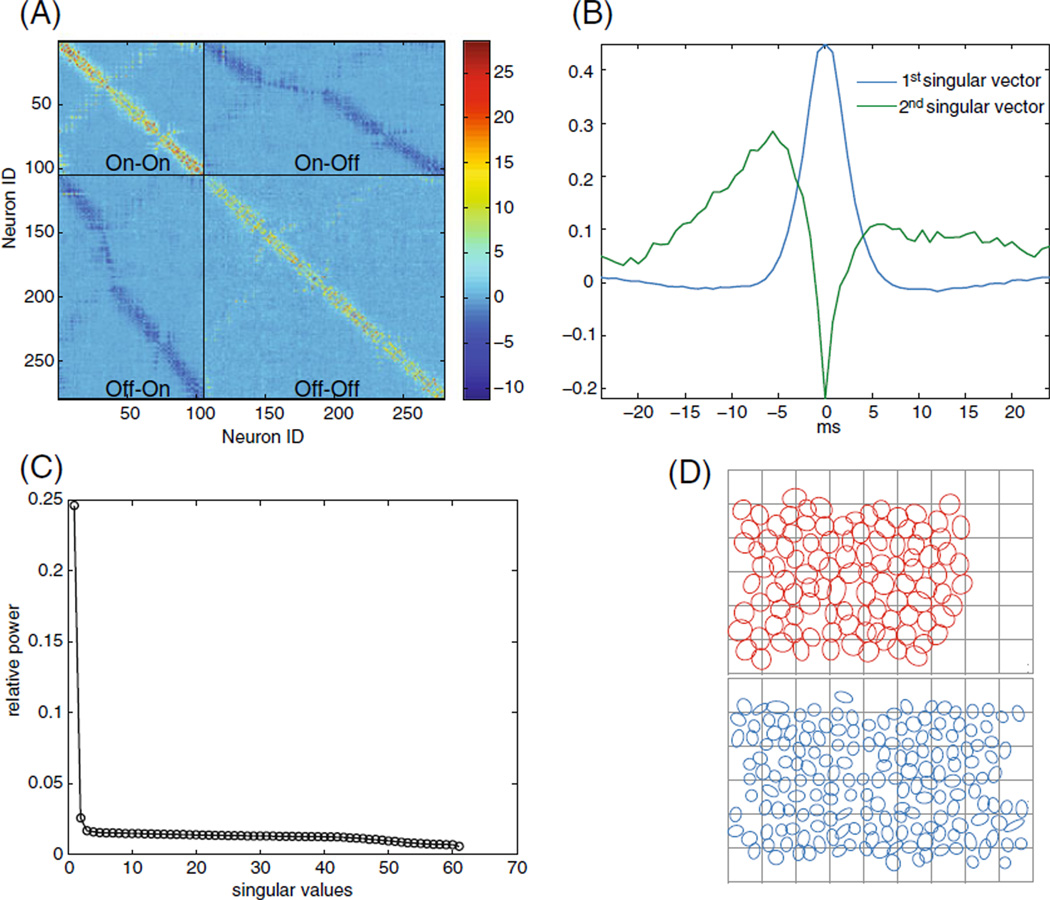
PSTH-based method (A) Approximate spatial covariance matrix of the inferred common noise composed of the first two spatial singular vectors. ${\tilde{C}}_{i,j}={\displaystyle {\sum }_{k=1}^2{\sigma }_k{U}_k}$ (the vectors are reshaped into matrix form). Note the four distinct regions corresponding to the ON–ON, OFF–OFF, ON–OFF, and OFF–ON. (B) First two temporal singular vectors, corresponding to the temporal correlations of the ‘same-type’ (ON–ON and OFF–OFF pairs), and ‘different type’(ON–OFF pairs). Note the asymmetry of the ON–OFF temporal correlations. (C) Relative power of all the singular values. Note that the first two singular values are well separated from the rest, indicating the correlation structure is well approximated by the first two singular vectors. (D) Receptive field centers and the numbering schema. Top in red: ON cells. Bottom in blue: OFF cells. The numbering schema starts at the top left corner and goes column-wise to the right. The ON cells are 1 through 104 and the OFF cells are 105 to 277. As a result, cells that are physically close are usually closely numbered

Stimulation and receptive field analysis

An optically reduced stimulus from a gamma-corrected cathode ray tube computer display refreshing at 120 Hz was focused on the photoreceptor outer segments. The low photopic intensity was controlled by neutral density filters in the light path. The mean photon absorption rate for the long (middle, short) wavelength-sensitive cones was approximately equal to the rate that would have been caused by a spatially uniform monochromatic light of wavelength 561 (530, 430) nm and intensity 9200 (8700, 7100) photons/µm²/s incident on the photoreceptors. The mean firing rate during exposure to a steady, spatially uniform display at this light level was 11 ± 3 Hz for ON cells and 17 ± 3.5 Hz for OFF cells. Spatiotemporal receptive fields were measured using a dynamic checkerboard (white noise) stimulus in which the intensity of each display phosphor was selected randomly and independently over space and time from a binary distribution. Root mean square stimulus contrast was 96%. The pixel size (60 µm) was selected to be of the same spatial scale as the parasol cell receptive fields. In order to outline the spatial footprint of each cell, we fit an elliptic two-dimensional Gaussian function to the spatial spike triggered average of each of the neurons. The resulting receptive field outlines of each of the two cell types (104 ON and 173 OFF RGCs) formed a nearly complete mosaic covering a region of visual space (Fig. 11(D)), indicating that most parasol cells in this region were recorded. These fits were only used to outline the spatial footprint of the receptive fields, and were not used as the spatiotemporal stimulus filters kⁱ, as discussed in more detail below.

2.2 Model structure

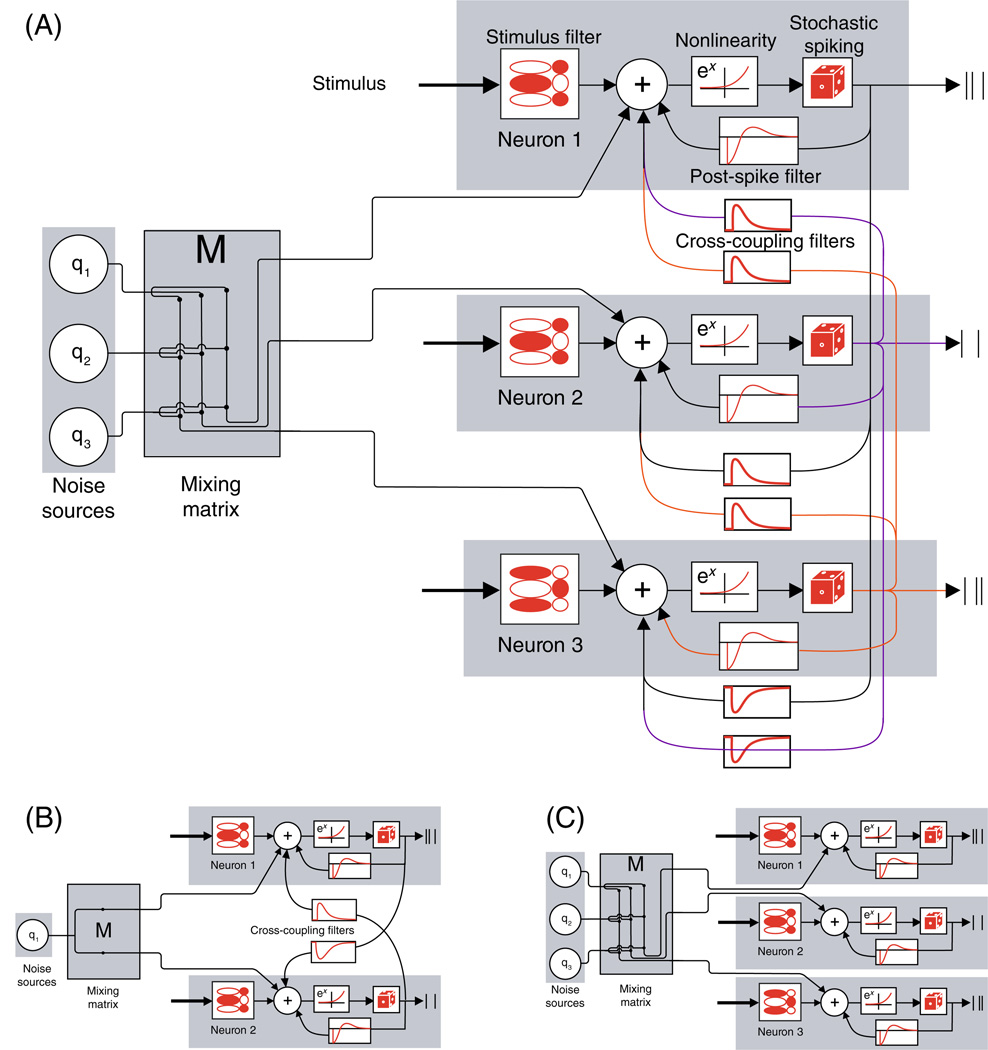
We begin by describing our model in its full generality (Fig. 1(A)). Later, we will examine two models which are different simplifications of the general model (Fig. 1(B)–(C)). We used a generalized linear model augmented with a state-space model (GLSSM). This model was introduced in Kulkarni and Paninski (2007) and is similar to methods discussed in Smith and Brown (2003) and Yu et al. (2006); see Paninski et al. (2010) for review. The conditional intensity function (instantaneous firing rate), ${\lambda }_t^i$ , of neuron i at time t was modeled as:

$$\text{log}{\lambda }_t^i={\mu }^i+{\mathbf{k}}^i·{\mathbf{x}}_t+{\mathbf{h}}^i·{\mathbf{y}}_t^i+{\displaystyle \sum _{j\ne i}^{n_{\text{cells}}}{\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j+{\displaystyle \sum _{r=1}^{n_q}{\mathbf{M}}_{i,r}·q_t^r.}}$$ (1)

Fig. 1.

Model schemas. (A) Fully general model. Each cell is modeled independently using a Generalized Linear model augmented with a state-space model (GLSSM). The inputs to the cell are: stimulus convolved with a linear spatio-temporal filter (kⁱ · x_t in Eq. (1)), past spiking activity convolved with a history filter ( ${\mathbf{h}}^i·{\mathbf{y}}_t^i$ ), past spiking activity of all other cells convolved with corresponding cross-coupling filters ( ${\displaystyle {\sum }_{j\ne i}^{n_{\text{cells}}}{\mathbf{L}}_{i,j}}·{\mathbf{y}}_t^j$ ), and a mixing matrix, M, that connects n_q common noise inputs $q_t^r$ to the n_cells observed RGCs. (B) Pairwise model. We simplify the model by considering pairs of neurons separately. Therefore, we have two cells and just one shared common noise. (C) Common-noise model where we set all the cross-coupling filters to zero and have n_cells independent common-noise sources coupled to the RGC network via the mixing matrix M

The right hand side of this expression is organized in terms of input-filter pairs; we will describe the inputs first and then the corresponding filters. μⁱ is a scalar offset, determining the cell’s baseline log-firing rate; x_t is the spatiotemporal stimulus history vector at time t; ${\mathbf{y}}_t^i$ is a vector of the cell’s own spike-train history in a short window of time preceding time t; ${\mathbf{y}}_t^j$ is the spike-train of the j^th cell preceding time t; $q_t^r$ is the r^th common noise component at time t. Correspondingly, kⁱ is the stimulus spatio-temporal filter of neuron i; hⁱ is the post-spike filter accounting for the i^th cell’s own post-spike effects; L_{i, j} are direct coupling filters from neuron j to neuron i which capture dependencies of the cell on the recent spiking of all other cells; and lastly, M_i,r is the mixing matrix which takes the r^th noise source and ‘injects’ it into cell i.

We experimented with two different distributions to model the spike count in each bin, given the rate ${\lambda }_t^i$ . First we used a Poisson distribution (with mean ${\lambda }_t^i\mathit{\text{dt}}$ , where dt = 0.8 ms was the temporal resolution used to represent the spike times here) in the exploratory analyses described in Sections 2.2 and 3.1 below; note that since ${\lambda }_t^i$ itself depends on the past spike times, this model does not correspond to an inhomogeneous Poisson process (in which the spiking in each bin would be independent). We also used the Bernoulli distribution with the same probability of not spiking, $p(\mathit{\text{no spike}})=\text{exp}(-{\lambda }_t^i\mathit{\text{dt}})$ .

The Poisson distribution constrains the mean firing rate to equal the variance of the firing rate, which is not the case in our data; the variance tends to be significantly smaller than the mean. In preliminary analyses, the Bernoulli model outperformed the Poisson model. Therefore, we used the Bernoulli model for the complete network with common noise with no direct coupling (described here and in Section 3.2). We did not explore the differences between the two models further, but in general expect them to behave fairly similarly due to the small dt used here.

Now we will discuss the terms in Eq. (1) in more detail. The stimulus spatio-temporal filter kⁱ was modeled as a five-by-five-pixels spatial field, by 30 frames (250 ms) temporal extent. Each pixel in kⁱ is allowed to evolve independently in time. The history filter was composed of ten cosine “bump” basis functions, with 0.8 ms resolution, and a duration of 188 ms, while the direct coupling filters were composed of 4 cosine-bump basis functions; for more details see Pillow et al. (2008).

The statistical model developed by Pillow et al. (2008) captured the joint firing properties of a complete subnetwork of 27 RGCs, but did not explicitly include common noise in the model. Instead, correlations were captured through direct reciprocal connections (corresponding to our L_{i, j} terms) between RGCs. (Similar models with no common noise term have been considered by many previous authors (Chornoboy et al. 1988; Utikal 1997; Keat et al. 2001; Paninski et al. 2004; Pillow et al. 2005; Truccolo et al. 2005; Okatan et al. 2005).) Because the cross-correlations observed in this network have a fast time scale and are peaked at zero lag, the direct connections in the model introduced by Pillow et al. (2008) were estimated to act almost instantaneously (with effectively zero delay), making their physiological interpretation somewhat uncertain. We therefore imposed a strict 3 ms delay on the initial rise of the coupling filters here to account for physiological delays in neural coupling. (However, the exact delay imposed on the cross-coupling filters did not change our results qualitatively, as long as some delay was imposed, down to 0.8 ms, our temporal resolution, as we discuss at more length below.) The delay in the cross-coupling filters effectively forces the common noise term to account for the instantaneous correlations which are observed in this network; see Fig. 5 and Section 3.1 below for further discussion.

Fig. 5.

Comparing real versus predicted cross-correlations. Example of 48 randomly selected cross-correlation functions of retinal responses and simulated responses of the common-noise model without direct cross-coupling (Fig. 1(C)). Each group of three panels shows the cross-correlation between a randomly selected reference ON/OFF (red/blue) cell and its three nearest neighbor cells (see schematic receptive field inset and enlarged example). In black is the data, in blue/red is the generated data using the common input model, and in green is the data generated with the common input turned off. The baseline firing rates are subtracted; also, recall that cells whose firing rate was too low or which displayed spike-sorting artifacts were excluded from this analysis. Each cross-correlation is plotted for delays between −96 to 96 ms. The Y-axis in each plot is rescaled to maximize visibility. The cross correlation between cells of the same type is always positive while opposite type cells are negatively cross correlated. Therefore, a blue positive cross correlation indicates an OFF–OFF pair, a red positive cross correlation indicates an ON–ON pair, and a blue/red negative cross-correlation indicates a OFF–ON/ON–OFF pair. Note that the cross-correlation at zero lag is captured by the common noise

The last term in Eq. (1) is more novel in this context, and will be our focus in this paper. The term $q_t^r$ is the instantaneous value of the r-th common noise term at time t, and we use ${\mathbf{q}}^r={\{q_t^r\}}_{t=1}^T$ to denote the time-series of common noise inputs, r. Each q^r is independently drawn from an autoregressive (AR) Gaussian process, q^r ~ 𝒩 (0, C_τ), with mean zero and covariance matrix C_τ. Since the inner layers of the retina are composed of non-spiking neurons, and since each RGC receives inputs from many inner layer cells, restricting q^r to be a Gaussian process seems to be a reasonable starting point. To fix the temporal covariance matrix C_τ, recall that Trong and Rieke (2008) reported that RGCs share a common noise with a characteristic time scale of about 4 ms, even in the absence of modulations in the visual stimulus. In addition, the characteristic width of the fast central peak in the cross-correlograms in this network is of the order of 4 ms (see, e.g., Shlens et al. 2006; Pillow et al. 2008, and also Fig. 5 below). Therefore, we imposed a 4 ms time scale on our common noise by choosing appropriate parameters for C_τ; we did this using the autoregressive formulation $q_t={\displaystyle {\sum }_{\tau =1}^n{\varphi }_{\tau }{q}_{t-\tau }+{\epsilon }_t}$ , and choosing appropriate parameters ϕ_τ and the variance of the white noise process, ε_t, using the Yule–Walker method, which solves a linear set of equations given the observed data autocorrelation (Hayes 1996). We use the Matlab implementation of the Yule–Walker method.

The common noise inputs in our model are independent of the stimulus, to maintain computational tractability; recall that Trong and Rieke (2008) observed that the common noise was strong and correlated even in the absence of a modulated stimulus. While the stimulus-independent AR model for the common noise was chosen for computational convenience (see Appendix A for details), this model proved sufficient for modeling the data, as we discuss at more length below. Models of this kind, in which the linear predictor contains a random component, are common in the statistical literature and are referred to as ‘random effects models’ (Agresti 2002), and ‘generalized linear mixed models’ (McCulloch et al. 2008).

The mixing matrix, M, connects the n_q common noise terms to the n_cells observed neurons; this matrix induces correlations in the noise inputs impacting the RGCs. More precisely, the interneuronal correlations in the noise arise entirely from the mixing matrix; this reflects our assumption that the spatio-temporal correlations in the common noise terms are separable. I.e. the correlation matrix can be written as a Kronecker product of two matrices, C = C_τ ⊗ C_s, where C_s = M^TM. Since the common noise sources q_t are independent, with identical distributions, and all the spatial correlations in the common noise are due to the mixing matrix, M, we may compute the spatial covariance matrix of the vector of mixed common noise inputs Mq_t as C_s = M^TM. (We have chosen the noise sources to have unit variance; this entails no loss of generality, since we can change the strength of any of the noise inputs to any cell by changing the mixing matrix M.) The number of noise sources in the model can vary to reflect modeling assumptions. In Section 2.2 we use one noise source for every pair of neurons, while in Section 2.2 we use the same number of noise sources as the number of cells in order to avoid imposing any further assumptions on the statistical structure of the noise. (One interesting question is how few common inputs are sufficient—i.e., how small can we make n_q while still obtaining an accurate model—but we have not yet pursued this direction systematically.)

Pairwise model (Fig. 1(B))

For simplicity, and for better correspondence with the experimental evidence of Trong and Rieke (2008), we began by restricting our model to pairs of RGCs. We fit our model to pairs of the same subset of 27 RGCs analyzed in the modeling paper by Pillow et al. (2008). The receptive fields of both ON and OFF cell types in this subset formed a complete mosaic covering a small region of visual space, indicating that every parasol cell in this region was recorded; see Fig. 1(b) of Pillow et al. (2008). We modeled each pair of neurons with the model described above, but we allowed one common noise to be shared by the cells. In other words, the two cells in the pair received the same time-series, q, scaled by M = [m₁, m₂]^T (Fig. 1(B)). Therefore, the conditional intensity is:

$${\lambda }_t^i=\text{exp}({\mu }^i+{\mathbf{k}}^i·{\mathbf{x}}_t+{\mathbf{h}}^i·{\mathbf{y}}_t^i+{\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j+m_i·q_t),$$ (2)

where we kept all the notation as above, but we have dispensed with the sums over the other cells and over the common noise inputs (since in this case there is only one other cell and one common noise term to consider). The probability of observing n spikes between time t and time t + dt for neuron i in this model is:

$$P(n_t^i)=\frac{{({\lambda }_t^i)}^{n_t^i}{e}^{-{\lambda }_t^i}}{n_t^i!};$$ (3)

This model is conceptually similar to the model analyzed by de la Rocha et al. (2007), with a GLM including the spike history ${\mathbf{y}}_t^i\text{and}{\mathbf{y}}_t^j$ in place of integrate and fire spiking mechanism used in that paper.

Common-noise model with no direct coupling (Fig. 1(C))

Encouraged by the results of the pairwise model, we proceeded to fit the GLSS model to the entire observed RGC network. The pairwise model results (discussed below) indicated that the cross-coupling inputs are very weak compared to all other inputs. Also, the experimental results of Trong and Rieke (2008) indicate only weak direct coupling between ON cells and no direct coupling between the OFF cells. Thus, in order to obtain a more parsimonious model we abolished all cross-coupling filters (Fig. 1(C)). Hence, the conditional intensity function, ${\lambda }_t^i$ is:

$${\lambda }_t^i=\text{exp}\left({\mu }^i+{\mathbf{k}}^i·{\mathbf{x}}_t+{\mathbf{h}}^i·{\mathbf{y}}_t^i+{\displaystyle \sum _{r=1}^{n_q}{\mathbf{M}}_{i,r}}·q_t^r\right).$$ (4)

As in the pairwise model, each cell has a spatiotemporal filter, kⁱ, and a history filter, hⁱ. In contrast with the pairwise model, we now have no direct coupling, L_{i, j}. As discussed above, the firing activity of all the cells was modeled here as a Bernoulli process, with probabilities

$$\begin{array}{c}P(n_t^i=0)=\text{exp}(-{\lambda }_t^i)\mathit{\text{dt}}\hfill \\ P(n_t^i=1)=1-\text{exp}(-{\lambda }_t^i)\mathit{\text{dt}}.\hfill \end{array}$$ (5)

The formulation of the model as conditionally independent cells given the common noise q, with no cross-coupling filters, interacting only through the covariance structure of the common inputs, lends itself naturally to computational parallelization, since the expensive step, the maximum likelihood estimation of the model parameters, can be performed independently on each cell if certain simplifying approximations are made, as discussed in the next section.

2.3 Model parameter estimation

Now that we have introduced the model structure, we will describe the estimation of the model parameters. We proceeded in three steps. First we obtained a preliminary estimate of the “private” GLM parameters (μ_i, kⁱ, hⁱ) using a standard maximum-likelihood approach in which the common noise inputs q and direct coupling terms L_i were fixed at zero: we maximized the GLM likelihood p(y|μ_i, kⁱ, hⁱ, L_i = 0, q = 0), computed by forming products over all timebins t of either the Poisson likelihood (Eq. (3), in the pairwise model) or the Bernoulli likelihood (Eq. (5), in the population model with no direct coupling). In parallel, we obtained a rough estimate of the spatial noise covariance C_s directly from the data using the PSTH method (explained briefly below, and in Appendix C). Then, in the second step, each cell’s GLSS model was fit independently given the rough estimate of C_s. Lastly, given the model parameters and data we determined the covariance structure of the common noise effects with greater precision using the method of moments (explained below and in Appendix B).

We now discuss each step in turn. Maximizing the GLM likelihood p(y|μ_i, kⁱ, hⁱ, L_i = 0, q = 0) followed standard procedures (Truccolo et al. 2005; Pillow et al. 2008). To obtain a first estimate of the spatial noise covariance C_s, we used a peri-stimulus time histogram- (PSTH-) based approach that was similar to the cross-covariogram method introduced by Brody (1999). Specifically, we analyzed another dataset in which we observed these neurons’ responses to a fixed repeating white noise stimulus with the same variance as the longer nonrepeating white noise stimulus used to fit the other model parameters. By averaging the neural responses to the repeated stimulus we obtained the PSTH. We subtracted each neuron’s PSTH from its response to each trial to obtain the neurons’ trial-by-trial deviations from the mean response to the stimulus. We then formed a covariance matrix of the deviations between the neurons for each trial, and estimated the spatial covariance C_s from this matrix via a singular value decomposition that exploits the spatiotemporally separable structure of the common noise in our model. (For more details see Appendix C.) It is important to note that even though the PSTH method gives a good estimate of the spatial covariance C_s, we only need a rough estimate of the magnitude of the common noise going into each cell in order to proceed to the next step in our estimation procedure.¹

In the second stage of the estimation procedure, we used a maximum marginal likelihood approach to update the parameters for each cell in parallel, using the rough estimate of the spatial covariance C_s obtained in the previous step. We abbreviate Θ = {μ_i, ‖k_i‖₂, h_i, L_i}.² In our model, since the common noise inputs q are unobserved, to compute the likelihood of the spike train given the parameters Θ, we must marginalize over all possible q:

$${\mathrm{\Theta }}^{\mathit{\text{opt}}}=\text{arg}\underset{\mathrm{\Theta }}{\text{max}}\text{log}p(\mathbf{y}|\mathrm{\Theta },{\mathbf{C}}_s)=\text{arg}\underset{\mathrm{\Theta }}{\text{max}}\text{log}{\displaystyle \int p(\mathbf{y}|\mathbf{q},\mathrm{\Theta };{\mathbf{C}}_s)p(\mathbf{q},\mathrm{\Theta };{\mathbf{C}}_s)\mathbf{\text{dq}},}$$ (6)

This marginal loglikelihood can be shown to be a concave function of Θ in this model (Paninski 2005). However, the integral over all common noise time series q is of very high dimension and is difficult to compute directly. Therefore, we proceeded by using the Laplace approximation (Kass and Raftery 1995; Koyama and Paninski 2010; Paninski et al. 2010):

$$\text{log}{\displaystyle \int p(\mathbf{y}|\mathbf{q},\mathrm{\Theta };{\mathbf{C}}_s)p(\mathbf{q},\mathrm{\Theta };{\mathbf{C}}_s)\mathbf{\text{dq}}\approx \text{log}p(\hat{\mathbf{q}})+\text{log}p(y|\hat{\mathbf{q}},\mathrm{\Theta };{\mathbf{C}}_s)}-\frac{1}{2}\text{log det}\left(\frac{{\partial }^{2}p(y|\hat{\mathbf{q}};\mathrm{\Theta };{\mathbf{C}}_s)}{{\partial }^2{\mathbf{q}}^2}\right),$$ (7)

with

$$\hat{\mathbf{q}}=\text{arg}\underset{\mathbf{q}}{\text{max}}[\text{log}p(\mathbf{q})+\text{log}p(y|\mathbf{q},\mathrm{\Theta };{\mathbf{C}}_s)].$$ (8)

While this approximation might look complicated at first sight, in fact it is quite straightforward: we have approximated the integrand p(y|q, Θ; C_s) p(q, Θ; C_s) with a Gaussian function, whose integral we can compute exactly, resulting in the three terms on the right-hand-side of Eq. (7). The key is that this replaces the intractable integral with a much more tractable optimization problem: we need only compute q̂, which corresponds to the maximum a posteriori (MAP) estimate of the common noise input to the cell on a trial by trial basis.³ The Laplace approximation is accurate when the likelihood function is close to Gaussian or highly concentrated around the MAP estimate; in particular, Pillow et al. (2011) and Ahmadian et al. (2011) found that this approximation was valid in this setting.

It should also be noted that the spatial covariance matrix, C_s, is treated as a fixed parameter and is not being optimized for in this second stage. The model parameters and the common noise were jointly optimized by using a Newton-Raphson method on the log-likelihood, Eq. (7). Taking advantage of the fact that the second derivative matrix of the log-posterior in the AR model has a banded diagonal structure, we were able to fit the model in time linearly proportional to the length of the experiment (Koyama and Paninski 2010; Paninski et al. 2010). For more details see Appendix A. In our experience, the last term in Eq. 7 does not significantly influence the optimization, and was therefore neglected, for computational convenience.

Over-fitting is a potential concern for all parametric fitting problems. Here one might worry, for example, that our common noise is simply inferred to be instantaneously high whenever we observe a spike. However, this does not happen, since we imposed that the common noise is an AR process with a nonvanishing time scale, and this time correlation, in essence, penalizes instantaneous changes in the common noise. Furthermore, in all the results presented below, we generated the predicted spike trains using a new realization of the AR process, not with the MAP estimate of the common noise obtained here, on a cross-validation set. Therefore, any possible over-fitting should only decrease our prediction accuracy.

In the third stage of the fitting procedure, we re-estimated the spatial covariance matrix, C_s, of the common noise influencing the cells. We use the method of moments to obtain C_s given the parameters obtained in the second step. In the method of moments, we approximated each neuron as a point process with a conditional intensity function, λ_t = exp(ΘX_t + q_t), where we have concatenated all the covariates, the stimulus and the past spiking activity of the cell and all other cells, into X. This allowed us to write analytic expressions for the different expected values of the model as a function of C_s given X_t. Then, we equated the analytic expressions for the expected values with the observed empirical expected values and solved for C_s. See details in Appendix B. The method of moments has the advantage that it permits an alternating optimization (iterating between the second and third steps described here). However, in practice we found that the two methods for estimating C_s (the PSTH approach and the method of moments) gave similar results.

2.4 Decoding

Once we found the model parameters, we solved the inverse problem and estimated the stimulus given the spike train and the model parameters. We will consider the decoding of the filtered stimulus input into the cells, uⁱ = kⁱ · x. For simplicity, we performed the decoding only on pairs of neurons, using the pairwise model (Fig. 1(B)) fit of Section 2.2 on real spike trains that were left out during the fitting procedure. We adopted a Bayesian approach to decoding, where the stimulus estimate, û(y), is based on the posterior stimulus distribution conditioned on the observed spike trains yⁱ. More specifically, we used the maximum a posteriori (MAP) stimulus as the Bayesian estimate. The MAP estimate is approximately equal to the posterior mean, E [u|y, Θ, C_s] in this setting (Pillow et al. 2011; Ahmadian et al. 2011). According to Bayes’ rule, the posterior p(u|y, Θ, C_s) is proportional to the product of the prior stimulus distribution p(u), which describes the statistics of the stimulus ensemble used in the experiment, and the likelihood p(y|u, Θ, C_s) given by the encoding model. The MAP estimate is thus given by

$$\hat{\mathbf{u}}(\mathbf{y})=\text{arg}\underset{\mathbf{u}}{\text{max}}p(\mathbf{u}|\mathbf{y},\mathrm{\Theta },{\mathbf{C}}_s)=\text{arg}\underset{\mathbf{u}}{\text{max}}[\text{log}p(\mathbf{u}|\mathrm{\Theta })+\text{log}p(\mathbf{y}|\mathbf{u},\mathrm{\Theta },{\mathbf{C}}_s)].$$ (9)

The prior p(u|Θ) depends on the model parameters through the dependence of uⁱ on the stimulus filters kⁱ. The marginal likelihood p(y|u, Θ, C_s) was obtained by integrating out the common noise terms as in Eq. (6), and as in Eq. (7), we used the Laplace approximation:

$$\text{log}p(\mathbf{y}|\mathbf{u},\mathrm{\Theta },{\mathbf{C}}_s)=\underset{\mathbf{q}}{\text{max}}[\text{log}p(\mathbf{q})+\text{log}p(\mathbf{y}|\mathbf{u},\mathbf{q},\mathrm{\Theta },{\mathbf{C}}_s)]$$ (10)

where, again, we retained just the first two terms of the Laplace approximation (dropping the log-determinant term, as in Eq. (7)). With this approximation the posterior estimate is given by

$$\hat{\mathbf{u}}(\mathbf{y})=\text{arg}\underset{\mathbf{u},\mathbf{q}}{\text{max}}[\text{log}p(\mathbf{u}|\mathrm{\Theta })+\text{log}p(\mathbf{q})+\text{log}p(\mathbf{y}|\mathbf{u},\mathbf{q},\mathrm{\Theta },{\mathbf{C}}_s)].$$ (11)

By exploiting the bandedness properties of the priors and the model likelihood, we performed the optimization in Eq. (11) in computational time scaling only linearly with the duration of the decoded spike trains; for more details see Appendix A.

3 Results

We began by examining the structure of the estimated GLM parameters. Qualitatively, the resulting filters were similar for the pairwise model, the common-noise model, and the model developed by Pillow et al. (2008). The stimulus filters closely resembled a time-varying difference-of-Gaussians. The post-spike filters produced a brief refractory period and gradual recovery with a slight overshoot (data not shown; see Fig. 1 in Pillow et al. 2008).

We will now first present our results based on the pairwise model. Then we will present the results of the analysis based on the common-noise model with no direct coupling; in particular, we will address this model’s ability to capture the statistical structure that is present in the full population data, and to predict the responses to novel stimuli. Finally, we will turn back to the pairwise model and analyze its decoding performance.

3.1 Pairwise model

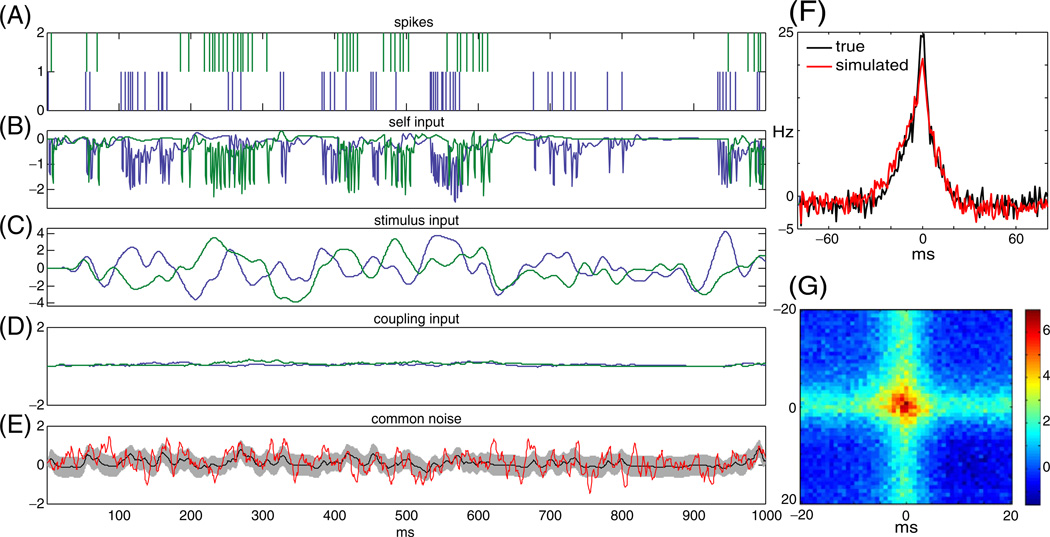
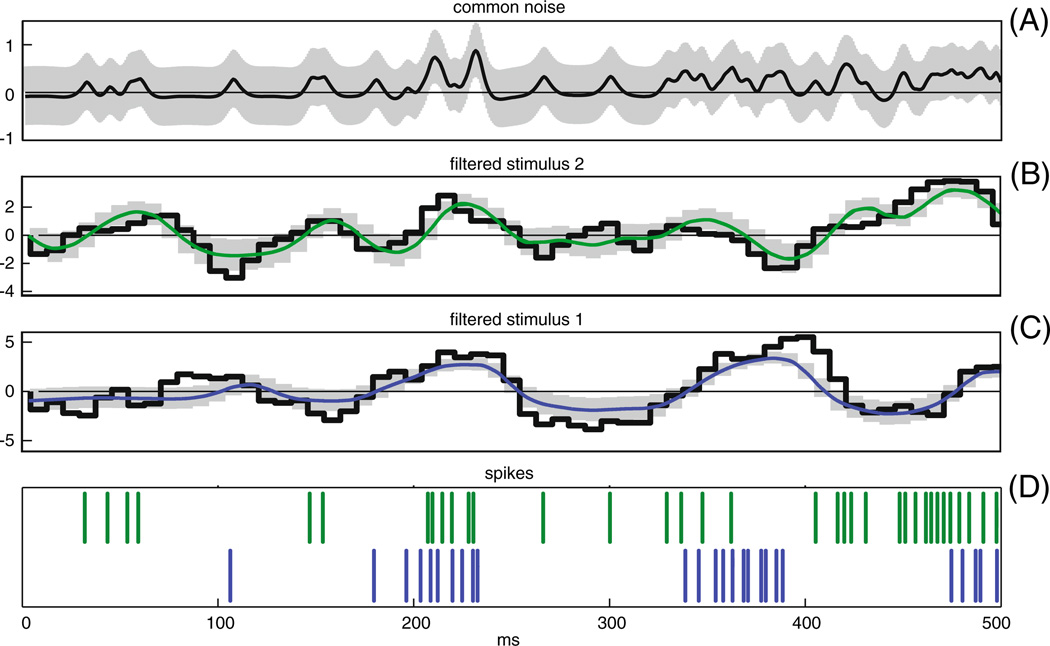
The pairwise model (Fig. 1(B)) allowed for the trial-by-trial estimation of the different inputs to the cell, including the common noise, q_t. To examine the relative magnitude of the inputs provided by stimulus and coupling-related model components, we show in Fig. 2 the net linear input to an example pair of ON cells on a single trial. The top panel (panel A) shows the spike-trains of two ON cells over 1 s. Below it are the different linear inputs. The post-spike filter input, ${\mathbf{h}}^i·{\mathbf{y}}_t^i$ , (panel B) imposes a relative refractory period after each spike by its fast negative input to the cell. The stimulus filter input, kⁱ · x_t, (panel C) is the stimulus drive to the cell. In panel D we show the cross-coupling input to the cells, ${\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j$ . The MAP estimate of the common noise, m_i · q_t, (panel E black line) is positive when synchronous spikes occur during negative stimulus periods or when the stimulus input is not strong enough to explain the observed spike times. This can be seen quantitatively in panel J, where we show the three point correlation function of the common noise and the two spike trains. In this case, m_i = m_j = 1, for simplicity, so m_i · q_t = q_t. The red line in panel E is an example of one possible realization of the common noise which is consistent with the observed spiking data; more precisely, it is a sample from the Gaussian distribution with mean given by the MAP estimate, q_t, (black line) and covariance given by the estimated posterior covariance of q_t (gray band) (Paninski et al. 2010). Note that the cross-coupling input, ${\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j$ , is much smaller than the stimulus, self-history, and the common noise.

Fig. 2.

Relative contribution of self post-spike, stimulus inputs, cross-coupling inputs, and common noise inputs to a pair of ON cells. In panels (A) through (D) blue indicates cell 1 and green cell 2. Panel (A): The observed spike train of these cells during this second of observation. Panel (B): Estimated refractory input from the cell, ${\mathbf{h}}^i·{\mathbf{y}}_t^i$ . In panels B through D the traces are obtained by convolving the estimated filters with the observed spike-trains. Panel (C): The stimulus input, kⁱ · x_t. Panel (D): Estimated cross-coupling input to the cells, ${\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j$ . Panel (E): MAP estimate of the common noise, q̂_t (black), with one standard deviation band (gray). Red trace indicates a sample from the posterior distribution of the common noise given the observed data. Note that the cross-coupling input to the cells are much smaller than all other three inputs to the cell. Panel (F): The cross-correlations of the two spike trains (black - true spike trains, red-simulated spike trains). Panel (G): The three point correlations function of the common-noise and the spike trains, C(τ₁, τ₂) = [〈q(t)y₁(t + τ₁)y₂(t + τ₂)〉 − 〈q(t)〉〈y₁(t)〉 〈y₂(t)〉]/(〈y₁(t)〉〈y₂(t)〉dt). Note that when the two cells fire in synchrony the common-noise tends to be high (as can be seen from the warm colors at the center of the figure)

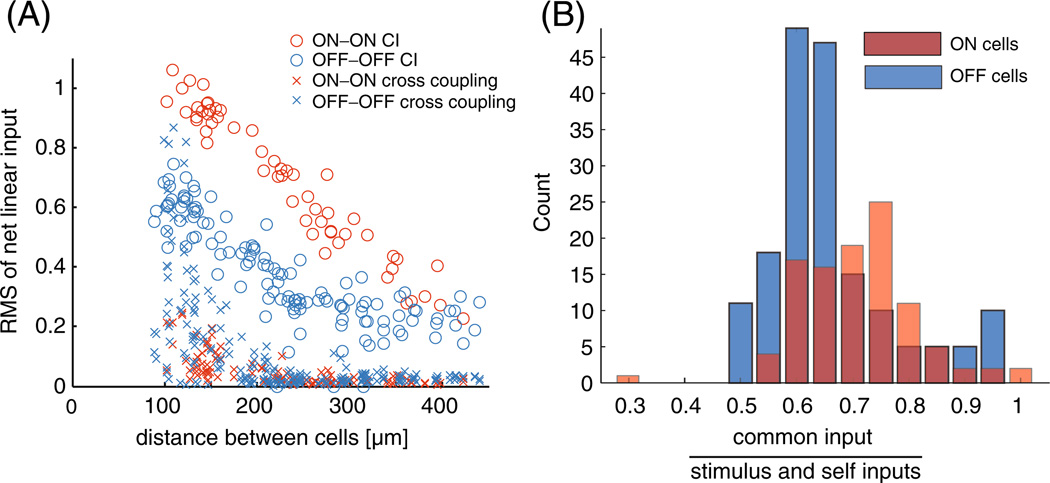
The relative magnitude of the different linear inputs is quantified in Fig. 3(A), where we show the root mean square (RMS) inputs to the ensemble of cells from q_t and ${\mathbf{L}}_{i,j}·{\mathbf{y}}_t^j$ as a function of the cells’ distance from each other. One can see that the common noise is significantly larger than the cross-coupling input in the majority of the cell pairs. It is important to note that we are plotting the input to the cells and not the magnitude of the filters; since the OFF population has a higher mean firing rate, the net cross-coupling input is sometimes larger than for the ON population. However, the magnitude of the cross-coupling filters is in agreement with Trong and Rieke (2008); we found that the cross-coupling filters between neighboring ON cells are stronger, on average, than the cross-coupling filters between neighboring OFF cells by about 25% (data not shown). It is also clear that the estimated coupling strength falls off with distance, as also observed in Shlens et al. (2006). The gap under 100 µm in Fig. 3(A) reflects the minimum spacing between RGCs of the same type within a single mosaic.

Fig. 3.

Population summary of the inferred strength of the inputs to the model. (A) Summary plot of the relative contribution of the common noise (circles) and cross-coupling inputs (crosses) to the cells as a function of the cells’ distance from each other in the pairwise model for the complete network of 27 cells. Note that the common noise is stronger then the cross-coupling input in the large majority of the cell pairs. Since the OFF cells have a higher spike rate on average, the OFF–OFF cross-coupling inputs have a larger contribution on average than the ON–ON cross-coupling inputs. However, the filter magnitudes agree with the results of Trong and Rieke (2008); the cross-coupling filters between ON cells are stronger, on average, than the cross-coupling filters between OFF cells (not shown). The gap under 100 µm is due to the fact that RGCs of the same type have minimal overlap (Gauthier et al. 2009). (B) Histograms showing the relative magnitude of the common noise and stimulus plus post-spike filter induced inputs to each cell under the common-noise model. The X-axis is the ratio of the RMS of each of these inputs $\left(\sqrt{\frac{\mathit{\text{var}}({\hat{q}}_t)}{\mathit{\text{var}}({\mathbf{h}}^i·{\mathbf{y}}_t^i+{\mathbf{k}}^i·{\mathbf{x}}_t)}}\right)$ . Common inputs tend to be a bit more than half as strong as the stimulus and post-spike inputs combined

Cells that are synchronized in this network have cross-correlations that peak at zero lag (as can be seen in Fig. 5 below and in Shlens et al. 2006 and Pillow et al. 2008). This is true even if we bin our spike trains with sub-millisecond precision. This is difficult to explain by direct coupling between the cells, since it would take some finite time for the influence of one cell to propagate to the other (though, gap junction coupling can indeed act on a submillisecond time scale and can explain fast time scale synchronization Brivanlou et al. 1998). Pillow et al. (2008) used virtually instantaneous cross-coupling filters with sub-millisecond resolution to capture these synchronous effects. To avoid this non-physiological instantaneous coupling, as discussed in the methods we imposed a strict delay on our cross-coupling filters L_{i, j}, to force the model to distinguish between the common noise and the direct cross-coupling. Therefore, by construction, the cross-coupling filters cannot account for very short-lag synchrony (under 4 ms) in this model, and the mixing matrix M handles these effects, while the cross-coupling filters and the receptive field overlap in the pairwise model account for synchrony on longer time scales. Indeed, the model assigns a small value to the cross-coupling and, as we will show below, we can in fact discard the cross-coupling filters while retaining an accurate model of this network’s spiking responses.

In the pairwise model, since every two cells share one common noise term, we may directly maximize the marginal log-likelihood of observing the spike trains given M (which is just a scalar in this case), by evaluating the log-likelihood on a grid of different values of M. For each pair of cells, we checked that the value of M obtained by this maximum-marginal-likelihood procedure qualitatively matched the value obtained by the method of moments procedure (data not shown). We also repeated our analysis for varying lengths of the imposed delay on the direct interneuronal cross-coupling filters. We found that the length of this delay did not appreciably change the obtained value of M, nor the strength of the cross-coupling filters, across the range of delays examined (0.8 – 4 ms).

3.2 Common-noise model with no direct coupling

We examined the effects of setting the cross-coupling filters to zero in the common-noise model in response to two considerations. The first consideration is the fact that the cross-coupling inputs to the cells were much smaller than all other inputs once we introduced the common noise effects and imposed a delay on the coupling terms. The second consideration is that Trong and Rieke (2008) reported that the ON RGCs are weakly coupled, and OFF cells are not directly coupled. This reduced the number of parameters in the model drastically since we no longer have to fit n_cells × (n_cells − 1) cross-coupling filters, as in the fully general model. When we estimated the model parameters with the direct coupling effects removed, we found that the inputs to the cell are qualitatively the same as in the pairwise model. For this new common-noise model, across the population, the standard deviation of the total network-induced input is approximately 1/2 the standard deviation of total input in the cells (Fig. 3(B)), in agreement with the results of Pillow et al. (2008). We also found that the inferred common noise strength shared by any pair of cells depended strongly on the degree of overlap between the receptive fields of the cells (Fig. 4), consistent with the distance-dependent coupling observed in Fig. 3(A).

In order to test the quality of the estimated model parameters, and to test whether the common noise model can account for the observed synchrony, we presented the model with a new stimulus and examined the resulting spike trains. As discussed in the methods, it is important to note that the common noise samples we used to generate spike trains are not the MAP estimate of the common noise we obtain in the fitting, but rather, new random realizations. This was done for two reasons. First, we used a cross-validation stimulus that was never presented to the model while fitting the parameters, and for which we have no estimate of the common noise. Second, we avoid over-fitting by not using the estimated common noise. Since we have a probabilistic model, and we are injecting noise into the cells, the generated spike trains should not be exact reproductions of the collected data; rather, the statistical structure between the cells should be preserved. Below, we show the two point (Fig. 5) and three point correlation (Fig. 6) functions of a set of randomly selected cells under the common-noise model. Both in the cross-correlation function and in the three-point correlation functions, one can see that the correlations of the data are very well approximated by the model.⁴ The results for the pairwise model are qualitatively the same and were previously presented in Vidne et al. (2009).

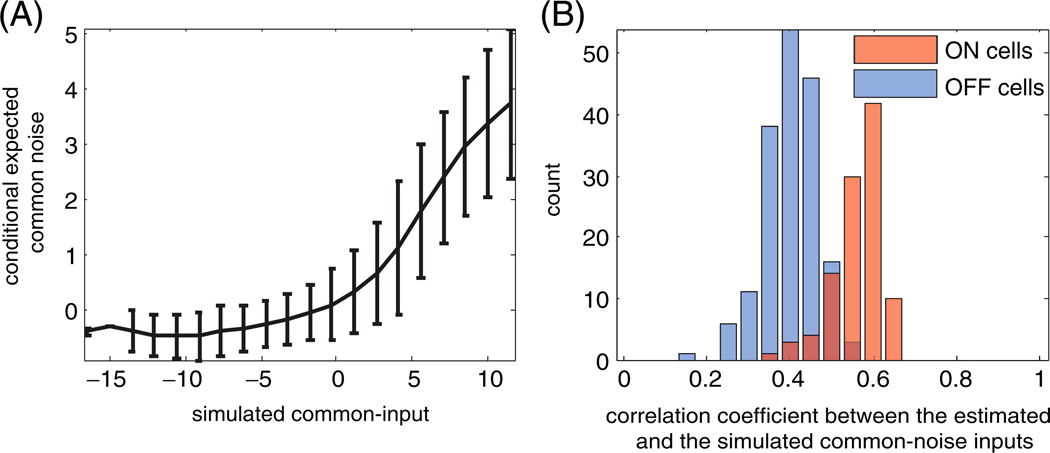
To further examine the accuracy of the estimated common noise terms q̂, we tested the model with the following simulation. Using the estimated model parameters and the true stimulus, we generated a new population spike-train from the model, using a novel sample from the common-noise input q. Then we estimated q given this simulated population spike-train and the stimulus, and examined the extent to which the estimated q̂ reproduces the true simulated q. We found that the estimated q̂ tracks the true q well when a sufficient number of spikes are observed, but shrinks to zero when no spikes are observed. This effect can be quantified directly by plotting the true vs. the inferred q_t values; we find that E(q̂_t|q_t) is a shrunk and half-rectified version of the true q_t (Fig. 7(A)), and when quantified across the entire observed population, we find that the correlation coefficient between the true and inferred simulated common-noise inputs in this model is about 0.5 (Fig. 7(B)).

Fig. 7.

Comparing simulated and inferred common-noise effects given the full population spike train. (A) The conditional expected inferred common-noise input q̂, averaged over all cells in the population, ± 1 s.d., versus the simulated common-noise input q. Note that the estimated input can be approximated as a rectified and shrunk linear function of the true input. (B) Population summary of the correlation coefficient between the estimated common-noise input and the simulated common-noise input for the entire population

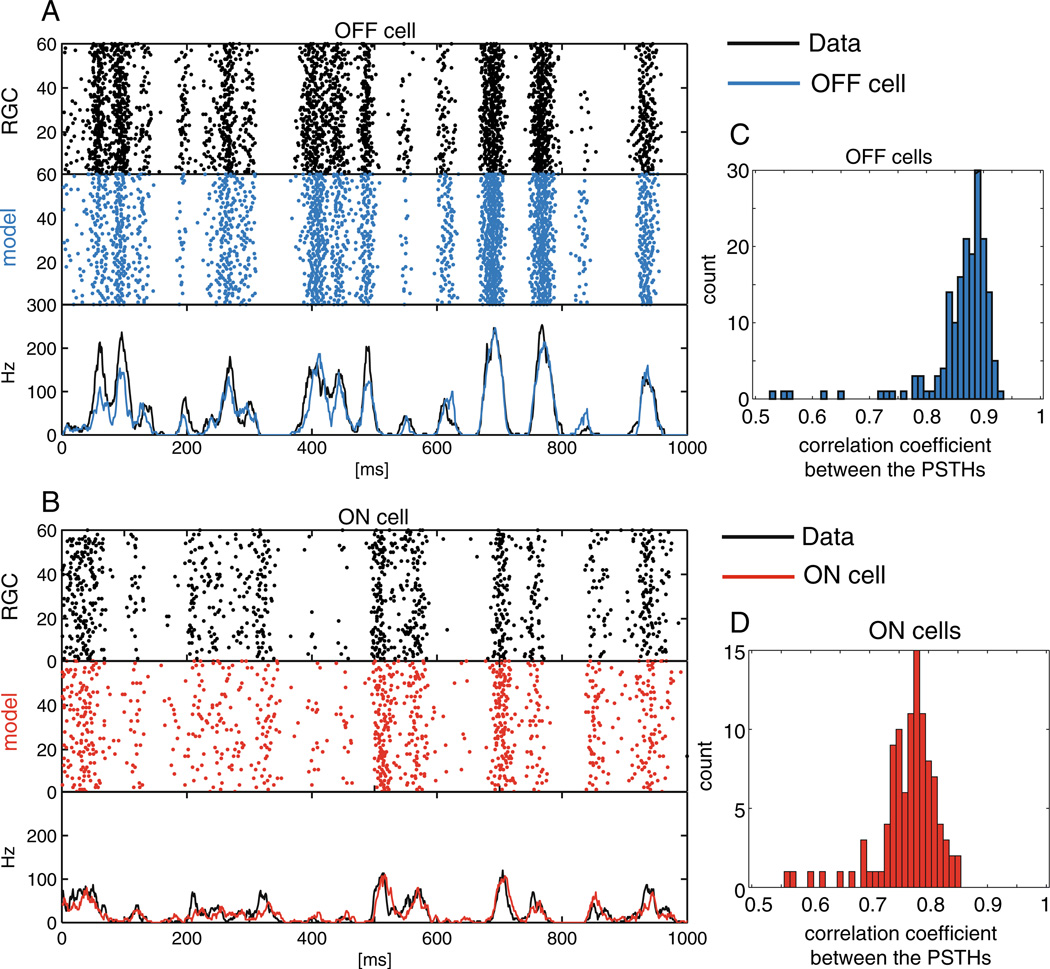
We also tested the model by examining the peristimulus time histogram (PSTH). We presented to the model 60 repetitions of a novel 10 s stimulus, and compared the PSTHs of the generated spikes to the PSTHs of the recorded activity of the cells (Fig. 8). The model does very well in capturing the PSTHs of the ON population and captures the PSTH of the OFF population even more accurately. In each case (PSTHs, cross-correlations, and triplet-correlations), the results qualitatively match those presented in Pillow et al. (2008). Finally, we examined the dependence of the inferred common noise on the stimulus; recall that we assumed when defining our model that the common noise is independent of the stimulus. We computed the conditional expectation E[q|x, y] as a function of x for each cell, where we use y to denote the cell’s observed spike train, q for the common noise influencing the cell, and x denotes the sum of all the other inputs to the cell (i.e., the stimulus input kⁱ · x_t plus the refractory input ${\mathbf{h}}^i·{\mathbf{y}}_t^i$ ). This function E[q|x, y] was well-approximated by a linear function with a shallow slope over the effective range of the observed x (data not shown). Since we can reabsorb any linear dependence in E[q|x, y] into the generalized linear model (via a suitable rescaling of x), we conclude that the simple stimulus-independent noise model is sufficient here.

Fig. 8.

Comparing real versus predicted PSTHs. Example raster of responses and PSTHs of recorded data and model-generated spike trains to 60 repeats of a novel 1 sec stimulus. (A) OFF RGC (black) and model cell (blue). (B) ON RGC (black) and model ON cell (red). (C)–(D) Correlation coefficient between the model PSTHs and the recorded PSTHs for all OFF (C) and ON cells (D). The model achieves high accuracy in predicting the PSTHs

The common noise model suggests that noise in the spike trains has two sources: the “back-end” noise due to the stochastic nature of the RGC spiking mechanism, and the “front-end” noise due to the common noise term, which represents the lump sum of filtered noise sources presynaptic to the RGC layer. In order to estimate the relative contribution of these two terms, we used the “law of total variance”:

$$E_x[\mathit{\text{var}}(y|x)]=E_x\left[{\mathit{\text{var}}}_{q|x}(E[y|q,x])\right]+E_x\left[E_{q|x}[\mathit{\text{var}}(y|q,x)]\right].$$ (12)

Here q, x, and y are as in the preceding paragraph. The first term on the right-hand side here represents the “front-end” noise: it quantifies the variance in the spike train that is only due to variance in q for different values of x. The second term on the right represents the “back-end” noise: it quantifies the average conditional variance in the spike train, given x and q (i.e., the variance due only to the spiking mechanism). We found that the front-end noise is approximately 60% as large as the back-end noise in the ON population, on average, and approximately 40% as large as the back-end noise in the OFF population.

3.3 Decoding

The encoding of stimuli to spike-trains is captured well by the GLSS model, as quantified in Figs. 5–8. We will now consider the inverse problem, the decoding of the stimuli given the spike-trains and the model parameters. This decoding analysis is performed using real spike trains that were left out during the fitting procedure of the pairwise model (Fig. 1B).

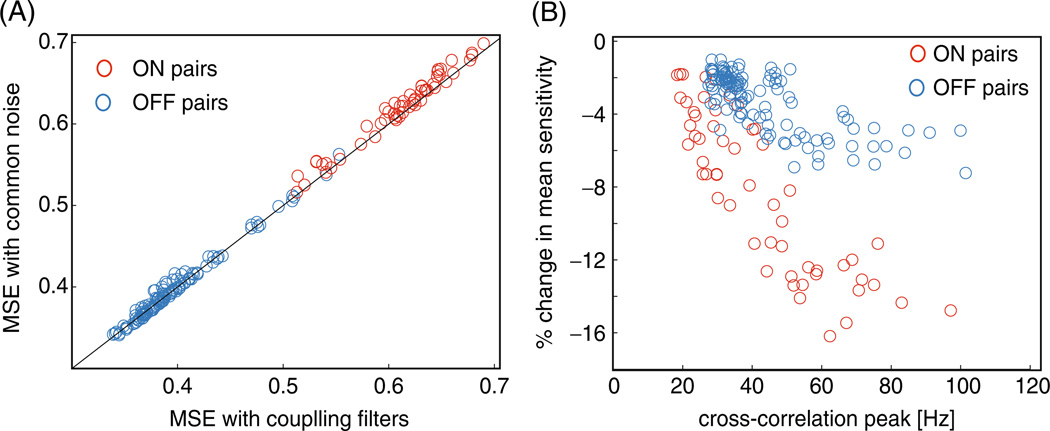
Figure 9 shows an example of decoding the filtered stimulus, uⁱ, for a pair of cells. Figure 10(A) shows a comparison of the mean-square decoding errors for MAP estimates based on the pairwise common-noise model, and those based on a GLM with no common noise but with post-spike filters directly coupling the two cells, as in Pillow et al. (2008). There is very little difference between the performance of the two models based on the decoding error.

Fig. 9.

Stimulus decoding given a pair of spike trains. In panels (B) through (D) blue indicates cell 1 and green cell 2. (A) MAP estimate of the common noise going into two cells (black) with one standard deviation of the estimate (gray). (B) and (C) panels: The true stimulus filtered by the estimated spatio-temporal filter trace, kⁱ · x_t, (black) and the MAP estimate of the filtered stimulus (green/blue) with one standard deviation (gray). Decoding performed following the method described in Section 2.4. (D) The spike trains of the two cells used to perform the decoding

Fig. 10.

Decoding jitter analysis. (A) Without any spike jitter, the two models decode the stimulus with nearly identical accuracy. Each point represents the decoding performance of the two models for a pair of cells. In red: ON–ON pairs. In blue: OFF–OFF. (B) Jitter analysis of the common noise model versus the direct coupling model from Pillow et al. (2008). The X axis denotes the maximum of the cross-correlation function between the neuron pair. Baseline is subtracted so that units are in spikes/s above (or below) the cells’ mean rate. The Y axis is the percent change ( $\frac{S_{\mathit{\text{common}}-\mathit{\text{noise}}}-S_{\mathit{\text{direct}}-\mathit{\text{coupling}}}}{S_{\mathit{\text{common}}-\mathit{\text{noise}}}}*100$ ) in the model’s sensitivity to jitter ( $S=\frac{\sqrt{{\mathbf{U}}_{\mathit{\text{jitter}}}-\mathbf{U}}}{|\mathrm{\Delta }t|}$ ) compared to the change in sensitivity of the direct coupling model: negative values mean that the common noise model is less sensitive to jitter than a model with direct cross-coupling. Note that the common-noise model leads to more robust decoding in every cell pair examined, and pairs that are strongly synchronized are much less sensitive to spike-train jitter in the common noise model than in the model with coupling filters

However, the decoder based on the common noise model turned out to be significantly more robust than that based on the direct, instantaneous coupling model. We studied robustness by quantifying how jitter in the spike trains changes the decoded stimulus, u(y_jitter), in the two models, where y_jitter is the jittered spike train (Ahmadian et al. 2009). Specifically, we analyzed a measure of robustness which quantifies the sensitivity to precise spike timing. To calculate a spike’s jitter sensitivity we compute the estimate u(y) for the original spike train and for a spike train in which the timing of that spike is jittered by a Gaussian random variable, with standard deviation Δt. We defined the sensitivity to be the root mean square distance between the two stimulus estimates divided by |Δt|, $S=\frac{\sqrt{{\mathbf{u}}_{\mathit{\text{jitter}}}-\mathbf{u}}}{|\mathrm{\Delta }t|}$ , where u_jitter is the decoded stimulus of the jittered spike train, and S is computed in the limit of small jitter, Δt → 0. The average value of these spike sensitivities quantifies how sensitively the decoder depends on small variations in the spike trains. Conversely, the smaller these quantities are on average, the more robust is the decoder.

Our intuition was that the direct coupling model has very precise spike-induced interactions, via the coupling filters L_{i, j}, but these interactions should be fragile, in the sense that if a spike is perturbed, it will make less sense to the decoder, because it is not at the right time relative to spikes of other cells. In the common-noise model, on the other hand, the temporal constraints on the spike times should be less precise, since the common noise term acts as an unobserved noise source which serves to jitter the spikes relative to each other, and therefore adding small amounts of additional spike-time jitter should have less of an impact on the decoding performance. We found that this was indeed the case: the spike sensitivities for ON–ON (OFF–OFF) pairs turned out to decrease by about 10% (5%) when using the decoder based on the common noise model instead of the instantaneous coupling model with no common noise. Furthermore, the percentage decrease in mean spike sensitivity was directly proportional to the strength of the common noise input between the two cells (Fig. 10(B)).

4 Discussion

The central result of this study is that multi-neuron firing patterns in large networks of primate parasol retinal ganglion cells can be explained accurately by a common-noise model with no direct coupling interactions (Figs. 1(C), 5–8), consistent with the recent intracellular experimental results of Trong and Rieke (2008). The common noise terms in the model can be estimated on a trial-by-trial basis (Figs. 2 and 7), and the scale of the common noise shared by any pair of cells depends strongly on the degree of overlap in the cells’ receptive fields (Fig. 4). By comparing the magnitudes of noise- versus stimulus-driven effects in the model (Fig. 3), we can quantify the relative contributions of this common noise source, versus spike-train output variability, to the reliability of RGC responses. Finally, optimal Bayesian decoding methods based on the common-noise model perform just as well as (and in fact, are more robust than) models that account for the correlations in the network by direct coupling (Fig. 10).

4.1 Modeling correlated firing in large networks

In recent years, many researchers have grappled with the problem of inferring the connectivity of a network from spike-train activity (Chornoboy et al. 1988; Utikal 1997; Martignon et al. 2000; Iyengar 2001; Paninski et al. 2004; Truccolo et al. 2005; Okatan et al. 2005; Nykamp 2005, 2008, 2009; Kulkarni and Paninski 2007; Stevenson et al. 2008, 2009). Modeling of correlated firing in the retina has been a special focus (Nirenberg et al. 2002; Schnitzer and Meister 2003; Schneidman et al. 2006; Shlens et al. 2006; Pillow et al. 2008; Shlens et al. 2009; Cocco et al. 2009). The task of disambiguating directed connectivity from common input effects involves many challenges, among them the fact that the number of model parameters increases with the size of the networks, and therefore more data are required in order to estimate the model parameters. The computational complexity of the task also increases rapidly. In the Bayesian framework, integrating over higher and higher dimensional distributions of unobserved inputs becomes difficult. Here, we were aided by prior knowledge from previous physiological studies—in particular, that the common noise in this network is spatially localized (Shlens et al. 2006; Pillow et al. 2008) and fast (with a timescale that was explicitly measured by Trong and Rieke 2008)—to render the problem more manageable. The model is parallelizable, which made the computation much more tractable. Also, we took advantage of the fact that the common noise may be well approximated as an AR process with a banded structure to perform the necessary computations in time that scales linearly with T, the length of the experiment. Finally, we exploited the separation of time scales between the common-noise effects and those due to direct connectivity by imposing a strict time delay on the cross-coupling filters; this allowed us to distinguish between the effects of these terms in estimating the model structure (Figs. 2 and 3).

Our work relied heavily on the inference of the model’s latent variables, the common noise inputs, and their correlation structure. If we fit our model parameters while ignoring the effect of the common noise, then the inferred coupling filters incorrectly attempt to capture the effects of the unmodeled common noise. A growing body of related work on the inference of latent variables given spike train data has emerged in the last few years, building on work both in neuroscience (Smith and Brown 2003) and statistics (Fahrmeir and Kaufmann 1991; Fahrmeir and Tutz 1994). For example, Yu et al. (2006, 2009) explored a dynamical latent variable model to explain the activity of a large number of observed neurons on a single trial basis during motor behavior. Lawhern et al. (2010) proposed to include a multi-dimensional latent state in a GLM framework to account for external and internal unobserved states, also in a motor decoding context. We also inferred the effects of the common noise on a single trial basis, but our method does not attempt to explain many observed spike trains on the basis of a small number of latent variables (i.e., our focus here is not on dimensionality reduction); instead, the model proposed here maintains the same number of common noise terms as the number of observed neurons, since these terms are meant to account for noise in the presynaptic network, and every RGC could receive a different and independent combination of these inputs.

Two important extensions of these methods should be pursued in the future. First, in our method the time scale of the common noise is static and preset. It will be important to relax this requirement, to allow dynamic time-scales and to attempt to infer the correct time scales directly from the spiking data, perhaps via an extension of the moment-matching or maximum likelihood methods presented here. Another important extension would be to include common noise whose scale depends on the stimulus; integrating over such stimulus-dependent common noise inputs would entail significant statistical and computational challenges that we hope to pursue in future work (Pillow and Latham 2007; Mishchenko et al. 2011).

4.2 Possible biological interpretations of the common noise

One possible source of common noise is synaptic variability in the bipolar and photoreceptor layers; this noise would be transmitted and shared among nearby RGCs with overlapping dendritic footprints. Our results are consistent with this hypothesis (Fig. 4), and experiments are currently in progress to test this idea more directly (Rieke and Chichilnisky, personal communication). It is tempting to interpret the mixing matrix M in our model as an effective connectivity matrix between the observed RGC layer and the unobserved presynaptic noise sources in the bipolar and photoreceptor layers. However, it is important to remember that M is highly underdetermined here: as emphasized in the Methods section, any unitary rotation of the mixing matrix will lead to the same inferred covariance matrix C_λ. Thus an important goal of future work will be to incorporate further biological constraints (e.g., on the sparseness of the cross coupling filters, locality of the RGC connectivity, and average number of photoreceptors per RGC), in order to determine the mixing matrix M uniquely. One possible source of such constraints was recently described by Field et al. (2010), who introduced methods for resolving the effective connectivity between the photoreceptor and RGC layers. Furthermore, parasol ganglion cells are only one of many retinal ganglion cell type; many researchers have found the other cell types to be synchronized as well (Arnett 1978; Meister et al. 1995; Brivanlou et al. 1998; Usrey and Reid 1999; Greschner et al. 2011). An important direction for future work is to model these circuits together, to better understand the joint sources of their synchrony.

4.3 Functional roles of synchrony and common noise

Earlier work (Pillow et al. 2008) showed that proper consideration of synchrony in the RGC population significantly improves decoding accuracy. Here, we showed that explaining the synchrony as an outcome of common noise driving the RGCs, as opposed to a model where the synchrony is the outcome of direct post-spike coupling, leads to less sensitivity to temporal variability in the RGC output spikes. One major question remains open: are there any possible functional advantages of this (rather large) common noise source in the retina? Cafaro and Rieke (2010) recently reported that common noise increases the accuracy with which some retinal ganglion cell types encode light stimuli. An interesting analogy to image processing might provide another clue: “dithering” refers to the process of adding noise to an image before it is quantized in order to randomize quantization error, helping to prevent visual artifacts which are coherent over many pixels (and therefore more perceptually obvious). It might be interesting to consider the common noise in the retina as an analog of the dithering process, in which nearby photoreceptors are dithered by the common noise before the analog-to-digital conversion implemented at the ganglion cell layer (Masmoudi et al. 2010). Of course, we emphasize that this dithering analogy represents just one possible hypothesis, and further work is necessary to better understand the computational role of common noise in this network.

Appendix A: O(T) optimization for parameter estimation and stimulus decoding for models with common noise effects

The common-noise model was formulated as conditionally independent cells, with no cross-coupling filters, interacting through the covariance structure of the common noise inputs. Therefore, the model lends itself naturally to parallelization of the computationally expensive stage, the maximum likelihood estimation of the model parameters. For each cell, we need to estimate the model parameters and the common noise the cell receives. The common noise to the cell on a given trial is a time series of the same length of the experiment itself (T discrete bins), and finding the maximum a posteriori (MAP) estimate of the common noise is a computationally intensive task because of its high dimensionality, but it can be performed independently on each cell. We used the Newton-Raphson method for optimization over the joint vector, ν = [Θ, q], of the model cell’s parameters and the common-noise estimate. Each iteration in the Newton-Raphson method requires us to find the new stepping direction, δ, by solving the linear set of equations, Hδ = ∇, where ∇ denotes the gradient and H the Hessian matrix (the matrix of second derivatives) of the objective function F. We need to solve this matrix equation for δ at every step of the optimization. In general, this requires O(T³) operations which renders naive approaches inapplicable for long experiments such as the one discussed here. Here we used a O(T) method for computing the MAP estimate developed in Koyama and Paninski (2010).

Because of the autoregressive structure of the common noise, q, the log posterior density of q_t can be written as:

$$F=\text{log}p(\{q_t\}|\{y_t\})=\text{log}p(q_o)+{\displaystyle \sum _{t=1}^T\text{log}p(q_t|q_{t-1})+{\displaystyle \sum _{t=1}^T\text{log}p(y_t|q_t)+\mathit{\text{const}},}}$$ (13)

where we denote the spike train as {y_t}, and for simplicity we have suppressed the dependence on all other model parameters and taken q to be a first order autoregressive process. Since all terms are concave in q, the entire expression is concave in q.

The Hessian, H, has the form:

$$\mathbf{H}=\left[\begin{array}{cc}\hfill \frac{{\partial }^{2}F}{{\partial }^{2}q}\hfill & \hfill \frac{{\partial }^{2}F}{\partial q\partial \mathrm{\Theta }}\hfill \\ \hfill \frac{{\partial }^{2}F}{\partial \mathrm{\Theta }\partial q}\hfill & \hfill \frac{{\partial }^{2}F}{{\partial }^2\mathrm{\Theta }}\hfill \end{array}\right];$$ (14)

note that the dimension of $J=\frac{{\partial }^{2}F}{{\partial }^{2}q}$ is T × T (in our case we have a 9.6 min recording and we use 0.8 ms bins, i.e. T = 720, 000), while the dimension of $H_{\mathrm{\Theta }\mathrm{\Theta }}=\frac{{\partial }^{2}F}{{\partial }^2\mathrm{\Theta }}$ is just N × N, where N is the number of parameters in the model (N < 20 for all the models considered here). Using the Schur complement of H we get:

$${\mathbf{H}}^{-1}={\left[\begin{array}{cc}\hfill J\hfill & \hfill H_{q\mathrm{\Theta }}\hfill \\ \hfill H_{\mathrm{\Theta }q}\hfill & \hfill H_{\mathrm{\Theta }\mathrm{\Theta }}\hfill \end{array}\right]}^{-1}=\left[\begin{array}{c}\hfill J^{-1}+J^{-1}{H}_{q\mathrm{\Theta }}{S}^{-1}{H}_{\mathrm{\Theta }q}J-J^{-1}{H}_{q\mathrm{\Theta }}{S}^{-1}\hfill \\ \hfill -S^{-1}{H}_{\mathrm{\Theta }q}{J}^{-1}{S}^{-1}\hfill \end{array}\right]$$ (15)

where we note the Schur complement of H as $S=J-H_{q\mathrm{\Theta }}{H}_{\mathrm{\Theta }\mathrm{\Theta }}^{-1}{H}_{\mathrm{\Theta }q}$ . The dimensions of $\frac{{\partial }^{2}F}{{\partial }^2\mathrm{\Theta }}$ are small (number of model parameters, N), and because of the autoregressive structure of the common noise, $J=\frac{{\partial }^{2}F}{{\partial }^{2}q}$ , is a tridiagonal matrix:

$$\mathbf{J}=\left[\begin{array}{cccccc}\hfill D_1\hfill & \hfill B_{1,2}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill B_{1,2}^T\hfill & \hfill D_2\hfill & \hfill B_{2,3}\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_{2,3}^T\hfill & \hfill D_3\hfill & \hfill \ddots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill B_{T-2,T-1}^T\hfill & \hfill D_{T-1}\hfill & \hfill B_{T-1,T}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill B_{T-1,T}^T\hfill & \hfill D_T\hfill \end{array}\right]$$ (16)

where

$$D_t=\frac{{\partial }^2}{\partial q_t^2}\text{log}p(y_t|q_t)+\frac{{\partial }^2}{\partial q_t^2}\text{log}p(q_t|q_{t-1})+\frac{{\partial }^2}{\partial q_t^2}\text{log}p(q_{t+1}|q_t)$$ (17)

and

$$B_{t,t+1}=\frac{{\partial }^2}{\partial q_t\partial q_{t+1}}\text{log}p(q_{t+1}|q_t).$$ (18)

In the case that we use higher order autoregressive processes, D_t and B_t are replaced by d × d blocks where d is the order of the AR process. The tridiagonal structure of J allows us to obtain each Newton step direction, δ, in O(d³T) time using standard methods (Rybicki and Hummer 1991; Paninski et al. 2010).

We can also exploit similar bandedness properties for stimulus decoding. Namely, we can carry out the Newton-Raphson method for optimization over the joint vector ν = (u, q), Eq. (11), in O(T) computational time. According to Eq. (11) (repeated here for convenience),

$$\hat{\mathbf{u}}(\mathbf{y})=\text{arg}\underset{\mathbf{u},\mathbf{q}}{\text{max}}[\text{log}p(\mathbf{u})+\text{log}p(\mathbf{q}|\mathrm{\Theta })+\text{log}p(\mathbf{y}|\mathbf{u},\mathbf{q},\mathrm{\Theta })].$$ (19)

the Hessian of the log-posterior, J, (i.e., the matrix of second partial derivatives of the log-posterior with respect to the components of ν = (u, q)) is:

$$\mathbf{J}=\frac{{\partial }^2\text{log}p(\mathbf{u})}{{\partial }^2\nu }+\frac{{\partial }^2\text{log}p(\mathbf{q}|\mathrm{\Theta })}{{\partial }^2\nu }+\frac{{\partial }^2\text{log}p(\mathbf{y}|\mathbf{u},\mathbf{q},\mathrm{\Theta })}{{\partial }^2\nu }.$$ (20)

Thus, the Hessian of the log-posterior is the sum of the Hessian of the log-prior for the filtered stimulus, $\mathbf{A}=\frac{{\partial }^2}{{\partial }^2\nu }\log p(\mathbf{u})$ , the Hessian, $\mathbf{B}=\frac{{\partial }^2}{{\partial }^2\nu }\log p(\mathbf{q}|\mathrm{\Theta })$ , of the log-prior for the common noise, and the Hessian of the log-likelihood, $\mathbf{D}=\frac{{\partial }^2}{{\partial }^2\nu }\log p(\mathbf{y}|\mathbf{u},\mathbf{q},\mathrm{\Theta })$ . Since we took the stimulus and common noise priors to be Gaussian with zero mean, A and B are constant matrices, independent of the decoded spike train.

We order the components of ν = (u, q) according to $(u_1^1,u_1^2,q_1,u_2^1,u_2^2,q_2,\cdots )$ , where subscripts denote the time step, i.e., such that components corresponding to the same time step are adjacent. With this ordering, D is block-diagonal with 3 × 3 blocks

$$\begin{array}{c}\mathbf{D}=\left(\begin{array}{ccc}\hfill {\mathbf{d}}_{1,1}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{d}}_{2,2}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right),\\ {\mathbf{d}}_{t,t}=\left(\begin{array}{lll}\hfill \frac{\partial 𝔏}{\partial u_t^1\partial u_t^1}\hfill & \hfill \frac{\partial 𝔏}{\partial u_t^1\partial u_t^2}\hfill & \hfill \frac{\partial 𝔏}{\partial u_t^1\partial q_t}\hfill \\ \hfill \frac{\partial 𝔏}{\partial u_t^2\partial u_t^1}\hfill & \hfill \frac{\partial 𝔏}{\partial u_t^2\partial u_t^2}\hfill & \hfill \frac{\partial 𝔏}{\partial u_t^2\partial q_t}\hfill \\ \hfill \frac{\partial 𝔏}{\partial q_t\partial u_t^1}\hfill & \hfill \frac{\partial 𝔏}{\partial q_t\partial u_t^2}\hfill & \hfill \frac{\partial 𝔏}{\partial q_t\partial q_t}\hfill \end{array}\right),\end{array}$$ (21)

where 𝔏 ≡ log p(y|u, q, Θ) is the GLM log-likelihood. The contribution of the log-prior for q is given by

$$\begin{array}{cc}\hfill \mathbf{B}=\left(\begin{array}{ccc}\hfill {\mathbf{b}}_{1,1}\hfill & \hfill {\mathbf{b}}_{1,2}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{b}}_{2,1}\hfill & \hfill {\mathbf{b}}_{2,2}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right),\hfill & \hfill {\mathbf{b}}_{t_1,t_2}\hfill \end{array}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill B_{t_1,t_2}\hfill \end{array}\right),$$ (22)

where, as above, the matrix [B_t1,t2] is the Hessian corresponding to the autoregressive process describing q (the zero entries in b_t1,t2 involve partial differentiation with respect to the components of u which vanish because the log-prior for q is independent of u). Since B is banded, B is also banded. Finally, the contribution of the log-prior term for u is given by

$$\begin{array}{cc}\hfill \mathbf{A}=\left(\begin{array}{ccc}\hfill {\mathbf{a}}_{1,1}\hfill & \hfill {\mathbf{a}}_{1,2}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{a}}_{2,1}\hfill & \hfill {\mathbf{a}}_{2,2}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right),\hfill & \hfill {\mathbf{a}}_{t_1,t_2}\hfill \end{array}=\left(\begin{array}{ccc}\hfill A_{t_1,t_2}^{1,1}\hfill & \hfill A_{t_1,t_2}^{1,2}\hfill & \hfill 0\hfill \\ \hfill A_{t_1,t_2}^{2,1}\hfill & \hfill A_{t_1,t_2}^{2,2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),$$ (23)

where the matrix A (formed by excluding all the zero rows and columns, corresponding to partial differentiation with respect to the common noise, from A) is the inverse covariance matrix of the uⁱ. The covariance matrix of the u_i is given by $C_{\mathbf{u}}^{\mathit{\text{ij}}}={\mathbf{k}}^i{C}_{\mathbf{x}}{\mathbf{k}}^{j^{\mathrm{T}}}$ where C_x is the covariance of the spatio-temporally fluctuating visual stimulus, x, and k^jT is cell j’s receptive field transposed. Since a white-noise stimulus was used in the experiment, we use C_x = c²I, where I is the identity matrix and c is the stimulus contrast. Hence we have $C_{\mathbf{u}}^{\mathit{\text{ij}}}=c^2{\mathbf{k}}^i{\mathbf{k}}^{j^{\mathrm{T}}}$ , or more explicitly⁵

$${\left[C_{\mathbf{u}}\right]}_{t_1,t_2}^{i,j}\equiv \text{Cov}[u_{t_1}^i,u_{t_2}^j]=c^2{\displaystyle \sum _{t,n}{k}^i(t_1-t,n)k^j(t_2-t,n).}$$ (24)

Notice that since the experimentally fit kⁱ have a finite temporal duration T_k, the covariance matrix, C_u is banded: it vanishes when |t₁ − t₂| ≥ 2T_k − 1. However, the inverse of C_u, and therefore A are not banded in general. This complicates the direct use of the banded matrix methods to solve the set of linear equations, Jδ = ∇, in each Newton-Raphson step. Still, as we will now show, we can exploit the bandedness of C_u (as well as B and D) to obtain the desired O(T) scaling.

In order to solve each Newton-Raphson step we need to recast our problem into an auxiliary space in which all our matrices are tridiagonal. Below we show how such a rotation can be accomplished. First, we calculate the (lower triangular) Cholesky decomposition, L, of C_u, satisfying LL^T = C_u. Since C_u is banded, L is itself banded, and its calculation can be performed in O(T) operations (and is performed only once, because C_u is fixed and does not depend on the vector (u, q)). Next, we form the 3T × 3T matrix L

$$\begin{array}{ccc}\hfill \mathbf{L}=\left(\begin{array}{ccc}\hfill {\mathbf{l}}_{1,1}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{l}}_{2,1}\hfill & \hfill {\mathbf{l}}_{2,2}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right),\hfill & & \hfill {\mathbf{l}}_{t_1,t_2}\hfill \end{array}=\left(\begin{array}{ccc}\hfill L_{t_1,t_2}^{1,1}\hfill & \hfill L_{t_1,t_2}^{1,2}\hfill & \hfill 0\hfill \\ \hfill L_{t_1,t_2}^{2,1}\hfill & \hfill L_{t_1,t_2}^{2,2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$ (25)

Clearly L is banded because L is banded. Also notice that when L acts on a state vector it does not affect its q part: it corresponds to the T × T identity matrix in the q-subspace. Let us define

$$\mathbf{G}\equiv {\mathbf{L}}^{\mathrm{T}}\mathbf{\text{JL}}.$$ (26)

Using the definitions of L and A, and L^T AL = I (which follows from $A=C_{\mathbf{u}}^{-1}$ and the definition of L), we then obtain

$$\mathbf{G}={\mathbf{I}}_{\mathbf{u}}+\mathbf{B}+{\mathbf{L}}^{\mathrm{T}}\mathbf{\text{DL}},$$ (27)

where we defined

$$\begin{array}{ccc}{\mathbf{I}}_{\mathbf{u}}=\left(\begin{array}{ccc}{\mathbf{i}}_{\mathbf{u}}& \mathbf{0}& \cdots \\ \mathbf{0}& {\mathbf{i}}_{\mathbf{u}}& \cdots \\ ⋮& ⋮& \ddots \end{array}\right),& & {\mathbf{i}}_{\mathbf{u}}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right).\end{array}$$ (28)

I_u is diagonal and B is banded, and since D is block-diagonal and L is banded, so is the third term in Eq. (27). Thus G is banded.

Now it is easy to see from Eq. (26) that the solution, δ, of the Newton-Raphson equation, Jδ = ∇, can be written as δ = Lδ̃ where δ̃ is the solution of the auxiliary equation Gδ̃ = L^T∇. Since G is banded, this equation can be solved in O(T) time, and since L is banded, the required matrix multiplications by L and L^T can also be performed in linear computational time. Thus the Newton-Raphson algorithm for solving Eq. (11) can be performed in computational time scaling only linearly with T.

Appendix B: Method of moments

The identification of the correlation structure of a latent variable from the spike-trains of many neurons, and the closely related converse problem of generating spike-trains with a desired correlation structure (Niebur 2007; Krumin and Shoham 2009; Macke et al. 2009; Gutnisky and Josic 2010), has received much attention lately. Krumin and Shoham (2009) generate spike-trains with the desired statistical structure by nonlinearly transforming the underlying nonnegative rate process to a Gaussian processes using a few commonly used link functions. Macke et al. (2009) and Gutnisky and Josic (2010) both use thresholding of a Gaussian process with the desired statistical structure, though these works differ in the way the authors sample the resulting processes. Finally, Dorn and Ringach (2003) proposed a method to find the correlation structure of an underlying Gaussian process in a model where spikes are generated by simple threshold crossing. Here we take a similar route to find the correlation structure between our latent variables, the common noise inputs. However, the correlations in the spike trains in our model stem from both the receptive field overlap as well as the correlations among the latent variable (the common noise inputs) which we have to estimate from the observed spiking data. Moreover, the GLM framework used here affords some additional flexibility, since the spike train including history effects is not restricted to be a Poisson process given the latent variable.

Our model for the full cell population can be written as:

$$\mathrm{\lambda }=\text{exp}(\mathbf{k}·\mathbf{x}+\mathbf{h}·\mathbf{y}+Q),$$ (29)

where Q ~ 𝒩 (0, C_τ ⊗ C_s) since we assume the spatiotemporal covariance structure of the common noise is separable (as discussed in Section 2.2). Here, we separate the covariance of the common noise inputs into two terms: the temporal correlation of each of the common noise sources which imposes the autoregressive structure, C_τ, and the spatial correlations between the different common inputs to each cell, C_s. Correlations between cells have two sources in this model. First, the spatio-temporal filters overlap. Second, the correlation matrix C_s accounts for the common noise correlation. The spatio-temporal filters’ overlap is insufficient to account for the observed correlation structure, as discussed in (Pillow et al. 2008); the RF overlap does not account for the large sharp peak at zero lag in the cross-correlation function computed from the spike trains of neighboring cells. Therefore, we need to capture this fast remaining correlation through C_s.

We approximated our model as: yⁱ ~ Poisson(exp(aⁱzⁱ + qⁱ)dt) where zⁱ = kⁱ · xⁱ + hⁱ · yⁱ. Since the exponential nonlinearity is a convex, log-concave, increasing function of z, so is E_q [exp(aⁱzⁱ + qⁱ)] (Paninski 2005). This guarantees that if the distribution of the covariate is elliptically symmetric, then we may consistently estimate the model parameters via the standard GLM maximum likelihood estimator, even if the incorrect nonlinearity is used to compute the likelihood (Paninski 2004), i.e, even when the correct values of the correlation matrix, C_s, are unknown. Consistency of the model parameter estimation holds up to a scalar constant. Therefore, we leave a scalar degree of freedom, aⁱ in front of zⁱ. We will now write the moments of the distribution analytically and afterwards we will equate them to the observed moments of the spike trains:

The average firing rate can be written as:

$$E[{\mathbf{y}}^i]=E_{z,\mathbf{q}}[\text{exp}(a^i{\mathbf{z}}^i+{\mathbf{q}}^i)]=E_z[\text{exp}(a^i{\mathbf{z}}^i)]E_{\mathbf{q}}[\text{exp}({\mathbf{q}}^i)]=G^i(a^i)r^i$$ (30)

and

$$E\left[{\mathbf{z}}^i{\mathbf{y}}^i\right]=E_{z,b}[z\text{exp}(a^i{\mathbf{z}}^i+q^i)]=E_z[z\text{exp}(a^i{\mathbf{z}}^i)]E_q[\text{exp}(q^i)]=\frac{d}{d{a}^i}{G}^i(a^i)r^i$$ (31)

where Gⁱ(aⁱ) = E[exp(aⁱzⁱ)] is the moment generating function (Bickel and Doksum 2001) of aⁱzⁱ and $r^i=E[\text{exp}(q^i)]=\text{exp}({\mu }^i+\frac{1}{2}{(C_s)}_{\mathit{\text{ii}}})$ may be computed analytically here (by solving the Gaussian integral over exp(q)). Therefore we have:

$$\frac{E[{\mathbf{z}}^i{\mathbf{y}}^i]}{E[{\mathbf{y}}^i]}=\frac{\frac{d}{d{a}^i}{G}_i(a_i)r_i}{G^i(a^i)r^i}=\frac{d}{d{a}^i}\text{log}{G}_i(a_i)$$ (32)

and we can solve for $a_{\mathit{\text{opt}}}^i$ .

Now, we can proceed and solve for C_s. We first rewrite C_s using the “law of total variance” saying that the total variance of a random variable is the sum of expected conditioned variance plus the variance of the expectations:

$${\mathbf{C}}_s=E\left[{\mathbf{y}}^i{\mathbf{y}}^j\right]-E\left[{\mathbf{y}}^i\right]E\left[{\mathbf{y}}^j\right]=E_{z,\mathbf{q}}[\mathit{\text{Cov}}(\mathbf{y}|z,\mathbf{q})]+{\mathit{\text{Cov}}}_{z,\mathbf{q}}(E[\mathbf{y}|z,\mathbf{q}]).$$ (33)

The first term in the right hand side can be written as:

$$E_{z,\mathbf{q}}[\mathit{\text{Cov}}(\mathbf{y}|z,\mathbf{q})]=E_{z,\mathbf{q}}[\mathit{\text{diag}}[\text{exp}(a^i{\mathbf{z}}^i+{\mathbf{q}}^i)]]=\mathit{\text{diag}}[E[{\mathbf{y}}^i]],$$ (34)

since the variance of a Poisson process equals its mean. The second term in the right hand side of Eq. (33) is

$$\begin{array}{c}{\mathit{\text{Cov}}}_{z,\mathbf{q}}(E[\mathbf{y}|z,\mathbf{q}])=E_{z,\mathbf{q}}[E[{\mathbf{y}}^i|{\mathbf{z}}^i,{\mathbf{q}}^i]E[{\mathbf{y}}^j|{\mathbf{z}}^j,{\mathbf{q}}^j]]-E_{z,\mathbf{q}}[E[{\mathbf{y}}^i|{\mathbf{z}}^i,{\mathbf{q}}^i]]E_{z,\mathbf{q}}[E[{\mathbf{y}}^j|{\mathbf{z}}^j,{\mathbf{q}}^j]]\hfill \\ =E_{z,\mathbf{q}}[\text{exp}(a^i{\mathbf{z}}^i+{\mathbf{q}}^i)\text{exp}(a^j{\mathbf{z}}^j+{\mathbf{q}}^j)]-E_{z,\mathbf{q}}[\text{exp}(a^i{\mathbf{z}}^i+{\mathbf{q}}^i)]E_{z,\mathbf{q}}[\text{exp}(a^j{\mathbf{z}}^j+{\mathbf{q}}^j)]\hfill \\ =E_z[\text{exp}(a^i{\mathbf{z}}^i+a^j{\mathbf{z}}^j)]E_{\mathbf{q}}[\text{exp}({\mathbf{q}}^i+{\mathbf{q}}^j)]-E\left[{\mathbf{y}}^i\right]E\left[{\mathbf{y}}^j\right]\hfill \\ =G^{i,j}(a^i,a^j)\text{exp}\left(\frac{1}{2}(C_s^{\mathit{\text{ii}}}+C_s^{\mathit{\text{jj}}}+2C_s^{\mathit{\text{ij}}})\right)-G^i(a^i)r^i{G}^j(a^j)r^j\hfill \end{array}$$ (35)

Putting them back together, we have

$${\mathbf{C}}_s=\mathit{\text{diag}}[E[{\mathbf{y}}^i]]+r^i{r}^j(G^{i,j}(a^{i,}{a}^j)\text{exp}\left({(C_s)}_{i,j}-G^i(a^i)G^j(a^j)\right).$$ (36)

Now we have all the terms for the estimation of C_s, and we can uniquely invert the relationship to obtain:

$${({\mathbf{C}}_s)}_{i,j}=\text{log}\left(\frac{{({\hat{\mathbf{C}}}_s)}_{i,j}-E[{\mathbf{y}}^i]}{r^i{r}^j{G}^{i,j}(a^i,a^j)}+\frac{G^i(a^i)G^j(a^j)}{G^{i,j}(a^i,a^j)}\right),$$ (37)

where we set G^{i, j}(aⁱ, a^j) = E[exp(aⁱzⁱ + a^jz^j)], and we denote the observed covariance of the time-series as Ĉ_s.

As a consequence of the law of total variance (recall Eq. (33) above), the Poisson mixture model (a Poisson model where the underlying intensity is itself stochastic) constrains the variance of the spike rate to be larger than the mean rate, while in fact our data is under-dispersed (i.e., the variance is smaller than the mean). This often results in negative eigenvalues in the estimate of C_s. We therefore need to find the closest approximant to the covariance matrix by finding the positive semidefinite matrix that minimizing the 2-norm distance to C_s which is a common approach in the literature, though other matrix norms are also possible. Therefore, in order that the smallest eigenvalue is just above zero, we must add a constant equal to the minimum eigenvalue to the diagonal, ${\mathbf{C}}_s^{\mathit{\text{psd}}}={\mathbf{C}}_s+\text{min}(\mathit{\text{eig}}({\mathbf{C}}_s))·1$ . For more details see (Higham 1988); a similar problem was discussed in (Macke et al. 2009). Finally, note that our estimate of the mixing matrix, M, only depends on the estimate of the mean firing rates and correlations in the network. Estimating these quantities accurately does not require exceptionally long data samples; we found that the parameter estimates were stable, approaching their final value even with as little as half the data.

Appendix C: PSTH-based method

A different method to obtain the covariance structure of the common noise involves analyzing the covariations of the residual activity in the cells once the PSTHs are subtracted (Brody 1999). Let $y_r^i(t)$ be the spike train of neuron i at repeat r. Where the the ensemble of cells is presented with a stimulus of duration T, R times. $s^i=E_r[y_r^i(t)]$ is the PSTH of neuron i. Let

$$\delta y_r^i(t)=y_r^i(t)-E_r[y_r^i(t)];\text{ie},$$ (38)

$\delta y_r^i(t)$ is each neuron’s deviation from the PSTH on each trial. This deviation is unrelated to the stimulus (since we removed the ‘signal’, the PSTH). We next form a matrix of cross-correlations between the deviations of every pair of neurons,

$$C_{i,j}(\tau )=E_r\left[\right(y_r^i(t)-E_r[y_r^i(t)])·(y_r^i(t+\tau )-E_r[y_r^i(t+\tau )]\left)\right]=E_r[\delta y_r^i(t)·\delta y_r^i(t+\tau )];$$ (39)

we can cast this matrix into a 2-dimensional matrix, C_k(τ), by denoting k = i · N + j. The matrix, C_k(τ), contains the trial-averaged cross-correlation functions between all cells. It has both the spatial and the temporal information about the covariations.

Using the singular value decomposition one can always decompose a matrix into C_k(τ) = U Σ V. Therefore, we can rewrite our matrix of cross-covariations as:

$$C_k(\tau )={\displaystyle \sum _i{\sigma }_i{U}_i·V_i^T.}$$ (40)

where U_i is the i^th singular vector in the matrix U and V_i is the i^th singular vector in the matrix V and σ_i are the singular values. Each matrix, ${\sigma }_i{U}_i·V_i^T$ , in the sum, is a spatio-temporally separable matrix. Examining the singular values, σ_i, in Fig. 11(C), we see a clear separation between the first and second singular values; this provides some additional support for the separable nature of the common noise in our model. The first two singular values capture most of the structure of C_k(τ). This means that we can approximate the matrix $C_k(\tau )\approx {\tilde{C}}_k={\displaystyle {\sum }_{i=1}^2{\sigma }_i{U}_i·V_i^T}$ (Haykin 2001). In Fig. 11(A), we show the spatial part of the matrix of cross-covariations composed of the first two singular vectors reshaped into matrix form, and in Fig. 11B we show the first two temporal counterparts. Note the distinct separation of the different subpopulations (ON–ON, OFF–OFF, ON–OFF, and OFF–ON) composing the matrix of the entire population in Fig. 11A.