Abstract
Divisive normalization in primary visual cortex has been linked to adaptation to natural image statistics in accordance to Barlow's redundancy reduction hypothesis. Using recent advances in natural image modeling, we show that the previously studied static model of divisive normalization is rather inefficient in reducing local contrast correlations, but that a simple temporal contrast adaptation mechanism of the half-saturation constant can substantially increase its efficiency. Our findings reveal the experimentally observed temporal dynamics of divisive normalization to be critical for redundancy reduction.
Author Summary
The redundancy reduction hypothesis postulates that neural representations adapt to sensory input statistics such that their responses become as statistically independent as possible. Based on this hypothesis, many properties of early visual neurons—like orientation selectivity or divisive normalization—have been linked to natural image statistics. Divisive normalization, in particular, models a widely observed neural response property: The divisive inhibition of a single neuron by a pool of others. This mechanism has been shown to reduce the redundancy among neural responses to typical contrast dependencies in natural images. Here, we show that the standard model of divisive normalization achieves substantially less redundancy reduction than a theoretically optimal mechanism called radial factorization. On the other hand, we find that radial factorization is inconsistent with existing neurophysiological observations. As a solution we suggest a new physiologically plausible modification of the standard model which accounts for the dynamics of the visual input by adapting to local contrasts during fixations. In this way the dynamic version of the standard model achieves almost optimal redundancy reduction performance. Our results imply that the dynamics of natural viewing conditions are critical for testing the role of divisive normalization for redundancy reduction.
Introduction
It is a long-standing hypothesis that the computational goal of the early visual processing stages is to reduce redundancies which are abundantly present in natural sensory signals [1], [2]. Redundancy reduction is a general information theoretic principle that plays an important role for many possible goals of sensory systems like maximizing the amount of information between stimulus and neural response [3], obtaining a probabilistic model of sensory signals [4], or learning a representation of hidden causes [3], [5]. For a population of neurons, redundancy reduction predicts that neuronal responses should be made as statistically independent from each other as possible [2].
Many prominent neural response properties such as receptive field structure or contrast gain control have been linked to redundancy reduction on natural images [2]. While an appropriate structure of linear receptive fields can always remove all redundancies caused by second order correlations, they have only little effect on the reduction of higher order statistical dependencies [6], [7]. However, one of the most prominent contrast gain control mechanisms—divisive normalization—has been demonstrated to reduce higher order correlations on natural images and sound [8]–[10]. Its central mechanism is a divisive rescaling of a single neuron's activity by that of a pool of other neurons [8, see also Figure 1a].
Recently, radial factorization and radial Gaussianization have been derived independently by [11] and [12], respectively, based on Barlow's redundancy reduction principle [1]. Both mechanisms share with divisive normalization the two main functional components, linear filtering and rescaling and have been shown to be the unique and optimal redundancy reduction mechanism for this class of transformations under certain symmetry assumptions for the data. Radial factorization is optimal for a more general symmetry class than radial Gaussianization [11], [13] and contains radial Gaussianization as a special case. As a consequence, radial factorization can achieve slightly better redundancy reduction for natural images than radial Gaussianization but the advantage is very small.
Here, we compare the redundancy reduction performance of divisive normalization to that of radial factorization in order to see to what extent divisive normalization can serve the goal of redundancy reduction. Our comparison shows that a non-adapting static divisive normalization is not powerful enough to capture the contrast dependencies of natural images. Furthermore, we show that (i) the shape of contrast response curves predicted by radial factorization is not consistent with that found in physiological recordings, and (ii) that for a static divisive normalization mechanism this inconsistency is a necessary consequence of strong redundancy reduction. Finally, we demonstrate that a dynamic adaptation of the half-saturation constant in divisive normalization may provide a physiologically plausible mechanism that can achieve close to optimal performance. Our proposed adaptation mechanism works via horizontal shifts of the contrast response curve along the log-contrast axis. Such shifts have been observed in experiments in response to a change of the ambient contrast level [14].
Results
Measures, Models, Mechanisms
We now briefly introduce divisive normalization, radial factorization, and the information theoretic measure of redundancy used in this study.
Redundancy reduction and multi-information
We consider a population of sensory neurons that transforms natural image patches  into a set of neural activities
into a set of neural activities  or
or  . We always use
. We always use 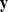 to denote responses to linear filters, and
to denote responses to linear filters, and  for the output of divisive normalization or radial factorization. The goal of redundancy reduction is to remove statistical dependencies between the single coefficients of
for the output of divisive normalization or radial factorization. The goal of redundancy reduction is to remove statistical dependencies between the single coefficients of 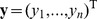 or
or 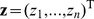 .
.
Redundancy is quantified by the information theoretic measure called multi-information
| (1) |
which measures how much the representation differs from having independent components. More precisely, the multi-information is the Kullback-Leibler divergence between the joint distribution and the product of its marginals or, equivalently, the difference between the sum of the marginal entropies and the joint entropy. In case of 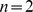 this equals the better known mutual information. If the different entries of
this equals the better known mutual information. If the different entries of 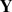 are independent, then its joint distribution equals the product of the single marginals or–-equivalently–-the joint entropy equals the sum of the marginal entropies. Thus, the multi-information is zero if and only if the different dimensions of the random vector
are independent, then its joint distribution equals the product of the single marginals or–-equivalently–-the joint entropy equals the sum of the marginal entropies. Thus, the multi-information is zero if and only if the different dimensions of the random vector 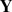 are independent, and positive otherwise. In summary, the multi-information measures all kinds of statistical dependencies among the single coefficients of a random vector. In the Methods Section, we describe how we estimate the multi-information for the various signals considered here.
are independent, and positive otherwise. In summary, the multi-information measures all kinds of statistical dependencies among the single coefficients of a random vector. In the Methods Section, we describe how we estimate the multi-information for the various signals considered here.
Divisive normalization
From all existing divisive normalization models considered previously in the literature, ours is most closely related to the one used by Schwartz and Simoncelli [9]. It consists of two main components: a linear filtering step and a rescaling step based on the Euclidean norm of the filter responses
| (2) |
While the linear filters 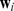 capture the receptive field properties, the rescaling step captures the nonlinear interactions between the single neurons. Most divisive normalization models use filters
capture the receptive field properties, the rescaling step captures the nonlinear interactions between the single neurons. Most divisive normalization models use filters 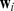 that resemble the receptive fields of complex cells [9], [15], [16]. Therefore, we use filters obtained from training an Independent Subspace Analysis (ISA) on a large collection of randomly sampled image patches [15], [16, see also Methods]. ISA can be seen as a redundancy reduction transform whose outputs are computed by the complex cell energy model [17], [18]. For this study, the algorithm has the advantage that it not only yields complex cell-like filter shapes, but also ensures that single filter responses
that resemble the receptive fields of complex cells [9], [15], [16]. Therefore, we use filters obtained from training an Independent Subspace Analysis (ISA) on a large collection of randomly sampled image patches [15], [16, see also Methods]. ISA can be seen as a redundancy reduction transform whose outputs are computed by the complex cell energy model [17], [18]. For this study, the algorithm has the advantage that it not only yields complex cell-like filter shapes, but also ensures that single filter responses 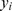 are decorrelated and already optimized for statistical independence. This ensures that the redundancies removed by divisive normalization and radial factorization are the ones that cannot be removed by the choice of linear filters [7], [19].
are decorrelated and already optimized for statistical independence. This ensures that the redundancies removed by divisive normalization and radial factorization are the ones that cannot be removed by the choice of linear filters [7], [19].
Several divisive normalization models exist in the literature. They differ, for instance, by whether a unit 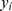 is contained in its own normalization pool, or in the exact form of the rescaling function
is contained in its own normalization pool, or in the exact form of the rescaling function 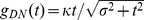 also known as Naka-Rushton function. From the viewpoint of redundancy reduction, the former distinction between models is irrelevant because the influence of a single unit on its normalization pool can always be removed by the elementwise invertible transformation
also known as Naka-Rushton function. From the viewpoint of redundancy reduction, the former distinction between models is irrelevant because the influence of a single unit on its normalization pool can always be removed by the elementwise invertible transformation 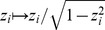 which does not change the redundancies between the responses [20] (the multi-information is invariant with respect to elementwise invertible transformations). Sometimes, a more general form of the Naka-Rushton function is found in the literature which uses different types of exponents
which does not change the redundancies between the responses [20] (the multi-information is invariant with respect to elementwise invertible transformations). Sometimes, a more general form of the Naka-Rushton function is found in the literature which uses different types of exponents
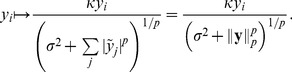 |
(3) |
The divisive normalization model considered in this study (equation (2)) differs from this more general version by the type of the norm used for rescaling the single responses: Where equation (3) uses the 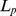 -norm
-norm  we use the Euclidean norm. Because radial factorization is defined for the more general
we use the Euclidean norm. Because radial factorization is defined for the more general 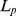 -norm (see Methods), all analyses in this paper could be carried out for this more general transform. However, we instead chose to use the Euclidean norm for simplicity and to make our model more comparable to the ones most commonly used in redundancy reduction studies of divisive normalization [9], [20]–[22].
-norm (see Methods), all analyses in this paper could be carried out for this more general transform. However, we instead chose to use the Euclidean norm for simplicity and to make our model more comparable to the ones most commonly used in redundancy reduction studies of divisive normalization [9], [20]–[22].
Also note that the Naka-Rushton function is often defined as the 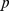 th power of equation (3). However, the form of equation (3) is more common in redundancy reduction studies in order to maintain the sign of
th power of equation (3). However, the form of equation (3) is more common in redundancy reduction studies in order to maintain the sign of 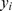 . We mention the consequences of this choice in the discussion.
. We mention the consequences of this choice in the discussion.
Radial factorization
Radial factorization is an optimal radial rescaling for redundancy reduction. We will now briefly introduce radial factorization starting from divisive normalization. For more mathematical details see the Methods Section.
On a population level, the rescaling step of divisive normalization is a nonlinear mapping that changes the Euclidean radius of the filter response population. This can be seen by decomposing divisive normalization into two multiplicative terms
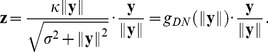 |
(4) |
The second term normalizes the response vector 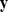 to length one while the Naka-Rushton function in the first term determines the new radius. Since the rescaling
to length one while the Naka-Rushton function in the first term determines the new radius. Since the rescaling 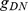 depends only on the norm, the new radius does not depend on any specific direction of
depends only on the norm, the new radius does not depend on any specific direction of 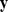 .
.
The redundancy between the coefficients of  is determined by three factors: The statistics of natural image patches
is determined by three factors: The statistics of natural image patches  which—together with the choice of filters
which—together with the choice of filters 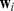 —determine the statistics of
—determine the statistics of 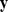 , and the radial transformation
, and the radial transformation 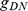 . If we allow the radial transformation to be a general invertible transform
. If we allow the radial transformation to be a general invertible transform 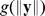 on the Euclidean norm, we can now ask how the different model components can be chosen in order to minimize the redundancy in
on the Euclidean norm, we can now ask how the different model components can be chosen in order to minimize the redundancy in  .
.
A substantial part of the redundancies in natural images are second order correlations, which can be removed by linear filters during whitening
[6]. Whitening does not completely determine the filters since the data can always be rotated afterwards and still stay decorrelated. Higher order decorrelation algorithms like independent component analysis use this rotational degree of freedom to decrease higher order dependencies in the filter responses 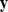 [3]. However, there is no set of filters that could remove all statistical dependencies from natural images [6], [7], because whitened natural images exhibit an approximately spherical but non-Gaussian joint distribution [7], [21], [23], [24]. Since spherical symmetry is invariant under rotation and because the only spherically symmetric factorial distribution is the Gaussian distribution [13], [25], the marginals cannot be independent.
[3]. However, there is no set of filters that could remove all statistical dependencies from natural images [6], [7], because whitened natural images exhibit an approximately spherical but non-Gaussian joint distribution [7], [21], [23], [24]. Since spherical symmetry is invariant under rotation and because the only spherically symmetric factorial distribution is the Gaussian distribution [13], [25], the marginals cannot be independent.
Hence, the remaining dependencies must be removed by nonlinear mechanisms like an appropriate radial transformation 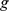 . Fortunately, the joint spherically symmetric distribution of the filter responses
. Fortunately, the joint spherically symmetric distribution of the filter responses 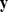 already dictates a unique and optimal way to choose
already dictates a unique and optimal way to choose 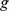 : Since a rescaling with
: Since a rescaling with 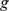 will necessarily result in a spherically symmetric distribution again,
will necessarily result in a spherically symmetric distribution again, 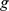 must be chosen such that
must be chosen such that  is jointly Gaussian distributed. Therefore, we need to choose
is jointly Gaussian distributed. Therefore, we need to choose 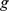 such that
such that 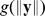 follows the radial distribution of a Gaussian or, in other words, a
follows the radial distribution of a Gaussian or, in other words, a 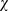 -distribution. This is a central point for our study: For a spherically symmetric distribution the univariate distribution on
-distribution. This is a central point for our study: For a spherically symmetric distribution the univariate distribution on 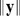 determines higher order dependencies in the multi-variate joint distribution of
determines higher order dependencies in the multi-variate joint distribution of 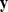 . This means that if we restrict ourselves to radial transformations, it is sufficient to look at radial distributions only. The fact that the Gaussian is the only spherically symmetric factorial distribution implies that the coefficients in
. This means that if we restrict ourselves to radial transformations, it is sufficient to look at radial distributions only. The fact that the Gaussian is the only spherically symmetric factorial distribution implies that the coefficients in  can only be statistically independent if
can only be statistically independent if  follows radial
follows radial 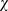 -distribution. Radial factorization finds a transformation
-distribution. Radial factorization finds a transformation 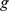 which achieves exactly that by using histogram equalization on the distribution of
which achieves exactly that by using histogram equalization on the distribution of 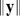 [11], [12, see also Methods]. All these considerations also hold for
[11], [12, see also Methods]. All these considerations also hold for 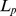 -spherically symmetric distributions [11], [13].
-spherically symmetric distributions [11], [13].
Note that this does not imply that the neural responses  must follow a Gaussian distribution if they are to be independent because the distribution of the single responses
must follow a Gaussian distribution if they are to be independent because the distribution of the single responses 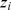 can always be altered by applying an elementwise invertible transformation
can always be altered by applying an elementwise invertible transformation 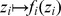 without changing the redundancy. The above considerations only mean that given the two main model components of divisive normalization (and the assumption of spherical symmetry), the best we can do is to choose the
without changing the redundancy. The above considerations only mean that given the two main model components of divisive normalization (and the assumption of spherical symmetry), the best we can do is to choose the 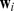 to be whitening filters and
to be whitening filters and 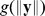 according to radial factorization.
according to radial factorization.
Radial factorization and divisive normalization are not equivalent
The goal of this study is to compare the redundancy reduction achieved by divisive normalization and radial factorization. Apart from all similarities between the two models, there is a profound mathematical difference showing that the two mechanisms are not equivalent (as noted by [12]).
Both mechanisms have the form
However, the radial rescalings of radial factorization and that of divisive normalization, 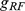 and
and 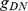 , have a different range. Since the
, have a different range. Since the 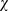 -distribution is non-zero on all of
-distribution is non-zero on all of 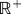 the range of
the range of 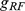 must be
must be 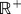 as well. However, in case of divisive normalization, the Naka-Rushton function
as well. However, in case of divisive normalization, the Naka-Rushton function 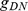 saturates at
saturates at  . This means that
. This means that 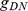 can never transform a radial distribution into a
can never transform a radial distribution into a 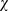 -distribution since values beyond
-distribution since values beyond  cannot be reached.
cannot be reached.
While this implies that the two mechanisms are mathematically not equivalent, it could still be that they perform similarly on data if the probability mass of the 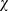 -distribution in the range beyond
-distribution in the range beyond  is small. Therefore, we choose
is small. Therefore, we choose  to be the
to be the 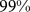 quantile of the
quantile of the 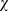 -distribution in all our experiments (see Methods).
-distribution in all our experiments (see Methods).
Comparison of the redundancy reduction performance
We compared the amount of redundancy removed by divisive normalization and radial factorization by measuring the multi-information in the plain filter responses 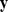 and the normalized responses
and the normalized responses  for a large collection of natural image patches (Figure 1b). In both cases the parameters of the radial transformation were chosen to yield the best possible redundancy reduction performance (see Methods). While both divisive normalization and radial factorization remove variance correlations (Figure 1a), the residual amount of dependencies for divisive normalization is still approximately
for a large collection of natural image patches (Figure 1b). In both cases the parameters of the radial transformation were chosen to yield the best possible redundancy reduction performance (see Methods). While both divisive normalization and radial factorization remove variance correlations (Figure 1a), the residual amount of dependencies for divisive normalization is still approximately 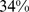 of the total redundancies removed by radial factorization (Figure 1a–b). This demonstrates that divisive normalization is not optimally tailored to the statistics of natural images.
of the total redundancies removed by radial factorization (Figure 1a–b). This demonstrates that divisive normalization is not optimally tailored to the statistics of natural images.
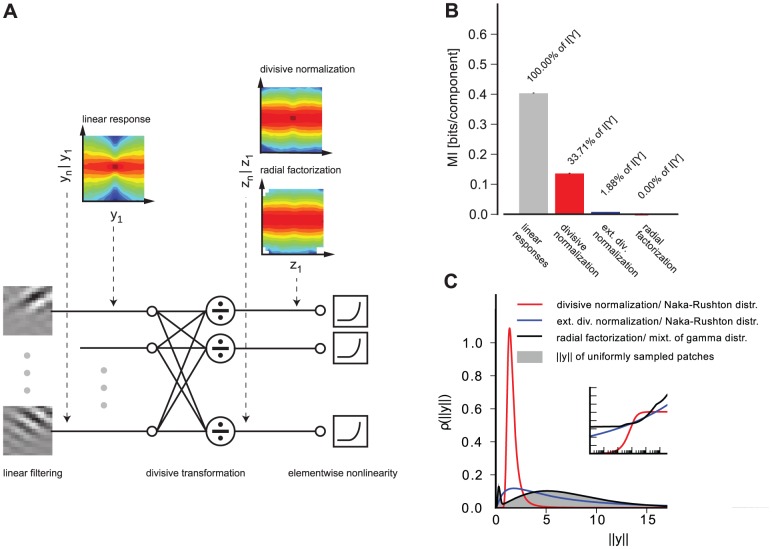
Figure 1. Redundancy reduction and radial distributions for different normalization models.
A: Divisive normalization model used in this study: Natural image patches are linearly filtered. These responses are nonlinearly transformed by divisive normalization or radial factorization (see text). After linear filtering the width of the conditional distribution 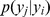 of two filter responses depends on the value of
of two filter responses depends on the value of 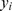 (conditional log-histograms as contour plots). This demonstrates the presence of variance correlations. These dependencies are decreased by divisive normalization and radial factorization. B: Redundancy measured by multi-information after divisive normalization, extended divisive normalization, and radial factorization: divisive normalization leaves a substantial amount of residual redundancy (error bars show standard deviation over different datasets). C: Distributions on the norm of the filter responses
(conditional log-histograms as contour plots). This demonstrates the presence of variance correlations. These dependencies are decreased by divisive normalization and radial factorization. B: Redundancy measured by multi-information after divisive normalization, extended divisive normalization, and radial factorization: divisive normalization leaves a substantial amount of residual redundancy (error bars show standard deviation over different datasets). C: Distributions on the norm of the filter responses 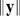 for which divisive normalization (red) and extended divisive normalization (blue) are the optimal redundancy reducing mechanisms. The radial transformation of radial factorization and its corresponding distribution (mixture of five
for which divisive normalization (red) and extended divisive normalization (blue) are the optimal redundancy reducing mechanisms. The radial transformation of radial factorization and its corresponding distribution (mixture of five  -distributions) is shown in black. While radial factorization (inset, black curve) and extended divisive normalization (inset, blue curve) achieve good redundancy reduction, they lead to physiologically implausibly shaped contrast response curves which are mainly determined by their respective radial transformations
-distributions) is shown in black. While radial factorization (inset, black curve) and extended divisive normalization (inset, blue curve) achieve good redundancy reduction, they lead to physiologically implausibly shaped contrast response curves which are mainly determined by their respective radial transformations 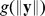 shown in the inset. The radial transformation of divisive normalization is shown for comparison (inset, red curve).
shown in the inset. The radial transformation of divisive normalization is shown for comparison (inset, red curve).
To understand this in more detail, we derived the distribution that 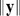 should have if divisive normalization were the optimal redundancy reducing mechanism and compared it to the empirical radial distribution of
should have if divisive normalization were the optimal redundancy reducing mechanism and compared it to the empirical radial distribution of 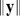 represented by a large collection of uniformly sampled patches from natural images. This optimal distribution for divisive normalization can be derived by transforming a
represented by a large collection of uniformly sampled patches from natural images. This optimal distribution for divisive normalization can be derived by transforming a 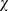 -distributed random variable with
-distributed random variable with 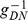 (see Methods). Since
(see Methods). Since 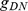 has limited range
has limited range 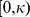 we actually have to use a
we actually have to use a 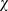 -distribution which is truncated at
-distribution which is truncated at  . The parametric form of the resulting distribution is given in the Methods Section. We refer to is as Naka-Rushton distribution in the following. The parameters of the Naka-Ruston distribution are
. The parametric form of the resulting distribution is given in the Methods Section. We refer to is as Naka-Rushton distribution in the following. The parameters of the Naka-Ruston distribution are  and
and 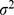 . Since
. Since  is already determined by fixing the range of
is already determined by fixing the range of 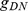 to the
to the 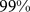 quantile of the
quantile of the 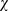 -distribution, the remaining free parameter is
-distribution, the remaining free parameter is 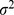 . In the Naka-Rushton function
. In the Naka-Rushton function 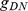 this parameter is called half-saturation constant and controls the horizontal position of the contrast response curve in model neurons.
this parameter is called half-saturation constant and controls the horizontal position of the contrast response curve in model neurons.
We fitted 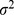 via maximum likelihood (see Methods) and found that even for the best fitting
via maximum likelihood (see Methods) and found that even for the best fitting 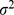 there is a pronounced mismatch between the Naka-Rushton distribution and the empirical distribution given by the histogram (Figure 1c). This explains the insufficient redundancy reduction because the Naka-Rushton distribution expects most of the responses
there is a pronounced mismatch between the Naka-Rushton distribution and the empirical distribution given by the histogram (Figure 1c). This explains the insufficient redundancy reduction because the Naka-Rushton distribution expects most of the responses 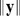 to fall into a much narrower range than responses to natural images do in reality. The Naka-Rushton function
to fall into a much narrower range than responses to natural images do in reality. The Naka-Rushton function 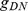 would map the red radial density in Figure 1c perfectly into a truncated
would map the red radial density in Figure 1c perfectly into a truncated 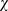 -distribution. However, it maps a profound part of the true radial distribution of
-distribution. However, it maps a profound part of the true radial distribution of 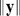 (gray histogram) close to
(gray histogram) close to  , since this part is located to the right of the mode of the Naka-Rushton distribution where it expects almost no probability mass. Additionally, the Naka-Rushton distribution exhibits a small gap of almost zero probability around zero. This gap, however, also contains a portion of empirical distribution. This part gets mapped close to zero. To understand why this leaves significant redundancies, imagine the most extreme case in which all the probability mass of
, since this part is located to the right of the mode of the Naka-Rushton distribution where it expects almost no probability mass. Additionally, the Naka-Rushton distribution exhibits a small gap of almost zero probability around zero. This gap, however, also contains a portion of empirical distribution. This part gets mapped close to zero. To understand why this leaves significant redundancies, imagine the most extreme case in which all the probability mass of 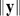 would either be mapped onto
would either be mapped onto  or on onto
or on onto  . The corresponding distribution on
. The corresponding distribution on  would consist of a point mass at zero and a spherical shell at
would consist of a point mass at zero and a spherical shell at  . Such a distribution would clearly exhibit strong dependencies.
. Such a distribution would clearly exhibit strong dependencies.
Augmenting divisive normalization by more parameters
It is clear that the suboptimal redundancy reduction performance of divisive normalization is due to its restricted parametric form. Therefore, we explored two options how to increase its degrees of freedom and thereby its redundancy reduction performance: the first option endows static divisive normalization with additional parameters 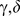 , the second option allows for a dynamic temporal adaptation of
, the second option allows for a dynamic temporal adaptation of 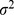 .
.
The simplest way to increase the degrees of freedom in divisive normalization is to introduce two additional parameters in the Naka-Rushton function
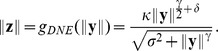 |
These parameters allow for more flexibility in the scale and shape of the corresponding Naka-Rushton distribution. We label all models that use this parametrization as extended in the following. Note that the extended Naka-Rushton function only saturates for 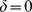 . This means that it could in principle transform
. This means that it could in principle transform 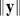 into
into  such that
such that  is
is 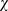 -distributed. For
-distributed. For 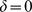 and
and 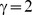 , the original Naka-Rushton function is recovered. As before, we derived the corresponding extended Naka-Rushton distribution by transforming a (truncated)
, the original Naka-Rushton function is recovered. As before, we derived the corresponding extended Naka-Rushton distribution by transforming a (truncated) 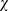 -distributed random variable with
-distributed random variable with 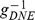 . We fitted the resulting distribution to a large collection of
. We fitted the resulting distribution to a large collection of 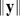 , used the maximum likelihood parameters for extended divisive normalization, and measured the redundancy via multi-information in the resulting normalized responses
, used the maximum likelihood parameters for extended divisive normalization, and measured the redundancy via multi-information in the resulting normalized responses 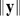 .
.
We found that an extended divisive normalization transform achieves substantially more redundancy reduction and that the extended Naka-Rushton distribution on 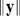 fits the image data significantly better (Figure 1b–c). However, we also find that the best extended Naka-Rushton function for redundancy reduction would yield biologically implausible contrast response curves which capture the firing rate of a neuron upon stimulation with gratings of different contrast at the neuron's preferred spatial frequency and orientation.
fits the image data significantly better (Figure 1b–c). However, we also find that the best extended Naka-Rushton function for redundancy reduction would yield biologically implausible contrast response curves which capture the firing rate of a neuron upon stimulation with gratings of different contrast at the neuron's preferred spatial frequency and orientation.
In the divisive normalization and the radial factorization model, the shape of the contrast response curve is determined by the shape of the radial rescaling function (Figure 1c, inset) [8]. In contrast to the normal Naka-Rushton function (Figure 1c, inset, red curve), the extended version (Figure 1c, inset, blue curve) exhibits a physiologically unreasonable shape: it starts at a non-zero value, increases without saturation, and does not resemble any sigmoidal shape at all. The non-zero level for low contrasts is a direct consequence of the optimization for redundancy reduction: redundancy reduction implies that the target radial distribution is a (truncated) 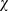 -distribution which has only very little probability mass close to zero. Therefore, the radial rescaling function must map the substantial portion of low contrast values in the empirical distribution upwards in order to match the
-distribution which has only very little probability mass close to zero. Therefore, the radial rescaling function must map the substantial portion of low contrast values in the empirical distribution upwards in order to match the 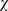 -distribution. This results in the immediate non-zero onset. This is a pronounced mismatch to the typical contrast response curves measured in cortical neurons (see Figure 2 in [14]). In fact, the addition of more parameters merely leads to a contrast response curve which is more similar to radial factorization (Figure 1, inset, black) which does not have a plausible shape, too. Therefore, we dismiss the option of adding more parameters to the Naka-Rushton function and turn to the option in which
-distribution. This results in the immediate non-zero onset. This is a pronounced mismatch to the typical contrast response curves measured in cortical neurons (see Figure 2 in [14]). In fact, the addition of more parameters merely leads to a contrast response curve which is more similar to radial factorization (Figure 1, inset, black) which does not have a plausible shape, too. Therefore, we dismiss the option of adding more parameters to the Naka-Rushton function and turn to the option in which 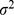 is allowed to dynamically adapt to the ambient contrast level.
is allowed to dynamically adapt to the ambient contrast level.
Figure 2. Simulated eye movements and adapted contrast distributions.
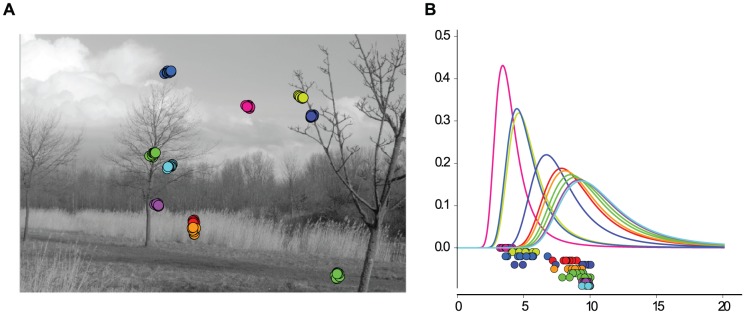
A: Simulated eye movements on a image from the van Hateren database [31]. Local microsaccades are simulated with Brownian motion with a standard deviation of 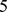 px. In this example,
px. In this example, 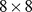 patches are extracted around the fixation location and whitened. B: Values of
patches are extracted around the fixation location and whitened. B: Values of 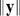 for the extracted patches plotted along the
for the extracted patches plotted along the  -axis. Vertical offset was manually introduced for visibility. Colors match the ones in A. The different curves are the maximum likelihood Naka-Rushton distributions estimated from the data points of the same color.
-axis. Vertical offset was manually introduced for visibility. Colors match the ones in A. The different curves are the maximum likelihood Naka-Rushton distributions estimated from the data points of the same color.
Dynamic divisive normalization
Previous studies found that single neurons adapt to the ambient contrast level via horizontal shifts of their contrast response curve along the log-contrast axis [8], [14]. In the divisive normalization model, this shift is realized by changes in the half-saturation constant 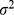 . This means, however, that there is not a single static divisive normalization mechanism, but a whole continuum whose elements differ by the value of
. This means, however, that there is not a single static divisive normalization mechanism, but a whole continuum whose elements differ by the value of 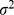 (Figure 2). This is equivalent to a continuum of Naka-Rushton distributions which can be adapted to the ambient contrast level by changing the value of
(Figure 2). This is equivalent to a continuum of Naka-Rushton distributions which can be adapted to the ambient contrast level by changing the value of 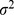 . Since this kind of adaptation increases the degrees of freedom, it could also lead to a better redundancy reduction performance.
. Since this kind of adaptation increases the degrees of freedom, it could also lead to a better redundancy reduction performance.
In order to investigate adaptation to the local contrast in a meaningful way, we used a simple model of saccades and micro-saccades on natural images to sample fixation locations and their corresponding filter responses 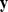 (see Methods). Previous studies on redundancy reduction with divisive normalization [9], [11], [12] ignored both the structure imposed by fixations between saccades in natural viewing conditions, and the adaptation of neural contrast response curves to the ambient contrast level via the adaptation of
(see Methods). Previous studies on redundancy reduction with divisive normalization [9], [11], [12] ignored both the structure imposed by fixations between saccades in natural viewing conditions, and the adaptation of neural contrast response curves to the ambient contrast level via the adaptation of 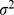 [14]. Figure 2 shows an example of simulated eye movements on a natural image from the van Hateren database. For each sample location, we computed the corresponding values of
[14]. Figure 2 shows an example of simulated eye movements on a natural image from the van Hateren database. For each sample location, we computed the corresponding values of 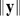 and fitted a Naka-Rushton distribution to it. The right hand side show the resulting Naka-Rushton distributions. One can see that the mode of the distribution shifts with the location of the data, which itself depends on the ambient contrast of the fixation location.
and fitted a Naka-Rushton distribution to it. The right hand side show the resulting Naka-Rushton distributions. One can see that the mode of the distribution shifts with the location of the data, which itself depends on the ambient contrast of the fixation location.
A dynamically adapting 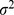 predicts that the distribution of
predicts that the distribution of 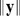 across time should be well fit by a mixture of Naka-Rushton distributions. Let
across time should be well fit by a mixture of Naka-Rushton distributions. Let 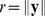 (we use
(we use  to emphasize that the radial distribution is a univariate density and not a multivariate density on
to emphasize that the radial distribution is a univariate density and not a multivariate density on 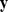 ), then averaged over all time points
), then averaged over all time points  , the distribution of
, the distribution of  is given by
is given by
| (5) |
where 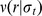 denotes a single Naka-Rushton distribution at a specific point in time.
denotes a single Naka-Rushton distribution at a specific point in time.
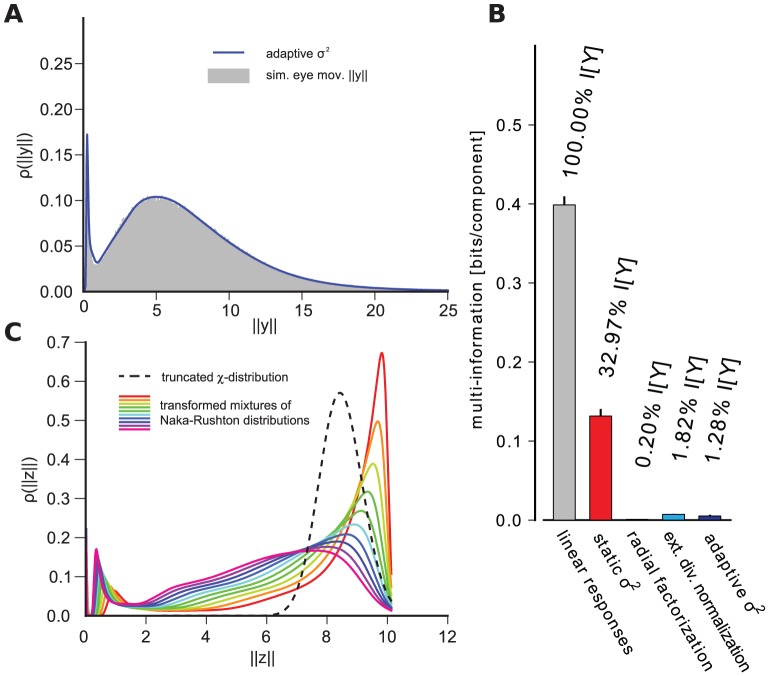
We fitted such a mixture distribution to samples 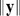 from simulated eye movements (see Methods). Figure 3a shows that the mixture of Naka-Rushton distributions fits the empirical data very well, thus confirming the possibility that a dynamic divisive normalization mechanism may be used to achieve optimal redundancy reduction.
from simulated eye movements (see Methods). Figure 3a shows that the mixture of Naka-Rushton distributions fits the empirical data very well, thus confirming the possibility that a dynamic divisive normalization mechanism may be used to achieve optimal redundancy reduction.
Figure 3. Radial distribution and redundancy reduction achieved by the dynamically adapting model.
A: Histogram of 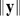 for natural image patches sampled with simulated eye movements: The distribution predicted by the dynamically adapting model closely matches the empirical distribution. B: Same as in Fig. 1B but for simulated eye movement data. The dynamically adapting
for natural image patches sampled with simulated eye movements: The distribution predicted by the dynamically adapting model closely matches the empirical distribution. B: Same as in Fig. 1B but for simulated eye movement data. The dynamically adapting 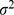 achieves an almost optimal redundancy reduction performance. C: Each colored line shows the distribution of a random variable from 3A transformed with a Naka-Rushton function. Different colors correspond to different values of
achieves an almost optimal redundancy reduction performance. C: Each colored line shows the distribution of a random variable from 3A transformed with a Naka-Rushton function. Different colors correspond to different values of  . The dashed curve corresponds to a truncated
. The dashed curve corresponds to a truncated 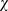 -distribution. A mixture of the colored distributions cannot resemble the truncated
-distribution. A mixture of the colored distributions cannot resemble the truncated 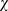 -distribution since there will either be peaks on the left or the right of the dashed distribution that cannot be canceled by other mixture components.
-distribution since there will either be peaks on the left or the right of the dashed distribution that cannot be canceled by other mixture components.
The next step is to find an explicit dynamic adaptation mechanism that can achieve optimal redundancy reduction. To this end, we sought for a way to adapt 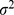 such that the redundancies between the output responses
such that the redundancies between the output responses  were small. Our temporally adapting mechanism chooses the current
were small. Our temporally adapting mechanism chooses the current 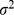 based on the recent stimulation history by using correlations between the contrast values at consecutive time steps. We estimated
based on the recent stimulation history by using correlations between the contrast values at consecutive time steps. We estimated 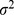 for the present set of filter responses
for the present set of filter responses 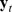 from the immediately preceding responses
from the immediately preceding responses 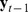 by sampling
by sampling 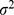 from a
from a  -distribution whose parameters were determined by the mean and the variance of the posterior
-distribution whose parameters were determined by the mean and the variance of the posterior 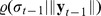 which was derived from the mixture distribution above (see Methods). We found that this temporal adaptation mechanism significantly decreased the amount of residual redundancies to about
which was derived from the mixture distribution above (see Methods). We found that this temporal adaptation mechanism significantly decreased the amount of residual redundancies to about 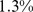 (Figure 3B). Note that the proposed mechanism is a simple heuristic that does not commit to a particular biophysical implementation of the adaptation, but it demonstrates that there is at least one mechanism that can perform well under realistic conditions a neural system would face.
(Figure 3B). Note that the proposed mechanism is a simple heuristic that does not commit to a particular biophysical implementation of the adaptation, but it demonstrates that there is at least one mechanism that can perform well under realistic conditions a neural system would face.
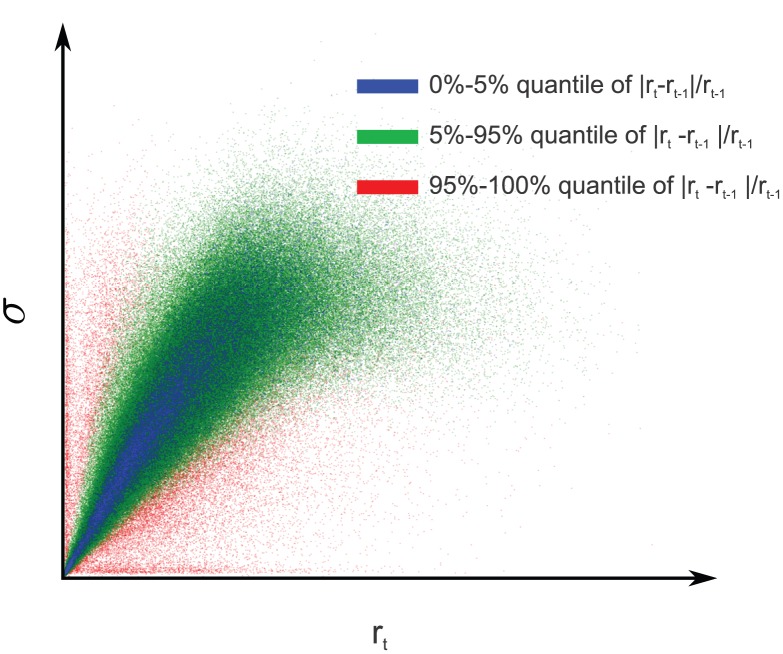
Looking at the joint dynamics of 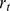 and its
and its  (Figure 4) we find them to be strongly and positively correlated. Therefore, a higher value of
(Figure 4) we find them to be strongly and positively correlated. Therefore, a higher value of 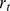 is accompanied by a higher value of
is accompanied by a higher value of  . This is analogous to the adaptation of neural contrast response curves observed in vivo where a higher contrast (higher
. This is analogous to the adaptation of neural contrast response curves observed in vivo where a higher contrast (higher 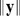 ) shifts the contrast response curve to the right (higher
) shifts the contrast response curve to the right (higher 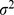 ), and vice versa [14].
), and vice versa [14].
Figure 4. Dynamics of the adaptive  .
.
The scatter plot shows the values of 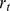 plotted against the
plotted against the  used to transform
used to transform 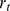 in the dynamic divisive normalization model. The two values are clearly correlated. This indicates that the shift of the contrast response curve, which is controlled by
in the dynamic divisive normalization model. The two values are clearly correlated. This indicates that the shift of the contrast response curve, which is controlled by  , tracks the ambient contrast level, which is proportional to
, tracks the ambient contrast level, which is proportional to 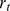 . Single elements in the plot are colored according to the quantile the value of
. Single elements in the plot are colored according to the quantile the value of 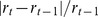 falls in. When the ambient contrast level changes abruptly (e.g. when a saccade is made), this value is large. If the ambient contrast level is relatively stable (e.g. during fixation), this value is small. In those situations (blue dots),
falls in. When the ambient contrast level changes abruptly (e.g. when a saccade is made), this value is large. If the ambient contrast level is relatively stable (e.g. during fixation), this value is small. In those situations (blue dots),  and
and 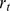 exhibit the strongest proportionality.
exhibit the strongest proportionality.
In order to demonstrate that improved redundancy reduction is a true adaptation mechanism which relies on correlations between temporally subsequent sample, we need to preclude the possibility that 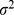 can be sampled independently (i.e. context independent). For strong redundancy reduction, the normalized responses
can be sampled independently (i.e. context independent). For strong redundancy reduction, the normalized responses  should follow a (possibly truncated)
should follow a (possibly truncated) 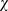 -distribution (see Methods). The history-independent choice of
-distribution (see Methods). The history-independent choice of 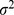 predicts that this truncated
predicts that this truncated 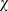 -distribution should be expressible as a mixture of distributions that result from transforming random variables, that follow a mixture of Naka-Rushton distributions from Figure 3C, with Naka-Rushton functions for different values of
-distribution should be expressible as a mixture of distributions that result from transforming random variables, that follow a mixture of Naka-Rushton distributions from Figure 3C, with Naka-Rushton functions for different values of 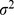 (see Methods for the derivation). We transformed the input distribution with Naka-Rushton functions that differed in the value of
(see Methods for the derivation). We transformed the input distribution with Naka-Rushton functions that differed in the value of 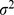 (Figure 3C, colored lines). Different colors in Figure 3C refer to different values of
(Figure 3C, colored lines). Different colors in Figure 3C refer to different values of 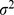 . If
. If 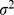 was history-independent, a positively weighted average of the colored distributions should be able to yield a truncated
was history-independent, a positively weighted average of the colored distributions should be able to yield a truncated 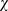 -distribution (Figure 3C, dashed line). It is obvious that this is not possible. Every component will either add a tail to the left of the
-distribution (Figure 3C, dashed line). It is obvious that this is not possible. Every component will either add a tail to the left of the 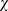 -distribution or a peak to the right of it. Since distributions can only be added with non-negative weight in a mixture, there is no way that one distribution can make up for a tail or peak introduced by another. Therefore,
-distribution or a peak to the right of it. Since distributions can only be added with non-negative weight in a mixture, there is no way that one distribution can make up for a tail or peak introduced by another. Therefore, 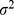 cannot be chosen independently of the preceding stimulation, but critically relies on exploiting the temporal correlation structure in the input.
cannot be chosen independently of the preceding stimulation, but critically relies on exploiting the temporal correlation structure in the input.
Discussion
In this study we have demonstrated that a static divisive normalization mechanism is not powerful enough to capture the contrast dependencies of natural images leading to a suboptimal redundancy reduction performance. Static divisive normalization could only exhibit close to optimal performance if the contrast distribution of the input data would be similar to a Naka-Rushton distribution that we derived in this paper. For the best fitting Naka-Rushton distribution, however, the interval containing most of the probability mass is too narrow and too close to zero compared to the contrast distribution empirically found for natural image patches. A divisive normalization mechanism that uses the 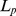 -norm as in equation (3) instead of the Euclidean norm would suffer from the same problem because the Naka-Rushton distribution for
-norm as in equation (3) instead of the Euclidean norm would suffer from the same problem because the Naka-Rushton distribution for 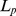 -norms other than
-norms other than 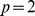 would have similar properties. However, the good performance of extended divisive normalization demonstrates that it is not necessary to model the contrast distribution perfectly everywhere but that it would be sufficient to match the range where most natural contrasts appear (Figure 1C).
would have similar properties. However, the good performance of extended divisive normalization demonstrates that it is not necessary to model the contrast distribution perfectly everywhere but that it would be sufficient to match the range where most natural contrasts appear (Figure 1C).
Not every mapping on natural contrasts that achieves strong redundancy reduction is also physiologically plausible: We showed that the extended static mechanism yields physiologically implausible contrast response curves. Extending the static mechanism of divisive normalization for better redundancy reduction simply makes it more similar to the optimal mechanism and, therefore, yields implausible tuning curves as well. We thus suggested to consider temporal properties of divisive normalization and devised a model that can resolve this conflict by temporally adapting the half-saturation constant 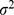 using temporal correlations between consecutive data points caused by fixations.
using temporal correlations between consecutive data points caused by fixations.
Another point concerning physiological plausibility is the relationship between divisive normalization models used to explain neurophysiological observations, and those used in redundancy reduction studies like ours. One very common neurophysiological model was introduced by Heeger [8] which uses half-squared instead of linear single responses:
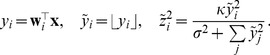 |
(6) |
In order to represent each possible image patch this model would need two neurons per filter: one for the positive part and one for the negative part 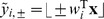 . Of course, these two units would be strongly anti-correlated since only one can be nonzero at a given point in time. Therefore, taking a redundancy reduction view requires considering the positive and the negative part. For this reason it is reasonable to use
. Of course, these two units would be strongly anti-correlated since only one can be nonzero at a given point in time. Therefore, taking a redundancy reduction view requires considering the positive and the negative part. For this reason it is reasonable to use 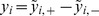 as the most basic unit and define the normalization as in equation (2). Since
as the most basic unit and define the normalization as in equation (2). Since 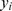 and
and 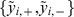 are just two different representations of the same information, the multi-information between
are just two different representations of the same information, the multi-information between  is the same as the multi-information between different tuples
is the same as the multi-information between different tuples 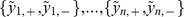 . Apart from this change of viewpoint, the two models are equivalent, because the normalized half-squared response of equation (6) can be obtained by half-squaring the normalized response of equation (2). Therefore, a model equivalent to the one in equation (6) can be obtained by using the model of equation (2) and representing its responses
. Apart from this change of viewpoint, the two models are equivalent, because the normalized half-squared response of equation (6) can be obtained by half-squaring the normalized response of equation (2). Therefore, a model equivalent to the one in equation (6) can be obtained by using the model of equation (2) and representing its responses  by twice as many half-squared coefficients afterwards.
by twice as many half-squared coefficients afterwards.
Previous work on the role of contrast gain control for efficient coding has either focused on the temporal domain [26], [27], or on its role in the spatial domain as a redundancy reduction mechanism for contrast correlations in natural images [9], [11], [12]. Our results emphasize the importance of combining both approaches by showing that the temporal properties of the contrast gain control mechanism can have a critical effect on the redundancies that originate from the spatial contrast correlations in natural images. Our analysis does not commit to a certain physiological implementation or biophysical constraints, but it demonstrates that the statistics of natural images require more degrees of freedom for redundancy reduction in a population response than a classical static divisive normalization model can offer. Our heuristic mechanism demonstrates that strong redundancy reduction is possible with an adaptation mechanism that faces realistic conditions, i.e. has only access to stimuli encountered in the past.
As we showed above, biologically plausible shapes of the contrast response curve and strong redundancy reduction cannot be easily brought together in a single model. Our dynamical model offers a possible solution to this problem. To what extent this model reflects the physiological reality, however, still needs to be tested experimentally.
The first aspect to test is whether the adaptation of the half-saturation constant reflects the temporal structure imprinted by saccades and fixations as predicted by our study. Previous work has measured adaptation timescales for 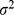 [14], [28]. However, these measurements are carried out in anesthetized animals and cannot account for eye movements. Since our adaptation mechanism mainly uses the fact that contrasts at a particular fixation location are very similar it predicts that that adaptive changes of
[14], [28]. However, these measurements are carried out in anesthetized animals and cannot account for eye movements. Since our adaptation mechanism mainly uses the fact that contrasts at a particular fixation location are very similar it predicts that that adaptive changes of 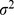 should be seen from one fixation location to another when measured under natural viewing conditions.
should be seen from one fixation location to another when measured under natural viewing conditions.
The mechanism we proposed is only one possible candidate for a dynamic contrast gain control mechanism that can achieve strong redundancy reduction. We conclude the paper with defining a measure that can be used to distinguish contrast gain control mechanisms that are likely to achieve strong redundancy reduction from those that do not. As discussed above, a necessary condition for strong redundancy reduction is that the the location and the width of the distribution of 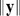 implied by a model must match the distribution of unnormalized responses
implied by a model must match the distribution of unnormalized responses 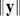 determined by the statistics of natural images. In order to measure the location and the width of the distributions in a way that does not depend on a particular scaling of the data, we plotted the median against the width of the
determined by the statistics of natural images. In order to measure the location and the width of the distributions in a way that does not depend on a particular scaling of the data, we plotted the median against the width of the 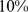 –
–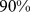 –percentile interval (Figure 5). For the empirical distributions generated by the statistics of the image data we always found a ratio greater than
–percentile interval (Figure 5). For the empirical distributions generated by the statistics of the image data we always found a ratio greater than 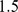 . We also included a dataset from real human eye movements by Kienzle et al. to ensure the generality of this finding [29] as real fixations could introduce a change in the statistics due to the fact that real observers tend to look at image regions with higher contrasts [30]. All models that yield strong redundancy reduction also exhibit a ratio greater than
. We also included a dataset from real human eye movements by Kienzle et al. to ensure the generality of this finding [29] as real fixations could introduce a change in the statistics due to the fact that real observers tend to look at image regions with higher contrasts [30]. All models that yield strong redundancy reduction also exhibit a ratio greater than 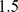 . Thus, the ratio of the median to the width of the contrast distribution is a simple signature that can be used to check whether an adaptation mechanism is potentially powerful enough for near-optimal redundancy reduction.
. Thus, the ratio of the median to the width of the contrast distribution is a simple signature that can be used to check whether an adaptation mechanism is potentially powerful enough for near-optimal redundancy reduction.
Figure 5. Median vs. width of 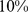 to
to 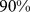 percentile interval of the models shown in Figure 3b.
percentile interval of the models shown in Figure 3b.
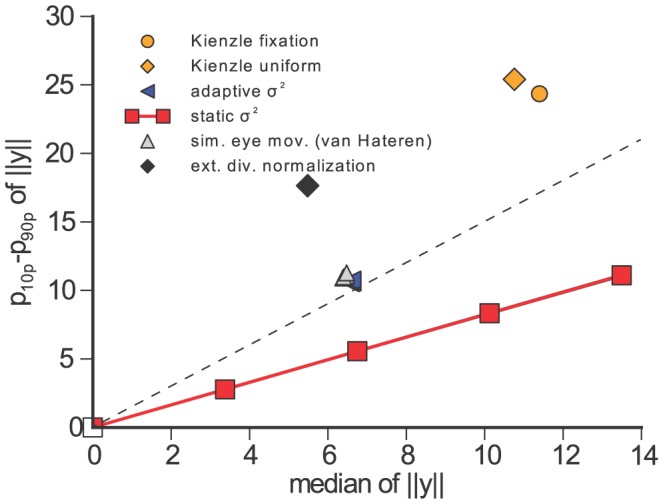
The red line corresponds to a static 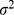 for different values of
for different values of 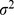 , the blue triangles correspond to the temporally adapting
, the blue triangles correspond to the temporally adapting 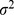 , the orange markers correspond to uniformly sampled (diamond) and fixational image patches with Brownian motion micro-saccades (circle) from Kienzle et al. [29], the gray markers to simulated eye movement datasets from van Hateren image data [31], and the black marker to the optimal extended divisive normalization model. All transforms that yield a strong redundancy reduction have models that exhibit a ratio greater than
, the orange markers correspond to uniformly sampled (diamond) and fixational image patches with Brownian motion micro-saccades (circle) from Kienzle et al. [29], the gray markers to simulated eye movement datasets from van Hateren image data [31], and the black marker to the optimal extended divisive normalization model. All transforms that yield a strong redundancy reduction have models that exhibit a ratio greater than 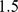 (dashed lines).
(dashed lines).
Methods
The code and the data are available online under http://www.bethgelab.org/code/sinz2012.
Data
van Hateren data
For the static experiments, we used randomly sampled 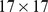 patches from the van Hateren database [31]. For all experiments we used the logarithm of the raw light intensities. We sampled
patches from the van Hateren database [31]. For all experiments we used the logarithm of the raw light intensities. We sampled 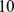 pairs of training and test sets of
pairs of training and test sets of 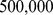 patches which we centered on the pixel mean.
patches which we centered on the pixel mean.
For the simulated eye movements, we also used  pairs of training and test sets. For the sampling procedure, we repeated the following steps until
pairs of training and test sets. For the sampling procedure, we repeated the following steps until 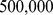 samples were drawn: We first drew an image randomly from the van Hateren database. For each image, we simulated ten saccades to random locations in that image. For each saccade location which was uniformly drawn over the entire image, we determined the number
samples were drawn: We first drew an image randomly from the van Hateren database. For each image, we simulated ten saccades to random locations in that image. For each saccade location which was uniformly drawn over the entire image, we determined the number  of patches to be sampled from around that location by
of patches to be sampled from around that location by 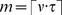 where
where 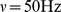 was the assumed sampling frequency and
was the assumed sampling frequency and  was a sample from an exponential distribution with average fixation time
was a sample from an exponential distribution with average fixation time 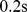 (i.e.
(i.e. 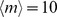 ). The actual locations of the patches were determined by Brownian motion starting at the saccade location and then propagating with a diffusion constant of
). The actual locations of the patches were determined by Brownian motion starting at the saccade location and then propagating with a diffusion constant of 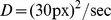 . This means that each patch location was drawn relative to the previous one based on an isotropic Gaussian centered at the current location with a standard deviation of
. This means that each patch location was drawn relative to the previous one based on an isotropic Gaussian centered at the current location with a standard deviation of 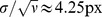 .
.
Kienzle data
The van Hateren database is a standard dataset for static natural image statistics. To make sure that our results also hold for real fixations, we sampled data from the images used by Kienzle et al. [29]. We computed the 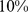 and
and 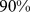 percentiles, as well as the width of the interval between them, for both datasets for Figure 5.
percentiles, as well as the width of the interval between them, for both datasets for Figure 5.
We constructed two datasets: One where the patches were uniformly drawn from the images, and one where we again used Brownian motion with a similar standard deviation around human fixation spots to simulate human fixational data. We applied the same preprocessing as for the van Hateren data: centering and whitening.
Models
Both the divisive normalization model and the optimal radial factorization consist of two steps: a linear filtering step and a radial rescaling step (Table 1). In the following, we describe the different steps in more detail.
Table 1. Model components of the divisive normalization and radial factorization model: Natural image patches are filtered by a set of linear oriented band-pass filters.
| divisive normalization model | radial factorization | |
| filtering |
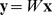
|
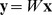
|
| normalization |
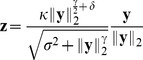
|
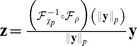
|
(static case 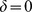 and and 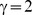 ) ) |
The filter responses are normalized and their norm is rescaled in the normalization step.
Filters
The receptive fields of our model neurons, i.e. the linear filters of our models, are given by the rows of a matrix 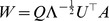 . In summary, the filters are obtained by (i) projecting the data onto the
. In summary, the filters are obtained by (i) projecting the data onto the  dimensional subspace that is insensitive to the DC component in the image patches, (ii) performing dimensionality reduction and whitening using principal component analysis, and (iii) training an independent subspace analysis algorithm (ISA) to obtain
dimensional subspace that is insensitive to the DC component in the image patches, (ii) performing dimensionality reduction and whitening using principal component analysis, and (iii) training an independent subspace analysis algorithm (ISA) to obtain 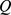 :
:
The projection of the data onto the
 dimensional subspace that is insensitive to the DC component is achieved via the matrix
dimensional subspace that is insensitive to the DC component is achieved via the matrix 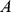 . This matrix is a fixed matrix for which the coefficients in each row sum to zero and all rows are mutually orthogonal. The matrix we used has been obtained via a QR-decomposition as described in the Methods Section of [7].
. This matrix is a fixed matrix for which the coefficients in each row sum to zero and all rows are mutually orthogonal. The matrix we used has been obtained via a QR-decomposition as described in the Methods Section of [7].The dimensionality reduction and whitening is achieved by
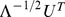 . The matrix
. The matrix 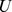 contains the principal components of
contains the principal components of 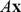 such that
such that 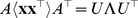 . As it is common practice, we kept only the first
. As it is common practice, we kept only the first 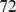 principal components to avoid “noisy” high frequency filters. However, our analysis would also be valid and lead to the same conclusions if we kept the full set of filters.
principal components to avoid “noisy” high frequency filters. However, our analysis would also be valid and lead to the same conclusions if we kept the full set of filters.The last matrix
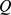 is constrained to be an orthogonal matrix because the covariance of whitened data remains white under orthogonal transformations. This additional degree of freedom is used by Independent Subspace Analysis (see below) to optimize the filter shapes for redundancy reduction beyond removing second-order correlations. While the matrix
is constrained to be an orthogonal matrix because the covariance of whitened data remains white under orthogonal transformations. This additional degree of freedom is used by Independent Subspace Analysis (see below) to optimize the filter shapes for redundancy reduction beyond removing second-order correlations. While the matrix 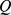 has a large effect on the particular filter shapes, the same results would have been obtained with any type of whitening filter, i.e. for any orthogonal matrix
has a large effect on the particular filter shapes, the same results would have been obtained with any type of whitening filter, i.e. for any orthogonal matrix 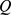 , because they only differ by an orthogonal rotation. Since we use the Euclidean norm in the divisive normalization model, the rotation would not change the norm of the filter responses and therefore all radial distributions would be the same. The only aspect in our analysis for which the filter choice would make a (small) difference is the multi-information of the raw filter responses. When using ICA filter, the multi-information could be a bit lower. However, since even for rather drastic changes of filter shapes (within the class of whitening filters) there is only a small effect on redundancy reduction [6], the particular choice of filter shapes does not affect any of our conclusions. The same is true for any choice of parametric filters as long as the covariance matrix of the filter responses is proportional to the identity matrix. Since the second-order correlations provide the dominant contribution to the multi-information any substantial deviation from the class of whitening filters is likely to yield suboptimal results.
, because they only differ by an orthogonal rotation. Since we use the Euclidean norm in the divisive normalization model, the rotation would not change the norm of the filter responses and therefore all radial distributions would be the same. The only aspect in our analysis for which the filter choice would make a (small) difference is the multi-information of the raw filter responses. When using ICA filter, the multi-information could be a bit lower. However, since even for rather drastic changes of filter shapes (within the class of whitening filters) there is only a small effect on redundancy reduction [6], the particular choice of filter shapes does not affect any of our conclusions. The same is true for any choice of parametric filters as long as the covariance matrix of the filter responses is proportional to the identity matrix. Since the second-order correlations provide the dominant contribution to the multi-information any substantial deviation from the class of whitening filters is likely to yield suboptimal results.
The independent subspace analysis (with two-dimensional subspaces) used to obtain the matrix 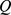 is based on the model by Hyvärinen [16]:
is based on the model by Hyvärinen [16]:
| (7) |
where 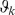 denotes the list of free parameters for each
denotes the list of free parameters for each 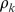 . More specifically,
. More specifically, 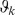 consists of the value
consists of the value 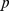 for the
for the 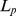 -norm and the parameters of the radial distribution for each of the
-norm and the parameters of the radial distribution for each of the 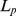 -spherically symmetric distributions. Each single
-spherically symmetric distributions. Each single 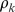 was chosen to be a two-dimensional
was chosen to be a two-dimensional 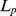 -spherically symmetric distribution [32]
-spherically symmetric distribution [32]
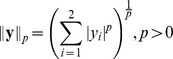 |
with a radial  -distribution
-distribution 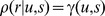 with shape
with shape  and scale
and scale  . Therefore, the parameters
. Therefore, the parameters  were given by
were given by 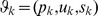 . In the denominator,
. In the denominator, 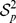 denotes the surface area of the
denotes the surface area of the 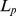 -norm unit sphere in two dimensions [32]. During training, we first fixed
-norm unit sphere in two dimensions [32]. During training, we first fixed 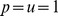 ; after initial convergence, we retrained the model with free
; after initial convergence, we retrained the model with free 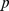 and
and  .
.
The likelihood of the data under equation (7) was optimized by alternating between optimizing 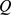 for fixed
for fixed 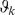 , and optimizing the
, and optimizing the 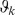 for fixed
for fixed 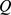 . The gradient ascent on the log-likelihood of
. The gradient ascent on the log-likelihood of 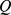 over the orthogonal group used the backprojection method by Manton [19], [33], [34]. Optimizing over
over the orthogonal group used the backprojection method by Manton [19], [33], [34]. Optimizing over 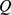 yields filter pairs that resemble quadrature pairs like in the energy model of complex cells [17], [18].
yields filter pairs that resemble quadrature pairs like in the energy model of complex cells [17], [18].
Radial rescaling
Optimal contrast gain control: radial factorization
In the following we describe the general mechanism of radial factorization. The spherical symmetric case mostly used in this study is obtained by setting 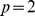 .
.
Radial factorization is the optimal redundancy reduction mechanism for 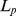 -spherically symmetric distributed data [11], [32]. Samples from
-spherically symmetric distributed data [11], [32]. Samples from 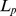 -spherically symmetric distributions with identical
-spherically symmetric distributions with identical 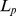 -norm
-norm 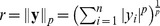 are uniformly distributed on the
are uniformly distributed on the 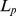 -sphere with that radius. A radial distribution
-sphere with that radius. A radial distribution 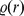 determines how likely it is that a data point is drawn from an
determines how likely it is that a data point is drawn from an 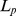 -sphere with that specific radius. Since the distribution on the sphere is uniform for any
-sphere with that specific radius. Since the distribution on the sphere is uniform for any 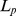 -spherically symmetric distribution, the radial distribution
-spherically symmetric distribution, the radial distribution  determines the specific type of distribution. For example,
determines the specific type of distribution. For example, 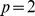 and
and 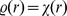 yields an isotropic Gaussian since the Gaussian distribution is spherically symmetric (
yields an isotropic Gaussian since the Gaussian distribution is spherically symmetric (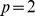 ) and has a radial
) and has a radial 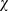 -distribution (
-distribution (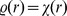 ). One can show that, for a fixed value of
). One can show that, for a fixed value of 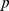 , there is only one type of radial distribution such that the joint distribution is factorial [13]. For
, there is only one type of radial distribution such that the joint distribution is factorial [13]. For 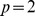 this radial distribution is the
this radial distribution is the 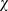 -distribution corresponding to a joint Gaussian distribution. For
-distribution corresponding to a joint Gaussian distribution. For 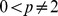 , the radial distribution is a generalization of the
, the radial distribution is a generalization of the 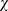 -distribution and the joint distribution is the so called
-distribution and the joint distribution is the so called 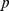 -generalized Normal [35].
-generalized Normal [35].
Radial factorization is a mapping on the 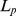 -norm
-norm 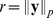 of the data points that transforms a given source
of the data points that transforms a given source 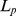 -spherically symmetric distribution into a
-spherically symmetric distribution into a 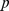 -generalized Normal. To this end, it first models the distribution of
-generalized Normal. To this end, it first models the distribution of  with a flexible distribution
with a flexible distribution  and then nonlinearly rescales
and then nonlinearly rescales  such that the radial distribution becomes a generalized
such that the radial distribution becomes a generalized 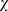 -distribution. This is achieved via histogram equalization
-distribution. This is achieved via histogram equalization 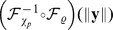 where the
where the 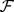 denote the respective cumulative distribution functions. On the level of joint responses
denote the respective cumulative distribution functions. On the level of joint responses 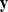 , radial factorization first normalizes the radius to one and then rescales the data point with the new radius:
, radial factorization first normalizes the radius to one and then rescales the data point with the new radius:
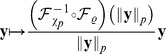 |
In our case  was chosen to be a mixture of five
was chosen to be a mixture of five  -distributions.
-distributions.
When determining the optimal redundancy reduction performance on the population response, we set 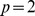 in order to use the same norm as the divisive normalization model. Only when estimating the redundancy of the linear filter responses, we use
in order to use the same norm as the divisive normalization model. Only when estimating the redundancy of the linear filter responses, we use 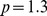 [11].
[11].
Note that the divisive normalization model and the radial factorization model used in this study are invariant with respect to the choice of 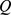 since the Euclidean norm (
since the Euclidean norm (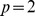 ) is invariant under orthogonal transforms. However, the choice of
) is invariant under orthogonal transforms. However, the choice of 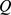 would affect the redundancies in the plain filter responses
would affect the redundancies in the plain filter responses 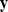 in Figure 1B. But even if we had chosen a different
in Figure 1B. But even if we had chosen a different 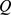 , i.e. another set of whitening filters, the redundancy between the coefficients of
, i.e. another set of whitening filters, the redundancy between the coefficients of 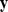 would not vary much as previous studies have demonstrated [6], [7].
would not vary much as previous studies have demonstrated [6], [7].
Divisive normalization model and Naka-Rushton distribution
We use the following divisive normalization transform
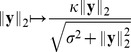 |
which is the common model for neural contrast gain control [8] and redundancy reduction [9].
Divisive normalization acts on the Euclidean norm of the filter responses 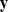 . Therefore, divisive normalization can only achieve independence if it outputs a Gaussian random variable. While in radial factorization the target and source distribution were fixed, and the goal was to find a mapping that transforms one into the other, we now fix the mapping to divisive normalization, the target distribution on the normalized response
. Therefore, divisive normalization can only achieve independence if it outputs a Gaussian random variable. While in radial factorization the target and source distribution were fixed, and the goal was to find a mapping that transforms one into the other, we now fix the mapping to divisive normalization, the target distribution on the normalized response  to be Gaussian (
to be Gaussian ( to be
to be  -distributed) and search for the corresponding source distribution that would lead to a factorial representation when divisive normalization is applied. Since divisive normalization saturates at
-distributed) and search for the corresponding source distribution that would lead to a factorial representation when divisive normalization is applied. Since divisive normalization saturates at  , we will actually have to use a truncated
, we will actually have to use a truncated 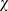 -distribution on
-distribution on 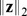 .
.  becomes the truncation threshold. Note that radial truncation actually introduces some dependencies, but we keep them small by choosing the truncation threshold
becomes the truncation threshold. Note that radial truncation actually introduces some dependencies, but we keep them small by choosing the truncation threshold  to be the
to be the 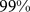 percentile of the radial
percentile of the radial 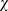 -distribution which is approximately
-distribution which is approximately 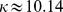 . The
. The 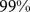 was chosen to keep the target distribution close to a factorial Gaussian. However, it could still be that another cut-off (value of
was chosen to keep the target distribution close to a factorial Gaussian. However, it could still be that another cut-off (value of  ) leads to a better redundancy reduction even though the target distribution is less factorial for lower values of
) leads to a better redundancy reduction even though the target distribution is less factorial for lower values of  (quantiles lower than
(quantiles lower than 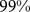 ). We made sure that this is not the case by choosing different values of
). We made sure that this is not the case by choosing different values of  , computing the best
, computing the best  via a maximum likelihood fit of a Naka-Rushton distribution (see below), and estimating the multi-information in the transformed outputs. We found that the choice of
via a maximum likelihood fit of a Naka-Rushton distribution (see below), and estimating the multi-information in the transformed outputs. We found that the choice of  has virtually no effect on the residual multi-infomation (it varies by
has virtually no effect on the residual multi-infomation (it varies by 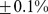 for
for 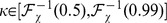 and takes its optimum within this interval). Therefore, we kept the
and takes its optimum within this interval). Therefore, we kept the 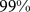 choice as it is most similar to the target distribution of radial factorization.
choice as it is most similar to the target distribution of radial factorization.
Note also that choosing a Gaussian target distribution does not contradict the finding that cortical firing rates are found to be exponentially distributed [36] since each single response  can always be transformed again to be exponentially distributed without changing the redundancy of
can always be transformed again to be exponentially distributed without changing the redundancy of  .
.
The distribution on  such that
such that
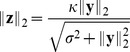 |
is truncated 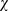 -distributed can be derived by a simple change of variables. In the resulting distribution
-distributed can be derived by a simple change of variables. In the resulting distribution
 |
the truncation threshold  , the half-saturation constant
, the half-saturation constant  , and the scale of the
, and the scale of the  -distribution become parameters of the model. The parameter
-distribution become parameters of the model. The parameter  of the Naka-Rushton distribution controls the variance of the corresponding Gaussian and was always chosen such that the Gaussian was white with variance one.
of the Naka-Rushton distribution controls the variance of the corresponding Gaussian and was always chosen such that the Gaussian was white with variance one.  was determined by the
was determined by the 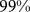 -percentile. The only remaining free parameter of the Naka-Rushton distribution is
-percentile. The only remaining free parameter of the Naka-Rushton distribution is  which simultaneously affects both shape and scale.
which simultaneously affects both shape and scale. 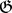 is the regularized-incomplete-gamma function which accounts for the truncation at
is the regularized-incomplete-gamma function which accounts for the truncation at  . We call the distribution Naka-Rushton distribution and denote it with
. We call the distribution Naka-Rushton distribution and denote it with 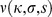 .
.
To derive the distribution on 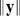 for which the extended divisive normalization transformation
for which the extended divisive normalization transformation 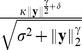 yields a
yields a  -distribution, the steps are exactly the same as for the plain divisive normalization transform above. This yields
-distribution, the steps are exactly the same as for the plain divisive normalization transform above. This yields
 |
for 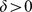 . The parameters of the distribution are now
. The parameters of the distribution are now 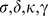 and
and  .
.
The parameters for all divisive normalization transforms were estimated via maximum likelihood of the Naka-Rushton distribution on the Euclidean norms 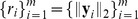 of the filter responses to natural image patches. As before, we did not optimize for
of the filter responses to natural image patches. As before, we did not optimize for  in the extended Naka-Rushton distribution but fixed it such that the corresponding Gaussian was white.
in the extended Naka-Rushton distribution but fixed it such that the corresponding Gaussian was white.
Dynamically adapting 
For the model with dynamically adapting  , we first model the Euclidean norms
, we first model the Euclidean norms 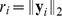 of the filter responses to the patches from the simulated eye movement data with a mixture of
of the filter responses to the patches from the simulated eye movement data with a mixture of 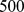 Naka-Rushton distributions
Naka-Rushton distributions
using EM [37]. 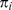 denotes the probability that
denotes the probability that 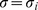 . The values of
. The values of 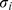 where chosen in
where chosen in 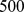 equidistant steps from
equidistant steps from 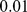 to
to 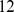 .
.
How much redundancy reduction can be achieved with a dynamically adapting  , depends on the dynamics according to which it is selected based on the recent history. While there might be many strategies, we chose a parsimonious one based on the mean and the standard deviation of the posterior over
, depends on the dynamics according to which it is selected based on the recent history. While there might be many strategies, we chose a parsimonious one based on the mean and the standard deviation of the posterior over 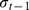 . Our heuristic consists of two steps: First the mean and the standard deviation of the posterior
. Our heuristic consists of two steps: First the mean and the standard deviation of the posterior 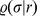 derived from the mixture distribution is approximated with piecewise linear functions
derived from the mixture distribution is approximated with piecewise linear functions 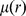 and
and 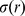 , then we sample
, then we sample 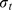 used to transform
used to transform  from a
from a  -distribution with mean and standard deviation
-distribution with mean and standard deviation 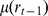 and
and 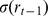 . This strategy emphasizes that the first two moments of the posterior are the important features for obtaining a good
. This strategy emphasizes that the first two moments of the posterior are the important features for obtaining a good 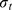 .
.
In more detail, we evaluated the posterior
of the mixture distribution at 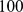 equidistant locations between
equidistant locations between 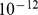 and
and 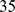 , computed the posterior mean and standard deviation at those locations, rescaled the standard deviation by
, computed the posterior mean and standard deviation at those locations, rescaled the standard deviation by 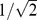 , and fitted the piecewise linear functions on the intervals
, and fitted the piecewise linear functions on the intervals 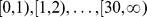 to each set of values. In the first interval, the linear function was constraint to start at zero. From these two functions
to each set of values. In the first interval, the linear function was constraint to start at zero. From these two functions 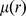 and
and 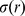 , we computed two functions for the scale
, we computed two functions for the scale  and the shape
and the shape  of a
of a  -distribution
-distribution
via moment matching. We obtained the value 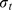 for transforming a value
for transforming a value 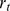 with a Naka-Rushton function by sampling
with a Naka-Rushton function by sampling 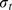 from a
from a  -distribution with shape and scale determined by
-distribution with shape and scale determined by 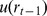 and
and 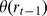 .
.
Computation of percentiles for Figure 5
For the dynamically adapting 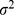 in Figure 5, we sampled from
in Figure 5, we sampled from
and computed the percentiles based on the sampled dataset. For the sampling procedure, we drew  from the
from the  -distribution
-distribution 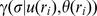 with shape and scale computed from
with shape and scale computed from 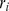 and then sampled
and then sampled  from the Naka-Rushton distribution
from the Naka-Rushton distribution 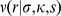 with that
with that  . We repeated that for all
. We repeated that for all 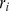 from a test set of simulated eye movement radii. This procedure was carried out for all pairs of training and test sets, and the distributions fitted to them.
from a test set of simulated eye movement radii. This procedure was carried out for all pairs of training and test sets, and the distributions fitted to them.
For the static case, we sampled data from single Naka-Rushton distributions for different values of  and computed the percentiles from the samples.
and computed the percentiles from the samples.
History-independent choice of 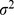
In the following, let 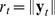 and
and 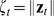 be the unnormalized and normalized responses at time
be the unnormalized and normalized responses at time  , respectively, and
, respectively, and 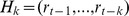 be the recent history of responses. The underlying generative structure of the model for temporally correlated data is the following: given a fixed history
be the recent history of responses. The underlying generative structure of the model for temporally correlated data is the following: given a fixed history 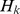 ,
, 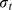 and
and 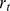 are sampled from
are sampled from 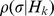 and
and 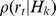 . Then,
. Then, 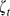 is generated from
is generated from 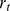 and
and 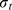 through divisive normalization.
through divisive normalization.
For strong redundancy reduction, 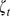 should follow a truncated
should follow a truncated 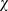 -distribution, which means that for given history
-distribution, which means that for given history 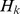 and
and 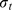 , the unnormalized response energy
, the unnormalized response energy 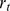 must have a Naka-Rushton distribution
must have a Naka-Rushton distribution
because normalizing this response via 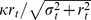 yields a truncated
yields a truncated 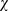 -distribution. Averaged over all histories
-distribution. Averaged over all histories 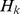 and half-saturation constants
and half-saturation constants 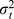 the distribution of
the distribution of 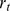 is a mixture of Naka-Rushton distributions
is a mixture of Naka-Rushton distributions
| (8) |
If 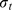 depends deterministically on
depends deterministically on 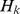 we obtain equation (5).
we obtain equation (5).
If 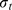 could be chosen independently of the preceding history the distribution of
could be chosen independently of the preceding history the distribution of 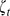 would be given by
would be given by
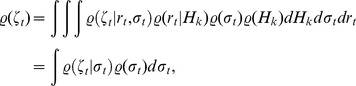 |
where 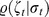 is the marginal distribution of
is the marginal distribution of 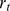 transformed with divisive normalization and a specific value of
transformed with divisive normalization and a specific value of 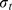 . Since redundancy reduction requires
. Since redundancy reduction requires 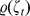 to be truncated
to be truncated  -distributed,
-distributed,  can be chosen independently only if the truncated
can be chosen independently only if the truncated  -distribution can be modelled as mixture of the different
-distribution can be modelled as mixture of the different 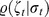 . Since we assume stationarity, we can drop the index
. Since we assume stationarity, we can drop the index  in the equation.
in the equation.
Multi-information estimation
We use the multi-information to quantify the statistical dependencies between the filter responses 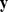 [38]. The multi-information is the
[38]. The multi-information is the  -dimensional generalization of the mutual-information. It is defined as the Kullback-Leibler divergence between the joint distribution and the product of its marginals or, equivalently, the difference between the sum of the marginal entropies and the joint entropy
-dimensional generalization of the mutual-information. It is defined as the Kullback-Leibler divergence between the joint distribution and the product of its marginals or, equivalently, the difference between the sum of the marginal entropies and the joint entropy
| (9) |
The multi-information is zero if and only if the different dimensions of the random vector 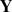 are independent. Since the joint entropy
are independent. Since the joint entropy 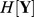 is hard to estimate we employ a semi-parametric estimate of the multi-information that is conservative in the sense that it is downward biased.
is hard to estimate we employ a semi-parametric estimate of the multi-information that is conservative in the sense that it is downward biased.
For the marginal entropies 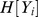 , we use a jackknifed estimator for the discrete entropy on the binned values [39]. We chose the bin size with the heuristic proposed by Scott [40]. We obtain an estimate for the differential entropy by correcting with the logarithm of the bin width (see e.g. [7]).
, we use a jackknifed estimator for the discrete entropy on the binned values [39]. We chose the bin size with the heuristic proposed by Scott [40]. We obtain an estimate for the differential entropy by correcting with the logarithm of the bin width (see e.g. [7]).
In order to estimate the joint entropy, we use the average log-loss to get an upper bound
Since the average log-loss overestimates the true entropy, replacing the joint entropy by 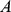 in equation (1) underestimates the multi-information. Therefore, we sometimes get estimates smaller than zero. Since the multi-information is always positive, we set the value to zero in that case. For computing errorbars on the multi-information estimations, we use the negative values but a mean zero in such cases, which effectively increases the standard deviation of the error.
in equation (1) underestimates the multi-information. Therefore, we sometimes get estimates smaller than zero. Since the multi-information is always positive, we set the value to zero in that case. For computing errorbars on the multi-information estimations, we use the negative values but a mean zero in such cases, which effectively increases the standard deviation of the error.
Since we want commit ourselves as little as possible to a particular model, we estimate 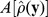 by making the assumption that
by making the assumption that 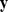 is
is 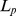 -spherically symmetric distributed but estimating everything else with non-parametric estimators. If
-spherically symmetric distributed but estimating everything else with non-parametric estimators. If 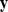 is
is 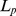 -spherically symmetric distributed, the radial component is independent from the directional component [32] and we can write
-spherically symmetric distributed, the radial component is independent from the directional component [32] and we can write
| (10) |
The entropy 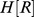 of the radial component is again estimated via a histogram estimator. The term
of the radial component is again estimated via a histogram estimator. The term 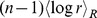 is approximated by the empirical mean.
is approximated by the empirical mean.
Putting all the equations together yields our estimator for the multi-information under the assumption of 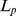 -spherically symmetric distributed
-spherically symmetric distributed 
where  are the univariate entropies estimated via binning.
are the univariate entropies estimated via binning.
Since the optimal value of 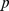 for filter responses
for filter responses 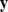 to natural image patches is approximately
to natural image patches is approximately 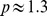 we use that value to estimate the multi-information of
we use that value to estimate the multi-information of 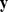 .
.
When estimating the multi-information of the responses  of either divisive normalization or radial factorization, we use the fact that
of either divisive normalization or radial factorization, we use the fact that
where 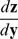 is the Jacobian of the normalization transformation. The mean is estimated by averaging over data points. The determinants of radial factorization, divisive normalization, and extended divisive normalization are given by
is the Jacobian of the normalization transformation. The mean is estimated by averaging over data points. The determinants of radial factorization, divisive normalization, and extended divisive normalization are given by
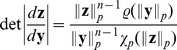 |
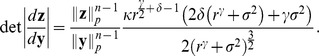 |
All multi-information values were computed on test data.
For the dynamically adapting model, the  for each data point
for each data point  is sampled from a
is sampled from a  -distribution whose parameters are determined from the previous value
-distribution whose parameters are determined from the previous value  and the posterior over
and the posterior over  obtained from the mixture of Naka-Rushton distributions. Since
obtained from the mixture of Naka-Rushton distributions. Since  changes from step to step it becomes part of the representation and should be included when computing the multi-information (i.e. the redundancy) between the outputs
changes from step to step it becomes part of the representation and should be included when computing the multi-information (i.e. the redundancy) between the outputs  . Therefore, the redundancy for the dynamically adapting model is measured by
. Therefore, the redundancy for the dynamically adapting model is measured by 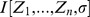 . For its computation, we use that
. For its computation, we use that 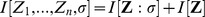 , where
, where 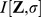 is the mutual information between
is the mutual information between 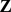 and
and  . In the following, we write
. In the following, we write 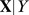 if
if 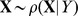 . Under the assumption that both
. Under the assumption that both 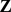 and
and 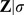 are spherically symmetric distributed, we can decompose respective random variables into the uniform (on the sphere) and the radial part:
are spherically symmetric distributed, we can decompose respective random variables into the uniform (on the sphere) and the radial part: 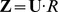 and
and 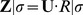 . This yields
. This yields
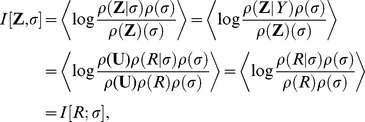 |
which means that we can restrict ourselves to the mutual information between the two univariate signals 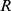 and
and  , which we estimate from a two-dimensional histogram with
, which we estimate from a two-dimensional histogram with  bins.
bins.
Acknowledgments
We thank P. Berens, L. Busse, S. Katzner and L. Theis for fruitful discussions and comments on the manuscript.
Funding Statement
This study was financially supported by the German Ministry of Education, Science, Research and Technology through the Bernstein award (BMBF; FKZ: 01GQ0601). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Barlow HB (1961) Possible Principles Underlying the Transformations of Sensory Messages. In: Rosenblith WA, editor. Sensory Communication. Cambridge, MA: MIT Press. pp. 217–234.
- 2. Simoncelli EP, Olshausen BA (2003) Natural Image Statistics and Neural Representation. Annual Review of Neuroscience 24: 1193–1216. [DOI] [PubMed] [Google Scholar]
- 3. Bell AJ, Sejnowski TJ (1997) The “independent components” of natural scenes are edge filters. Vision Research 37: 3327–3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Barlow HB (1989) Unsupervised Learning. Neural Computation 1: 295–311. [Google Scholar]
- 5. Lewicki MS, Olshausen BA (1999) Probabilistic framework for the adaptation and comparison of image codes. Journal of the Optical Society of America A 16: 1587–1601. [Google Scholar]
- 6. Bethge M (2006) Factorial coding of natural images: how effective are linear models in removing higher-order dependencies? Journal of the Optical Society of America A 23: 1253–1268. [DOI] [PubMed] [Google Scholar]
- 7. Eichhorn J, Sinz F, Bethge M (2009) Natural Image Coding in V1: How Much Use Is Orientation Selectivity? PLoS Comput Biol 5: e1000336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Heeger DJ (1992) Normalization of cell responses in cat striate cortex. Vis Neurosci 9: 181–197. [DOI] [PubMed] [Google Scholar]
- 9. Schwartz O, Simoncelli EP (2001) Natural signal statistics and sensory gain control. Nat Neurosci 4: 819–825. [DOI] [PubMed] [Google Scholar]
- 10. Carandini M, Heeger DJ (2011) Normalization as a canonical neural computation. Nature reviews Neuroscience 13: 51–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sinz F, Bethge M (2009) The Conjoint Effect of Divisive Normalization and Orientation Selectivity on Redundancy Reduction. In: Koller D, Schuurmans D, Bengio Y, Bottou L, editors. Advances in neural information processing systems 21: 22nd Annual Conference on Neural Information Processing Systems 2008. Red Hook, NY, USA: Curran Associates. pp. 1521–1528.
- 12. Lyu S, Simoncelli EP (2009) Nonlinear extraction of independent components of natural images using radial gaussianization. Neural Computation 21: 1485–1519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Sinz F, Gerwinn S, Bethge M (2009) Characterization of the p-generalized normal distribution. Journal of Multivariate Analysis 100: 817–820. [Google Scholar]
- 14. Bonds AB (1991) Temporal dynamics of contrast gain in single cells of the cat striate cortex. Vis Neurosci 6: 239–255. [DOI] [PubMed] [Google Scholar]
- 15. Hyvärinen A, Hoyer P (2000) Emergence of Phase- and Shift-Invariant Features by Decomposition of Natural Images into Independent Feature Subspaces. Neural Computation 12: 1705–1720. [DOI] [PubMed] [Google Scholar]
- 16. Hyvärinen A, Koester U (2007) Complex cell pooling and the statistics of natural images. Network: Computation in Neural Systems 18: 81–100. [DOI] [PubMed] [Google Scholar]
- 17. Pollen D, Ronner S (1981) Phase relationships between adjacent simple cells in the visual cortex. Science 212: 1409–1411. [DOI] [PubMed] [Google Scholar]
- 18. Adelson EH, Bergen JR (1985) Spatiotemporal energy models for the perception of motion. Journal of the Optical Society of America A 2: 284–299. [DOI] [PubMed] [Google Scholar]
- 19.Sinz F, Simoncelli EP, Bethge M (2009) Hierarchical Modeling of Local Image Features through Lp-Nested Symmetric Distributions. In: Bengio Y, Schuurmans D, Lafferty J, Williams C, Culotta A, editors. Advances in Neural Information Processing Systems 22: 23rd Annual Conference on Neural Information Processing Systems 2009. Red Hook, NY, USA: Curran Associates. pp. 1696–1704.
- 20. Lyu S (2011) Dependency Reduction with Divisive Normalization: Justification and Effectiveness. Neural Computation 23: 2942–2973. [DOI] [PubMed] [Google Scholar]
- 21. Wainwright MJ, Simoncelli EP (2000) Scale mixtures of Gaussians and the statistics of natural images. Neural Information Processing Systems 12: 855–861. [Google Scholar]
- 22.Wainwright MJ, Schwartz O, Simoncelli EP (2002) Natural image statistics and divisive normalization: modeling nonlinearities and adaptation in cortical neurons. In: Statistical theories of the brain. MIT Press. pp. 203–222.
- 23. Field DJ (1987) Relations between the statistics of natural images and the response properties of cortical cells. Journal of the Optical Society of America A 4: 2379–2394. [DOI] [PubMed] [Google Scholar]
- 24. Ruderman DL, Bialek W (1994) Statistics of natural images: Scaling in the woods. Physical Review Letters 73: 814. [DOI] [PubMed] [Google Scholar]
- 25. Kac M (1939) On a Characterization of the Normal Distribution. American Journal of Mathematics 61: 726–728. [Google Scholar]
- 26. Brenner N, Bialek W, De Ruyter Van Steveninck R (2000) Adaptive rescaling maximizes information transmission. Neuron 26: 695–702. [DOI] [PubMed] [Google Scholar]
- 27. Wark B, Lundstrom BN, Fairhall A (2007) Sensory adaptation. Current Opinion in Neurobiology 17: 423–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hu M, Wang Y (2011) Rapid Dynamics of Contrast Responses in the Cat Primary Visual Cortex. PLoS ONE 6: e25410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Kienzle W, Franz MO, Schölkopf B, Wichmann FA (2009) Center-surround patterns emerge as optimal predictors for human saccade targets. Journal of Vision 9: 7.1–15. [DOI] [PubMed] [Google Scholar]
- 30. Reinagel P, Zador AM (1999) Natural scene statistics at the centre of gaze. Network 10: 341–350. [PubMed] [Google Scholar]
- 31. Van Hateren JH, Van Der Schaaf A (1998) Independent component filters of natural images compared with simple cells in primary visual cortex. Proceedings of the Royal Society B Biological Sciences 265: 359–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Gupta AK, Song D (1997) Lp-norm spherical distribution. Journal of Statistical Planning and Inference 60: 241–260. [Google Scholar]
- 33. Manton JH (2002) Optimization algorithms exploiting unitary constraints. Signal Processing, IEEE Transactions on 50: 635–650. [Google Scholar]
- 34. Sinz F, Bethge M (2010) Lp -Nested Symmetric Distributions. Journal of Machine Learning Research 11: 3409–3451. [Google Scholar]
- 35. Goodman IR, Kotz S (1973) Multivariate theta]-generalized normal distributions. Journal of Multivariate Analysis 3: 204–219. [Google Scholar]
- 36. Baddeley R, Abbott LF, Booth MC, Sengpiel F, Freeman T, et al. (1997) Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proceedings of the Royal Society B Biological Sciences 264: 1775–1783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B Methodological 39: 1–38. [Google Scholar]
- 38. Perez A (1977) ε-admissible simplification of the dependence structure of a set of random variables. Kybernetika 13: 439–444. [Google Scholar]
- 39. Paninski L (2003) Estimation of Entropy and Mutual Information. Neural Computation 15: 1191–1253. [Google Scholar]
- 40. Scott DW (1979) On optimal and data-based histograms. Biometrika 66: 605–610. [Google Scholar]