Boosting for detection of gene-environment interactions

Abstract

In genetic association studies, it is typically thought that genetic variants and environmental variables jointly will explain more of the inheritance of a phenotype than either of these two components separately. Traditional methods to identify gene-environment interactions typically consider only one measured environmental variable at a time. However, in practice, multiple environmental factors may each be imprecise surrogates for the underlying physiological process that actually interacts with the genetic factors. In this paper we develop a variant of L₂ boosting that is specifically designed to identify combinations of environmental variables that jointly modify the effect of a gene on a phenotype. Because the effect modifiers might have a small signal compared to the main effects, working in a space that is orthogonal to the main predictors allows us to focus on the interaction space. In a simulation study that investigates some plausible underlying model assumptions our method outperforms the lasso, and AIC and BIC model selection procedures as having the lowest test error. In an example for the WHI-PAGE study, the dedicated boosting method was able to pick out two single nucleotide polymorphisms for which effect modification appears present. The performance was evaluated on an independent test set and the results are promising.

1. Introduction

In genetic association studies, it is typically thought that important insight will be obtained through joint modeling of genetic variants and environmental variables. However, weak effect of gene-environment interactions, and imprecise measurement of the environment make it difficult to identify “statistically significant” interaction effects. In many situations, however, there may be a combination of the measured environmental variables that could interact with a particular gene, either because these measured variables are all imprecise surrogates for the actual underlying factor that interacts with the gene, or because multiple environmental factors each trigger the same biological mechanism.

Traditional methods to identify gene-environment interactions typically consider only one measured environmental variable at a time. The power to identify such variables is then typically very limited. Chatterjee at al. use Tukey’s 1-df model to combine multiple levels of environmental factors but not multiple environmental factors [1]. Thomas mentions multiple relevant susceptibility factors (environmental factors) as one of the future challenges in identifying gene-environment interactions [2]. In this paper we develop a variant of L₂ boosting that is specifically designed to identify combinations of environmental variables that jointly modify the effect of a gene on a phenotype.

Boosting was initially developed as a classification procedure [3], and has since been adapted to the regression and general prediction settings. In the original boosting algorithms, a weak classifier is applied iteratively to re-weighted versions of the data based on its performance on a training set. The estimated predictions from each of the classifiers are then averaged to obtain the final estimator. Friedman adapted boosting to the regression setting as an optimization problem with a squared error loss function [4]. Boosting has been shown to produce consistent estimates in very high dimensional settings where the number of predictors increases on the order of exp(sample size) [5].

Forward stage-wise linear regression, a version of boosting, has been shown to produce solutions approximately equivalent to that of the lasso (Least absolute shrinkage and selection), a regularized regression method [6], when using small step sizes [7]. The lasso, initially proposed by Tibshirani, minimizes the residual sum of squares under the condition that the sum of the absolute values of the coefficients are less than a constant λ. Due to this L₁ penalty, the lasso is able to simultaneously perform shrinkage and variable selection and performs well when the number of potential predictors is large.

The L₂ boosting procedure iteratively fits a learner, a simple fitting procedure, to the residuals from the previous model’s fitted values [4]. The learner can be linear or non-parametric. The number of boosting iterations, k, is a smoothing parameter generally chosen by cross-validation.

We investigate moderate to high dimensional regression problems where particular interest lies in determining a set of effect modifiers with low individual signal. We propose a variation to the usual L₂ boosting procedure which focuses on the interaction search in contrast to most boosting methods which address overall model prediction or classification. To be able to focus on the interaction space, the main predictors are regressed out of the response variable and the interactions. The usual L₂ boosting procedure is then applied to the resulting residuals. Because the effect modifiers may have small signal compared to the main effects, working in a space which is orthogonal to the main predictors allows improved performance of the algorithm as compared to applying the usual boosting algorithm which combines both main effects and interactions as learners. The dedicated boosting method is not intended for GWAS studies. Rather, due to computational demands, it is better suited for follow-up studies where focus lies on a small number of SNPs.

A similar and broader problem referred to as “mandatory covariates” has been recently addressed by Hothorn and Boulesteix [8]. The mandatory covariates are necessarily included in the model and the aim is to determine the additional predictive value of other variables, such as high dimensional molecular data. In their paper, the authors suggest the utilization of a two stage boosting procedure, implemented in the R package globalboosttest. The mandatory variables are regressed out of the outcome and then boosting is performed to determine a model with the additional covariates. While the idea is similar, further considerations need to be taken into account when dealing with interactions.

Since the interactions and the main effects are expected to be correlated, taking the extra step of regressing out the main effects from the interactions, rather than just the outcome variable allows for better performance and detection of the interaction effects. We compare the performance of dedicated boosting to the algorithm globalboosttest in simulations and a real data example.

In Section 2 we describe the dedicated boosting algorithm in detail and its implementation. We apply this method to a genetic association study within the Women’s Health Initiative (WHI) set in Section 3. A simulation study of the properties of dedicated boosting is presented in Section 4. We compare its performance to linear regression, the AIC and BIC stepwise model selecting procedures, the lasso [6], and globalboosttest.

2. Dedicated Boosting

We are interested in identifying groups of environmental factors that may modify the effect of a gene on a phenotype. To that effect, we have developed a method to build a model consisting of an ensemble of interactions with potentially small effects. The group of interactions is treated as a profile. The individual membership of factors in this profile is considered only suggestive as the method does not establish significance for the individual interactions but rather investigates the ensemble as a whole.

Methods for the identification of interactions using stepwise model selection with criterions such as the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) establish the significance of individual factors, and thus require a strong signal. The lasso [6] and boosting are geared towards building ensembles with weaker effects. Our intent is to develop a method for the purpose of interaction search that has the good performance of boosting when there is little signal.

2.1. L₂ boosting

We first describe the usual L₂ boosting algorithm with component-wise linear least squares as base procedure [9, 5, 10]. The algorithm iteratively refits the residuals at each step and performs a linear least squares regression against the single best predictor variable.

For a continuous outcome Y and a potentially large set of predictors X_j the L₂ boosting algorithm can be summarized as (following [10]):

1. Initialize f̂⁽⁰⁾ = Ȳ and set k = 0, let ν be a small fixed number.

2. Increase k by 1. Compute the vector of residuals R^(k−1) = Y − f̂^(k−1)(X) for all observations i.

3. Fit a simple linear regression for each X_j to the residual vector R^(k−1). Choose the X_b which best predicts the residuals, let β̂_b be the regression coefficient of X_b.

4. Set ĝ^(k) = β̂_bX_b, the fitted values from the best fit in step 3.

5. Update f̂^(k) = f̂^(k−1) + νĝ^(k)

Iterate steps 2 – 5 until k = k_stop. The value k_stop is determined via cross-validation of the mean squared error of (Y − f̂^(k)) on the validation sample.

The boosting estimator is the sum of the base procedures scaled by ν. The scalar ν is a shrinkage parameter used to avoid over-fitting. In general, good results are achieved with small ν, but the procedure is relatively insensitive to the size of ν. Of course, smaller ν will require the algorithm to run a larger number of iterations. Note that that model can be written as

$${\widehat{f}}^{(k)}=\nu \sum _{k=1}^k{\widehat{g}}^{(k)}+{\widehat{f}}^{(0)}.$$

Step 3 is

$$g^{(k)}={\widehat{\beta }}_b{X}_b,$$

where

$$b=\underset{1\le j\le J}{argmin}\sum _i{(R_i^{(k-1)}-{\widehat{\beta }}_j{X}_{ij})}^2.$$

We select the predictor at iteration k in the simple linear model setting, which implies that we pick the predictor X_j which is most highly correlated with the residuals R^(k−1) from iteration k − 1. Note that the predictors X_j used at consecutive steps can be the same or different (thus formally we should add an additional superscript ^k to X_j, which we omit for simplicity). In the remainder we assume that the candidates X_j are the same at each step; in some applications the X_j are changing during the procedure, for example when splines or regression trees on the X_j are considered.

The fitted function is updated in a linear fashion; as the number of steps of the algorithm gets large the estimates converge to the least squares solution. The coefficient estimates are added at each iteration as well; the coefficient associated with the X_b at that step is updated. Therefore,

$${\widehat{\beta }}^{(k)}={\widehat{\beta }}^{(k-1)}+\nu {\widehat{\beta }}_b;$$

so we can also write

$${\widehat{f}}^{(k)}=\sum _j{\widehat{\beta }}_j^{(k-1)}{X}_j.$$ (1)

2.2. Dedicated boosting

For ease of notation we will assume that we are looking for an environmental effect that may depend on multiple environmental variables E_t = {E₁, …, E_p} that modifies a genetic single nucleotide polymorphism (SNP) effect G on a regression outcome Y.

Let Y be a n × 1 continuous response vector and G an n × 1 vector be a SNP of interest. (We discuss extension of the dedicated boosting algorithm to a binary response Y in the discussion.) Let E be a n × p matrix of environmental variables. Let the matrix of potential interaction factors be I = G × E. We refer to M = (G, E₁, …, E_p) as the set of main effects and I = (I₁, …, I_p) as the set of interactions. We start by standardizing all continuous environmental variables to mean 0 and variance 1 prior to constructing the matrix of interactions with categorical variables transformed to 0/1. Results are transformed later back to the original scale. To be able to focus on the interaction space, the main predictors are regressed out of both the response variable and the interactions up-front. The L₂ boosting procedure described in Section 2.1 is then applied to the resulting residuals, using the residuals of I as the predictors X_j. In particular, the dedicated boosting procedure is now:

1. Regress the main effects out of the outcome Y and the interaction terms I

   $$Y={\sum }_{j=1}^{p+1}{\widehat{\alpha }}_j{M}_j+\mathit{res}(Y),$$ (2)

   $$\begin{array}{c}{I}_1={\sum }_{j=1}^{p+1}{\widehat{\gamma }}_{j1}{M}_j+\mathit{res}(I_1),\\ \cdots \end{array}$$ (3)

   $$I_p={\sum }_{j=1}^{p+1}{\widehat{\gamma }}_{jp}{M}_j+\mathit{res}(I_p),$$ (4)

   where the notation res(Z) is used to indicate the residuals of the regression model with Z as response and the main effects M as predictors. These models are fit using ordinary least squares.

2. Apply the L₂ boosting procedure with outcome res(Y) and predictor set res(I₁), …, res(I_p). In particular, let

   $$\mathit{res}(Y)=\sum _{j=1}^p{\widehat{\beta }}_j^{(k)}\mathit{res}(I_j)+\mathit{residuals},$$

   be the equivalent of (1) for the L₂ boosting procedure, and let β̂^(k) be the coefficients from the boosting procedure.

Then the fitted values of the whole boosting algorithm can be retrieved by adding ${\sum }_{j=1}^p{\widehat{\beta }}_j^{(k)}$ to (Y − res(Y)), so that the fit of the dedicated boosting solution can be expressed as

$$\sum _{j=1}^{p+1}{\widehat{\alpha }}_j{M}_j+\sum _{t=1}^p{\widehat{\beta }}_t^{(k)}\left(I_t-\sum _{j=1}^{p+1}{\widehat{\gamma }}_{jt}{M}_j\right).$$

We see that the interaction coefficients are identical to the boosting coefficients β̂^(k). Because we applied boosting to the residuals, the main effect coefficient for M_j becomes ${\widehat{\alpha }}_j+{\sum }_{t=1}^p{\widehat{\beta }}_t^{(k)}{\widehat{\gamma }}_{jt}$.

In this manuscript we do not consider interactions between environmental variables. If such interactions are known a priori we would regress them out together with the main effects. Our interest lies in modifiers of a particular gene and we are not looking for interactions between environmental factors. However, the method we propose can also be used to explore interactions between a specific gene with several other genes. While the examples in this paper focus only on one SNP at a time and the potential interactions between that SNP and the environmental factors, multiple SNPs and their pairwise interactions can also be added. The algorithm will be applied in the same way. All main effects including the SNPs under consideration and all environment factors will be regressed out of the outcome variable and the gene-environment and gene-gene interaction terms. The boosting algorithm will then be applied with both gene-environment and gene-gene interactions are learners.

3. WHI data

The Women’s Health Initiative (WHI) is a long-term national health study that focuses on strategies for preventing chronic diseases, such as heart disease, breast and colorectal cancer and fracture in postmenopausal women. The WHI consisted of an observational study of 93,773 postmenopausal women and four clinical trials studying various interventions in 68,035 postmenopausal women [11]. Participants were recruited between 1992 and 1998. The active intervention of the clinical trials was stopped between 2002 and 2005 (e.g. [12],[13]). Follow-up of subjects is ongoing.

At time of enrollment in the study, extensive environmental exposure data on WHI participants were collected. A blood collection also took place. Using the DNA extracted from this blood collection, a number of genetic studies among WHI participants were initiated.

Population Architecture using Genomics and Epidemiology (PAGE) is a National Human Genome Research Institute (NHGRI) funded consortium that includes WHI, the Multi Ethnic Cohort, Causal Variants Across the Life Course (CALiCo, a consortium of five cardiovascular cohorts), and Epidemiologic Architecture for Genes Linked to Environment (EAGLE, which studies the NHANES cohort). As part of PAGE tens of thousands of subjects are genotyped for SNPs that were identified as genome-wide significant in other studies (“putative causal SNPs”) to study the genetic architecture of the phenotypes for which the SNPs were identified. Each of the four PAGE groups genotyped a number of SNPs associated with obesity or body mass index (BMI).

In the current paper we analyze the WHI-PAGE data on obesity consisting of 11 SNPs previously identified, mostly in GWAS studies, to be associated with obesity. Genotype, demographic, and environmental data assumed to be associated with obesity and collected at recruitment are available on 17,049 women. These data include age, current exercise (expressed as METs/week, a continuous variable), whether the subject exercised at each of age 18, 35, and 50 years (binary), education (eleven levels, treated as continuous), ever smoking (binary), current smoking (binary) and alcohol consumption (five levels, treated as continuous), ethnicity (Caucasian, African American, Hispanic, Asian/Pacific Islander, American Indian), region (three levels corresponding to North-South, as a surrogate for sun (vitamin D) exposure), and estimated percent of calories from fat, protein, and carbohydrates based on food-frequency questionnaires. The response is measured BMI (weight in kilograms divided by height in meters squared). The study design is described in detail by Fesinmeyer et al. “Genetic risk factors for body mass index and obesity in an ethnically diverse population: results from the Population Architecture using Genomics and Epidemiology (PAGE) Study” (submitted, 2011).

We want to investigate the possibility of effect modification of the association between each of the SNPs and BMI by some of the environmental and demographic variables. Because this effect modification is likely to be on a small scale, the dedicated boosting algorithm is a good candidate method of analysis. The particular composition of the group of environmental and demographic variables is only intended to provide an illustration of our methodology: we consider this a group of predictors that may be associated with BMI and that could be interacting with the SNP effect on BMI.

We present results for linear regression, stepwise model building using AIC and BIC model selection (described below), the lasso, globalboosttest, and dedicated boosting. The data are randomly divided into a training set with 13,049 subjects and a test set with 4,000 subjects. For each of the 11 SNPs, each method is applied to the training data set which contains a specific SNP, all the environmental and demographic variables and the interactions between the SNP and the other variables. We reserve the test set for evaluating the performance of the models. With the exception of the three FTO SNPs, the linkage disequilibrium as measured by the absolute value of the correlations between the SNPs is less than 0.12. The three FTO SNPs are in high linkage disequilibrium with correlations between 0.78 and 0.89.

To ensure comparability across methods, the main effects of all variables are included (unpenalized) in each method. The AIC and BIC model selection is done in a forward fashion starting with the main effects model and adding the interaction effects one at a time. A penalization for the lasso is applied only to the interaction terms, ensuring that all main effects are included in the final model. For dedicated boosting we standardize the continuous predictors. All results are back-transformed and presented on the original scale. For the simulations presented in Section 4, we also apply an AIC procedure which honors model hereditary constraints. In other words, interactions are considered only once both main effects have been selected by the stepwise algorithm to be included in the model. Results for BIC with hereditary constraint procedure are not presented since very rarely was an interaction term selected.

Based on our initial experiments we concluded that, like for the regular boosting algorithm, the value of ν is mostly irrelevant, as long as it is small enough. Therefore, we took ν = 0.1 throughout.

We started our analysis by applying the dedicated boosting algorithm for each of the SNPs, as well as to versions of the data with the response permuted. When comparing the number of steps that the dedicated boosting algorithm took on the real data, as selected with cross-validation, with the number of steps it took on the permuted data, it appeared that for SNP rs10938397 there was evidence of some possible interactions. For SNP rs17782313 there were maybe some interactions, but these interactions appeared to be weaker. In our analysis we focus on these two SNPs, providing some limited results for the other nine SNPs.

The interactions, as found by the dedicated boosting algorithm between rs10938397 and age, current exercise and exercise at 18, and Asian/Pacific Islander ethnicity (see Table 1) have a negative effect on BMI, while the interactions with percent calories from protein in the diet, education, smoking, and Hispanic, African American and American Indian ethnicity have a positive effect. For exercise at 18, education level, Hispanic and American Indian ethnicities the interactions are in the opposite direction of the main effects, while the rest of the selected interactions strengthen the corresponding main effects. We note that the magnitude of the coefficients from the dedicated boosting algorithm are smaller than those from (unpenalized) linear regression and stepwise model selection using AIC. The lasso coefficients are neither consistently smaller nor bigger than those of the boosting algorithm. The BIC method selects no interactions for this data set while the globalboosttest algorithm selects only one interaction term.

Table 1.

rs10938397: Comparison of interaction terms chosen by the five methods. The dedicated boosting algorithm took 92 steps. Cells that are labeled “-” mean that a particular approach did not select that variable. Each approach first fits (the same) main effects; “Full” refers to fitting all interaction terms using a linear model; “GlobalB” is the globallboosttest algorithm; “Boosting” is the dedicated boosting algorithm.

	Main Effects			Interaction Effects
	Estimate	Std. Error	p-value	Full	AIC	BIC	Lasso	GlobalB	Boosting
(Intercept)	40.597	1.928	< 0.001
rs10938397	0.209	0.082	0.011
Age	−0.195	0.008	< 0.001	−0.016	−0.018	-	-	-	−0.014
Amount of exercise	−0.066	0.005	< 0.001	−0.013	−0.013	-	−0.009	-	−0.010
Exercise at 18	1.387	0.138	< 0.001	−0.358	−0.318	-	−0.227	-	−0.215
Exercise at 35	0.345	0.147	0.019	0.074	-	-	-	-	-
Exercise at 50	−0.518	0.134	< 0.001	−0.067	-	-	−0.005	-	-
% Calories from carbo.	−0.007	0.017	0.665	−0.002	-	-	-	-	-
% Calories from protein	0.183	0.024	< 0.001	0.031	-	-	-	-	0.016
% Calories from fat	0.096	0.019	< 0.001	−0.005	-	-	-	-	-
Education level	−0.359	0.030	< 0.001	0.093	0.091	-	0.041	-	0.060
Ever smoking	0.401	0.121	0.001	0.278	0.261	-	0.191	-	0.164
Current smoking	−3.153	0.218	< 0.001	−0.093	-	-	-	-	-
Alcohol	−0.612	0.055	< 0.001	−0.007	-	-	-	-	-
Hispanic	−0.329	0.216	0.127	0.263	-	-	0.143	-	0.019
African American	2.532	0.160	< 0.001	0.525	0.469	-	0.467	0.030	0.362
Asian/Pacific Islander	−3.936	0.275	< 0.001	−0.389	-	-	−0.269	-	−0.229
American Indian	−0.603	0.565	0.286	1.336	1.308	-	0.991	-	0.816
Region middle	−0.315	0.144	0.029	−0.080	-	-	-	-	-
Region south	−0.361	0.137	0.008	−0.069	-	-	-	-	-

In Table 2 we present results for SNP rs17782313. We again note that for those variables where AIC and boosting selected the same terms, the boosting coefficients are smaller than the AIC coefficients. For this SNP, the group of variables selected by dedicated boosting include age, current exercise, exercise at 18 and 35 years of age, percent calories from carbohydrates in the diet, smoking, and Hispanic and African American ethnicity. Of these smoking and African American ethnicity are in the opposite direction of the corresponding main effects.

Table 2.

rs17782313: Comparison of interaction terms chosen by the five methods. The dedicated boosting algorithm took 63 steps. Cells that are labeled “-” mean that a particular approach did not select that variable. Each approach first fits (the same) main effects; “Full” refers to fitting all interaction terms using a linear model; “GlobalB” is the globallboosttest algorithm; “Boosting” is the dedicated boosting algorithm.

	Main Effects			Interaction Effects
	Estimate	Std. Error	p-value	Full	AIC	BIC	Lasso	GlobalB	Boosting
(Intercept)	40.730	1.927	< 0.001
rs17782313	0.185	0.094	0.049
Age	−0.195	0.008	< 0.001	−0.034	−0.035	-	-	-	−0.018
Amount of exercise	−0.066	0.005	< 0.001	−0.009	-	-	-	-	−0.004
Exercise at 18	1.382	0.138	< 0.001	0.218	0.327	-	-	-	0.123
Exercise at 35	0.352	0.147	0.017	0.166	-	-	-	-	0.075
Exercise at 50	−0.517	0.134	< 0.001	0.048	-	-	-	-	-
% Calories from carbo.	−0.008	0.017	0.656	−0.010	−0.019	-	-	-	−0.010
% Calories form protein	0.183	0.024	< 0.001	0.015	-	-	-	-	-
% Calories from fat	0.096	0.019	< 0.001	0.006	-	-	-	-	-
Education level	−0.360	0.030	< 0.001	−0.021	-	-	-	-	-
Ever smoking	0.398	0.121	0.001	−0.572	−0.558	-	-	-	−0.368
Current smoking	−3.157	0.218	< 0.001	0.234	-	-	-	-	-
Alcohol	−0.611	0.055	< 0.001	−0.010	-	-	-	-	-
Hispanic	−0.320	0.216	0.139	−0.861	−0.811	-	-	-	−0.352
African American	2.440	0.157	< 0.001	−0.473	−0.441	-	-	0.058	−0.152
Asian/Pacific Islander	−3.984	0.274	< 0.001	0.165	-	-	-	-	-
American Indian	−0.610	0.565	0.280	−0.066	-	-	-	-	-
Region middle	−0.316	0.144	0.028	−0.003	-	-	-	-	-
Region south	−0.361	0.137	0.008	0.026	-	-	-	-	-

Table 3 summarizes for each of the 11 SNPs the performance of each of the models. It also includes the minor allele frequencies of each of the SNPs included in the study. We compute the vector $U={\sum }_{j=1}^{18}{\widehat{\beta }}_j\text{res}(I_j)$, where β̂ is the set of estimated interaction terms for the model and res(I_j) are the residuals left from regressing the main effects out of interaction term I_j in the test data set (see (3)–(4)). We compute res(Y) (2), the test set BMI residual vector after regressing out the main effects and the residual sums of squares $\mathit{RSS}={\sum }_{i=1}^{4000}{(\text{res}(Y_i)-U_i)}^2$. We report RSS − RSS_main, the residual sums of squares less the residual sums of squares of the main effects model. We compute this quantity for a random split of the data in a test set of 4,000 subjects and a training set of 13,049 subjects and nine random splits with the same division and average the resulting RSS − RSS_main over all ten splits.

Table 3.

RSS for the 11 SNPs from the WHI-PAGE data based on the 5 examined approaches. Results are averages of ten random test sets with 4000 subjects that were not used in any aspect of the model building or selection; “Full” refers to fitting all interaction terms using a linear model; “GlobalB” is the globallboosttest algorithm; “Boosting” is the dedicated boosting algorithm. In bold is the best performing method for each SNP.

Nearest Gene	SNP	Minor allele freq.	Full	AIC	BIC	Lasso	GlobalB	Boosting
MTCH2	rs10838738	0.297	0.0272	0.0130	0.0000	−0.0006	0.0005	−0.0017
GNPDA2	rs10938397	0.387	0.0100	0.0019	0.0096	0.0182	−0.0015	0.0013
KCTD15	rs11084753	0.355	0.0058	0.0012	0.0091	−0.0029	0.0030	−0.0108
MC4R	rs17782313	0.236	0.0677	0.0534	0.0000	0.0010	0.0001	0.0124
NEGR1	rs2815752	0.367	0.0805	0.0551	0.0000	0.0017	−0.0018	0.0060
CTNNBL1	rs6013029	0.093	0.0762	0.0433	0.0000	0.0000	−0.0020	0.0049
TMEM18	rs6548238	0.155	0.0613	0.0533	0.0000	0.0072	0.0026	0.0095
SH2B1	rs7498665	0.355	0.0440	0.0062	0.0128	−0.0003	−0.0011	−0.0095
FTO	rs3751812	0.327	0.0360	0.0440	0.0110	0.0085	0.0039	0.0050
FTO	rs8050136	0.394	0.0054	−0.0048	0.0000	−0.0049	0.0050	−0.0051
FTO	rs9930506	0.378	0.0605	0.0328	0.0000	0.0000	0.0046	−0.0023

As far as RSS is concerned, globalboosttest and dedicated boosting have the best performance (Table 3), but while close dedicated boosting identifies more interactions that appear real. globalboosttest identifies some interactions but also misses some. In fact, we will see later in the simulation study that globalboosttest has fewer true positives and fewer false positives. For SNP rs17782313 the lowest error is achieved with the BIC model, which selected no interactions for any of the splits. This would signify that even though we have some evidence that dedicated boosting is selecting interaction terms that are associated with the outcome, these interactions are not strong enough to improve the predictive properties of the model.

Permutation Test

Next we discuss the results of a permutation test for SNPs rs10938397 and rs17782313. We permuted the response variable BMI 1000 times after the main effects were regressed out to generate data under the null hypothesis of no interaction effects. Each time we applied the dedicated boosting algorithm using the permutation of BMI as response variable. Note that this is not a typical global permutation test, as we are only removing the interactions, rather than removing both main effects and interactions.

Table 4 summarizes the results for SNP rs10938397. For each of the covariates that were selected by the dedicated boosting algorithm in the original analysis, we count how often the variable is selected during the 1000 permutations, and, if it is selected, whether the absolute value of the coefficient β̂ is larger during the simulations than the original version or that it is smaller. We do the same for the variables that were not selected, except that here if a variable is selected during the permutations, its coefficient is larger in magnitude than the original analysis, since in that case the coefficient was zero.

Table 4.

rs10938397: Results for permutation study based on 1000 permutations of the null. While the dedicated boosting algorithm on the original data took 92 steps, only 95 out of the 1000 permutations had number of steps greater than or equal to 20 and none had number of steps larger than 85.

	Coef	Selected	Larger coef	Smaller coef
Age	−0.014	122	14	108
Amount of exercise	−0.010	126	4	122
Exercise at age 18	−0.215	119	8	111
% Calories from protein	0.016	126	43	83
Education level	0.060	115	5	110
Ever smoking	0.164	120	20	100
Hispanic	0.019	121	121	0
African American	0.362	127	4	123
Asian/Pacific Islander	−0.229	144	50	94
American Indian	0.816	123	20	103
Exercise at age 35		105	105	-
Exercise at age 50		131	131	-
% Calories from carbo.		67	67	-
% Calories from fat		100	100	-
Current smoking		129	129	-
Alcohol		107	107	-
Region middle		127	127	-
Region south		116	116	-

With the exception of Hispanic ethnicity the number of permutation models which included a larger coefficient than the original coefficient were less than or equal to 50. The Hispanic ethnicity interaction term had a larger coefficient in 121 of the permuted data samples. This suggests that if there were no true interactions for this SNP, as is the case for the permutated data sets, results from the dedicated boosting model would be unlikely to be observed for all covariates that were selected except for Hispanic ethnicity. On the other hand, for all the covariates that were not selected in the original model, the analysis of the permuted data sets frequently selected a larger coefficient.

We also note that in none of the 1000 permutations the boosting algorithm took as many steps as the algorithm took on the original data. This suggests that the dedicated boosting algorithm indeed found a “signal” that is beyond noise.

Table 5 presents the permutation results for SNP rs17782313, organized the same way as Table 4. The interactions for exercise and exercise at age 35 resulted in coefficients more extreme than the original in more than 50 of the permutations, suggesting that these covariates may have ended up by chance in the original model. The rest of the interactions had coefficients large enough to make them unlikely if there were truly no effect modifications present for this SNP.

Table 5.

rs17782313: Results for permutation study based on 1000 permutations of the null. On the original data, the dedicated boosting algorithm took 63 steps; 14 permutation runs had number of steps greater than or equal to 63.

	Coef	Selected	Larger coef	Smaller coef
Age	−0.018	122	6	116
Amount of exercise	−0.004	132	59	73
Exercise at age 18	0.123	139	47	92
Exercise at age 35	0.075	122	63	59
% Calories from carbo.	−0.010	93	18	75
Ever smoking	−0.368	134	2	132
Hispanic	−0.352	124	27	97
African American	−0.152	130	43	87
Exercise at age 50		130	130	-
% Calories from protein		148	148	-
% Calories from fat		100	100	-
Education level		149	149	-
Current smoking		153	153	-
Alcohol		126	126	-
Asian/Pacific Islander		152	152	-
American Indian		146	146	-
Region middle		135	135	-
Region south		137	137	-

In 14 out of the 1000 permutations the dedicated boosting algorithm took as many steps or more as the algorithm took on the real data. This suggests that there likely is a true interaction effect for this data, but that the signal is not as strong as for rs10938397.

4. Simulation study

We conducted a simulation study to further examine the performance of dedicated boosting based on the results that we obtained for SNP rs10938397 on the analysis of the WHI data. In particular, we simulate only a new response variable and use the original data set for the prediction variables. Results are presented for the least squares model without model selection, AIC and BIC based forward stepwise model selection of interactions, the lasso, applied to the interaction terms only, globalboosttest, AIC with hereditary constraint and dedicated boosting. We consider the model

$$Y=\underset{\text{main}\text{effect}}{\underbrace{{\gamma }_0+{\gamma }_{1}G+\sum _{j=2}^{19}{\gamma }_j{E}_j}}+\underset{\begin{array}{c}\text{interaction}\\ [\text{via}\text{dedicated}\text{boosting}]\end{array}}{\underbrace{\sum _{j=1}^{18}{\beta }_j(E_j\times G)}}+\epsilon$$

where

$$\epsilon =N(0,{6.42}^2);$$

note that 6.42 is the residual variance in the WHI data.

The β coefficients were taken from the dedicated boosting results in Table 1 and the γ coefficients are the main effects from the same table. For the interactions there are 10 non-zero coefficients and 8 zero coefficients. In particular, the non-zero coefficients were

$$\beta =(-0.014,-0.010,-0.215,0.016,0.060,0.164,0.019,0.362,-0.229,0.816),$$

for age, amount of exercise, exercise at 18, % of calories from protein, education level, ever smoking, Hispanic, African American, and American Indian ethnicity, and region middle, respectively. Note that these are the coefficients shown in Table 4. The random error is based on the residual variance of the same model.

To compare the five methods we compute

$$U=\sum _{j=1}^{18}{\widehat{\beta }}_j\text{res}(I_j)$$

and compare it to the true linear combination (TLC) of the interactions

$$\mathit{TLC}=\sum _{j=1}^{18}{\beta }_j\text{res}(I_j),$$

where res(I) represent the residuals from the linear regression models of the main effects on the interaction terms. We report the MIaSE = n⁻¹ Σ (TLC − U)², an overall measure of the distance between the true and fitted coefficients for each model.

Table 6 presents the results from 1000 replications of the simulation model. We note that the dedicated boosting algorithm has the best performance out of all the methods with respect to RSS. For the 10 terms with non-zero β’s we report on average how many times the model assigned non-zero coefficients (“True positive”). The dedicated boosting algorithm has the highest proportion of true positives averaged over the 1000 runs. The procedure assigned a non-zero coefficient to the Hispanic variable only 21% of the times. The row “False positive” counts how often one of the eight covariates with zero coefficients was selected. Not surprisingly, the BIC model, which rarely picked any interactions, has the best false positive performance. Dedicated boosting has less false positives than the lasso, but slightly more than AIC. Globalboosttest performs similarly to BIC, with very false positives and very few true positives.

Table 6.

Simulation study results based on 1000 replications. “Full” refers to fitting all interaction terms using a linear model; “GlobalB” is the globallboosttest algorithm; “HAIC” is the hereditary constraints AIC model; “Boosting” is the dedicated boosting algorithm.

	Full	AIC	HAIC	BIC	Lasso	GlobalB	Boosting
Non-zero coefficients
Age	1.00	0.46	0.14	0.09	0.09	0.00	0.57
Amount of exercise	1.00	0.49	0.11	0.05	0.47	0.18	0.53
Exercise at age 18	1.00	0.42	0.11	0.02	0.40	0.12	0.44
% Calories from protein	1.00	0.25	0.06	0.01	0.11	0.00	0.28
Education level	1.00	0.50	0.13	0.03	0.22	0.00	0.50
Ever smoking	1.00	0.33	0.08	0.03	0.41	0.10	0.42
Hispanic	1.00	0.16	0.02	0.00	0.29	0.04	0.21
African American	1.00	0.60	0.16	0.11	0.66	0.53	0.66
Asian/Pacific Islander	1.00	0.23	0.06	0.01	0.39	0.13	0.30
American Indian	1.00	0.38	0.01	0.02	0.46	0.19	0.43
Zero coefficients
Exercise at age 35	1.00	0.22	0.04	0.00	0.25	0.03	0.22
Exercise at age 50	1.00	0.17	0.04	0.00	0.28	0.05	0.24
% Calories from carbo.	1.00	0.26	0.03	0.00	0.06	0.00	0.19
% Calories from fat	1.00	0.26	0.03	0.00	0.10	0.00	0.17
Current smoking	1.00	0.17	0.04	0.01	0.32	0.06	0.23
Alcohol	1.00	0.20	0.05	0.00	0.21	0.01	0.24
Region middle	1.00	0.16	0.02	0.00	0.29	0.03	0.23
Region south	1.00	0.15	0.03	0.00	0.26	0.02	0.22
Overall summary
MIaSE	0.0570	0.0532	0.0440	0.0456	0.0380	0.0395	0.0312
True Positive	1.0000	0.3819	0.0879	0.0369	0.3492	0.1293	0.4337
False Positive	1.0000	0.1979	0.0331	0.0033	0.2218	0.0249	0.2172

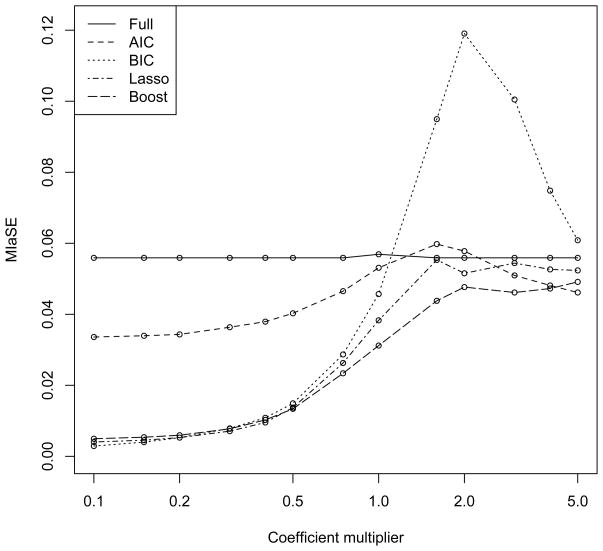
Further, we investigate the performance of the dedicated boosting algorithm in a range of scenarios, varying from very weak to very strong interaction effects. Figure 1 presents the MIaSE based on the same simulation setup as above. However, all of the interaction coefficients are multiplied by a factor between 0.1 and 5. Thus, the coefficients in these models are aβ_j where a is between 0.1 and 5, and the β_j are the same as above. For these models still a fixed number of the environmental factors (but not all) have interactions. The strength of these interactions varies between very weak and very strong. Results are based on 50 simulations. As expected the BIC model performs very well when the interaction terms are very small, as it in general rarely selects interactions for inclusion in the model. All methods perform very similarly once the interaction effects are large, as essentially every method finds the right model. Boosting outperforms the other methods for a range of values of the multiplier a between 0.75 and 3, which importantly contains a = 1 which corresponds to the interaction effects seen in the real data.

Figure 1.

Simulation study results based on 50 replications for varying magnitude of interaction terms. “Full” refers to fitting all interaction terms using a linear model; “Boosting” is the dedicated boosting algorithm.

5. Discussion

In many genetic epidemiological studies, it is not just of interest to identify SNPs that are associated with particular phenotypes, but it is also of interest to identify environmental and demographical factors that modify these genetic effects. The search for such effect modifiers has often had limited success, both because the effect modifications are small, and because various of the variables are measured with error.

Dedicated boosting is a variation of L₂ boosting which focuses on the search for effect modifiers. We were interested in developing a method that is able to pick out ensembles of weaker effects of covariates that interact with another risk factor, such as a SNP. Well known methods such as AIC and BIC model selection with stepwise model building can be modified to be used for finding interactions. However, when using these methods, the effect of the interactions needs to be fairly strong for them to be included in the final model. Penalized regression methods, such as the lasso and boosting are well suited for finding solutions which consist of combinations of weaker effects. Our interest was in adapting such a method for low signal in a search for interactions.

In a simulation study our method outperforms the lasso, globalboosttest, AIC, and BIC model selection procedures as having the lowest test error. In the WHI-PAGE data example the dedicated boosting method was able to pick out two SNPs for which effect modification appears present. The performance was evaluated on an independent test set and the results are promising. For most SNPs no effect modification was detected by any of the methods. In these cases the performance of dedicated boosting is not markedly different than the rest of the methods. However, when some effect modification is present dedicated boosting gives lower error rates on the independent test set, as was the case with SNP rs10938397.

Future work that we intend to pursue includes extending our approach to settings beyond linear regression to binary outcomes using a binomial loss function and beyond linear covariate effects, and to extend ways to “export” the fitted profiles that identify the effect modifiers from one epidemiological cohort to another cohort. This may in fact turn out to be quite challenging as environmental covariates are often measured slightly different in different cohorts. The PAGE consortium will be an excellent place to apply such a method, as other cohorts that are part of this consortium have the same outcome, the same SNPs, and similar covariates measured.