Improved Encoding Pulses for Bloch-Siegert $B_1^{+}$ Mapping

Abstract

A new family of optimized encoding pulses for Bloch-Siegert (BS) $\left|B_1^{+}\right|$ mapping is introduced, as well as an algorithm to design them. The pulses are designed by numerical maximization of BS sequence sensitivity, subject to constraints that ensure low on-resonance excitation. The pulses are in all cases characterized by a constant envelope and U-shaped frequency sweep. They are validated in simulations, 7 T in vivo experiments, and an experiment to measure their on-resonance excitation, and are compared to a Fermi pulse conventionally used in the BS method. The pulses are shown to produce larger phase shifts in a shorter time and with lower on-resonance excitation than the Fermi pulse, which results in lower SAR and improved $\left|B_1^{+}\right|$ accuracy in areas of the body with large main field inhomogeneities.

1. Introduction

For magnetic resonance imaging at high field (≥ 3 T), and in parallel transmission [1, 2], it is important to consider subject-dependent spatial variations of the magnitude of the transmit RF magnetic field $\left(\left|B_1^{+}\right|\right)$, and many methods have been developed to measure $\left|B_1^{+}\right|$ maps. Recently, a $\left|B_1^{+}\right|$ field mapping method based on the Bloch-Siegert (BS) shift has been proposed [3], which uses a high-amplitude RF pulse played with a frequency offset far from resonance to impart a phase shift in the MR signal that is approximately proportional to ${\left|B_1^{+}\right|}^2$. The method has received significant attention for its ease of implementation and robustness to relaxation effects. It is also accurate and sensitive over a relatively wide range of $\left|B_1^{+}\right|$ and inhomogeneities in the main (B₀) field. While other phase-based methods exist (such as Ref. [4]), prior to this method most $\left|B_1^{+}\right|$ mapping was performed using magnitude-based techniques [5, 6, 7] that suffer from poor dynamic range and are sensitive to errors due to T₁ relaxation, necessitating relatively long repetition times (TRs) that limit their speed and applicability. Various T₁-insensitive AFI and double angle methods have been introduced [8, 9], but these still generally require longer TRs than phase-based methods due to the large amount of gradient spoiling required [9] or the need to accomodate saturation modules [8].

However, BS $\left|B_1^{+}\right|$ mapping is challenging at 7 T and higher due to SAR limitations and signal loss resulting from the high amplitude and long duration of the $\left|B_1^{+}\right|$–encoding pulse used in the sequence (typically 4–6 ms at full RF power [10]). Hence, it is desirable to shorten the pulse while maintaining the sequence's sensitivity. The pulse also must negligibly tip on-resonant spins towards or away from the z-axis. To achieve this we propose a new method for BS pulse design in which both RF envelope and frequency waveforms are optimized to maximize sensitivity, subject to a constraint requiring negligible on-resonance excitation. Our method produces distinctive and interpretable waveforms. We present the results of simulations and in vivo (human head) and phantom experiments at 7 T to validate the performance of the designed pulses, in terms of BS phase shift and on-resonance excitation. The pulses are compared to Fermi pulses conventionally used in BS $\left|B_1^{+}\right|$ mapping [3]. Results show that the designed pulses possess higher $\left|B_1^{+}\right|$ sensitivity than much longer Fermi pulses, while producing similar or lower on-resonance excitation. We also show that the shorter duration of thepulses enables BS $\left|B_1^{+}\right|$ mapping in anatomical regions with large B₀ inhomogeneities, such as the lower brain at 7 T.

2. Theory

A BS acquisition is typically based on a gradient-recalled echo (GRE) sequence and comprises an excitation pulse, followed by the off-resonance $\left|B_1^{+}\right|$-encoding pulse that is surrounded by bipolar crusher gradients, followed by the signal readout. Denoting the magnetization after the excitation pulse as $(M_{\mathit{\text{xy}}}^{-},M_z^{-})$, the transverse magnetization after the $\left|B_1^{+}\right|$-encoding pulse and its crushers is [11]:

$$M_{\mathit{\text{xy}}}^{+}={\text{(}{\alpha }^{\ast }\text{)}}^{\text{2}}{M}_{\mathit{\text{xy}}}^{-}-{\beta }^2{M}_{\mathit{\text{xy}}}^{-\ast }{e}^{i2\phi (\overrightarrow{x})}+2{\alpha }^{\ast }\beta M_z^{-}{e}^{i\phi (\overrightarrow{x})},$$ (1)

where α and β are the net spinor parameters of the $\left|B_1^{+}\right|$-encoding pulse, and φ(x⃗) is the phase applied by each crusher gradient. The crusher gradients are intended to attenuate the second two terms in Eq. 1, which correspond to magnetization flipped towards and away from the z-axis. The goal of a BS $\left|B_1^{+}\right|$-encoding pulse is to impart as large a phase shift as possible to $M_{\mathit{\text{xy}}}^{-}$ per unit $\left|B_1^{+}\right|$, without tipping magnetization towards or away from the z-axis. In terms of spinor parameters, these requirements correspond to an α parameter with magnitude one and a phase that changes as rapidly as possible as a function of $\left|B_1^{+}\right|$, and zero β.

For a fixed pulse duration, we define the optimal BS pulse as the one that has maximum average sensitivity (the derivative of ∠α with respect to $\left|B_1^{+}\right|$) over a target $\left|B_1^{+}\right|$ range, and satisfies a small |β| limit of β_max over that range, as well as over a specified range of off-resonance frequencies (Δf₀). Discretizing the pulse to N_t samples and the $\left|B_1^{+}\right|$ and Δf₀ axes to N_b1 and N_f0 points, respectively, we can state the corresponding pulse optimization problem as:

$$\begin{array}{c}\text{maximize}{\sum }_{i=\text{2}}^{N_{b1}}{\sum }_{j=1}^{N_{f0}}\angle \left({\alpha }_{i,j}{\alpha }_{i-1,j}^{\ast }\right)\\ \text{subject to}{a}_k^2\le 1k=1,\dots ,N_t\\ {\left|{\beta }_{\mathit{\text{ij}}}\right|}^2\le {\beta }_{\mathit{\text{max}}}^{2}i=1,\dots ,N_{b1},j=1,\dots ,N_{f0},\end{array}$$ (2)

where i and j index a discretized range of $\left|B_1^{+}\right|$ and Δf₀ values, $\mathit{\text{a}}={\left\{a_k\right\}}_{k=1}^{N_t}$ are the amplitudes of the RF pulse samples to be optimized, and $\mathit{\text{f}}={\left\{f_k\right\}}_{k=1}^{N_t}$ are the frequency offsets of the RF pulse samples to be optimized. α and β are implicitly dependent on a, f, $\left|B_1^{+}\right|$, and off-resonance frequency Δf₀. The maximized term in this problem is proportional to the average sensitivity of the pulse over the discretized $\left|B_1^{+}\right|$−Δf₀ grid, while the $|{\beta }_{ij}{|}^2\le {\beta }_{\mathit{\text{max}}}^2$ constraints ensure small excitation over the same range, and the $a_k^{\text{2}}\le 1$ constraints ensure that the resulting pulse is normalized. We note also that the problem in Eq. 2 is non-convex. For a given pulse (a, f) and ( $\left|B_1^{+}\right|$, Δf₀) pair, α and β can be calculated using a standard spin-domain RF pulse simulation code¹[11] to evaluate:

$$\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)=\left(\begin{array}{cc}cos\left({\theta }_{N_t}/2\right)& -\iota sin\left({\theta }_{N_t}/2\right)\\ -\iota sin\left({\theta }_{N_t}/2\right)& cos\left({\theta }_{N_t}/2\right)\end{array}\right)\left(\begin{array}{cc}{e}^{\iota \phi N_t/2}& 0\\ 0& e^{\iota \phi N_t/2}\end{array}\right)\cdots \left(\begin{array}{cc}cos\left({\theta }_1/2\right)& -\iota sin\left({\theta }_1/2\right)\\ -\iota sin\left({\theta }_1/2\right)& cos\left({\theta }_1/2\right)\end{array}\right)\left(\begin{array}{cc}{e}^{\iota {\phi }_1/2}& 0\\ 0& e^{\iota {\phi }_1/2}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right),$$ (3)

where ${\theta }_k\triangleq \gamma \left|B_1^{+}\right|a_k{\Delta }_t$, and ${\phi }_k\triangleq 2\pi {\Delta }_t\left(\Delta f_0+f_k\right)$.

3. Methods

3.1. Pulse designs

A 2 ms pulse duration was initially selected with time a step of Δ_t = 6.4 μs, yielding N_t = 312 amplitude and frequency samples to be optimized, for a total of 624 variables. The optimization was performed on a discretized $\left|B_1^{+}\right|$−Δf₀ grid spanning 1–20 μT and ±600 Hz with 1 μT and 15 Hz steps, respectively [10]. β_max was set to 0.01. The maximization problem was solved using the fmincon function in MATLAB (The Mathworks, Natick, USA), which was set to use an interior-point algorithm with a termination tolerance (‘TolX’) of 10⁻¹², and was initialized with a 2 ms Fermi pulse with a constant 4 kHz frequency offset. The frequency offset samples were optimized in units of kHz.

In addition to the 2 ms pulse we designed a library of pulses across a range of durations {0.5, 1.0, 1.5, 2.0} ms and resonance frequency bandwidths {600, 1200, 1800} Hz. The designs used the same β_max = 0.01 as the initial 2 ms pulse.

3.2. Simulations and Experiments

We performed simulations and experiments to compare the optimized 2 ms waveform to 2 ms block and 6 ms Fermi pulses with constant frequency offsets of 2.3 and 4 kHz, respectively. While the Fermi pulse is a common BS pulse selection, the block pulse was chosen as a comparison since it closely resembles our optimized pulses, yet as will be shown lacks subtle features that are critical to their performance.

3.2.1. Simulations

To compare the pulses' performance over wide $\left|B_1^{+}\right|$ and Δf₀ ranges, Bloch simulations were performed to calculate the BS phase shift and |β| of each pulse over a $\left|B_1^{+}\right|$ range of 0 to 25 μT and a ±1200 Hz Δf₀ range. We also used the simulation results to elucidate the optimized pulses' function.

3.2.2. In-Vivo Experiments

An adult volunteer was recruited to serve as an imaging subject for this study. All protocols were approved by the local Institutional Review Board (IRB). Experiments were conducted on a 7 T Philips Achieva whole-body scanner (Philips Healthcare, Cleveland, OH) based on a Magnex 90 cm magnet and a single-channel, volume quadrature transmit/receive head coil from Nova Medical (Wilmington, MA) with a 29 cm inner diameter. $\left|B_1^{+}\right|$ maps were acquired using the 6 ms/4 kHz Fermi and optimized 2 ms pulses. 2D scans of a central axial slice and a lower axial slice (2 mm slice thickness) were acquired with FOV 24×24 cm and matrix size 120×120, with TR/TE=1500 ms/shortest. The actual TE's thereby depended on the duration of the BS pulse (8.4 ms for the 6 ms Fermi pulse and 4.5 ms for the optimized 2 ms BS waveform). A pair of 1 ms crushers with maximum gradient amplitudes (33 mT/m) were placed around the BS pulses in all experiments. The two slices were chosen to best demonstrate the performance of the pulses in a typical range of $\left|B_1^{+}\right|$−Δf₀ values (central brain) and in areas were Δf₀ variations are especially large (lower brain). As is required in BS $\left|B_1^{+}\right|$ mapping, for each pulse and slice two images were acquired with opposite frequency offsets. To enable calculation of $\left|B_1^{+}\right|$ from the phase difference between these images and from Δf₀ maps, $\left|B_1^{+}\right|$ lookup tables were generated for the two pulses using high-resolution Bloch equation simulations (grid resolution: 0.1 μT, 1.5 Hz). Linear interpolation was then used to calculate $\left|B_1^{+}\right|$ at each image voxel from the lookup tables, phase differences and Δf₀ maps.

3.2.3. Experimental measurement of |β|

To validate that the optimized 2 ms pulse produces negligible on-resonance excitation (as measured by |β|), we performed an experiment to measure the Fermi, block, and optimized 2 ms pulses' |β| distribution in a phantom. To do this, two BS pulse sequences were used that are shown in Fig. 1. The signal magnitude for the sequence with bipolar G_z crushers (i.e. the standard GRE BS sequence) is:

Figure 1.

The gradient-recalled echo Bloch-Siegert sequence with a Fermi pulse and bipolar (solid) and unipolar (dashed) crushers used for measurement of Bloch-Siegert phase (bipolar) and residual on-resonance magnetization (unipolar and bipolar). Note that readout gradients are omitted.

$$\left|S_1\right|\approx \left|{\left({\alpha }^{\ast }\right)}^2\right|\left|M_{\mathit{\text{xy}}}^{-}\right|.$$ (4)

The signal equation for the sequence with unipolar crushers (a standard crushed spin echo sequence) is [11]:

$$\left|S_2\right|\approx \left|{\beta }^2\right|\left|M_{\mathit{\text{xy}}}^{-\ast }\right|$$ (5)

Taking the ratio of the signals and applying the spinor unitary condition (|α|² + |β|² = 1), yields:

$$\left|\frac{S_2}{S_1}\right|\approx \frac{{\left|\beta \right|}^2}{\left|{\left({\alpha }^{\ast }\right)}^2\right|}=\frac{{\left|\beta \right|}^2}{1-{\left|\beta \right|}^2},$$ (6)

which can be solved for |β|:

$$\left|\beta \right|\approx \sqrt{\frac{\left|S_2\right|}{\left|S_1\right|+\left|S_2\right|}}$$ (7)

A 17 cm diameter spherical dielectric phantom, containing realistic concentrations of common brain metabolites and doped with paramagnetic agent to reduce T₁ (T₁ ≈ 300 ms), was used to experimentally measure the |β| of each pulse. 10 averages were acquired. The TR was set to 1384 ms for all pulses, and the TE's were set to their minimum values for each pulse: 8.4 ms/4.5 ms/4.5 ms for Fermi/block/optimized.

4. Results

Figure 2 plots the 6 ms/4 kHz Fermi, 2 ms block, and optimized 2 ms pulses. The optimized 2 ms pulse has a block amplitude waveform, but a frequency waveform that sweeps in a ‘U’ shape from far away from resonance, to near-resonance, and back away from resonance. The frequency spikes at either end are present in all the optimized pulses and differentiate the pulses from a block pulse with a constant frequency offset. The optimized 2 ms waveform has 57% lower SAR $\left(\text{SAR}\propto {\sum }_{k=1}^{N_t}{a}_k^2\right)$ than the 6 ms Fermi pulse, but we will show that it induces larger BS phase shifts. The 2 ms block pulse was included in the simulations to show how critical the time-varying frequency sweep is to the optimized 2 ms pulse's performance.

Figure 2.

Comparison of pulse shapes. The 6 ms Fermi pulse (left) has a time-varying amplitude waveform that is tapered at the ends to reduce its bandwidth and prevent the excitation of on-resonance spins. It uses a constant frequency offset, which is relatively large (4 kHz here). A 2 ms block pulse with a constant frequency offset of 2.3 kHz (a least-squares fit of a constant frequency offset to the frequency waveform of the optimized 2 ms pulse) is shown in the middle. The optimized 2 ms pulse is plotted on the right. Note the characteristic constant amplitude shape and U-shaped frequency sweep. Figure 3 shows that the optimized 2 ms pulse has a similar sensitivity to the 6 ms/4 kHz Fermi pulse, despite its much shorter duration.

4.1. Simulations

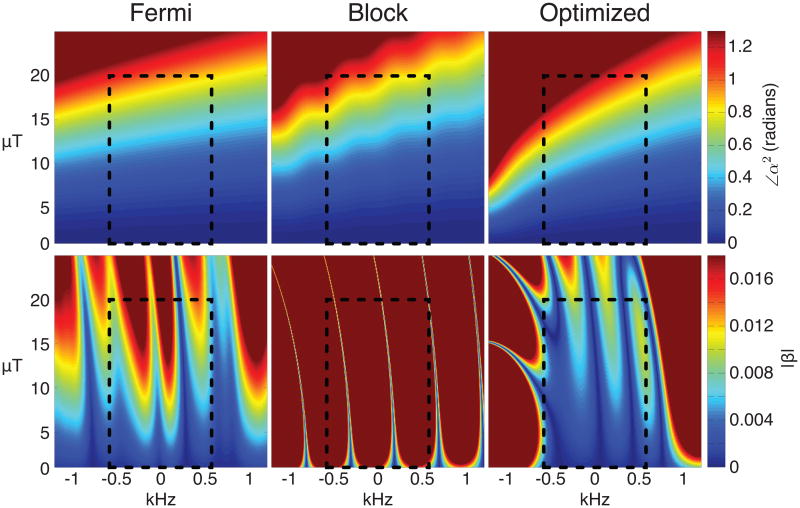
Figure 3 compares the on-resonance phase shift versus $\left|B_1^{+}\right|$ for each pulse, and Fig. 4 compares ∠α² and |β| for each pulse over wide $\left|B_1^{+}\right|$−Δf₀ ranges. Figure 3 shows that the optimized 2 ms pulse produces larger BS phase shifts than the other two pulses on-resonance. The K_BS values [3] of the pulses are 67.66 radians/(Gauss)² (6 ms/4 kHz Fermi), 49.51 radians/(Gauss)² (2 ms/2.3 ms block), and 69.85 radians/(Gauss)² (optimized 2 ms). The differences increase with $\left|B_1^{+}\right|$. The block pulse's phase shift is only slightly lower than the Fermi pulse's throughout the entire $\left|B_1^{+}\right|$ range. The top row of Fig. 4 shows that the optimized pulse produces larger phase shifts than the other two pulses throughout almost the entire $\left|B_1^{+}\right|$−Δf₀ grid. For fixed $\left|B_1^{+}\right|$, all pulses' phase shift increases with decreasing Δf₀. This is because each pulse has a strictly positive frequency offset, so that decreasing Δf₀ brings the pulses closer to resonance, resulting in a larger BS phase shift (Ref. [3], Equation 5). The bottom row shows that the optimized 2 ms pulse produces significantly smaller on-resonance excitation than the other two pulses. The mean/maximum |β| values for the three pulses within the 0–20 μT and ±600 Hz range over which the pulse was optimized 2 ms were: 0.008/0.028 (Fermi); 0.119/0.366 (block); 0.004/0.010 (optimized). The optimized 2 ms pulse satisfiedthe target β_max of 0.01.

Figure 3.

Simulated on-resonance BS phase shift ∠α² versus $\left|B_1^{+}\right|$ for the Fermi, block and optimized 2 ms pulses. The optimized 2 ms pulse produces larger phase shifts than the other two pulses.

Figure 4.

Simulated BS phase shift ∠α² and excitation |β| for the Fermi, block, and optimized 2 ms pulses across wide $\left|B_1^{+}\right|$ −Δf₀ ranges. The dashed black boxes demarcate the region over which the optimized 2 ms pulse was designed. The optimized 2 ms pulse produces larger BS phase shifts and smaller excitation than the other two pulses over the design region.

Figure 5 illustrates the optimized 2 ms pulse's operation via the evolution of the (on-resonance/Δf₀ = 0) phase shift ∠α², and |β| over the pulse duration. Just after the first frequency spike (time point 1), there is very little BS phase shift, but a large on-resonant excitation (|β|) is generated by the sharp (high-bandwidth) edge at the beginning of the pulse. The majority of the phase shift is built up in the middle of the pulse (between time points 1 and 2), but this also generates on-resonance excitation. After the second frequency spike the phase shift is only slightly larger but the on-resonance excitation is completely destroyed, suggesting that together the high frequency spikes on either end of the pulse serve to cancel excitation created throughout the pulse duration, but mostly by the envelope edges. Note that at the end of the pulse (time point 3) |β| is negligible across the entire simulated $\left|B_1^{+}\right|$ range and on-resonance (|β| ≤ 10⁻⁵, corresponding to flip angles of 0.0011 degrees or less).

Figure 5.

Evolution of on-resonance BS phase shift (∠α²) and excitation (|β|) over the duration of the optimized 2 ms pulse. Most of the BS phase shift arises in the middle of the pulse (between time points 1 and 2), when the offset frequency is low, but this is accompanied by undesirable on-resonant excitation (|β|) generated during this period and prior to time point 1. The frequency spikes at the beginning and end of the pulse spoil the |β| developed in the middle.

Figure 6 shows the resulting $\left|B_1^{+}\right|$ errors when a Δf₀ map is not used in conjunction with the BS phase difference to determine $\left|B_1^{+}\right|$ (i.e., a zero Δf₀ map is assumed in the lookup table operation). While the pattern of errors is similar for the Fermi and optimized pulses, the maximum error for the optimized pulse is approximately 5× higher than the maximum error for the Fermi pulse (1.39 μT and 0.27 μT, respectively). The higher error of the optimized pulse is also suggested by the pattern of phase shifts in Fig. 4, which shows that the optimized pulse's BS phase shift has a stronger dependence on Δf₀ than the Fermi pulse. However, over most of the $\left|B_1^{+}\right|$ and Δf₀ grid the optimized pulse's errors are less than 1 μT, and the largest errors are concentrated in regions where both $\left|B_1^{+}\right|$ and Δf₀ are high. Furthermore, we note that a) it is common to acquire Δf₀ maps for shimming [12], parallel transmit RF pulse design [13], and image reconstruction [14], and that these maps can be rapidly acquired [12], and that b) the Fermi pulses' longer minimum TE's and smaller phase shifts will generally lead to lower SNR in their phase difference maps, which will result in increased $\left|B_1^{+}\right|$ error relative to the optimized pulses' maps when a Δf₀ map is not used in the $\left|B_1^{+}\right|$ estimation.

Figure 6.

Simulated $\left|B_1^{+}\right|$ errors for the Fermi and optimized 2 ms pulses, when a zero Δf₀ map is assumed when calculating $\left|B_1^{+}\right|$ from measured BS phase differences. The shape of the errors are similar, but the maximum $\left|B_1^{+}\right|$ errors are larger for the optimized 2 ms pulse.

The frequency waveforms and mean sensitivities of the pulses in the optimized library are shown in Fig. 7. All of the pulses have the characteristic U-shaped frequency sweep. The optimized amplitude waveforms (not shown) were all approximately constant, with insignificant amplitude variations between 0.9988 and 0.9999. All of the pulses satisfied the β_max constraint. Figure 7 also shows that the average sensitivity (explicitly maximized though the optimization problem defined in Eq. 2) is a monotonically decreasing function of target stop-bandwidth and monotonically increasing function of BS pulse duration. Interestingly, doubling the duration more than doubles sensitivity while doubling of the stop-bandwidth does decrease the pulses' sensitivity but by a much smaller factor. A least-squares polynomial fit was performed for each frequency waveform, comprising even powers from 0 to 18. The fitted coefficients are given in Table 1, and the frequency waveforms can be reconstructed from these coefficients as:

Figure 7.

Frequency modulation (in kHz) for optimized BS pulses of different durations (dur) and bandwidth (BW) and their corresponding average sensitivity (units of rad/μT). Each of the pulses had a constant amplitude waveform.

Table 1.

Frequency waveform polynomial coefficients, mean sensitivities (s̄) and maximum |β| of the approximated waveforms.

Dur (ms)	0.5			1			1.5			2
BW (Hz)	600	1200	1800	600	1200	1800	600	1200	1800	600	1200	1800
c0	2.52	3.22	3.19	1.40	1.77	2.36	1.25	1.47	1.80	1.01	1.34	1.56
c2	-1.69e1	-5.33e1	-8.75e-1	4.51e1	2.57e1	-2.67e1	-2.73e1	2.00e1	5.26	6.09	-2.10e1	3.89e1
c4	1.12e3	2.49e3	1.08e3	-2.49e3	-1.66e3	-1.12e3	2.98e3	-1.30e3	-2.63e2	-4.81e2	2.34e3	-3.81e3
c6	-4.05e4	-8.03e4	-6.11e4	8.17e4	7.99e4	1.52e5	-1.25e5	3.32e4	1.92e4	1.30e4	-8.82e4	1.44e5
c8	9.38e5	1.71e6	1.50e6	-1.67e6	-2.07e6	-4.59e6	2.86e6	-3.06e5	-5.83e5	-3.91e4	1.73e6	-2.48e6
c10	-1.26e7	-2.20e7	-1.95e7	2.11e7	2.98e7	6.72e7	-3.79e7	-3.50e5	8.36e6	-2.55e6	-2.02e7	2.07e7
c12	9.91e7	1.70e8	1.44e8	-1.64e8	-2.46e8	-5.46e8	2.97e8	2.83e7	-5.97e7	4.00e7	1.50e8	-6.89e7
c14	-4.49e8	-7.62e8	-6.05e8	7.58e8	1.16e9	2.51e9	-1.36e9	-2.24e8	2.04e8	-2.61e8	-6.89e8	-7.26e7
c16	1.08e9	1.82e9	1.34e9	-1.89e9	-2.90e9	-6.08e9	-3.36e9	7.61e8	-2.61e8	8.13e8	1.78e9	1.02e9
c18	-1.07e9	-1.77e9	-1.22e9	1.94e9	2.96e9	6.03e9	-3.44e9	-9.82e8	-2.49e7	-9.93e8	-1.96e9	-1.78e9
s̄ (rad/μT)	0.012	0.010	0.009	0.034	0.030	0.027	0.064	0.055	0.049	0.097	0.083	0.073
max |β|	0.010	0.010	0.010	0.010	0.010	0.011	0.011	0.010	0.011	0.011	0.012	0.013

$$f\left(t\right)=c_0+c_2{\left(\frac{t}{T}\right)}^2+\cdots +c_{18}{\left(\frac{t}{T}\right)}^{18},$$ (8)

where f(t) is in units of kHz, T is the duration of each pulse, and t ∈ (−T/2,T/2). Table 1 also shows the mean sensitivities (s̄) and maximum |β| of the fitted waveforms, when paired with constant amplitude waveforms. In comparison with the mean sensitivities of the original pulses (shown in Fig. 7), the sensitivities are not significantly affected, and the maximum |β| values are only slightly higher in some cases.

4.2. In-Vivo Experiments

Figure 8 shows magnitude images, $\left|B_1^{+}\right|$ maps and the Δf₀ map of the central axial brain slice. Indicated by the arrows in that figure, the magnitude images of the Fermi pulse contain significant ringing along the Δf₀ gradient in the front of the brain. The ringing agrees well with ringing along the Δf₀ axis in the Fermi pulse's simulated |β| pattern, suggesting that it may be caused by magnetization being significantly flipped towards or away from the z-axis by the Fermi pulse itself. In spite of the ringing though, the $\left|B_1^{+}\right|$ maps for the two pulses largely agree. Figure 9 shows magnitude images, $\left|B_1^{+}\right|$ maps and the Δf₀ map of the lower axial slice. The magnitude images of the Fermi pulse, in particular the negative frequency image, again contains ringing in the front of the brain, and in this slice the ringing significantly degrades the $\left|B_1^{+}\right|$ map in the front of the brain. In addition, the 4 ms longer TE of the Fermi BS pulse sequence leads to significant through-plane signal loss in the front of the brain and above the ear canals. In comparison, there are no visible artifacts in the $\left|B_1^{+}\right|$ map acquired with the optimized 2 ms pulse.

Figure 8.

In vivo comparison of the 6 ms/4 kHz Fermi and optimized 2 ms pulse in the brain at 7 T. (a) Magnitude images for the positive and negative frequency offsets. The Fermi pulse images contain a significant amount of ringing along the Δf₀ gradient in the front of the brain (white arrows). (b) $\left|B_1^{+}\right|$ maps in this slice derived from the Fermi and optimized 2 ms images. (c) The Δf₀ map of this slice contains a left-right gradient in the front of the brain (white arrow).

Figurer 9.

In vivo comparison of the 6 ms/4 kHz Fermi and optimized 2 ms pulses in the lower brain at 7 T. (a) Magnitude images for the positive and negative frequency offsets. Like the higher slice, the Fermi pulse images again contain a significant amount of ringing along the Δf₀ gradient in the front of the brain, particularly the negative frequency image (white arrow). (b) $\left|B_1^{+}\right|$ maps in this slice derived from the Fermi and optimized 2 ms images. The Fermi map is significantly degraded by through-plane signal loss and large frequency offsets above the sinuses. (c) The Δf₀ map of this slice contains typical large offset above the sinuses and mouth.

4.3. Experimental measurement of |β|

Figure 10 shows the distribution of |β| values measured in the phantom for each pulse. $\left|B_1^{+}\right|$ inside the phantom ranged between 3 and 11.5 μT, and Δf₀ ranged between -40 and 20 Hz. Rayleigh noise significantly biased all three measurements towards larger mean |β| values. Nevertheless, it is clear that the Fermi and optimized pulses produce similarly low mean |β|, while the block pulse produces much larger mean |β|. Furthermore, the optimized pulse's |β| distribution tends toward zero more rapidly with increasing |β|, while the Fermi pulse's distribution contains significant energy above |β| = 0.2.

Figure 10.

Distribution of |β| in a phantom for the 6 ms/4 kHz Fermi, the 2 ms block, and the optimized 2 ms pulse. Shaded bins at |β| = 1 correspond to voxels outside the phantom. The Fermi and optimized pulses produce similarly low average |β|, while the block pulse produces significantly larger excitation.

5. Discussion and conclusions

We have introduced and evaluated a new family of $\left|B_1^{+}\right|$-to-phase encoding pulses for Bloch-Siegert $\left|B_1^{+}\right|$ mapping that have improved performance (lower on-resonance excitation over wide frequency bandwidths) and shorter durations than conventional pulses with similar sensitivities. We described the design of these pulses and demonstrated an optimized 2 ms pulse in 7 T human head $\left|B_1^{+}\right|$ mapping of central and lower axial brain slices, which comprised wide ranges of $\left|B_1^{+}\right|$ and Δf₀ values. The optimized pulse yielded similar $\left|B_1^{+}\right|$ maps to a conventional Fermi pulse in the upper brain, but produced much more accurate maps in the lower brain where large resonance frequency variations severely degraded the performance of the Fermi pulse. In addition, the optimized 2 ms pulse had 57% lower SAR than a 6 ms/4 kHz Fermi and 27% higher average on-resonance sensitivity. We also developed and performed an experiment to validate the low on-resonance excitation of the pulses.

Current pulses used in the Bloch-Siegert method are either a) narrow-band pulse envelopes, such as Fermi or Gaussian, which are modulated far from resonance by a constant frequency offset, or b) locally-optimized versions of these pulses [10]. All these pulse choices are based on the assumption that, while the objective of a large phased shift per unit $\left|B_1^{+}\right|$ dictates that the pulse envelope should have as high a magnitude as possible for as long as possible (i.e., a constant magnitude or ‘hard’ pulse shape), the simultaneous requirement of small on-resonance excitation dictates that a tradeoff must be made and a shaped envelope that is tapered at the ends must be used to reduce the envelope's frequency bandwidth. We showed that a hard pulse envelope with a constant frequency offset has a wide bandwidth, so that it produces large on-resonance excitation and is thus unsuitable as a Bloch-Siegert pulse. In contrast, our pulse design formulation yielded a high-sensitivity hard pulse shape and a time-varying frequency waveform instead of a constant frequency offset, which in all designs was characterized by a flat region in the middle of the pulse and two frequency spikes at either end of the pulse. The spikes at the ends of the frequency waveform served to cancel excitation produced primarily by the edges of the pulse.

Previously, Khalighi et al described another approach to Bloch-Siegert pulse optimization [10]. What distinguishes our approach from that method is the setup of optimization problem, in that we maximize the pulse's sensitivity directly, and use a non-convex optimization algorithm to seek the global maximum of the sensitivity objective (though we note that finding the global maximum cannot be guaranteed). We do not make any approximations regarding the functional dependence of BS phase on $\left|B_1^{+}\right|$ or the BS pulse's frequency waveform. Most importantly in that method the frequency offset of the BS pulse was held fixed, while we directly optimized the frequency waveform along with the envelope. More recently, in parallel to our work Khalighi et al have developed Bloch-Siegert pulses that have a similar near-constant envelope and U-shaped frequency sweep, but derived those pulses using an analysis of adiabatic excitation [15]. Our approach again differs from their work in that our algorithm enables the explicit specification of $\left|B_1^{+}\right|$ and Δf₀ ranges over which sensitivity is to be maximized and on-resonance excitation is to be minimized, as well as the specification of a maximum allowed on-resonance excitation (β_max).

We note that while the optimization problem formulation in Eq. 2 did not necessarily guarantee a pulse that produces a one-to-one mapping of the measured BS phase shift back to $\left|B_1^{+}\right|$, in practice we found that maximizing the average sensitivity (the average derivative of the BS phase shift with respect to $\left|B_1^{+}\right|$) always resulted in solutions that produced strictly positive phase derivatives, so that the phase curves monotonically increased with $\left|B_1^{+}\right|$ and were thus invertible. If solutions with non-monotonic phase curves were encountered, one could incorporated a strictly positive derivative constraint in the optimization problem.

Computation times for the optimized pulses varied between approximately 1/2 hour (0.5 ms pulse duration) to 3 hours (2 ms pulse duration),on a 2.0 GHz PC with 8 GB RAM. However, we have found that these rather long design times can be mitigated by assuming that, as is supported by our results, the optimal amplitude waveform will be constant, and that the frequency waveform can be parameterized by an polynomial with even orders (maximum order of 20) (results not shown). With this pulse parameterization the number of variables to be optimized can be decreased from several hundred to about 10 for a 2 ms pulse. This subsequently reduces the design times to at most several minutes, and improves the feasibility of performing multiple optimizations with different initializations to improve the likelihood of finding the globally-optimal frequency waveform.

• A new family of short RF pulses for Bloch-Siegert (BS) $\left|B_1^{+}\right|$ mapping is introduced.

• The pulses are shown to produce larger BS phase shifts than pulse currently utilized.

• They produce lower on-resonance excitation than pulses currently utilized.

• They result in improved $\left|B_1^{+}\right|$ accuracy in areas with large B₀ field inhomogeneities.

• Pulses result in lower SAR in areas with large B₀ field inhomogeneities.