Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 1;3:1194. doi: 10.1038/srep01194

Angle-Insensitive Structural Colours based on Metallic Nanocavities and Coloured Pixels beyond the Diffraction Limit

Yi-Kuei Ryan Wu 1,3, Andrew E Hollowell 1,2,3, Cheng Zhang 1,3, L Jay Guo 1,a
PMCID: PMC3561620  PMID: 23378925

Abstract

To move beyond colorant-based pigmentation display technologies, a variety of photonic and plasmonic crystal based structures have been designed and applied as colour filters. Nanostructure based colour filtering offers increased efficiencies, low power consumption, slim dimensions, and enhanced resolution. However, incident angle tolerance still needs to be improved. In this work, we propose a new scheme through localized resonance in metallic nanoslits by light funneling. Angle insensitive colour filters up to ±80 degrees have been achieved, capable of wide colour tunability across the entire visible band with pixel size beyond the diffraction limit (~λ/2). This work opens the door to angle insensitive manipulation of light with structural filtering.

Structural colour is an attractive replacement for colorant pigmentation employed by the current display technologies. However, such chemical pigments are vulnerable to a variety of processing chemicals, cannot withstand constant illumination with strong light intensities, and require extensive multilayer processing to pattern individual pixels1,2,3. Inspired by natural colour filtering, as found in the wings of Morpho butterflies and the feathers of peacocks2,4,5,6,7, many structural colour designs have been developed based on photonic crystals8,9 and plasmonic nano-structures2,3,10,11,12,13. However, the iridescence of these devices leads to drastic changes in colour with different incident angles of light, which is the key challenge to be addressed for practical applications of structural colours. For plasmonic nanostructures, this angle dependence is directly related to surface plasmon polariton (SPP) excitation via grating coupling2,3,10,14,15. This approach has led to high coupling efficiencies16, but is inherently angle-dependent due to momentum matching conditions. Overcoming this angle-dependent spectrum response will allow these structural filters to be integrated into practical applications such as high resolution visual displays, miniature hyperspectral imaging, and high sensitivity sensors17,18,19.

To obtain angle-insensitivity, one has to avoid relying on grating coupling for plasmonic mode excitation. In contrast to grating coupling, plasmonic based resonators and antennas have been demonstrated as candidates for structure colours20,21,22,23,24. Additionally, horizontally deployed plasmonic antennas and resonators have gained attention on angle insensitive spectrum response in Near-IR, Mid-IR, and THz band25,26,27. However, as pointed out by Kumar et. al.7, increasing the density of these plasmonic resonators is necessary to effectively scatter light to viewers' eyes (or detector) at visible wavelengths. In order to increase the scattering efficiency and generate more vivid colours, we employ a vertical plasmonic resonator array with specially designed periodicity to avoid angle variation. In this design, light funneling into nanoslits is exploited to generate strong absorption for transverse magnetic (TM) polarized incident light28,29,30. Utilizing light funneling, extremely small physical dimensions have large scattering cross sections, and therefore possess plasmonic mode coupling with efficiency comparable to that of grating coupling. In this letter, we theoretically and experimentally study angle robust optical devices with near-perfect absorption, as large as 96%, in the visible spectrum. Moreover, wide colour tunability throughout the entire visible spectrum and pixel size beyond the diffraction limit are demonstrated. We also suggest a design principle for angle-robust reflection by investigating the angular response of the reflection spectra with respect to the periodicity of arrayed one-dimensional structures. We further discuss the influence of periodicity on field confinement within the nano-cavities, and conclude through discussion of a variety of applications for angle robust field confinement and spectrum filtering.

Results

Plasmonic-nanoresonantor-based angle robust colour filtering

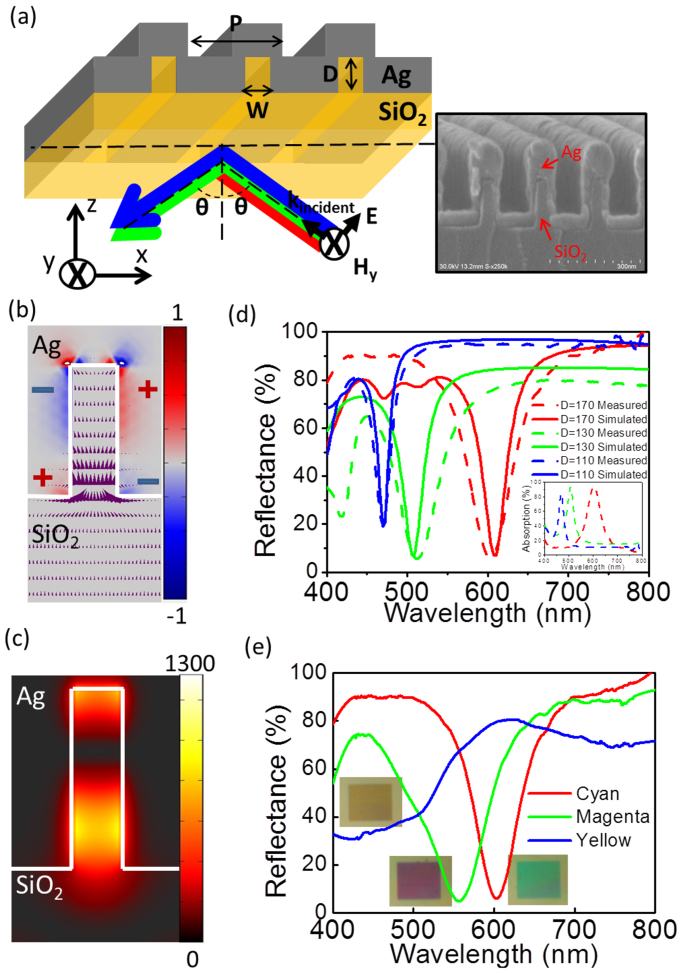
A schematic diagram of our plasmonic nanostructure is illustrated in Figure 1(a) as well as a corresponding SEM image of a fabricated device. Silver (Ag) is conformally deposited on a fused silica grating defined with the pitch, depth, and width of the grating as P, D, and W respectively. As opposed to trapping the incident light into surface plasmon modes through grating coupling, the dimensions and periodicity of the structure have been designed to concentrate the light into the silica nano-grooves based on a phenomena recognized as light funneling. As light is incident on the nano-groove array, an induced polarization charge pair accumulates at the top corners of the grooves. This charge pair acts as a dipole and further alters the E-field of incident light, redirecting the light into the groove. Figure 1(b) shows this effect with a red-blue surface plot and arrow plot which represent the normalized polarization charge distribution induced by the scattered field31 and propagation direction of the field's Poynting vector, respectively. It is noticed that the purple arrows near the Ag and silica interface point toward the groove verifying this funneling effect. The intensity distribution of the magnetic field |Hy|2, under the funneling condition, is depicted in Figure 1(c) showing that the light is well confined in the groove at the resonant wavelength.

Figure 1. Plasmonic-nanocavity-based angle robust colour filtering.

Figure 1

Open in a new tab

(a) A schematic of the proposed structure and corresponding SEM image of a fabricated device with width (W) = 45 nm, depth (D) = 160 nm, and period (P) = 180 nm with θ as the incident angle of light. (b) Polarization charge and Poynting vector distribution of light funneled into these nano-grooves, presented with the red–blue surface plot and purple arrows, respectively. (c) Intensity distribution of the magnetic-field Hy at resonance, P = 180, W = 50, and D = 170 nm. (d) Reflection (simulated in solid lines and measured in dash lines) and measured absorption spectra (inset, dashed lines) at D = 110, 130, and 170 nm in blue, green, and red curves, given fixed P = 180 and W = 50 nm at normal incidence. (e) Reflection spectra at fixed P = 180 nm and D = 170 nm demonstrating the three basic colours of the CMY colour model, cyan (C), magenta (M), and yellow (Y), with varying W = 40, 60, and 90 nm at normal incidence.

The above angle insensitive colour filtering results from the fact that light is funneled into metal-insulator-metal Fabry-Perot (MIMFP) cavity modes. By varying the optical path length in the MIMFP cavity through changing the width and depth of the nano-grooves, the resonance of the structure is able to be tuned across the entire visible spectrum. The MIMFP resonant wavelength, λ, is determined by the effective refractive index, neff, and the depth, D, in the Fabry Perot resonance equation, 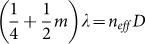Inline graphic, where m is a positive integer and neff is the effective refractive index of MIM waveguide modes. The effective index is insignificantly dependent on the nano-groove depth, D24, but is highly dependent on acute changes in the width, W. The effective indices, neff, are calculated for changing values in width, W28,32. For example, when the insulator SiO2 width W = 50 nm, the effective index dispersion relation of even modes in a MIM waveguide is found to be neff = 1.85, 1.90, and 2.02 for wavelengths of λ = 620, 532, and 460 nm, respectively. When W = 60 nm, neff = 1.91, 1.99, and 2.11, respectively. This design can be integrated into various applications as well as accommodate different manufacturing processes, since there is a wide degree of freedom in modifying the filtered colour by changing either D or W. Especially by simply changing the nano-grove width but maintaining the grove depths, the fabrication process can be greatly simplified and can be easily scaled to large area devices. This coupling to the MIMFP by means of funneling, as opposed to grating coupling into waveguide or plasmonic modes, allows angle insensitive performance.

Ultra-high resolution, widely tunable colour filtering

First a description is given on how resonant wavelength, namely the wavelength of the absorption peaks (reflections dips), can be tuned throughout the entire visible spectrum through adjusting the groove depth D. In this set of simulation and experiment, the groove width, W, and period, P, are held constant at 50 nm and 180 nm respectively. The groove depths D corresponding to yellow, cyan, and magenta reflective colours are found to be 110, 130, and 170 nm, respectively. Figure 1(d) presents the simulated and measured reflection spectra (and measured absorption spectra in the inset) of the above three devices with different D at normal incidence and TM polarized light. These devices are able to trap light as much as 96% at the resonance wavelength and reflect all other wavelengths. The optical propagation loss in silver at shorter wavelengths is non-negligible, resulting in an 80% absorption peak at the shorter wavelength. This strong absorption at the selected wavelength range can be exploited for high purity reflective colour filtering.

In addition to the colour tuning based on changing D, Figure 1(e) shows that the three basic colours of the cyan, magenta, and yellow (CMY) colour scheme can also be achieved by adjusting the width of the nano-groove W from 40 nm to 90 nm, given fixed P = 180 nm and D = 170 nm. It is noticed that the broad resonance dip on the yellow device is due to larger propagation loss of the MIM waveguides at higher frequencies. A better reflection dip for yellow can be achieved by changing D to 110 nm with W = 50 nm as shown in the blue solid and dotted lines in Figure 1(d). This method of holding the period and depth constant while varying the widths of the groove presents a more viable method for manufacturing where the depth of reactive ion etching (RIE) is held constant and the width of each coloured pixel is altered, allowing multiple colour pixels to be produced on a single wafer.

In order to demonstrate the visual performance of these colour filters, we have designed and fabricated coloured images in the format of the Olympic Rings. Figure 2(a) and its insets show SEM images of the devices. The corresponding optical image of these reflective colour filters is in Figure 2(b). The period, P, and depth, D, of each ring are held constant while the widths, W, vary from 40 nm to 90 nm to generate the different colours. The angular dependence of these images was measured only up to 30 degree because of the small size of the structure and the limitation of the optical path in the microscope. Within this range, the color appears unchanged. The next section presents large scale devices fabricated through nanoimprint lithography in which we were able to measure the angled reflection spectrum and confirm angle insensitivity. With this technique, cyan, magenta, and yellow, as well as intermediate colours can be achieved. Note that the purple colour from the rope held by the gymnast in the top middle ring is produced by two nano-grooves. Moreover, the magenta colour from the bow area is produced by several isolated and segmented short lines, as small as 100 nm in length and 60 nm in width, demonstrating ultra-high colour resolution. In the supporting information, we further include simulation results to prove that even single and double slits of tens nm width can have colour filtering effect. This colour demonstration proves that the proposed plasmonic structural colour is capable of creating pixels with sizes beyond the diffraction limit of light. This opens up the possibility of realizing super-pixels imaging5, in which colours are mixed between multiple super-pixels before their combined size is comparable to the diffraction limit. In addition, an Olympic ring with two colours has been fabricated to present an application of the polarization dependence of these filters. Figure 2(c) shows an image with two sets of gratings. As the polarization of incident light is changed, the displayed image is altered. Particularly, the central pattern in Figure 2(c) is concealed when the incident light polarization changes from TM polarized light to TE. This polarization dependence can be utilized in applications of cryptography and anti-counterfeiting. One specific example would be to put such images on a personal identification card. Counterfeiters may be able to reproduce the colour of the symbol but it would be increasingly difficult for them to make the image additionally dependent on polarization of light, adding another element to the validity of the identification card. This polarization dependence is also advantageous for implementation in visual display technologies by creating a multifunctional component that can serve as a conductive electrode, polarizer, and colour filter simultaneously3.

Figure 2. Colour demonstrations with ultra-high resolution and polarization dependent images.

Figure 2

Open in a new tab

(a) The SEM images and (b) optical image under white light illumination of fabricated coloured images in the format of the Olympic rings. The full range of CMY colours are achieved by sweeping W from 40 to 90 nm, with P and D fixed at 180 nm and 170 nm respectively. (b) Shows that even a single short segmented nano-groove demonstrates colour response. (c) Demonstrates utilizing polarization dependence to actively change the displayed image, where grooves with W = 40 for cyan and W = 60 nm for magenta under TM illumination.

Design rules for angle insensitivity

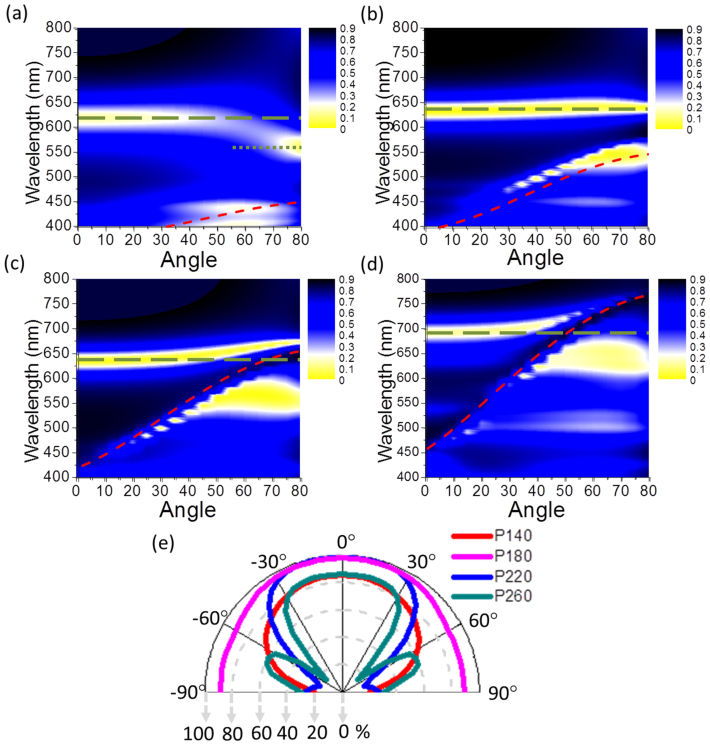
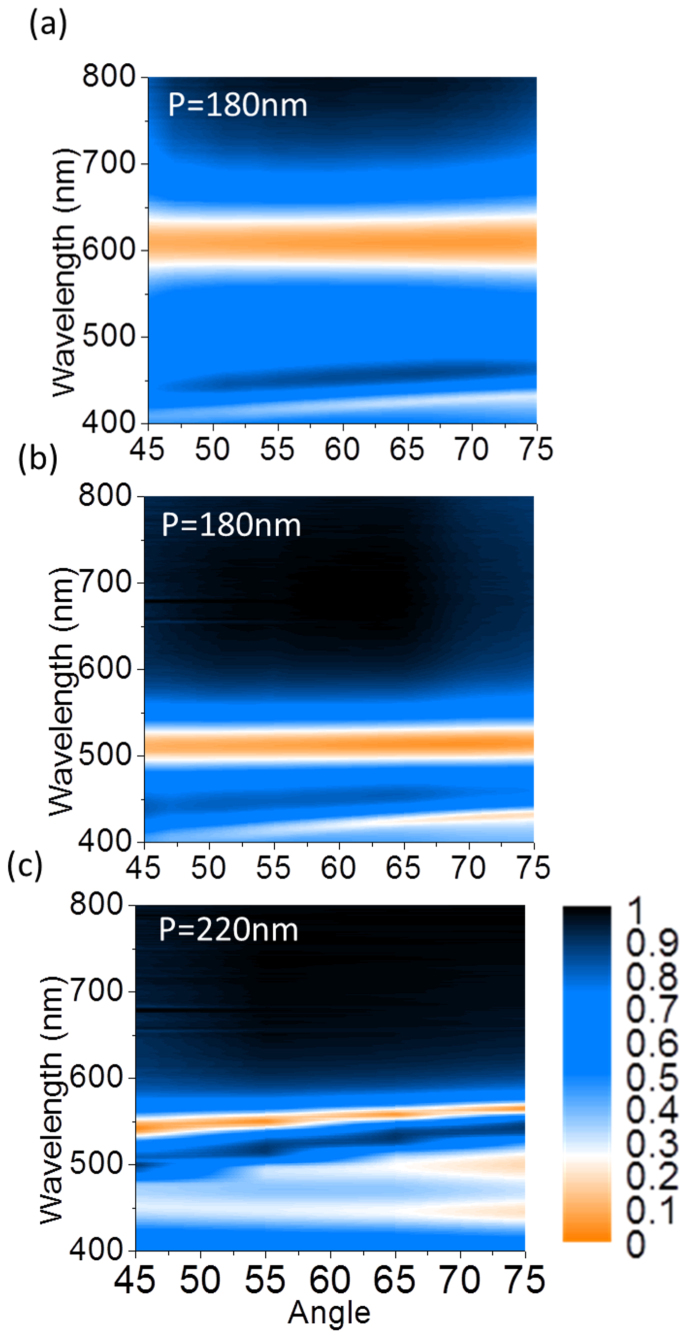
The effect of periodicity on the angle robustness of these metallic nano-grooves is investigated here. Given W = 50 nm and D = 180 nm, the simulated angle resolved reflection spectra contour plots at periods of P = 140, 180, 220, and 260 nm are shown in Figure 3(a), (b), (c), and (d). Incremental changes of 40 nm in the period are chosen to illustrate three different regimes: grating coupling, localized resonance, as well as cavity coupling between neighboring waveguides which is explained further in the next section of this letter. Figure 3(a) and (d) indicate higher angle dependence than Figures 3(b) and (c). When the period P = 140 nm, 220 nm, and 260 nm, the MIMFP resonance position shifts with increasing incident angle of light, whereas the spectrum at the periods of 180 nm remains at a relatively constant wavelengths over all incident angles. Furthermore, the angular behavior of absorption at the resonance wavelength 630 nm with P = 140, 180, 220 and 260 nm are presented in Figure 3(e) showing that the absorption reaches over 90% for ±90° angle range with P = 180 nm. This shows that angle independence is achieved at a periodicity of 180 nm for visible wavelengths of light. Above or below P = 180 nm, the resonance wavelength corresponding to the absorption peak is angle dependent and therefore less efficient. The angle resolved reflection spectra from angles of 45° to 75° were measured on various large scale fabricated devices based on nanoimprint lithography. Two of them are shown in Figures 4(a) and (b) with a period of 180 nm and depths D, of 130 and 170 nm, respectively. A device fabricated with a period of 220 nm exhibited angle dependence further validating this design. The angle resolved reflection spectra of this device, with P = 220 nm, W = 45 nm, and D = 160 nm, is displayed in Figure 4(c). 25 nm Δλ is observed per 30° change in incident illumination angle. This change in reflection dip is not observed at P = 180 nm (Figures 4(a) and (b)) showing strong agreement between measured and simulated spectra. Through this analysis we conclude that a colour filter structure with a range of periods from 160 nm to 200 nm possess angle robust spectrum response.

Figure 3. Simulated angle resolved reflection spectra with various periods.

Figure 3

Open in a new tab

The simulated angle resolved reflection spectra contour plots at periods P = 140 (a), P = 180 (b), P = 220 (c), and P = 260 nm (d). The green dash lines in all four figures indicate metal-insulator-metal Fabry-Perot (MIMFP) cavity mode, whereas the red dash lines refer to the grating assisted surface plasmon (GASP) modes whose dispersion is dependent on the grating period. The crossing between MIMFP and GASP when P = 220 and 260 nm indicates coupling between the two modes. The green dash line in (a) refers to the dispersion of odd mode defined in Figure 5(c). (e) The simulated angular absorption maxima in terms of various period from 140, 180, 220, and 260 nm.

Figure 4. Experimental angle insensitive spectrum filtering.

Figure 4

Open in a new tab

(a) The angle resolved reflection spectra of this design with sweeping incident illumination angle from 45° to 75° are presented with the following device dimensions (a) P = 180, W = 50, and D = 130 nm, (b) P = 180, W = 50, and D = 170 nm, and (c) P = 220 nm, W = 50 nm, and D = 160 nm. (a) and (b) show flat band absorption response indicating angle insensitivity, while (c) shows 25 nm resonance wavelength shift per 30° change in incident illumination angle representing coupling between MIMFP and GASP modes.

We would now like to further elaborate on the mechanism for angle dependence when the period is away from the optimal range, P > 200 nm and P < 160 nm. Clearly shown in Figures 3(e), the side lobes of the absorption maxima develop at large angles of incidence. Therefore we further analyzed the resonant modes at these larger degrees of incidence. For P > 200 nm, two modes are involved in this phenomenon. MIMFP resonances are angle independent modes, illustrated as green straight dash lines, and grating assisted surface plasmon modes (GASP) generated under the Bragg coupling condition15 are highly angle dependent, illustrated by the red dashed lines in Figures 3(a), (b), (c) and (d). The increasing angle leads to the interaction between the MIMFP modes and the grating assisted surface plasmon modes (GASP) due to momentum matching. For TM-polarized waves, the momentum matching equation for grating assisted surface plasmon resonance excitation of dielectric—metal interfaces is governed by the following relationship, 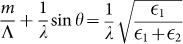Inline graphic. 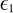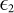In this equation, m represents the diffraction order, Λ the period (denoted in the figures as P), λ the wavelength, θ the incident angle, and Inline graphic and Inline graphic are the permittivity of the metal and dielectric materials respectively. The red curves in Figures 3(a), (b), (c), and (d) extend from the ultraviolet to the visible region with increasing periodicity, and finally result in a strong coupling between the GASP and the MIMFP cavity modes. The field distribution of this coupling will be discussed at the end of this paper. Moreover, Λ is found to be proportional to λ in the above equation, which provides a guideline of selecting the appropriate period for angle independent plasmonic resonance at desired wavelength bands.

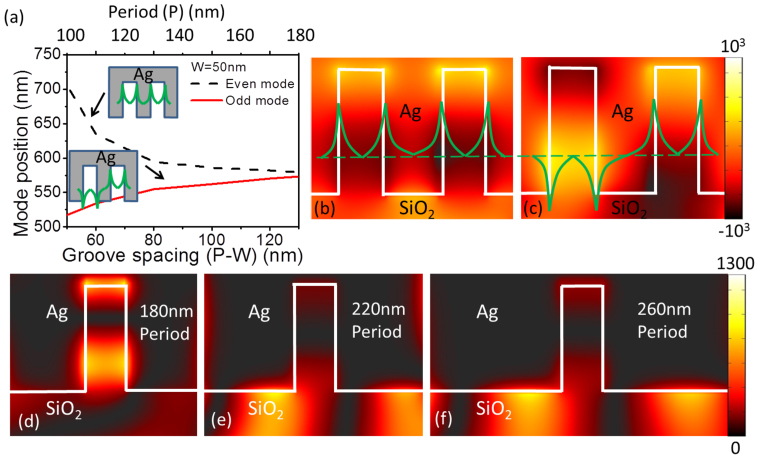
When P < 160 nm, the MIMFP resonance band blue shifts at incident angles greater than 60°. This is due to the breakdown of the assumption that nano-groove structures are well separated (nano-groove size W ≪ Period P). When the thickness of the groove spacing (P-W = groove spacing) is too small, the dispersion has to be reconsidered due to coupling between neighboring metal-insulator-metal (MIM) waveguides33,34. Figure 5(a) shows the mode dispersion with respect to the groove spacing (P-W) and Period. In this scheme, even and odd modes are defined in Figure 5(a), which indicate whether the field is in-phase or out-of-phase in the neighboring grooves, respectively. The fields of both even and odd modes at an incident angle of 75° are plotted in Figures 5(b) and (c), respectively. Moreover, the dispersion in Figure 5(a) clearly indicates that the splitting between even and odd modes increases as the groove spacing (P-W) reduces. This trend follows the observation found in Figures 3(a) and (b) denoted by the green dashed lines and green dotted lines for the even and odd modes. Only when the incident angle of light is large enough can the odd mode be excited due to phase requirement, which causes the resonance shift to shorter wavelengths at incident angles greater than 60°.

Figure 5. Optical mode coupling and period dependent field confinement.

Figure 5

Open in a new tab

(a) shows mode dispersion with respect to the groove spacing (P-W) and Period, as well as the definition of even and odd modes in the insets. The field distribution of Hy with defined even and odd modes is plotted in (b) and (c), respectively. The intensity distribution of magnetic field Hy at the incident illumination angle of 45° is presented at P = 180 nm (d), 220 nm (e), 260 nm (f). (d) confirms that the field is well confined within the nano-groove corresponding to a MIMFP mode, while (d) and (f) show strong surface modes illustrating coupling to the GASP modes.

The intensity distributions of the Hy field at the resonance wavelength for periods of 180, 220 and 260 nm further illustrates this coupling between GASP and MIMFP modes, as shown in Figures 5(d), (e), and (f) for 45° angle of incidence. The resonance mode for a period of 180 nm indicates that the field is mostly concentrated within the groove. Alternatively, when the period is greater than 220 nm the field is both in the groove and on top of the grating. This indicates strong coupling between MIMFP and GASP modes, leading to the angular dependence of the reflection dips. The information in this set of the figures also confirms that the angle independent reflection spectra occur at periods < 200 nm for visible wavelengths of light. Moreover, the light confinement is manipulated with respect to periodicity P in the Figures 5(d), (e), and (f) with stronger coupling into GASP modes for larger periods. The period controllable optical field confinement in this nanostructure can be a design principle for applications that require strong field confinement such as optical trapping, high sensitivity nanofluidic index sensors, and plasmonic enhanced nanoscale emitters.

Discussion

We have designed, fabricated and analyzed one dimensional nanostructure with angle-robust colour response. Light funneling is employed as a method for angle independent coupling into localized resonances in metallic nanoslits. Colour tunability across the visible spectrum and pixel size beyond the diffraction limit has been demonstrated. Such principle could also be exploited for super-high resolution optical storage. Through simulation and experimental confirmation, design principles have been developed for angle tolerant spectrum response. Angle dependence has been avoided with a designed periodic structure for visible wavelength resonances employing MIMFP modes. Finally, field confinement and manipulation within these nano-grooves induced through sub-wavelength periodic effects are discussed. This device is capable of wide colour tunability in the visible wavelength regime and can be used as a guideline for designing devices that require consistent performance independent of incident angles of light.

Methods

Simulation

In the simulations and experiments in this letter, broad-band collimated light illumination in the wavelength range λ = 400–800 nm is supplied as the input. The simulation is performed using finite difference time domain (FDTD) method for the field distribution details and rigorous coupled wave analysis (RCWA) is used to calculate the angle resolved reflection and absorption spectra.

Device fabrication

The devices described are fabricated by nanoscale lithography, reactive ion etching (RIE), and metal deposition. Nanoimprint lithography (NIL) is used to fabricate samples with large enough areas for angle resolved reflection measurements to confirm angle insensitive colour response. Electron beam (e-beam) lithography is used to create patterned images in the form of the Olympic Rings and demonstrate colours with resolution beyond the diffraction limit. The respective lithography techniques are used to create a resist template on a fused silica substrate. For NIL an angled evaporation is used to tune the width of patterned resist. Nickel (Ni) is then e-beam evaporated over the patterned substrate and a lift off process is performed. The Ni is then used as an etch mask for a RIE process defining the depth, D, of the silica grating. After the silica etch, the Ni mask is removed in nitric acid and Ag is then sputter deposited conformally covering the silica grating and finalizing the fabrication process.

Optical characterization

The optical measurement is conducted using two systems to obtain the reflection/absorption spectra at normal and angled incidence. Reflection spectra at normal incidence are measured using Nikon TE300 inverted microscope with a halogen lamp for the light source. Reflection spectra with angled incidence are measured from 45° to 75° (2° increment) swept perpendicular to the grating orientation (the definition of the the sweeping orientation is shown in the supporting information), as depicted in Figure 1(a), with a J. A. Woollam M-2000 ellipsometer. The numerical apertures of the collection optics in both systems are as low as 0.04 to ensure high angular resolution. We would like to note that sweeping the incident angle along the grating direction does not exhibit iridescence.

Author Contributions

Y.K.W. is responsible for theoretical design and simulation; A.E.H. is responsible for optimizing RIE and metal deposition processes and fabricating large scale devices based on Nano-imprinting lithography. C.Z. is responsible for complex graphic colour demonstration based on e-beam lithography. L.J.G. and Y.K.W. conceived the idea. L.J.G. directed the project. All authors performed device characterization, discussed the results and contributed to the article.

Supplementary Material

Supplementary Information

Supplementary materials

srep01194-s1.pdf (355.5KB, pdf)

Acknowledgments

We acknowledge the financial support from AFOSR (Dr. H. Weinstock) and NSF. The device fabrications were performed at the Lurie Nanofabrication Facility (LNF) and SEM images taken at Electron MicroAnalysis Lab at the University of Michigan.

References

  1. Cho E. et al. Two-dimensional photonic crystal color filter development. Optics Express 17, 8621–8629 (2009). [DOI] [PubMed] [Google Scholar]
  2. Xu T. et al.. Structural Colors: From Plasmonic to Carbon Nanostructures. Small 7, 3128–3136 (2011). [DOI] [PubMed] [Google Scholar]
  3. Xu T., Wu Y., Luo X. & Guo L. J. Plasmonic nanoresonators for high-resolution colour filtering and spectral imaging. Nature Communications 1, 59 (2010). [DOI] [PubMed] [Google Scholar]
  4. Vukusic P., Sambles J. R. & Lawrence C. R. Structural colour - Colour mixing in wing scales of a butterfly. Nature 404, 457–457 (2000). [DOI] [PubMed] [Google Scholar]
  5. Zi J. et al. Coloration strategies in peacock feathers. Proc. Natl. Acad. Sci. U. S. A. 100, 12576–12578 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wu Z., Lee D., Rubner M. F. & Cohen R. E. Structural color in porous, superhydrophilic, and self-cleaning SiO2/TiO2 Bragg stacks. Small 3, 1445–1451 (2007). [DOI] [PubMed] [Google Scholar]
  7. Kumar K. et al.. Printing colour at the optical diffraction limit. Nature Nanotechnology 7, 557–561 (2012). [DOI] [PubMed] [Google Scholar]
  8. Kinoshita S., Yoshioka S. & Miyazaki J. Physics of structural colors. Reports on Progress in Physics 71, 076401–076401 (2008). [Google Scholar]
  9. Kim H. et al. Structural colour printing using a magnetically tunable and lithographically fixable photonic crystal. Nature Photonics 3, 534–540 (2009). [Google Scholar]
  10. Kaplan A. F., Xu T. & Guo L. J. High efficiency resonance-based spectrum filters with tunable transmission bandwidth fabricated using nanoimprint lithography. Appl. Phys. Lett. 99, 143111 (2011). [Google Scholar]
  11. Yokogawa S., Burgos S. P. & Atwater H. A. Plasmonic Color Filters for CMOS Image Sensor Applications. Nano Letters 12 (2012). [DOI] [PubMed] [Google Scholar]
  12. Laux E., Genet C., Skauli T. & Ebbesen T. W. Plasmonic photon sorters for spectral and polarimetric imaging. Nature Photonics 2 (2008). [Google Scholar]
  13. Lee H., Yoon Y., Lee S., Kim S. & Lee K. Color filter based on a subwavelength patterned metal grating. Optics Express 15 (2007). [DOI] [PubMed] [Google Scholar]
  14. Diest K., Dionne J. A., Spain M. & Atwater H. A. Tunable Color Filters Based on Metal-Insulator-Metal Resonators. Nano Letters 9, 2579–2583 (2009). [DOI] [PubMed] [Google Scholar]
  15. Zhou W., Gao H. & Odom T. W. Toward Broadband Plasmonics: Tuning Dispersion in Rhombic Plasmonic Crystals. Acs Nano 4, 1241–1247 (2010). [DOI] [PubMed] [Google Scholar]
  16. Genet C. & Ebbesen T. W. Light in tiny holes. Nature 445, 39–46 (2007). [DOI] [PubMed] [Google Scholar]
  17. Lee K. et al. Enhancing Surface Plasmon Detection Using Template-Stripped Gold Nanoslit Arrays on Plastic Films. Acs Nano 6, 2931–2939 (2012). [DOI] [PubMed] [Google Scholar]
  18. Yao J. et al. Soft Embossing of Nanoscale Optical and Plasmonic Structures in Glass. Acs Nano 5, 5763–5774 (2011). [DOI] [PubMed] [Google Scholar]
  19. Schmidt M. A., Lei D. Y., Wondraczek L., Nazabal V. & Maier S. A. Hybrid nanoparticle-microcavity-based plasmonic nanosensors with improved detection resolution and extended remote-sensing ability. Nature communications 3, 1108 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Brown L. V., Sobhani H., Lassiter J. B., Nordlander P. & Halas N. J. Heterodimers: Plasmonic Properties of Mismatched Nanoparticle Pairs. Acs Nano 4, 819–832 (2010). [DOI] [PubMed] [Google Scholar]
  21. Aksu S. et al. High-Throughput Nanofabrication of Infrared Plasmonic Nanoantenna Arrays for Vibrational Nanospectroscopy. Nano Letters 10, 2511–2518 (2010). [DOI] [PubMed] [Google Scholar]
  22. Ross B. M., Wu L. Y. & Lee L. P. Omnidirectional 3D Nanoplasmonic Optical Antenna Array via Soft-Matter Transformation. Nano Letters 11, 2590–2595 (2011). [DOI] [PubMed] [Google Scholar]
  23. Pasquale A. J., Reinhard B. M. & Dal Negro L. Engineering Photonic-Plasmonic Coupling in Metal Nanoparticle Necklaces. Acs Nano 5, 6578–6585 (2011). [DOI] [PubMed] [Google Scholar]
  24. Ikeda K. et al. Structural Tuning of Optical Antenna Properties for Plasmonic Enhancement of Photocurrent Generation on a Molecular Mono layer System. Journal of Physical Chemistry C 116, 20806–20811 (2012). [Google Scholar]
  25. Hao J. et al. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 96, 251104 (2010). [Google Scholar]
  26. Cattoni A. et al. lambda(3)/1000 Plasmonic Nanocavities for Biosensing Fabricated by Soft UV Nanoimprint Lithography. Nano Letters 11, 3557–3563 (2011). [DOI] [PubMed] [Google Scholar]
  27. Le Perchec J., Desieres Y., Rochat N. & de Lamaestre R. E. Subwavelength optical absorber with an integrated photon sorter. Appl. Phys. Lett. 100, 113305 (2012). [Google Scholar]
  28. Le Perchec J., Quemerais P., Barbara A. & Lopez-Rios T. Why metallic surfaces with grooves a few nanometers deep and wide may strongly absorb visible light. Phys. Rev. Lett. 100, 066408 (2008). [DOI] [PubMed] [Google Scholar]
  29. Pardo F., Bouchon P., Haidar R. & Pelouard J. Light funneling mechanism explained by magnetoelectric interference. Phys. Rev. Lett. 107 (2011). [DOI] [PubMed] [Google Scholar]
  30. Polyakov A. et al. Plasmonic light trapping in nanostructured metal surfaces. Appl. Phys. Lett. 98, 203104 (2011). [Google Scholar]
  31. Marty R., Baffou G., Arbouet A., Girard C. & Quidant R. Charge distribution induced inside complex plasmonic nanoparticles. Optics Express 18, 3035–3044 (2010). [DOI] [PubMed] [Google Scholar]
  32. Dionne J. A., Sweatlock L. A., Atwater H. A. & Polman A. Plasmon slot waveguides: Towards chip-scale propagation with subwavelength-scale localization. Physical Review B 73, 035407 (2006). [Google Scholar]
  33. Economou E. N. Surface Plasmons in Thin Films. Physical Review 182, 539–& (1969). [Google Scholar]
  34. Fan X., Wang G. P., Lee J. C. W. & Chan C. T. All-angle broadband negative refraction of metal waveguide arrays in the visible range: Theoretical analysis and numerical demonstration. Phys. Rev. Lett. 97, 073901 (2006). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary materials

srep01194-s1.pdf (355.5KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES