Abstract
Computer simulations are useful in evolutionary biology for hypothesis testing, to verify analytical methods, to analyze interactions among evolutionary processes, and to estimate evolutionary parameters. In particular, the simulation of DNA sequences with recombination may help in understanding the role of recombination in diverse evolutionary questions, such as the genome structure. Consequently, plenty of computer simulators have been developed to simulate DNA sequence data with recombination. However, the choice of an appropriate tool, among all currently available simulators, is critical if recombination simulations are to be biologically meaningful. This review provides a practical survival guide to commonly used computer programs and methodologies for the simulation of coding and non-coding DNA sequences with recombination. It may help in the correct design of computer simulation experiments of recombination. In addition, the study includes a review of simulation studies investigating the impact of ignoring recombination when performing various evolutionary analyses, such as phylogenetic tree and ancestral sequence reconstructions. Alternative analytical methodologies accounting for recombination are also reviewed.
Keywords: simulation, recombination, recombination breakpoints, recombination hotspots, DNA sequences, recombination phylogenetic bias
Introduction
Recombination constitutes a basic and dominant mechanism in molecular evolution, increasing genetic diversity before natural selection operates on the new sequence. Recombination is widespread across nuclear genomes (e.g., Awadalla, 2003; Tsaousis et al., 2005; Fraser et al., 2007; Gaut et al., 2007; Duret and Arndt, 2008) and the importance of its understanding has been long recognized, with crucial implications for genome structure (Reich et al., 2001), phenotypic diversity (Zhang et al., 2002), and genetic diseases (Daly et al., 2001). Moreover, ignoring recombination may bias phylogenetic reconstructions (e.g., Posada, 2001; Posada and Crandall, 2002; Beiko et al., 2008), and the derived inferences (e.g., Schierup and Hein, 2000a; Feil et al., 2001; Anisimova et al., 2003; Arenas and Posada, 2010a,b,c).
The evolutionary importance of recombination (e.g., Robertson et al., 1995; Lukashev, 2005) calls for its accurate detection and measurement (see, Martin et al., 2011). Although some analytical methods have shown an overall better performance than others (Posada and Crandall, 2001; Wiuf et al., 2001), the choice of an appropriate tool also depends on the particular analysis (e.g., detection of recombination breakpoints or estimation of recombination rates), computational costs (some methods are computationally expensive), and the genetic marker. I recommend the following two reviews for helping users to make choices for appropriate methods and computer tools for recombination inference (Posada et al., 2002; Martin et al., 2011).
Computer simulations aim to mimic real world processes. They allow the study of mechanisms that may alter processes or the understanding of complex systems that are analytically intractable (Peck, 2004). Indeed, the simulation of evolutionary histories is commonly used for hypothesis testing (e.g., Arenas et al., 2008; Pierron et al., 2011), to verify and compare analytical methods or programs (e.g., Westesson and Holmes, 2009; Marttinen et al., 2012), to analyze interactions among evolutionary processes (e.g., Arenas et al., 2012, 2013), or to estimate evolutionary parameters (e.g., Wilson et al., 2009; Beaumont, 2010). Importantly, the choice of an appropriate simulator is critical because simulations should be as realistic as possible in order to mimic a given biological scenario. Although several studies have already reviewed computer simulators in population genetics from global perspectives (e.g., Liu et al., 2008; Arenas, 2012; Arenas and Posada, 2012; Hoban et al., 2012), they have not explored particular methodologies for the simulation of DNA sequences with recombination.
The present study provides an overview of the capabilities of available computer tools and methodologies, and suggests recommendations, for the simulation of DNA sequences with recombination. It also describes some applications of simulated datasets with recombination to show the importance of including recombination in evolutionary analyses. Alternative analytical methodologies that consider recombination are also suggested.
Computer Programs for the Simulation of DNA Data Under Recombination
Recombination can be simulated by the two major simulation approaches commonly used in population genetics, the forward in time (forward-time, where the evolutionary history of an entire population is simulated from the past to the present; e.g., Epperson et al., 2010) and the coalescent (backward-time, which describes a backward in time genealogical process from a sample of genes to a single ancestral copy; e.g., Nordborg, 2007; Wakeley, 2008). The forward-time approach can simulate complex processes, including gene–gene interactions and complex selection (e.g., Calafell et al., 2001; Peng et al., 2007), but coalescent simulations are computationally faster and can be recommended for extensive simulation studies (e.g., Beaumont et al., 2002). Table 1 shows an overview of currently available computer programs, for both coalescent and forward-time approaches, to simulate DNA sequences with recombination.
Table 1.
Commonly used software for direct simulation of DNA sequences under recombination.
| Program | Evolutionary history | Recombination algorithm | Recombination hotspots | Other evolutionary processes | Substitution model | Rate variation | Intracodon recombination | Indels | OS | Citation |
|---|---|---|---|---|---|---|---|---|---|---|
| CodonRecSim | Coalescent | SCR | No | No | Codb: GY94 | No | No | No | SC, Win | Anisimova et al. (2003) |
| Recodon/NetRecodon | Coalescent | SCRa | No | D, Pm | Nt: All; Codb: GY94 | G, I | Yes (NetRecodon) | No | All | Arenas and Posada (2007, 2010a) |
| SIMCOAL2 | Coalescent | SCR | Yes | D, Pm | Nt: JC, K2P | No | No | No | Linux, Win | Laval and Excoffier (2004) |
| Fastsimcoal | Coalescent | SMC | Yes | D, Pm | Nt: JC, K2P | No | No | No | Linux, Mac, Win | Excoffier and Foll (2011) |
| Mlcoalsim | Coalescent | SCR | Yes | D, Pm | Nt: JC, K2P | G, I | No | No | All | Ramos-Onsins and Mitchell-Olds (2007) |
| TREEEVOLVE | Coalescent | SCR | No | D, Pm | Nt: All | G | No | No | SC, Mac | Grassly and Rambaut (1997) |
| SPLATCHE2 | Forward, coalescent | SCR | No | D, Pm | Nt: JC, K2P | No | No | No | Linux, Win | Ray et al. (2010) |
| GenomePop | Forward | CO | Yes | D, Pm, S | Nt: JC, GTR; Cod: MG94 | No | Yes | No | SC, Linux, Win | Carvajal-Rodriguez (2008) |
| SFS_CODE | Forward | CO, SB | Yes | D, Pm, S | Nt: All; Cod: Ntc | G | No | Yes | All | Hernandez (2008) |
| SimuPop | Forward | CO | Yes | D, Pm, S | Nt: All | No | No | Yes | All | Peng and Kimmel (2005) |
“Recombination algorithm”: “SCR” means the standard coalescent with recombination to simulate the ARG (Hudson, 1983); “SMC” indicates the sequential Markovian coalescent, which is an approximation of the SCR (further details in, McVean and Cardin, 2005); “CO” means crossing over recombination model (see Padhukasahasram et al., 2008); “SB” indicates sex-biased recombination. “Other evolutionary processes”: “D,” “Pm,” and “S” mean demographics, population structure with migration, and selection, respectively. “Substitution model” refers to substitution models based on nucleotide “Nt” or codon “Cod” sequences; “Nt: All” means all nucleotide substitution models (JC, …, GTR). “Rate variation” indicates variable substitution rate across sites (G, gamma distribution; I, proportion of invariable sites). “Intracodon recombination” indicates if recombination breakpoints can occur at any codon position (Yes) or are forced to occur between codons (No). “OS” shows the availability of executable files in different operating systems (“All” means available for Macintosh, Windows, and Linux), “SC” means that the source code is available.
aThe simulated ARG can be exported from NetRecodon and then can be visualized and analyzed using NetTest (Arenas et al., 2010).
bUnder codon models, dN/dS can vary across codons.
cCoding sequences are simulated by nucleotide substitution models, avoiding stop codons.
Simulation of coding DNA sequences with recombination
Direct simulation of coding DNA sequences with recombination can be only performed with a few programs. Using the coalescent approach, the programs Recodon (Arenas and Posada, 2007), CodonRecSim (Anisimova et al., 2003), and NetRecodon (Arenas and Posada, 2010a) allow such simulation, but only the latter program does not force recombination breakpoints to occur between codons, thus allowing more realistic simulations (see Arenas and Posada, 2010a). Concerning the forward-time approach, only the programs GenomePop (Carvajal-Rodriguez, 2008) and SFS_CODE (Hernandez, 2008) implement the simulation of coding sequences with recombination.
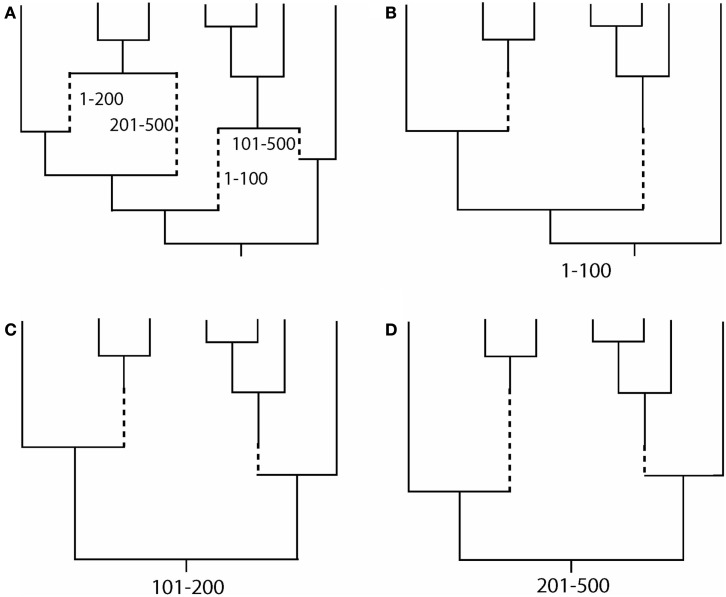
Evolutionary scenarios that are not implemented in these programs can be simulated by the following alternative methodology, which is based on the concatenation of two different simulators. First, we simulate an evolutionary history with recombination [an ancestral recombination graph (ARG, see Figure 1A), which contains a tree for each recombinant fragment; Figures 1B–D]. This procedure can be carried out using, for example, the program ms (Hudson, 2002); see also other evolutionary history simulators in (Hoban et al., 2012). Next, we simulate molecular evolution of each coding fragment, according to a user-specified codon-substitution model, along its corresponding simulated tree (further details in Yang, 2006; Fletcher and Yang, 2009). Finally, we just concatenate the simulated coding fragments. The simulation of coding sequence evolution along given trees can be performed, for example, with the program INDELible (Fletcher and Yang, 2009); see also other software in (Arenas, 2012; Arenas and Posada, 2012). The limitation of this methodology is that recombination breakpoints are always assumed to occur between codons and not within codons.
Figure 1.
Example of an ancestral recombination graph (ARG) with the corresponding embedded trees for each recombinant fragment. (A) ARG based on two recombination events with breakpoints at positions 100 and 200. Dashed lines indicate branches for recombinant fragments. (B–D) Embedded tree for each recombinant fragment. Note that topologies and branch lengths may differ across trees. Finally, the simulation of sequence evolution can be performed site by site along the corresponding tree (see, Yang, 2006; Fletcher and Yang, 2009).
Simulation of nucleotide sequences with recombination
A number of computer programs can directly simulate non-coding DNA sequences under recombination (see Table 1). Similarly to the previous subsection, the simulation of non-coding DNA sequences under other evolutionary scenarios, which are not described in the Table 1, can be performed by combining two computer tools. We can use a simulator of recombination evolutionary histories (e.g., ms or msms; Ewing and Hermisson, 2010) followed by a non-coding DNA sequence evolution simulator (e.g., INDELible, Seq-Gen, Rambaut and Grassly, 1997; EVOLVER, Yang, 1997; or indel-Seq-Gen, Strope et al., 2009).
Simulation of genomes with recombination hotspots
It is known that the recombination rate is not homogeneous throughout the genome and some regions (hotspot regions) are more likely to suffer recombination (e.g., Gabriel et al., 2002; Zhuang et al., 2002). Consequently, recombination hotspots should be considered for realistic genome simulation.
The simulation of genomes with recombination requires robust and memory-efficient simulators. Programs like fastsimcoal (Excoffier and Foll, 2011) or mlcoalsim (Ramos-Onsins and Mitchell-Olds, 2007) allow for efficient simulations of non-coding genomic regions under recombination (including recombination hotspots). However, these tools do not implement a variety of substitution models (e.g., codon models), or particular evolutionary mechanisms like selection; this may be problematic if we are trying to mimic genome-wide data (see, Arbiza et al., 2011).
Again, an alternative methodology consists of the use of two simulators. A few programs currently implement the simulation of recombination hotspots, namely, SNPsim (Wiuf and Posada, 2003), cosi (Schaffner et al., 2005), GENOME (Liang et al., 2007), mbs (Teshima and Innan, 2009), and msHOT (Hellenthal and Stephens, 2007). Although all these programs simulate particular genetic markers (such as SNPs or STRs), DNA sequence evolution can be simulated upon phylogenetic trees produced by these programs if we use the two-step procedure described above.
Simulation of recombination phylogenetic networks
In order to represent a full evolutionary history with recombination, phylogenetic networks should be used instead of forcing the genealogy onto a single tree (Huson and Bryant, 2006). There are two commonly used methodologies for the simulation of recombination networks: direct simulation of the ARG (e.g., Figure 1A) or combining the simulated trees for each recombinant fragment (e.g., Figures 1B–D). To my knowledge, only two programs can really output a simulated ARG, namely, Serial NetEvolve (Buendia and Narasimhan, 2006) and NetRecodon (Arenas and Posada, 2010a), where the ARG can be visualized and analyzed using the NetTest web server (Arenas et al., 2010)1. On the other hand, trees can be combined to generate a network using tools like CombineTrees (see for a review, Woolley et al., 2008)2.
Recombination Simulation for Analyzing the Influence of Recombination on Phylogenetic Inferences
This section outlines three computer simulation studies where ignoring recombination leads to biased phylogenetic inferences. Alternative phylogenetic inference methodologies considering recombination are also suggested.
Influence of recombination on phylogenetic tree reconstruction
Schierup and Hein (2000a) simulated samples under the coalescent with recombination (Hudson, 1983). Then, from the simulated genealogy, they simulated nucleotide sequence evolution under the Jukes-Cantor (JC) and Kimura’s two-parameter (K2P) nucleotide substitution models of evolution. The simulated datasets were analyzed using programs for phylogenetic tree reconstruction by both distance-based methods and maximum-likelihood (ML) methods. Ignoring recombination biased the inferred phylogenetic trees toward larger terminal branches, smaller times to the most recent common ancestor (MRCA) and incorrect topologies (Schierup and Hein, 2000a). In addition, ignoring recombination led to overestimation of the substitution rate heterogeneity, apparent homoplasies and loss of molecular clock (Schierup and Hein, 2000a,b). Later, Posada (2001) analyzed the molecular clock hypothesis on four empirical datasets. In particular, the author applied a triplet likelihood ratio test (test for equality of evolutionary rates among three species, called a relative-rate test, RRT), which is independent of topology and might be unbiased by recombination. Results showed that recombinant data did not allow a good fit to the molecular clock when using classical likelihood ratio tests (LRT). However, the molecular clock was not rejected when using the RRT test. Thus, this test could be recommended for testing a molecular clock in the presence of recombination. In addition, phylogenetic incongruence in empirical data was also observed as a consequence of ignoring recombination (e.g., Worobey and Holmes, 1999; Feil et al., 2001).
These findings, consequently, suggest biases in derived evolutionary analyses based on phylogenetic reconstructions that ignore recombination. As an alternative, there are two methodologies of phylogenetic reconstruction accounting for recombination:
-
–
Inference of a single phylogenetic network (e.g., Figure 1A; Griffiths and Marjoram, 1997; Huson and Bryant, 2006). Recombination networks can be inferred by using computer programs like SplitsTree (Huson, 1998; Huson and Bryant, 2006).
-
–
Inference of a set of phylogenetic trees, where each tree corresponds to the evolutionary history of each recombinant fragment (e.g., Figures 1B–D). The methodology consists of the detection of recombination breakpoints (see for a review, Martin et al., 2011) followed by a phylogenetic tree reconstruction for each recombinant fragment.
Both methodologies correctly account for recombination and the choice should be based on the posterior application. For example, the phylogenetic network may help for an easy visualization of clades and phylogenetic relationships (e.g., Maughan and Redfield, 2009). By contrast, the simulation of sequence evolution requires a phylogenetic tree for each recombinant fragment (e.g., Fletcher and Yang, 2009).
Influence of recombination on ancestral sequence reconstruction
Recently, Arenas and Posada (2010c) analyzed the effect of considering recombination on ancestral sequence reconstruction (ASR). They performed extensive simulations of nucleotide, codon, and amino acid data by using the coalescent with recombination approach implemented in NetRecodon. They then reconstructed ancestral sequences with different ASR methods (joint ML, marginal ML, and empirical Bayes). Results clearly indicated that ignoring recombination biases the reconstruction of ancestral sequences, regardless of the method or software used. This ASR error can be partially reduced if recombination is considered (Arenas and Posada, 2010c). The methodology consists of four steps: the detection of recombination breakpoints, the reconstruction of a phylogenetic tree for each recombinant fragment, the reconstruction of ancestral fragments by using the corresponding trees and, finally, the concatenation of the ancestral fragments to generate the entire ancestral sequence. The Datamonkey web server (Kosakovsky Pond and Frost, 2005)3 and the Hyphy package (Kosakovsky Pond et al., 2005) have automated the whole procedure described above to infer ancestral sequences with consideration of recombination.
Arenas and Posada (2010c) also analyzed empirical data, in particular two datasets of the env region of HIV-1. They inferred ancestral sequences both ignoring and considering recombination, using the methodology described above, and observed a different number of CTL epitopes depending on whether recombination was considered or not.
Influence of recombination on the detection of molecular adaptation
The detection of molecular adaptation (based on the non-synonymous/synonymous substitution rate ratio, hereafter dN/dS) is commonly used at both global (entire sequence) and local (codon) levels. Indeed, these analyses have commonly been applied to datasets collected from highly recombinant viruses and bacteria (e.g., Perez-Losada et al., 2009, 2011; Bozek and Lengauer, 2010). Several studies have shown the impact of recombination on the estimation of dN/dS (e.g., Anisimova et al., 2003; Arenas and Posada, 2010a). After simulating coding data under a variety of codon-substitution models for heterogeneous selection pressure (see, Yang et al., 2000) and different levels of recombination, they selected those heterogeneous codon models that best fitted the simulated data by using LRTs. Results showed a weak impact of recombination on the estimation of global dN/dS but a strong effect on the estimation of local dN/dS, in particular by increasing the number of false-positively selected sites (PSS). An alternative methodology to reduce these errors consists of the detection of recombination breakpoints followed by the reconstruction of a phylogenetic tree for each recombinant fragment and, finally, the estimation of dN/dS by using the corresponding trees (see, Kosakovsky Pond et al., 2006). This methodology was applied in (Perez-Losada et al., 2009, 2011). Again, the Datamonkey web server and the Hyphy package have automated this whole procedure to estimate dN/dS while accounting for recombination.
Recombination might also affect other evolutionary inferences. For example, it could bias those analytical methods based on the coalescent without recombination (e.g., BEAST; Drummond and Rambaut, 2007). However these influences have not yet been rigorously evaluated.
Another interesting question concerns the influence of recombination on genetic diversity. Spencer et al. (2006) studied this in humans and found that recombination only affects genetic diversity at recombination hotspots. However, such hotspots did not alter substitution rates, perhaps because recombination rates were always low. By contrast, large recombination rates (common in a variety of viruses and bacteria) may strongly increase genetic diversity and bring novel lineages (e.g., He et al., 2010).
At this point, I would suggest the approximate Bayesian computation (ABC) approach (see for a review, Beaumont, 2010) to estimate evolutionary parameters accounting for recombination. ABC is based on computer simulations and provides an alternative for those analyses where the likelihood function cannot be computed. Simulations can be performed according to a prior distribution for recombination rate (among other parameters) and then, by a rejection or a regression method, a posterior distribution can be computed to obtain the parameter estimates (Beaumont et al., 2002). For example, Wilson et al. (2009) applied ABC for joint estimation of a set of evolutionary parameters, such as substitution rate, dN/dS and recombination rate. By this methodology, the influence of recombination on other evolutionary mechanisms is accounted for, but only if it is indeed implemented in the computer simulator.
Conclusion
This review provides a practical guide to the state of the art in software, and recommends methodologies, for simulating coding and non-coding sequence data with recombination, including recombination hotspots. Currently, only three programs implement the direct simulation of coding data with recombination. These programs will not cover every evolutionary scenario, but this problem can be circumvented by the use of two simulators, one for the evolutionary history and another for sequence evolution. It is also important to consider intracodon recombination (Arenas and Posada, 2010a), because 2/3 of recombination events are expected to occur within codons. By contrast, the simulation of non-coding sequences with recombination can be performed by a variety of programs. Here again, two simulators may be combined where necessary.
Among many other applications (e.g., Sun et al., 2011; Marttinen et al., 2012), the simulation of DNA data with recombination has been especially important for demonstrating the strong influence of recombination on phylogenetic tree reconstruction and derived analyses, such as ASR or dN/dS estimation. However, some alternative methodologies have been developed for phylogenetic inference accounting for recombination.
The current set of computer tools to simulate DNA sequences with recombination can cover a wide range of evolutionary scenarios. However, some scenarios are still difficult to simulate and will require the development of more complex simulators. For example, next-generation sequencing (NGS) technologies now deliver fast and accurate genome sequences (Metzker, 2010) that may call for simulations of entire genomes accounting for recombination (including recombination hotspots; e.g., Westesson and Holmes, 2009; Marttinen et al., 2012), as well as other evolutionary mechanisms like natural selection. Indeed, the simulation of DNA evolution should be performed by using different substitution models for each genomic region (Arbiza et al., 2011). Moreover, I would expect interactions between the different evolutionary forces, such as joint influences of natural selection and recombination on dN/dS (e.g., Anisimova et al., 2003; Kryazhimskiy and Plotkin, 2008) or of structural protein energies on sequence evolution (e.g., Bastolla et al., 2007; Arenas et al., 2009; Grahnen et al., 2011). To my knowledge, there is currently no tool to simulate sequences accounting for all these evolutionary features, including interactions among them. On the other hand, there is also a demand for fast simulations, in particular for applying ABC or Bayesian model-choice approaches that require extensive simulations (see recombination examples in, Wilson et al., 2009; Nunes and Balding, 2010; Sohn et al., 2012).
In conclusion, there is a need to innovate continuously in fast and complex simulators of DNA sequences with recombination and I expect future advances in this area.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I want to thank Badri Padhukasahasram, Guest Associate Editor of Frontiers in Evolutionary and Population Genetics, for the invitation to contribute with this review to the Research Topic “Inference of recombination and gene-conversion from whole genome sequence variation data.” Indeed, I also want to thank the Journal Frontiers in Evolutionary and Population Genetics for a waiver to cover publication costs. I thank Dr Richard M. Gunton for helpful comments. I thank two reviewers for insightful comments and suggestions. I thank the Spanish Government for the “Juan de la Cierva” fellowship, JCI-2011-10452.
Footnotes
References
- Anisimova M., Nielsen R., Yang Z. (2003). Effect of recombination on the accuracy of the likelihood method for detecting positive selection at amino acid sites. Genetics 164, 1229–1236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbiza L., Patricio M., Dopazo H., Posada D. (2011). Genome-wide heterogeneity of nucleotide substitution model fit. Genome Biol. Evol. 3, 896–908 10.1093/gbe/evr080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M. (2012). Simulation of molecular data under diverse evolutionary scenarios. PLoS Comput. Biol. 8:e1002495. 10.1371/journal.pcbi.1002495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Francois O., Currat M., Ray N., Excoffier L. (2013). Influence of admixture and paleolithic range contractions on current European diversity gradients. Mol. Biol. Evol. 30, 57–61 10.1093/molbev/mss203 [DOI] [PubMed] [Google Scholar]
- Arenas M., Patricio M., Posada D., Valiente G. (2010). Characterization of phylogenetic networks with nettest. BMC Bioinformatics 11:268. 10.1186/1471-2105-11-268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Posada D. (2007). Recodon: coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinformatics 8:458. 10.1186/1471-2105-8-458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Posada D. (2010a). Coalescent simulation of intracodon recombination. Genetics 184, 429–437 10.1534/genetics.109.109736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Posada D. (2010b). Computational design of centralized HIV-1 genes. Curr. HIV Res. 8, 613–621 10.2174/157016210794088263 [DOI] [PubMed] [Google Scholar]
- Arenas M., Posada D. (2010c). The effect of recombination on the reconstruction of ancestral sequences. Genetics 184, 1133–1139 10.1534/genetics.109.109736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Posada D. (2012). “Simulation of coding sequence evolution,” in Codon Evolution, eds Cannarozzi G. M., Schneider A. (Oxford: Oxford University Press; ), 126–132 [Google Scholar]
- Arenas M., Ray N., Currat M., Excoffier L. (2012). Consequences of range contractions and range shifts on molecular diversity. Mol. Biol. Evol. 29, 207–218 10.1093/molbev/msr187 [DOI] [PubMed] [Google Scholar]
- Arenas M., Valiente G., Posada D. (2008). Characterization of reticulate networks based on the coalescent with recombination. Mol. Biol. Evol. 25, 2517–2520 10.1093/molbev/msn219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Villaverde M. C., Sussman F. (2009). Prediction and analysis of binding affinities for chemically diverse HIV-1 PR inhibitors by the modified SAFE_p approach. J. Comput. Chem. 30, 1229–1240 10.1002/jcc.21147 [DOI] [PubMed] [Google Scholar]
- Awadalla P. (2003). The evolutionary genomics of pathogen recombination. Nat. Rev. Genet. 4, 50–60 10.1038/nrg964 [DOI] [PubMed] [Google Scholar]
- Bastolla U., Porto M., Roman H. E., Vendruscolo M. (2007). Structural Approaches to Sequence Evolution. Berlin: Springer [Google Scholar]
- Beaumont M. A. (2010). Approximate Bayesian computation in evolution and ecology. Annu. Rev. Ecol. Evol. Syst. 41, 379–405 10.1146/annurev-ecolsys-102209-144621 [DOI] [Google Scholar]
- Beaumont M. A., Zhang W., Balding D. J. (2002). Approximate Bayesian computation in population genetics. Genetics 162, 2025–2035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beiko R. G., Doolittle W. F., Charlebois R. L. (2008). The impact of reticulate evolution on genome phylogeny. Syst. Biol. 57, 844–856 10.1080/10635150802559265 [DOI] [PubMed] [Google Scholar]
- Bozek K., Lengauer T. (2010). Positive selection of HIV host factors and the evolution of lentivirus genes. BMC Evol. Biol. 10:186. 10.1186/1471-2148-10-186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buendia P., Narasimhan G. (2006). Serial netevolve: a flexible utility for generating serially-sampled sequences along a tree or recombinant network. Bioinformatics 22, 2313–2314 10.1093/bioinformatics/btl387 [DOI] [PubMed] [Google Scholar]
- Calafell F., Grigorenko E. L., Chikanian A. A., Kidd K. K. (2001). Haplotype evolution and linkage disequilibrium: a simulation study. Hum. Hered. 51, 85–96 10.1159/000022963 [DOI] [PubMed] [Google Scholar]
- Carvajal-Rodriguez A. (2008). GENOMEPOP: a program to simulate genomes in populations. BMC Bioinformatics 9:223. 10.1186/1471-2105-9-223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daly M. J., Rioux J. D., Schaffner S. F., Hudson T. J., Lander E. S. (2001). High-resolution haplotype structure in the human genome. Nat. Genet. 29, 229–232 10.1038/ng1001-229 [DOI] [PubMed] [Google Scholar]
- Drummond A. J., Rambaut A. (2007). BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol. Biol. 7:214. 10.1186/1471-2148-7-214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duret L., Arndt P. F. (2008). The impact of recombination on nucleotide substitutions in the human genome. PLoS Genet. 4:e1000071. 10.1371/journal.pgen.1000071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epperson B. K., McRae B. H., Scribner K., Cushman S. A., Rosenberg M. S., Fortin M. J., et al. (2010). Utility of computer simulations in landscape genetics. Mol. Ecol. 19, 3549–3564 10.1111/j.1365-294X.2010.04678.x [DOI] [PubMed] [Google Scholar]
- Ewing G., Hermisson J. (2010). MSMS: a coalescent simulation program including recombination, demographic structure and selection at a single locus. Bioinformatics 26, 2064–2065 10.1093/bioinformatics/btq322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L., Foll M. (2011). Fastsimcoal: a continuous-time coalescent simulator of genomic diversity under arbitrarily complex evolutionary scenarios. Bioinformatics 27, 1332–1334 10.1093/bioinformatics/btr124 [DOI] [PubMed] [Google Scholar]
- Feil E. J., Holmes E. C., Bessen D. E., Chan M.-S., Day N. P. J., Enright M. C., et al. (2001). Recombination within natural populations of pathogenic bacteria: Short-term empirical estimates and long-term phylogenetic consequences. Proc. Natl. Acad. Sci. U.S.A. 98, 182–187 10.1073/pnas.98.1.182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher W., Yang Z. (2009). INDELible: a flexible simulator of biological sequence evolution. Mol. Biol. Evol. 26, 1879–1888 10.1093/molbev/msp098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser C., Hanage W. P., Spratt B. G. (2007). Recombination and the nature of bacterial speciation. Science 315, 476–480 10.1126/science.1127573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel S. B., Schaffner S. F., Nguyen H., Moore J. M., Roy J., Blumenstiel B., et al. (2002). The structure of haplotype blocks in the human genome. Science 296, 2225–2229 10.1126/science.1069424 [DOI] [PubMed] [Google Scholar]
- Gaut B. S., Wright S. I., Rizzon C., Dvorak J., Anderson L. K. (2007). Recombination: an underappreciated factor in the evolution of plant genomes. Nat. Rev. Genet. 8, 77–84 10.1038/nrg1970 [DOI] [PubMed] [Google Scholar]
- Grahnen J. A., Nandakumar P., Kubelka J., Liberles D. A. (2011). Biophysical and structural considerations for protein sequence evolution. BMC Evol. Biol. 11:361. 10.1186/1471-2148-11-361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassly N. C., Rambaut A. (1997). Treevolve: A Program to Simulate the Evolution of DNA Sequences Under Different Population Dynamic Scenarios. Oxford: Department of Zoology, Wellcome Centre for Infectious Disease, Oxford University [Google Scholar]
- Griffiths R. C., Marjoram P. (1997). “An ancestral recombination graph,” in Progress in Population Genetics and Human Evolution, eds Donelly P., Tavaré S. (Berlin: Springer-Verlag; ), 257–270 [Google Scholar]
- He C. Q., Ding N. Z., He M., Li S. N., Wang X. M., He H. B., et al. (2010). Intragenic recombination as a mechanism of genetic diversity in bluetongue virus. J. Virol. 84, 11487–11495 10.1128/JVI.01216-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellenthal G., Stephens M. (2007). msHOT: modifying Hudson’s ms simulator to incorporate crossover and gene conversion hotspots. Bioinformatics 23, 520–521 10.1093/bioinformatics/btl622 [DOI] [PubMed] [Google Scholar]
- Hernandez R. D. (2008). A flexible forward simulator for populations subject to selection and demography. Bioinformatics 24, 2786–2787 10.1093/bioinformatics/btn522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoban S., Bertorelle G., Gaggiotti O. E. (2012). Computer simulations: tools for population and evolutionary genetics. Nat. Rev. Genet. 13, 110–122 [DOI] [PubMed] [Google Scholar]
- Hudson R. R. (1983). Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 23, 183–201 10.1016/0040-5809(83)90013-8 [DOI] [PubMed] [Google Scholar]
- Hudson R. R. (2002). Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18, 337–338 10.1093/bioinformatics/18.suppl_1.S337 [DOI] [PubMed] [Google Scholar]
- Huson D. H. (1998). Splitstree: analyzing and visualizing evolutionary data. Bioinformatics 14, 68–73 10.1093/bioinformatics/14.1.68 [DOI] [PubMed] [Google Scholar]
- Huson D. H., Bryant D. (2006). Application of phylogenetic networks in evolutionary studies. Mol. Biol. Evol. 23, 254–267 10.1093/molbev/msj030 [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Frost S. D. (2005). Datamonkey: rapid detection of selective pressure on individual sites of codon alignments. Bioinformatics 21, 2531–2533 10.1093/bioinformatics/bti320 [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Frost S. D., Muse S. V. (2005). HYPHY: hypothesis testing using phylogenies. Bioinformatics 21, 676–679 10.1093/bioinformatics/bti079 [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Posada D., Gravenor M. B., Woelk C. H., Frost S. D. (2006). Automated phylogenetic detection of recombination using a genetic algorithm. Mol. Biol. Evol. 23, 1891–1901 10.1093/molbev/msl051 [DOI] [PubMed] [Google Scholar]
- Kryazhimskiy S., Plotkin J. B. (2008). The population genetics of dN/dS. PLoS Genet. 4:e1000304. 10.1371/journal.pgen.1000304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laval G., Excoffier L. (2004). SIMCOAL 2.0: a program to simulate genomic diversity over large recombining regions in a subdivided population with a complex history. Bioinformatics 20, 2485–2487 10.1093/bioinformatics/bth264 [DOI] [PubMed] [Google Scholar]
- Liang L., Zollner S., Abecasis G. R. (2007). GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics 23, 1565–1567 10.1093/bioinformatics/btm138 [DOI] [PubMed] [Google Scholar]
- Liu Y., Athanasiadis G., Weale M. E. (2008). A survey of genetic simulation software for population and epidemiological studies. Hum. Genomics 3, 79–86 10.1186/1479-7364-3-1-79 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukashev A. N. (2005). Role of recombination in evolution of enteroviruses. Rev. Med. Virol. 15, 157–167 10.1002/rmv.457 [DOI] [PubMed] [Google Scholar]
- Martin D. P., Lemey P., Posada D. (2011). Analysing recombination in nucleotide sequences. Mol. Ecol. Resour. 11, 943–955 10.1111/j.1755-0998.2011.03026.x [DOI] [PubMed] [Google Scholar]
- Marttinen P., Hanage W. P., Croucher N. J., Connor T. R., Harris S. R., Bentley S. D., et al. (2012). Detection of recombination events in bacterial genomes from large population samples. Nucleic Acids Res. 40, e6. 10.1093/nar/gkr928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maughan H., Redfield R. J. (2009). Tracing the evolution of competence in Haemophilus influenzae. PLoS ONE 4:e5854. 10.1371/journal.pone.0005854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. A., Cardin N. J. (2005). Approximating the coalescent with recombination. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 1387–1393 10.1098/rstb.2005.1673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzker M. L. (2010). Sequencing technologies – the next generation. Nat. Rev. Genet. 11, 31–46 10.1038/nrg2626 [DOI] [PubMed] [Google Scholar]
- Nordborg M. (2007). “Coalescent theory,” in Handbook of Statistical Genetics, 3rd Edn, eds Balding D. J., Bishop M., Cannings C. (Chichester: John Wiley & Sons Ltd; ), 843–877 [Google Scholar]
- Nunes M. A., Balding D. J. (2010). On optimal selection of summary statistics for approximate Bayesian computation. Stat. Appl. Genet. Mol. Biol. 9, 34. [DOI] [PubMed] [Google Scholar]
- Padhukasahasram B., Marjoram P., Wall J. D., Bustamante C. D., Nordborg M. (2008). Exploring population genetic models with recombination using efficient forward-time simulations. Genetics 178, 2417–2427 10.1534/genetics.107.085332 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peck S. L. (2004). Simulation as experiment: a philosophical reassessment for biological modeling. Trends Ecol. Evol. (Amst.) 19, 530–534 10.1016/j.tree.2004.07.019 [DOI] [PubMed] [Google Scholar]
- Peng B., Amos C. I., Kimmel M. (2007). Forward-time simulations of human populations with complex diseases. PLoS Genet. 3:e47. 10.1371/journal.pgen.0030047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng B., Kimmel M. (2005). Simupop: a forward-time population genetics simulation environment. Bioinformatics 21, 3686–3687 10.1093/bioinformatics/bti584 [DOI] [PubMed] [Google Scholar]
- Perez-Losada M., Jobes D. V., Sinangil F., Crandall K. A., Arenas M., Posada D., et al. (2011). Phylodynamics of HIV-1 from a phase III AIDS vaccine trial in Bangkok, Thailand. PLoS ONE 6:e16902. 10.1371/journal.pone.0016902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Losada M., Posada D., Arenas M., Jobes D. V., Sinangil F., Berman P. W., et al. (2009). Ethnic differences in the adaptation rate of HIV gp120 from a vaccine trial. Retrovirology 6, 67. 10.1186/1742-4690-6-67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierron D., Chang I., Arachiche A., Heiske M., Thomas O., Borlin M., et al. (2011). Mutation rate switch inside Eurasian mitochondrial haplogroups: impact of selection and consequences for dating settlement in Europe. PLoS ONE 6:e21543. 10.1371/journal.pone.0021543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posada D. (2001). Unveiling the molecular clock in the presence of recombination. Mol. Biol. Evol. 18, 1976–1978 10.1093/oxfordjournals.molbev.a003802 [DOI] [PubMed] [Google Scholar]
- Posada D., Crandall K. A. (2001). Evaluation of methods for detecting recombination from DNA sequences: computer simulations. Proc. Natl. Acad. Sci. U.S.A. 98, 13757–13762 10.1073/pnas.241370698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posada D., Crandall K. A. (2002). The effect of recombination on the accuracy of phylogeny estimation. J. Mol. Evol. 54, 396–402 [DOI] [PubMed] [Google Scholar]
- Posada D., Crandall K. A., Holmes E. C. (2002). Recombination in evolutionary genomics. Annu. Rev. Genet. 36, 75–97 10.1146/annurev.genet.36.040202.111115 [DOI] [PubMed] [Google Scholar]
- Rambaut A., Grassly N. C. (1997). Seq-gen: an application for the Monte carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 13, 235–238 [DOI] [PubMed] [Google Scholar]
- Ramos-Onsins S. E., Mitchell-Olds T. (2007). Mlcoalsim: multilocus coalescent simulations. Evol. Bioinform. Online 3, 41–44 [PMC free article] [PubMed] [Google Scholar]
- Ray N., Currat M., Foll M., Excoffier L. (2010). SPLATCHE2: a spatially explicit simulation framework for complex demography, genetic admixture and recombination. Bioinformatics 26, 2993–2994 10.1093/bioinformatics/btq581 [DOI] [PubMed] [Google Scholar]
- Reich D. E., Cargill M., Bolk S., Ireland J., Sabeti P. C., Richter D. J., et al. (2001). Linkage disequilibrium in the human genome. Nature 411, 199–204 10.1038/35075590 [DOI] [PubMed] [Google Scholar]
- Robertson D. L., Sharp P. M., McCutchan F. E., Hahn B. H. (1995). Recombination in HIV-1. Nature 374, 124–126 10.1038/374124a0 [DOI] [PubMed] [Google Scholar]
- Schaffner S. F., Foo C., Gabriel S., Reich D., Daly M. J., Altshuler D. (2005). Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 15, 1576–1583 10.1101/gr.3709305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schierup M. H., Hein J. (2000a). Consequences of recombination on traditional phylogenetic analysis. Genetics 156, 879–891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schierup M. H., Hein J. (2000b). Recombination and the molecular clock. Mol. Biol. Evol. 17, 1578–1579 10.1093/oxfordjournals.molbev.a026256 [DOI] [PubMed] [Google Scholar]
- Sohn K. A., Ghahramani Z., Xing E. P. (2012). Robust estimation of local genetic ancestry in admixed populations using a nonparametric Bayesian approach. Genetics 191, 1295–1308 10.1534/genetics.112.140228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer C. C., Deloukas P., Hunt S., Mullikin J., Myers S., Silverman B., et al. (2006). The influence of recombination on human genetic diversity. PLoS Genet. 2:e148. 10.1371/journal.pgen.0020148 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strope C. L., Abel K., Scott S. D., Moriyama E. N. (2009). Biological sequence simulation for testing complex evolutionary hypotheses: indel-seq-gen version 2.0 . Mol. Biol. Evol. 26, 2581–2593 10.1093/molbev/msp174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun S., Evans B. J., Golding G. B. (2011). “Patchy-tachy” leads to false positives for recombination. Mol. Biol. Evol. 28, 2549–2559 10.1093/molbev/msr076 [DOI] [PubMed] [Google Scholar]
- Teshima K. M., Innan H. (2009). Mbs: modifying Hudson’s ms software to generate samples of DNA sequences with a biallelic site under selection. BMC Bioinformatics 10:166. 10.1186/1471-2105-10-166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsaousis A. D., Martin D. P., Ladoukakis E. D., Posada D., Zouros E. (2005). Widespread Recombination in Published Animal mtDNA Sequences. Mol. Biol. Evol. 22, 925–933 10.1093/molbev/msi084 [DOI] [PubMed] [Google Scholar]
- Wakeley J. (2008). Coalescent Theory: An Introduction. Greenwood Village: Roberts and Company Publishers [Google Scholar]
- Westesson O., Holmes I. (2009). Accurate detection of recombinant breakpoints in whole-genome alignments. PLoS Comput. Biol. 5:e1000318. 10.1371/journal.pcbi.1000318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson D. J., Gabriel E., Leatherbarrow A. J., Cheesbrough J., Gee S., Bolton E., et al. (2009). Rapid evolution and the importance of recombination to the gastroenteric pathogen Campylobacter jejuni. Mol. Biol. Evol. 26, 385–397 10.1093/molbev/msn264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiuf C., Christensen T., Hein J. (2001). A simulation study of the reliability of recombination detection methods. Mol. Biol. Evol. 18, 1929–1939 10.1093/oxfordjournals.molbev.a003733 [DOI] [PubMed] [Google Scholar]
- Wiuf C., Posada D. (2003). A coalescent model of recombination hotspots. Genetics 164, 407–417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley S. M., Posada D., Crandall K. A. (2008). A comparison of phylogenetic network methods using computer simulation. PLoS ONE 3:e1913. 10.1371/journal.pone.0001913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worobey M., Holmes E. C. (1999). Evolutionary aspects of recombination in RNA viruses. J. Gen. Virol. 80, 2535–2543 [DOI] [PubMed] [Google Scholar]
- Yang Z. (1997). PAML: a program package for phylogenetic analysis by maximum likelihood. Comput. Appl. Biosci. 13, 555–556 [DOI] [PubMed] [Google Scholar]
- Yang Z. (2006). Computational Molecular Evolution. Oxford: Oxford University Press [Google Scholar]
- Yang Z., Nielsen R., Goldman N., Pedersen A.-M. K. (2000). Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics 155, 431–449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. X., Perry K., Vinci V. A., Powell K., Stemmer W. P., del Cardayre S. B. (2002). Genome shuffling leads to rapid phenotypic improvement in bacteria. Nature 415, 644–646 10.1038/415644a [DOI] [PubMed] [Google Scholar]
- Zhuang J., Jetzt A. E., Sun G., Yu H., Klarmann G., Ron Y., et al. (2002). Human immunodeficiency virus type 1 recombination: rate, fidelity, and putative hot spots. J. Virol. 76, 11273–11282 10.1128/JVI.76.22.11273-11282.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]