Forelimb kinematics during swimming in the pig-nosed turtle, Carettochelys insculpta, compared with other turtle taxa: rowing versus flapping, convergence versus intermediacy

SUMMARY

Animals that swim using appendages do so by way of rowing and/or flapping motions. Often considered discrete categories, rowing and flapping are more appropriately regarded as points along a continuum. The pig-nosed turtle, Carettochelys insculpta, is unusual in that it is the only freshwater turtle to have limbs modified into flippers and swim via synchronous forelimb motions that resemble dorsoventral flapping, traits that evolved independently from their presence in sea turtles. We used high-speed videography to quantify forelimb kinematics in C. insculpta and a closely related, highly aquatic rower (Apalone ferox). Comparisons of our new data with those previously collected for a generalized freshwater rower (Trachemys scripta) and a flapping sea turtle (Caretta caretta) allow us to: (1) more precisely quantify and characterize the range of limb motions used by flappers versus rowers, and (2) assess whether the synchronous forelimb motions of C. insculpta can be classified as flapping (i.e. whether they exhibit forelimb kinematics and angles of attack more similar to closely related rowing species or more distantly related flapping sea turtles). We found that the forelimb kinematics of previously recognized rowers (T. scripta and A. ferox) were most similar to each other, but that those of C. insculpta were more similar to rowers than to flapping C. caretta. Nevertheless, of the three freshwater species, C. insculpta was most similar to flapping C. caretta. ‘Flapping’ in C. insculpta is achieved through humeral kinematics very different from those in C. caretta, with C. insculpta exhibiting significantly more anteroposterior humeral motion and protraction, and significantly less dorsoventral humeral motion and depression. Based on several intermediate kinematic parameters and angle of attack data, C. insculpta may in fact represent a synchronous rower or hybrid rower-flapper, suggesting that traditional views of C. insculpta as a flapper should be revised.

INTRODUCTION

Animals that propel themselves using appendages (e.g. fins or limbs) do so by way of rowing and/or flapping motions. Rowing is characterized by anteroposterior oscillatory motions of the limbs with distinct recovery and power strokes (Blake, 1979; Blake, 1980; Vogel, 1994; Walker and Westneat, 2000; Rivera and Blob, 2010), whereas flapping is characterized by dorsoventral oscillatory motions of the limbs, in which a distinct recovery stroke may not be present (Aldridge, 1987; Rayner, 1993; Walker and Westneat, 1997; Wyneken, 1997; Walker and Westneat, 2000; Rivera, A. R. V. et al., 2011). During rowing, propulsory structures attain low-drag orientations (i.e. small angles of attack ≈0 deg) during recovery strokes, but rotate to high-drag orientations (i.e. large angles of attack ≈90 deg) during power strokes (Walker and Westneat, 2002b). In contrast, flapping motions, which generate thrust via lift-based mechanisms, display intermediate angles of attack (Walker and Westneat, 2000; Walker and Westneat, 2002b). Aquatic locomotion via rowing and flapping has been reported for a diverse range of taxa, including invertebrates (Plotnick, 1985; Seibel et al., 1998), fishes (Walker and Westneat, 2000; Walker, 2002; Walker and Westneat, 2002a; Walker and Westneat, 2002b), turtles (Davenport et al., 1984; Pace et al., 2001; Rivera and Blob, 2010; Rivera, A. R. V. et al., 2011), birds (Baudinette and Gill, 1985) and mammals (Feldkamp, 1987; Fish, 1993; Fish, 1996).

Rowing and flapping fishes, in particular, have provided productive systems for examining the functional consequences and correlates of these two methods of swimming. Flapping has been shown to be a more energetically efficient mode of swimming than rowing, regardless of swimming speed (Walker and Westneat, 2000). This suggests that flapping should be employed by species that require energy conservation (Walker and Westneat, 2000), such as those that swim great distances. However, rowing appendages were found to generate more thrust during the power stroke, and to be better for maneuvers such as accelerating, braking and turning (Walker and Westneat, 2000), suggesting that aquatic species that require substantial maneuvering should employ rowing. A strong correlation between swimming mode and limb morphology also exists, with rowing appendages typically distally expanded or paddle shaped, whereas flapping appendages are typically distally tapering and wing-shaped (Walker, 2002; Walker and Westneat, 2002a; Walker and Westneat, 2002b). In addition, many rowing species are not fully aquatic like fishes, but instead are semi-aquatic. Semi-aquatic animals must function effectively on land, as well as in water, and limbs suited for rowing are better suited for terrestrial locomotion than those used for flapping (Vogel, 1994; Fish, 1996; Walker and Westneat, 2000).

Although the qualitative difference between rowing and flapping is established, empirical quantification of the kinematic distinctions between these locomotor styles has been rare. Such quantitative comparisons would be particularly useful for comparisons of lineages in which these styles have arisen multiple times, as these data could aid understanding of evolutionary diversification in locomotor function and the nature of functional transitions (e.g. gradual versus abrupt) in such groups. In this context, turtles provide an ideal study system. As a result of their immobilized axial skeleton and reduced tail, thrust in swimming turtles is generated exclusively by the movements of forelimbs and hindlimbs (Zug, 1971; Wyneken, 1997; Pace et al., 2001; Blob et al., 2008; Rivera, G. et al., 2011). Thus, evaluations of differences in swimming kinematics across taxa are not confounded significantly by the contributions of other structures to propulsion, such as flexible bodies, tails or specialized fins (Blake et al., 1995; Walker, 2000; Fish, 2002; Fish and Nicastro, 2003; Rivera et al., 2006).

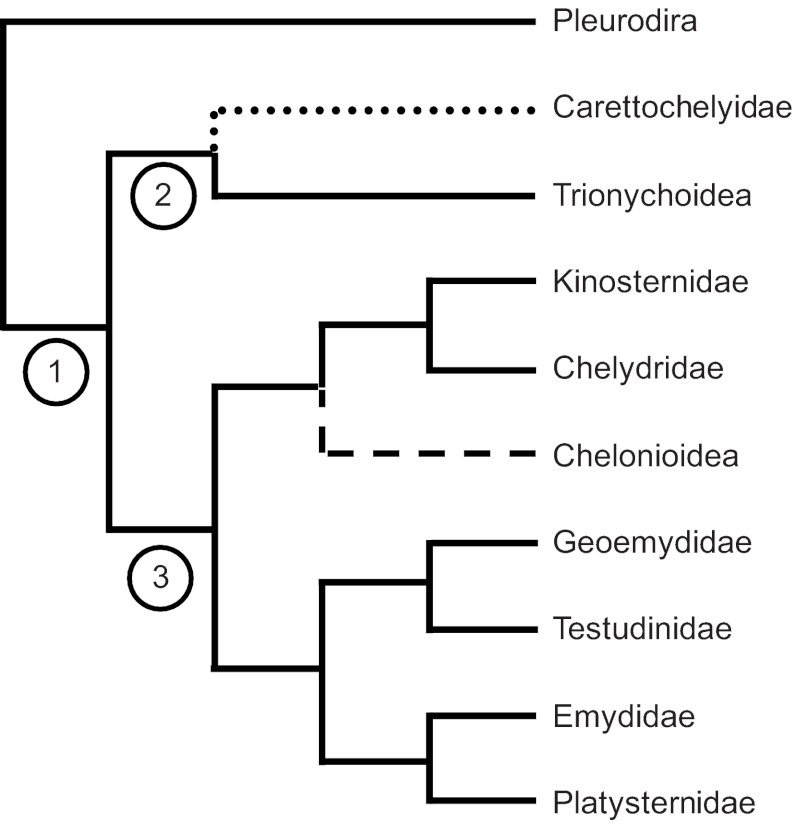
While there are many differences among species of aquatic turtle (>200 species) with regard to their locomotion in aquatic habitats (Webb, 1962; Zug, 1971; Walker, 1973; Davenport et al., 1984; Pace et al., 2001; Blob et al., 2008; Renous et al., 2008), one of the most striking examples is in the use of rowing versus flapping in swimming taxa. Asynchronous rowing is the more common and ancestral form of swimming in turtles (Joyce and Gauthier, 2004) and has been reported as the exclusive swimming mode for all but one freshwater species (Fig. 1). In rowing turtles, the forelimb of one side moves essentially in phase with the contralateral hindlimb, so that forelimbs (and hindlimbs) of opposite sides move asynchronously (Pace et al., 2001; Rivera et al., 2006; Rivera and Blob, 2010; Rivera, G. et al., 2011). Rowing species also tend to possess moderate to extensive webbing between the digits of the forelimb and hindlimb (Pace et al., 2001) [i.e. distally expanded and paddle-shaped (Walker and Westneat, 2002b)] (Fig. 2). Synchronous flapping is a much more rare locomotor style among turtles, definitively employed by the seven extant species of sea turtle (Wyneken, 1997) (Fig. 1). Flapping turtles swim via synchronous motions of forelimbs that have been modified into flat, elongate, semi-rigid flippers [i.e. distally tapering wing-like appendages (Walker and Westneat, 2002b)] (Fig. 2). Foreflippers may produce thrust on both upstroke and downstroke, but the hindlimbs have a negligible propulsive role (Walker, 1971; Walker, 1973; Davenport et al., 1984; Renous and Bels, 1993; Walker and Westneat, 2000). In addition, synchronous flapping-style swimming has been reported for a single freshwater species, the pig-nosed turtle Carettochelys insculpta (Walther, 1921; Rayner, 1985; Georges et al., 2000; Walker, 2002), which would represent an independent convergence on this swimming style within the chelonian lineage. Carettochelys insculpta is the sole extant member of the carettochelyid lineage that forms the sister taxon to the trionychid clade (Fig. 1) (Engstrom et al., 2004; Fujita et al., 2004; Iverson et al., 2007; Barley et al., 2010). While trionychids are highly specialized rowers with extensive webbing between the digits of the forelimb (Pace et al., 2001), this morphology is even further hypertrophied in C. insculpta through elongation of both the digits and webbing, so that the forelimbs of this species converge on at least a superficial resemblance to the foreflipper anatomy of sea turtles (Fig. 2) (Walther, 1921). Yet, while described as using flapping forelimb motions (Rayner, 1985; Ernst and Barbour, 1989; Georges et al., 2000), neither kinematic nor angle of attack measurements from C. insculpta are currently available that would allow quantitative comparisons with flapping by sea turtles and evaluations of the similarity of these purportedly convergent locomotor styles.

Fig. 1.

Recent phylogeny of turtles based on 14 nuclear genes, showing familial relationships. Solid lines indicate asynchronous anteroposterior rowing motions of forelimbs and hindlimbs for swimming (presumptive ancestral condition), dashed line indicates synchronous dorsoventral flapping motions of forelimbs for swimming in sea turtles (derived), and dotted line indicates swimming in Carettochelys insculpta (the only extant member of the family Carettochelyidae, and the only freshwater turtle species with forelimbs modified into flippers that swims using synchronous forelimb motions). The family Emydidae includes Trachemys scripta, Chelonioidea includes Caretta caretta and Trionychoidea includes Apalone ferox. Branch lengths do not reflect time since divergence. Time since divergence of focal lineages is indicated at nodes: 1=175 mya; 2=155 mya; 3=94 mya. Phylogeny is based on Barley et al. (Barley et al., 2010). Estimates of divergence times are based on Near et al. (Near et al., 2005).

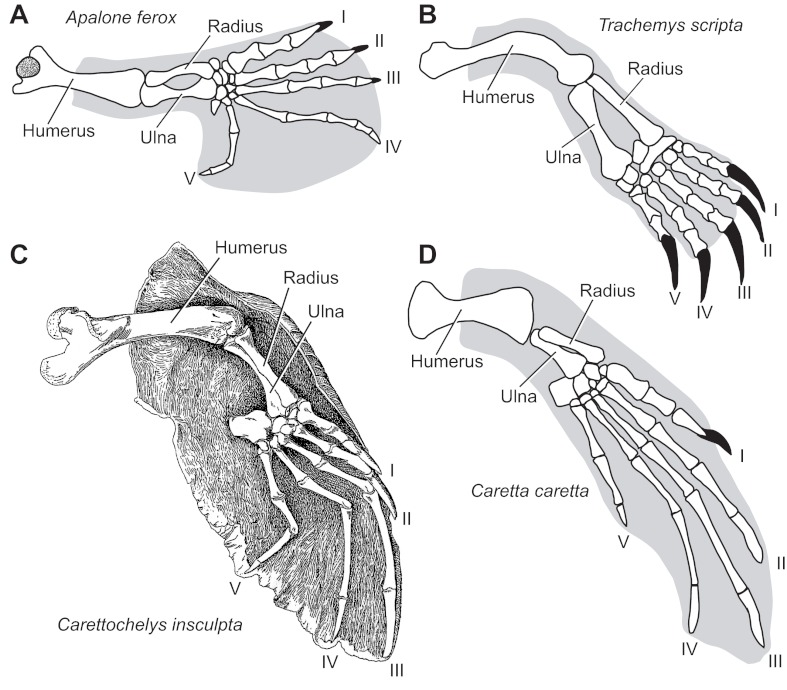
Fig. 2.

Ventral view of the left forelimb showing skeletal anatomy and outlines of the paddle/flipper in (A) Apalone ferox, (B) Trachemys scripta, (C) Carettochelys insculpta and (D) Caretta caretta. Outlines of the paddle/flipper end mid-humerus to indicate where the limb protrudes from the shell. Stippling on the humerus of A. ferox (A) indicates the depression of the intertubercular fossa. The humerus of T. scripta (B) is rotated 90 deg posteriorly, providing a posterior view that highlights the dorsally oriented curvature of the bone. The radius is anterior, lateral and ventral to the ulna for each species. Digits I–V are indicated. Images are redrawn and modified from source material [A. ferox (Sheil, 2003), T. scripta (Hall, 2000; Sheil and Portik, 2008), C. insculpta (Walther, 1921) and C. caretta (Wyneken, 2001; Sanchez-Villagra et al., 2007)].

Although descriptions of appendicular motions during swimming are commonly framed dichotomously as either rowing or flapping, these characterizations may be more correctly viewed as extremes along a continuum of possible limb motions (Gatesy, 1991; Carrano, 1999; Walker and Westneat, 2002b). Understanding appendicular swimming kinematics beyond just the predominant plane of motion (i.e. anteroposterior versus dorsoventral) would allow for a better understanding of whether suites of kinematic parameters (e.g. humeral and elbow kinematics, forefoot feathering) in turtles can rightfully be described as ‘rowing’ or ‘flapping’. Moreover, the angle of attack of the limb, which is determined by the combination of these kinematic parameters, can also provide telling information regarding the correct classification of these two locomotor styles. Although summaries of patterns of forelimb motion have been reported for some species of turtle (Walker, 1971; Davenport et al., 1984; Renous and Bels, 1993; Wyneken, 1997), detailed kinematic data from the forelimb during swimming are available for only a few species, including rowing by the emydid Trachemys scripta (red-eared slider) (Pace et al., 2001; Rivera and Blob, 2010) and the trionychid Apalone spinifera (spiny softshell turtle) (Pace et al., 2001), and flapping employed by the loggerhead sea turtle, Caretta caretta (Rivera, A. R. V. et al., 2011). Among rowers, there are some notable kinematic differences between the lentic, semi-aquatic generalist T. scripta and the lotic, aquatic specialist A. spinifera; in particular, the aquatic specialist greatly restricts the range of anteroposterior (less than half that of T. scripta) and dorsoventral (less than a third that of T. scripta) motions of the forelimb (Pace et al., 2001). These findings indicate that in addition to differences in kinematics between modes of locomotion (i.e. flapping versus rowing), significant variation can also exist within locomotor modes. Finally, the lack of data on the angle of attack of limbs for all but a few species of sea turtle (Davenport et al., 1984) limits the ability to fully interpret the hydrodynamic significance of kinematic results found in the literature.

The goals of this study were to: (1) examine forelimb kinematics within and between locomotor modes across turtle species to more precisely quantify and characterize the range of limb motions used by flappers and rowers, and (2) determine how C. insculpta uses synchronous forelimb movements to swim, allowing us to evaluate whether the limb motions displayed by this distinctive freshwater species are more strongly correlated with its phylogenetic relationships with other species, or with its locomotor mode (i.e. synchronous use of the foreflippers). To address these questions, we quantified forelimb kinematics during swimming by pig-nosed turtles (C. insculpta Ramsay 1886) and rowing Florida softshell turtles (Apalone ferox Schneider 1783), and compared these results with data from two additional species: our previous measurements of forelimb kinematics from the slider [T. scripta Schoepff 1972 (Rivera and Blob, 2010)] and the loggerhead sea turtle [C. caretta Linnaeus 1758 (Rivera, A. R. V. et al., 2011)], representing generalized rowing and characteristic flapping, respectively. Apalone ferox is an aquatic specialist and member of the sister group to C. insculpta; unlike other Apalone species [such as the previously studied A. spinifera (Pace et al., 2001)], A. ferox prefers the lentic conditions of lakes and ponds rather than lotic rivers and, when found in rivers, usually prefers the slower portions (Ernst and Lovich, 2009). As such, A. ferox may provide a more appropriate comparison to C. insculpta [which also prefers slow currents (Ernst and Barbour, 1989; Georges et al., 2000; Georges and Wombey, 1993)] than A. spinifera. Furthermore, data from A. ferox will provide an additional point of comparison among the diversity of rowing species, and, as a lentic species, provides an important comparison to T. scripta. Thus, the comparisons we perform in this study allow us to evaluate the extent to which carettochelyids and sea turtles have converged on similar flapping kinematics and angles of attack, or whether aspects of forelimb function in C. insculpta bear closer resemblance to those of their close relatives, such as A. ferox.

MATERIALS AND METHODS

Experimental animals

Access to turtles was provided by a commercial vendor (Turtles and Tortoises, Brooksville, FL, USA). Data were collected from two C. insculpta (carapace length=23.8±1.8 cm) and nine A. ferox (carapace length=15.1±1.1 cm). The number and size of C. insculpta were limited because of infrequent availability of this species. Turtles were housed in 600 liter (150 gallon) stock tanks equipped with pond filters; A. ferox were provided with dry basking platforms. Tanks were located in a temperature-controlled greenhouse facility, thus exposing turtles to ambient light patterns during the course of experiments. Carettochelys insculpta were fed a diet of commercially available algae wafers (Hikari, Hayward, CA, USA) and fresh kiwi and bananas. Apalone ferox were fed a diet of commercially available reptile food (ReptoMin, Tetra, Blacksburg, VA, USA), supplemented with earthworms. All animal care and experimental procedures were conducted in accordance with Clemson University IACUC guidelines (protocols 50110, 2008-013 and 2008-080). Experimental procedures followed those of our previous studies of slider turtles (Rivera and Blob, 2010) and sea turtles (Rivera, A. R. V. et al., 2011) as closely as possible to facilitate comparisons among the four species.

Collection and analysis of kinematic data

Kinematic data were collected simultaneously in lateral and ventral views (100 Hz) using two digitally synchronized high-speed video cameras (Phantom V4.1, Vision Research, Wayne, NJ, USA) from swimming C. insculpta and A. ferox. Locomotor trials for C. insculpta were conducted in a glass aquarium and those for A. ferox were conducted in a custom-built recirculating flow tank with a transparent glass side and bottom (see supplementary material Table S1). Ventral views were obtained by directing the ventral camera at a mirror oriented at a 45 deg angle to the transparent bottom of the tank. Swimming trials were collected from each turtle, yielding 17 and 22 cycles from each C. insculpta and 20–25 limb cycles from each A. ferox. For A. ferox, water flow was adjusted to elicit forward swimming behavior (Pace et al., 2001; Rivera and Blob, 2010); once the turtle was swimming, flow was adjusted to keep pace with the swimming speed of the animal so that it remained in the field of view of the cameras. As C. insculpta would not readily swim in flow, and because it was necessary for turtles to stay in the field of view of the camera for several consecutive limb cycles, the posterior margin of the carapace of C. insculpta was gently held, restricting forward movement of the animal while eliciting normal swimming motions of the limbs. Validity of this method was supported by the lack of a significant difference in the values of kinematic variables (N=8, see statistical analysis below) compared between free-swimming (N=4) and restrained (N=17) trials for one individual (MANOVA: Wilks lambda=0.386, F=2.389, d.f.=8, 12, P=0.084).

To facilitate digitization of animal movement from videos, a combination of white correction fluid and black marker pen were used to draw high-contrast points on the following 13 anatomical landmarks (Fig. 3): tip of the nose; shoulder; elbow; wrist (A. ferox only); digits 1, 3 and 5; an anterior and posterior point on the bridge of the shell (visible in lateral and ventral view); and right, left, anterior and posterior points on the plastron (plastral points visible in ventral view only). Landmark positions were digitized frame-by-frame in each video using DLTdataViewer2 (Hedrick, 2008). The three-dimensional coordinate data generated were then processed using custom MATLAB (Student Ver. 7.1, MathWorks, Natick, MA, USA) routines to calculate limb kinematics during swimming, including protraction and retraction of the humerus, elevation and depression of the humerus, extension and flexion of the elbow, forefoot orientation angle, and displacement of the tip of digit 3 in the anteroposterior and dorsoventral directions. Calculated values for kinematic variables from each limb cycle were fit to a quintic spline (Walker, 1998) to smooth the data, and interpolated to 101 values, representing 0 through 100% of the limb cycle. Transformation of the duration of each cycle to a percentage allowed us to compare locomotor cycles of different absolute durations and calculate average kinematic profiles and standard errors for each variable through the course of the limb cycle.

Fig. 3.

Representative still images from lateral (A,C) and ventral (B,D) videos showing landmarks digitized for kinematic analysis. (A,B) Apalone ferox. Points 1–9 are the same in lateral and ventral view; points 10–13 are only visible in ventral view. Landmarks include: 1, tip of the nose; 2, shoulder; 3, elbow; 4, wrist; 5, digit 1; 6, digit 3; 7, digit 5; 8, anterior point on bridge; 9, posterior point on bridge; 10, point on left side of plastron; 11, point on right side of plastron; 12, posterior point on plastron; and 13, anterior point on plastron. (C,D) Carettochelys insculpta. Points 1–8 are the same in lateral and ventral view; points 9–12 are only visible in ventral view. Landmarks include: 1, tip of the nose; 2, shoulder; 3, elbow; 4, digit 1; 5, digit 3; 6, digit 5; 7, anterior point on bridge; 8, posterior point on bridge; 9, point on left side of plastron; 10, point on right side of plastron; 11, posterior point on plastron; and 12, anterior point on plastron. A representative video of swimming in C. insculpta is provided in supplementary material Movie 1.

A humeral protraction/retraction angle of 0 deg indicates that the humerus is perpendicular to the midline of the turtle, while an angle of 90 deg indicates a fully protracted forelimb with the distal end of the humerus directed anteriorly (an angle greater than 90 deg would indicate that the distal end of the humerus was medial to the shoulder, whereas an angle of –90 deg would indicate a fully retracted forelimb with the distal tip of the humerus directed posteriorly). A humeral elevation/depression angle of 0 deg indicates that the humerus is in the horizontal plane. Angles greater than zero indicate elevation above the horizontal (distal end above proximal end), whereas negative angles indicate depression of the humerus (distal end lower than proximal end). Extension of the elbow is indicated by larger extension/flexion angles and flexion is indicated by smaller values. An elbow angle of 0 deg indicates a hypothetical fully flexed elbow (i.e. humerus perfectly parallel to radius and ulna), 180 deg indicates a fully extended elbow and 90 deg indicates that the humerus is perpendicular to the radius and ulna. Forefoot orientation angle was also calculated as the angle between a vector pointing forwards along the anteroposterior midline (also the path of travel) and a vector emerging from the palmar surface of a plane defined by the tips of digits 1 and 5 and the elbow (C. insculpta) or wrist (A. ferox); this angle was transformed by subtracting 90 deg from each value (Pace et al., 2001; Rivera and Blob, 2010; Rivera, A. R. V. et al., 2011). A high-drag orientation of the forefoot paddle with the palmar surface of the paddle directed opposite the direction of travel (and in the same direction as the flow of water) is indicated by an angle of 90 deg, and a perfect low-drag orientation of the forefoot paddle is indicated by an angle of 0 deg. Angle of attack was calculated as the angle between (1) a motion vector that describes the motion of the tip of the forefoot paddle relative to the position of the shoulder, and (2) a vector rotated 90 deg from the normal to the paddle (described above) so that the vector points in the direction of the leading edge of the paddle. Angle of attack ranges from –180 deg to 180 deg. Negative angles of attack refer to a leading edge that is oriented clockwise relative to the motion vector, whereas positive angles of attack refer to a leading edge that is oriented counterclockwise relative to the motion vector.

Statistical analysis

To assess general patterns of movement, the overall mean and standard error of each variable were calculated for all swimming trials. Kinematic variables include: (i) maximum protraction, retraction, elevation and depression of the humerus, (ii) maximum elbow extension and flexion, (iii) anteroposterior and dorsoventral excursion of the humerus, (iv) elbow excursion, (v) percentage of the cycle at which maximum elbow extension occurs, (vi) percentage of the limb cycle at which a switch from protraction to retraction occurs, (vii) maximum, minimum and range of feathering of the forefoot, (viii) ratio of dorsoventral to anteroposterior excursion of the tip of digit 3 and (ix) angle of attack at the midpoint of the two phases of the limb cycle. Because the maximum values for each limb cycle do not always occur at the same percentage of the limb cycle, it is possible that the average of the maximum values calculated for all limb cycles may be masked (appear lower) in average kinematic profiles. We compare our data for C. insculpta and A. ferox with those previously published for rowing-style swimming in the generalized freshwater slider T. scripta (Rivera and Blob, 2010) and flapping-style swimming in loggerhead sea turtles (C. caretta) (Rivera, A. R. V. et al., 2011). We used SYSTAT 13 (Systat Software, Chicago, IL, USA) and R 2.12 (R Development Core Team, 2010) for statistical analyses, and P<0.05 as the criterion for significance.

To determine whether swimming kinematics differed overall among the four species, we conducted a two-way nested MANOVA, with species as a fixed factor and individual (nested within species) as a random factor. All multivariate analyses used standardized values (Z-scores) (Gotelli and Ellison, 2004) for eight angular kinematic variables: maximum humeral protraction, retraction, elevation and depression; maximum elbow extension and flexion; and maximum and minimum forefoot feathering. Excursions were not included in multivariate analyses because they are compositional data (i.e. the difference between minimum and maximum values), and as such are highly correlated with the variables used to calculate them. Next, kinematic differences were visualized using principal components analysis (PCA). While PCA can visually demonstrate the difference in kinematics among the species, viewing only a subset of PC axes does not accurately illustrate the true multidimensional difference among them, and it can be difficult to interpret plots of more than two or three axes at a time. To illustrate the multidimensional differences more clearly, the Euclidean distances (D) between all pairs of species means were calculated using the eight variables described above. Euclidean distances provide information on the magnitude of difference (or similarity) between pairs of species, with smaller values indicating greater similarity than larger values. To determine which pairs of species differed, we used a permutation procedure (Adams and Collyer, 2009; Marsteller et al., 2009), in which the observed Euclidean distances between the least-squares means for the proper species–turtle assignments were compared with a distribution of possible values obtained by randomizing trial data among species–individual assignments. This randomization process was repeated 9999 times and the proportion of randomly generated values that exceeded the observed values was treated as the significance level (P_rand) (Adams and Collyer, 2007; Collyer and Adams, 2007; Adams and Collyer, 2009; Marsteller et al., 2009).

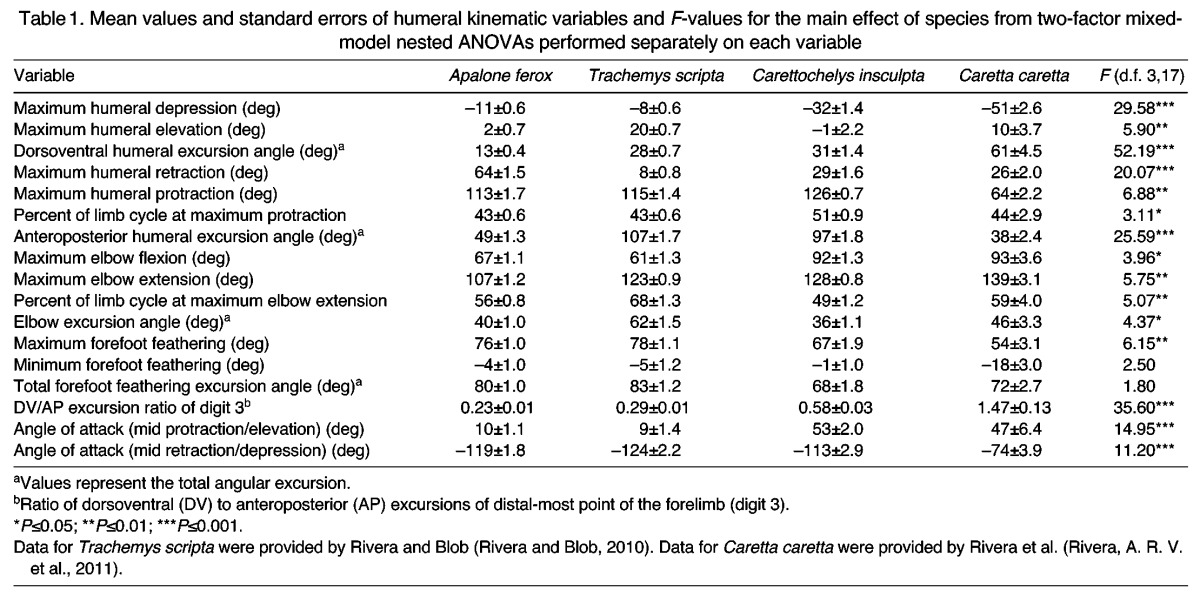
To evaluate differences among the species with respect to the 17 kinematic variables that characterize swimming in each species, we conducted separate two-way mixed-model nested ANOVAs (corrected for unbalanced sampling), with species as a fixed factor and individual (nested within species) as a random factor. For each significant ANOVA, we conducted post hoc Tukey’s pair-wise mean comparison tests to determine which species pairs differed. In tabular data summaries we provide d.f. and F-values to clarify the potential effects of making multiple comparisons (Table 1).

Table 1.

Mean values and standard errors of humeral kinematic variables and F-values for the main effect of species from two-factor mixed-model nested ANOVAs performed separately on each variable

To compare overall kinematic trajectories (i.e. the shapes of kinematic profiles) for each of the major limb motions across species, we computed time-average vectors from the values of four variables (anteroposterior and dorsoventral humeral motion, elbow motion and forefoot orientation) over the duration of the limb cycle (1–100%). Then, for each variable, we used standard vector equations (Hamilton, 1989; Hankison et al., 2006) to calculate the angle between these vectors for each pair-wise combination of species. Angles between these vectors indicate the degree of similarity or difference between the trajectories (i.e. shapes) of the average kinematic profiles for each variable. An angle of 90 deg between kinematic vectors indicates orthogonal, or independent, trajectories, and thus different kinematic patterns. In contrast, an angle of 0 deg indicates positively correlated, similar kinematic patterns, whereas angles near 180 deg would indicate negatively correlated (e.g. phase shifted) kinematic patterns.

RESULTS

Herein we report new data on the kinematics of swimming in C. insculpta (39 cycles from two turtles) and A. ferox (195 cycles from nine turtles); we compare our new data to previously published findings for T. scripta [136 cycles from seven turtles (Rivera and Blob, 2010)] and C. caretta [33 cycles from three turtles (Rivera, A. R. V. et al., 2011)]. Similar to C. insculpta, the smaller number of individuals from which data were collected for C. caretta reflects their rare and threatened status (Rivera, A. R. V. et al., 2011). Kinematic plots depicting the general pattern of limb motion during swimming in each species were constructed using our new data for C. insculpta and A. ferox and published data for T. scripta (Rivera and Blob, 2010) and C. caretta (Rivera, A. R. V. et al., 2011). Turtles of each species swam using similar forelimb cycle frequencies (C. insculpta: 1.78±0.06 cycles s^–1; A. ferox: 2.24±0.03 cycles s^–1; T. scripta: 2.29±0.04 cycles s^–1; C. caretta: 1.85±0.05 cycles s^–1). A summary of sample sizes from each individual, by species, is given for statistical analyses (see supplementary material Table S1).

Kinematics of swimming in C. insculpta and A. ferox

Limb motions in swimming C. insculpta are characterized by a threefold greater degree of anteroposterior humeral motion (97±1.8 deg) than dorsoventral motion (31±1.4 deg; Fig. 4A,B, Table 1). Hence, following previous conventions, a limb cycle in C. insculpta is defined similarly to that in rowing species, beginning at the start of humeral protraction and ending at the start of the next protraction cycle (Pace et al., 2001; Blob et al., 2008; Rivera and Blob, 2010). Protraction in C. insculpta occupies slightly more than the first half (51±0.9%) of the limb cycle (Fig. 4A, Table 1). The humerus reaches a single peak of protraction (126±0.7 deg), followed by a return of the humerus to the retracted position (maximum retraction angle=29±0.6 deg; Fig. 4A, Table 1). Throughout the limb cycle, the humerus of C. insculpta is held depressed relative to the horizontal, and displays a bimodal pattern of elevation and depression, reaching a first peak during protraction and a second peak during retraction (Fig. 4A,B). The elbow is at its most flexed position at the beginning and end of the limb cycle (92±1.3 deg). The elbow gradually extends throughout protraction, reaching a single peak of 128±0.8 deg at 49±1.2% of the limb cycle, approximately coincident with the timing of maximal humeral protraction (51±0.9%), followed by a return to the fully flexed position by the end of the cycle (Fig. 4C, Table 1). During the first ∼10% of the limb cycle, the forefoot of C. insculpta is rotated into a low-drag, feathered orientation; the forefoot remains feathered throughout the recovery (i.e. protraction) phase (Fig. 4D, Table 1). Concurrent with the start of humeral retraction (i.e. thrust phase), the forefoot is rotated into a high-drag orientation, nearly perpendicular to the direction of flow (67±1.9 deg; Fig. 4D, Table 1). Maximum high-drag forefoot orientation is achieved near the end of the thrust phase, after which the forefoot is rotated back to a feathered orientation for the remainder of the swimming stroke.

Fig. 4.

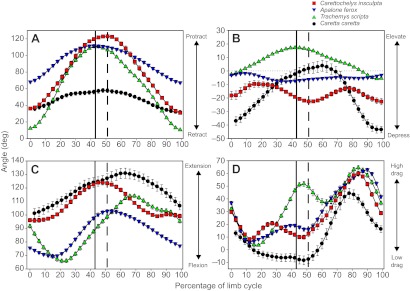
Mean kinematic profiles of swimming in four species of turtle: Carettochelys insculpta (red squares), rowing Apalone ferox (inverted blue triangles), rowing Trachemys scripta (green triangles) and flapping Caretta caretta (black circles). Data for T. scripta were provided by Rivera and Blob (Rivera and Blob, 2010). Data for C. caretta were provided by Rivera et al. (Rivera, A. R. V. et al., 2011). Each trial was normalized to the same duration and angle values were interpolated to represent 0–100% of the limb cycle. For C. insculpta, A. ferox and T. scripta, the limb cycle is defined as protraction of the humerus followed by retraction; for C. caretta, the limb cycle is defined as elevation of the humerus followed by depression. Mean ± s.e.m. angle values are plotted for every third increment (every 3% through the cycle) for all individuals. Solid vertical lines demarcate the switch from protraction to retraction in A. ferox and T. scripta at 43% of the limb cycle. Dashed vertical lines indicate the switch from protraction to retraction in C. insculpta and from elevation to depression in C. caretta at 51% of the limb cycle. (A) Humeral protraction and retraction (i.e. angle from the transverse plane). An angle of 0 deg indicates that the humerus is perpendicular to the midline of the turtle, while an angle of 90 deg indicates a fully protracted forelimb with the distal end of the humerus directed anteriorly (an angle of –90 deg would indicate a fully retracted forelimb with the distal tip of the humerus directed posteriorly). (B) Humeral elevation and depression (i.e. angle from the horizontal plane). An angle of 0 deg indicates that the humerus is in the horizontal plane. Angles greater than zero indicate elevation above the horizontal (distal end above proximal end) and negative angles indicate depression of the humerus (distal end lower than proximal end). Peak elevation is coincident with peak protraction for T. scripta and C. caretta, meaning that limb protraction happens at the same time as elevation and retraction is concurrent with depression. (C) Elbow flexion and extension. Extension is indicated by larger angles and flexion is indicated by smaller angles. An angle of 0 deg indicates complete flexion, 180 deg indicates a fully extended elbow, and 90 deg indicates that the humerus is perpendicular to the radius and ulna. (D) Forefoot orientation angle is calculated as the angle between a vector pointing forwards along the anteroposterior midline (also the path of travel) and a vector emerging from the palmar surface of a plane defined by the tips of digits 1 and 5 and the elbow; this angle is transformed by subtracting 90 deg from each value. A high-drag orientation of the forefoot paddle with the palmar surface of the paddle directed opposite the direction of travel (and in the same direction as the flow of water) is indicated by a feathering angle of 90 deg, and a perfect low-drag orientation of the forefoot paddle is indicated by a feathering angle of 0 deg.

Because A. ferox swims via rowing motions of the limbs, we follow the previously established convention of defining the limb cycle as starting at the beginning of humeral protraction and ending at the start of the next protraction cycle (Pace et al., 2001; Blob et al., 2008; Rivera and Blob, 2010). The limb cycle can be divided into two separate phases; humeral protraction represents the ‘recovery’ phase, followed by retraction of the humerus through the ‘thrust’ phase. In A. ferox, humeral protraction comprises the first 43±0.6% (mean ± s.e.m.) of the limb cycle (Fig. 4A; Table 1). A single peak of humeral protraction (113±1.7 deg) is followed by a return of the forelimb to the retracted position (maximum retraction angle=64±1.5 deg; Fig. 4A, Table 1). Throughout the limb cycle, the humerus of A. ferox shows very little elevation or depression, primarily being held at a slightly depressed angle relative to the horizontal plane (Fig. 4B). Hence, the range of anteroposterior humeral motion (49±1.3 deg) is far greater than the dorsoventral range (13±0.4 deg; Fig. 4A,B, Table 1). The elbow flexes at the beginning of protraction, but then gradually extends throughout the remainder of protraction, reaching a single peak of 107±1.2 deg at 56±0.8% of the limb cycle, followed by flexion (Fig. 4C, Table 1). During the first ∼10% of the limb cycle, the forefoot of A. ferox is rotated into a low-drag, feathered orientation; the forefoot remains feathered throughout the recovery (i.e. protraction) phase (Fig. 4D, Table 1). Shortly after the start of humeral retraction (i.e. thrust phase), the forefoot is rotated into a high-drag orientation, nearly perpendicular to the direction of flow (76±1.0 deg; Fig. 4D, Table 1). Maximum high-drag forefoot orientation is achieved near the end of the thrust phase, after which the forefoot is rotated back to a feathered orientation for the remainder of the swimming stroke.

Multi-species comparisons of the kinematics of rowing and flapping

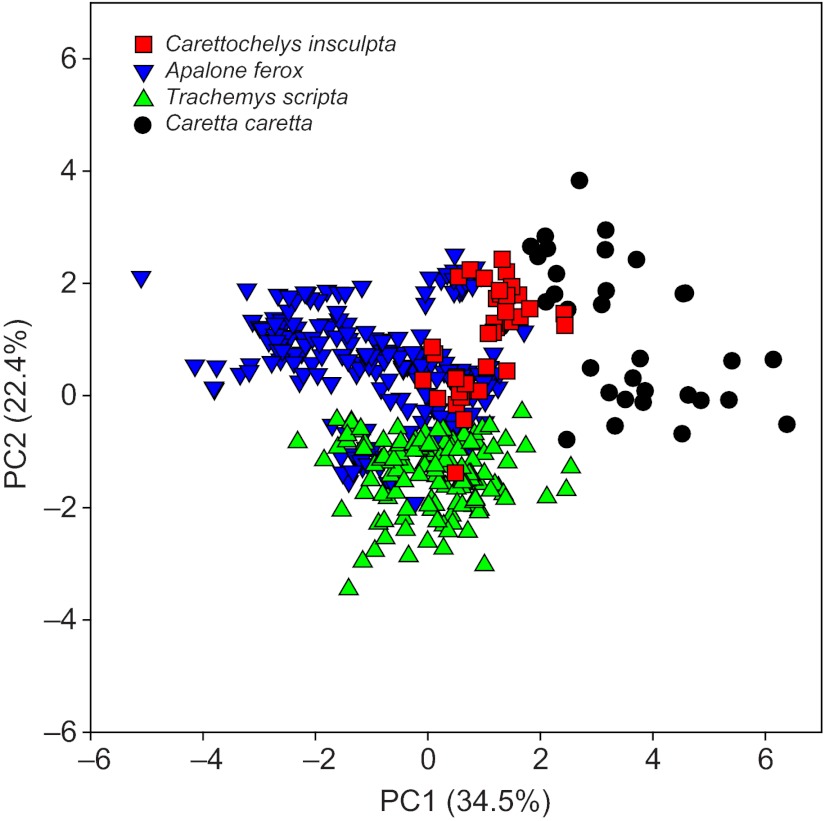
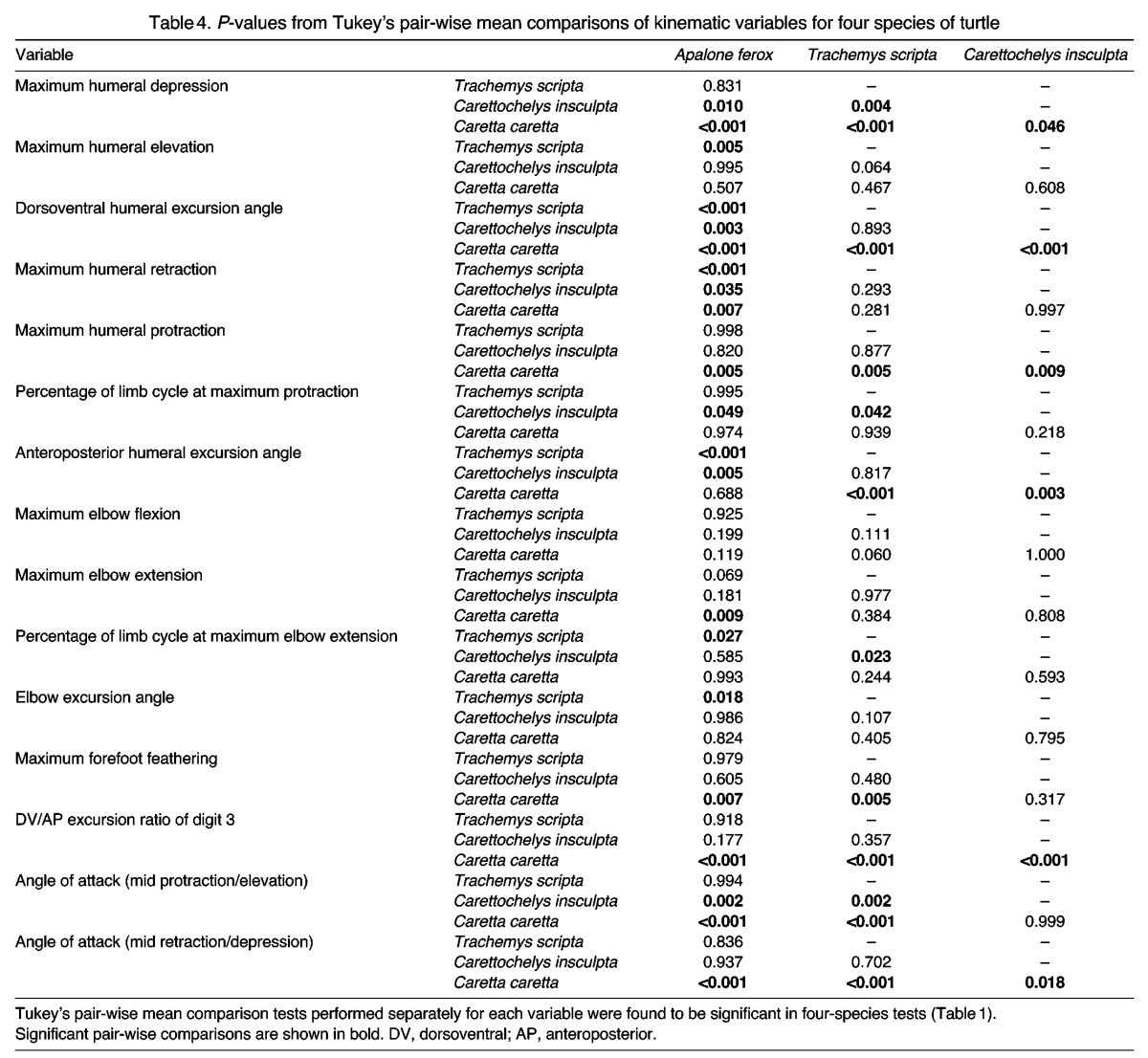
Using nested MANOVA, we found significant differences in the kinematics of swimming among C. insculpta, A. ferox, T. scripta and C. caretta (Wilks lambda=0.002, F=8.74, d.f.=24, 29, P<0.001). PCA visually demonstrates the differences in overall swimming kinematics among these species (Fig. 5, see Table 2 for PC loadings). While the first two PC axes account for 56.9% of the total variation in angular forelimb kinematics among species, the true multidimensional difference among them is depicted more clearly by the pair-wise Euclidean distances between species means (Table 3). Listed from smallest to largest, these were: A. ferox–T. scripta, A. ferox–C. insculpta, T. scripta–C. insculpta, C. insculpta–C. caretta, T. scripta–C. caretta and A. ferox–C. caretta (Table 3). All pair-wise species comparisons were found to be significant using permutation tests (P_rand<0.001). Two-way nested ANOVAs showed significant differences among the species for 13 out of 15 kinematic variables; only minimum forefoot feathering and total forefoot feathering excursion angle were found to not differ (Table 1). Tukey’s pair-wise species comparison results for each significant ANOVA are given in Table 4.

Fig. 5.

Plot of the first two axes of a principal components analysis of swimming kinematics for eight variables in four species of turtle: Carettochelys insculpta (red squares), rowing Apalone ferox (blue inverted triangles), rowing Trachemys scripta (green triangles) and flapping Caretta caretta (black circles). The first two axes explain 56.9% of the total variation in forelimb swimming kinematics. See Table 2 for axis loadings.

Table 2.

PC loadings from a principal components analysis of swimming kinematics for eight variables in four species of turtle

Table 3.

Euclidean distance matrix comparing kinematics of swimming in four species of turtle

Table 4.

P-values from Tukey’s pair-wise mean comparisons of kinematic variables for four species of turtle

While the predominant direction of humeral motion for all three freshwater species is anteroposterior, the range of motion in A. ferox (49±1.3 deg) and C. caretta (38±2.4 deg) is similarly small and differs significantly from that of C. insculpta (97±1.8 deg) and T. scripta (107±1.7 deg), which do not differ (Fig. 4A, Tables 1, 4). With its narrow anteroposterior range of humeral motion and a peak value of protraction similar to that of C. insculpta and T. scripta, A. ferox retracts the humerus significantly less than other species (Fig. 4A, Tables 1, 4). Additionally, flapping C. caretta protract the humerus significantly less than the three freshwater species (Fig. 4, Tables 1, 4). While the limb cycle was defined as protraction followed by retraction for the three freshwater species, for sea turtles (C. caretta) it was defined as humeral elevation (at 51±2.5% of the limb cycle) followed by depression (Rivera, A. R. V. et al., 2011). Despite this difference, all species exhibit humeral protraction during the first phase of the limb cycle (Fig. 4A), and only slight (though significant) differences were found in the timing of maximum protraction between C. insculpta (51±0.9%) and both A. ferox (43±0.6%) and T. scripta (43±0.6%) (Fig. 4A, Tables 1, 4). Similarly, the timing of maximum protraction in C. caretta (44±2.9%) did not differ from that of freshwater species.

Three distinct patterns of dorsoventral motion are evident among the four species (Fig. 4B). Rowing T. scripta and flapping C. caretta are both characterized by a single peak of elevation (coincident with the timing of peak protraction), while C. insculpta displays a bimodal pattern of humeral elevation, and A. ferox displays minimal humeral dorsoventral movement (Fig. 4B). Despite differences in the general pattern or presence of a peak in elevation, only minimal differences were found in the peak values of humeral elevation: T. scripta elevates the humerus significantly more than A. ferox (20±0.7 versus 2±0.7 deg), with values for C. insculpta (–1±2.2 deg) approaching a significant difference from T. scripta (P=0.064; Fig. 4B, Tables 1, 4). Similarly, dorsoventral humeral excursion also exhibits three distinct patterns among the four species (Fig. 4B). Apalone ferox displays significantly less dorsoventral motion (13±0.4 deg) than the other species, C. insculpta and T. scripta display ranges of motion similar to each other (31±1.4 and 28±0.7 deg) that are intermediate and significantly different than others, and, finally, C. caretta displays the greatest range of dorsoventral motion (61±4.5 deg; P<0.001 for all comparisons; Fig. 4B, Tables 1, 4). Maximum humeral depression was significantly greater in C. caretta (–51±2.6 deg) than in C. insculpta (–32±1.4 deg), and was significantly greater in C. insculpta and C. caretta than in rowers, but rowing A. ferox (–11±0.6 deg) and T. scripta (–8±0.6 deg) did not differ (Fig. 4B, Tables 1, 4).

Motion at the elbow displays a generally similar pattern in all four species, extending during the first phase of the limb cycle with flexion beginning at roughly the same time as the second phase of the limb cycle (Fig. 4C). However, the pattern in A. ferox and T. scripta begins with a period of elbow flexion, reaching a similar maximum elbow flexion angle of 67±1.1 and 61±1.3 deg, respectively, at ∼20% of the limb cycle (Fig. 4C, Tables 1, 4). Carettochelys insculpta and C. caretta begin and end each cycle with a maximally flexed elbow (92±1.3 and 93±3.6 deg; Fig. 4C, Tables 1, 4). Both rowers and species typically viewed as ‘flappers’ display degrees of elbow flexion that are similar within these two categories, visibly different between categories, and show significant differences via two-way ANOVA (Table 1); however, only the greatest difference, between rowing T. scripta and flapping C. caretta, approaches significance (P=0.060; Table 4). Similarly, only minimal differences were found with regard to maximum elbow extension: only A. ferox and C. caretta differ (107±1.2 versus 139±3.1 deg; Fig. 4C, Tables 1, 4). Elbow excursion angle differs significantly only between T. scripta (62±1.5 deg) and A. ferox (40±1.0 deg), though C. insculpta displays the least motion at the elbow (36±1.1 deg); this discrepancy is likely due to the smaller sample size for the rare species, leading to a less powerful but more conservative statistical test. Finally, maximum elbow extension occurs significantly later in the limb cycle for T. scripta (68±1.3%) than for A. ferox (56±0.8%) or C. insculpta (49±1.2%), but does not differ from that of C. caretta (59±4.0%; Fig. 4C, Tables 1, 4).

The four species display the fewest kinematic differences in forefoot feathering orientation (Fig. 4D), with only maximum (i.e. high-drag) forefoot orientation displaying significant differences (Table 1). All species display the same general pattern of rotating the forefoot (also called the flipper in C. insculpta and C. caretta) into a maximally feathered (i.e. low-drag) orientation during the first phase of the limb cycle (‘recovery phase’), followed by rotation to a high-drag orientation during the second phase of the limb cycle (‘thrust phase’) (Fig. 4D). Caretta caretta is the only species to exhibit a negative inclination of the forefoot at any point of the swimming cycle (Fig. 4D). Apalone ferox and T. scripta display significantly greater high-drag forefoot angles than C. caretta (76±1.0 and 78±1.1 deg versus 54±3.1 deg), with C. insculpta also achieving higher, though not significantly different, values (67±1.9 deg) (Fig. 4D, Tables 1, 4).

Results of our kinematic vector analysis (Table 5) are concordant with other statistical analyses. For example, although A. ferox holds the humerus in a more protracted orientation than C. caretta throughout the limb cycle, the kinematic vector angle of only 2 deg between profiles for anteroposterior humeral motion of these species indicates that the shapes of these curves are highly correlated (Fig. 4A, Table 5). Conversely, C. caretta and T. scripta display very different profiles of dorsoventral humeral motion (Fig. 4B) and a kinematic vector angle of 94 deg (Table 5), indicating nearly orthogonal trajectories – making these two species excellent turtle examples of stereotypical flapping and rowing, respectively. Additionally, small kinematic vector angles for each pair-wise species comparison support the assertion that species are displaying generally similar patterns of elbow motion (Table 5, Fig. 4C).

Table 5.

Pair-wise angles between kinematic trajectory vectors

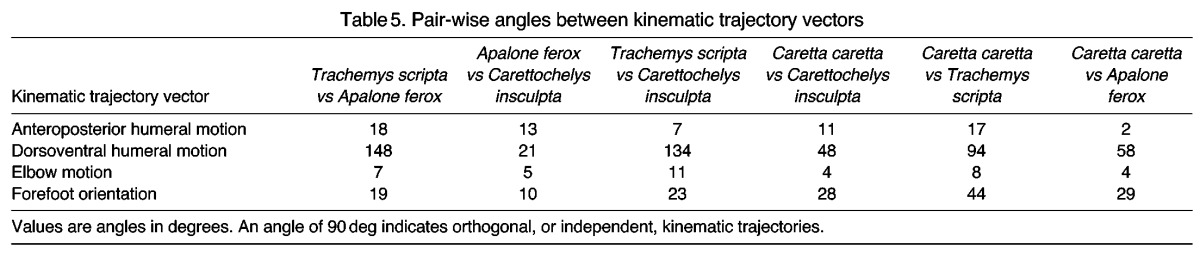
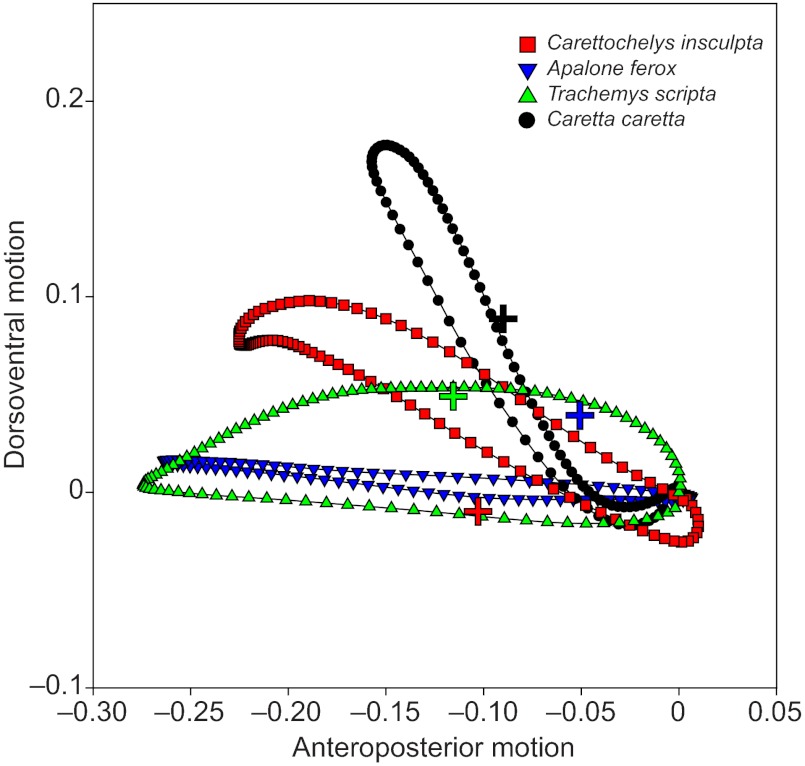
Species also differed with respect to motion of the distal-most point of the forelimb (digit 3) (Fig. 6, Table 1). Despite greater dorsoventral motion in T. scripta, the trajectories of digit 3 for both A. ferox and T. scripta (asynchronous rowers) are horizontal and the ratios of dorsoventral to anteroposterior motion of digit 3 (DV/AP) in each do not differ significantly (A. ferox DV/AP=0.23±0.01, T. scripta DV/AP=0.29±0.01; Fig. 6, Table 4). Flapping C. caretta approach (but do not attain) a vertical trajectory, with a DV/AP ratio that differs significantly from that of A. ferox and T. scripta (C. caretta DV/AP=1.47±0.13; Fig. 6, Table 4). Finally, C. insculpta exhibit a trajectory of the tip of the flipper that is intermediate between that of A. ferox/T. scripta and C. caretta, with a DV/AP ratio that differs significantly from that of C. caretta but does not differ significantly from those of A. ferox and T. scripta (C. insculpta DV/AP=0.58±0.03; Fig. 6, Table 4).

Fig. 6.

Lateral view of the paths taken by the distal-most point of the forelimb (digit 3; tip of the flipper in Carettochelys insculpta and Caretta caretta) for C. insculpta (red squares), Apalone ferox (blue inverted triangles), Trachemys scripta (green triangles) and C. caretta (black circles) showing the amount of anteroposterior and dorsoventral motion relative to the turtle’s body throughout the limb cycle. Coordinate positions of X and Z throughout the swimming cycle were smoothed and interpolated to 101 points. Paths are the average of all trials for each species, and have been scaled to unit size to facilitate comparisons of trajectories. Paths start at the origin. Position of the shoulder relative to the path is indicated for each species with a color-coded cross. Despite greater dorsoventral motion in T. scripta, the trajectories of A. ferox and T. scripta (rowers) are both horizontal. Caretta caretta (flapper) approaches (but does not attain) a vertical trajectory. Finally, in C. insculpta, the trajectory of the tip of the flipper is intermediate between A. ferox/T. scripta and C. caretta. The ratios of dorsoventral to anteroposterior motion of digit 3 designate A. ferox, T. scripta and C. insculpta as rowers (ratios less than 1: DV/AP=0.23±0.01, 0.29±0.01 and 0.58±0.03, respectively) and C. caretta as a flapper with a ratio greater than 1 (DV/AP=1.47±0.13).

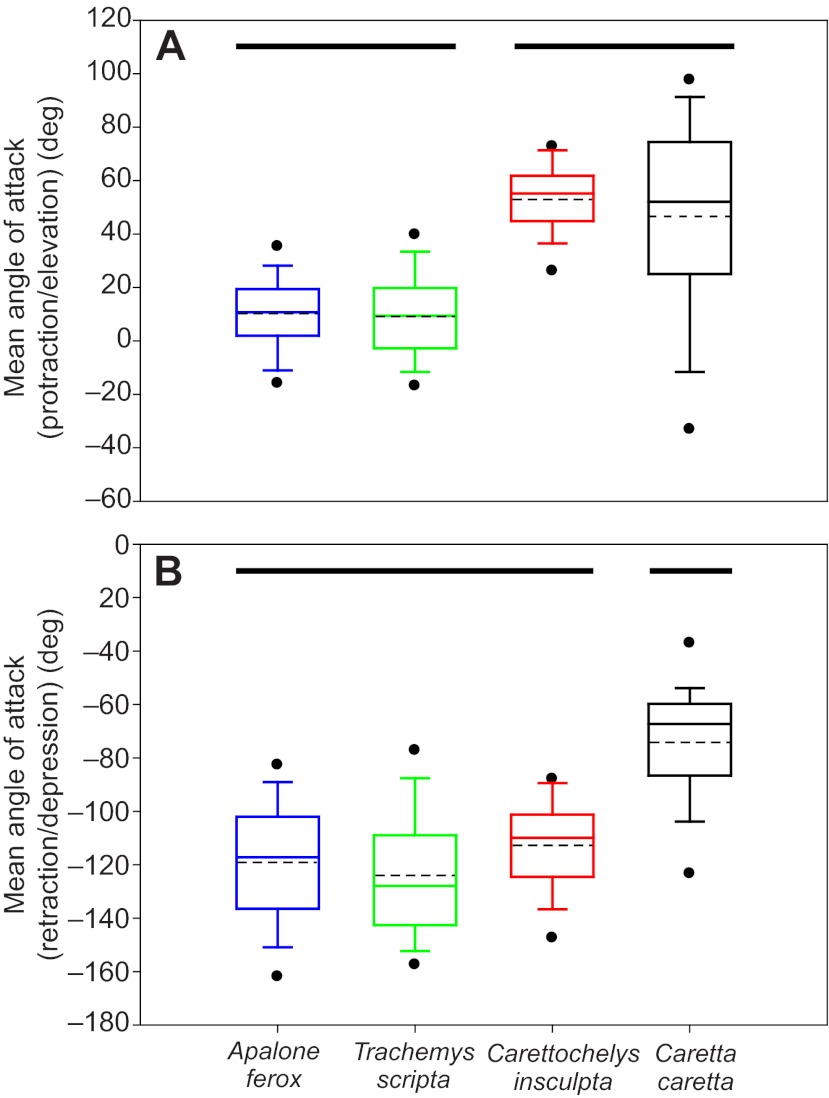
Significant differences between species were also identified for angle of attack at the midpoint of both phases of the limb cycle (Fig. 7, Table 1). For rowing A. ferox and T. scripta, angle of attack during protraction was near the theoretical optimum of 0 deg (Walker and Westneat, 2002b). In contrast, C. insculpta and C. caretta both exhibit values of ∼50 deg during the early phase of the cycle. Results of Tukey’s tests indicate that rowing A. ferox and T. scripta form one homogenous subset, and C. insculpta and C. caretta form a second homogenous subset (Fig. 7, Table 4). For the latter phase of the cycle, A. ferox, T. scripta and C. insculpta exhibit angles of attack of approximately –120 deg (Fig. 7; Table 4), and form a homogenous subset that is distinct from C. caretta (angle of attack=–74±3.9 deg).

Fig. 7.

Comparison of hydrodynamic angle of attack of the forelimb at mid-phase for protraction/elevation (A) and retraction/depression (B) in four species of turtle. For each trial, a representative midstroke protraction/elevation value was calculated as the mean of the five central values during this phase, and a representative midstroke retraction/depression value was calculated as the mean of the five central values during this phase. Box plots are based on the distributions of these representative values: solid lines indicate medians, dashed lines indicate means, box margins represent 50th and 75th percentiles, whiskers show 10th and 90th percentiles, and circles show 5th and 95th percentiles. Angle of attack was calculated as the angle between a vector representing the path of motion of the tip of the forelimb (digit 3) and a vector emerging from the palmar surface of a plane defined by the tips of digits 1 and 5 and the elbow. Small angular values indicate a shallow angle between the path of limb motion and the forefoot; an angle of 0 deg during protraction/elevation indicates the leading edge of the forefoot is oriented perfectly along the path of motion in a low-drag orientation. Maximum drag orientation of the forefoot paddle relative to the path of motion of the forefoot is indicated by an angle of 90 deg during protraction/elevation, and an angle of –90 deg during retraction/depression. Results of post hoc multiple comparison Tukey’s tests are indicated with solid black lines above the boxplots. During protraction/elevation, two groups were identified; rowing Apalone ferox and Trachemys scripta do not differ from one another, and Carettochelys insculpta groups with flapping Caretta caretta. However, during retraction/depression, C. insculpta groups with rowing species.

DISCUSSION

Overview of multivariate comparisons of forelimb kinematics across swimming styles in turtles

Based on multivariate comparisons of kinematic variables representative of the overall pattern of forelimb kinematics, we found significant differences among all of the species. In our analysis of Euclidean distances, the two freshwater species that use asynchronous rowing (A. ferox and T. scripta) were found to have the most similar forelimb kinematics (D=2.48; Fig. 5, Table 3). Between these rowers and the species typically considered ‘flappers’, forelimb kinematics were most similar between the sister taxa A. ferox and C. insculpta (D=2.66; Fig. 5, Table 3), followed by T. scripta and C. insculpta (D=2.96; Fig. 5, Table 3). The three largest pair-wise distances were between flapping sea turtles (C. caretta) and the three freshwater species, but with C. insculpta being most similar to C. caretta (D=3.33; Fig. 5, Table 3). Finally, the rowing-style forelimb kinematics of swimming in T. scripta (a semi-aquatic generalist) were more similar to the flapping kinematics of C. caretta (T. scripta–C. caretta, D=4.45) than were those of the highly aquatic A. ferox (A. ferox–C. caretta, D=4.56). These results highlight the overall intermediacy of swimming forelimb kinematics in C. insculpta to those of typical ‘rowers’ and ‘flappers’, as well as the distinctiveness of the flapping forelimb kinematics employed by sea turtles.

Comparison of rowing in A. ferox and T. scripta

Although rowing and flapping are really points along a continuum of possible limb motions, our data also support the conclusion that rowing should, itself, be viewed as a continuum. While forelimb kinematics are most similar between the two asynchronously rowing species, we found some strong differences between the kinematics employed by generalist rowers and specialist rowers. For example, A. ferox restricts the range of both anteroposterior and dorsoventral humeral motions by limiting humeral retraction and elevation compared with T. scripta. This is similar to the differences reported for T. scripta and another softshell species, A. spinifera (Pace et al., 2001). Rowing appears to be fairly similar between A. ferox and A. spinifera, though the latter primarily holds the humerus elevated with respect to the horizontal while the humerus of the former is generally depressed. In addition, when compared with A. spinifera, A. ferox displays a narrower range of anteroposterior motion [49 versus 74 deg (Pace et al., 2001)] and extends the elbow less [maximum elbow extension angle of 107 versus 149 deg (Pace et al., 2001)]. Although the limb cycle frequencies exhibited by each species were similar (A. ferox=2.24±0.3 cycles s^–1 and A. spinifera=1.66±0.12 cycles s^–1), it is possible that differences in swimming speed contribute to the kinematic differences observed between Apalone species. Nevertheless, among rowing turtles, aquatic specialists may be more efficient swimmers than more generalized taxa by limiting extraneous humeral motions. Whether the tendency to limit motion in aquatic specialists is an adaptation for increased swimming efficiency, or the greater range of motion exhibited by the semi-aquatic generalist T. scripta is related to the greater extent to which it moves over land, remains to be determined.

Comparison of swimming between C. insculpta and other turtles

Carettochelys insculpta and sea turtles are distantly related, yet both have evolved a similar derived forelimb morphology (flippers) and synchronous mode of swimming through convergent evolution. Swimming in C. insculpta has commonly been described as flapping and being like that of sea turtles (Walther, 1921; Rayner, 1985; Georges et al., 2000), though formal comparisons of quantified kinematics had not been performed. Our measurements indicate that C. insculpta and sea turtles have not converged on an identical flapping style of swimming through use of similar humeral kinematics. While both sea turtles (C. caretta) and C. insculpta swim via synchronous motions of the flippers, their movements are only superficially similar, as their patterns of humeral motion differ substantially. Whereas the primary humeral motions in C. caretta are elevation and depression, this is not the case in C. insculpta, which shows a unique bimodal pattern of dorsoventral motion and does not depress the humerus nearly as much as C. caretta (Fig. 4). Carettochelys insculpta also protract the humerus significantly more than C. caretta (and slightly more than the asynchronous rowers in our comparison), leading to a much greater anteroposterior excursion range despite nearly identical levels of humeral retraction. Although these two species differ in the predominant directions of humeral motion (i.e. dorsoventral for C. caretta and anteroposterior for C. insculpta), they are quite similar with regard to motion at the elbow (Fig. 4C), indicating that this might be an aspect of kinematics important for producing dorsoventral motion of the flippers in both species.

Despite common statements to the contrary, we found the humeral kinematics of swimming in C. insculpta to be more similar to the rowing kinematics used by A. ferox and T. scripta than to the flapping kinematics of our sea turtle species (C. caretta), with multivariate analyses showing the three freshwater species to be most similar (Fig. 5, Table 3). Humeral motion during the dorsoventrally restricted rowing of A. ferox is more similar to that of C. insculpta than is the rowing of T. scripta. This similarity may reflect the close phylogenetic relationship between A. ferox and C. insculpta (Fig. 1) (Barley et al., 2010). Given the limited amount of humeral depression and retraction observed in A. ferox relative to T. scripta, it is clear why both dorsoventral and anteroposterior ranges of motion differ. Trachemys scripta also shows less humeral depression than C. insculpta, and while the pattern of anteroposterior movement is very similar between the two, C. insculpta reaches peak elbow extension significantly earlier. Patterns of forefoot feathering are nearly identical between A. ferox and C. insculpta, and with the exception of a mid-cycle high-drag peak, the pattern in T. scripta is also quite similar. While the humeral kinematics used by both asynchronous rowers were more similar to those of C. insculpta, and while A. ferox is most similar to C. insculpta, the biggest pair-wise species difference observed was between A. ferox and C. caretta. Apalone ferox differs from C. caretta with regard to aspects of dorsoventral motion and maximum protraction, and in addition, retracts the humerus and extends the elbow significantly less. Apalone ferox and T. scripta also both achieve higher-drag forefoot orientations than observed in C. caretta. Differences between T. scripta and C. caretta have been reported previously (Rivera, A. R. V. et al., 2011), with T. scripta showing greater anteroposterior motion due to significantly greater protraction, whereas C. caretta shows greater dorsoventral motion due to significantly greater humeral depression.

How does C. insculpta swim?

Our quantitative evaluation of forelimb kinematics during swimming in C. insculpta shows that this unusual freshwater species, which is commonly described as a flapper, displays limb motions that are similar to flappers for some parameters, but that more closely resemble the kinematics of rowers overall. So, how does C. insculpta swim? Humeral kinematics of swimming in C. insculpta are more similar to the rowing kinematics of A. ferox and T. scripta; they are not flapping the humerus up and down as in C. caretta. Carettochelys insculpta shows a great amount of humeral protraction (slightly greater peak values than the rowers) and retraction, and a much smaller amount of elevation and depression than C. caretta. The key to how this species accomplishes what looks like flapping-style locomotion (and likely the reason it has historically been described as a flapper) appears to lie in humeral rotation. As the humerus is protracted, the marked elevation of the tips of the digits that occurs while humeral elevation remains minimal (Figs 3, 5) indicates that substantial medial rotation occurs while the elbow is extended. This rotation causes the flipper blade to elevate even as the distal end of the humerus starts to depress, resulting in what appears to be an upstroke of the limb and the first peak in humeral elevation (Fig. 4B). As the humerus is retracted it appears to rotate laterally while the elbow is flexed, causing the flipper blade to depress while the distal end of the humerus slightly elevates, and resulting in an apparent downstroke of the limb and the second peak in elevation (Fig. 4B). Carettochelys insculpta reaches peak high-drag forefoot orientation concurrent with the slight second peak in humeral elevation (Fig. 4B,D), and then returns to the starting position. While the pattern of forefoot orientation in C. insculpta is very similar to that of the other freshwater species (both rowers), particularly A. ferox, rotation of the humerus in combination with a pattern of elbow motion that more closely resembles that of flapping C. caretta produces a pattern of limb motion in C. insculpta that bears a strong, though somewhat superficial, resemblance to movements typically viewed as ‘flapping’. Thus, C. insculpta and C. caretta show some components of convergence on what appears to be a flapping-style of swimming, though it is achieved with significant kinematic differences. While the pattern of motion at the elbow might play an important role in the generation of the upstroke and downstroke characteristic of flapping-style swimming, humeral elevation and depression appear to be crucial for generating flapping in C. caretta whereas humeral rotation is more important in the generation of the ‘upstroke’ and ‘downstroke’ of C. insculpta.

Humeral motion does not support the classification of C. insculpta as a flapper. However, given the strong visual resemblance of the motions of C. insculpta limbs to flapping, might other kinematic variables indicate that C. insculpta swims via dorsoventral flapping, even though the most prominent humeral movements are not dorsoventral (i.e. upstroke and downstroke)? An additional way that species could be classified as flappers or rowers is by evaluating the amount of dorsoventral motion of the foot relative to its anteroposterior motion. Whereas equal amounts of dorsoventral and anteroposterior motion yield a ratio of 1, greater values indicate flapping and smaller values indicate rowing. A comparison of the path traveled by the tip of the flipper (digit 3) shows that although C. insculpta exhibits far greater dorsoventral excursion than rowing A. ferox and T. scripta, there is still a greater amount of anteroposterior than dorsoventral motion in C. insculpta (Fig. 6). Based on the ratio of dorsoventral to anteroposterior motion of the distal-most tip of the forelimb, A. ferox and T. scripta are classified as rowers (A. ferox DV/AP=0.23±0.01, T. scripta DV/AP=0.29±0.01), C. caretta as a flapper (DV/AP=1.47±0.13) and C. insculpta as intermediate between these two groups (DV/AP=0.58±0.03), though still on the rowing side of this index. Thus, with forelimb kinematics showing aspects resembling both rowers and flappers, but more closely aligned with rowers based on multivariate results as well as overall flipper motion (i.e. DV/AP ratio less than 1), kinematically, C. insculpta is perhaps best described as a rower (albeit with forelimbs moved synchronously). This kinematic classification is further justified by the statistical findings (based on the ratio of dorsoventral to anteroposterior motion of the digit 3) that indicated that C. insculpta forelimb movements are statistically different from flapping Caretta, but not from the traditionally classified rowers, T. scripta and A. ferox.

However, beyond kinematic analyses, designations of ‘rower’ or ‘flapper’ also relate to how measured kinematic parameters culminate in the production of hydrodynamic force: rowers produce drag-based thrust whereas flappers produce lift-based thrust. Values of angles of attack can provide insight into hydrodynamically based characterizations. Our results demonstrate that during the early phase of the limb cycle (protraction/elevation), both C. insculpta and C. caretta display statistically concordant values of angle of attack. These angles are within the range previously shown to produce lift-based thrust (Davenport et al., 1984; Walker and Westneat, 2000). Furthermore, because previous studies of sea turtles have demonstrated that hydrodynamic thrust is produced on the upstroke (Davenport et al., 1984), these findings provide the first evidence that C. insculpta may in fact utilize lift-based thrust, albeit only during the first phase of the limb cycle. In contrast, during the latter phase of the limb cycle (retraction/depression), C. insculpta, A. ferox and T. scripta display statistically concordant angles of attack that differ from those of C. caretta. Moreover, during the second phase, the values displayed by C. insculpta and the two other freshwater species are consistent with the high-drag orientation used by rowers, while only the intermediate values used by C. caretta are consistent with those shown to generate lift-based thrust (Walker and Westneat, 2002b). These findings, for the latter phase of the cycle, are consistent with the kinematic analyses that found that C. insculpta is most similar to rowers. Thus, angle of attack data suggest that C. insculpta is less of an intermediate and more of a hybrid: flapping during protraction/elevation and rowing during retraction/depression. To our knowledge, this is the first time such a locomotor style has been proposed for a turtle, though there is some precedent for a hybrid stroke in secondarily aquatic vertebrates with flippers [see Feldkamp (Feldkamp, 1987) for a description in sea lions]. In the case of a hybrid, one general assumption is that thrust is still more dominant than lift. For both freshwater rowers and marine flappers, the retraction/depression phase of the cycle generates considerably more force than the protraction/elevation phase (Davenport et al., 1984). Thus, even if lift-based thrust is being produced by C. insculpta, more thrust is likely being produced from the rowing component of the cycle. Our data thus lead to two general conclusions: (1) it is incorrect to refer to C. insculpta as a ‘flapper’, and (2) although the angle of attack during the early phase is consistent with angles known to produce lift-based thrust, until this is tested using techniques such as digital particle image velocimetry, it is most conservative to classify C. insculpta as a ‘synchronous rower’ rather than a ‘hybrid rower-flapper’.

We have shown that C. insculpta does not show the close convergence with the flapping motions of sea turtles that has commonly been described, and instead exhibits a suite of swimming forelimb kinematics different from other species. Interspecific variation in locomotor behaviors can arise through modification of anatomical structures, modification of patterns of muscle activation, or some combination of both (Westneat and Wainwright, 1989; Lauder and Reilly, 1996). With the identification of these patterns of kinematic differences, a next step would involve determining how divergence in motor patterns contributes to this diversity. A recent examination of the forelimb motor patterns that power swimming in T. scripta and C. caretta showed strong conservation in the activation patterns of several muscles (e.g. coracobrachialis, latissimus dorsi), but marked differences in others (e.g. deltoid, triceps), indicating that the evolution of flapping in sea turtles was achieved through modification of motor patterns as well as anatomical structures (Rivera, A. R. V. et al., 2011). Given the similarity of limb kinematics in C. insculpta to rowing in A. ferox and T. scripta for much of the swimming cycle, it is possible that C. insculpta might exhibit motor patterns more similar to those of other rowing freshwater species, particularly those in the more closely related and more similar genus Apalone (A. ferox and A. spinifera). Testing how patterns of muscle activation compare among a broad range of rowing and flapping turtles could provide additional insight into how novel patterns of locomotion arise.