Optimization of Stimulus Parameters for Selective Peripheral Nerve Stimulation with Multi-Contact Electrodes

Abstract

This study describes a method for optimizing selective stimulus parameters for multi-contact peripheral electrodes. Overlap between pairs of contacts is quantified by the deviation in their combined response from linear addition of their individual responses. Mathematical models are fit to recruitment and overlap data, and a cost function is defined to maximize recruitment and minimize overlap between all contacts. Results are presented for two four-contact nerve-cuff electrodes stimulating bilateral femoral nerves of one human subject with spinal cord injury. Knee extension moments between 11.6 and 17.2 Nm are achieved through two contacts of each nerve-cuff with less than 10% overlap between each pair of contacts. These results suggest that optimization can provide an automated means of determining stimulus parameters to achieve strong, selective muscle contractions through multi-contact peripheral nerve electrodes.

I. Introduction

Multi-contact stimulating electrodes have been gaining popularity as a means for interfacing with (FNS) systems [1–3]. These electrodes allow for a high density of contacts to be placed around or in peripheral nerves to independently activate multiple fascicles and motor units.

Independent activation can allow for the control of multiple functions with a single electrode and for recruitment of multiple populations of agonist motor units within a single muscle [4, 5]. Control of multiple functions with a single electrode could reduce the number of implantation sites required to produce a variety of functional joint moments for FNS systems [4]. Control of multiple agonist motor units with a single electrode could allow for better control of joint moment by varying the number of motor units recruited by the electrode [5]. Further, by alternating stimulation of multiple agonist motor unit populations, it may be possible to reduce stimulation duty cycle and prolong the time of muscle contraction before the onset of fatigue [6].

Determining selective stimulus parameters when multiple contacts stimulate agonist populations of motor units is a complex problem. Populations of agonist motor units cannot be separated based on their lines of action or resultant joint moments. Instead, previous work has utilized the dynamics of neural stimulation to quantify and minimize the overlap between a pair of contacts within a multi-contact electrode [2, 3]. By stimulating through two contacts, one after the other with a slight time delay between them, it is possible to avoid summation of their currents, and if the time delay is sufficiently short (less than 2.2 ms), any motor units that respond to stimulation through the first contact will be refractory and will not respond to stimulation through the second contact [2, 3, 7, 8]. With this type of stimulation, if there is overlap between two contacts, the force produced when they are stimulated together will be less than the linear sum of the individual forces produced when stimulating through the two contacts separately. Conversely, if there is no overlap between the two contacts, the response will be the linear sum of the individual forces.

While this method provides a useful way to quantify overlap between two contacts, it does not easily scale to larger numbers of contacts. Others have used this method to quantify overlap between pairs of contacts within an electrode, and then averaged all of those overlaps [3, 6]. While averaging provides some insight into the general amount of overlap for a multi-contact electrode, it does not provide a clear means of tuning stimulus parameters for each individual contact. Furthermore, as the number of contacts within the electrode increases, the number of pairwise combinations of contacts that must be considered for this method increases exponentially. This can quickly lead to impossibly large data sets as the number of contacts increases.

In this report, we propose a method for choosing selective stimulus parameters for multi-contact electrodes by minimizing overlap between adjacent contacts while maximizing the joint moment produced by each contact. We rely on the method described above to quantify overlap between pairs of contacts, then fit a set of mathematical models to reduce the data requirements for characterizing the electrodes, and use a cost function that minimizes all pairwise overlaps while simultaneously maximizing all joint moments. We show that this method can select stimulus parameters that produce strong muscle contractions with little overlap between stimulated motor unit populations.

II. Methods

The process we propose to quantify and optimize selective stimulation for multi-contact electrodes includes four steps. First, the response to stimulation through the multi-contact electrode and the overlap between pairs of contacts are quantified. These responses are twitches, elicited by single stimulus pulses, which are less likely to cause fatigue and can be collected more quickly than tetanic responses. Next, the relationship between twitch and tetanic stimulation is quantified. This relationship provides a scaling factor so that the twitch responses, which are more easily collected, can be converted to more functionally relevant tetanic responses. Third, mathematical models are fit to the scaled recruitment and overlap data. These models serve the dual purposes of reducing the size of the data set required for optimization and providing a mathematical framework over which optimization can be performed. Finally, the recruitment and overlap models are used in a cost function that can be minimized to achieve optimal selective stimulus parameters.

A. Subject Selection and Multi-Contact Electrodes

The Case Western Reserve University self-sizing four contact spiral nerve-cuff electrode was used to develop this method for optimizing selective stimulus parameters. Two nerve-cuffs were implanted around bilateral femoral nerves of one volunteer with motor-complete spinal cord injury (level C7, ASIA B). The nerve-cuff electrodes, which have four contacts that can be controlled independently, were sized so that any two adjacent contacts were separated by 90° around the circumference of the nerve. All contacts were connected to an implanted stimulator capable of generating monopolar, charge-balanced biphasic stimulus pulses. For this study, all stimuli had a current amplitude of 1.4 mA.

Informed consent was acquired prior to all experiments, and all protocols were approved by the Institutional Review Board of MetroHealth Medical Center, Cleveland, OH.

B. Recruitment and Overlap Characterization

For the first step in optimizing selective stimulus parameters, recruitment and overlap between pairs of contacts were characterized. With the knee fixed at 20° of flexion and a load cell aligned with the knee joint center, isometric knee extension moment was recorded in response to stimulus pulses applied to the femoral nerve through each contact of the nerve-cuff electrodes. Data were low-pass filtered at 31.25 Hz and sampled at 150 Hz. To characterize recruitment, pulse width modulated recruitment curves were collected. To characterize overlap between pairs of contacts, a stimulus was applied through one contact, followed by a 2 ms time delay, and then a pulse through a second contact. All stimulus pulse widths were varied between 1 and 255 μs.

For some multi-contact electrodes, it is possible to reduce the number of pairwise combinations by ignoring pairs that are not adjacent to each other, since elimination of overlap between adjacent contacts will also eliminate overlap between non-adjacent contacts. In the case of the four-contact nerve-cuff, all contacts are adjacent to each other, so all six pairwise combinations were considered.

C. Twitch/Tetany Relationship

While twitch stimulation is far more practical for characterizing the response to stimulation and overlap, tetanic stimulation is more functionally relevant. Previous studies demonstrated that there is a linear relationship between the shape of isometric twitch and tetanic recruitment curves, and that a simple linear scaling factor can describe the difference between these [5]. To quantify this scaling factor, twitch and tetanic responses to stimulation were recorded with the knee held at 20° of flexion. The ratio of the maximum twitch and tetanic responses was used as a scaling factor.

D. Mathematical Models of Recruitment and Overlap

Fitting mathematical models to recruitment and overlap data reduces the size of the data set required for characterizing the electrodes while also providing a framework for optimization of stimulus parameters. To determine the best type of models for recruitment and overlap, sets of 32 recruitment or overlap data points were fit to a variety of models and separate sets of 16 data points were used to test for goodness-of-fit. For recruitment, 1^st through 5^th order polynomial, sigmoid, Gaussian, and Gompertz functions were tested. For overlap, which are two-dimensional since pulse width can be controlled for both contacts in a pairwise combination, 1^st through 5^th order polynomials were tested. To determine goodness-of-fit, the corrected Akaike Information Criterion (AICc) was calculated for each model. Models with the highest AICc were implemented in the optimization.

E. Optimization of Selective Stimulus Parameters

Achieving selectivity of stimulation necessarily creates a trade-off between larger stimuli with large joint moments and smaller stimuli with low overlap. It is, therefore, useful to treat selectivity as an optimization problem, where the goal is to choose stimulus parameters to maximize joint moment while minimizing overlap, using a cost function of the form

$$C\left(\overline{PW}\right)=-{\omega }_0{M}_T\left(\overline{PW}\right)+{\omega }_1{O}_T\left(\overline{PW}\right),$$ (1)

where PW is an N-dimensional vector of stimulus pulse widths for an N-contact electrode, O_T is the overlap of all contacts, M_T is the joint moment generated by all contacts, and ω₀ and ω₁ are weighting factors.

The joint moment term, M_T, is defined here as

$$M_T\left(\overline{PW}\right)=\sum _{i=1:N}{M}_i\left({PW}_i\right)/\sum _{i=1:N}max\left(M_i\right),$$ (2)

where M_i is the moment generated when stimulating through contact i, which is described mathematically by the model function previously fit to recruitment data. The sum of these functions is divided by the sum of the maxima of the functions to normalize the joint moment term. In this way, overall joint moment is normalized with respect to overlap, but joint moments from all contacts are weighted equally.

Overlap is quantified by the deviation from linear addition when stimulation is applied by two contacts with a short inter-contact delay. This is expressed as

$$M_{i\cap j}\left({PW}_i,{PW}_j\right)=M_i\left({PW}_i\right)+M_j\left({PW}_j\right)-M_{i\cup j}\left({PW}_i,{PW}_j\right)$$ (3)

where M_i∩j is the overlap between contacts i and j, M_i and M_j are the moments generated when stimulating through contacts i and j, and M_i∪j is a mathematical function fit to overlap data generated by stimulating through two contacts with a short inter-contact time delay. To include all pairwise overlaps while normalizing with respect to M_T, O_T is defined as

$$O_T\left(\overline{PW}\right)=\frac{2}{N^2-N}\sum _{i=1:N-1}\sum _{j=2:N}\frac{M_{i\cap j}\left({PW}_i,{PW}_j\right)}{M_{i\cup j}\left({PW}_i,{PW}_j\right)},$$ (4)

which ranges between 0 and 1.

Since both O_T and M_T are normalized, the weighting factors, ω, can be used to emphasize larger joint moments or lower overlap, depending on the particular application. For this study, the terms were weighted equally.

To ensure that either sufficiently large joint moments or sufficiently small overlaps are achieved, a linear penalty was added to the function if joint moment was less than 5 Nm or overlap was greater than 10% between any two contacts. A direct search optimization algorithm (Matlab, Natick, MA) determined the minimum of the cost function and the optimal set of stimulus pulse widths for selectivity.

III. Results

A. Electrode Characterization and Mathematical Models

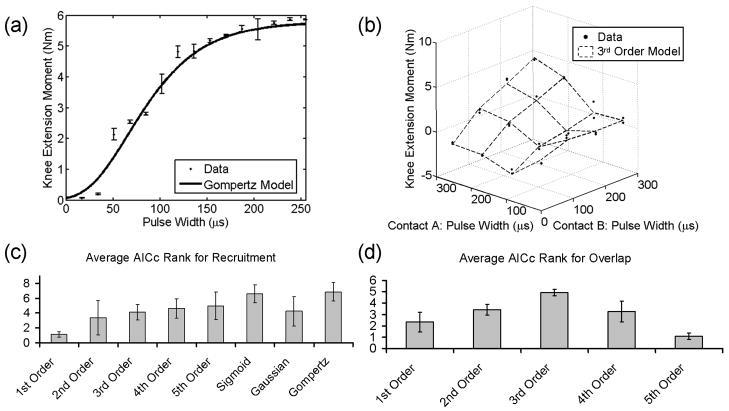
Fig. 1(a) shows the response to stimulation through one contact of the nerve-cuff electrode and a Gompertz model fit to those data. Fig. 1(c) shows the average AICc calculated for all eight contacts within the nerve-cuff electrodes. From these results, the Gompertz function has the highest AICc and is the most appropriate model of the response to stimulation.

Fig. 1.

(a) Recruitment data for a single contact fit with a Gompertz model. (b) Overlap data for two contacts fit with a third-order polynomial model. (c) The average AICc of eight models fit to recruitment data, where a higher score denotes a better fit. (d) The average AICc of five models fit to overlap data.

Fig. 1(b) shows an example of overlap data between two contacts within a nerve-cuff electrodes as well as an example of a third-order polynomial fit to those data. Fig. 1(d) shows the average AICc for all twelve pairwise combinations of contacts for the two nerve-cuff electrodes. From these results, the third-order polynomial is the most appropriate model of overlap in stimulation between two contacts.

B. Twitch/Tetany Relationship

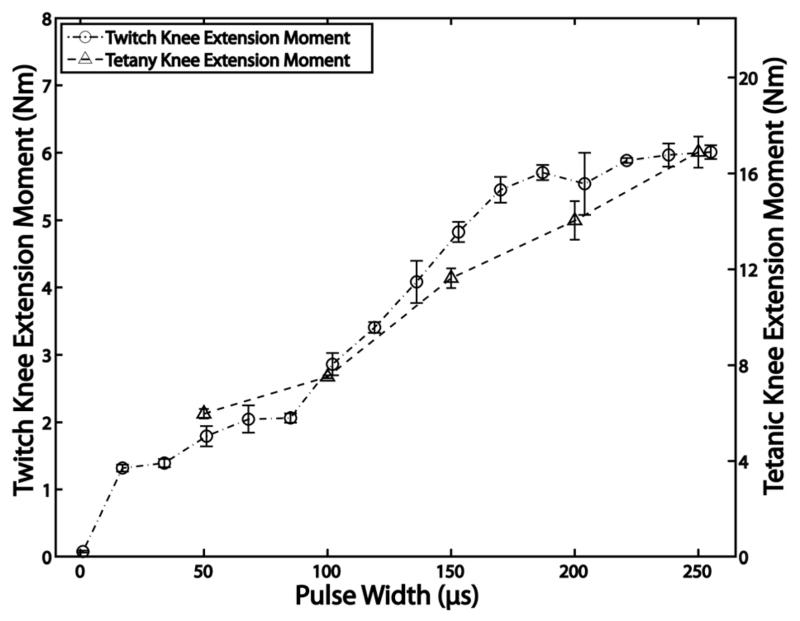
Examples of typical twitch and tetanic recruitment curves are shown in Fig. 2. For all eight contacts within the two nerve-cuff electrodes, the shape of twitch and tetanic recruitment curves were similar, and a linear scaling factor was calculated as the ratio of the maxima of the two curves (mean ± standard deviation = 2.67±0.3). Scaling factors for all contacts are shown in Table I.

Fig. 2.

An example of the relationship between twitch (circles) and tetanic (triangles) recruitment curves. A linear scaling factor is calculated as the ratio of maxima of these curves.

TABLE I.

Selective Stimulus Parameters

Contact	Selective Pulse Width (μs)	Selective Twitch Moment (Nm)	Twitch/Tetany Scaling Factor	Estimated Selective Tetanic Moment (Nm)
Left 1	N/Aa	N/Aa	2.94	N/Aa
Left 2	255	5.86	2.22	13.01
Left 3	N/Aa	N/Aa	2.81	N/Aa
Left 4	90	3.74	3.11	11.64
Right 1	N/Aa	N/Aa	2.55	N/Aa
Right 2	255	7.33	2.35	17.23
Right 3	N/Aa	N/Aa	2.79	N/Aa
Right 4	96	5.59	2.60	14.54

^aThe optimization produced larger selective moments when some contacts were excluded from the cost function.

C. Optimization of Selective Stimulus Parameters

Table I shows the optimal stimulus parameters for both nerve-cuffs, as determined by a direct search which minimized the cost function defined above. Also shown are joint moments in response to those parameters.

Note that only two contacts for either nerve-cuff electrode have non-zero stimulus parameters. The results of the optimization demonstrated that removing two contacts from the cost function produced significantly higher joint moments with less overlap than if all contacts were included. Optimal selective stimulus parameters resulted in 7% overlap between contacts 2 and 4 of the left nerve-cuff, and 5% overlap between contacts 2 and 4 of the right nerve-cuff.

IV. Discussion

These results suggest that the optimization method can select a set of stimulus parameters to provide large joint moments with low overlap. For these two nerve-cuff electrodes, the optimization determined that 4 of the 8 nerve-cuff contacts could produce between 11.6 and 17.2 Nm of knee extension moment with less than 10% overlap.

While the optimization method was applied to an electrode with four contacts, it is scalable to higher density electrodes. By focusing only on overlap between adjacent pairs of electrodes, and by fitting mathematical models to overlap and recruitment, it should be possible to select optimal stimulus parameters for electrodes with any number of contacts. Also, by adjusting the weighting factors in the cost function, the procedure can be tailored to applications with different requirements, such as when low overlap is more important than producing large joint moments or vice versa.

For both of these nerve-cuff electrodes, the optimization produced better results if only two contacts were used. In both cases, these contacts sit opposite one another around the nerve, so it is expected that they would have less overlap than contacts that are directly adjacent. While this means that only one pairwise overlap was used in each optimization, this need not always be the case, and, for electrodes with higher densities of contacts, it is likely that more contacts would be used in the final set of optimal stimulus parameters.

Future work should include repeating these experiments with more subjects, extending this method to electrodes with higher densities of contacts, and using the selective stimulus parameters to improve function in FNS systems. This could be achieved, for example, by alternating stimulation between selective contacts to reduce duty cycle of stimulation while maintaining a constant joint moment to delay fatigue.

V. Conclusion

This study presents a method for optimizing stimulus parameters for multi-contact peripheral stimulating electrodes. By using twitch responses and fitting mathematical models to recruitment and overlap, the method reduces the data requirements for optimizing selective stimulation. A cost function that includes terms representing recruitment and pairwise overlap for all contacts allows for maximization of the moment generated by each contact while minimizing overlap between all pairs of contacts. This method provides an objective and automated means of selecting stimulus parameters for electrodes with high-densities of contacts.

The results of this study also suggest these nerve-cuff electrodes can generate strong contractions with little or no overlap between contacts. For the two electrodes in this study, it was possible to produce between 11.6 and 17.2 Nm of knee extension moment with less than 10% overlap between contacts. When used simultaneously, these joint moments would likely be sufficient to achieve a sit-to-stand transition, and the moments generated by each contact may be enough to keep the knees locked during standing.