Guanine base stacking in G-quadruplex nucleic acids

Abstract

G-quadruplexes constitute a class of nucleic acid structures defined by stacked guanine tetrads (or G-tetrads) with guanine bases from neighboring tetrads stacking with one another within the G-tetrad core. Individual G-quadruplexes can also stack with one another at their G-tetrad interface leading to higher-order structures as observed in telomeric repeat-containing DNA and RNA. In this study, we investigate how guanine base stacking influences the stability of G-quadruplexes and their stacked higher-order structures. A structural survey of the Protein Data Bank is conducted to characterize experimentally observed guanine base stacking geometries within the core of G-quadruplexes and at the interface between stacked G-quadruplex structures. We couple this survey with a systematic computational examination of stacked G-tetrad energy landscapes using quantum mechanical computations. Energy calculations of stacked G-tetrads reveal large energy differences of up to 12 kcal/mol between experimentally observed geometries at the interface of stacked G-quadruplexes. Energy landscapes are also computed using an AMBER molecular mechanics description of stacking energy and are shown to agree quite well with quantum mechanical calculated landscapes. Molecular dynamics simulations provide a structural explanation for the experimentally observed preference of parallel G-quadruplexes to stack in a 5′–5′ manner based on different accessible tetrad stacking modes at the stacking interfaces of 5′–5′ and 3′–3′ stacked G-quadruplexes.

INTRODUCTION

G-quadruplex nucleic acids can adopt a wide range of sequence-dependent structures with stacked guanine assemblies called G-tetrads at their core (Figure 1A). G-quadruplex-forming sequences are found in many areas of the chromosomes including the telomere (1,2), gene promoters (1,3) and mini-satellite regions (4,5). Stabilization of G-quadruplexes by small-molecule binding in the telomeric and oncogenic promoter regions are attractive anti-cancer strategies. Additionally, G-quadruplex-based aptamers have been identified with a host of physiologically beneficial properties (6,7).

Figure 1.

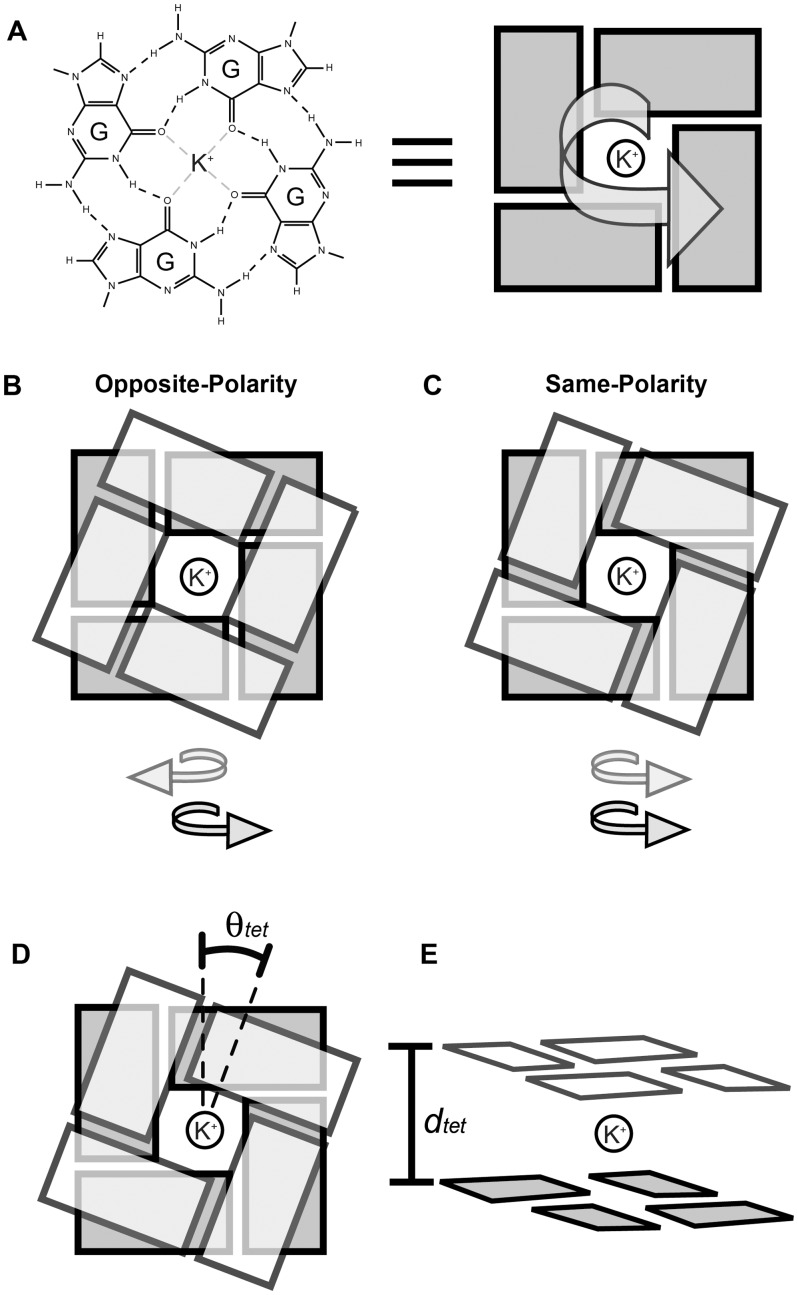
G-tetrad stacking: (A) G-tetrads have a polarity as defined by direction of the Hoogsteen hydrogen bond donor-to-acceptor pattern. Tetrad stacking can be primarily described as (B) opposite-polarity or (C) same-polarity stacking. Model stacked G-tetrad geometries used in this study varied by (D) relative rotation angle (θ_tet) and (E) G-tetrad separation distance (d_tet).

Study of the physical interactions that govern G-quadruplex formation and their higher-ordered assemblies is important to understand the structure and function of biologically relevant G-quadruplexes and facilitates the engineering of aptamer molecules. Like more canonical nucleic acid structures, the π–π stacking of aromatic bases is central to the formation of G-quadruplexes. Consequently, a great deal of research has gone into understanding the relative energies of stacked nucleic acid bases in varying geometries (8–13), including G-tetrad geometries found in G-quadruplexes (14–16).

Besides being fundamental to G-quadruplex formation, guanine base stacking plays an important role in higher-ordered G-quadruplex assemblies. Individual G-quadruplex units have the capacity to stack on one another at their G-tetrad interfaces, as seen in both X-ray crystallographic (17–27) and nuclear magnetic resonance (NMR) solution structures (28–34). Unlike in the G-quadruplex core, base stacking geometries at free-stacking interfaces are not constrained by covalent linkage through the backbone. Understanding the roles of base stacking at the interface of stacked G-quadruplexes is particularly important considering that high-order assemblies have been observed in vitro for telomeric DNA (20) and telomeric repeat-containing RNA (TERRA) (35,36), and that a number of G-quadruplex-based aptamers are formed from stacked G-quadruplexes (32,34,37). With this in mind, we set out to quantitatively characterize the base stacking geometries of G-quadruplexes. We report on the results of an extensive structural survey of G-quadruplex structures published in the Protein Data bank (PDB).

We also investigate base stacking on a fundamental level, examining how G-tetrad stacking energy differs with varying geometry. Previous quantum mechanical (QM) computational studies have looked at the relative stacking energies between some optimized geometries of stacked G-tetrads coordinated with central cations (14–16). The present study expands on previous works by generating comprehensive QM energy landscapes at the MP2 level for both same-polarity and opposite-polarity stacked tetrads by systematically varying the separation and relative rotation of stacked K⁺-coordinated tetrads (Figure 1). Comparison of our experimental survey results and QM energy calculations gives insight into the relative energies of stacked G-tetrad geometries, both within a single G-quadruplex and at the interface of stacked G-quadruplexes.

We also set out to investigate the role of base stacking in high-order assemblies of G-quadruplexes. Molecular dynamics (MD) has been used in past studies to investigate the energy differences of G-quadruplexes with varying structural features (38–40). In this work, we evaluate the ability of an AMBER molecular mechanics (MM) description of energy to accurately represent the base stacking energy of coordinated guanine-tetrads in comparison with QM calculations. MM-computed energy differences between base stacking modes are discussed with special attention paid to their implications toward high-order G-quadruplex assemblies. MD simulations are carried out to investigate the observed preference in our survey of G-quadruplexes to stack in a 5′–5′ manner, with the G-tetrad stacking interface occurring between the 5′-end of individual parallel G-quadruplex units. MD simulations provide some explanation for this observation in terms of different accessible base stacking geometries between 3′–3′ and 5′–5′ stacked G-quadruplexes.

Nomenclature

The stacking of adjacent G-tetrads can be described by the relative polarity of the Hoogsteen hydrogen bond pattern (Figure 1). Within a single G-tetrad, the hydrogen bond polarity is defined in the direction of hydrogen bond donor to acceptor, from N2-H to N7 and from N1-H to O6. Two neighboring G-tetrads can therefore be described as belonging to one of two classes of stacking: (i) ‘same-polarity’ if the polarities are in the same direction (Figure 1C); or (ii) ‘opposite-polarity’ if in the opposite direction (Figure 1B). The possible geometries of stacked guanine bases are fundamentally different between same- and opposite-polarity stacked G-tetrads. Nomenclature of commonly occurring base stacking modes is based on a description of the aromatic ring overlap of stacked guanines. For example, stacking geometry characterized by overlapping of the 5-member rings of guanine bases is termed ‘5-ring’ stacking. Within the G-quadruplex core, the geometries of stacked guanines are related to the glycosidic conformation of the bases (41) and are therefore sometimes referred to in these terms. For example, the ‘Syn/Anti’ nomenclature describes the base stacking geometry of the 5′-‘Syn→Anti’-3′ dinucleotide step.

In the literature, it is common for same-polarity and opposite-polarity classifications to be further divided and referred to as head-to-tail or tail-to-head belonging to same-polarity stacking and head-to-head or tail-to-tail belonging to opposite-polarity stacking (42). In this notation, head and tail refer to the different faces of a guanine base. In the isolated planar G-tetrad models used in our QM studies, there is no energy difference between head-to-head and tail-to-tail models or the head-to-tail and tail-to-head models of similar separation and relative rotation. For this reason, we classify stacking primarily as belonging to either the same-polarity or opposite-polarity type.

The G-tetrad models used for both energy calculations and structural characterization are symmetric planar guanine assemblies. We allow the relative rotation angle, termed θ_tet (Figure 1D), and the separation distance d_tet defined as the distance between parallel planar tetrads (Figure 1E), to vary in our models. Because of the nature of G-tetrads and the symmetry of our models, the geometries of stacked guanines repeat, as θ_tet varies over 90° intervals. In the case of opposite-polarity stacked tetrads, the θ_tet angle between stacked tetrads is defined to be the rotation of one tetrad, in the direction of its hydrogen bond polarity, with respect to the other through the central axis perpendicular to the tetrad plane (Figure 1). In the case of same-polarity stacked tetrads, the θ_tet angle is defined arbitrarily to be the rotation of the tetrad containing the 5′-end guanine in the direction of its hydrogen bond polarity. The θ_tet angle is defined to be zero when O6 atoms of stacked tetrads are on top of each other such that the inter-tetrad O6–O6 distance of stacked guanines is at its minimum and is equal to d_tet, the separation between G-tetrads (Supplementary Figure S1).

Figure 2.

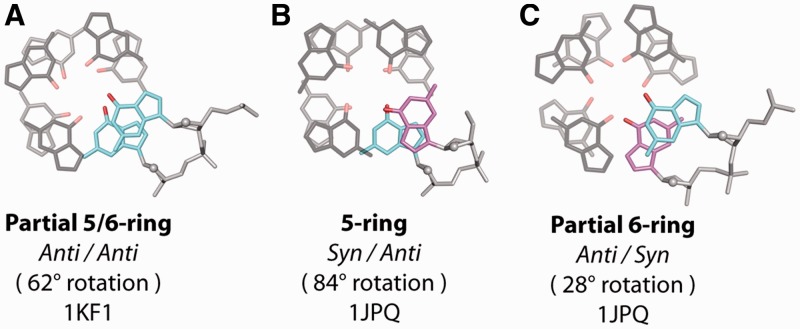
Illustrative examples of core base stacking modes from the structural survey. (A) ‘Partial 5/6-ring’ stacking of the ‘Anti/Anti’ step, (B) ‘5-ring’ stacking of the ‘Syn/Anti’ step and (C) ‘Partial 6-ring stacking’ of the ‘Anti/Syn’ as observed in crystallographic structures. ‘Syn’ and ‘Anti’ glycosidic conformations are depicted as magenta and cyan, respectively. Stacking modes are labeled along with the θ_tet rotation value and the PDB ID code of the experimental structure from which the geometries are taken.

The QM-computed interaction energy, termed ‘stacking energy’ or ΔE, represents the gas-phase energy difference between a complex of stacked K⁺-coordinated G-tetrads and isolated fragments as shown in equation 1.

(1)

The counterpoise procedure is used to correct for basis set superposition errors (43). Here, E^complex is the total energy of the complex, whereas E^tetrad1, E^tetrad2 and E^ion are the energies of individual tetrads and a central coordinating ion, respectively. For QM-computed energy landscapes, ΔE^norm represents the normalized stacking energy, determined relative to the minimum ΔE observed across both same- and opposite-polarity landscapes. For higher-level MP2/6-311 + G(2 d,2 p) calculations, ΔE^norm was determined relative to the lowest ΔE across the geometries computed. For MM-computed energy landscapes, E^Amber represents the total MM description of system energy for a given geometry, normalized relative to the minimum across both same- and opposite-polarity landscapes. Let us note how interaction energy differs from the free energy of a system. Interaction energy, or stacking energy, is the energy associated with molecules interacting in gas phase. This energy is calculated to describe how favorable the geometry of a molecular ensemble is compared with sum of each molecule in isolation. These calculations are limited to a quantum description of interactions in the absence of solvent. In fully represented and solvated systems, other interactions such as hydrophobic interactions and the polarization of solute molecules by solvent influence the total free energy of the system.

METHODS

Model tetrads

Tetrad models were created by first performing QM geometry optimization of a single G-tetrad at the MP2/6-31(d,p) level (44,45). The optimized structure consisted of a planar G-tetrad displaying C4 symmetry stabilized by two centrally located cations, located above and below the tetrad plane. The optimized tetrad was then used to create models for single-point energy calculations and structural characterization, which contain two parallel-centered G-tetrads with a single central K⁺ ion. The geometries of stacked planar tetrads were varied by their separation (d_tet) and relative rotation (θ_tet) (Figure 1).

Structural characterization

A survey of G-quadruplex structures published in the PDB was carried out using the following keywords: quadruplex(es), tetrad(s) and tetraplex(es). Search results of X-ray crystallographic structures of G-quadruplexes containing neighboring G-tetrads, as of June 16, 2011, are examined. A selection of NMR G-quadruplex solution structures containing stacked G-tetrads is also presented. The relative rotation (θ_tet) and separation (d_tet) (Figure 1) of individual pairs of stacked guanine bases in experimentally determined structures were quantified by comparison with a library of stacked guanines taken from our models of stacked tetrads with geometries varying in rotation and separation with increments of 0.05° and 0.005 Å, respectively. The characterization of guanines within G-quadruplexes involved the alignment of >1000 experimentally determined stacked guanine pairs (from 40 crystallographic and 16 NMR PDB structures) to a library of model stacked guanines. The pair of model stacked guanines that best fit a given experimental pair was determined by the lowest root-mean-square deviation (RMSD) alignment (C, N, O atoms) of the guanine bases (Supplementary Figure S2). A single RMSD minimum was observed in rotation-separation space for every guanine pair cataloged. Stacked guanines within G-tetrads tend to be parallel, although G-tetrads are not always planar. Characterization of individual stacked base separations is an accurate measure of inter-base stacking distance and is relevant to our computational study involving planar G-tetrad stacks. Structural characterization code was written using MATLAB software (version R2008B, The Mathworks Inc.). Structural visualization was performed using PyMOL molecular visualization software (version 0.99, http://www.pymol.org/).

Quantum mechanical computations

QM computations were carried out using the Gaussian 03 software (46). Single-point interaction energy calculations used to create energy landscapes were performed at the MP2 level (44) using the modified split valance basis set 6-31G*(0.25) (47) in which the polarization d-function exponent from the standard 6-31G* basis set (45) is changed from 0.8 to 0.25 for C, N, and O atoms as well as for K⁺ ions. Previous works by Hobza and Sponer (9) and Sponer et al. (12) have demonstrated the 6-31G*(0.25) basis set to be an inexpensive choice for modeling stacking interactions. The 6-31G*(0.25) basis set was further tested here (Supplementary Figure S3).

Energy landscapes were determined for both same-polarity and opposite-polarity stacked G-tetrads. Single-point interaction energy was computed over a tetrad separation distance (d_tet) of 3.0–3.6 Å with a 0.1 Å resolution and a relative rotation angle (θ_tet) of 0°–90° with 5° resolution. In total, 266 single-point interaction energy calculations were performed at the MP2/6-31 G*(0.25) level. Single-point energy calculations were also performed for average geometries of base stacking modes observed in crystal structures at the MP2/6-311 + G(2d,2p) level (44,45). Stacking energies (ΔE) in this work have been determined using the counterpoise procedure (43) to correct for basis set superposition errors, treating each tetrad layer and central ion as individual fragments.

Molecular mechanics and molecular dynamics computations

MM and MD computations were performed with the AMBER 10 software (48) using the force field of Cornell et al. (49) with the Parmbsc0 force field modification (50) commonly used for nucleic acid simulations. The intermolecular terms affecting the energy landscape of MM-computed stacked G-tetrads include Van der Waals and electrostatic terms as described by the original force field of Cornell et al. (49). Single-point energy calculations used to generate energy landscapes were performed using the same models used in QM computation. Energy landscape calculations were performed in vacuum with no cutoff used for non-bonded interactions. Force field parameters for isolated guanines used in our models were derived by standard AMBER protocols. RESP partial atomic charges were calculated at Hartree–Fock/6-31G* level using the R.E.D. software (51) (Supplementary Table S1).

MD simulations of stacked G-quadruplexes were generated from an NMR-based model of the sequence d[TT(G₃T)₄] (52). Flanking ends were removed to generate a model for the d[(G₃T)₃G₃] sequence used in our simulations. The chemistry of strand termini was modified to reflect that observed in experimentally synthesized oligonucleotides with the 3′-end capped with a C3′-O3′-H chemistry and the 5′-end capped with a C5′-O5′-H chemistry. Two individual G-quadruplex units were then manually stacked in a 5′–5′ and 3′–3′ orientation. The relative rotation of these units was varied in ∼30° intervals to generate three unique starting structures for each of the 5′–5′ and 3′–3′ stacking models. Starting structures ranged over two of the four possible stacking quadrants (Supplementary Figure S4). K⁺ ions were manually added between tetrads in the core and at the interface of stacked G-quadruplexes. Additional K⁺ ions (for a total of 28) were added to neutralize the systems. The systems were solvated with a TIP3P (53) water truncated octahedral box with water molecules ranging in number from 5500 to 7500 over the models explored.

Periodic boundary conditions were used in our simulations. Pressure and temperature were held constant at 1 bar and 300 K, respectively, according to the Berendsen algorithm (54). A 2-fs time step was used while constraining covalent hydrogen bonds using SHAKE (55). The particle mesh Ewald method (56) was used to calculate long-range electrostatic interactions. Non-bonded interactions were calculated within a 9 Å cutoff in our MD simulations, and the list of non-bonded pairs was updated, and the center-of-mass motion was removed at 10 ps intervals. Systems underwent a series of initial constrained minimizations and equilibration dynamics. Systems were first minimized with harmonic potential position restraints (25 kcal mol⁻¹ Å⁻²) on DNA atoms and ions within the G-quadruplex core/interface over 500 steps of steepest decent minimization followed by 500 step of conjugated gradient minimization. Systems were then heated from 100 to 300 K over 10 ps and equilibrated at 300 K for 90 ps under constant volume while maintaining 25 kcal mol⁻¹ Å⁻² position restraints on aforementioned atoms. Systems underwent further steps of minimization and equilibration in which the positional restraints were gradually reduced to 5, 4, 3, 2, 1 and 0.5 kcal mol⁻¹ Å⁻². We take the start of simulations as the first segment of unrestrained simulation. Structures were examined every 25 ps in the first 3 ns and every 100 ps thereafter. The guanines at the interface were compared with model stacked guanines of variable separation and relative rotation. All four stacked guanine pairs at the interface were cataloged for each snapshot, and the average rotational values are presented.

RESULTS AND DISCUSSION

Structural survey and characterization: guanine stacking within the G-tetrad core

A structural survey of the PDB was performed to characterize the guanine base stacking geometries observed between tetrads within the G-tetrad core of crystallographic G-quadruplex structures (Supplementary Table S2). Individual G-quadruplex units were found to have three common stacking geometries within the G-tetrad core (Figure 2), which are intrinsically related to the glycosidic conformation of the bases: (i) ‘Partial 5/6-ring’ stacking (Figure 2A) of the ‘Anti/Anti’ step is formed from same-polarity stacked tetrads with a partial overlap of the 5-member ring of one guanine with the 6-member ring of another; (ii) ‘5-ring’ stacking (Figure 2B) of the ‘Syn/Anti’ step is a result of opposite-polarity stacking with an overlap of the 5-member rings of stacked guanines; (iii) ‘Partial 6-ring’ stacking (Figure 2C) of the ‘Anti/Syn’ step is also formed by opposite-polarity stacked tetrads and exhibits a partial overlap of the 6-member rings of stacked guanines.

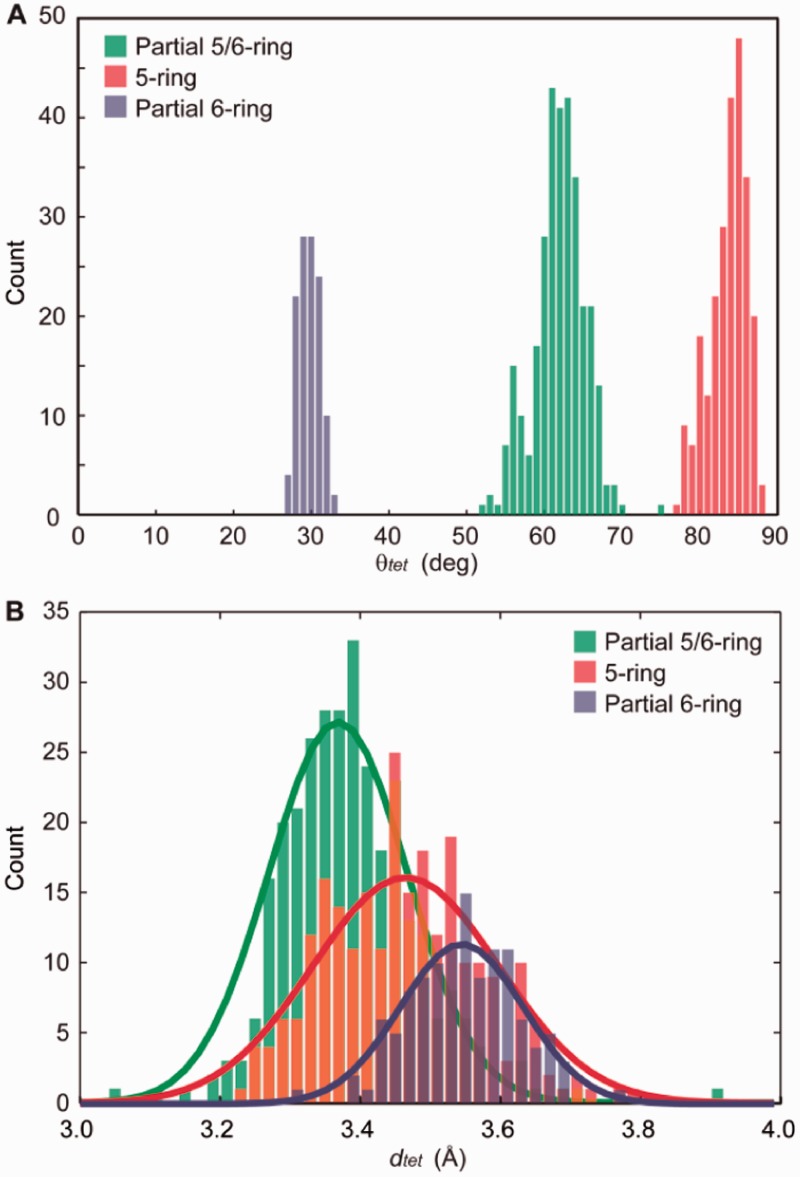
To quantify the stacking geometries of different core guanine–guanine steps, stacked guanines from the tetrads of experimentally determined structures were compared with a library of stacked guanines from model G-tetrads varying over relative rotation (θ_tet) and separation (d_tet) space (Figure 1). Values of these parameters were assigned to experimental pairs of stacked guanines via lowest RMSD alignment with model tetrads (see ‘Methods’ section). The results of our characterization of experimental guanine base stacking geometries are shown in Figure 3 and Table 1. Expectedly, there exist discrete regions of θ_tet for the ‘Anti/Anti’, ‘Anti/Syn’ and ‘Syn/Anti’ steps (Figure 3A). Unexpectedly, the average d_tet was found to vary among stacking modes (Figure 3B and Table 1). Average d_tet values of 3.39, 3.47 and 3.55 Å were observed for the ‘Anti/Anti’, ‘Syn/Anti’ and ‘Anti/Syn’ steps, respectively. However, regions of d_tet for different base stacking modes are highly overlapped. To account for a possible bias of experimental conditions on our statistical results of base stacking geometries, subclasses of G-quadruplex structures were also analyzed. When appropriate, crystallographic structures were further classified by their varying structural features (Supplementary Table S3), including whether the oligonucleotide chemistry was DNA or RNA, the type of coordinating ion, the presence of a drug molecule, strand directionality and strand stoichiometry. No significant differences are observed among the features investigated in this work. To see whether our statistical findings were specific to crystallographic structures, a set of NMR structures were also examined (Table 1 and Supplementary Table S4). Similar average values of d_tet and θ_tet were observed for the ‘Anti/Anti’, ‘Syn/Anti’ and ‘Anti/Syn’ core stacking modes (Table 1 and Supplementary Figures S5–S7). It is important to state that there was a notable occurrence of ‘Anti/Syn’ geometries surveyed from crystal structures in which the stacked guanines were non-parallel, containing varying pitch angles about the C2–C8 axis of an individual guanine. While our study is focused on understanding the effects of θ_tet and d_tet on stacking energy, it would be interesting to understand the effects of other degrees of freedom on stacked coordinated G-tetrad systems.

Figure 3.

Histograms representing the (A) relative rotation (θ_tet) and (B) separation (d_tet) values observed for stacked guanines within the G-tetrad core of cataloged crystallographic G-quadruplexes. Counts are binned every 1° (θ_tet) and 0.02 Å (d_tet). Separation histograms are fitted with Gaussian distributions for visualization purposes. For a detailed explanation of how geometrical parameters are extracted from experimental structures, see ‘Methods’ section.

Table 1.

Statistics of base stacking modes as observed in experimentally determined structures

Stacking Mode	Counta	X-ray				Countc	NMRb
		θtet (°)		dtet (Å)			θtet (°)		dtet (Å)
		Average	First SDd	Average	First SDd		Average	First SDd	Average	First SDd
Core
Partial 5/6-ring (Anti/Anti)	310	61.5	3.3	3.39	0.10	23	61.1	5.5	3.28	0.17
5-ring (Syn/Anti)	245	83.2	2.4	3.47	0.11	44	84.5	4.7	3.54	0.29
Partial 6-ring (Anti/Syn)	118	29.2	1.4	3.55	0.08	8	30.7	8.2	3.57	0.29
Interfacee
Partial 6-ring	4	26.2		3.50
6-ring	4	41.6		3.41
5/6-ring	3	56.5		3.41		15	61.8		3.43
5-ring	33	83.2	1.4	3.52	0.08	5	81.4		3.11

^aThe number of observed base stacking geometries that are defined uniquely within the unit cell or at the interface of symmetry mates.

^bA selection of NMR structures (Supplementary Table S4) were cataloged to determine if there exist fundamental differences between the base stacking modes exhibited in X-ray and NMR structures.

^cFor NMR structures, the base stacking geometry of a single count of stacked guanines is an average across all of the models present in a given PDB file.

^dStandard deviation (SD) values highlight the ensemble spread of our characterized geometries used to determine θ_tet and d_tet. They do not reflect the uncertainty in experimental measurements.

^e‘Partial 6-ring' stacking was observed for a mixed 5′-3′ stacked structure (PDB ID: 2AVJ) and ‘6-ring' stacking was observed for a 3′-3′ stacked structure (PDB ID: 2HRI) while ‘5/6-ring' and ‘5-ring' stacking were observed for 5′-5′ stacked G-quadruplexes. The interface geometries of some NMR structures (PDB ID: 1MY9 and 2RQJ) were observed to contain mixed base stacking modes at their stacking interface.

The statistical information in Table 1 offers insight into the differences between core guanine base stacking geometries. Although different average θ_tet angles are fundamental to unique stacking modes, perhaps unintuitive is the observed differences in average d_tet of stacked guanines. Another feature of note is that the variation in the first standard deviation (SD) of θ_tet of crystallographic structures with ‘Anti/Anti’ > ‘Syn/Anti’ > ‘Anti/Syn’. Additionally, stacked guanines within the core of NMR structures demonstrate larger first SD values compared with those in crystallographic structures. This variation may reflect the different nature of crystal and solution environments or limitations of NMR-based models in providing the atomic precision necessary for a rigorous discussion of base stacking geometry. Considering the limitations in accuracy of experimentally determined structures, we must be cautious in our interpretation of statistical results dealing with small structural differences such as the average d_tet values for core stacking modes.

To better interpret the statistical data of Table 1, let us discuss the structural motifs included in this study. The ‘Anti/Anti’ step is abundant in crystallographic structures of dimeric and monomeric telomeric G-quadruplexes (20,26,27,36,57,58) as well as structures of some tetrameric G-quadruplexes (17–19,21,22,24,25,59–63). The ‘Syn/Anti’ and ‘Anti/Syn’ steps are abundant in G-quadruplexes formed from Oxytricha telomeric sequences (64–69) containing the G₄T₄G₄ motif and its variants. Additionally, ‘Syn/Anti’ steps are observed in some bulged RNA tetramer G-quadruplexes (60,70) (Supplementary Supporting Text 1). The ‘Syn/Syn’ stacking mode (Supplementary Figure S8) is observed in some NMR structures of unique folding topologies (41,71–74). Similar to ‘Anti/Anti’ steps, ‘Syn/Syn’ steps also exhibit a ‘Partial 5/6-ring’ stacking geometry. The ‘Syn/Syn’ step is not discussed here in length, as it has not been observed in crystallographic G-quadruplex structures, which to date are less diverse than NMR structures in terms of sequence and folding topology.

Structural survey and characterization: guanine stacking at the G-tetrad interface of stacked G-quadruplexes

In our survey of the PDB, we also cataloged the base stacking geometries at the interface of stacked G-quadruplexes. The G-tetrad stacking interfaces of stacked G-quadruplexes arise because of the dimerization of individual G-quadruplex units in solution or in a crystal packing environment. We include both crystallographic and NMR structures in our survey because of the limited number of stacked G-quadruplex complexes published to date. Experimentally observed interface geometries may be classified into four modes (Figure 4). These stacking geometries are termed ‘Partial 6-ring’, ‘6-ring’, ‘5/6-ring’ and ‘5-ring’. We note that all interface stacking exhibits an opposite-polarity orientation. Additionally, almost all parallel G-quadruplexes that exhibit interface stacking do so at their 5′-end. The preference for 5′–5′ interface stacking is examined further in subsequent sections.

Figure 4.

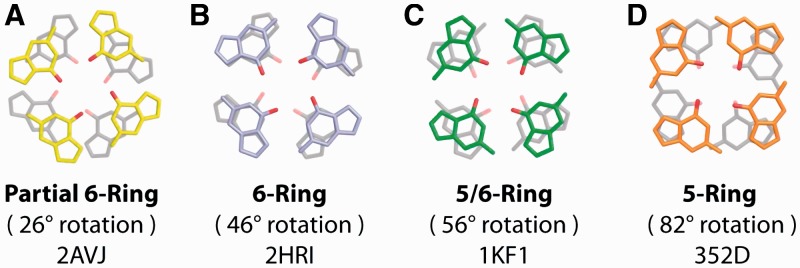
Illustrative examples of G-tetrad base stacking modes at the interface of stacked G-quadruplexes as identified in our structural survey. (A) ‘Partial 6-ring’, (B) ‘6-ring’, (C) ‘5/6-ring’ and (D) ‘5-ring’ as observed in crystallographic structures. Stacking modes are labeled along with the θ_tet rotational value and the PDB ID code of the experimental structure from which the G-tetrads are taken.

The ‘6-ring’, ‘5/6-ring’ and ‘5-ring’ stacking modes are observed at the interfaces of crystallographic tetrameric (17–19,21,22,24,25) as well as monomeric and dimeric human telomeric (20,26) G-quadruplex structures (Supplementary Tables S2 and S4). A single instance of ‘Partial 6-ring’ stacking is observed in an G-quadruplex structure formed by the sequence d[G₄^BrUT₂G₄]₂ demonstrating 2 + 2 (↑•↑•↓•↓) strand directionality (23). Interface stacked G-tetrad geometries in crystallographic structures exhibited mostly ‘5-ring’ stacking (Table 1), largely owing to the high number of tetrameric structures formed from the d[TG₄T] sequence.

NMR structures containing G-quadruplex interfaces were mostly propeller-type and demonstrated either the ‘5/6-ring’ or the ‘5-ring’ stacking geometries. Interface base stacking geometries are sometimes found within interlocked G-quadruplexes such as the ‘Partial 6-ring’ stacking of the interlocked V4 folding topology (75). Interlocked structures (29,32,75) are dimeric G-quadruplexes without a free-stacking interface, consisting of two stacked G-quadruplex units, each contributing guanines to G-tetrad core of the other. These unique geometries are not considered in our statistics.

QM computational studies: energy landscapes of K⁺-coordinated stacked G-tetrads

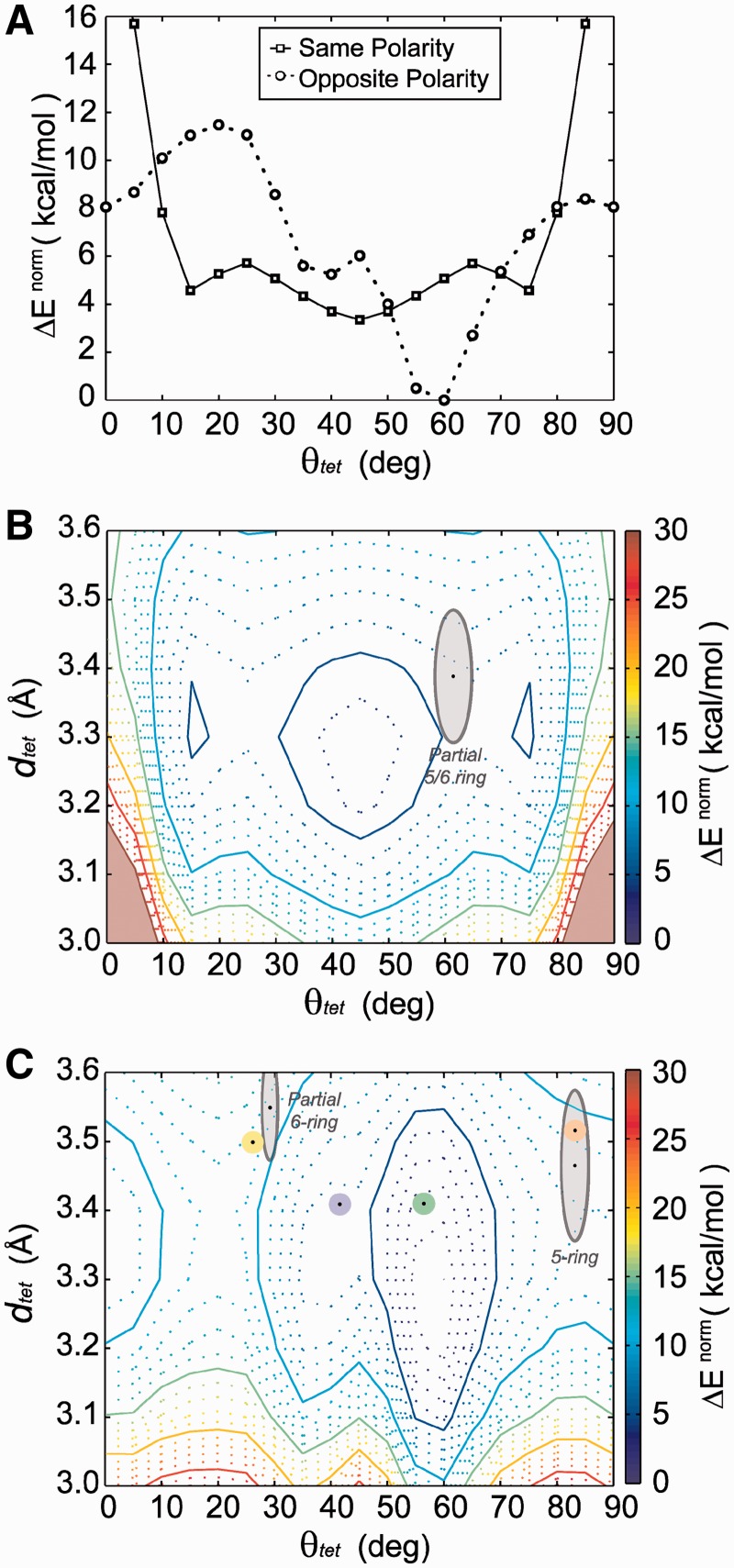
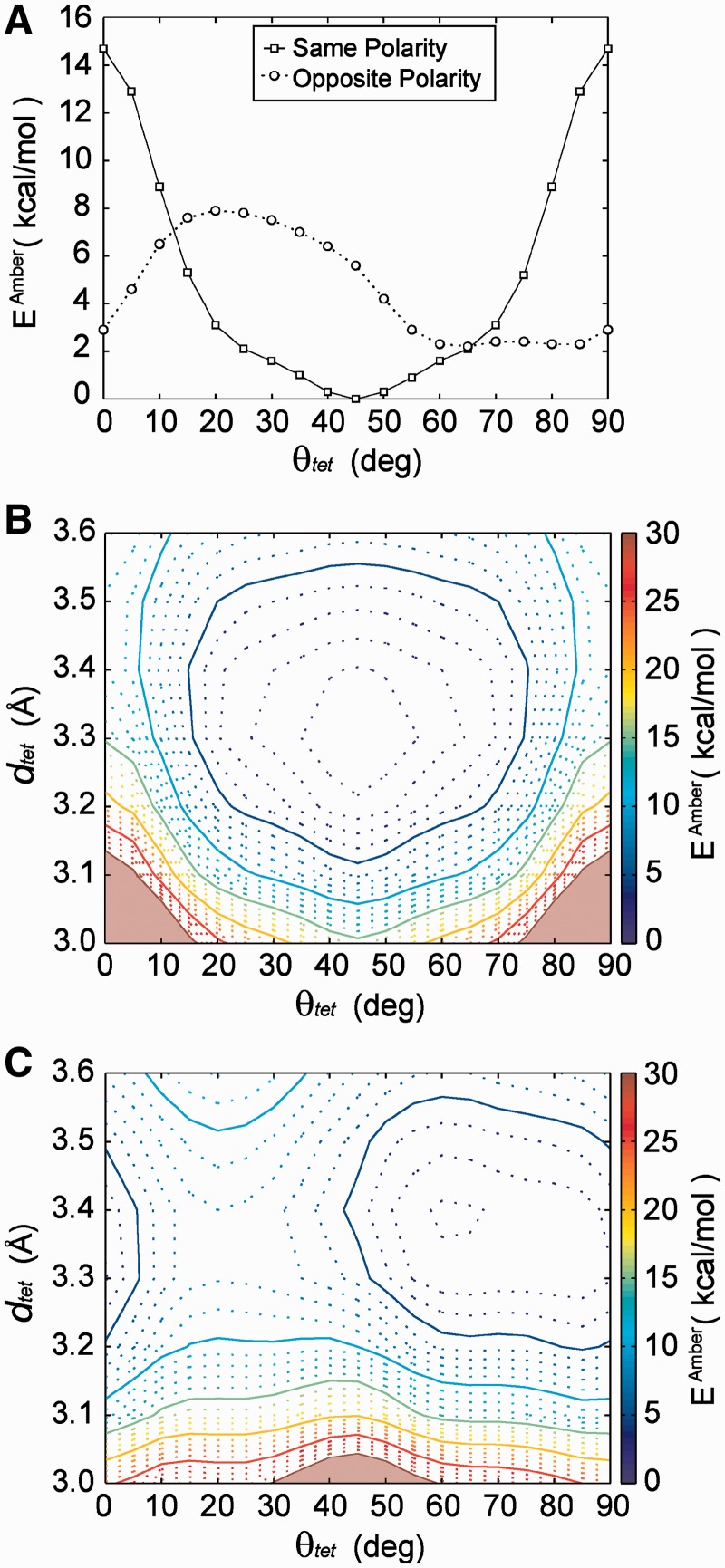
We used a series of QM computations to calculate stacking energies (see ‘Nomenclature’ section), of stacked G-tetrad geometries coordinated by a centralized K⁺ ion. The θ_tet and d_tet values of stacked tetrads were systematically varied to generate energy landscapes of same-polarity and opposite-polarity stacked tetrads at the MP2/6-31G*(0.25) level (Figure 5). Slices of energy landscapes at a d_tet value of 3.3 Å illustrate the θ_tet energy dependence of same- and opposite-polarity stacked tetrads (Figure 5A). Examples of the d_tet dependence of energy curves are shown in Supplementary Figure S9).

Figure 5.

QM energy landscapes. (A) The rotational (θ_tet) energy profile of same-polarity and opposite-polarity stacked G-tetrads at a d_tet value of 3.3 Å separation. Energy landscapes of (B) same-polarity and (C) opposite-polarity stacked tetrads are presented with stacking modes as determined from cataloged crystallographic structures superimposed. Average core G-tetrad stacking modes are shown with average geometries indicated by a black dot and gray outlined regions having dimensions of the first SD for θ_tet and d_tet values. Average G-tetrad stacking modes at the interface of stacked G-quadruplexes are presented, color-coded as shown in Figure 4: ‘Partial 6-ring’ (yellow), ‘6-ring’ (purple), ‘5/6-ring’ (green) and ‘5-ring’ (orange).

The θ_tet energy profile of same-polarity stacking is characterized by highly unfavorable stacking energy in the areas of θ_tet <15° and >75° and a broad energy minimum elsewhere (15°–75°) with a global minimum at 45° and two minima of comparable energy at 15° and 75° separated by a small energy barrier of roughly 2.5 kcal/mol. The energy landscape of the same-polarity stacked tetrad is presented (Figure 5B), superimposed with regions indicating average geometries of base stacking modes cataloged from crystal structures (Table 1). There exists a broad low-energy basin within the d_tet range of 3.2–3.4 Å and 15°–75°. The ‘Anti/Anti’ core stacking geometry is observed to fall well within this energy basin (Figure 5B and Supplementary Figures S6 and S7) in close proximity to the landscapes low-energy states. It is interesting to note that the most favorable same-polarity stacking occurs at rotation angle of 45° when there is little aromatic ring overlap of stacked bases.

In contrast, the θ_tet energy profile of opposite-polarity stacking is characterized by a deep global minimum at 55°–60° and local minima at 35°–45° and 85°–5° of roughly 6 and 8 kcal/mol, respectively (Figure 5A). There is a sizable energy barrier of 4 kcal/mol separating the 85°–5° and 35°–45° minima. The energy landscape of opposite-polarity stacked tetrads (Figure 5C) is a diverse landscape characterized by narrow energy minima. The ‘Anti/Syn Partial 6-ring’ and ‘Syn/Anti 5-ring’ core stacking modes, as well as interface stacking modes, can be seen superimposed on the opposite-polarity stacking landscape (Figure 5C). Interestingly, the ‘Partial 6-ring' and the ‘5-ring' geometries found in the core and at the interface of G-quadruplexes do not fall within calculated minima. Alternatively, the ‘5/6-ring’ interface stacking mode occupies the global minimum (55°–60°), with the ‘6-ring’ interface stacking mode being found in the neighboring energy minimum (35°–45°). It is interesting that stacking at the interface of G-quadruplexes, which is not constrained by a backbone, is capable of occupying the energy minima of the QM-computed energy landscapes. We note that the most favorable interface stacking geometry, the ‘5/6-ring’ mode, is found in both crystallographic and NMR structures.

The stacking energies of average G-tetrad stacking geometries from experimentally determined structures were interpolated from the energy landscape and are presented in Table 2. Additionally, stacking energies were computed at a higher level of theory, MP2/6-311 + G(2d,2p), for stacked G-tetrads that mimic the average experimental stacking geometries observed in our survey (Table 2). ΔE^norm stacking energies of core tetrad stacking geometries were found to be ranked ‘Anti/Anti Partial 5/6-ring’ < ‘Syn/Anti 5-ring’ < ‘Anti/Syn Partial 6-ring’ with values of 4.21, 7.81 and 11.88 kcal/mol, respectively. For interface tetrad stacking geometries, ΔE^norm is ranked as follows: ‘5/6-ring’ < ‘6-ring’ < ‘5-ring’ < ‘Partial 6-ring’ with values of 0.00, 4.88, 9.14 and 11.69 kcal/mol, respectively. The stacking energies interpolated from MP2/6-31G*(0.25) calculations of average experimental geometries are in agreement with higher level MP2/6-311 + G(2d,2p) calculations (Table 2). It is important to remember that relative energies discussed here are for entire stacked tetrads, not a single pair of stacked guanines. As a large number of cataloged structures contain Na⁺ ions instead of K⁺ ions, the effects of Na⁺ on the energy profiles of stacked tetrads were also investigated (Supplementary Figure S10, Tables S5–S7 and Text S2).

Table 2.

Calculated tetrad stacking energies (kcal/mol) of experimentally observed stacking modes

Stacking mode	MP2 6-31G*(0.25)a		MP2 6-311 + G(2d,2p)		AMBER
	ΔE	ΔEnorm	ΔE	ΔEnorm	EAmber
Core
Partial 5/6-ring	−153.56	5.74	−157.37	4.21	2.07
5-ring	−150.74	8.56	−153.77	7.81	3.64
Partial 6-ring	−147.71	11.59	−149.70	11.88	10.09
Interface
Partial 6-ring	−147.78	11.52	−149.90	11.69	9.24
6-ring	−153.72	5.58	−156.71	4.88	5.27
5/6-ring	−157.66	1.64	−161.58	0.00	2.29
5-ring	−149.99	9.31	−152.45	9.14	4.76

Rotation and separation coordinates corresponding to these energies are the averages presented in Table 1.

^aEnergies determined by interpolation from available data on the energy landscapes of the same- and opposite-polarity stacked tetrads.

One should use caution when comparing quantitative relative energies from gas phase energy calculations of isolated tetrads with experimentally observed tetrad stacking geometries. For reasons discussed earlier (see ‘Nomenclature’ section), the energy dependence of tetrad geometries calculated in gas phase can be altered by a water environment. For example, interactions of tetrad edges with ions and water are energetic contributions that can differ with varying tetrad geometries (27,36,57,58). As crystallographic structures are expected to have less atomic coordinate uncertainty than their NMR counterparts, we focus on crystallographic structures when relating to our computational models. Despite these uncertainties, the results of our survey of crystallographic structures, particularly interface stacking geometries, are in good agreement with our computational studies suggesting that computed energy landscapes provide a good general description of preferable G-tetrad stacking geometries in G-quadruplex systems. Results from fully represented and solvated MD simulations of G-quadruplexes (discussed later) further support these findings.

Previous quantum chemical studies of G-tetrad stacking have also examined some of the base stacking geometries discussed in this study (14–16). A study by Gu and Leszczynski. (15) in 2002 examined two geometries of stacked G-tetrad complexes with different coordinated cations. Initial geometries were similar to those found in crystallographic structures and then optimized at the Hartree–Fock level of theory. Optimized tetrad geometries of ‘5/6-ring’ stacking were observed for an opposite-polarity model, and an optimized θ_tet of ∼45° was observed for a same-polarity model. Although far from their starting geometries, optimized tetrads in this study are in agreement with the two global minima observed in our study. In 2005, Meyer et al. (16) examined such tetrads in a similar manner using density functional theory. Three optimized geometries were obtained based on model tetrads of different symmetries. These included the two geometries discussed earlier and a third corresponding to the global maximum of our same-polarity landscape with a θ_tet of ∼0°. These past studies have examined G-tetrad stacking geometries for same- and opposite-polarity stacked tetrads and give an idea of the energy differences between them. The current study expands on previous works by a systematic assessment of stacking energy landscapes at a high level of theory, MP2/6-31G*(0.25), and couples this investigation with a structural survey of experimental G-tetrad stacking geometries.

MM energy landscapes of stacked G-tetrads

In addition to our QM investigation of G-tetrad stacking, we decided to assess the accuracy of a commonly used MM force field in representing G-tetrad stacking. Energy landscapes were computed for K⁺-coordinated stacked G-tetrads using the ff94 AMBER force field (49) description of intermolecular Van der waals and electrostatic terms, which is commonly used for nucleic acid simulations. The results of these studies are shown in Figure 6. The shape of the MM same-polarity energy landscape (Figure 6B) is similar to that of the QM landscape, with a similar broad energy basin observed. The low θ_tet regions of the same-polarity energy landscape are again observed to be unfavorable. The opposite-polarity stacking landscape computed via the AMBER force field (Figure 6C) is also generally similar in shape to that of the QM landscape, except with smaller and less defined energy barriers. More specifically, the energy barriers between the ‘5/6-ring’ and ‘5-ring’, as well as between the ‘Partial 6-ring’ and the ‘6-ring’ base stacking modes, are negligible.

Figure 6.

MM energy landscapes. (A) Rotational energy profile of same-polarity and opposite-polarity stacked tetrads at a d_tet value of 3.3 Å separation. (B) MM energy landscapes of same-polarity and (C) opposite-polarity stacked tetrads.

The differences between the QM and the MM energy landscapes lead to some notable differences in the relative energies of various stacking modes (Table 2), particularly for the ‘Partial 5/6-ring’ and ‘5-ring’ modes of the core and the ‘5/6-ring’ and ‘5-ring’ modes of the interface. The less defined energy minima of the opposite-polarity energy landscape computed via AMBER should be considered when using such techniques in modeling G-quadruplex structures. Generally speaking, however, the AMBER force field shows a good agreement with QM computations, and favors the ‘5/6-ring’ and ‘5-ring’ interface stacking modes, which are seen occupied by all NMR-based experimental structures and most crystallographic structures. This agreement is interesting considering that the description of intermolecular interactions in the AMBER force field is limited to Van der Waals and electrostatic interactions.

Recently, studies have used free energy analysis of MD simulations to explore the effects of varying structural features on the energy of G-quadruplex systems (39,40). Studies by Cang et al. examined energy differences of different dinucleotide steps in the context of G-quadruplex DNA (39). A difference of 15 kcal/mol, calculated using MM-PBSA free energy analysis of MD simulations, is observed between two-layered G-quadruplexes containing all ‘Syn/Anti’ steps and one containing less favorable ‘Anti/Anti’ steps. Our ranking of ‘Anti/Anti Partial 5/6-ring’ < ‘Syn/Anti 5-ring’ < ‘Anti/Syn Partial 6-ring’ for core base stacking geometries does not directly contrast these results, as our work seeks to understand the energy contribution of base stacking, which is only one component driving the formation of G-quadruplex structures. In a fully represented (with base, sugar and backbone atoms) and solvated system, it is apparent that many other factors play a role. It is interesting to note that a comparison of QM and MM energy landscapes suggests a relative energy difference of 3.4 and 1.6 kcal/mol, respectively, between the more favorable ‘Anti/Anti Partial 5/6-ring’ and the ‘Syn/Anti 5-ring’ stacking geometries (Table 2) suggesting some discrepancy between the QM-computed landscapes and the MM description of G-tetrad stacking energy. Nevertheless, the MM energy landscapes reproduce the general trends observed in QM energy landscapes, suggesting a fairly accurate description of the relative stacking energy between stacked G-tetrad geometries.

Investigating 3′–3′ and 5′–5′ G-quadruplex stacking using molecular dynamics

Individual G-quadruplex blocks are sometimes observed to stack on each other at the interface of their outermost exposed G-tetrads. Parallel-stranded G-quadruplexes contain well-defined 3′- and 5′-ends giving rise to four possible stacking combinations (76), 5′–5′, 3′–3′, 5′–3′ and 3′–5′. Stacking that is 5′–5′ or 3′–3′ arises from opposite-polarity tetrad stacking, whereas 5′–3′ and 3′–5′ arises from same-polarity tetrad stacking. No instances of 5′–3′ stacking at the G-tetrad interface of G-quadruplexes have been reported, although unpublished data from our laboratory suggest that 5′–3′ stacking can occur at the interface of two G-quadruplexes connected by a linker. In our survey, G-quadruplex stacking interfaces are almost entirely observed to be 5′–5′ in nature. In tetramer G-quadruplex-forming sequences, stacking is observed in a 5′–5′ manner despite the presence of 3′- and 5′-flanking ends for most sequences (17–19,21,24,25). Of sequences with well-defined free-stacking interfaces, the only exception observed to stack in 3′–3′ manner is a bimolecular telomeric G-quadruplex whose 5′-end is occupied by small molecule binding (26). NMR studies of the 5′-TTAGGG sequence demonstrate that when the 5′-end of a tetrameric G-quadruplex is occupied by a sizable flanking sequence, 3′–3′ stacking still readily occurs (77). These studies suggest that 3′–3′ stacking is possible, but less favorable compared with the more readily observed 5′–5′ stacking. It is also interesting to note that some instances have been observed of drug-mediated 5′–5′ stacking (58).

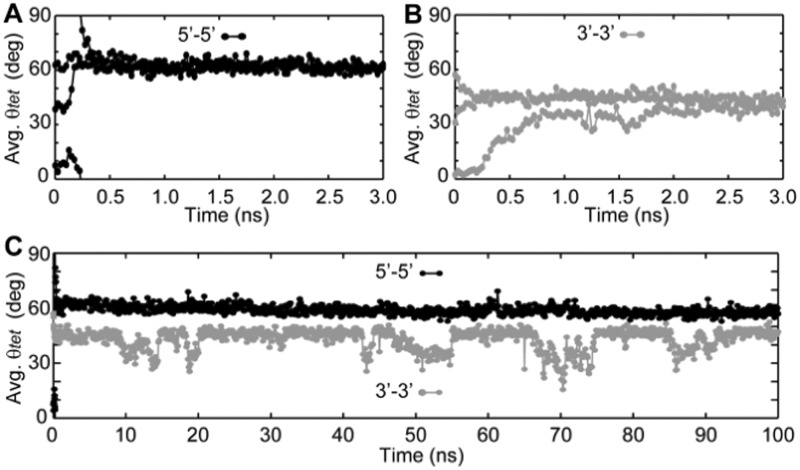
To shed light on the observed 5′–5′ stacking preference, a series of MD simulations was performed. Using a variant from an NMR-based model (52), we simulated the stacking of two propeller structures formed by the sequence d[G₃(TG₃)₃]. Individual G-quadrupex units were oriented in a 3′–3′- or 5′–5′ manner in multiple starting geometries (See ‘Methods’ section). The θ_tet of interface stacked guanines was determined along the trajectories to understand the base stacking modes occupied by 3′–3′ and 5′–5′ stacked G-quadruplexes (Figure 7 and Supplementary Figure S11).

Figure 7.

MD investigation of G-quadruplex G-tetrad stacking interfaces: 5-ns trajectories of stacked propeller G-quadruplexes formed by the sequences d[(G₃T)₃G₃] were run for (A) 5′–5′ and (B) 3′–3′ stacked G-quadruplexes. The trajectories of three different starting geometries of G-quadruplex stacking arrangements (Interface θ_tet varying by ∼30°) are shown. (C) Long 100-ns trajectories were computed for a 5′–5′ and a 3′–3′ stacked G-quadruplex complex. Average relative rotation (θ_tet) of the four interface guanine stacks was characterized at regular intervals.

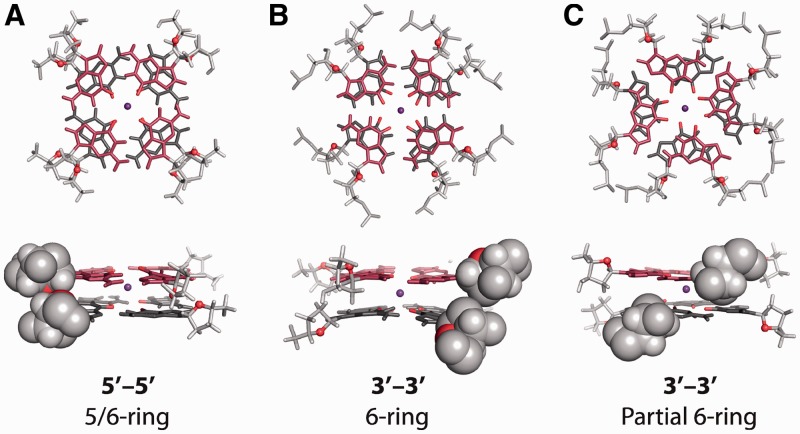
For all trajectories, the θ_tet values of tetrads at the interface of the stacked propeller G-quadruplexes equilibrate within the first few nanoseconds of simulation. More interestingly, each of the three trajectories run for the 3′–3′ and 5′–5′ models equilibrate to a single θ_tet value, regardless of their initial θ_tet value. What is perhaps most interesting is that the 3′–3′ and 5′–5′ stacking models equilibrate to different interface geometries. The interface geometries of the 3′–3′ model equilibrate to θ_tet value of roughly 40°–45° corresponding to the ‘6-ring’ stacking mode, as seen experimentally (22), whereas the 5′–5′ model equilibrates to 60°–65°, similar to ‘5/6-ring’ stacking. Longer MD simulations of 100 ns were computed for select trajectories to investigate whether these stacking geometries are maintained over a longer time scale (Figure 8C and Supplementary Figure S12). Both the 3′–3′ and the 5′–5′ models remain folded and stacked throughout the 100 ns trajectories. The 3′–3′ stacked G-quadruplexes are observed to periodically shift from the more favorable of ‘6-ring’ stacking to a ‘Partial 6-ring’ stacking geometry with a θ_tet of roughly 30°. The 5′–5′ model remains in an equilibrium interface geometry exhibiting ‘5/6-ring’ stacking over the entire 100-ns trajectory.

Figure 8.

Illustrative interface geometry of MD trajectories: (A) A ‘5/6-ring’ stacking equilibrium is maintained across the 100-ns trajectory for the 5′–5′ stacking model. (B) The interface of the 3′–3′ model is mostly found in a ‘6-ring’ stacking geometry. (C) Occasionally the 3′–3′ model occupies a ‘Partial 6-ring’ stacking mode. Backbone atoms are shown in light gray and the O1′ atoms of sugar are shown in red. Spherical representation of backbone atoms are the approximate Van der Waals surface of atoms as visualized in PyMOL.

Structural analysis suggests that the 3′–3′ model cannot occupy the interfacial ‘5/6-ring’ stacking mode, as this would result in a clash between the sugars of the stacked guanines (Figure 8). Conversely, the ‘5/6-ring’ stacking of the 5′–5′ model is easily achieved without unfavorable backbone interactions. Calculations at the MP2/6-311 + G(2d,2p) level described in Table 2 suggest that the ‘6-ring’ and ‘5/6-ring’ stacking modes are energetically different by roughly 5 kcal/mol. Based on the QM and MD studies described in this work, we provide evidence that accessible base stacking modes are fundamentally different for 3′–3′ and 5′–5′ stacked G-quadruplexes. Furthermore, we suggest that sizable energetic differences between accessible base stacking modes play a role in the observed preference for G-quadruplexes to stack primarily in a 5′–5′ manner.

Understanding the relative energies of accessible interfacial base stacking modes has important implications in high-order stacking of G-quadruplexes. Past studies have suggested that long telomeric repeats form a ‘bead-on-a-string’ model in which long telomeric nucleic acids form a series of intramolecular quadruplex ‘beads’ (78,79). Other studies (20,35,76,80) suggest that further structural organization is possible, in which individual beads stack on each other on the 3′-end and/or the 5′-end G-tetrad interfaces. Stacking models have been suggested in which telomeric G-quadruplex beads stack in a 5′–3′ (20,80), 3′–3′ (35) and 5′–5′ manner (35,76). Crystallographic structural data have shown drug-mediated 5′–3′ stacking interactions in two-repeat human telomeric DNA (57). Additionally, 5′–5′ stacking has been observed in two-repeat (27) and four-repeat (20) human telomeric DNA. NMR solution studies have observed 5′–5′ G-tetrad stacking in two-repeat human telomeric RNA (35). Additionally, recent studies have suggested that TERRA stacks preferentially in a two-block manner (76,81). This observation is in line with a 5′–5′ or 3′–3′ model, as 5′–3′ stacking is expected to demonstrate continuous stacking beyond two blocks. The preference of 5′–5′ stacking observed in our survey supports 5′–5′ stacking models of higher-ordered telomeric repeat structures and is in agreement with recent studies by Martadinata et al. (76), which report a ‘5/6-ring’ interface stacking geometry of the 5′–5′ stacked TERRA based on experimental and MD studies. Although it is probable that multiple types of high-order G-quadrupex assemblies can form in dynamic long telomeric nucleic acids, further work needs to be done to understand which are most readily adopted in the context of biologically relevant environments.

CONCLUSION

The current study seeks to understand the roles of guanine base stacking in the formation and interaction of G-quadruplex nucleic acids. We undertake an extensive survey of the PDB to characterize guanine base stacking geometries within the core and at the interface of G-quadruplexes. We couple this survey with systematic QM and MM computations of G-tetrad stacking energy landscapes, in order to understand the base stacking energy contributions for different G-tetrad geometries observed experimentally. We also perform MD simulations to investigate the roles of base stacking in high-order G-quadruplex assemblies. We conclude the following from our studies:

1. There exists three well-defined base stacking modes within the G-tetrad core of G-quadruplexes, as well as numerous commonly occurring stacked G-tetrad geometries at the interface of stacked G-quadruplex structures. Base stacking geometries within the core were unique for the ‘Anti/Anti’, ‘Syn/Anti’ and ‘Anti/Syn’ dinucleotides steps (Figure 2) Additional base stacking geometries were observed at the interface, with the ‘5-ring’ and ‘5/6-ring’ stacking modes being most readily observed (Figure 4).

2. In our survey of the PDB, G-tetrad stacking at the interface of G-quadruplexes in both NMR and crystallographic structures always displayed opposite-polarity stacking (Figure 1) and was primarily stacked in a 5′–5′ manner.

3. QM energy landscapes of K⁺-coordinated stacked G-tetrads were calculated for different stacking polarities. Tetrad stacking energy for experimental geometries are ranked as follows, core stacking modes: ‘Anti/Anti Partial 5/6-ring’ < ‘Syn/Anti 5-ring’ < ‘Anti/Syn Partial 6-ring’, interface stacking modes: ‘5/6-ring’ < ‘6-ring’ < ‘5-ring’ < ‘Partial 6-ring’. G-tetrad stacking geometries at the interface of G-quadruplex units are found to be energetically different in terms of stacking energy by up to 12 kcal/mol.

4. Aside a few small differences, MM-computed G-tetrad stacking energy landscapes are in good agreement with QM landscapes suggesting that relative G-tetrad stacking energies are well represented in MD simulations.

5. MD simulations suggest that 5′–5′ and 3′–3′ stacking of parallel-stranded G-quadruplexes have different accessible base stacking modes, with 5′–5′ stacking being more energetically stable in terms of tetrad stacking energy. The results of our survey and computational studies suggest that a 5′–5′ arrangement with the ‘5/6-ring’ base stacking geometry of the interfacial G-tetrads is a favorable arrangement of stacked parallel G-quadruplexes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Tables S1–S7, Figures S1–S12, Texts S1 and S2, Supplementary References [82–89].

FUNDING

Singapore Ministry of Education and Nanyang Technological University (to A.T.P). Funding for open access charge: Nanyang Technological University.

Conflict of interest statement. None declared.