Categorical spectral analysis of periodicity in human and viral genomes

Abstract

Periodicity in nucleotide sequences arises from regular repeating patterns which may reflect important structure and function. Although a three-base periodicity in coding regions has been known for some time and has provided the basis for powerful gene prediction algorithms, its origins are still not fully understood. Here, we show that, contrary to common belief, amino acid (AA) bias and codon usage bias are insufficient to create base-3 periodicity. This article applies the rigorous method of spectral envelope to systematically characterize the contributions of codon bias, AA bias and protein structural motifs to the three-base periodicity of coding sequences. The method is also used to classify CpG islands in the human genome. In addition, we show how spectral envelope can be used to trace the evolution of viral genomes and monitor global sequence changes without having to align to previously known genomes. This approach also detects reassortment events, such as those that led to the 2009 pandemic H1N1 virus.

INTRODUCTION

Genomic nucleotide sequences contain functional and structural information at multiple levels. Even though consensus sequence motifs resulting from local alignments have provided fundamental units of information, e.g. specific recognition sites for DNA-binding factors, several recent studies highlight the limitations of this approach. For example, the conformational states of DNA under negative superhelical stress critically depend on long-distance coupling of base-pairs (1), and motif analyses can account for only half of nucleosome-free regions in yeast (2). Furthermore, traditional motif analyses have failed to explain how long non-coding RNAs (ncRNAs) find their target genomic locations and direct chromatin remodeling. These limitations suggest that new perspectives are necessary to extract information from genomic sequences. Identifying subtle features specific to coding sequences, regulatory sites, introns and intergenic regions will facilitate our understanding of the principles that have guided DNA sequence evolution.

One compelling idea is to analyze sequences from a dual picture of frequency space and study hidden periodic features without having to perform local alignments. This idea of searching for patterns in frequency space has been successfully applied to protein-coding sequences which often have three-nucleotide periodicity. This periodic phenomenon has intrigued many biologists for several decades (3–8). For example, it has led to the proposal that the ancestral forms of present-day genes might have consisted of repeating RNY (purine-any-pyrimidine) triplets (3); as a support, it was further shown that the presence of RNY periodicity can be used to identify the correct reading frame (4). Thus, patterns recurring at a period of three bases suggest principles behind gene evolution from small building blocks. Furthermore, powerful modern algorithms utilize the periodicity to predict coding regions in unannotated genomes (9–12). Carefully understanding the source and pattern of periodicity in genomic sequences thus represents an important problem in biology. As described below, however, several explanations for the periodicity are now available, providing sometimes conflicting views and creating confusion in the field. This article presents a rigorous mathematical analysis to clarify our understanding and demonstrates the utility of analyzing genomes in the frequency space.

Some competing explanations for the three-base periodicity and our extensions are

• (G-non G-N) repeat which may be important for ribosomal RNA guiding (5). The motif (G-non G-N) is found to belong to 130 diverse species of animals, plants, bacteria, viruses, organelles, plasmids and transposons. A local disruption of this periodical (G-non G-N) pattern is strongly correlated with instances of ribosome slippage. Interestingly, this (G-non G-N) pattern is found to disappear in the area of ribosome slippage sites. The (G-non G-N) pattern reemerges immediately downstream of the slippage site, but now in a new frame, reflecting the new translation reading frame. This may indicate that the (G-non G-N) repeat in mRNA is needed to monitor the correct reading frame during translation. (Note: In this article, however, we show that the most predominant triplet in proteins that show statistically significant periodicity is in fact NWS (any-[A/T]-[G/C]).

• Periodic G or C base at third codon position. Lió et al. (13) searched for subcodes while viewing the DNA sequences as being composed of ‘strong’ (S = G or C) and ‘weak’ (W = A or T) base-pairs. The three-nucleotide periodicity of S was found only in protein-coding sequences and primarily in structural genes playing important roles in cell metabolism. This periodicity was specifically prevalent in sequences of prokaryotes living in extreme environments. The authors suggested that the conservation of the periodicity is due to increased stability and translation accuracy, since the G and C pairing in the third codon position can help messenger RNA bind more effectively to ribosomes. (Note: In line with this observation, we also find that NWS repeats are prevalent in human protein domains that show statistically significant three-base periodicity.)

• Amino acid (AA) usage bias: the preponderance of only a few AAs in a given protein. Tsonis et al. (7) randomly selected 100 proteins from the Protein Information Resource database. Their analysis showed that in 80% of these proteins, only four AAs, which share the same first base in their codons, make up 32% of the protein length. As for the rest of the analyzed proteins, three or fewer AAs, possibly having different first bases in codons, make up nearly 40% of the protein length. In comparison, introns do not exhibit this same structure, and the authors concluded that this is why non-coding sequences do not possess the period-3 property. (Note: Table 1 shows the bias in the genome-wide AA usage in human. We will demonstrate in this article that even if all 64 codons are equally represented, simply removing stop codons from a fixed reading frame in random sequences can create fictitious periodicity. We also use Markov Chain Monte Carlo (MCMC) minimization to show that AA bias by itself is not sufficient to create periodicity.)

• Species-specific synonymous codon usage bias. Eskesen et al. (14) simulated random coding sequences by sampling triplet nucleotides from the codon usage frequencies estimated from Drosophila melanogaster, Homo sapiens and Caenorhabditis elegans and found that the periodicity observed in these simulations was highly similar to the periodicity in the actual exons. The authors also simulated coding sequences by sampling non-stop codons at equal frequency and found only minor periodicities in A and T nucleotides. Finally, the authors simulated sequences by sampling all codons at equal frequency, including the stop codons and found that the DNA periodicity completely disappeared. Based on these results, the authors suggested that the period-3 property is due to the codon usage bias specific to a given organism. The species-specific codon usage bias may potentially be due to different tRNA abundance (15). However, Ohno observed that the number of tRNA can quickly change through gene duplication and that the codon bias may actually be an artifact of primitive heptameric repeats (6). (Note: As the above discussion shows, codon usage bias is only one component of the periodicity, and we will quantify the contribution of codon bias.)

• Differential multinomial probabilities of nucleotides across the three codon positions. Gutiérrez et al. (16) analyzed the Fourier spectra of the four numerical series obtained by assigning a particular nucleotide to 1 and all others to 0; they found that the height of the spectrum at period 3 is proportional to the variance of each nucleotide across codon positions. It suggests that an asymmetric distribution of nucleotides across the three codon positions provides a mathematical explanation of the periodicity. (Note: By decomposing the multinomial probabilities into a sum product of conditional and marginal probabilities, we will show that there exist infinitely many combinations of codon and AA frequencies that lead to uniform multinomial probabilities across codon positions. We will thus show that codon and AA biases are not sufficient to create the three-base periodicity.)

Table 1.

AA usage in the human genome

Amino acid	%	Amino acid	%	Amino acid	%
L	10.0	K	5.7	N	3.6
S	8.3	R	5.7	Y	2.7
E	7.1	T	5.3	H	2.6
A	7.0	Q	4.7	C	2.3
G	6.6	D	4.7	M	2.1
P	6.3	I	4.3	W	1.2
V	6.0	F	3.7

Although a spectral analysis was performed for a few sequences in (7), the Fourier spectrum of categorical data crucially depends on how the data are represented as real numbers. The first mathematically rigorous method for studying periodicity in categorical data was developed by Stoffer et al. (8) and previously applied to DNA sequence analysis (8,17). By taking advantage of multi-core processing in modern computers, we have used this method called spectral envelope, explained in the ‘Materials and Methods’ section, to compute the spectrum of all coding DNA sequences (CDSs) and select regulatory regions in the human genome. CpG islands are shown to have different classes of spectra, depending on their evolutionary origin.

We further develop a projection method for visualizing global sequence evolution and show how our approach can be used to trace the spectral evolution of H1N1 influenza A virus. In addition to gradual shifts in genomic sequence content, we demonstrate how to classify abrupt jumps corresponding to reassortments, such as those that led to the 2009 pandemic H1N1 virus.

MATERIALS AND METHODS

Spectral envelope calculation

We will follow the convention used in (8). Let be a real-valued function, called the scaling function. Given any DNA sequence of length n, where , the scaling function then defines a real-valued series . The spectral envelope of X_k is defined as

(1)

where the maximization is taken over β not proportional to the identity map that maps all letters to 1, f_β(ω) is the spectral density of X_k and is the population variance of X_k (8). The β that maximizes the quantity in Equation 1 is unique up to scaling and translation. Thus, for DNA sequences, we can use these two degrees of freedom to set β(T) = 0 and , where is the upper hemisphere of a unit sphere. The spectral envelope λ(ω) thus gives an upper bound on the spectral energy of any representation of the DNA sequence s_{1 …} s_n at frequency ω, i.e. it is the maximum possible spectral energy at frequency ω. A spike in the spectral energy may therefore indicate a dominant harmonic. We used a modified version of the R code included in (17) to compute the sample spectral envelope, with a modified Daniell kernel (0.0625, 0.25, 0.375, 0.25, 0.0625) for smoothing the periodogram. In the following, we will use λ to denote the sample spectral envelope.

Markov Chain Monte Carlo

Let a₁a_{2 …} a_n be a protein sequence, where a_k is an AA with M_k codons. Let s₁s₂s_{3 …} s_3n be a DNA sequence that codes for this protein. There are distinct DNA sequences that code for the same protein sequence. We would like to find DNA sequences that have the maximum or minimum spectral energy at period 3. Explicitly computing the spectral envelope for all M distinct sequences is usually not feasible, because this number M is very large even for a short protein sequence. For example, for the protein motif NLNTLTLDHNLIDHIAEGTFVQ of length only 22, there are roughly 49 billion distinct synonymous DNA sequences. Thus, we used MCMC methods rather than exhaustive enumeration in order to approximately find the optima of the spectral energy function for each protein motif. In general, MCMC methods consist of algorithms that simulate from a probability density by generating an ergodic Markov chain with this probability density as its equilibrium distribution. The two MCMC methods used in this work are simulated annealing (18) and parallel tempering MCMC (19) (PTMCMC). These two methods are advantageous because these algorithms avoid getting trapped in local minima indefinitely and are easy to implement.

Simulated annealing

Simulated annealing is guaranteed to find the minimum if the temperature decreases slowly enough, but in practice the technique can only find a decent approximation to a global optimum. In terms of the simulated annealing algorithm, suppose we are looking for the global minimum of a complicated function. We proceed by sampling the large search space for possible solutions according to a candidate distribution. During each sampling, we decide whether to update our current solution with this new solution. Initially, when the temperature is large, we accept the proposed solution with relatively high probability; when the temperature decreases, however, we are more likely to accept whichever solution is lower.

Specifically, for a given protein motif, the simulated annealing method that was used in this article is described below as follows:

1. Let X₀ be any DNA sequence that codes for the protein motif.

2. Using the current X_t sequence generate a candidate sequence X* by randomly choosing a codon of X_t and replacing it with a synonymous codon.

3. Calculate the following expression:

   

where λ(X*) is the spectral envelope of the candidate sequence X* at frequency 1/3, λ(X_t) is the spectral envelope of the current sequence X_t at frequency 1/3 and the function T_t is the cooling schedule. We use the geometric decline

We accept the candidate sequence with probability α_SA. If we accept X*, then we set X_t+1 = X* and return to Step (ii). Otherwise, we set X_t+1 = X_t and return to Step (ii). We used 8 as T₀ and 20 000 as n.

Parallel tempering MCMC

Although simulated annealing uses a single chain to find the global optimum, PTMCMC simultaneously simulates from multiple non-interacting MCMC chains, each one at a different temperature. That is, if the target distribution from which we aim to sample is given by

for some small T₀, then we make an extended system:

where and Z(T_i) are normalization constants. Higher temperatures have the effect of flattening the target distribution. Periodically during the iterations, two neighboring chains set at, say, temperatures T_i and T_i+1, will swap their respective configurations X_i and X_i+1 with probability defined by:

In this way, parallel tempering uses several Markov chains to improve mixing and efficiently sample complicated landscapes. Note that in parallel tempering, two types of operations are used: the update operation, which generates a new sample for each chain using a Metropolis kernel and an exchange operation, which swaps the samples between two neighboring chains. We used seven chains, i.e. n = 6. T₀ was chosen so that the acceptance probability of a move that increases the spectral envelope by 1% of the original spectrum at frequency 1/3 is 1%. Succeeding temperatures were chosen as T_i = 2ⁱT₀. We used 10 000 simulations.

Protein domains and sequences

We obtained the annotated protein domains in human from PROSITE Release 20.81 (20) and converted them to CDSs by using the genome version HG19. Gene features and sequences in the human genome were obtained from GENCODE version 11 (21).

Position-specific frequency of nucleotides

Let be the set of codons coding for AA α, and let N_i be the nucleotide at position i = 1, 2, 3. Then, we can factorize the nucleotide frequency P(N_i) at the ith position as

(2)

where P(N_i|C) is 1 if the ith nucleotide in C is N_i and 0 otherwise. P(C|α) represents the codon usage bias for the AA α, and P(α) represents the AA usage bias in the genome. We can rewrite this equation in a matrix form

(3)

where N is a column vector of nucleotide frequencies P(N_i), A is a column vector of AA usage frequencies P(α) and C is the remaining sum product in Equation 2. It will be shown subsequently that there exist infinitely many combinations of AA and codon usage biases, P(α) and P(C|α), such that P(N_i = A) = P(N_i = T) = 0.3 and P(N_i = G) = P(N_i = C) = 0.2 for i = 1, 2, 3.

Area-preserving 2D projection of the scaling function

As previously mentioned, we use the convention where β(T) = 0 and (x,y,z) = (β(G),β(C),β(A)) lies on the upper unit hemisphere , where z ≥ 0. To compute the density of β at frequency 1/3, we would like to project the distribution of β onto a plane by using an area preserving map. Note that neither the usual stereographic projection nor the map preserves area and can lead to density artifacts. A simple calculation shows that

(4)

is an area preserving projection of the upper hemisphere onto a disk of radius .

Annotation of CpG islands

CpG islands (28 691) in the human genome (HG19) were obtained from http://genome.ucsc.edu/. To search for CpG islands that do not contain coding exons, we removed CpG islands that overlap UCSC known genes, human mRNAs from GenBank, expressed sequence tag or Yale pseudogenes (Release 60), also obtained from http://genome.ucsc.edu/. This filtering resulted in 1819 non-coding CpG islands.

Influenza A virus sequences

Nucleotide sequences of 4222 human, 411 swine and 89 avian H1N1 influenza A viruses were obtained from the NCBI Influenza Virus Resource (22) (http://www.ncbi.nlm.nih.gov/genomes/FLU/).

RESULTS

Spectral envelope of protein domains

We calculated the spectral envelope of 20 491 DNA sequences corresponding to human protein domains from PROSITE. To test for significance of periodicity at frequency 1/3 for each protein motif, we permuted the corresponding DNA sequence 100 times, calculated the spectral envelope for each permutation and calculated the resultant mean envelope. For each protein motif at frequency 1/3, we counted how many permuted spectral envelopes were greater than the spectral envelope of the original DNA sequence to determine an empirical P-value. We found that 3381 (16.5%) DNA sequences had a spectral envelope at frequency 1/3 that was greater than the spectral envelope of all 100 permuted sequences. We have defined the corresponding 3381 protein domains to have a significant period-3 property at P-value cutoff of 0.01. Supplementary Figure S1a shows a histogram of the calculated P-values for all the analyzed protein domains.

The periodic protein domains were significantly longer than the protein domains that lacked the period-3 property (Wilcoxon Rank Sum Test, P-value ). The median length of periodic protein domains was 57 AAs, while that of non-periodic protein domains was 31. In addition, the periodic protein domains were enriched for the fork head domain (binomial P-value ) and the basic-leucine zipper (bZIP) domain (binomial P-value ).

To assess the contribution of codon bias to periodicity, we uniformly sampled 100 synonymous DNA sequences for each protein motif and calculated the spectral envelope, as well as the resultant mean envelope. We found that 3839 (18.7%) sequences had a spectral envelope value at frequency 1/3 that was greater than the spectral envelope of all 100 synonymous sequences. Supplementary Figure S1b shows a histogram of the P-values calculated from this simulation. To determine the fraction of spectral envelope at frequency 1/3 that can be explained by codon usage bias, we computed the N-statistic defined as:

where λ is the spectral envelope at frequency 1/3 and is the mean envelope from 100 corresponding synonymous DNA sequences. Figure 1a shows the distribution of the N-statistic for significant period-3 protein domains. The mean N-statistic is 0.46, with a confidence interval of [0.44, 0.48].

Figure 1.

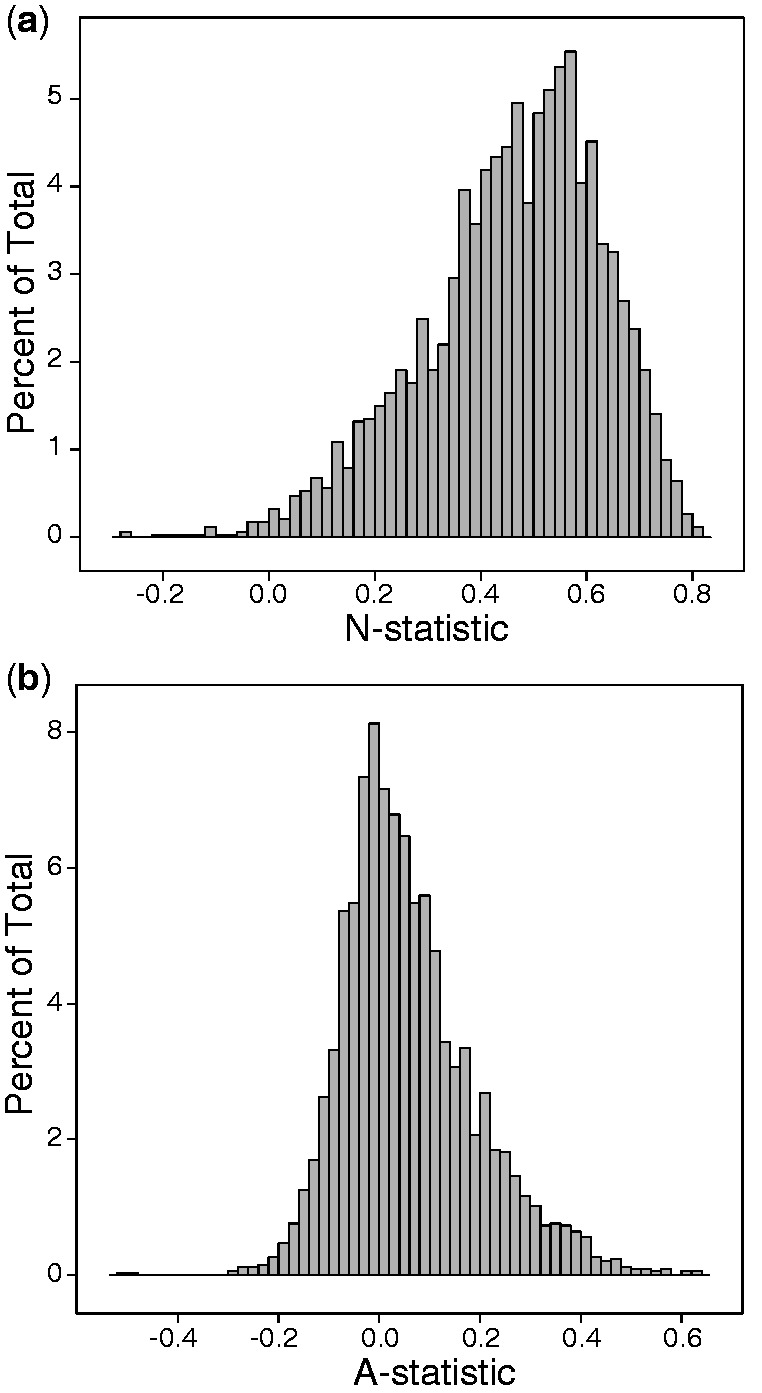
(a) Histogram of the N-statistic (quantification of the contribution of codon bias to periodicity) for protein domains with significant three-nucleotide periodicity. (b) Histogram of the A-statistic (quantification of the contribution of AA position to periodicity) for protein domains with significant three-nucleotide periodicity.

While previous research has found that the three-nucleotide periodicity is attributable to the uneven distribution of base compositions at different codon positions, to the best of our knowledge, the possible contribution of AA positions have not yet been characterized. For example, the DNA sequences CCT AAA CCT GCT TGG CCT GAT CCT GAG CCT AGT CCT TAA CCT and CCT CCT CCT CCT CCT CCT CCT AAA GCT TGG GAT AGT TAA GAG each have the same numbers of AA types, and even the same base compositions at the three codon sites, yet the spectrum for the second sequence at frequency 1/3 is 0.1695 while the spectrum for the first is 0.1321. To determine the fraction of the spectral envelope at frequency 1/3 that can be explained by the AA position, we computed the A-statistic defined as:

where λ is the spectral envelope at frequency 1/3 and is the mean envelope from 100 DNA sequences each with permuted AA locations. Figure 1b shows the distribution of the A-statistic for significant protein domains. The mean A-statistic is 0.059, with a confidence interval of [0.055, 0.063].

To study the nucleotide content of periodic sequences, we projected the scaling functions for the periodic protein domains onto a disk by using an area-preserving map. Figure 2 shows the projection onto the GC plane and indicates that for periodic protein domains, the scaling function predominantly maps nucleotides C and G to similar values. Supplementary Figures S2 and S3 show the projection of the distribution of the scaling functions for periodic domains onto the AC and AG planes, respectively; these figures further show that the scaling function frequently maps the nucleotide A to values near 0. Recalling that the scaling function maps T to 0 by definition, these particular assignments suggest that a strong–weak signal is the dominant signal at frequency 1/3. The GC content was 56.6, 39.2 and 77.8% at the three positions of the consensus codon for periodic protein domains, demonstrating the prevalence of NWS triplets.

Figure 2.

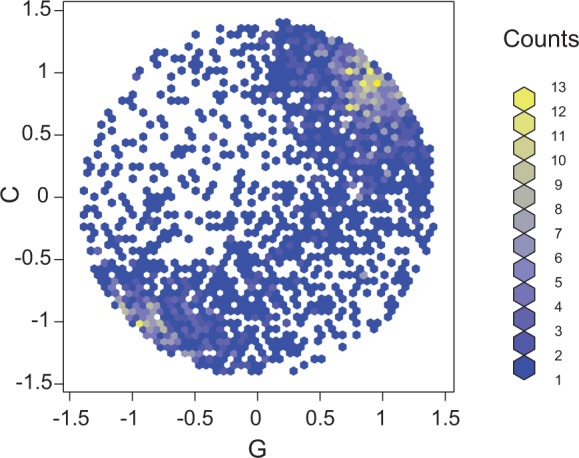
Area-preserving 2D projection of the scaling function of protein domains with significant period-3 property.

Spectral envelope of full-length proteins

To examine the three-base periodicity globally in the human genome, we computed the spectral envelope for 75 979 GENCODE transcripts that contain a CDS. We removed the UTRs in the computation. To assess the significance of the spectral density, we also computed the spectral envelope for 100 random permutations of each original transcript; a transcript was then considered to possess significant three-base periodicity if its spectral envelope at frequency 1/3 is greater than the maximum of the envelopes of the 100 permuted sequences at frequency 1/3. According to this definition, 18 200 (24.0%) transcripts did not show significant periodicity. Periodic sequences were significantly longer than non-periodic sequences (Wilcoxon Rank Sum Test, P-value ): the median length of AAs was 416 for periodic and 122 for non-periodic transcripts. Gene ontology analysis showed that the non-periodic genes were significantly involved in alternative splicing, mitochondrial parts and ncRNA metabolic processes (23).

Compared with periodic sequences, non-periodic sequences had a 5.4-fold enrichment for transcripts that are being targeted for non-sense-mediated decay (Fisher’s exact test, P-value ); the difference in distribution of AA lengths was still present between the two classes even after removing those transcripts: median AA length was 432 for periodic and 147 for non-periodic protein-coding sequences (Wilcoxon Rank Sum Test, P-value ).

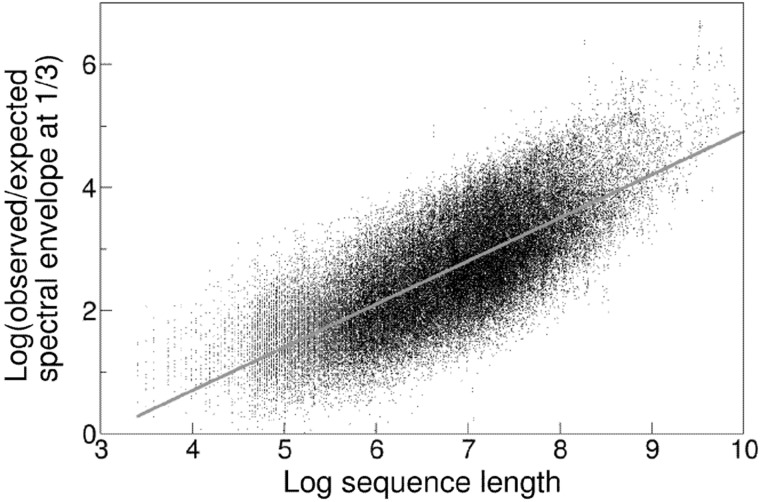
The Pearson correlation between the log ratio of observed over expected spectral envelopes at frequency 1/3 and the log length of protein was 0.74, where the expected spectral envelope was obtained by averaging the envelopes for 100 permuted sequences. Figure 3 shows the scatter plot of the log ratio and the log CDS length for each GENCODE transcript.

Figure 3.

The ratio of observed over expected spectral envelope at frequency 1/3 is highly correlated with the length of protein.

To assess whether a particular codon position can dominate in creating periodicity, we performed three sets of controlled permutations of GENCODE sequences by fixing the nucleotides at codon position 1, 2 or 3, and permuting the remaining nucleotides. Compared with the original sequences, permutations fixing the first position nucleotides led to a median decrease of 64% in the spectral envelope at frequency 1/3. In contrast, permutations fixing the second position or the third position nucleotides led to a median decrease of only 26 or 33%, respectively. These results suggest that the first codon position may be much less important than the second and third positions for creating periodicity.

AA usage bias is insufficient to create periodicity

To assess the extent to which human coding sequences have evolved to maximize or minimize the spectrum at frequency 1/3, we used MCMC optimization techniques of simulated annealing and PTMCMC to search for synonymous DNA sequences that have the maximum or minimum spectral envelope at frequency 1/3. For 3380 of the 3381 protein domains with significant periodicity, using either simulated annealing or PTMCMC, we found a synonymous DNA sequence whose spectrum at frequency 1/3 is lower than the minimum spectrum at frequency 1/3 of 100 random permutations by nucleotide. Thus, given nearly any protein motif, we have shown that we can construct a synonymous DNA sequence that does not have the typical period-3 property; that is, we can almost always choose codons that destroy the peak at frequency 1/3.

DV TITT LRDSGTFTCIASN AAGEA TAPVEVC is the protein domain with significant periodicity which the MCMC optimization techniques failed to find a synonymous DNA sequence whose spectrum at frequency 1/3 is lower than the minimum spectrum at frequency 1/3 of 100 random permutations. However, upon inspecting the sequence, one can see that each of the AAs in the second block of the domain (TITT) are encoded by nucleotide triplets beginning with A. Similarly, all AAs in the fourth block (AAGEA) are encoded by nucleotide triplets beginning with G. Because of this close positioning of the same nucleotide in the same codon position, synonymous DNA sequences tend to have a spectrum at frequency 1/3 that is higher than that of random permutations by nucleotide. Indeed, if we randomly switch AAs between block 2 and block 4, and then perform PTMCMC for this resulting DNA sequence, we are able to find a synonymous sequence whose spectrum at frequency 1/3 is lower than the minimum spectrum of 100 random permutations by nucleotide.

This shows that the AA usage bias itself is not sufficient to create a significant periodicity. In addition, either by PTMCMC or by simulated annealing, we found a synonymous DNA sequence for each protein domain whose spectrum at frequency 1/3 is higher than the maximum spectrum of 100 random permutations by nucleotide. In this regard, it is interesting to see that the natural DNA sequence coding for a particular protein motif does not exhibit the maximum spectral envelope value for frequency 1/3.

As an example, Figure 4 shows the spectral envelope calculation for the protein motif PS00108 (serine/threonine protein kinases active-site signature). Supplementary Figures S4 and S5 show additional spectral envelope plots for other protein motifs.

Figure 4.

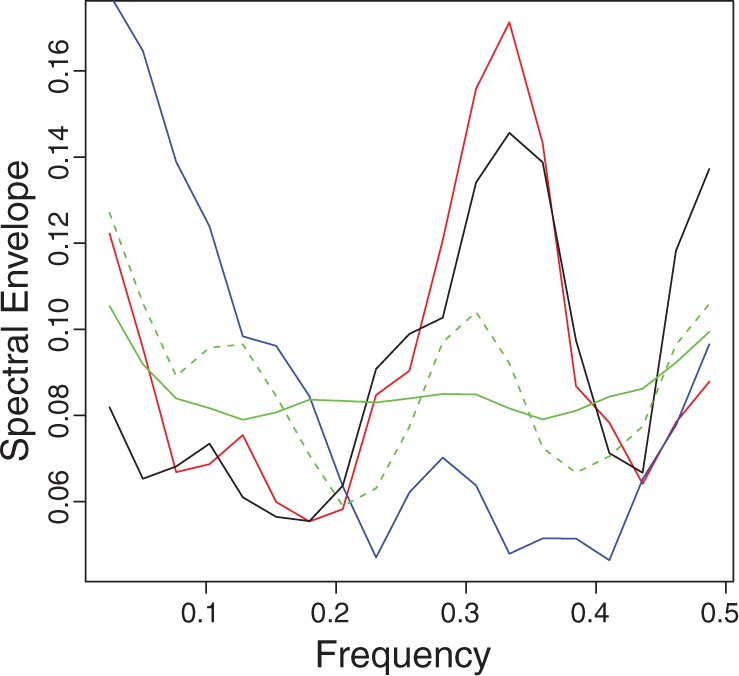
Spectral envelope calculations for the protein motif PS00108 which has a significant period-3 property. Black line is the spectral envelope of the original DNA sequence; blue, spectral envelope of synonymous DNA sequence found by MCMC minimization at frequency 1/3; red, spectral envelope of the synonymous DNA sequence found by MCMC maximization; dashed green, average spectral envelopes of 100 random synonymous sequences and solid green, average spectral envelope of 100 random permutations.

The absence of stop codons contributes to periodicity

Figure 3 shows that the spectrum at frequency 1/3 in coding regions depends on the length of sequence. In contrast, intronic and intergenic sequences have position-independent multinomial distributions of nucleotides (Table 2) and thus do not possess three-base periodicity even as the length increases, as shown in Figure 5a. However, Figure 5b shows that simply removing stop codons from intronic sequences in a fixed reading frame is sufficient to create fictitious periodicity, and the spectrum at 1/3 also increases with the length of intron. This artificial periodicity results from the fact that all stop codons (TAA, TAG and TGA) begin with T and that two of them have A in the second and third positions. Removing stop codons thus breaks the symmetry in the multinomial distribution of nucleotides across the three positions, as shown in Table 2, and this asymmetry is able to create three-base periodicity for sufficiently long sequences. This finding is consistent with the previous analysis that attributed the periodicity in coding regions to the differential multinomial probability (16). It also highlights the fact that the absence of stop codons alone may be sufficient to create periodicity in long coding sequences.

Table 2.

Position-specific nucleotide frequency in the human genome

Region	Nucleotide	Position 1 (%)	Position 2 (%)	Position 3 (%)
Coding	A	26.7	31.1	19.4
	C	24.9	23.7	29.7
	G	31.4	19.1	28.6
	T	17.0	26.1	22.3
Whole genome	A	29.9	29.9	29.9
	C	20.1	20.1	20.1
	G	20.1	20.1	20.1
	T	29.9	29.9	29.9
Whole genome (no stop codon)	A	31.6	27.9	27.2
	C	21.3	21.2	21.3
	G	21.3	19.2	19.9
	T	25.8	31.6	31.6

For whole genome, all triplets in the human genome were enumerated, and the nucleotide frequencies were derived from these triplet frequencies.

Figure 5.

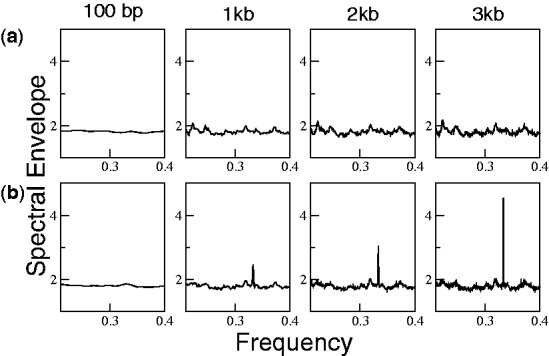
Spectral envelope of intronic sequences. (a) Period 3 is not present in 1000 random introns of length 100 bp, 1 kb, 2 kb and 3 kb. (b) Removing the stop codons (TAA, TGA and TAG) in a fixed frame from the sequences in (a) increases the spectrum at period 3.

Codon and AA biases are insufficient to create periodicity

In Equation 2, set P(A_i) = P(T_i) = 0.3 and P(G_i) = P(C_i) = 0.2, for i = 1, 2, 3, which are the expected nucleotide frequencies in the human genome; we shall demonstrate here that there exist continuous families of codon and AA biases which lead to these nucleotide frequencies and thus do not yield three-base periodicity in coding sequences. We simulated the codon bias frequencies 10 000 times as follows: for each AA α with m_α distinct codons, we sampled the order statistics of standard uniform random variables and defined to be the kth codon bias , where and . Using these values, Equation 2 gives 12 linear equations in 20 unknowns P(α). For each simulated codon bias matrix C in Equation 3, we performed constrained least-square optimization with the constraint , for all AA α, and solved for A. Supplementary Figure S6 shows the distribution of the relative residuals and shows that for 48.2% of randomly chosen codon bias matrices, we can find AA frequencies P(α) such that the relative residual is <10⁻⁷. The null space of C has dimension 10, so the solutions form a 10-dimensional affine space. Thus, there are infinitely many instances of codon and AA usage biases that nevertheless have the same multinomial nucleotide frequencies P(N_i) at all three codon positions i = 1, 2, 3, and that do not lead to three-base periodicity in coding regions. An example is given in Supplementary Table S1.

Periodicity in non-coding CpG islands

We now give examples of some other applications of the spectral envelope. Periodicity in non-coding regulatory regions might also indicate repeating units of information associated with their evolutionary origin and function. We computed the spectral envelope for 1819 non-coding CpG islands. As described in ‘Materials and Methods’ section, we removed any CpG island that has previously annotated coding potential. A CpG island was considered to possess statistically significant periodicity if its spectral envelope was greater than all spectral envelopes for 100 permuted sequences, corresponding to an empirical P-value cutoff of 0.01. We found 89 CpG islands to possess significant spectrum at frequency 1/3. Out of 89, 39 CpG islands consisted of tandem repeat sequences and had several spectral peaks (Figure 6a). Tandem repeat CpG islands tend to be methylated and lie in heterochromatin; some of them also regulate imprinted genes (24). At least 11 of the remaining 50 CpG islands arose from segmental duplications of genomic loci that harbor protein-coding genes. For example, Figure 6b shows the spectral envelope for a CpG island that had several segmental duplications on chromosome 11. A significant peak can be seen at frequency 1/3. This observation points toward the exonic origin of some CpG islands, which might have lost their coding potential after duplication through evolution and now function as regulators for other nearby genes.

Figure 6.

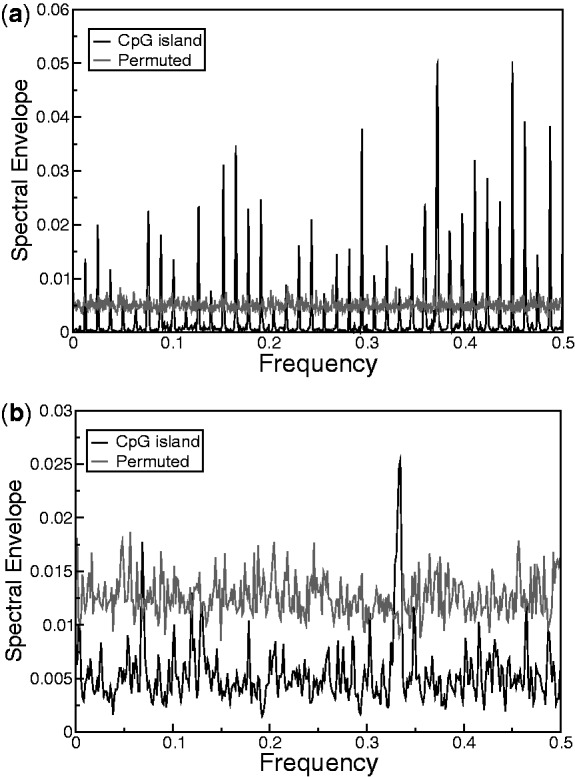
Spectral envelope for CpG islands at (a) chr4:3565311-3567185 consisting of 78-mer tandem repeats and (b) chr11:89713070-89713801 having several segmental duplications on chromosome 11. The coordinates are in HG19.

Spectral evolution of H1N1 influenza A virus

Influenza viruses affect millions of people every year and continue to outwit our immune system by evolving through mutations and reassortment of genetic information among related strains. From a disease control perspective, the two major properties of an influenza virus are its pathogenicity and its transmissibility, either from person to person or from species to species. The recent 2009 H1N1 pandemic virus has segments of human, avian and swine origin; this strain was in fact first detected in 2005, but was dormant between 2006 and 2008. It is highly transmissible between humans, but its pathogenicity is not high. On the other hand, the avian H5N1 virus is highly virulent, but it does not transmit easily to humans. It is thus important to monitor the evolution of these viruses and detect changes associated with their adaptation and newly acquired transmissibility or pathogenicity. We here show that we can use our projection map of the scaling function at frequency 1/3 to trace the evolution of H1N1 virus and detect the triple reassortment event that was first found in a 2005 strain and that subsequently led to the 2009 pandemic.

The 2009 pandemic H1N1 virus has the PA protein of avian origin and NP protein of classical swine origin. Figure 7a and b traces the changes in the projected scaling functions for these two proteins during the past 80 years. A sudden jump is clearly seen in year 2005 for both proteins. Interestingly, the scaling functions revert back to those from previous years in years 2006–2008, agreeing with the fact that the reassortant H1N1 was dormant during this period. From 2009 onward, the reassortant virus became the prevalent H1N1, and this pattern is well reflected in Figure 7a and b. Note that β(A), β(C) and β(G) are all positive for these viral sequences; as a result, their distribution on the unit sphere is invariant under changing the constraint on the scaling function from β(A) > 0 to either β(C) > 0 or β(G) > 0, and the above separation of avian and swine sequences from human is independent of our choice.

Figure 7.

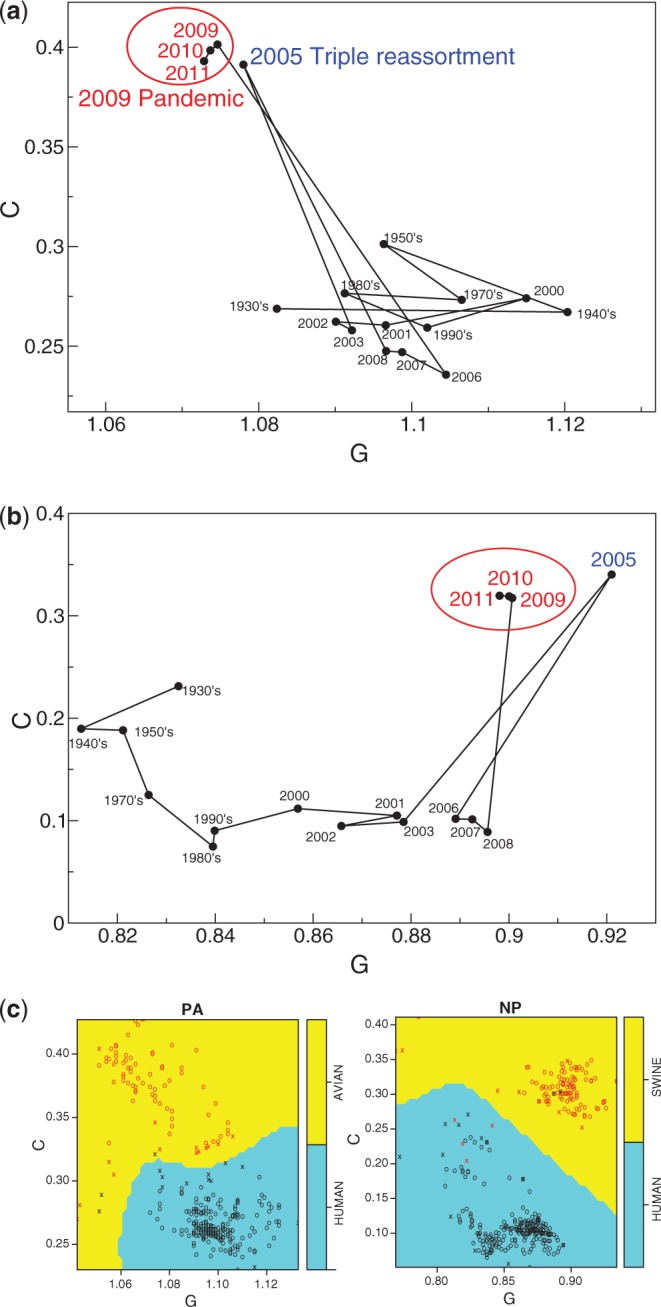
Evolutionary trace of the scaling function for the human H1N1 (a) PA protein and (b) NP protein. Each dot corresponds to the median projected scaling functions of all sequences from the indicated year. (c) SVM decision boundaries and training data points are shown. Support vectors are indicated as x and other training data points are indicated as circles. Human data points are in black and avian or swine data points are in red.

Motivated by this finding, we trained a support vector machine (SVM) using radial basis kernels on scaling functions from avian and human PA sequences as well as those from swine and human NP sequences. All avian H1N1 sequencing data from NCBI were used. As H1N1 was the predominant strain in swine before 1998, when H3N2 subtypes began infecting pigs, we restricted to pre-1998 swine sequences in order to avoid contamination of reassorted sequences. For human, pre-reassortant H1N1 sequences prior to 2005 were used. Figure 7c shows the decision boundaries for the trained SVM. We then tested the predictor on 3276 post-reassortment human H1N1 sequences from 2005 and 2009–11, and 430 sequences from pre-2005. Our SVM predicts 99.3% human for pre-2005 and 92.4% avian for post-reassortment PA sequences. It predicts 99.5% human for pre-2005 and 92.4% classical swine for post-reassortment NP sequences.

DISCUSSION

This study uses the rigorous method of spectral envelope to comprehensively analyze the period-3 property of protein-CDSs. The method selects the optimal mapping of categorical data to real numbers at each frequency and allows us to test the statistical significance of periodicity in the entire human genome. We provide a thorough quantitative investigation of sequence properties that contribute to the phenomenon. The two main questions that we consider are (i) How can we quantify different sources of the base-3 periodicity? (ii) What is a minimal set of attributes sufficient for periodicity?

It has been previously reported that the three-base periodicity depends only on the occurrence frequencies of the nucleotides in each of the three codon positions of a DNA sequence (25). However, another possible source of three-base periodicity is the particular ordering of AAs; for example, two DNA sequences that have exactly the same nucleotide distributions across the three codon positions, but with different orderings of AAs, can have different spectral envelopes as we have illustrated. Here, we report that, on average, the fraction of the spectral envelope at frequency 1/3 that can be attributed to the AA ordering is ∼6% for human protein domains.

Previous studies have implicated AA usage bias, i.e. the prevalence of a few of AAs, as a dominant source of periodicity (7). This bias creates a difference in nucleotide frequencies across codon positions. For instance, all but three AAs have the same first base in their synonymous codons, so the preponderance of a single AA could yield a periodic appearance of the first-position nucleotide. In this study, however, we found that AA usage bias cannot be the sole explanation for the three-base periodicity in human structural protein domains. MCMC optimization showed that for any DNA sequence corresponding to a protein domain, one can construct a synonymous DNA sequence that destroys any existing three-base periodicity. Thus, even though most protein-coding sequences consist of only a few AAs, the extent of AA usage bias in human protein domains is insufficient to create a significant periodicity.

Furthermore, contrary to previous reports (14), we found that the synonymous codon usage bias in human protein structural motifs is likewise insufficient to generate significant three-base periodicity. On average, we have determined that the fraction of the spectral envelope at frequency 1/3 that can be explained by the codon bias is ∼46% for protein structural domains. Our method of projecting the scaling function onto a two-dimensional disk provides an intuitive way of assessing the sequence content of periodic nucleotides and demonstrates the prevalence of NWS triplets, in contrast to the previous suggestions of RNY (3) or GHN repeats (5). Our genome-wide analysis thus does not support the hypothesis that the present-day genes have evolved from an ancestral form of RNY repeats.

Interestingly, removing stop codons from long introns in a fixed reading frame forces them to lose their position-independent multinomial distributions of nucleotides and creates significant three-base periodicity. This simulation suggests that the absence of stop codons within long coding sequences is sufficient to create periodicity, as demonstrated in Figure 3. Thus, even though our observations indicate that AA bias and codon bias are each insufficient to create base-3 periodicity in human protein domains, the asymmetry in the multinomial distribution of nucleotides across the three codon positions is enough to create this phenomenon, at least in long protein sequences. Note that periodicity can depend on other biases besides this asymmetry; as noted above, factors such as AA position can also contribute.

Using rigorous mathematics to supplement our spectral envelope approach, we have additionally shown that there are infinitely many pairs of codon and AA usage biases that will lead to the expected background nucleotide frequencies. Our work thus demonstrates that the presence of codon and AA biases in itself is not sufficient to generate three-base periodicity. That is, in theory, it would be possible to have a genome with both codon and AA usage biases, but no period-3 periodicity. Thus, even though the codon and AA usage biases observed in biological sequences do contribute to the periodicity, the true source of periodicity lies not in the fact that the biases exist, but in that the observed biases lead to unequal multinomial distributions of nucleotides across codon positions. This subtle difference has not been previously appreciated.

In addition to facilitating the analysis of periodicity, spectral envelope also provides a novel technique for studying evolution. Traditional phylogenetic analyses require sequence alignments and do not readily yield a summary statistic that can effectively capture genome-wide sequence changes. This article demonstrated how to use spectral envelope to detect residues of coding potential in CpG islands that arose through segmental duplication from protein-coding regions. These select CpG islands retained a significant peak at frequency 1/3 even though they no longer coded for a functional protein. CpG islands consisting of tandem repeats could be also distinguished by their regular spectral peaks. We further introduced the concept of spectral evolution, which represents genome-wide changes in sequences as changes in the scaling function that maximizes periodicity. This approach is unique in that it does not require sequence alignments and succinctly summarizes genome-wide sequence evolution in two dimensions. We applied this concept to the H1N1 influenza A virus by mapping the evolution of the scaling function at frequency 1/3 during the past 80 years. The projection method illustrates both random drift and abrupt changes in the viral genome. The gradual change in scaling function is similar to the previously observed random drift from G,C to A,U in human influenza H1N1 virus, which may reflect a species-specific mutational bias (26). Our approach captures a higher order pattern in sequence evolution, corresponding to changes in genome-wide periodicity. Importantly, our method is also able to detect reassortment events that may correspond to inter-species jumps resulting in sudden changes in pathogenicity and transmissibility. The method of spectral evolution thus provides an efficient new tool to monitor the evolutionary trends in influenza and other viruses.

CONCLUSION

Understanding the structure and function of genetic information encoded in diverse genomes represents a major challenge. Traditional local alignment and sequence motif analyses have fundamental limitations and fail to answer several important problems in biology. There is thus an emerging need for a paradigm shift in sequence analysis that goes beyond alignment-based information. Here, we have proposed one alternative approach of spectral envelope to gain new insight into the human three-base periodicity and the spectral evolution of the H1N1 influenza A viral genome. This article highlights the possibility that non-local properties of DNA relying on long-distance sequence patterns may mark distinct functional sites and also help summarize genome-wide sequence evolution.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Table 1 and Supplementary Figures 1–6.

FUNDING

The NSF CAREER Award [1144866, in part]. Funding for open access charge: National Science Foundation.

Conflict of interest statement. None declared.