A population model for genotyping indels from next-generation sequence data

Abstract

Insertion and deletion polymorphisms (indels) are an important source of genomic variation in plant and animal genomes, but accurate genotyping from low-coverage and exome next-generation sequence data remains challenging. We introduce an efficient population clustering algorithm for diploids and polyploids which was tested on a dataset of 2000 exomes. Compared with existing methods, we report a 4-fold reduction in overall indel genotype error rates with a 9-fold reduction in low coverage regions.

INTRODUCTION

Single-nucleotide polymorphisms (SNPs) and copy number variants (CNVs) are pervasive in the human genome and have been well established as sources of genetic and phenotypic variation. Insertion and deletion (indel) polymorphisms are comparably abundant and functionally significant but remain relatively unexplored, mainly due to the fact that they cannot be efficiently detected using microarray platforms.

The advent of next-generation sequencing (NGS) has offered new prospects for exploring the impact of indels on the genetic landscape of both plants and animals. As a result, both assembly-based methods (1) as well as gapped-alignment-based methods have been used for indel discovery. Assembly-based methods rely on high-coverage whole-genome sequence data and can only resolve homozygous indels. Gapped alignment methods aim to distinguish between actual indels and spurious results caused by sequencing errors, including base calling and mapping errors, as well as errors due to polymerase slippage during polymerase chain reaction amplification. Further challenges are faced when trying to identify indels using exome sequencing data. The intermediate microarray hybridization step that is designed to capture coding sequences of interest results in less efficient capture of non-reference reads and uneven coverage across the genome. Existing methods attempt to overcome such biases using a variety of strategies. Dindel (2) utilizes a Bayesian framework to account for the various errors, which requires prior knowledge of context-dependent error rates currently restricted to Illumina platforms. Other methods, such as piCALL (3), involve computationally expensive numerical approximations in order to model population-scale sequence data. QCALL attempts to sample from the space of potential ancestral recombination graphs relating the history of the population in order to improve SNP genotyping accuracy from NGS data (4). This method, however, poses significant computational challenges and has not yet been applied to indel genotyping. Furthermore, none of the current methods has the ability to detect and genotype indels in polyploid genomes.

We present SOAP-popIndel, a novel probabilistic framework for fast and sensitive indel genotyping at the population level. By modelling site-specific indel error rates across thousands of samples, our method achieves high genotyping and detection accuracy, while minimizing the computational burden. Particularly for targeted exome capture data, we demonstrate that SOAP-popIndel outperforms competing methods, despite their more complex and resource-intensive approaches. SOAP-popIndel is the only indel genotyping algorithm that is not restricted to diploid genomes, thus constituting an unparalleled tool for ongoing plant population re-sequencing efforts, such as the 1001 Genomes Project (5) and the rice re-sequencing project (6).

MATERIALS AND METHODS

SOAP-popIndel pipeline

The SOAP-popIndel pipeline is shown in Supplementary Figure S1. The first step is to use the Burrows–Wheeler Aligner (BWA) with default parameters to perform gapped alignment of the sequencing reads to the reference genome. The resulting alignments comprise the candidate indel dataset. A rigorous filtering process is required to eliminate spurious alignments from further analysis. The average density of indels across the human genome has been reported to be one indel per 7.2 kb (7). Therefore, it was deemed necessary to discard alignments that exhibit more than one gap per read. We also filter out alignments with gaps located towards either ends of the read, as they most likely correspond to sequencing artefacts. When multiple indel alleles arise in the population, we consider up to K (1 ≤ K ≤ K_max) non-reference alleles for which the average number of supporting reads among the samples in which we observe the non-reference allele, is greater than or equal to two. K_max is a pre-defined parameter representing the maximum number of alternative alleles which the program will model. Finally, we filter putative indel sites on the basis of average depth of coverage (Supplementary Methods).

Next, we create K alternative reference sequences at each putative indel site, each consisting of a 2*L window flanking the indel, together with the indel allele itself (where L denotes the read length). For example, the alternative reference will be missing the equivalent section from the reference where there is a putative deletion and will have incorporated extra sequence relative to the reference where we have identified a putative insertion.

Subsequently, we perform un-gapped alignment for all individuals j = 1… M using BWA on the combined alternative and the reference genome sequence (such that each read can only be assigned to the reference or one of the alternative sequences). We then record the number of reads N_i,j,k which align to the k^th allele of the i^th indel with less than five mismatches and such that breakpoints are >5 bp from the read ends. The vector of these read counts is denoted by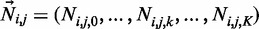, where k = 0 indicates the reference allele. These quantities are the summary statistics which we use for all subsequent inference in SOAP-popIndel.

Algorithm for modelling read counts

We model the probability of the data (D_i) over all samples j = 1… M conditional on the vector of total depth of coverage at position i as:

(1)

where 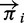denotes the underlying population allele frequencies and E_i the matrix of site-specific read assignment errors. We condition our probabilities on the total depth, 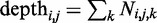, to mitigate the influence of the variable depth of coverage on our inference. Such variability can be caused by uneven hybridization of the capture array in exome sequence datasets, by variation in repeat content or by differences in alignability for whole-genome datasets. Intuitively, we consider our data as being the allele-specific depths conditioned on the total depth at each position. Equation (1) also assumes that these allele-specific depths from different individuals are independent, conditional on the total read depth and the population allele frequency.

We expand Equation (1), dropping the i, j subscripts for convenience:

(2)

where the genotype g comes from all the possible genotypes for ploidy Pl and number of alleles K + 1. For example, G(2,3) = {AAA,AAB,ABB,BBB}. We further expand Equation (2) using the multinomial

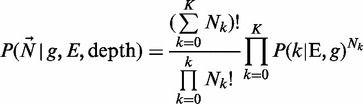(3)

where vector P(k|E,g) denotes the probability of observing a read k conditional on genotype 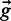and assignment matrix E. This can be thought of as a probability of success in a multinomial ‘dice-throw’ model, adjusted to reflect the rate of mis-assignment of indel reads to reference reads and vice versa:

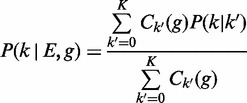(4)

where k′ denotes the hidden real underlying allele of the read, P(k|k′) = E_k,k′ denotes the ‘error-rate’ of aligning the allele k′ to k, and C_k′ (g) denotes the number of alleles k in the genotype g. Note that is the ploidy and that for all k′ = 0, … , K. So that there are K·(K − 1) free parameters in the matrix E, consisting of all the off-diagonal elements. We make the simplifying assumption that E_k,0 = e^ref→indel for all k = 1, … , K and that E_0,k = e^indel→ref for all k = 1, … , K and E_k,k′ = e^{indel→indel} for all k,k′ = 1, … , K. We express the prior probability of genotype g, P(g) from Equation (3) in terms of the Hardy–Weinberg equilibrium frequencies:

(5)

The parameters of this model are initialized to:

and trained separately at each site, using a generalized expectation–maximization algorithm. It is important to note that if e_i^indel→ref = 0, then the likelihood in Equation (3) will be zero for reference homozygotes if we observe at least one supporting indel read (and vice versa if e_i^ref→indel = 0), which results in the program inferring an excess of heterozygotes as a result of misalignment errors. In the expectation step, we calculate the posterior probability of observing each genotype in each individual conditional on the current parameter set. These posterior probabilities are summed to calculate the expected number of indel alleles in the population, which we use to update the allele frequency vector of the indel. The posterior probabilities also enable us to assign probabilistically each data point 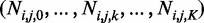to each genotype cluster. Thus, for given values of e_i^indel→ref, e_i^ref→indel and e^{indel→indel}, we can calculate the probability of each data point being generated by each genotype cluster using Equations (3) and (4), and by calculating a sum of these values weighted by their assignment probability, we evaluate the likelihood of this assigned data conditional on the parameter values. We can then use a numerical maximization algorithm to find the values of e_i^indel→ref, e_i^ref→indel and e^{indel→indel} that maximize this likelihood conditional on the posterior genotype assignments. We train the model for 25 iterations, which we observed to be sufficient for convergence. After training, we report the final posterior probability of each indel genotype in each individual.

Data

We used paired-end exome sequence data generated on 2000 samples that were collected for a case–control study of type II diabetes (8). Exons were captured using the Agilent 47 Mb ‘All Exon Kit’ (v2) and subsequently sequenced at high depth using Illumina HiSeq platform. These data consisted of an average depth of coverage of 56.42× on the capture region, with a SD of 8.64×. The target read length was 100 bp and the target insert size was 500 bp.

The simulated dataset was constructed by introducing indels of known size into a 1 Mb region on chromosome 17 (chr17:11.2 Mb-12.2 Mb, NCBI Build 36, hg18). The indels ranged from 1 to 50 bp, with a length distribution as previously reported (9). In total, we simulated 1000 indel sites equally divided between insertions and deletions. Next, we randomly assigned a population frequency f to each indel, f ∈ {0.05,0.10,0.20,0.50,0.80,0.90,0.95} and generated 2000 diploid genomes as well as a separate 2000 triploid genomes. Finally, we used WGSIM (with options −e 0.01 –d 500 –s 50 –N 200000 −1 100 −2 100 –r 0.001 –R 0.10 –X 0.30 –h) (10) to simulate paired-end reads from each of the 2000 genomes with a base error rate of 1% and a mutation rate of 0.1% (of which 10% were indels). The read length was set to 100 bp, whereas the average insert size was set to 500 bp. We simulated data at a depth of coverage of 40×, then randomly down-sampled depths of 4× and 20×, respectively, for the diploid dataset only. We also simulated tri-allelic data at 40× coverage using the same simulation strategy and total non-reference allele frequency, except that each indel site was assumed to have two alternative alleles, which are selected with equal probability.

Benchmarking of indel calling software

We analysed the simulated dataset with SOAP-popIndel, Dindel, SAMtools and piCall. We used Dindel version 1.01 (linux 64 bit), filtering indels with less than three supporting reads as recommended, running in ‘pool’ mode in 200 bins of 10 samples each to avoid out-of-memory errors. We further filtered out predicted indels, which had less than 100 samples with observed data (using the ‘Number of Samples with Data’ field from the merged vcf file) in order to remove the majority of predicted 284 759 indels that were false positives, resulting in 913 indels for comparison. We used SAMtools version 0.1.17 and the mpileup command with options –u −d 1000 −m 3. We run SAMtools in two batches of 1000 samples to avoid out-of-memory errors. We analysed the real dataset with Dindel with the same parameters as well as SOAP-popIndel.

RESULTS

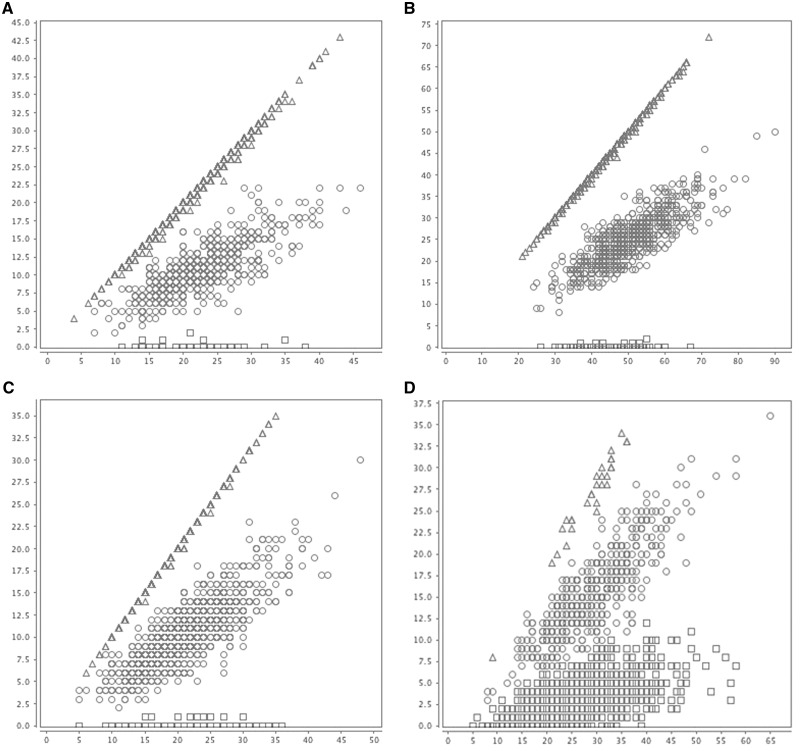
We applied SOAP-popIndel to an exome sequencing dataset consisting of 2000 samples sequenced at an average depth of 56×. Because of the difficulty in experimentally validating multi-allelic indel genotypes, we ran SOAP-popIndel with K_max = 1, thus only considering bi-allelic indels. To visualize our results, we generated plots of the number of reads aligned to the indel reference N_i,j,1 against the total number of aligned reads (N_i,j,0 + N_i,j,1) at different putative bi-allelic indel sites across all individuals in the population, annotated by SOAP-popIndel genotype (Figure 1). Despite the varying levels of coverage and rates of misalignment of indel reads to the reference and vice versa, SOAP-popIndel’s ability to update its site-specific error rate via a population model allowed it to accurately identify three genotype clouds in each case.

Figure 1.

Illustration of population clustering method on real data. (A–D) Clustering at different putative indel sites, with different depth of coverage, as well as site-specific error rates. Each point represents the total number of aligned reads (X-axis), as well as the number of indel aligned reads (Y-axis) for each individual in the population. Shapes indicate the genotype called by SOAP-popIndel: squares, circles and triangles indicate homozygous reference, heterozygous and homozygous indels, respectively. (A and C) low-to-medium depth of coverage, low error rate. Panel B: medium-to-high depth of coverage, low error rate. (D) low-to-medium depth of coverage, high error rate.

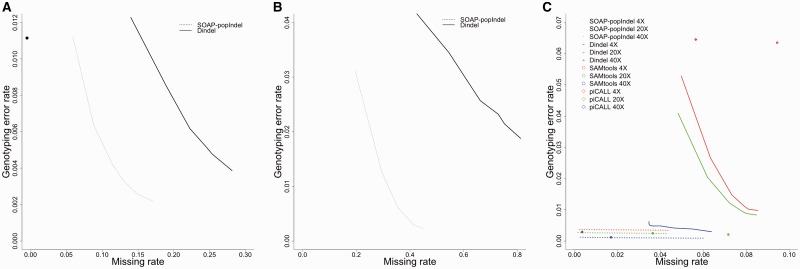
We randomly chose 50 indels detected by SOAP-popIndel for validation, three of which were subsequently removed due to differences between the hg18 and hg19 genome builds. Using a Sequenom assay, we validated 44 of the 47 indels indicating a false discovery rate of <6.4%. These 44 validated indels were also detected by Dindel. We further assessed SOAP-popIndel and Dindel genotyping accuracy at these validated sites (Figure 2A). SOAP-popIndel achieved a genotyping error rate of 0.26% versus 1.02% for Dindel at the same missing rate of 15%. When we restricted to sites with less than 5× coverage, the error rates were 0.5 and 4.5%, respectively, at a higher missing rate of 37.5% (Figure 2B).

Figure 2.

Genotyping accuracy and missing rates. Dashed-line, solid line, circles and diamonds represent SOAP-popIndel, Dindel, SAMTools and piCALL, respectively. Black: real exome data; Red: 4× simulation; Green: 20× simulation and Blue: 40× simulation. Lines for Dindel and SOAP-popIndel are based on posterior probability thresholds between 0.90 and 0.99. SAMTools and piCALL do not report probability of assignment, so are represented by a single point. (A) Results on 44 Sequenom validated sites. (B) Restricted to sites within samples that had <5× coverage. (C) Results on simulated data.

It was difficult to benchmark indel detection sensitivity and specificity on this dataset due to a lack of a gold standard. Thus, we used a simulated dataset of 2000 samples to more extensively compare SOAP-popIndel with Dindel (2), piCALL (3) and SAMtools (10). At 4× coverage, our method achieved a sensitivity of 99.8% with a false-discovery rate (FDR) of 0.22%, which was an order of magnitude lower than the best competing method, Dindel, which also had a lower sensitivity of 99.0% (Table 1). As reported in Neuman et al. (11), Dindel was more accurate than methods other than SOAP-popIndel, particularly at low coverage. SOAP-popIndel did not miss indels detected by the other algorithms, while Dindel missed seven (∼1% of simulated indels) which were detected by SOAP-popIndel and SAMtools (Supplementary Figure S2). At higher coverage (Supplementary Figure S2B and C), the FDR of competing methods decreased, while that of SOAP-popIndel did not, indicating that 4× is sufficient to enable accurate detection of indels, providing population-level information is properly exploited. Our method achieved comparable accuracy (sensitivity of 99.13% and FDR of 0.66%) in indel detection for triploid data. Our method achieved a comparable FDR of 0.34% for tri-allelic diploid simulated data but had a lower sensitivity of 96.8% due to sites for which only one of the two indel alleles were correctly identified (Supplementary Table S4).

Table 1.

Comparison of false-discovery and false-negative rates of different methods in detecting indels on simulated data

Method		Diploid (%)			Triploid (%)
		4x	20x	40x	40x
SOAP_popIndel	FN	0.22	0.33	0.55	0.66
	FD	0.22	0.11	0.22	0.87
Dindel	FN	0.99	0.99	1.20	NA
	FD	9.60	5.54	1.20	NA
SAMtools	FN	1.20	11.8	18.84	NA
	FD	64.28	63.10	63.55	NA
piCALL	FN	11.83	1.42	1.42	NA
	FD	53.18	57.18	64.19	NA

NA, not applicable; FD, false discovery; FN, false-negative.

We also benchmarked genotyping accuracy using the simulated dataset. SOAP-popIndel had lower missing rate and a substantially lower genotyping error than competing methods, particularly for low depth of coverage (Figure 2C). SOAP-popIndel results for 4x coverage are superior to those achieved by other algorithms even at 20x coverage. Although the SOAP-popIndel genotyping error rate for triploid data is similar to that for diploid data, the missing rate is higher (Supplementary Figure S3), which was, however, mostly due to difficulty in distinguishing the AAB and ABB heterozygotes (Supplementary Table S3). The genotyping error rate of 1.2% at diploid tri-allelic sites is higher than for diploid bi-allelic sites, but the missing rate remains low (Supplementary Figure S4).

We observed that SOAP-popIndel requires considerably less CPU time than other indel callers (Supplementary Table S1). SOAP-popIndel memory requirements were higher on the simulated dataset of 2000 samples, reflecting the fact that we arbitrarily batched regions into ∼1000 indels per run. Adjusting the number of indels batched into a single run can be used to maintain the same memory footprint for larger datasets, e.g. 100 indels per run for 20 000 samples.

DISCUSSION

We have described SOAP-popIndel, a novel fast algorithm for genotyping indels at the population level using exome NGS data. We address the problem of uneven capture efficiency by conditioning on site- and sample-specific total depth of coverage. However, the main strength of our approach is that it models indel genotypes across the entire population, using a model which incorporates site-specific read misalignment rates, as well as the indel population allele frequency. This enables our method to call highly accurate genotypes even on low coverage sequence data and in the presence of significant rates of misalignment. Our genotyping error rates of 0.25% are significantly lower than competing methods, although indel callers that consider more than one alternative allele, such as Dindel, may have been artificially penalized on the bi-allelic simulation data. SOAP-popIndel is insensitive to depth of coverage—achieving lower error rates at 4× than competing methods at 20× coverage. As a result, our reported indel genotyping error rates are now comparable with those reported for SNP genotyping (12). Further gains in accuracy may be achieved by using SNP/indel haplotype clustering (13) to borrow information locally across individuals sharing haplotypes. The ability to accurately call indel genotypes at low coverage is extremely helpful even for high coverage exome sequence data, which usually contain many regions of low coverage due to variability in exon capture efficiency mediated in part by GC compositional biases. Benchmarking of SOAP-popIndel on simulated polyploid data demonstrated the feasibility of calling indel genotypes in polyploid plant genomes. However, there may be other features of plant genomes, such as differences in indel heterozygosity, repeat and GC composition, as well as divergence of homologous chromosomes, which may further complicate indel genotyping. In particular, Neuman et al. (11) demonstrate that indel calling becomes progressively more difficult as the density of indels increases, which may be a problem for genomes with high levels of heterozygosity.

SOAP-popIndel provides a comprehensive solution for accurate and efficient sequencing-based indel detection that will help elucidate their largely unexplored role in phenotypic diversity. SOAP-popIndel’s performance, coupled with its unique ability to accommodate polyploids, renders it invaluable for exploring the impact of indels on both animal and plant genomes.

The software is available from http://soap.genomics.org.cn/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Tables 1–4, Supplementary Figures 1–4 and Supplementary Methods.

FUNDING

Major State Basic Research Development Program of China—973 Program [2011CB809201, 2011CB809202, 2011CB809203]; Major Program of National Natural Science Foundation of China [30890032]; Shenzhen Key Laboratory of Transomics Biotechnologies [CXB201108250096A]; the BBSRC research grant [award number BB/H024808/1 to L.J.M.C. and E.B.]. Funding for open access charge: Imperial College open access fund.

Conflict of interest statement. None declared.